Равенство и подобие треугольников: Признаки равенства и подобия треугольников

Подобие и равенство треугольников

Вопросы занятия:

·  поговорить о равенстве и подобии треугольников;

·  сформулировать и доказать три признака равенства треугольников;

·  сформулировать и доказать три признака подобия треугольников.

Материал урока

Напомним, что две фигуры называют равными, если их можно совместить.

Давайте, возьмём два равных треугольника  и . И наложим их друг на друга.

Видим, они совместились, то есть попарно совместились их вершины и стороны. А значит, попарно совместились и углы этих треугольников.

Следовательно, можем сделать вывод: если два треугольника равны, то стороны и углы одного треугольника соответственно равны сторонам и углам другого треугольника.

Также следует отметить, что в равных треугольниках против соответственно равных сторон лежат равные углы, и наоборот: против соответственно равных углов лежат равные стороны

.

Равенство треугольников  и  обозначают следующим образом:

И говорят «треугольник А Б Ц равен треугольнику А₁ Б₁ Ц₁».

Исходя из рассмотренного, можно сказать, что равенство треугольников мы можем установить не только наложением их друг на друга, но и сравнивая их элементы.

Для установления равенства треугольников пользуются соответствующими признаками равенства треугольников.

Итак, первый признак равенства треугольников.

Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.

Докажем это утверждение. Пусть  и  – треугольники, у которых , , . Докажем, что .

Так как , то  совместится с , а  и  совместятся с лучами  и .

Так как , а , то  совместится с , а  – с .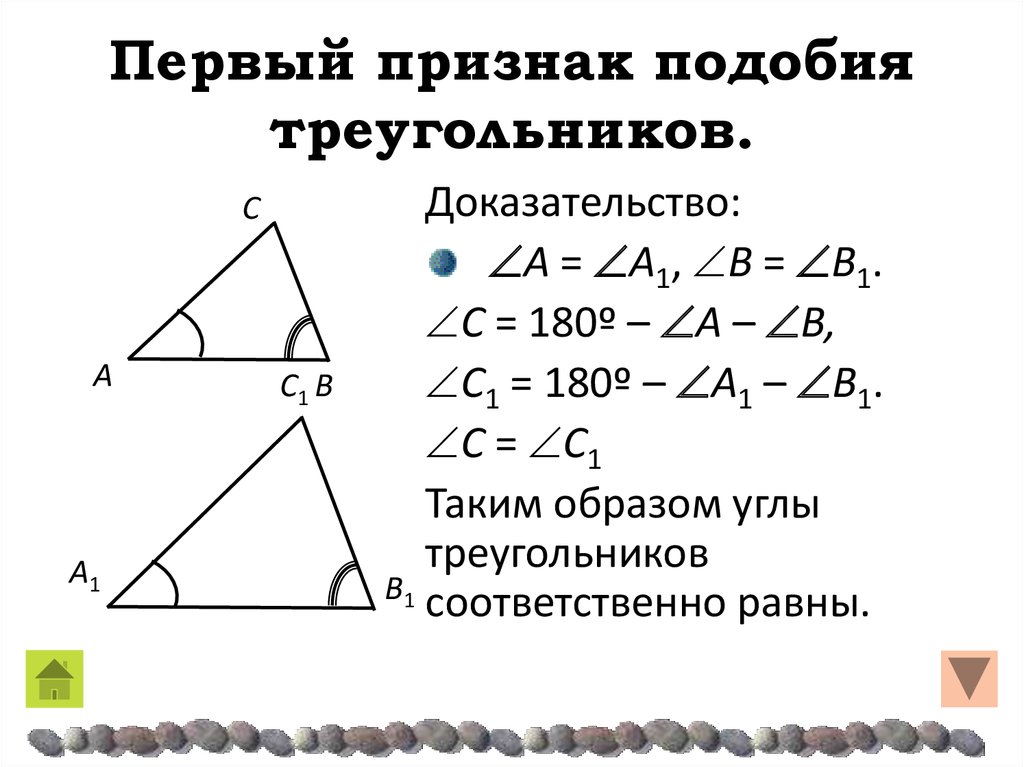 Исходя из этого, точка  совместится с ,  – с . Следовательно,  совместится с .

Тогда имеем, треугольники  и  полностью совместились. Значит, .

Таким образом, теорема доказана.

Задача.

На рисунке , . Доказать, что .

Так как , , то .

Рассмотрим два треугольника  и . У них стороны  равны по условию задачи. Выше мы выяснили, что , а угол  – общий угол. Следовательно, данные треугольники равны  по первому признаку равенства треугольников. Значит, у них соответственные стороны и углы равны. То есть . Что и требовалось доказать.

Сформулируем второй признак равенства треугольников.

Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны

.

Докажем это утверждение. Пусть  и  – треугольники, у которых , , . Докажем, что .

Совместим треугольник  с треугольником 1 таким образом, чтобы вершина А совместилась с вершиной А₁, сторона АВ – с равной ей стороной А₁В₁, а вершины С и С₁ оказались по одну сторону от прямой А₁В₁.

Так как  и , то  совместится с , а  – с . Поэтому вершина С – общая точка сторон АС и ВС, окажется лежащей и на лучах А₁С₁ и В₁С₁, а следовательно, совместится с общей точкой этих лучей – вершиной С₁. Значит, совместятся стороны  и ,  и . Получаем, что треугольники  и  полностью совместятся. А значит, .

Теорема доказана.

Задача.

Отрезки  и  пересекаются в точке , которая является серединой отрезка , а . Доказать, что .

Рассмотрим  и . У них , так как Е – середина отрезка АВ. Углы  равны по условию задачи. А углы  равны как вертикальные. Получаем, что треугольники  равны по второму признаку.

Прежде чем сформулировать третий признак равенства треугольников, давайте немного подробнее поговорим о равнобедренных треугольниках.

Напомним, что треугольник называется равнобедренным, если две его стороны равны.

Возьмём, к примеру, треугольник , у которого стороны . Как мы уже отмечали, эти стороны называют боковыми сторонами

. Третья сторона  называется основанием равнобедренного треугольника. Точка  называется вершиной равнобедренного треугольника, а точки  и  – вершинами при его основании. Угол  называется углом при вершине, а углы  и  – углами при основании.

Теперь сформулируем некоторые теоремы о свойствах равнобедренного треугольника.

Первая теорема звучит следующим образом: в равнобедренном треугольнике углы при основании равны.

И вторая теорема: в равнобедренном треугольнике биссектриса, проведённая к основанию, является медианой и высотой.

Ну а теперь давайте перейдём к третьему признаку равенства треугольников.

Если три стороны одного треугольника соответственно равны трём сторонам другого треугольника, то такие треугольники равны

.

Докажем это утверждение. Пусть  и  – два треугольника, у которых , , . Докажем, что .

Приложим треугольник  к треугольнику  таким образом, чтобы вершина А совместилась с вершиной А₁, вершина В – с вершиной В₁, а вершины С и С₁ оказались по разные стороны от прямой А₁В₁. Тогда возможны три случая.

Рассмотрим первый случай.

Так как по условию теоремы , , то треугольники  и  являются равнобедренными. По теореме о свойстве углов равнобедренного треугольника , . Поэтому .

Итак мы знаем, что ,  и . Следовательно, треугольник  по первому признаку равенства треугольников.

Рассмотрим второй случай.

Так как по условию теоремы , то треугольник  является равнобедренным. По теореме о свойстве углов равнобедренного треугольника углы при основании . Можем сказать, что треугольники  по первому признаку равенства треугольников, так как , , .

И третий случай.

По условию теоремы  и . Из этого следует, что треугольники  и  являются равнобедренными. Тогда по теореме о свойстве углов при основании равнобедренного треугольника . А, следовательно, . Итак, треугольники  по первому признаку равенства треугольников, так как  и  по условию теоремы, а .

Теорема доказана.

Задача.

Отрезок  – общее основание равнобедренных  и.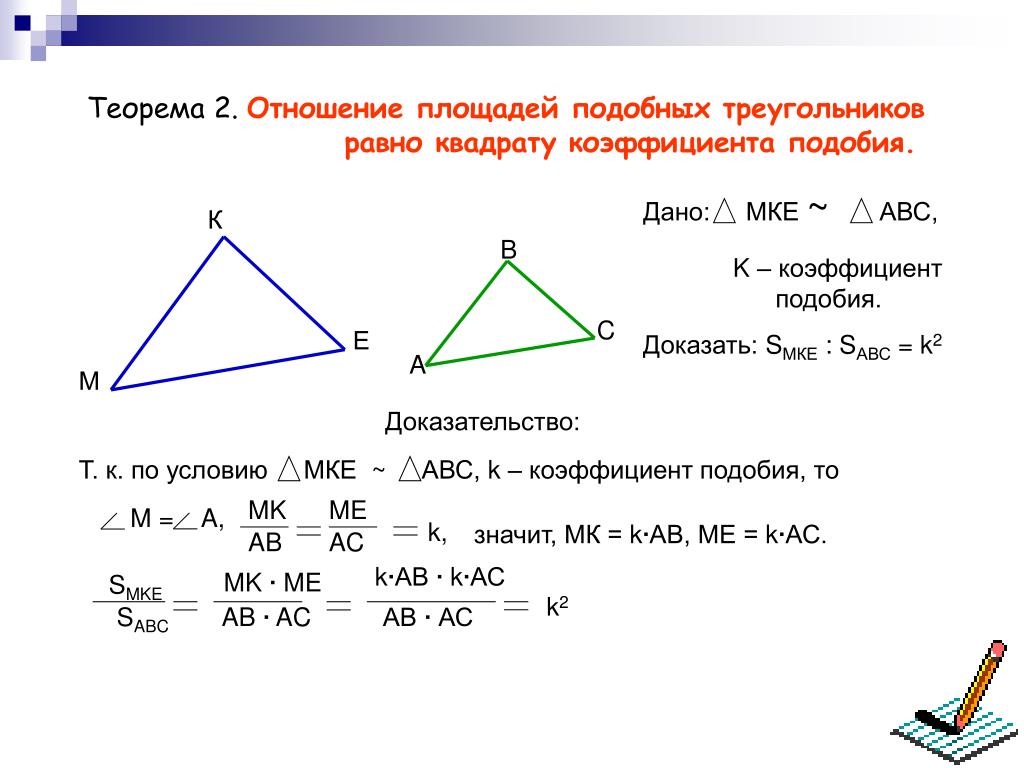 Докажите, что .

Доказательство. Рассмотрим треугольники  и . У этих треугольников , , а сторона  – общая. Тогда получаем, что треугольники  по третьему признаку равенства треугольников.

Что и требовалось доказать.

Теперь перейдём к признакам подобия треугольников.

Вспомним, что подобными называются треугольники, у которых углы соответственно равны, а сходственные стороны пропорциональны.

Подобные треугольники обозначают следующим образом: .

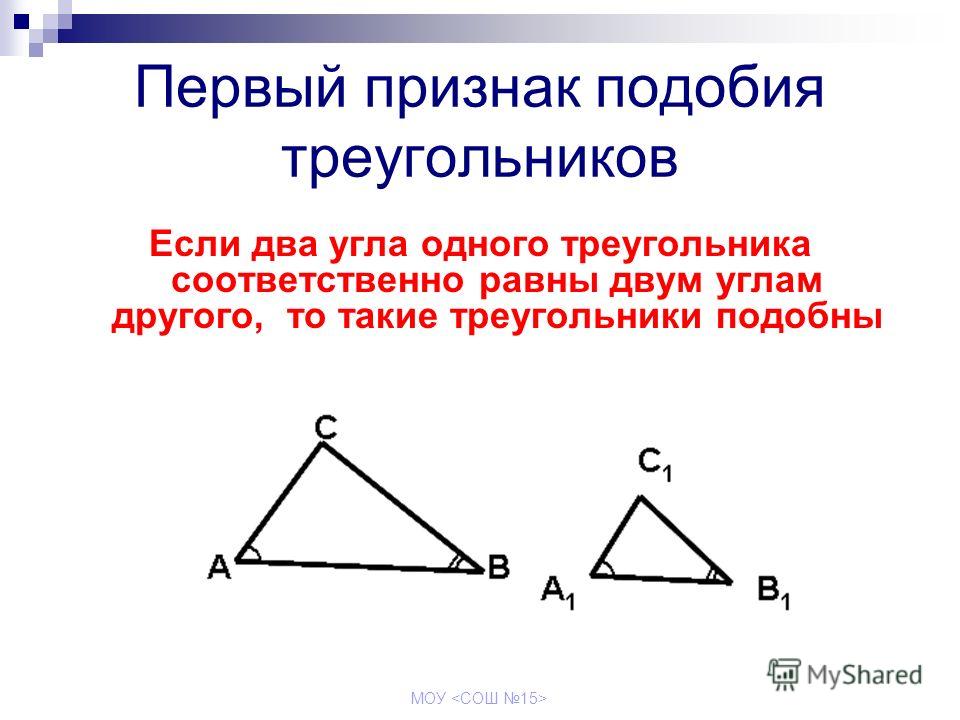
Сформулируем первый признак подобия треугольников.

Если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны.

Доказательство. Пусть у треугольников  и  , .

Напомним, что сумма углов треугольника равна 180^о. Значит, для наших треугольников можем записать следующие равенства:

Выразим из первого равенства , а из второго – угол .

Так как по условию , , то, следовательно, . То есть у рассматриваемых треугольников углы соответственно равны.

Теперь докажем, что сходственные стороны этих треугольников пропорциональны.

Так как , то по теореме: если угол одного треугольника равен углу другого треугольника, то площади этих треугольников относятся как произведения сторон, заключающих равные углы; площадь треугольника .

Углы , а тогда отношение площадей наших треугольников равно .

Заметим, что у этих равенств левые части одинаковые, а тогда можно приравнять их правые части:

Упростим, получившееся равенство. Для этого обе части равенства разделим на , а затем умножим на . И получим,

Аналогично, так как , , то имеют место следующие равенства:

Их левые части равны, а тогда можем приравнять их правые части. Упростим, получившееся равенство. И получим,

Таким образом, из полученных равенств следует .

То есть мы получили, что сходственные стороны треугольников  и  пропорциональны. Выше мы доказали, что соответственные углы этих треугольников равны, а значит, .

Что и требовалось доказать.

Задача.

На рисунке:  см,  см,  см, а . Найти .

Рассмотрим треугольники  и . У них углы  по условию задачи, а  – общий. Значит,  по первому признаку.

Из подобия треугольников следует пропорциональность их сходственных сторон: . Подставим известные значения сторон из условия задачи: . Выразим . Запишем ответ.

Сформулируем и докажем второй признак подобия треугольников.

Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы между ними равны, то такие треугольники подобны

.

Рассмотрим треугольники  и , у которых , .

Построим на стороне  треугольника  треугольник , у которого , . Тогда треугольники  по первому признаку. Для сходственных сторон можем записать, что .

По условию, . А тогда их этих двух равенств получим, что .

Рассмотрим треугольники  и . У них . Сторона  – общая. , так как  и . А значит, треугольники  по двум сторонам и углу между ними, то есть по первому признаку равенства треугольников.

Таким образом, мы получили, что треугольник , а построенный треугольник . Отсюда следует, что треугольник .

Что и требовалось доказать.

Задача.

На одной из сторон  отложены отрезки  и , равные соответственно  см и  см. На другой стороне этого же угла отложены отрезки  и , соответственно равные  см и  см. Подобны ли  и ?

Рассмотрим треугольники  и . У них  – общий. Составим отношения сторон , , образующих . Видим, что эти отношения равны, а значит, .

А, следовательно, треугольники  по двум сторонам и углу между ними, то есть по второму признаку подобия треугольников.

Ну а теперь сформулируем третий признак подобия треугольников.

Если три стороны одного треугольника соответственно пропорциональны трём сторонам другого треугольника, то такие треугольники подобны.

Доказательство. Рассмотрим треугольники  и , у которых стороны соответственно пропорциональны .

Построим на стороне  треугольника  треугольник , у которого , .

Тогда треугольники  по первому признаку подобия треугольников. Поэтому стороны .

По условию стороны . Сравнивания эти равенства, получаем, что ; .

Тогда треугольники  по третьему признаку равенства треугольников, так как только что мы получили, что ; , а сторона  у них общая. Следовательно, у этих треугольников углы соответственно равны, то есть .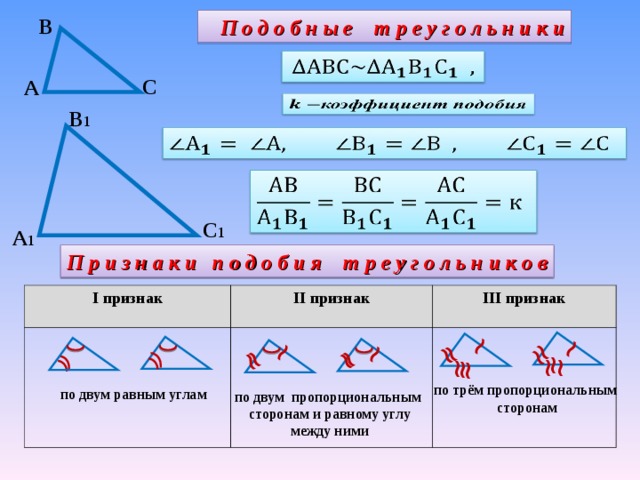 А так как , то .

Таким образом, мы получаем, что у треугольников  и  стороны пропорциональны и . Следовательно,  по второму признаку подобия треугольников.

Что и требовалось доказать.

Задача.

Выяснить, подобны ли  и , если  см,  см,  см,  см,  см,  см?

Так как нам известны длины всех сторон данных треугольников, то проверим, пропорциональны ли стороны треугольника  сторонам треугольника .

Найдём отношения сторон:

Видим, что эти отношения равны, а значит, . Следовательно,  по третьему признаку подобия треугольников.

Итоги урока

На этом уроке мы говорили о равенстве и подобии треугольников. Сформулировали и доказали три признака равенства треугольников. А также сформулировали и доказали три признака подобия треугольников.

Доказательства равных треугольников: как доказать равенство углов, 3 признака равенства, подобие треугольников

Геометрия как отдельный предмет начинается у школьников в 7 классе. До этого времени они касаются геометрических задач достаточно лёгкой формы и в основном того, что можно рассмотреть на наглядных примерах: площади комнаты, земельного участка, длины и высоты стен в помещениях, периметра плоских предметов и прочее. В нача ле изучения непосредственно геометрии появляются первые сложности, такие, например, как понятие прямой, так как потрогать руками эту прямую нет возможности. Что касается треугольников -это самый простой вид многоугольников, содержащий всего три угла и три стороны.

Оглавление:

• Как доказать, что треугольники равны
• 3 признака равенства треугольников
• Доказательство подобия треугольников

Тема треугольников одна из основных важных и больших тем школьной программы в геометрии 7−9 классов. Усвоив её хорошо, возможно решать очень сложные задачи. При этом можно изначально рассматривать совершенно другую геометрическую фигуру, а затем разделить её для удобства на подходящие треугольные части.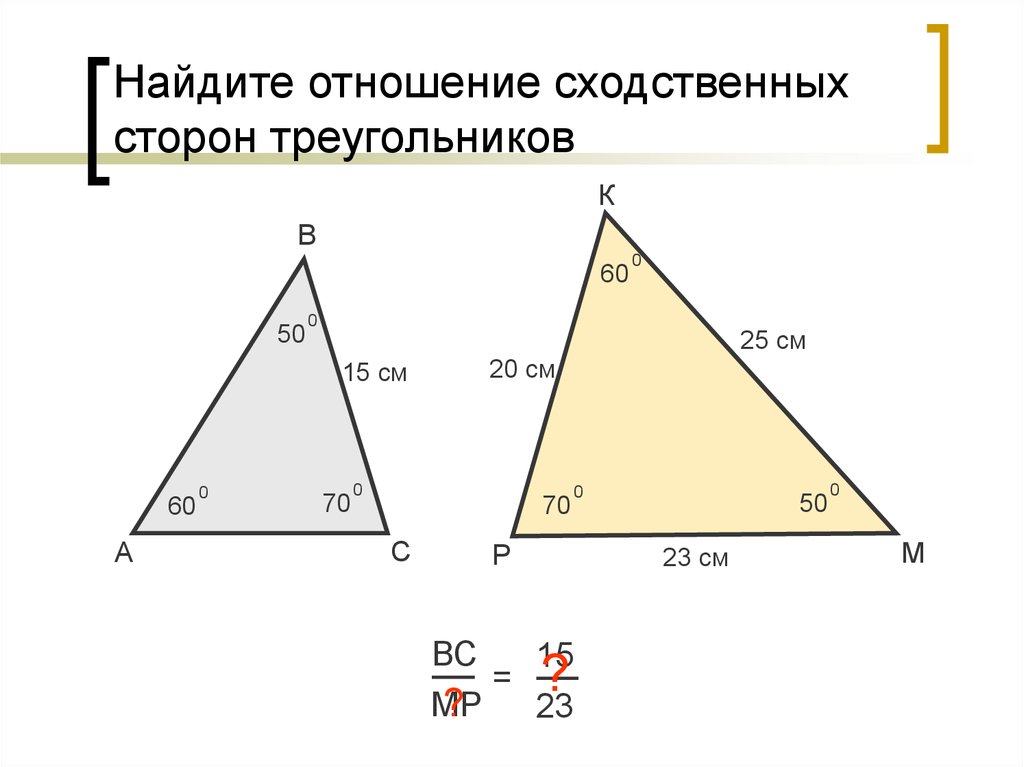

Содержание

Как доказать, что треугольники равны

Для работы над доказательством равенства ∆ ABC и ∆A1B1C1 нужно хорошо усвоить признаки равенства фигур и уметь ими пользоваться. Перед изучением признаков необходимо научиться определять равенство сторон и углов простейших многоугольников.

Чтобы доказать, что углы треугольников равны, помогут следующие варианты:

1. ∠ α = ∠ β исходя из построения фигур.
2. Дано в условии задания.
3. При двух параллельных прямых и наличии секущей могут образоваться как внутренние накрест лежащие, так и соответственные ∠ α = ∠ β.
4. Прибавляя (вычитая) к (из) ∠ α = ∠ β равные углы.
5. Всегда сходны вертикальные ∠ α и ∠ β
6. Общий ∠ α, одновременно принадлежащий ∆ MNK и ∆ MNH .
7. Биссектриса делит ∠ α на два равнозначных.
8. Смежный с ∠ 90° — угол, равный исходному.
9. Смежные равным углам равны.
10. Высота образует два смежных ∠ 90° .
11. В равнобедренном ∆ MNK при основании ∠ α = ∠ β.
12. В равных ∆ MNK и ∆ SDH соответствующие ∠ α = ∠ β.
13. Доказанное ранее равенство ∆ MNK и ∆ SDH .

Это интересно: Как найти периметр треугольника.

3 признака равенства треугольников

Доказательство равенства ∆ ABC и ∆A1B1C1 очень удобно производить, опираясь на основные признаки тождественности этих простейших многоугольников. Существует три таких признака. Они являются очень важными при решении многих геометрических задач. Стоит рассмотреть каждый.

• I признак. Две стороны и угол между ними ∆ ABC соответственно = двум сторонам и углу ∆ A1B1C1 , следовательно, треугольники равны.
• II признак. Сторона и два прилежащих к ней угла ∆ ABC соответственно = стороне и двум углам ∆ A1B1C1 , =&gt, треугольники равны.
• III признак. Если все стороны ∆ ABC соответственно = сторонам ∆ A1B1C1 , то имеющиеся треугольники равны.

Перечисленные выше признаки являются теоремами и доказываются методом наложения одной фигуры на другую, соединения вершин соответственных углов и начала лучей.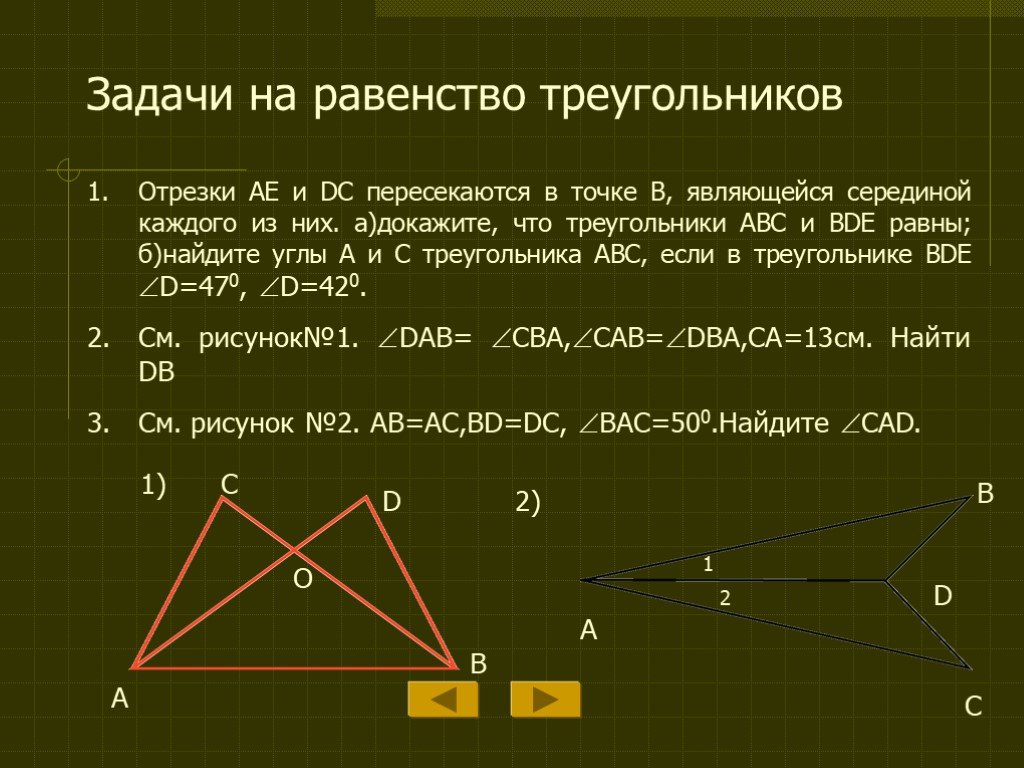 Доказательства равенства треугольников в 7 классе описаны в очень доступной форме, но сложны в изучении школьниками на практике, так как содержат большое количество элементов, обозначенных заглавными латинскими буквами. Это не совсем привычно для многих учеников на момент начала изучения предмета. Подростки путаются в названиях сторон, лучей, углов.

Доказательство подобия треугольников

Чуть позже появляется ещё одна важная тема «Подобие треугольников». Само определение «подобие» в геометрии означает схожесть формы при различии размеров. Для примера можно взять два квадрата, первый со стороной 4 см, а второй 10 см. Эти виды четырёхугольников будут похожи и, одновременно, иметь отличие, поскольку второй будет больше, причём каждая сторона увеличена в одинаковое количество раз.

В рассмотрении темы подобия также приводятся 3 признака:

• Первый о двух соответственно равных углах двух рассматриваемых треугольных фигур.
• Второй об угле и образующих его сторонах ∆ MNK , которые равны соответственным элементам ∆ SDH .
• Третий указывает на пропорциональность всех соответственных сторон двух нужных фигур.

Нужно знать! Что такое горизонталь?

Как же доказать, что треугольники подобны? Достаточно воспользоваться одним из выше перечисленных признаков и грамотно описать весь процесс доказательства задания. Тема подобия ∆ MNK и ∆ SDH проще воспринимается школьниками исходя из того, что к моменту её изучения ученики уже свободно пользуются обозначениями элементов в геометрических построениях, не путаются в огромном количестве названий и умеют читать чертежи.

Завершая прохождение обширной темы треугольных геометрических фигур, учащиеся уже в совершенстве должны знать, как доказать равенство ∆ MNK = ∆ SDH по двум сторонам, установить равны два треугольника или нет. Учитывая, что многоугольник, имеющий ровно три угла — это одна из важнейших геометрических фигур, к усвоению материала следует подойти серьёзно, уделяя особое внимание даже мелким фактам теории.

Урок: Подобие треугольников | Нагва

В этом уроке мы научимся определять и доказывать, подобны ли два треугольника, используя равенство соответствующих углов или пропорциональность соответствующих сторон, и как использовать подобия для нахождения неизвестных длин и углов.

План урока

Учащиеся смогут

• определить и доказать подобие двух треугольников в силу того, что две пары соответствующих углов равны по величине,
• определить и доказать подобие двух треугольников в силу того, что соответствующие стороны имеют одинаковую пропорцию,
• написать заявления о сходстве двух подобных треугольников,
• используют подобие двух треугольников для нахождения неизвестных углов, неизвестных длин и периметров.

Видео урока

16:16

Объяснитель урока

Список воспроизведения уроков

• 03:15

• 02:03

Рабочий лист урока

Q1:

Похож ли треугольник 𝑀𝑁𝐿 на треугольник 𝑋𝑍𝑌?

Q2:

Какой из следующих треугольников подобен показанному на данном рисунке?

Q3:

Учитывая, что 𝐴𝐵 и 𝐷𝐶 параллельны, подобны ли треугольники 𝐸𝐶𝐷 и 𝐸𝐴𝐵? Если да, то почему?

Nagwa использует файлы cookie, чтобы обеспечить вам максимальное удобство на нашем веб-сайте. Узнайте больше о нашей Политике конфиденциальности.

Геометрия — треугольники — равные, углы, углы и подобные

Треугольники представляют собой плоские фигуры, определяемые тремя не лежащими на одной прямой точками, называемыми «вершинами». Они состоят из сегментов, называемых сторонами, которые соединяются с ними. Хотя стороны представляют собой сегменты, а не лучи, каждая их пара составляет один из углов треугольника.

Треугольники можно классифицировать по размеру их углов или по длине их сторон. Треугольники, все углы которых меньше прямых, называются остроугольными. Те, у которых один угол прямой, являются «прямыми» треугольниками. Те, у которых один угол больше прямого, называются «тупыми». (В прямоугольном треугольнике сторона, противоположная прямому углу, называется «hy potenuse», а две другие стороны — «каттерами».) Треугольники, у которых нет равных сторон, являются «разносторонними» треугольниками. Те, у кого две равные стороны, являются «равнобедренными». Те, у кого три равные стороны, являются «равносторонними». Прямой связи между величиной углов треугольника и длинами его сторон нет. Однако самая длинная сторона будет находиться напротив наибольшего угла; и самая короткая сторона, противоположная наименьшему углу. Против равных углов будут лежать равные стороны.

При сравнении треугольников полезно устанавливать соответствие между ними и называть соответствующие вершины в том же порядке. Если CXY и PST — два таких треугольника, то углы C и P соответствуют; стороны CY и PT соответствуют; и так далее.

Два треугольника конгруэнтны, если их шесть соответствующих частей равны. Конгруэнтные треугольники имеют одинаковый размер и форму, хотя один из них может быть зеркальным отражением другого. Треугольники ABC и FDE равны, если стороны и углы, которые кажутся равными, на самом деле равны.

Можно показать, что два треугольника равны, не устанавливая равенство всех шести частей. Два треугольника будут конгруэнтны, если

1. Две стороны и угол между ними равны двум сторонам и углу между ними другого (конгруэнтность SAS).
2. Два угла и сторона, прилежащая к одному, равны двум углам и стороне, прилежащей к другому (конгруэнтность ASA).
3. Три стороны одного равны трем сторонам другого (конгруэнтность SSS).

Конгруэнтность треугольников применима не только к двум различным треугольникам. Это также относится к одному треугольнику в два разных момента времени или к одному треугольнику, рассматриваемому двумя разными способами. Например, когда балки моста укреплены треугольными раскосами, каждый треугольник остается конгруэнтным самому себе в течение определенного периода времени и делает это благодаря конгруэнтности SSS.

Два треугольника тоже могут быть подобны. Подобные треугольники имеют одинаковую форму, но не обязательно одинаковый размер. Они похожи так же, как похожи снимок и его увеличенное изображение. Когда два треугольника подобны, соответствующие углы равны, а соответствующие стороны пропорциональны.

Можно показать, что два треугольника подобны, не показывая, что все углы равны и все стороны пропорциональны. Два треугольника будут подобны, если

1. Две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы между ними равны (подобие SAS).
2. Два угла одного треугольника равны двум углам другого треугольника (подобие АА).
3. Три стороны одного треугольника пропорциональны трем сторонам другого треугольника (подобие SSS).

Широко используются свойства подобных треугольников. Художники, например, используют их для создания уменьшенных или увеличенных версий изображения. Создатели карты используют их для рисования карт; и пользователи, читая их.

На рис. 3 показан прямоугольный треугольник, в котором высота BD проведена к гипотенузе AC. По подобию АА треугольники ABC, ADB и BDC подобны друг другу.

В силу этих сходств можно написать AC/BC = BC/DC и AC/AB = AB/AD. Затем, используя AD + DC = AC и немного алгебры, получаем (AB) ² + (BC) ² = (AC) ² , или теорема Пифагора : «В прямоугольном треугольнике сумма квадратов на катетах равна гипотенуза». Это изящное доказательство было обнаружено Бхаскарой, упомянутой ранее.

Высота BD на рис. 3 также является средним значением , пропорциональным между AD и DC. То есть AD/BD = BD/DC.

В треугольнике ABC, если DE — линия, проведенная параллельно AC, она образует треугольник, подобный ABC. Следовательно, он делит AB и BC пропорционально. И наоборот, линия, которая пропорционально делит две стороны треугольника, параллельна третьей стороне. Частным случаем этого является отрезок, соединяющий середины двух сторон треугольника. Он параллелен третьей стороне и равен половине ее длины.

С каждым треугольником связано четыре набора линий: медианы, высоты, биссектрисы углов и биссектрисы сторон. В каждом наборе три линии, что примечательно, параллельны, то есть все они проходят через одну точку. В случае медиан, которые представляют собой линии от вершины до середины противоположной стороны, точкой пересечения является «центроид», центр тяжести. Биссектрисы угла совпадают в «центре вписанной окружности», в центре окружности, касательной к трем сторонам.