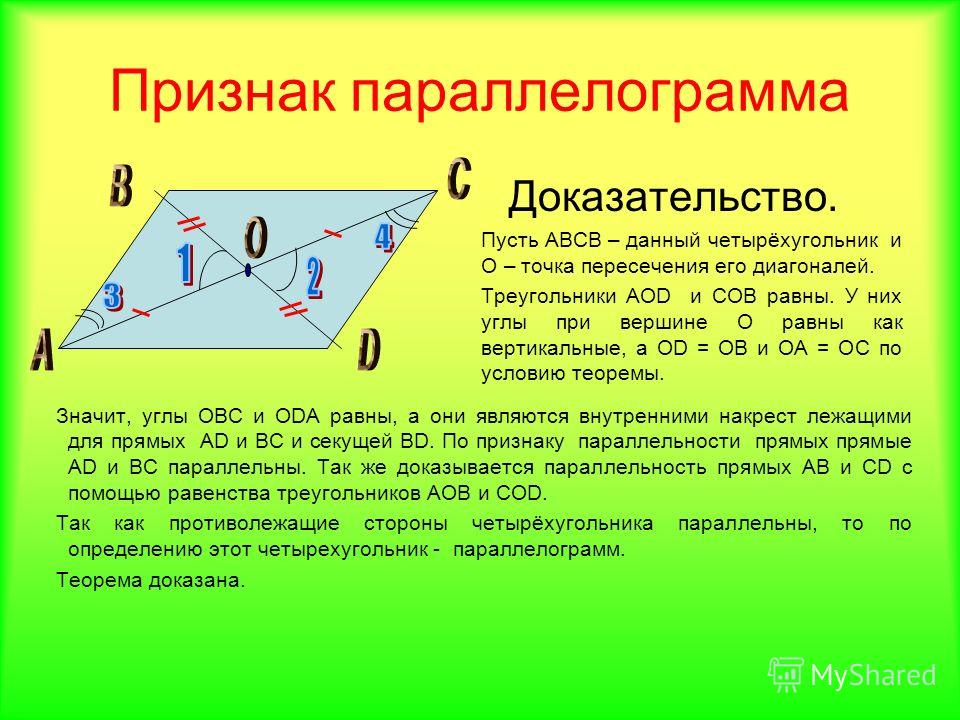
Первое свойство параллелограмма и его доказательство
Теорема о сумме внутренних углов > Первое свойство параллелограмма и его доказательство
|
3. Скалярное произведение. Гильбертово пространство.
 Аксиомы и свойства. Ортонормированные системы. Ортогонализация по Шмидту. Тождество параллелограмма.
Аксиомы и свойства. Ортонормированные системы. Ортогонализация по Шмидту. Тождество параллелограмма.Определение 2. Линейное пространство Н называется предгильбертовым пространством, если указано правило, которое позволяет сопоставить каждой паре элементов x и y пространства Н вещественное (или комплексное) число, называемое скалярным произведением векторов x и y и обозначенное , удовлетворяющее следующим условиям:
а) (в случае комплексного значения )
б)
в) для любого вещественного числа ;
г) при и при ;
Число назовём нормой элемента х.
Ниже мы покажем, что эта величина
удовлетворяет всем требованиям нормы.
В случае, если Н полное
пространство по этой норме, его называют гильбертовым.
Таким образом, гильбертово пространство
есть частный случай банахова пространства.
Пример 9. Пространство l2 становится гильбертовым, если для любых двух его элементов и положить
Сходимость этого ряда для любых x и y из l2 вытекает из неравенства Буняковского для рядов.
Пример 10. Пространство . Это пространство (вещественных) функций, определённых и измеренных на отрезке [a, b] и таких, что
,
где почти всюду на [a, b]. будет гильбертовым пространством, если положить для
Существование этого интеграла при любом и из вытекает из неравенства Гельдера для интегралов.
Рассмотрим простейшие свойства гильбертовых пространств.
Из аксиом б) и в) легко получается общая формула
справедливая для произвольных векторов и произвольных вещественных чисел
Установим теперь
для скалярного произведения неравенство
Коши — Буняковского. Для любых и любого R,
имеем или Рассматривая это выражение как квадратный
трехчлен относительно ,
получаем, что условием его неотрицательности
является неположительность его
дискриминанта, т.е.(х, у)2 – (у, у)(х, х)
0 или |(x, y)|
– это и есть неравенство Коши –
Буняковского.
Для любых и любого R,
имеем или Рассматривая это выражение как квадратный
трехчлен относительно ,
получаем, что условием его неотрицательности
является неположительность его
дискриминанта, т.е.(х, у)2 – (у, у)(х, х)
0 или |(x, y)|
– это и есть неравенство Коши –
Буняковского.
Теорема 6. Величина является нормой в пространстве со скалярным произведением.
Доказательство. 1.
Неотрицательность следует из неотрицательности скалярного произведения.2.
3. . По неравенству Коши-Буняковского,
.
Извлекая из обеих частей квадратный корень, получим неравенство .
Легко доказывается непрерывность скалярного произведения.
Теорема 7. Скалярное произведение есть непрерывная функция относительно сходимости по норме.
Доказательство. Пусть и . Тогда числа и ограничены; пусть М
– их верхняя
граница.
Тогда числа и ограничены; пусть М
– их верхняя
граница.
Имеем
Так как и при ,то и при , что и требовалось доказать.
Наличие скалярного произведения позволяет ввести в гильбертовом пространстве понятие длины (нормы) вектора и угла между векторами по формулам
Из неравенства Коши – Буняковского следует корректность этих формул. Эти определения согласуются с обычными формулами аналитической геометрии.
Два вектора х и y Н называются ортогональными (в этом случае записывают ), если . Если и , то это определение, в соответствии с общим определением угла между векторами, означает, что x и y образуют угол в . Нулевой вектор оказывается ортогональным любому вектору х Н.
В пространстве условие ортогональности векторов и имеет вид
.
Легко проверить, вычислив соответствующие интегралы, что в пространстве любые два вектора тригонометрической системы
взаимно ортогональны.
Отметим несколько простых свойств, связанных с понятием ортогональности.
1) Если вектор х ортогонален векторам то он ортогонален и любой линейной комбинации этих векторов.
2) Если векторы ортогональны вектору х и , то вектор у также ортогонален вектору х.
Действительно, в силу непрерывности скалярного произведения , что и требовалось доказать.
Из свойств 1) и 2) следует, что совокупность всех векторов ортогональных вектору х (или произвольному фиксированному множеству Х векторов в Н), образует замкнутое подпространство – ортогональное дополнение к вектору х (к множеству Х).
Система векторов пространства Н называется ортонормальной системой, если
.
Бесконечная система элементов линейного пространства называется линейно независимой, если любая конечная подсистема этой системы линейно независима.
Любую систему линейно независимых элементов можно превратить в ортонормальную с помощью следующего процесса ортогонализации Шмидта.
Полагаем . Пусть . Подберем число так, чтобы было ортогональным . Имеем . Отсюда следует, что для этого следует взять . Полагаем ; при этом , так как в противном случае и вектора и будут линейно зависимы, что противоречит условию. Пусть уже построены. Возьмем
и подберем числа так, чтобы было ортогонально ; для этого следует взять . Полагаем , причем снова и т.д.
Пример 11.
Если совокупность степеней ортогонализовать
в пространстве то мы придём к системе многочленов называемых многочленами Лежандра. Можно
показать, что n-ый многочлен Лежандра
имеет вид .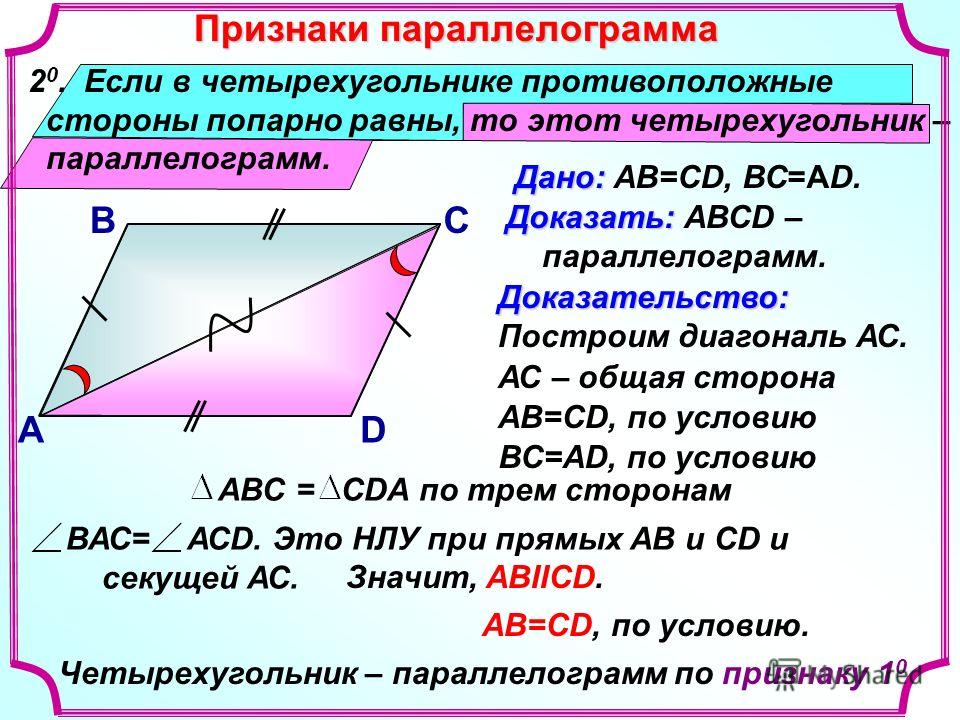
Пример 12. Функции, получающиеся при ортогонализации выражений в пространстве , называются функциями Эрмита. Можно показать, что n-ая функция Эрмита имеет вид .
Пример 13. Функции, получающиеся при ортогонализации выражений в пространстве называется функциями Лагерра. Можно показать, что n-ая функция Лагерра имеет вид .
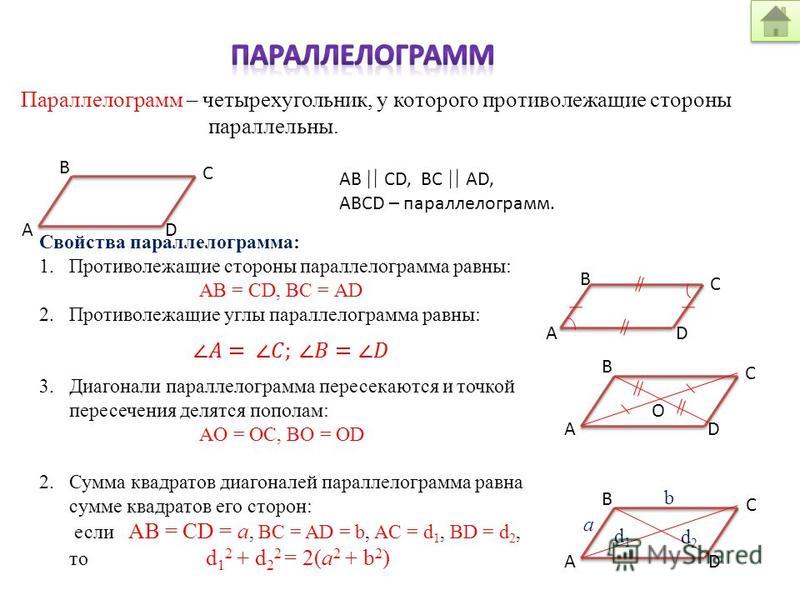
Теорема 8. (равенство параллелограмма) В пространстве со скалярным произведением выполняется следующее тождество:
||x + y||2 + ||x y||2 = 2||x||2 + 2||y||2.
Доказательство. В пространстве со скалярным произведением выполняются равенства
||x + y||2 = (x + y, x + y
||x y||2 = (x y, x y) = (x,
x) 2(x,
y) + (y,
y) = ||x||2 2(x,
y) + ||y||2.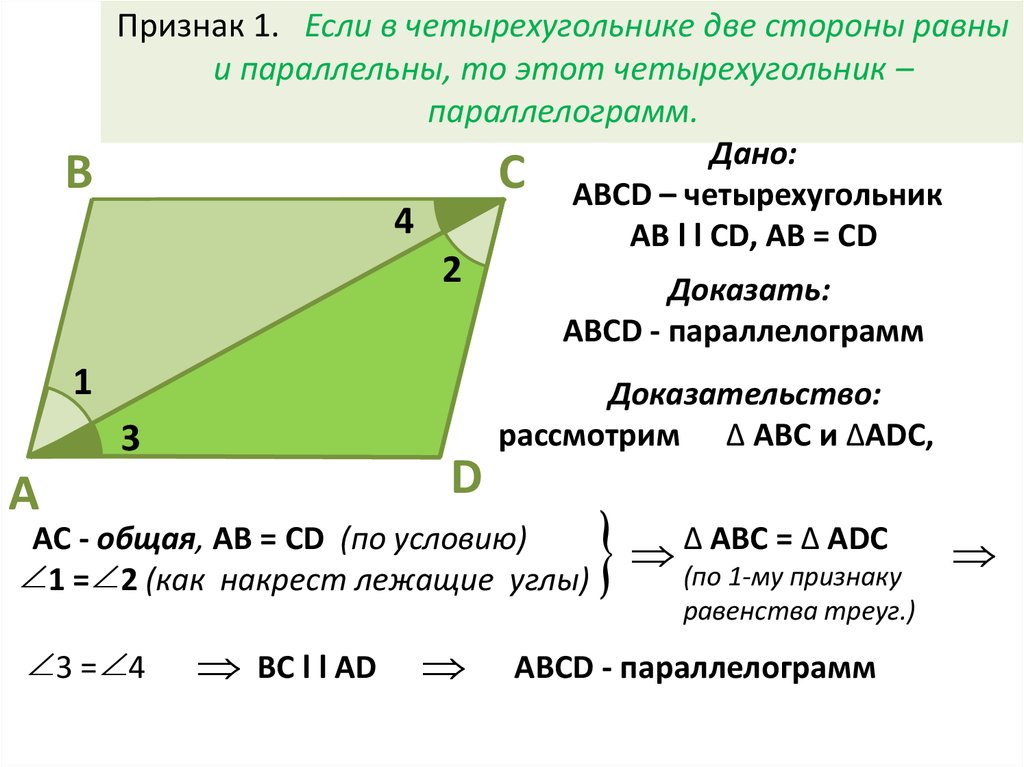 2\right).$$ Мы имеем дело с действительных векторных пространств и отложите обработку сложного случая до шага 4 ниже.
2\right).$$ Мы имеем дело с действительных векторных пространств и отложите обработку сложного случая до шага 4 ниже.
Шаг 0. $\langle x, y \rangle = \langle y, x\rangle$ и $\Vert x \Vert = \sqrt{\langle x, x\rangle}$.
Очевидно.
Шаг 1. Функция $(x,y) \mapsto \langle x,y \rangle$ непрерывна относительно $\Vert \cdot \Vert$.
Непрерывность по норме $\Vert\cdot\Vert$ следует из того, что сложение и отрицание $\Vert\cdot\Vert$-непрерывны, что сама норма непрерывна, а суммы и композиции непрерывных функций являются непрерывными. 92\справа)\\ & = \langle x, z \rangle + \langle y, z \rangle \end{выравнивание*}$$ по желанию.
Шаг 3. $\langle \lambda x, y \rangle = \lambda \langle x, y \rangle$ для всех $\lambda \in \mathbb{R}$.
Очевидно, что это верно для $\lambda = -1$, и по шагу 2 и по индукции имеем $\langle \lambda x, y \rangle = \lambda \langle x, y \rangle$ для всех $\lambda \in \ mathbb{N}$, то есть для всех $\lambda \in \mathbb{Z}$. Если $\lambda = \frac{p}{q}$ с $p,q \in \mathbb{Z}, q \neq 0$, мы получаем с $x’ = \dfrac{x}{q}$, что
$$q \langle \lambda x, y \rangle = q\langle p x’, y \rangle = p \langle q x’, y \rangle = p\langle x,y \rangle,$$
поэтому деление этого на $q$ дает
$$\langle \lambda x , y \rangle = \lambda \langle x, y \rangle \qquad\text{для всех} \lambda \in \mathbb{Q}.$$
Мы только что видели, что при фиксированных $x,y$ непрерывная функция $\displaystyle t \mapsto \frac{1}{t} \langle t x,y \rangle$, определенная на $\mathbb{R} \smallsetminus \{0 \}$ равно $\langle x,y \rangle$ для всех $t \in \mathbb{Q} \smallsetminus \{0\}$, поэтому равенство выполняется для всех $t \in \mathbb{R} \ маленький набор минус \{0\}$. Случай $\lambda = 0$ тривиален, и мы закончили. 92\geq0$ (это также доказывает, что $\|x\|=\sqrt{\langle x,x\rangle}$.)
Если $\lambda = \frac{p}{q}$ с $p,q \in \mathbb{Z}, q \neq 0$, мы получаем с $x’ = \dfrac{x}{q}$, что
$$q \langle \lambda x, y \rangle = q\langle p x’, y \rangle = p \langle q x’, y \rangle = p\langle x,y \rangle,$$
поэтому деление этого на $q$ дает
$$\langle \lambda x , y \rangle = \lambda \langle x, y \rangle \qquad\text{для всех} \lambda \in \mathbb{Q}.$$
Мы только что видели, что при фиксированных $x,y$ непрерывная функция $\displaystyle t \mapsto \frac{1}{t} \langle t x,y \rangle$, определенная на $\mathbb{R} \smallsetminus \{0 \}$ равно $\langle x,y \rangle$ для всех $t \in \mathbb{Q} \smallsetminus \{0\}$, поэтому равенство выполняется для всех $t \in \mathbb{R} \ маленький набор минус \{0\}$. Случай $\lambda = 0$ тривиален, и мы закончили. 92\geq0$ (это также доказывает, что $\|x\|=\sqrt{\langle x,x\rangle}$.)
$\langle x,y\rangle=\langle y,x\rangle$, очевидно.
Теперь нам нужно доказать, что $\langle x+y,z\rangle=\langle x,z\rangle+\langle y,z\rangle$ и что $\langle cx,y\rangle=c\langle x, y\rangle$ для всех $x,y,z\in X$ и $c\in\mathbb{R}$.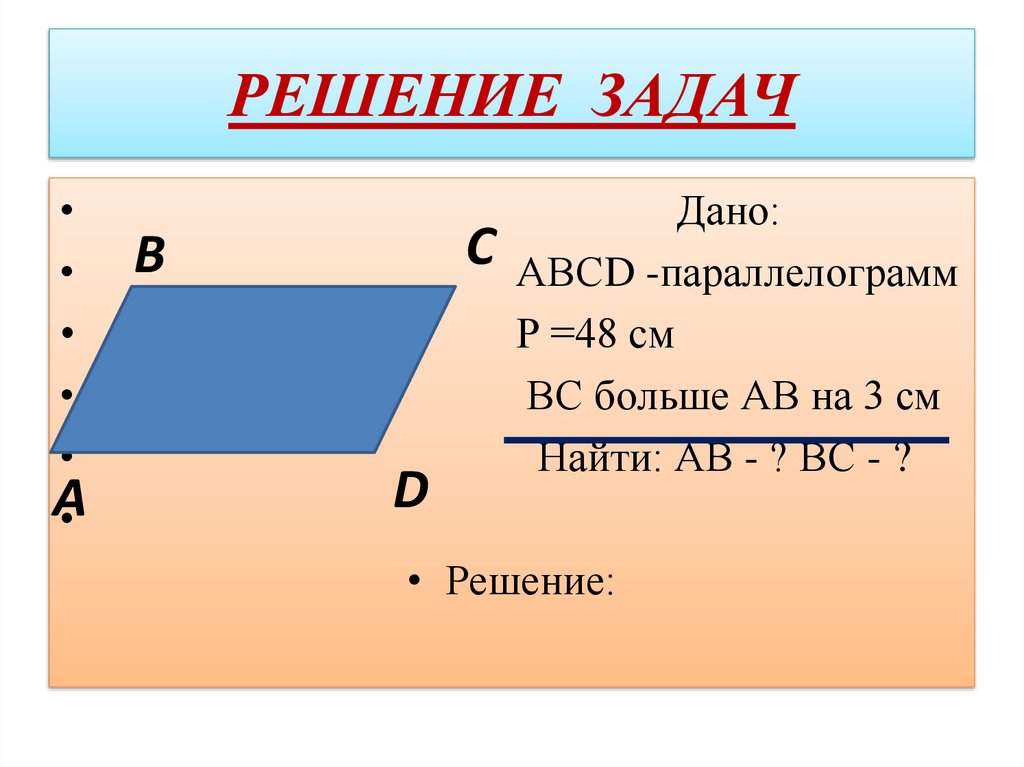 Я оставлю первое свойство недоказанным, так как это всего лишь вопрос простых, но жестких вычислений и приложений предполагаемого свойства.
Посмотрим, как доказать второе свойство (будем использовать первое). 92) = -\langle x,y \rangle$.
Я оставлю первое свойство недоказанным, так как это всего лишь вопрос простых, но жестких вычислений и приложений предполагаемого свойства.
Посмотрим, как доказать второе свойство (будем использовать первое). 92) = -\langle x,y \rangle$.
Теперь докажем, что если свойство верно для $c_1,c_2\in\mathbb{R}$, то оно верно и для $c_1\cdot c_2$. Действительно, это $\langle (c_1\cdot c_2)x,y\rangle=\langle c_1\cdot(c_2 x),y\rangle=c_1\langle c_2x,y\rangle=c_1c_2\langle x,y\rangle $.
Применяя последнее свойство для $c_1=n\in\mathbb{N}$ и $c_2=-1$, мы получаем, что желаемое свойство выполняется для $c\in\mathbb{Z}$.
Пусть $n\in\mathbb{Z}-\{0\}$. Это $\langle x,y\rangle=\langle \frac{n}{n}x,y\rangle=n\langle \frac{1}{n}x,y\rangle$, поэтому $\langle\ frac{1}{n}x,y\rangle=\frac{1}{n}\langle x,y\rangle$.
Используя свойство $c_1,c_2$ для $c_1=1/n$ для некоторых $n\in\mathbb{Z}$ и $c_2=m\in\mathbb{Z}$, получаем, что наш результат верно для каждого $c\in\mathbb{Q}$.
Итак, мы доказали, что для всех $c\in\mathbb{Q}$ это $\langle cx,y\rangle=c\langle x,y\rangle$.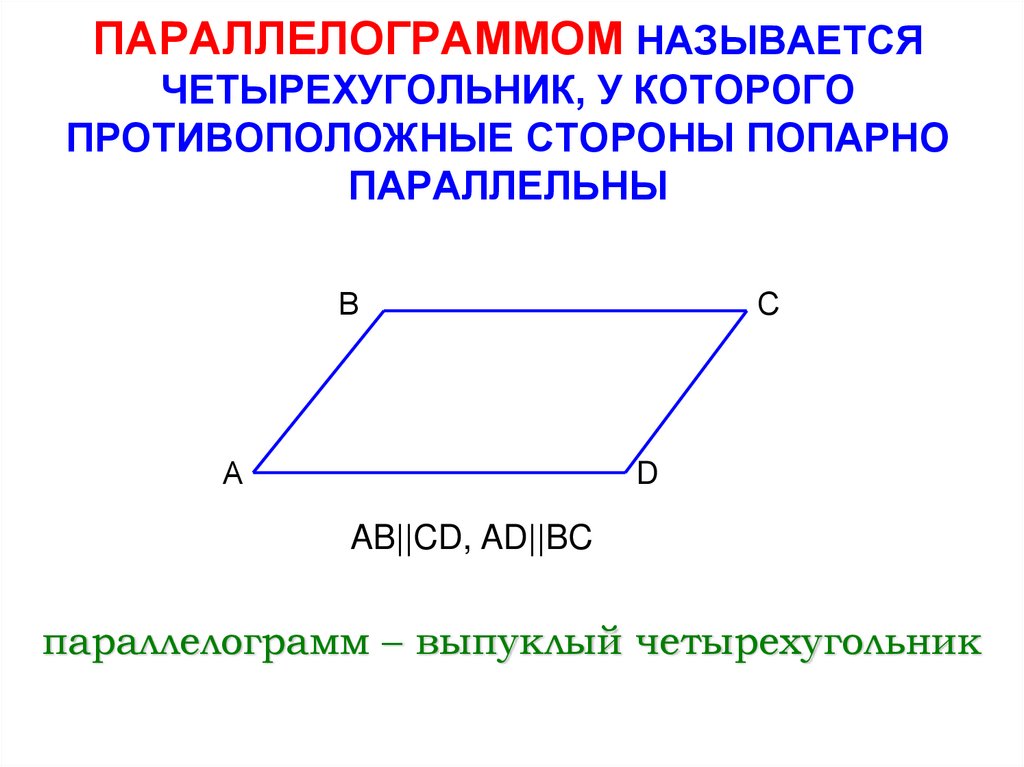

 Эта сторона является секущей при параллельных прямых .
Эта сторона является секущей при параллельных прямых .