Равнобедренная трапеция формулы: Равнобедренная трапеция. «Формулы, признаки и свойства равнобедренной трапеции» (11 класс)

Равнобедренная трапеция. Формулы, признаки и свойства равнобедренной трапеции

Навигация по странице: Определение равнобедренной трапеции Признаки равнобедренной трапеции Основные свойства равнобедренной трапеции Стороны равнобедренной трапеции Средняя линия равнобедренной трапеции Высота равнобедренной трапеции Диагонали равнобедренной трапеции Площадь равнобедренной трапеции Окружность описанная вокруг равнобедренной трапеции

Формулы и свойства трапеции

Определение.

Равнобедренная трапеция — это трапеция у котрой боковые стороны равны.

На этой странице представленны формулы характерные равнобедренной трапеции. Не забывайте, что для равнобедренной трапеции выполняются все формулы и свойства трапеции.

Рис.1

Признаки равнобедренной трапеции

Трапеция будет равнобедренной если выполняется одно из этих условий:

1. Углы при основе равны:

∠ABC = ∠BCD и ∠BAD = ∠ADC

2. Диагонали равны:

AC = BD

3. Одинаковые углы между диагоналями и основаниями:

∠ABD = ∠ACD, ∠DBC = ∠ACB, ∠CAD = ∠ADB, ∠BAC = ∠BDC

4. Сумма противоположных углов равна 180°:

∠ABC + ∠ADC = 180° и ∠BAD + ∠BCD = 180°

5. Вокруг трапеции можно описати окружность

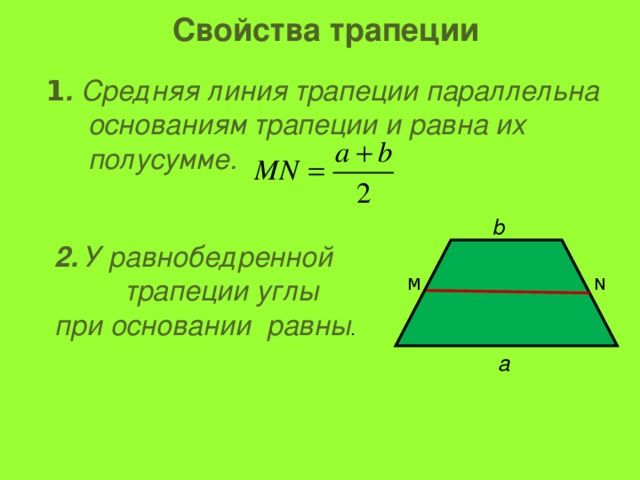
Основные свойства равнобедренной трапеции

1. Сумма углов прилегающих к боковой стороне равнобедренной трапеции равна 180°:

∠ABC + ∠BAD = 180° и ∠ADC + ∠BCD = 180°

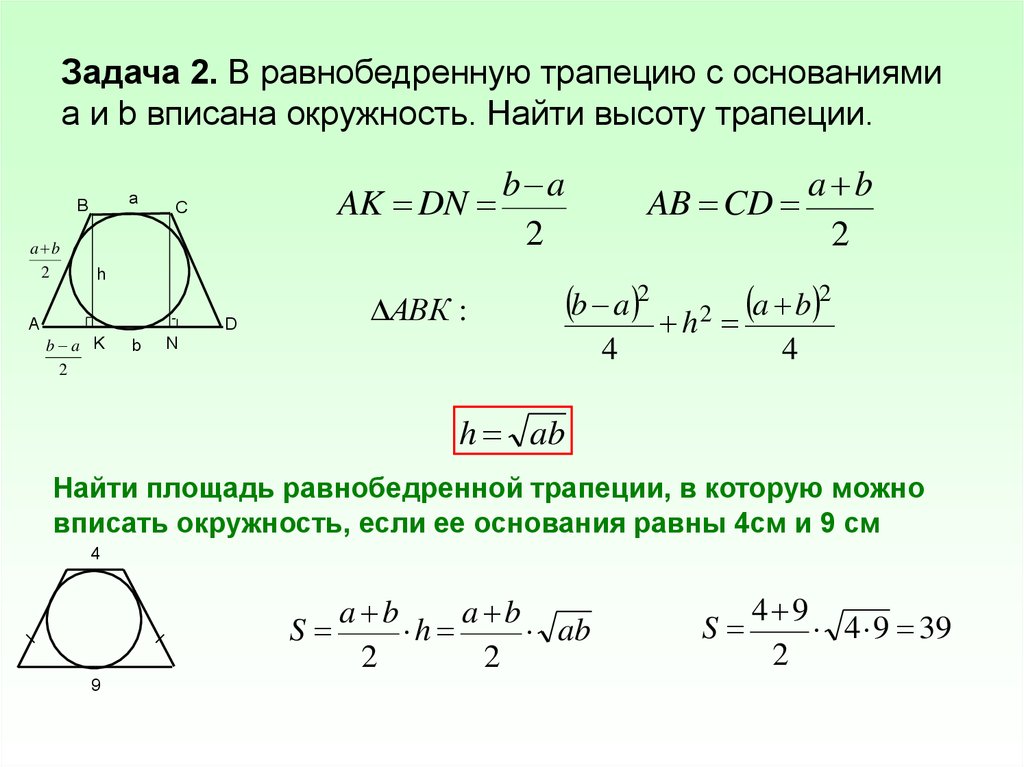
2. Если в равнобедренную трапецию можно вписать окружность, то боковая сторона равна средней лини трапеции:

AB = CD = m

3. Вокруг равнобедренной трапеции можно описать окружность

4. Если диагонали взаимно перпендикулярны, то высота равна полусумме оснований (средней лини):

h = m

5. Если диагонали взаимно перпендикулярны, то площадь трапеции равна квадрату высоты:

S_ABCD = h²

6. Если в равнобедренную трапецию можно вписать окружность, то квадрат высоты равен произведению основ трапеции:

h² = BC · AD

7. Сумма квадратов диагоналей равна сумме квадратов боковых сторон плюс удвоенному произведению основ трапеции:

AC² + BD² = AB² + CD² + 2BC · AD

8. Прямая, проходящая через середины оснований, перпендикулярна основаниям и является осью симметрии трапеции:

HF ┴ BC, HF ┴ AD

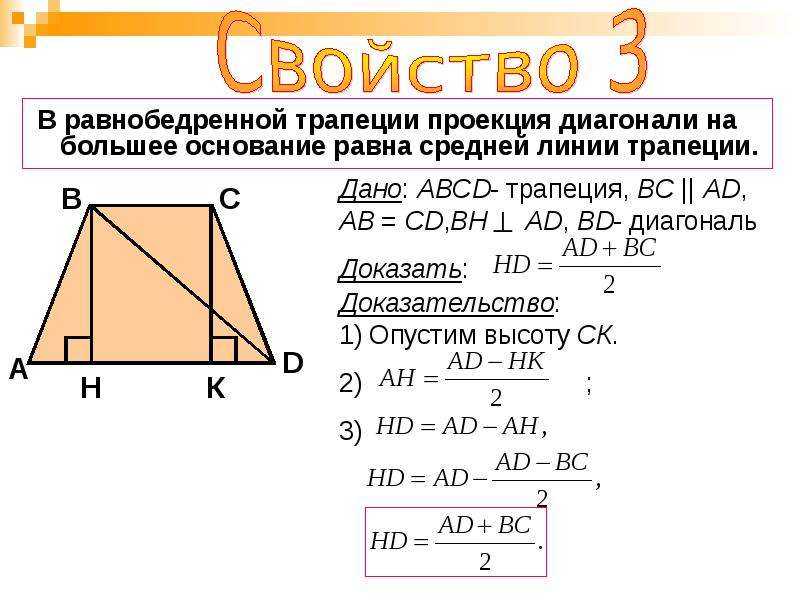
9. Высота (CP), опущенная из вершины (C) на большее основание (AD), делит его на большой отрезок (AP), который равен полусумме оснований и меньший (PD) — равен полуразности оснований:

AP =	BC + AD
	2

PD =	AD — BC
	2

10. Также смотрите свойства трапеции

Стороны равнобедренной трапеции

Формулы длин сторон равнобедренной трапеции:

1. Формулы длины сторон через другие стороны, высоту и угол:

a = b + 2h ctg α = b + 2c cos α

b = a — 2h ctg α = a — 2c cos α

c =	h	=	a — b
	sin α		2 cos α

2. Формула длины сторон трапеции через диагонали и другие стороны:

a =	d 12 — c2	b =	d12 — c2	c = √d12 — ab
	b		a

3. Формулы длины основ через площадь, высоту и другую основу:

a =	2S	— b      b =	2S	— a
	h		h

4. Формулы длины боковой стороны через площадь, среднюю линию и угол при основе:

с =	S
	m sin α

5. Формулы длины боковой стороны через площадь, основания и угол при основе:

с =	2S
	(a + b) sin α

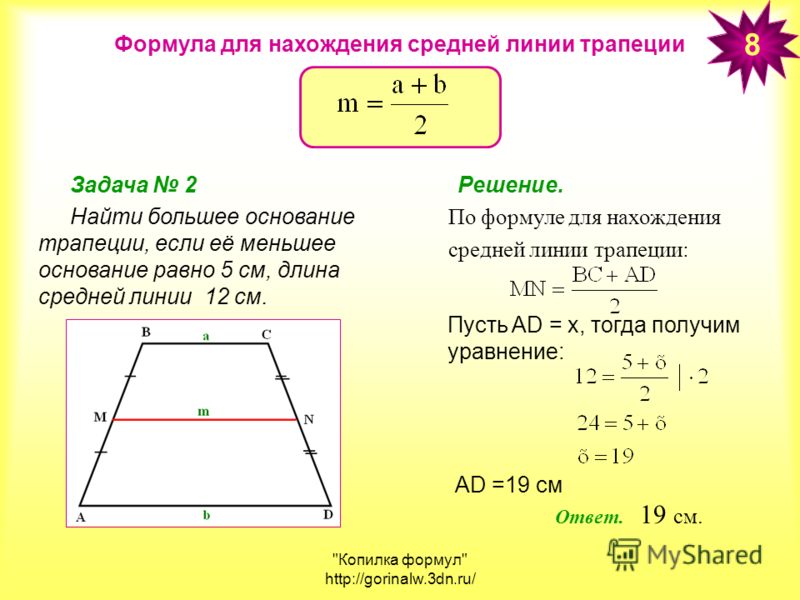
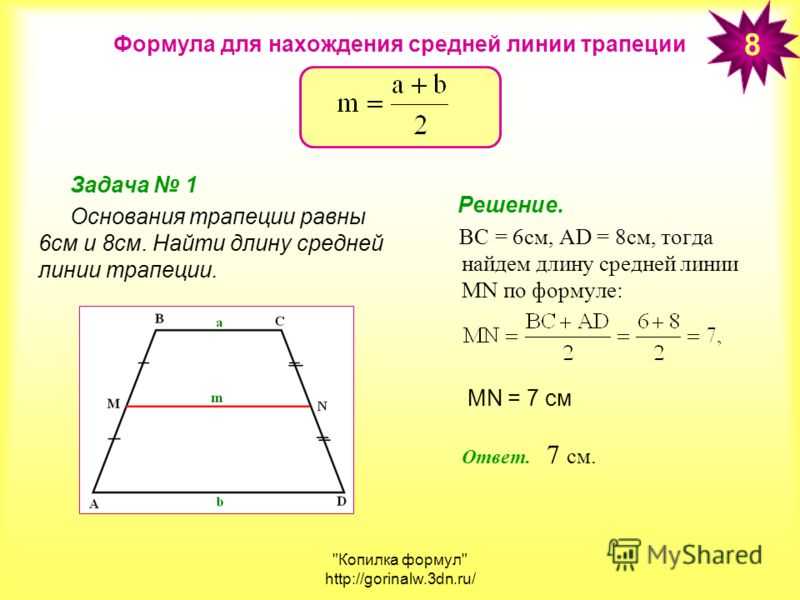
Средняя линия равнобедренной трапеции

Формулы длины средней линии равнобедренной трапеции:

1. Формула определения длины средней линии через основания, высоту и угол при основании:

m = a — h ctg α = b + h ctg α = a — √c² — h² = b + √c² — h²

2. Формула средней линии трапеции через площадь и сторону:

m =	S
	c sin α

Высота равнобедренной трапеции

Формулы определения длины высоты равнобедренной трапеции:

1. Формула высоты через стороны:

h =	1	√4c2 — (a — b)2
	2

2. Формула высоты через стороны и угол прилегающий к основе:

h =	a — b	tg β	= c sin β
	2

Диагонали равнобедренной трапеции

Диагонали равнобедренной трапеции равны:

d₁ = d₂

Формулы длины диагоналей равнобедренной трапеции:

1. Формула длины диагонали через стороны:

d₁ = √с² + ab

2. Формулы длины диагонали по теореме косинусов:

d₁ = √a² + c² — 2ac cos α

d₁ = √b² + c² — 2bc cos β

3. Формула длины диагонали через высоту и среднюю линию:

d₁ = √h² + m²

4. Формула длины диагонали через высоту и основания:

d1 =	1	√4h2 + (a + b)2
	2

Площадь равнобедренной трапеции

Формулы площади равнобедренной трапеции:

1. Формула площади через стороны:

S =	a + b	√4c2 — (a — b)2
	4

2. Формула площади через стороны и угол:

S = (b + c cos α) c sin α = (a — c cos α) c sin α

3. Формула площади через радиус вписанной окружности и угол между основой и боковой стороной:

S =	4 r 2	=	4 r 2
	sin α		sin β

4. Формула площади через основания и угол между основой и боковой стороной:

S =	ab	=	ab
	sin α		sin β

5. Формула площади ранобедренной трапеции в которую можно вписать окружность:

S = (a + b) · r = √ab·c = √ab·m

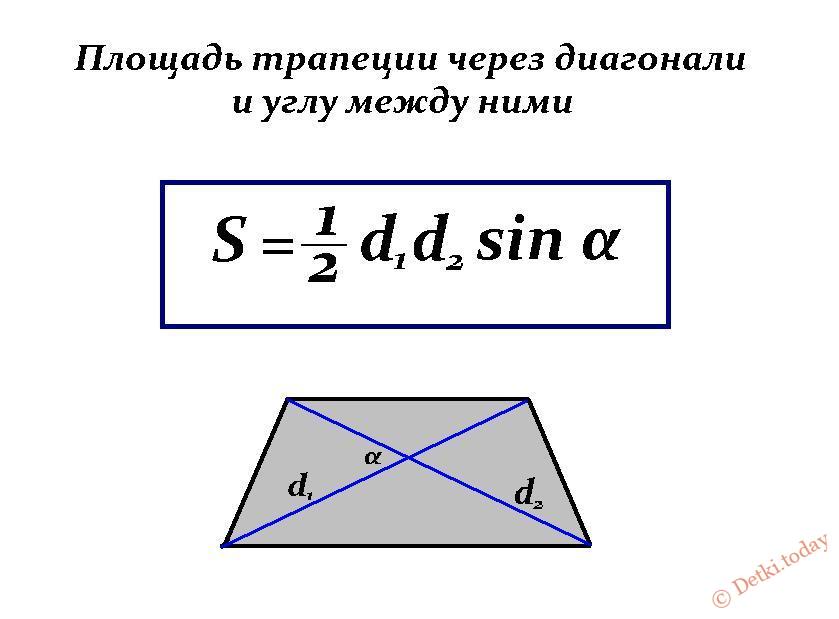
6. Формула площади через диагонали и угол между ними:

S =	d12	· sin γ	=	d12	· sin δ
	2			2

7. Формула площади через среднюю линию, боковую сторону и угол при основании:

S = mc sin α = mc sin β

8. Формула площади через основания и высоту:

S =	a + b	· h
	2

Окружность описанная вокруг трапеции

Окружность можно описать только вокруг равнобедренной трапеции!!!

Формула определения радиуса описанной вокруг трапеции окружности:

1.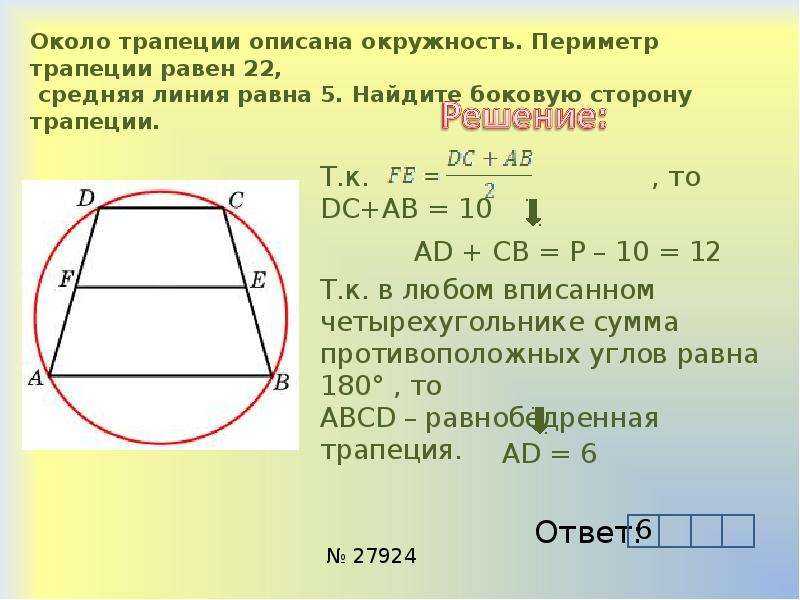 Формула радиуса через стороны и диагональ:

R =	a·c·d1
	4√p(p — a)(p — c)(p — d1)

где

p =	a + c + d1
	2

a — большее основание

Все таблицы и формулы

Равнобедренная трапеция. Формулы, признаки и свойства равнобедренной трапеции

Навигация по странице: Определение равнобедренной трапеции Признаки равнобедренной трапеции Основные свойства равнобедренной трапеции Стороны равнобедренной трапеции Средняя линия равнобедренной трапеции Высота равнобедренной трапеции Диагонали равнобедренной трапеции Площадь равнобедренной трапеции Окружность описанная вокруг равнобедренной трапеции

Формулы и свойства трапеции

Определение.

Равнобедренная трапеция — это трапеция у котрой боковые стороны равны.

На этой странице представленны формулы характерные равнобедренной трапеции. Не забывайте, что для равнобедренной трапеции выполняются все формулы и свойства трапеции.

Рис.1

Признаки равнобедренной трапеции

Трапеция будет равнобедренной если выполняется одно из этих условий:

1. Углы при основе равны:

∠ABC = ∠BCD и ∠BAD = ∠ADC

2. Диагонали равны:

AC = BD

3. Одинаковые углы между диагоналями и основаниями:

∠ABD = ∠ACD, ∠DBC = ∠ACB, ∠CAD = ∠ADB, ∠BAC = ∠BDC

4. Сумма противоположных углов равна 180°:

∠ABC + ∠ADC = 180° и ∠BAD + ∠BCD = 180°

5. Вокруг трапеции можно описати окружность

Основные свойства равнобедренной трапеции

1. Сумма углов прилегающих к боковой стороне равнобедренной трапеции равна 180°:

∠ABC + ∠BAD = 180° и ∠ADC + ∠BCD = 180°

2. Если в равнобедренную трапецию можно вписать окружность, то боковая сторона равна средней лини трапеции:

AB = CD = m

3. Вокруг равнобедренной трапеции можна описать окружность

4. Если диагонали взаимно перпендикулярны, то высота равна полусумме оснований (средней лини):

h = m

5. Если диагонали взаимно перпендикулярны, то площадь трапеции равна квадрату высоты:

S_ABCD = h²

6. Если в равнобедренную трапецию можно вписать окружность, то квадрат высоты равен произведению основ трапеции:

h² = BC · AD

7. Сумма квадратов диагоналей равна сумме квадратов боковых сторон плюс удвоенному произведению основ трапеции:

AC² + BD² = AB² + CD² + 2BC · AD

8. Прямая, проходящая через середины оснований, перпендикулярна основаниям и является осью симметрии трапеции:

HF ┴ BC ┴ AD

9. Высота (CP), опущенная из вершины (C) на большее основание (AD), делит его на большой отрезок (AP), который равен полусумме оснований и меньшый (PD) — равен полуразности оснований:

AP =	BC + AD
	2

PD =	AD — BC
	2

10. Также смотрите свойства трапеции

Стороны равнобедренной трапеции

Формулы длин сторон равнобедренной трапеции:

1. Формулы длины сторон через другие стороны, высоту и угол:

a = b + 2h ctg α = b + 2c cos α

b = a — 2h ctg α = a — 2c cos α

c =	h	=	a — b
	sin α		2 cos α

2. Формула длины сторон трапеции через диагонали и другие стороны:

a =	d12 — c2	b =	d12 — c2	c = √d12 — ab
	b		a

3. Формулы длины основ через площадь, высоту и другую основу:

a =	2S	— b      b =	2S	— a
	h		h

4. Формулы длины боковой стороны через площадь, среднюю линию и угол при основе:

с =	S
	m sin α

5. Формулы длины боковой стороны через площадь, основания и угол при основе:

с =	2S
	(a + b) sin α

Средняя линия равнобедренной трапеции

Формулы длины средней линии равнобедренной трапеции:

1. Формула определения длины средней линии через основания, высоту и угол при основании:

m = a — h ctg α = b + h ctg α = a — √c² — h² = b + √c² — h²

2. Формула средней линии трапеции через площадь и сторону:

m =	S
	c sin α

Высота равнобедренной трапеции

Формулы определения длины высоты равнобедренной трапеции:

1. Формула высоты через стороны:

h =	1	√4c2 — (a — b)2
	2

2. Формула высоты через стороны и угол прилегающий к основе:

h =	a — b	tg β	= c sin β
	2

Диагонали равнобедренной трапеции

Диагонали равнобедренной трапеции равны:

d₁ = d₂

Формулы длины диагоналей равнобедренной трапеции:

1. Формула длины диагонали через стороны:

d₁ = √с² + ab

2. Формулы длины диагонали по теореме косинусов:

d₁ = √a² + c² — 2ac cos α

d₁ = √b² + c² — 2bc cos β

3.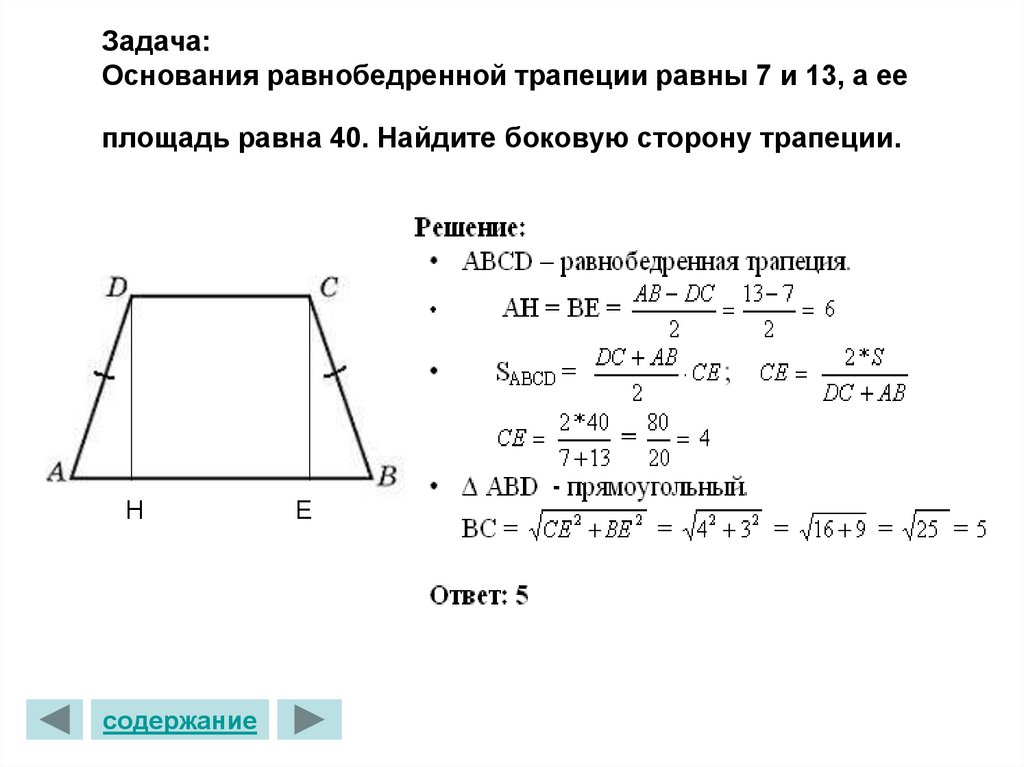 Формула длины диагонали через высоту и среднюю линию:

d₁ = √h² + m²

4. Формула длины диагонали через высоту и основания:

d1 =	1	√4h2 + (a + b)2
	2

Площадь равнобедренной трапеции

Формулы площади равнобедренной трапеции:

1. Формула площади через стороны:

S =	a + b	√4c2 — (a — b)2
	4

2. Формула площади через стороны и угол:

S = (b + c cos α) c sin α = (a — c cos α) c sin α

3. Формула площади через радиус вписанной окружности и угол между основой и боковой стороной:

S =	4 r 2	=	4 r 2
	sin α		sin β

4. Формула площади через основания и угол между основой и боковой стороной:

S =	ab	=	ab
	sin α		sin β

5. Формула площади ранобедренной трапеции в которую можно вписать окружность:

S = (a + b) · r = √ab·c = √ab·m

6. Формула площади через через диагонали и угол между ними:

S =	d12	· sin γ	=	d12	· sin δ
	2			2

7. Формула площади через через среднюю линию, боковую сторону и угол при основании:

S = mc sin α = mc sin β

8. Формула площади через через основания и высоту:

S =	a + b	· h
	2

Окружность описанная вокруг трапеции

Окружность можно описать только вокруг равнобедренной трапеции!!!

Формула определения радиуса описанной вокруг трапеции окружности:

1. Формула радиуса через стороны и диагональ:

R =	a·c·d1
	4√p(p — a)(p — c)(p — d1)

где

p =	a + c + d1
	2

a — большее основание

Формулы по геометрии Квадрат. Формулы и свойства квадрата Прямоугольник. Формулы и свойства прямоугольника Параллелограмм. Формулы и свойства параллелограмма Ромб. Формулы и свойства ромба Трапеция. Формулы и свойства трапеции — Равнобедренная трапеция. Формулы и свойства равнобедренной трапеции — Прямоугольная трапеция. Формулы и свойства прямоугольной трапеции Формулы площади геометрических фигур Формулы периметра геометрических фигур Формулы объема геометрических фигур Формулы площади поверхности геометрических фигур

Все таблицы и формулы

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Равнобедренная трапеция – формула, свойства, определение, примеры

Равнобедренная трапеция – это трапеция с конгруэнтными углами при основании и конгруэнтными непараллельными сторонами. Трапеция – это четырехугольник, у которого параллельна только одна сторона. Равнобедренная трапеция обладает многими интересными свойствами, которые делают ее уникальной и помогают нам отличить ее от других четырехугольников. Давайте обсудим их подробно.

1.	Равнобедренная трапеция Определение
2.	Свойства равнобедренной трапеции
3.	Формула равнобедренной трапеции
4.	Часто задаваемые вопросы о равнобедренной трапеции

Определение равнобедренной трапеции

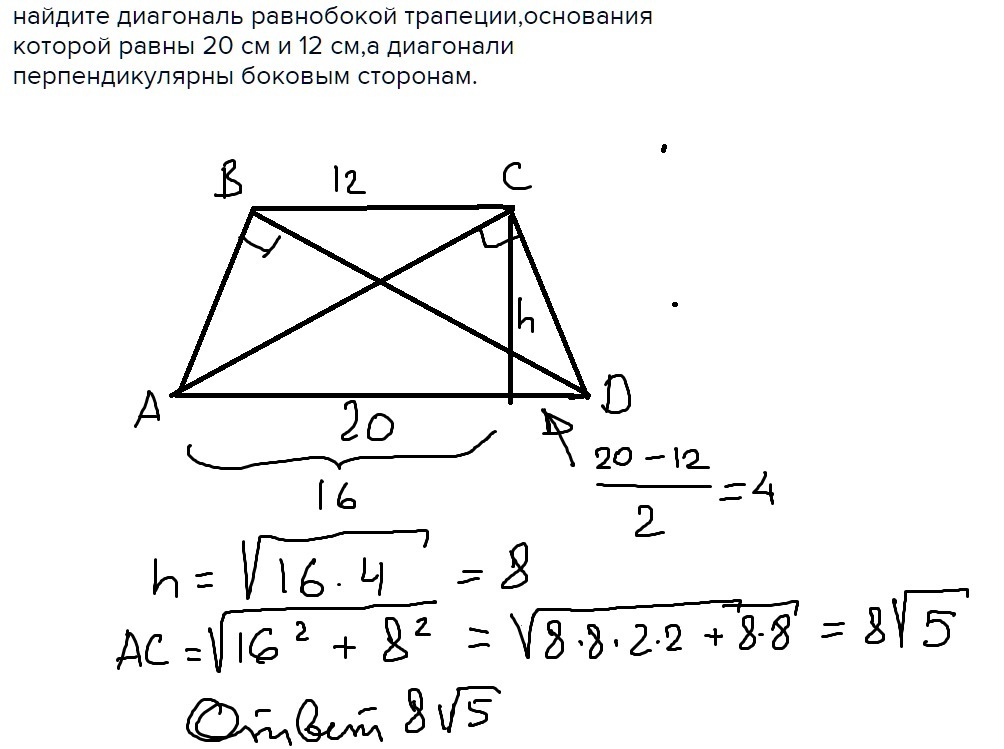
Равнобедренная трапеция может быть определена как трапеция, у которой непараллельные стороны и углы при основании имеют одинаковую величину. Другими словами, если две противоположные стороны (основания) трапеции параллельны, а две непараллельные стороны имеют одинаковую длину, то это равнобедренная трапеция.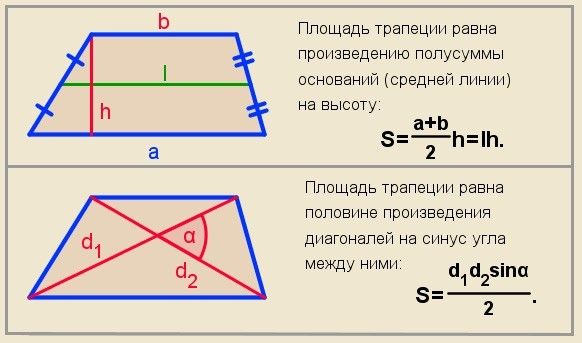 Посмотрите на изображение ниже: стороны c и d равны по длине, а противоположные стороны a и b (основания трапеции) параллельны друг другу.

Свойства равнобедренной трапеции

Ниже приведены свойства равнобедренной трапеции согласно рисунку, приведенному ниже.

• Имеет ось симметрии. Он не имеет вращательной симметрии и имеет одну линию симметрии, соединяющую середины параллельных сторон.
• Одна пара сторон параллельна и является базовой стороной. (AB II DC на данном изображении)
• Остальные стороны, кроме основания, непараллельны и равны по длине. (c = d на данном изображении)
• Диагонали имеют одинаковую длину. (АС = БД)
• Углы основания одинаковые. (∠D = ∠C, ∠A=∠B)
• Сумма противоположных углов равна 180° или дополнительным. (∠A + ∠C = 180° и ∠B + ∠D = 180°)
• Отрезок, соединяющий середины параллельных сторон, перпендикулярен основаниям. (PQ ⊥ DC)

Формула равнобедренной трапеции

Ниже приведены формулы для расчета площади и периметра равнобедренной трапеции.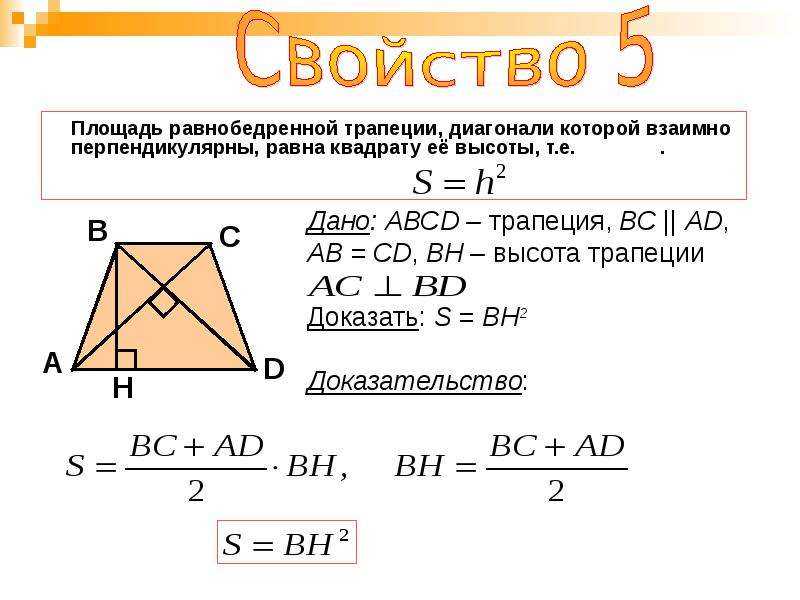

Площадь равнобедренной трапеции

Чтобы найти площадь равнобедренной трапеции, мы должны сложить стороны основания или параллельные стороны и разделить на 2, а затем умножить результат на высоту.
Площадь равнобедренной трапеции = (сумма параллельных сторон ÷ 2) × h

Периметр равнобедренной трапеции

Чтобы найти периметр равнобедренной трапеции, мы должны сложить все стороны равнобедренной трапеции.
Периметр равнобедренной трапеции = сумма всех сторон

Похожие статьи о равнобедренной трапеции

Ознакомьтесь с интересными темами, чтобы узнать больше о равнобедренной трапеции.

• Формула трапеции
• Площадь трапеции
• Периметр трапеции Формула
• Калькулятор равнобедренных трапеций

 

Примеры на равнобедренной трапеции

1. Пример 1: Найдите высоту равнобедренной трапеции, если ее площадь равна 128 дюймов ² и длины оснований 12 дюймов и 20 дюймов.
   Решение: Данная площадь = 128 дюймов ² , основания = 12 дюймов и 20 дюймов
   мы знаем, что площадь равнобедренной трапеции = (сумма параллельных сторон ÷ 2) × высота
   следовательно, 128 = [(12 + 20) ÷ 2] × высота
   Высота = 128/16 = 8 дюймов

2. Пример 2: Найдите площадь равнобедренной трапеции, если ее основания 3 дюйма и 5 дюймов, а высота 4 дюйма.
   Решение: Площадь равнобедренной трапеции = (сумма параллельных сторон ÷ 2) × высота
   дано, основания = 3 дюйма и 5 дюймов, высота = 4 дюйма
   Площадь = [(3 + 5) ÷ 2] × 4
   Площадь = 16 дюймов ²

3. Пример 3: Найдите периметр равнобедренной трапеции, если ее основания равны 20 и 25 дюймов, а непараллельные стороны по 30 дюймов каждая.
   Решение: Периметр равнобедренной трапеции = сумма всех сторон равнобедренной трапеции
   Периметр равнобедренной трапеции = 20 + 25 + 30 + 30 = 105 дюймов

перейти к слайду перейти к слайду перейти к слайду

Отличное обучение в старшей школе с использованием простых подсказок

Увлекаясь зубрежкой, вы, скорее всего, забудете понятия.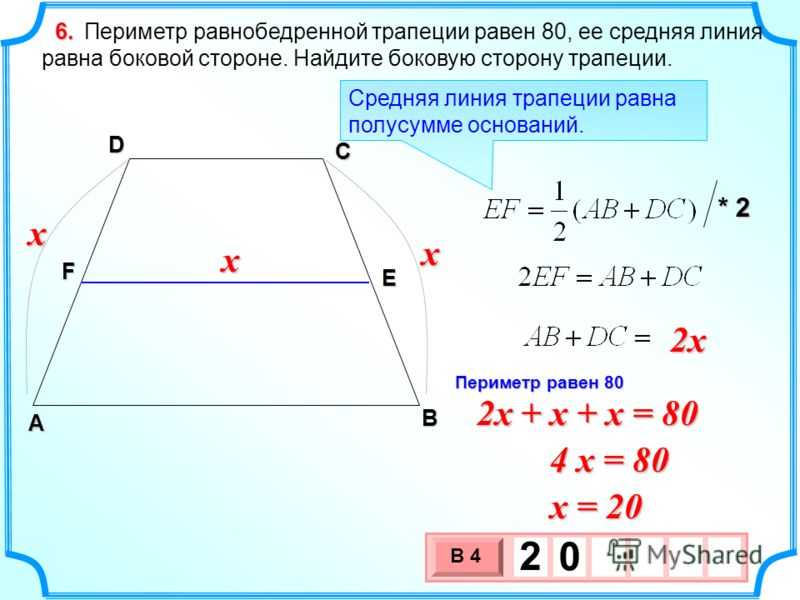 С Cuemath вы будете учиться визуально и будете удивлены результатами.

Записаться на бесплатный пробный урок

Практические вопросы по равнобедренной трапеции

 

перейти к слайдуперейти к слайду

Часто задаваемые вопросы о равнобедренной трапеции

Что такое равнобедренная трапеция?

Равнобедренная трапеция — это тип трапеции, у которой непараллельные стороны равны друг другу. Равнобедренная трапеция — это тип четырехугольника, в котором линия симметрии делит пополам одну пару противоположных сторон. Основания равнобедренной трапеции параллельны друг другу, а стороны равны по размеру.

Каковы свойства равнобедренной трапеции?

У равнобедренной трапеции четыре стороны. Две противоположные стороны (основания) параллельны друг другу, а две другие стороны равны по длине, но не параллельны друг другу.

Если один угол при основании равнобедренной трапеции равен 30°. Найдите другой угол при основании.

Согласно свойству равнобедренной трапеции углы при основании равны, поэтому если один угол при основании равен 30°, то и другой угол при основании будет равен 30°.

В чем разница между трапецией и равнобедренной трапецией?

В трапеции каждая сторона имеет разную длину и диагонали не равны, тогда как в равнобедренной трапеции непараллельные стороны равны, углы при основании равны, диагонали равны, а противоположные углы дополняют друг друга.

Какая формула площади равнобедренной трапеции?

Формула для расчета площади равнобедренной трапеции: Площадь = (сумма параллельных сторон ÷ 2) × высота.

Какая формула для периметра равнобедренной трапеции?

Формула для расчета периметра равнобедренной трапеции Периметр = сумма всех сторон равнобедренной трапеции

Скачать БЕСПЛАТНЫЕ учебные материалы

Рабочие листы по геометрии

Калькулятор площади равнобедренной трапеции

030D 90D Zzc Создано Анна 2 Отзыв от Davide Borchia

Последнее обновление: 02 февраля 2023 г.

Содержание:

• Какова площадь равнобедренной трапеции?
• Полезные трапециевидные ресурсы
• Часто задаваемые вопросы

Калькулятор площади равнобедренной трапеции поможет вам рассчитать именно эти трапеции. Напомним, мы говорим, что трапеция равнобедренная , если ее стороны имеют одинаковую длину . У вас не возникнет проблем с использованием калькулятора площади равнобедренной трапеции Omni, но мы знаем, что жизнь тяжела, и иногда вам приходится считать с ручкой и бумагой. Не беспокойтесь — мы научим вас находить площадь равнобедренной трапеции с помощью специальных формул.

Какова площадь равнобедренной трапеции?

Существует несколько специальных формул площади равнобедренной трапеции:

• основания a,b и высота h дано: A = (a + b) * h / 2

• основания a,b и катет c дано: вычислить h по теореме Пифагора ( h есть квадратный корень из c² - (ab)²/4 ) и A = (a-b)²/4 ) и +б)*ч/2

• основания a,b и угол α дано: вычислить h как tan(α) * (ab)² / 4 и затем A = (a + b) * h / 2

• основание a , катет c и угол α дано: вычислить h как c * sin(α) и b как a - 2) c * 9, тогда А = (а + b) * ч / 2

Выберите формулу площади равнобедренной трапеции, соответствующую имеющимся данным (обозначения см. на рисунке ниже). Или просто воспользуйтесь нашим калькулятором площади равнобедренной трапеции!

Полезные ресурсы по трапециям

Помимо калькулятора площади равнобедренных трапеций, в Omni есть обширная коллекция инструментов, связанных с трапециями. Обязательно взгляните на:

• Калькулятор трапеций
• Калькулятор площади трапеции
• Калькулятор периметра трапеции
• Калькулятор стороны трапеции
• Калькулятор угла трапеции
• Калькулятор высоты трапеции
• Средняя часть трапеции
• Калькулятор равнобедренных трапеций
• Калькулятор правой трапеции
• Калькулятор площади правой трапеции
• Калькулятор площади неправильной трапеции

Часто задаваемые вопросы

Как вычислить площадь равнобедренной трапеции по диагонали?

Вы можете вычислить площадь равнобедренной трапеции как:

A = 0,5 × d² × sin(φ)

где:

• A — площадь трапеции;
• d — длина диагонали; и
• φ угол между диагоналями.

  No related posts.