Равномерное распределение случайной величины – Равномерное распределение

Равномерное распределение

Перейдем теперь к часто используемым на практике распределениям непрерывной случайной величины.

Непрерывная с.в. Х называется равномерно распределенной на отрезке [a,b], если плотность ее вероятности постоянна на этом отрезке, а вне его равна 0 (т.е. случайная величина Х сосредоточена на отрезке [a,b], на котором имеет постоянную плотность). По данному определению плотность равномерно распределенной на отрезке [a,b] случайной величины Х имеет вид:

,

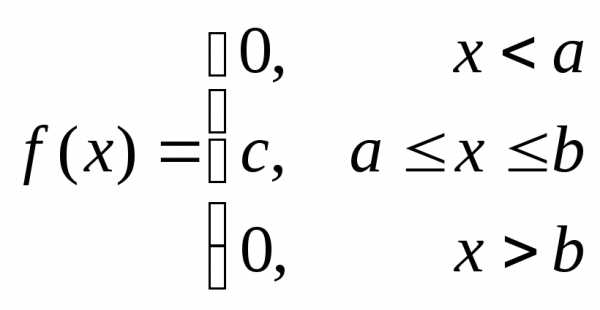где с есть некоторое число. Впрочем, его легко найти, используя свойство плотности вероятности для с.в., сосредоточенных на отрезке [

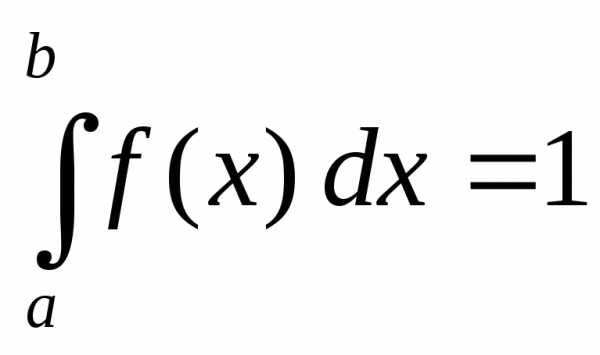a,b]: . Отсюда следует, что, откуда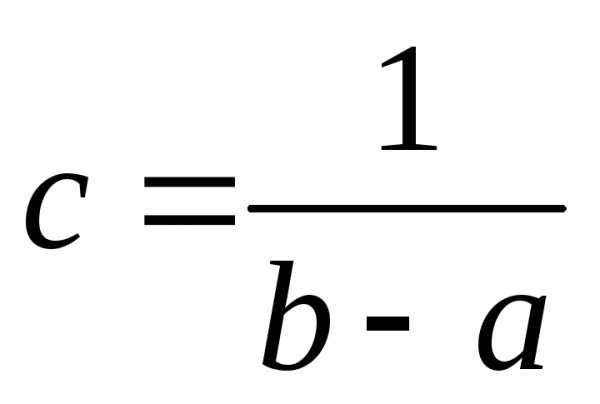. Поэтомуплотность равномерно распределенной на отрезке [a,b] случайной величины Х имеет вид: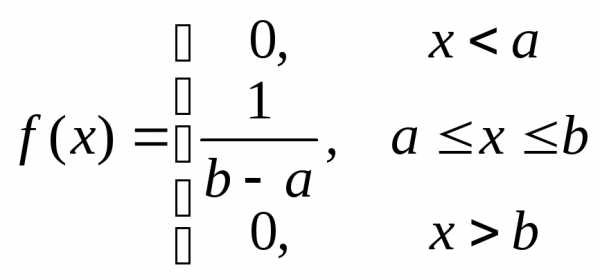

.

Судить о равномерности распределения н.с.в. Х можно из следующего соображения. Непрерывная случайная величина имеет равномерное распределение на отрезке [a,b], если она принимает значения только из этого отрезка, и любое число из этого отрезка не имеет преимущества перед другими числами этого отрезка в смысле возможности быть значением этой случайной величины.

К случайным величинам, имеющим равномерное распределение относятся такие величины, как время ожидания транспорта на остановке (при постоянном интервале движения длительность ожидания равномерно распределена на этом интервале), ошибка округления числа до целого (равномерно распределена на [−0.5

, 0.5]) и другие.

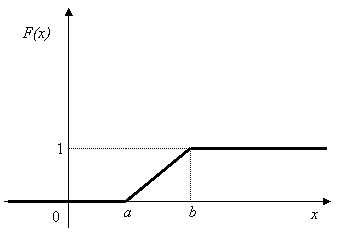
Вид функции распределения F(x) равномерно распределенной отрезке [a,b] случайной величины Х ищется по известной плотности вероятности f(x) c помощью формулы их связи 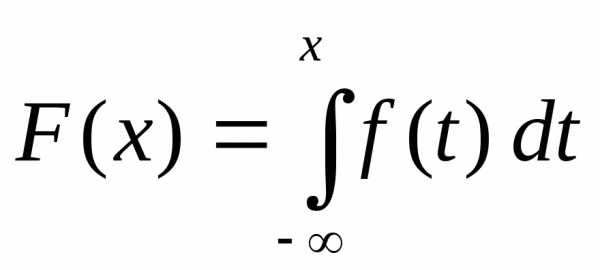. В результате соответствующих вычислений получаем следующую формулу для функции распределенияF(x) равномерно распределенной отрезке [a,b] случайной величины Х :

.

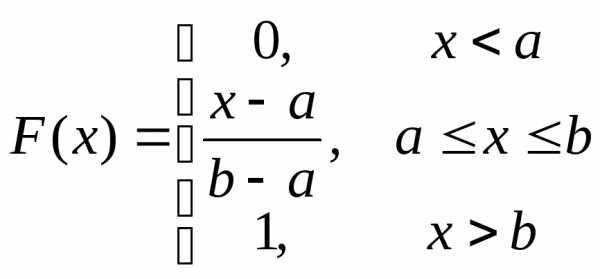На рисунках приведены графики плотности вероятности f

(x) и функции распределения f(x) равномерно распределенной отрезке [a,b] случайной величины Х :

Математическое ожидание, дисперсия, среднее квадратическое отклонение, мода и медиана равномерно распределенной отрезке [a,b] случайной величины Х вычисляются по плотности вероятности f(x) обычным образом (и достаточно просто из-за простого вида f(x)). В результате получаются следующие формулы:

,

а модой d(X) является любое число отрезка [a,b].

Найдем вероятность попадания равномерно распределенной отрезке [a,b] случайной величины Х в интервал 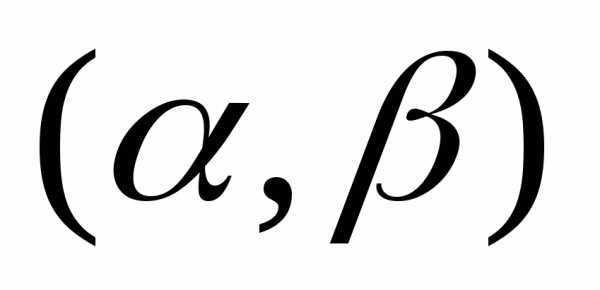, полностью лежащий внутри [

a,b]. Учитывая известный вид функции распределения, получаем:

.

Таким образом, вероятность попадания равномерно распределенной отрезке [a,b] случайной величины Х в интервал 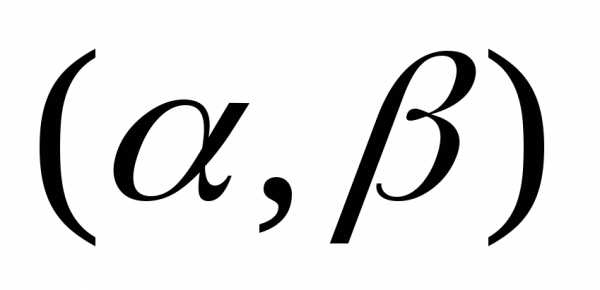, полностью лежащий внутри [a,b], не зависит от положения этого интервала, а зависит только от его длины и прямо пропорциональна этой длине.

Пример. Интервал движения автобуса составляет 10 минут. Какова вероятность того, что пассажир, подошедший к остановке, прождет автобус менее 3 минут? Каково среднее время ожидания автобуса?

Нормальное распределение

Это распределение наиболее часто встречается на практике и играет исключительную роль в теории вероятностей и математической статистике и их приложениях, поскольку такое распределение имеют очень многие случайные величины в естествознании, экономике, психологии, социологии, военных науках и так далее. Данное распределение является предельным законом, к которому приближаются (при определенных естественных условиях) многие другие законы распределения. С помощью нормального закона распределения описываются также явления, подверженные действию многих независимых случайных факторов любой природы и любого закона их распределения. Перейдем к определениям.

Непрерывная случайная величина называется распределенной по нормальному закону (или закону Гаусса), если ее плотность вероятности имеет вид:

,

где числа а и σ (σ>0) являются параметрами этого распределения.

Как уже было сказано, закон Гаусса распределения случайных величин имеет многочисленные приложения. По этому закону распределены ошибки измерений приборами, отклонение от центра мишени при стрельбе, размеры изготовленных деталей, вес и рост людей, годовое количество осадков, количество новорожденных и многое другое.

Приведенная формула плотности вероятности нормально распределенной случайной величины содержит, как было сказано, два параметра а и σ , а потому задает семейство функций, меняющихся в зависимости от значений этих параметров. Если применить обычные методы математического анализа исследования функций и построения графиков к плотности вероятности нормального распределения, то можно сделать следующие выводы.

1. Плотность вероятности f(x)>0 для всех значений х, а потому график функции расположен над осью х.

2. Ось х является асимптотой графика при х → ± ∞, поскольку . Поэтому на бесконечности график «прижимается» к осих.

3. Функция f(х) имеет единственную точку максимума

   х=а, а максимальное значение .

4. График функции симметричен относительно вертикальной прямой с уравнением х=а.

5. С помощью второй производной можно убедиться, что точки графика

являются точками его перегиба.

Исходя из полученной информации, строим график плотности вероятности f(x) нормального распределения (он называется кривой Гаусса − рисунок).

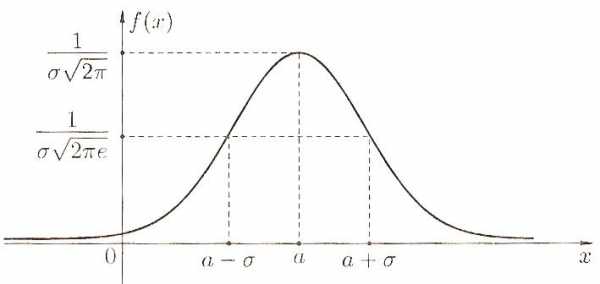
Выясним, как влияет изменение параметров а и σ на форму кривой Гаусса. Очевидно (это видно из формулы для плотности нормального распределения), что изменение параметра а не меняет форму кривой, а приводит лишь к ее сдвигу вправо или влево вдоль оси

х. Зависимость от σ сложнее. Из проведенного выше исследования видно, как зависит величина максимуму и координаты точек перегиба от параметра σ . К тому же надо учесть, что при любых параметрах а и σ площадь под кривой Гаусса остается равной 1 (это общее свойство плотности вероятности). Из сказанного следует, что с ростом параметра σ кривая становится более пологой и вытягивается вдоль оси х. На рисунке изображены кривые Гаусса при различных значениях параметра σ ( σ₁< σ< σ₂ ) и одном и том же значении параметра а.

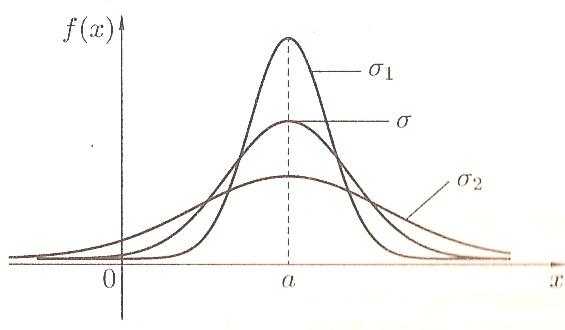
Выясним вероятностный смысл параметров а и σ нормального распределения. Уже из симметричности кривой Гаусса относительно вертикальной прямой, проходящей через число а

на оси х понятно, что среднее значение (т.е. математическое ожидание М(Х)) нормально распределенной случайной величины равно а. Из этих же соображений мода и медиана тоже должны быть равны числу а. Точные расчеты по соответствующим формулам это подтверждают. Если же мы выписанное выше выражение для f(x) подставим в формулу для дисперсии , то после (достаточно непростого) вычисления интеграла получим в ответе числоσ². Таким образом, для случайной величины Х, распределенной по нормальному закону, получились следующие основные ее числовые характеристики:

.

Поэтому вероятностный смысл параметров нормального распределения а и σ следующий. Если с.в. Х распределена нормально с параметрами а и σ, то ее среднее значение равно а, а среднее квадратическое отклонение равно σ.

Найдем теперь функцию распределения

F(x) для случайной величины Х, распределенной по нормальному закону, используя выписанное выше выражение для плотности вероятности f(x) и формулу 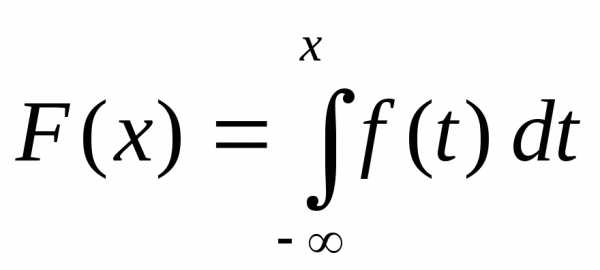. При подстановкеf(x) получается «неберущийся» интеграл. Все, что удается сделать для упрощения выражения для F(x), это представление этой функции в виде:

,

где Ф(х) − так называемая функция Лапласа, которая имеет вид

.

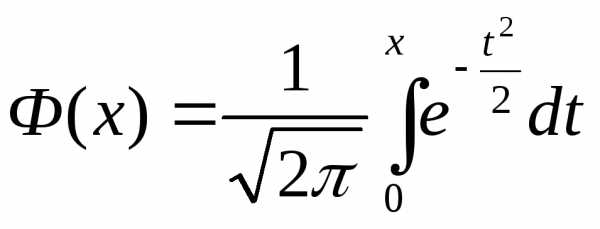Интеграл, через который выражается функция Лапласа, тоже является неберущимися (но при каждом х этот интеграл может быть вычислен приближенно с любой наперед заданной точностью). Однако вычислять его и не потребуется, так как в конце любого учебника по теории вероятностей есть таблица для определения значений функции

Ф(х) при заданном значении х. В дальнейшем нам понадобится свойство нечетности функции Лапласа: Ф(−х)= −Ф(х) для всех чисел х.

Найдем теперь вероятность того, что нормально распределенная с.в. Х примет значение из заданного числового интервала (α, β). Из общих свойств функции распределения Р(α<X< β)=F(β) − F(α). Подставляя α и β в выписанное выше выражение для F(x), получим

.

Как сказано выше, если с.в. Х распределена нормально с параметрами а и σ, то ее среднее значение равно а, а среднее квадратическое отклонение равно σ. Поэтому среднее отклонение значений этой с.в. при испытании от числа а равно σ. Но это среднее отклонение. Поэтому возможны и бо´льшие отклонения. Узнаем, насколько возможны те или иные отклонения от среднего значения. Найдем вероятность того, что значение распределенной по нормальному закону случайной величины Х отклониться от ее среднего значения М(Х)=а менее, чем на некоторое число δ, т.е. Р(|X−a|<δ ) : . Таким образом,

.

Подставляя в это равенство δ=3σ, получим вероятность того, что значение с.в. Х (при одном испытании) отклонится от среднего значения менее чем на утроенное значение σ (при среднем отклонении, как мы помним, равном σ): (значениеФ(3) взято из таблицы значений функции Лапласа). Это почти 1 ! Тогда вероятность противоположного события (что значение отклонится не менее, чем на 3σ) равна 1−0.997=0.003, что очень близко к 0. Поэтому это событие «почти невозможно» − случается крайне редко (в среднем 3 раза из 1000). Это рассуждение является обоснованием широко известного «правила трех сигм».

Правило трех сигм. Нормально распределенная случайная величина при единичном испытании практически не отклоняется от своего среднего далее, чем на 3σ.

Еще раз подчеркнем, что речь идет об одном испытании . Если испытаний случайной величины много, то вполне возможно, что какое-либо ее значение и удалится от среднего далее, чем 3σ. Это подтверждает следующий

Пример. Какова вероятность, что при 100 испытаниях нормально распределенной случайной величины Х хотя бы одно ее значение отклонится от среднего более, чем на утроенное среднее квадратическое отклонение? А при 1000 испытаниях?

Решение. Пусть событие А означает, что при испытании случайной величины Х ее значение отклонилось от среднего более, чем на 3σ. Как только что было выяснено, вероятность этого события р=Р(А)=0.003 . Проведено 100 таких испытаний. Надо узнать вероятность того, что событие А произошло хотя бы раз, т.е. произошло от 1 до 100 раз. Это типичная задача схемы Бернулли с параметрами n=100 (число независимых испытаний), р=0.003 (вероятность события А в одном испытании), q=1−p=0.997. Требуется найти Р₁₀₀(1≤k≤100). В данном случае, конечно, проще найти сначала вероятность противоположного события Р₁₀₀(0) − вероятность того, что событие А не произошло ни разу ( т.е. произошло 0 раз) . Учитывая связь вероятностей самого события и ему противоположного, получим:

.

Не так уж мало. Вполне может произойти (происходит в среднем в каждой четвертой такой серии испытаний). При 1000 испытаний по такой же схеме можно получить, что вероятность хотя бы одного отклонения далее, чем на 3σ, равно: . Так что можно с большой уверенностью дождаться хотя бы одного такого отклонения.

Пример. Рост мужчин определенной возрастной группы распределен нормально с математическим ожиданием a, и среднеквадратическим отклонением σ. Какую долю костюмов k-го роста следует предусмотреть в общем объеме производства для данной возрастной группы, если k-ый рост определяется следующими пределами:

1 рост: 158 − 164см 2 рост: 164 − 170см 3 рост: 170 − 176см 4 рост: 176 − 182см

Решение. Решим задачу при следующих значениях параметров: а=178, σ=6, k=3. Пусть с.в. Х − рост случайно выбранного мужчины (она распределена по условию нормально с заданными параметрами). Найдем вероятность того, что наугад выбранному мужчине понадобится 3-й рост. Пользуясь нечетностью функции Лапласа Ф(х) и таблицей ее значений: P(170<X<176) =Ф((176−178)/6) − Ф((170−178)/6) = Ф(−0.3333) −Ф(−1.3333)= Ф(1.3333) −Ф(0.3333)=0.4082−0.1293=0.2789. Поэтому в общем объеме производства надо предусмотреть 0.2789*100%=27.89% костюмов 3-го роста.

studfiles.net

Равномерное распределение непрерывной случайной величины

Равномерным распределением непрерывной случайной величины называется распределение, в котором значения случайной величины с двух сторон ограничены и в границах интервала имеют одинаковую вероятность. Это означает, что в в данном интервале плотность вероятности постоянна.

Таким образом, при равномерном распределении плотность вероятности имеет вид

Значения f(x) в крайних точках a и b участка (a, b) не указываются, так как вероятность попадания в любую из этих точек для непрерывной случайной величины равна нулю.

Кривая равномерного распределения имеет вид прямоугольника, опирающегося на участок (a, b) (рисунок ниже), в связи с чем равномерное распределение иногда называют «прямоугольным».

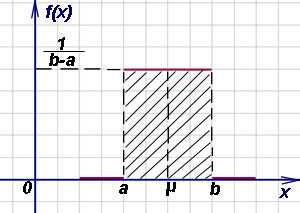
Как найти вероятность попадания случайной величины X, равномерно распределённой на участке (a, b) на любую часть (α, β) участка (a, b) ?

Эта вероятность находится по формуле

и геометрически представляет собой площадь, дважды заштрихованную на рисунке ниже и опирающуюся на часть (α, β) участка (a, b):

Функция распределения F(x) непрерывной случайной величины при равномерном распределении имеет вид

Характеристики равномерного распределения:

• среднее значение (математическое ожидание) ;
• дисперсия ;
• стандартное отклонение ;
• равномерное распределение не имеет моды.

Пример 1. Наблюдения показали, что вес ящика, предназначенного для транспортировки овощей, является равномерно распределённой случайной величиной в интервале от 985 г. до 1025 г. Случайно выбран один ящик. Найти характеристики равномерно распределённой случаной величины при условиях, которые будут указаны в решении.

Решение. Найдём вероятность того, что вес данного ящика будет в интервале от 995 г. до 1005 г. :

.

Найдём среднее значение непрерывной случайной величины:

.

Найдём стандартное отклонение:

.

Определим, у скольки процентов ящиков вес находится на удалении одного стандартного отклонения от среднего значения (т. е. в интервале ):

.

Пример 2. Поезда метрополитена идут регулярно с интервалом 2 (мин.). Пассажир выходит на платформу в случайный момент времени, никак не связанный с расписанием поездов. Случайная величина T — время, в течение которого ему придётся ждать поезда, имеет равномерное распределение. Найти плотность распределения f(x) случайной величины T, её математическое ожидание, дисперсию и стандартное отклонение. Найти вероятность того, что ждать придётся не больше полминуты.

Решение. Найдём плотность распределения f(x):

f(x) = 1/2 (0 < x < 2).

Найдём математическое ожидание случайной величины:

μ = (2 + 0)/2 = 1.

Найдём дисперсию:

σ² = 2²/12 = 1/3.

Стандартное отклонение:

σ = (√3)/3.

Найдём вероятность того, что пассажиру придётся ждать поезда не больше полминуты:

P{T < 1/2} = 1/4.

Пример 3. Случайная величина X распределена равномерно на участке (a, b). Найти вероятность того, что в результате опыта она отклонится от своего математического ожидания больше, чем на 3σ.

Решение. Найдём стандартное отклонение:

σ = (b — a)/(2√3);

3σ = 3(b — a)/(2√3) = √3(b — a)/2;

При равномерном распределении на участке (a, b) крайние точки a и b, ограничивающие участок возможных значений случайной величины, отстоят от её математического ожидания μ = (a + b)/2 на расстояние (b — a)/2, которое меньше, чем √3(b — a)/2. Следовательно, вероятность события, обозначенного в условии задачи, равна нулю.

Начало темы «Теория вероятностей»

function-x.ru

Пример (Гипотеза случайности).

МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ИНСТИТУТ ЭЛЕКТРОНИКИ И МАТЕМАТИКИ

Кафедра теории вероятностей и математической статистики

РЕФЕРАТ

по математической статистике

на тему:

«Равномерное распределение»

Выполнил: студенты группы М-65

Ражева А.А.

Кнутова А.С.

Проверил: Заведующий Кафедрой

Ивченко Г. И.

Москва 2012 г.

Непрерывное равномерное распределение — в теории вероятностей распределение, характеризующееся тем, что вероятность любого интервала зависит только от его длины.

Равномерное распределение полезно при описании переменных, у которых каждое значение равновероятно, иными словами, значения переменной равномерно распределены в некоторой области.

Определение

Говорят, что случайная величина имеет непрерывное равномерное распределение на отрезке [a,b], где 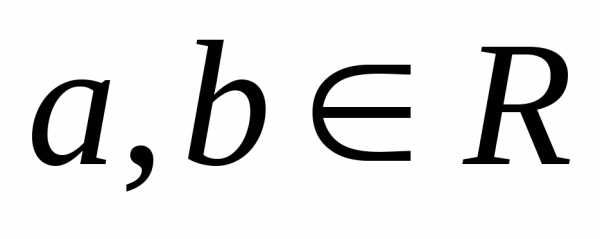, если её плотность имеет вид:

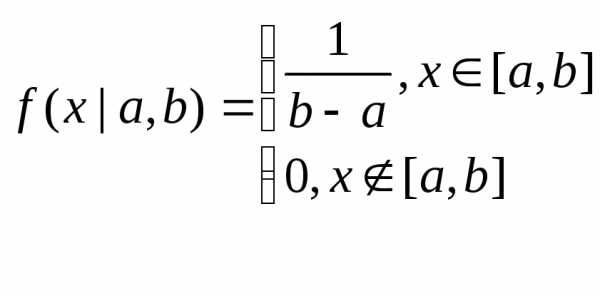
Пишут: X ~ U (a,b) или

Иногда значения плотности в граничных точках x = a и x = b меняют на другие, например 0 или 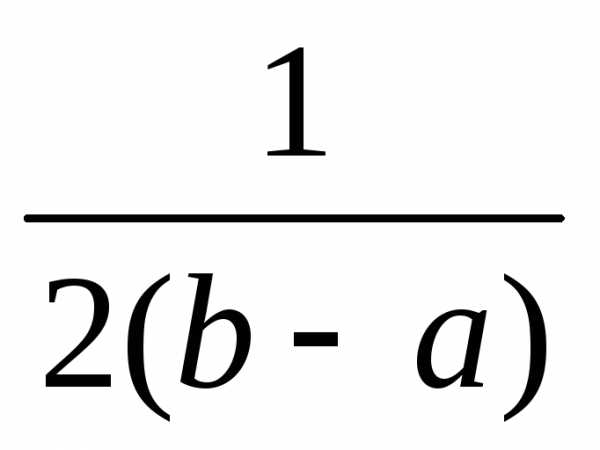. Так как интеграл Лебега от плотности не зависит от поведения последней на множествах меры нуль, эти вариации не влияют на вычисления связанных с этим распределением вероятностей.

Если L(ξ) = U(a,b), то

Равномерное распределение U (a,b) описывает процесс «выбора точки наудачу» в интервале [a,b]. Так, если [a,b] – интервал между последовательными отправлениями автобуса от остановки, то время ожидания пассажира, не знающего расписания и пришедшего на остановку, есть случайная величина с распределением U (0,1). Распределение U (0,1) играет особую роль в методах моделирования с помощью компьютеров случайных величин с заранее заданными распределениями. Такие методы широко используют для приближенных вычислений интегралов, решений дифференциальных и интегральных уравнений и т.д.

В некоторых случаях априори предполагается (постулируется), что исходные данные представляют собой случайную выборку из некоторого распределения, т.е. компоненты вектора данных X=(независимы и одинаково распределены. Как правило, это предположение бывает оправдано, так как вытекает из самого характера задачи, и не подвергается сомнению. Но иногда это исходное предположение само нуждается в проверке, т.е. оно рассматривается как статистическая гипотеза 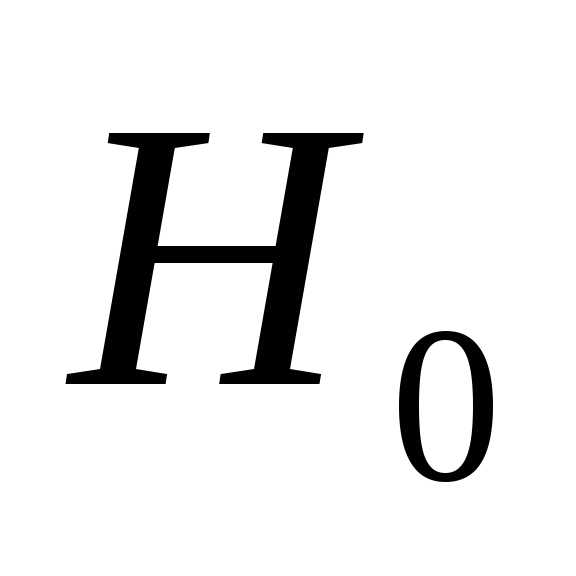, называемая гипотезой случайности. Формализуется такая гипотеза следующим образом. Пусть обозначает функцию распределения выборки , тогда подлежащая проверки гипотеза означает утверждени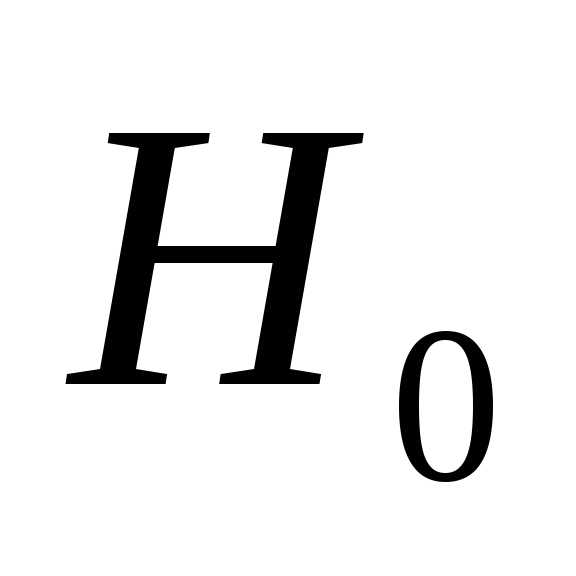е : , где 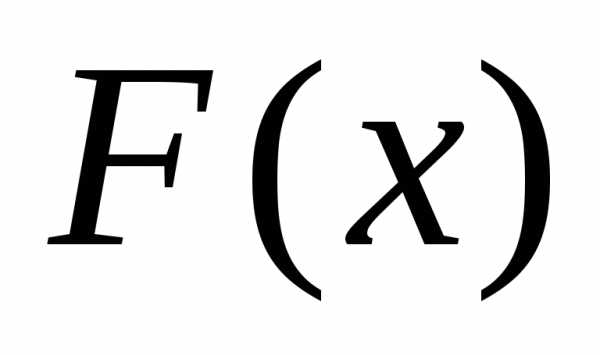— некоторая одномерная функция распределения (она может быть полностью задана, либо задано семейство, которому она принадлежит, либо никак не специфицируется). Типичным примером ситуации, когда возникает необходимость проверки гипотезы случайности, является работа генератора (датчика) случайных чисел. Под случайными числами понимается последовательность независимых и равномерно распределённых на отрезке [0,1] случайных величин. Такие числа широко используются в различных областях: в статистике – для моделирования случайных выборок из различных распределений, в криптографии – при получении ключей для шифрования информации, в численном анализе и т.д. В практических задачах последовательность строят либо с использованием готовых таблиц случайных чисел, либо генерируют с помощью специальных датчиков, встроенных непосредственно в ЭВМ, либо получают программным способом по некоторому вспомогательному алгоритму (в последнем случае получаются так называемые псевдослучайные числа т.е. «очень похожие» на случайные). Во всех случаях (особенно в последнем) требуется осуществлять контроль за «качеством» вырабатываемой последовательности (т.е. чтобы эти числа были практически неотличимы от независимых одинаково распределенных чисел), что в математическом плане сводится к проверке гипотезы случайности.

Функция распределения

Интегрируя определённую выше плотность, получаем:

Так как плотность равномерного распределения разрывна в граничных точках отрезка [a,b], то функция распределения в этих точках не является дифференцируемой. В остальных точках справедливо стандартное равенство:

Характеристическая функция случайной величины X ~ U(a,b):

Математическое ожидание и дисперсия по определению равны:

Вообще,

Стандартное равномерное распределение

Если a = 0, а b = 1, то есть X ~ U[0,1], то такое непрерывное равномерное распределение называют стандартным. Имеет место элементарное утверждение:

Если случайная величина X ~ U[0,1], и Y = a + (b − a)X, где a < b, тo Y ~ U[0,1].

Таким образом, имея генератор случайной выборки из стандартного непрерывного равномерного распределения, легко построить генератор выборки любого непрерывного равномерного распределения.

Более того, имея такой генератор и зная функцию обратную к функции распределения случайной величины, можно построить генератор выборки любого непрерывного распределения (не обязательно равномерного) с помощью метода обратного преобразования. Поэтому, стандартно равномерно распределённые случайные величины иногда называют базовыми случайными величинами.

Линейное преобразование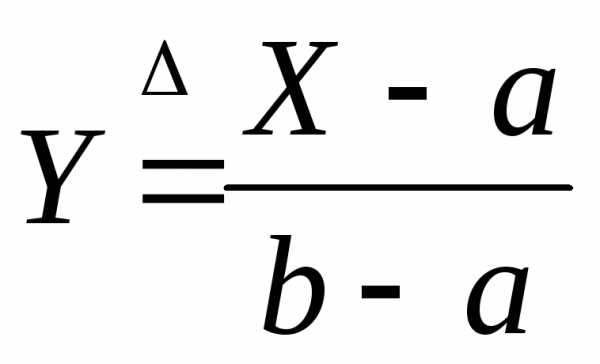

переводит СВ X ~ R(a,b) в СВ Y ~ R(0,1). Действительно,

Равномерное распределение является непрерывным аналогом дискретного распределения вероятностей для опытов с равновероятными исходами.

studfiles.net

Равномерное распределение.

Непрерывная случайная величина считается равномерно распределенной на отрезке (a,b), если ее плотность вероятности имеет вид:

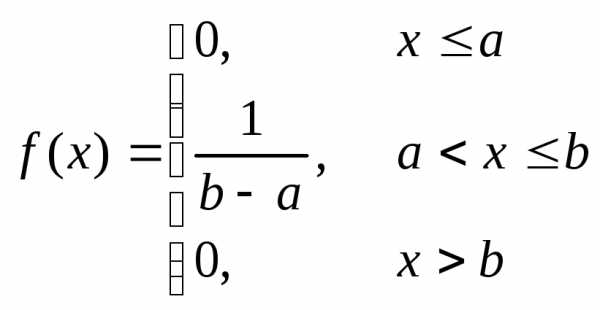
График плотности вероятности для равномерного распределения

Математическое ожидание и дисперсия непрерывной случайной величины, имеющей равномерное распределение, равны соответственно:

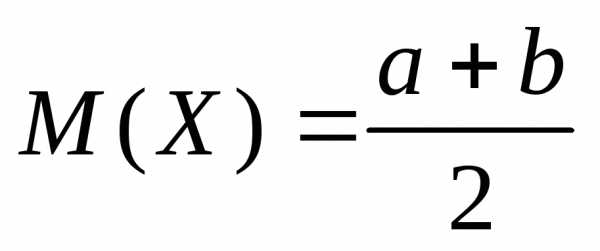
Пример. Интервал движения автобуса равен 15 мин. Какова вероятность того, что пассажир на остановке будет ждать автобус не более 5 минут?

Решение. Пусть случайная величина 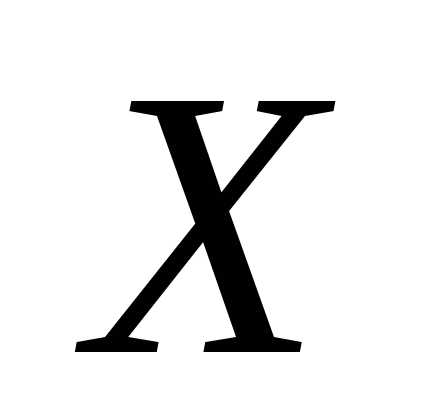— время ожидания автобуса. Она имеет равномерное распределение на отрезке [0,15]. Имеем

В рассматриваемом случае

Показательное распределение.

Показательным (экспоненциальным) распределением непрерывной случайной величины 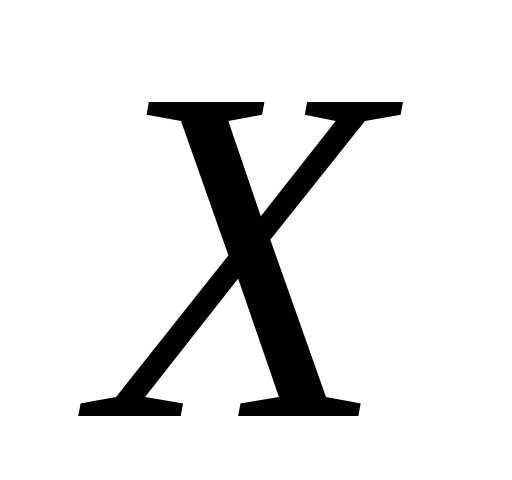называется распределение, имеющее плотность вероятности вида:

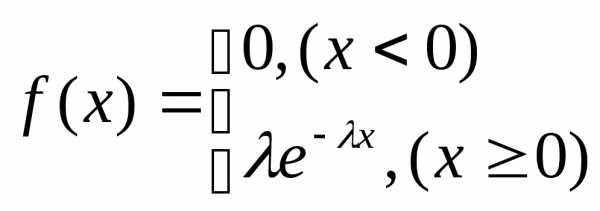
где – постоянная положительная величина. Плотность вероятностей для показательного распределения дляприведена ниже

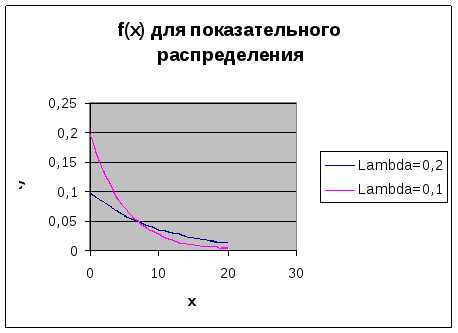
Функция распределения вероятности для показательного распределения имеет вид:

Функция распределения для приведена ниже

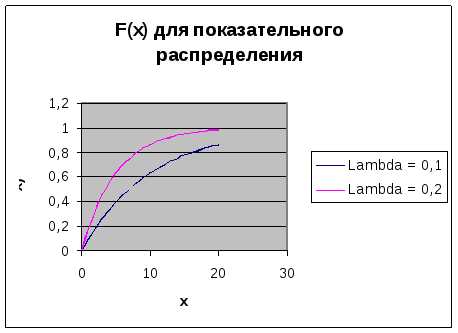
Можно показать, что математическое ожидание и дисперсия случайной величины, имеющей экспоненциальное распределение, равны:

Пример. Установлено, что время горения электрической лампочки (Т) является случайной величиной, распределенной по показательному закону. Считая, что среднее значение этой величины равно 6 месяцам, найти вероятность того, что лампочка будет исправна более года.

Решение. Так как и функция распределения случайной величиныT имеет вид

Поэтому

Лекция 9. Нормальное распределение. Вероятностный смысл входящих в него параметров. Функция Лапласа и ее свойства. Отклонение нормальной случайной величины от ее математического ожидания. Правило “трех сигм”

Непрерывная случайная величина 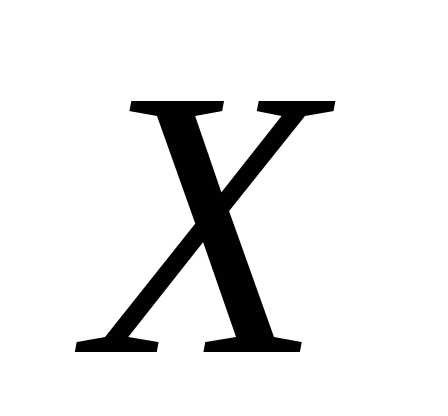имеет нормальный закон распределения с параметрамии, если ее плотность вероятности имеет вид функции Гаусса

где 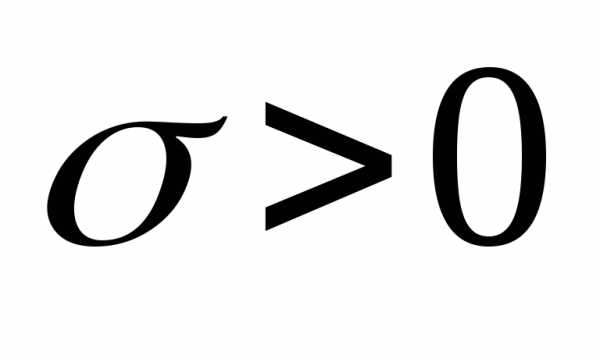. С помощью непосредственного вычисления математического ожидания и дисперсии нормального распределения легко выяснить вероятностный смысл его параметров:– есть математическое ожидание, а— среднее квадратическое отклонение нормального распределения. Прираспределение называетсястандартным нормальным распределением.

Графики 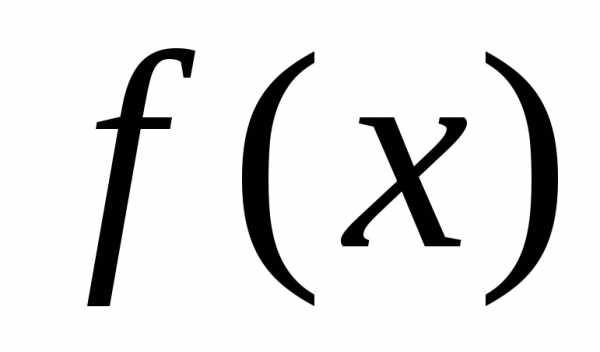для ряда конкретных значений математического ожидания и среднего квадратического отклонения приведены ниже.

Рис. 1. Изменение вида функции 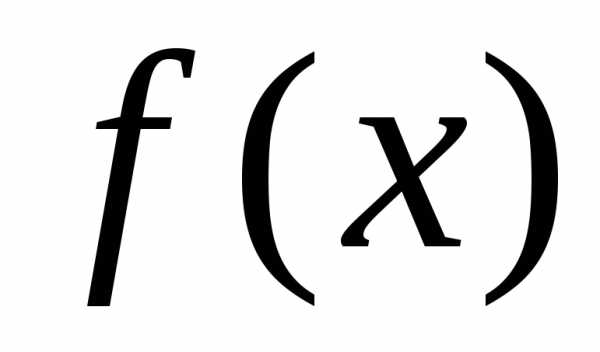при изменении математического ожидания

Рис. 2. Изменение 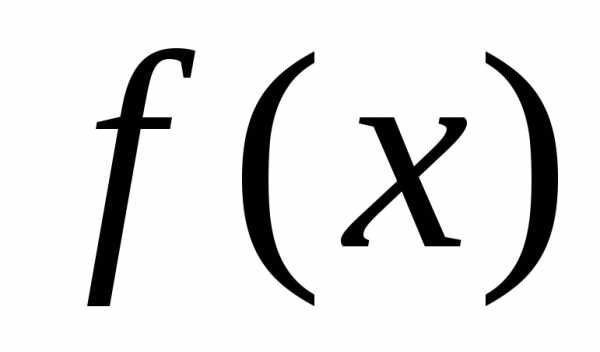при изменении среднего квадратического отклонения

Функция распределенияв случае нормального распределения, очевидно, равна

.

Графики функции 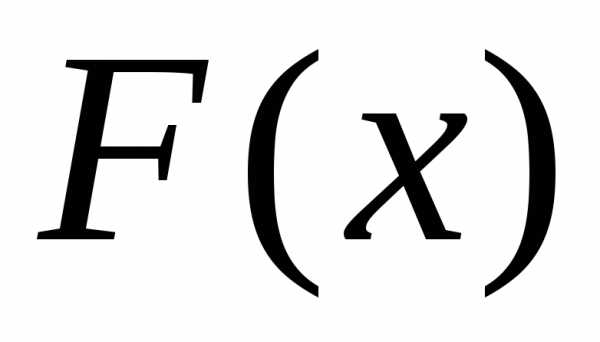для ряда значений математического ожидания и среднего квадратического отклонения изображены на приводимых ниже рисунках

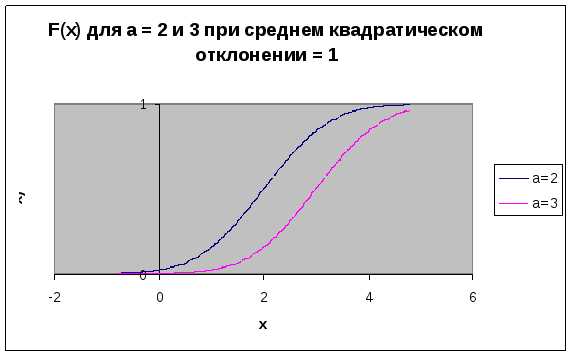
Рис. 3. Зависимость функции распределения от величины

Рис. 4. Зависимость функции распределения от величины

Нормальное распределение имеет исключительно важное значение для практических применений, так как многие непрерывные случайные величины описываются именно этим распределением. Оказывается, что суммирование большого числа случайных величин с различными законами распределения приводит к нормальному распределению результирующей суммы. Это свойство подтверждается центральной предельной теоремой (теорема Ляпунова). Смысл этой теоремы состоит в следующем. Если случайная величина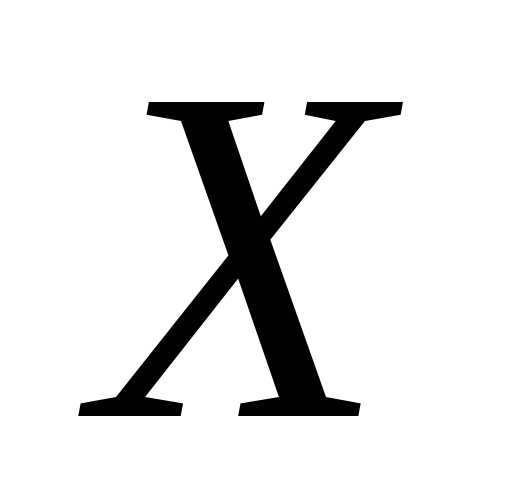представляет собой сумму очень большого числа взаимно независимых случайных величин, влияние каждой из которых на всю сумму ничтожно мало, то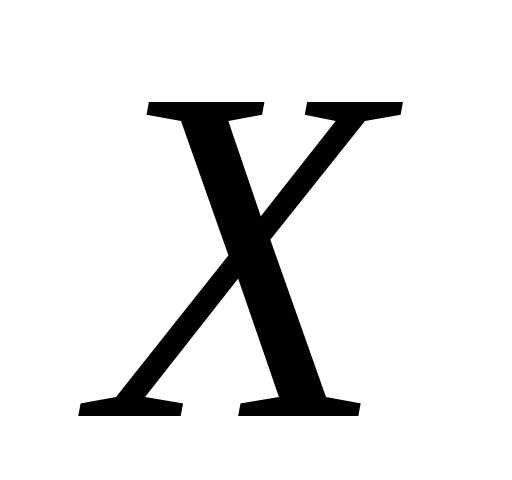имеет распределение, близкое к нормальному.

Следует иметь в виду, что при усилении влияния отдельных факторов могут появляться отклонения от нормального распределения результирующего параметра. Поэтому большое значение на практике уделяется экспериментальной проверке выдвинутых гипотез, в том числе и гипотезы о нормальном распределении.

studfiles.net

19.Равномерный закон распределения

19. Равномерный закон распределения и его числовые характеристики.

На практике встречаются случайные величины, о которых заранее известно, что они могут принять какое-либо значение в строго определенных границах, причем в этих границах все значения случайной величины имеют одинаковую вероятность (обладают одной и той же плотностью вероятностей).

Например, при поломке часов остановившаяся минутная стрелка будет с одинаковой вероятностью (плотностью вероятности) показывать время, прошедшее от начала данного часа до поломки часов. Это время является случайной величиной, принимающей с одинаковой плотностью вероятности значения, которые не выходят за границы, определенные продолжительностью одного часа. К подобным случайным величинам относится также и погрешность округления. Про такие величины говорят, что они распределены равномерно, т. е. имеют равномерное распределение.

Определение. Непрерывная случайная величина Х имеет равномерное распределение на отрезке [а, в], если на этом отрезке плотность распределения вероятности случайной величины постоянна, т. е. если дифференциальная функция распределения f(х) имеет следующий вид:

Иногда это распределение называют законом равномерной плотности. Про величину, которая имеет равномерное распределение на некотором отрезке, будем говорить, что она распределена равномерно на этом отрезке.

Найдем значение постоянной с. Так как площадь, ограниченная кривой распределения и осью Ох, равна 1(исходя из св-в плотности вероятности ), то

откуда с=1/(b-a).

Таким образом, непрерывная случайная величина X имеет равномерный закон распределения, на отрезке [a, b], если её плотность вероятности

Построим функцию распределения F(x), для чего найдем выражение F(x) на интервале [a, b]:

Теорема. Функция распределения случайной величины X, распределённой по равномерному закону, есть

её математическое ожидание

а её дисперсия

Графики функций f(x) и F(x) имеют вид:

Равномерный закон распределения используется при анализе ошибок округления при проведении числовых расчётов (например, ошибка округления числа до целого распределена равномерно на отрезке [-0,5; 0,5]), в ряде задач массового обслуживания, при статистическом моделировании наблюдений, подчинённых заданному распределению. Так, случайная величина X, распределённая равномерно на отрезке [0; 1], называемая «случайным числом от 0 до 1», служит исходным материалом для получения случайных величин с любым законом распределения.

Найдем числовые характеристики.

Используя формулу для вычисления математического ожидания НСВ, имеем:

Таким образом, математическое ожидание случайной величины, равномерно распределенной на отрезке [a, b] совпадает с серединой этого отрезка.

Найдем дисперсию равномерно распределенной случайной величины:

откуда сразу же следует, что среднее квадратическое отклонение:

Найдем теперь вероятность попадания значения случайной величины, имеющей равномерное распределение, на интервал (a,b), принадлежащий целиком отрезку [a, b]:

Геометрически эта вероятность представляет собой площадь заштрихованного прямоугольника. Числа а и b называются параметрами распределения и однозначно определяют равномерное распределение.

Пример1. Автобусы некоторого маршрута идут строго по расписанию. Интервал движения 5 минут. Найти вероятность того, что пассажир, подошедший к остановке. Будет ожидать очередной автобус менее 3 минут.

Решение:

СВ- время ожидания автобуса имеет равномерное распределение. Тогда искомая вероятность будет равна:

Пример2. Ребро куба х измерено приближенно. Причем

Рассматривая ребро куба как случайную величину, распределенную равномерно в интервале (a, b), найти математическое ожидание и дисперсию объема куба.

Решение:

Объем куба- случайная величина, определяемая выражением У= Х3. Тогда математическое ожидание равно:

Дисперсия:

studfiles.net

Равномерный закон распределения вероятностей. Пример решения задачи на Викиматик

Пожалуй, равномерное распределение является самым простым из всех законов распределений непрерывных случайных величин. Непрерывная случайная величина $X$ является равномерно распределенной на отрезке $\left[a;b\right]$, если ее плотность распределения вероятностей имеет следующий вид:

$$f\left(x\right)=\left\{\begin{matrix}
0,\ x\le a\\ 
{{1}\over {b-a}},\ a < x\le b\\ 
0,\ x>b
\end{matrix}\right.$$

Тогда соответствующая функция распределения имеет вид:

$$F\left(x\right)=\left\{\begin{matrix}
0,\ x\le a\\ 
{{x-a}\over {b-a}},\ a < x\le b\\ 
1,\ x>b
\end{matrix}\right.$$ 

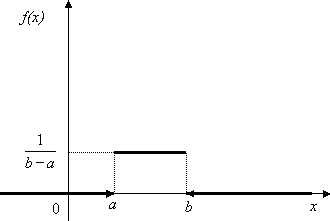
Графики функций плотности $f\left(x\right)$ и распределения $F\left(x\right)$ представлены на рисунке.

Для равномерного закона распределения числовые характеристики могут быть вычислены по известным формулам. Математическое ожидание:

$$M\left(X\right)={{a+b}\over {2}}.$$ 

Дисперсия:

$$D\left(X\right)={{{\left(b-a\right)}^2}\over {12}}.$$ 

Равномерно распределенная случайная величина $X$ принимает все свои значения лишь в конечном промежутке $\left[a;b\right]$, причем все эти значения случайной величины $X$ равновероятны. Примерами случайных величин, распределенных по равномерному закону, могут быть:

• Время ожидания автобуса, при условии, что пассажир приходит на остановку в случайный момент времени и автобусы ходят с постоянным интервалом.
• Ошибки при взвешивании.
• Ошибка округления числа до целочисленного значения. Очевидно, что такая случайная величина распределена равномерно на отрезке $\left[-0,5;0,5\right]$.

Пример 1. Плотность распределения вероятностей случайной величины $X$ имеет вид $f\left(x\right)=\left\{\begin{matrix}
0,\ x\le 2\\ 
{{1}\over {5}},\ 2 < x\le 7\\ 
0,\ x>7
\end{matrix}\right.$.

Тогда математическое ожидание $M(X)=(a+b)/2=(2+7)/2=4,5$, дисперсия $D(X)={\left(b-a\right)}^2/12={\left(7-2\right)}^2/12=25/12\approx 2,083.$

Пример 2. Вычислить вероятность того, что при семи испытаниях менее трех раз случайная величина $X$ попадет в интервал $\left[0;1,5\right]$, если распределено по равномерному закону на отрезке $\left[0;6\right]$.

Запишем функцию распределения равномерно распределенной случайной величины $X\sim R\left[0;6\right]$.

$$F\left(x\right)=\left\{\begin{matrix}
0,\ при\ x < 0\\ 
{{x}\over {6}},\ при\ 0\le x\le 6\\ 
1,\ при\ x>6
\end{matrix}\right.$$ 

Математическое ожидание равномерно распределенной случайной величины $X$ вычисляется по формуле:

$$M\left(X\right)={{a+b}\over {2}}={{0+6}\over {2}}=3.$$ 

Тогда вероятность того, что $X\in \left[0;1,5\right]$ равна разности значений функции распределения $F\left(x\right)$ на концах этого интервала: $P(0\le X\le 1,5)=F(1,5)-F(0)=1,5/6-0=0,25.$

Вероятность того, что при $n=7$ независимых испытаниях $X$ попадет в интервал $\left[0;1,5\right]$ менее трех раз, вычисляем по формуле: $P_7\left(k < 3\right)=P_7\left(0\right)+P_7\left(1\right)+P_7\left(2\right)=C^0_7\cdot {0,25}^0\cdot {0,75}^7+C^1_7\cdot 0,25\cdot {0,75}^6+C^2_7\cdot {0,25}^2\cdot {0,75}^5=0,133+0,311+0,311=0,755$.

Данная статья полезна?

Да Нет

wikimatik.ru

22. Закон равномерного распределения.

Равномерный закон распределения.

На практике встречаются случайные величины, о которых заранее известно, что они могут принять какое-либо значение в строго определенных границах, причем в этих границах все значения случайной величины имеют одинаковую вероятность (обладают одной и той же плотностью вероятностей).

Например, при поломке часов остановившаяся минутная стрелка будет с одинаковой вероятностью (плотностью вероятности) показывать время, прошедшее от начала данного часа до поломки часов. Это время является случайной величиной, принимающей с одинаковой плотностью вероят ности значения, которые не выходят за границы, определенные продолжительностью одного часа. К подобным случайным величинам относится также и погрешность округления. Про такие величины говорят, что они распределены равномерно, т. е. имеют равномерное распределение.

 Определение. Непрерывная случайная величина Х имеет равномерное распределение на отрезке [а, в], если на этом отрезке плотность распределения вероятности случайной величины постоянна, т. е. если дифференциальная функция распределения f(х)имеет следующий вид:

Иногда это распределение называют законом равномерной плотности. Про величину, которая имеет равномерное распределение на некотором отрезке, будем говорить, что она распределена равномерно на этом отрезке.

Найдем значение постоянной с. Так как площадь, ограниченная кривой распределения и осью Ох, равна 1, то

откуда с=1/(b—a).

 Теперь функцию f(x) можно представить в виде

  

Построим функцию распределения F(x), для чего найдем выражение F(x) на интервале [a, b]:

Графики функций f(x) и F(x) имеют вид:

 Найдем числовые характеристики.

Используя формулу для вычисления математического ожидания НСВ, имеем:

Таким образом, математическое ожидание случайной вели чины, равномерно распределенной на отрезке [a, b] совпадает с серединой этого отрезка.

Найдем дисперсию равномерно распределенной случайной величины:

откуда сразу же следует, что среднее квадратическое отклонение:

Найдем теперь вероятность попадания значения случайной величины, имеющей равномерное распределение, на интервал (,), принадлежащий целиком отрезку [a, b]: 

Геометрически эта вероятность представляет  собой площадь заштрихованного прямоугольника. Числа а и b называютсяпараметрами распределения и однозначно определяют равномерное распределение.

23. Экспонентный закон распределения.

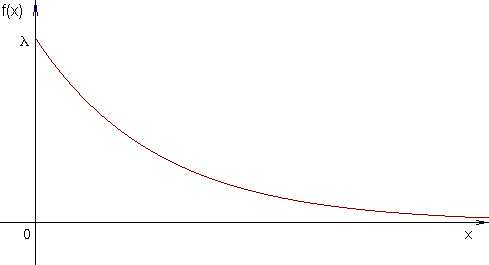
Определение. Непрерывная случайная величина X имеет показательный (экспоненциальный) закон распределения с параметром , если её плотность вероятности f(x) имеет вид:

Кривая распределения  f(x)  приведена на рисунке

Теорема. Функция распределения случайной величины X, распределённой по показательному закону, есть

её математическое ожидание

а её дисперсия

Доказательство.

График функции распределения F(x) случайной величины X, имеющей показательное распределение представлен на рисунке

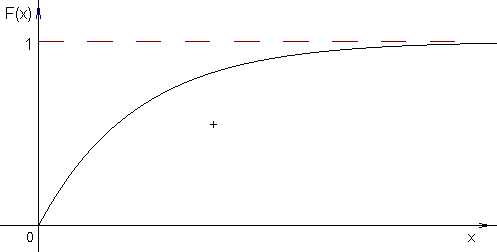
Следствие. Для случайной величины, распределённой по показательному закону, математическое ожидание равно среднему квадратическому отклонению, т. е.

Показательный закон распределения играет большую роль в теории массового обслуживания и теории надёжности. Так, например, интервал времени Т между двумя соседними событиями в простейшем потоке событий имеет

studfiles.net
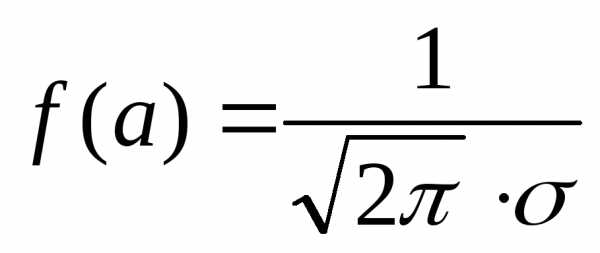