Равный вектор: Понятие вектора. Равенство векторов. Откладывание вектора от данной точки 9 класс онлайн-подготовка на Ростелеком Лицей

Понятие вектора. Равенство векторов. Откладывание вектора от данной точки 9 класс онлайн-подготовка на Ростелеком Лицей

Тема 23.

Понятие вектора. Равенство векторов. Откладывание вектора от данной точки.

Сегодня мы вспомним что такое вектор, дадим определение равным векторам.

Многие физические величины, скорость, характеризуется не только своим числовым значением, но и направлением в пространстве. Такие физические величины называются векторными величинами или векторами.

Рассмотрим произвольный отрезок. Его концы называются так же граничными точками отрезка.

На отрезке можно указать два направления: от одной граничной точки до другой и наоборот.

Чтобы выбрать одно из направлений, одну граничную точку назовем началом отрезка, а другую – концом и будем считать, что отрезок направлен от начала к концу.

Определение:

Отрезок, для которого указано, какая из его граничных точек считается началом, а какая – концом, называется направленным отрезком или

вектором.

Вектор изображается отрезком со стрелкой, показывающей направление вектора. Векторы обозначают двумя заглавными латинскими буквами со стрелками над ними, например, АВ⃗. Первая буква обозначает начало вектора, вторая – конец. Векторы часто обозначают и одной строчной латинской буквой со стрелкой над ней: a,⃗b⃗,c⃗.

Любая точка плоскости также является вектором. В этом случае вектор называется нулевым. Начало нулевого вектора совпадает с его концом, на рисунке такой вектор изображается одной точкой. Если, например, точка, изображающая нулевой вектор, обозначена буквой М, то данный нулевой вектор можно обозначить так: ММ⃗. Нулевой вектор обозначается так же символом 0⃗.

Длиной или модулем ненулевого вектора АВ⃗ называется длина отрезка АВ.

Обозначается так: АВ⃗. Длина нулевого вектора ММ⃗=0.

Рассмотрим движение тела, при котором все его точки движутся с одной и той же скоростью и в одном и том же направлении.

Скорость каждой точки М тела является векторной величиной, поэтому ее можно изобразить направленным отрезком, начало которого совпадает с точкой М. Так как все точки тела движутся с одной и той же скоростью, то все направленные отрезки, изображающие скорости этих точек, имеют одно и то же направление и длины их равны.

Введем понятие коллинеарных векторов.

Ненулевые векторы называются коллинеарными, если они лежат либо на одной прямой, либо на параллельных прямых; нулевой вектор считается коллинеарным любому вектору.

Если два ненулевых вектора коллинеарны, то они могут быть направлены либо одинаково, либо противоположно. В первом случае векторы называются сонаправленными, а во втором – противоположно направленными.

Сонаправленность векторов a⃗ и b⃗ обозначается следующим образом: a⃗↑↑b⃗. Если же векторы a⃗ и b⃗ противоположно направлены, то обозначают так: a⃗↑↓b⃗.

Дадим теперь определение равных векторов.

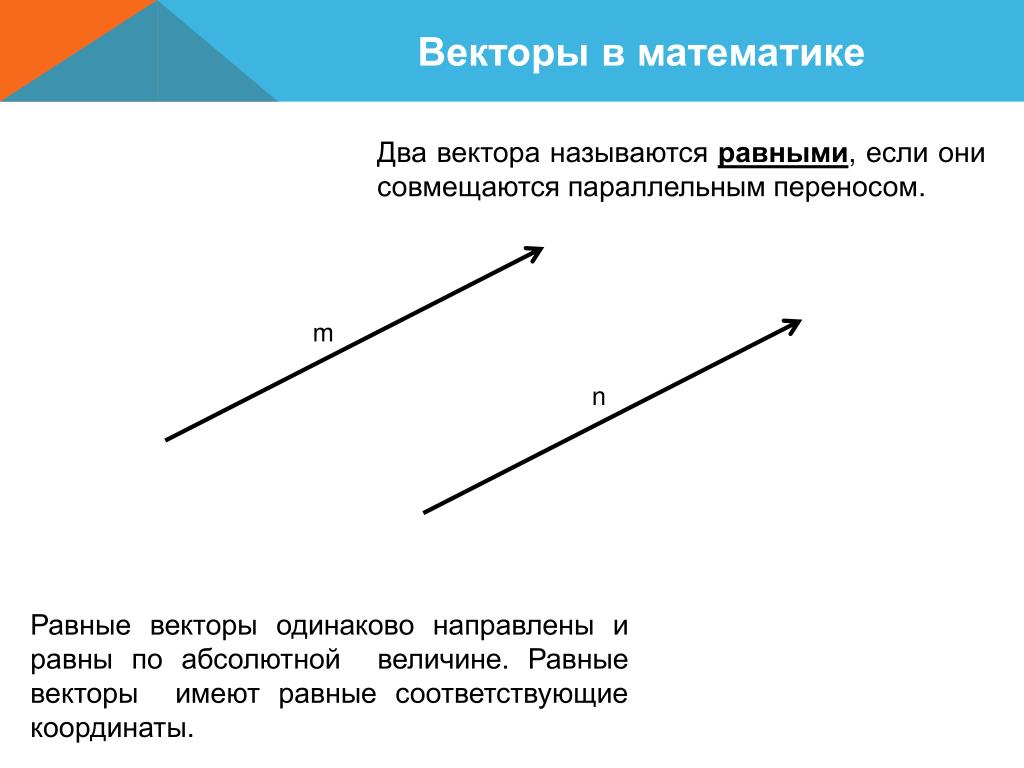
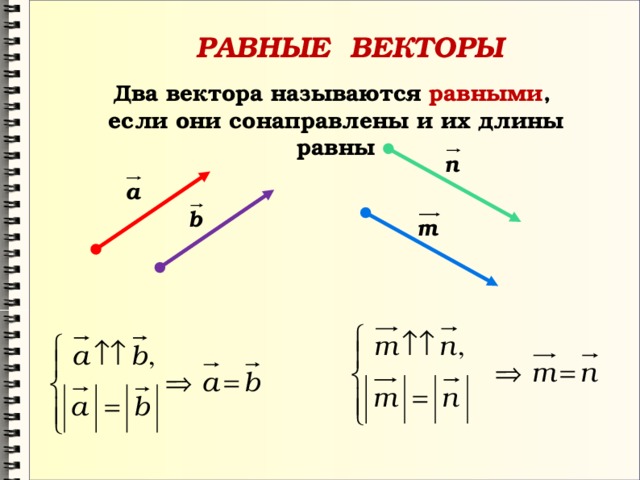
Определение: Векторы называются равными, если они сонаправлены и их длины равны.

Таким образом векторы a⃗ и b⃗ равны, если a⃗↑↑b⃗ и a⃗=b⃗. Равенство векторов обозначается так: a⃗=b⃗.

Если точка А – начало вектора a⃗, то говорят, что вектор a⃗ отложен от точки А.

Итак, от любой точки М можно отложить вектор, равный данному вектору a⃗ и притом только один.

Замечание:

Равные векторы, отложенные от разных точек, часто обозначают одной и той же буквой. Иногда про такие векторы говорят, что это один и тот же вектор, но отложенный от разных точек.

Равные вектора

Равные вектора

Навигация по странице:

• Определение равных векторов
• Условие равенства векторов
• Примеры задач на равенство векторов
  • плоские задачи
  • пространственные задачи

Определение. Вектора a и b называются равными, если они имеют одинаковую длину, лежат на параллельных прямых или на одной прямой, и направлены в одном направлении. (рис. 1).

То есть, два вектора равны, если они коллинеарные, сонаправленые и имеют равные длины:

a = b, если a↑↑b и |a| = |b|.

Условие равенства векторов.Вектора равны, если их координаты равны.

рис. 1

Примеры плоских задач на равенство векторов

Пример 1. Определить какие из векторов равны a = {1; 2}, b = {1; 2}, c = {3; 2}.

Решение:

a = b — так как их координаты равны,
a ≠ c — так как их координаты не равны,
b ≠ c — так как их координаты не равны.

Пример 2. При каком значении параметра n вектора a = {1; 8;} и b = {1; 2n} равны.

Решение:

Проверим равенство компонентов векторов
a_x = b_x = 1
a_y = b_y => 8 = 2n => n = 8/2 = 4

Ответ: при n = 4 вектора a и b равны.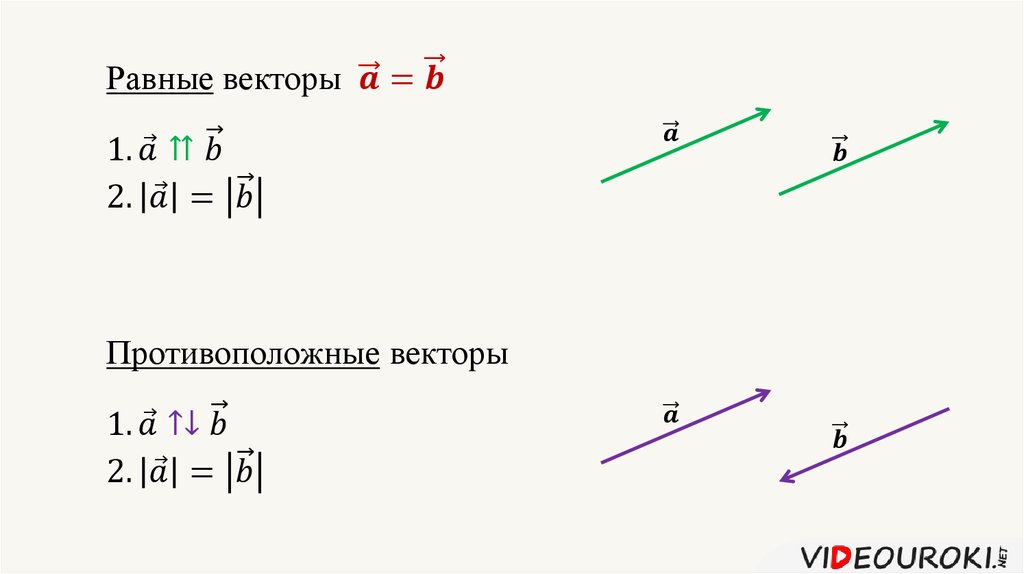

Примеры пространственных задач на равенство векторов

Пример 3. Определить какие из векторов равны a = {1; 2; 4}, b = {1; 2; 2}, c = {1; 2; 4}.

Решение:

a = c — так как их координаты равны,
a ≠ b — так как их координаты не равны,
b ≠ c — так как их координаты не равны.

Пример 4. При каком значении параметра n вектора a = {1; 2; 4} и b = {1; 2; 2n} равны.

Решение:

Проверим равенство компонентов векторов
a_x = b_x = 1
a_y = b_y = 2
a_z = b_z => 4 = 2n => n = 4/2 = 2

Ответ: при n = 2 вектора a и b равны.

Вектора Вектор: определение и основные понятия Определение координат вектора заданного координатами его начальной и конечной точки Модуль вектора.

Длина вектора Направляющие косинусы вектора Равенство векторов Ортогональность векторов Коллинеарность векторов Компланарность векторов Угол между векторами Проекция вектора Сложение и вычитание векторов Умножение вектора на число Скалярное произведение векторов Векторное произведение векторов Смешанное произведение векторов Линейно зависимые и линейно независимые вектора Разложение вектора по базису

Онлайн калькуляторы с векторами

Онлайн упражнения с векторами на плоскости

Онлайн упражнения с векторами в пространстве

Равный вектор — определение, формула, угол, примеры, часто задаваемые вопросы Проще говоря, мы можем сказать, что два или более вектора называются равными векторами, если их длина одинакова и все они указывают в одном направлении. Как правило, мы можем проверить равенство векторов, сравнив их координаты. Если все координаты двух или более векторов одинаковы, то они являются равными векторами.

Следовательно, говорят, что вектор A равен вектору B, если они имеют равные координаты.

Далее в этой статье мы рассмотрим понятие вектора равенства, его определение и формулу. Мы также поймем диаграмму равных векторов и угол между равными векторами с помощью некоторых решенных примеров для лучшего понимания концепции.

1.	Что такое равный вектор?
2.	Равная векторная диаграмма
3.	Определение равного вектора
4.	Формула равного вектора
5.	Равный угол вектора
6.	Часто задаваемые вопросы о Equal Vector

Что такое равный вектор?

Вектор A называется вектором, равным вектору B, если они имеют одинаковую величину и направлены в одном направлении. Мы также можем сказать, что два или более вектора равны, если они сонаправлены (направлены в одном направлении), коллинеарны (лежат на одной прямой) и имеют одинаковую величину (имеют одинаковую длину).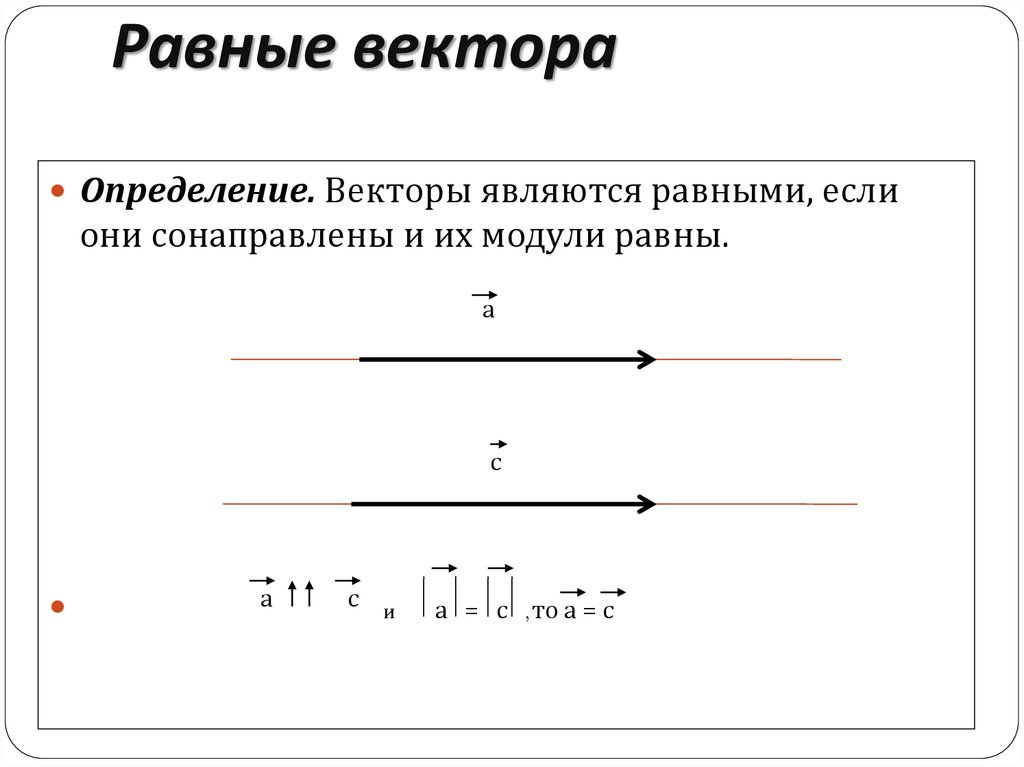

Это означает, что равные векторы также являются параллельными векторами. Мы также можем проверить вектор на равенство, если он имеет те же компоненты x, y, z, что и компоненты другого вектора. Нет необходимости, чтобы равные векторы начинались с одной и той же точки.

Равная векторная диаграмма

Ниже приведена диаграмма вектора A, равного вектору B. Два вектора равны, но не совпадают с начальными векторами, то есть они не начинаются из одной и той же точки. Следовательно, равные векторы не обязательно должны иметь одинаковые начальные точки. Это параллельные и сонаправленные векторы одинаковой величины. Если у нас есть два вектора с одинаковой величиной, но антипараллельными (действующими в противоположных направлениях), то они не являются равными векторами.

Определение равного вектора

Равные векторы определяются как два или более векторов, имеющих одинаковую величину и одинаковое направление. Это означает, что вектор A называется вектором, равным вектору B, если они имеют одинаковую длину и указывают в одном направлении.

Векторы с одинаковыми координатами (с одинаковым знаком) называются равными векторами. Следовательно, мы можем сказать, что равные векторы являются параллельными векторами, но параллельные векторы не могут быть равными векторами.

Формула равного вектора

Формула для проверки равенства векторов: если у нас есть два вектора \(\overrightarrow{A} = x\hat{i} + y\hat{j} + z\hat{k}\) и \( \overrightarrow{B} = p\hat{i} + q\hat{j} + r\hat{k}\), то векторы A и B равны тогда и только тогда, когда x = p, y = q и z = r, то есть имеют равные координаты. Чтобы понять эту формулу, рассмотрим пример:

Пример: Если два вектора A = 2i + 3j — 8k и B = xi — yj — 8k равны, то найдите значения x и y.

Решение:

Поскольку векторы A и B равны, то они должны иметь одинаковые компоненты. Отсюда имеем

2 = x, 3 = -y, -8 = -8

⇒ x = 2 и y = -3

Следовательно, значения x и y равны x = 2 и y = -3 .

Равный угол вектора

Как мы знаем, равные векторы также являются параллельными векторами и угол между параллельными векторами равен нулю радиан. Теперь мы докажем это, используя формулу скалярного произведения векторов. Рассмотрим два равных вектора A и B с координатами (x, y), то есть A = xi + yj и B = xi + yj, и пусть θ — угол между ними. Теперь возьмем скалярное произведение векторов A и B:

А.В = |А| |Б| cos θ

⇒ cos θ = (A.B)/(|A| |B|)

⇒ cos θ = [(xi + yj)(xi + yj)]/[√(x ² + y ² )√(x ² + y ² )]

⇒ cos θ = [(xi + yj)(xi + yj)]/[√(x ² + y ² (x )√ ² + y ² )]

⇒ θ = arccos [(x ² + y ² )/(x ² + y в обеих сторонах]

⇒ θ = arccos (1)

⇒ θ = 0

Следовательно, угол между двумя равными векторами равен нулю.

☛ Связанные темы:

• Радиан
• Типы векторов
• Направление вектора

Важные замечания о равных векторах

• Если два вектора имеют одинаковую величину и одинаковое направление, говорят, что они равны.
• Угол между равными векторами равен нулю градусов.
• Вектор A равен вектору B, если они имеют одинаковые координаты.

Часто задаваемые вопросы о Equal Vector

Что такое равный вектор в математике?

Говорят, что вектор X равен другому вектору Y, если они оба имеют одинаковую величину и одинаковое направление. Проще говоря, мы можем сказать, что равные векторы имеют одинаковую длину и указывают в одном направлении.

Что такое формула для равного вектора?

Формула для равных векторов: Два вектора A = xi + yj + zk и B = pi + qj + rk называются равными векторами тогда и только тогда, когда x = p, y = q и z = r.

Когда два вектора считаются равными?

Два или более вектора называются равными векторами, если они имеют одинаковую величину (длину) и действуют в одном направлении.

Чему равен угол между двумя равными векторами?

Угол между двумя равными векторами равен нулю градусов, так как они параллельны и действуют в одном направлении. Кроме того, скалярное произведение двух равных векторов равно 1, следовательно, угол равен нулю.

Что такое скалярное произведение двух равных векторов?

Скалярное произведение двух равных векторов равно 1, так как они имеют одинаковую величину и направление. Поскольку их скалярное произведение равно единице, это означает, что угол между ними равен нулю.

Какое условие должно быть выполнено, чтобы два вектора были равными?

Чтобы два вектора были равны, они должны иметь одинаковую длину и указывать в одном направлении. Другими словами, мы можем сказать, что равные векторы имеют одинаковые координаты.

Как определить, равны ли два вектора?

Чтобы проверить, равны ли два вектора, мы проверяем, одинаковы ли их величины и должны ли они быть сонаправлены, то есть действовать в одном направлении.

Равные векторы

Равные векторы

Навигация по странице:

• Равные векторы — определение
• Условия равенства векторов
• Примеры задач
  • самолетные задачи
  • пространственные задачи

Определение.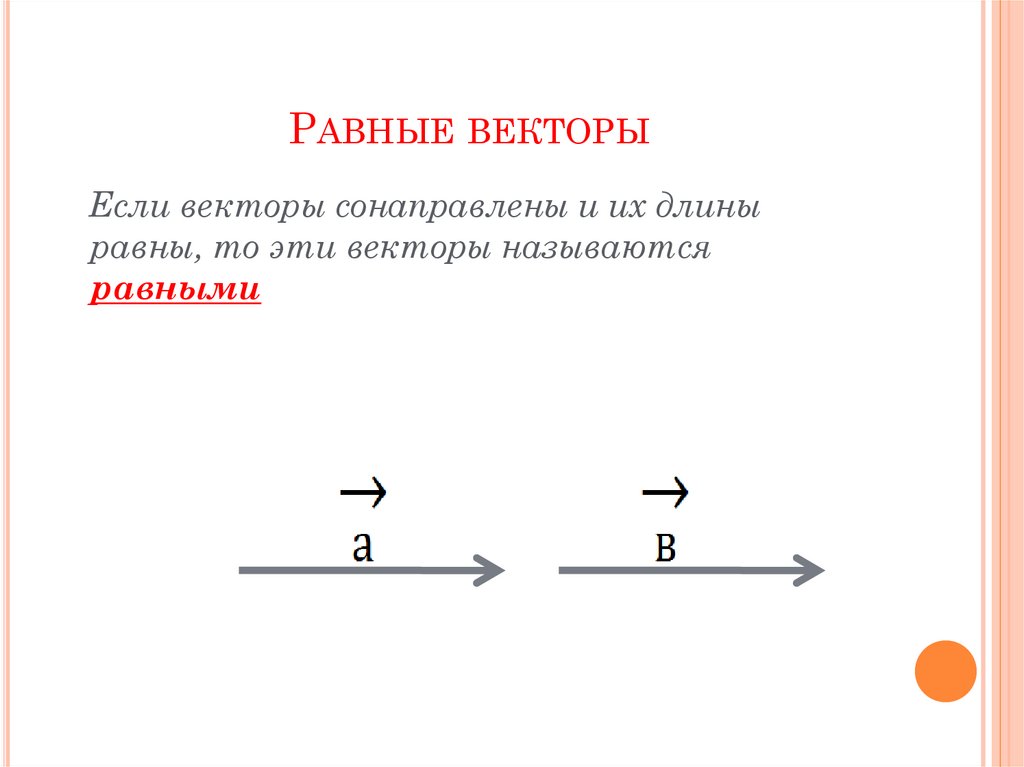 Векторы a и b равны равны вектора , если они лежат на одной или параллельных прямых, их направления совпадают и длины равны (рис. 1).

Два вектора равны, если они коллинеарны, сонаправлены и имеют одинаковую длину:

a = b, если a↑↑b и |a| = |б|.

Условия равенства векторов. Векторы равны , если их координаты равны.

Рис. 1

Примеры плоских задач

Пример 1. Определить, какие из векторов равны a = {1; 2}, б = {1; 2}, с = {3; 2}.

Решение:

a = b — так как их координаты равны,
a ≠ c — так как их координаты не равны,
b ≠ c — так как их координаты не равны.

Пример 2. При каком значении параметра n векторы a = {1; 8;} и b = {1; 2n} равны.

Решение:

Проверить равенство компонентов векторов
а _х = б _х = 1
a _y = b _y => 8 = 2n => n = 8/2 = 4

Ответ: при n = 4 векторы a и b равны.