Математический анализ. Продолжение курса
Математический анализ. Продолжение курса
ОглавлениеПРЕДИСЛОВИЕГлава 1. ЧИСЛОВЫЕ РЯДЫ § 1. ПОНЯТИЕ ЧИСЛОВОГО РЯДА 2. Критерий Коши сходимости ряда. § 2. РЯДЫ С НЕОТРИЦАТЕЛЬНЫМИ ЧЛЕНАМИ 2. Признаки сравнения. 3. Признаки Даламбера и Коши. 4. Интегральный признак Коши—Маклорена. 5. Признак Раабе. 6. Отсутствие универсального ряда сравнения. § 3. АБСОЛЮТНО И УСЛОВНО СХОДЯЩИЕСЯ РЯДЫ 2. О перестановке членов условно сходящегося ряда. 3. О перестановке членов абсолютно сходящегося ряда. § 4. ПРИЗНАКИ СХОДИМОСТИ ПРОИЗВОЛЬНЫХ РЯДОВ § 5. АРИФМЕТИЧЕСКИЕ ОПЕРАЦИИ НАД СХОДЯЩИМИСЯ РЯДАМИ § 6. БЕСКОНЕЧНЫЕ ПРОИЗВЕДЕНИЯ 2. Связь между сходимостью бесконечных произведений и рядов. 3. Разложение функции sin x в бесконечное произведение. § 7. ОБОБЩЕННЫЕ МЕТОДЫ СУММИРОВАНИЯ РАСХОДЯЩИХСЯ РЯДОВ 1. Метод Чезаро (метод средних арифметических). 2. Метод суммирования Пуассона—Абеля. § 8. ЭЛЕМЕНТАРНАЯ ТЕОРИЯ ДВОЙНЫХ И ПОВТОРНЫХ РЯДОВ Глава 2.  ФУНКЦИОНАЛЬНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ И РЯДЫ§ 1. ПОНЯТИЯ СХОДИМОСТИ В ТОЧКЕ и РАВНОМЕРНОЙ СХОДИМОСТИ НА МНОЖЕСТВЕ 2. Сходимость функциональной последовательности (функционального ряда) в точке и на множестве. 3. Равномерная сходимость на множестве. 4. Критерий Коши равномерной сходимости последовательности (ряда). § 2. ДОСТАТОЧНЫЕ ПРИЗНАКИ РАВНОМЕРНОЙ СХОДИМОСТИ ФУНКЦИОНАЛЬНЫХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ И РЯДОВ § 3. ПОЧЛЕННЫЙ ПЕРЕХОД К ПРЕДЕЛУ § 4. ПОЧЛЕННОЕ ИНТЕГРИРОВАНИЕ И ПОЧЛЕННОЕ ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИОНАЛЬНЫХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ И РЯДОВ 2. Почленное дифференцирование. 3. Сходимость в среднем. § 5. РАВНОСТЕПЕННАЯ НЕПРЕРЫВНОСТЬ ПОСЛЕДОВАТЕЛЬНОСТИ ФУНКЦИИ 2. Непрерывность суммы степенного ряда. 3. Почленное интегрирование и почленное дифференцирование степенного ряда. § 7. РАЗЛОЖЕНИЕ ФУНКЦИИ В СТЕПЕННЫЕ РЯДЫ 2. Разложение некоторых элементарных функций в ряд Тейлора. 3. Элементарные представления о функциях кемплексной переменной. 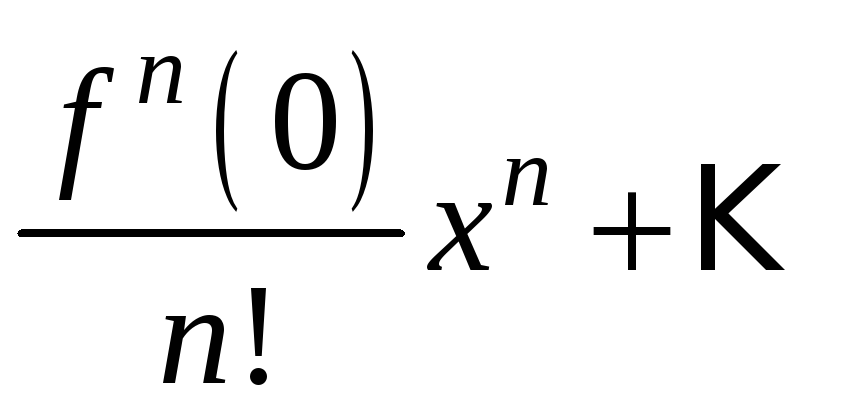 4. Теорема Вейерштрасса о равномерном приближении непрерывной функции многочленами. Глава 3. ДВОЙНЫЕ И n-КРАТНЫЕ ИНТЕГРАЛЫ § 1. ОПРЕДЕЛЕНИЕ И УСЛОВИЯ СУЩЕСТВОВАНИЯ ДВОЙНОГО ИНТЕГРАЛА 2. Условия существования двойного интеграла для прямоугольника. 3. Определение и условия существования двойного интеграла для произвольной области. 4. Общее определение двойного интеграла. § 2. ОСНОВНЫЕ СВОЙСТВА ДВОЙНОГО ИНТЕГРАЛА § 3. СВЕДЕНИЕ ДВОЙНОГО ИНТЕГРАЛА К ПОВТОРНОМУ ОДНОКРАТНОМУ 2. Случай произвольной области. § 4. ТРОЙНЫЕ И n-КРАТНЫЕ ИНТЕГРАЛЫ § 5. ЗАМЕНА ПЕРЕМЕННЫХ В n-КРАТНОМ ИНТЕГРАЛЕ § 6. ВЫЧИСЛЕНИЕ ОБЪЕМОВ n-МЕРНЫХ ТЕЛ § 7. ТЕОРЕМА О ПОЧЛЕННОМ ИНТЕГРИРОВАНИИ ФУНКЦИОНАЛЬНЫХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ И РЯДОВ § 8. КРАТНЫЕ НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ 2. Два признака сходимости несобственных интегралов от неотрицательных функций. 3. Несобственные интегралы от знакопеременных функций. 4. Главное значение кратных несобственных интегралов. Глава 4.  n.3. Преобразования базисов. Ковариантные и контрвариантные координаты вектора. 4. Инварианты линейного оператора. Дивергенция и ротор. 5. Выражения для дивергенции и ротора линейного оператора в ортонормированном базисе. § 2. СКАЛЯРНЫЕ И ВЕКТОРНЫЕ ПОЛЯ. ДИФФЕРЕНЦИАЛЬНЫЕ ОПЕРАТОРЫ ВЕКТОРНОГО АНАЛИЗА 2. Дивергенция, ротор и производная по направлению векторного поля. 4. Заключительные замечания. § 3. ОСНОВНЫЕ ИНТЕГРАЛЬНЫЕ ФОРМУЛЫ АНАЛИЗА 2. Формула Остроградского—Гаусса. 3. Формула Стокса. § 4. УСЛОВИЯ НЕЗАВИСИМОСТИ КРИВОЛИНЕЙНОГО ИНТЕГРАЛА НА ПЛОСКОСТИ ОТ ПУТИ ИНТЕГРИРОВАНИЯ § 5. НЕКОТОРЫЕ ПРИМЕРЫ ПРИЛОЖЕНИИ ТЕОРИИ ПОЛЯ 2. Выражение объема через поверхностный интеграл. ДОПОЛНЕНИЕ К ГЛАВЕ 6. ДИФФЕРЕНЦИАЛЬНЫЕ ФОРМЫ В ЕВКЛИДОВОМ ПРОСТРАНСТВЕ § 1. ЗНАКОПЕРЕМЕННЫЕ ПОЛИЛИНЕЙНЫЕ ФОРМЫ 2. Билинейные формы. 3. Полилинейные формы. 4. Знакопеременные полилинейные формы. 5. Внешнее произведение знакопеременных форм.  6. Свойства внешнего произведения знакопеременных форм. 7. Базис в пространстве знакопеременных форм. § 2. ДИФФЕРЕНЦИАЛЬНЫЕ ФОРМЫ 2. Внешний дифференциал. § 3. ДИФФЕРЕНЦИРУЕМЫЕ ОТОБРАЖЕНИЯ 2. Свойства отображения. § 4. ИНТЕГРИРОВАНИЕ ДИФФЕРЕНЦИАЛЬНЫХ ФОРМ 2. Дифференцируемые цепи. 3. Формула Стокса. 4. Примеры. Глава 7. ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРОВ § 1. РАВНОМЕРНОЕ ПО ОДНОЙ ПЕРЕМЕННОЙ СТРЕМЛЕНИЕ ФУНКЦИИ ДВУХ ПЕРЕМЕННЫХ К ПРЕДЕЛУ ПО ДРУГОЙ ПЕРЕМЕННОЙ 2. Критерий Коши равномерного стремления функции к предельной. 3. Применения понятия равномерного стремления к предельной функции. § 2. СОБСТВЕННЫЕ ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРА 2. Случай, когда пределы интегрирования зависят от параметра. § 3. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРА 2. Несобственные интегралы второго рода, зависящие от параметра. § 4. ПРИМЕНЕНИЕ ТЕОРИИ ИНТЕГРАЛОВ, ЗАВИСЯЩИХ ОТ ПАРАМЕТРА, К ВЫЧИСЛЕНИЮ НЕКОТОРЫХ НЕСОБСТВЕННЫХ ИНТЕГРАЛОВ § 5.  ИНТЕГРАЛЫ ЭЙЛЕРА2. В-функция. 3. Связь между эйлеровыми интегралами. 4. Примеры. § 6. ФОРМУЛА СТИРЛИНГА 2. Несобственные кратные интегралы, зависящие от параметра. Глава 8. РЯДЫ ФУРЬЕ § 1. ОРТОНОРМИРОВАННЫЕ СИСТЕМЫ И ОБЩИЕ РЯДЫ ФУРЬЕ 2. Понятие об общем ряде Фурье. § 2. ЗАМКНУТЫЕ И ПОЛНЫЕ ОРТОНОРМИРОВАННЫЕ СИСТЕМЫ § 3. ЗАМКНУТОСТЬ ТРИГОНОМЕТРИЧЕСКОЙ СИСТЕМЫ И СЛЕДСТВИЯ ИЗ НЕЕ 2. Доказательство замкнутости тригонометрической системы. 3. Следствия замкнутости тригонометрической системы. § 4. ПРОСТЕЙШИЕ УСЛОВИЯ РАВНОМЕРНОЙ СХОДИМОСТИ И ПОЧЛЕННОГО ДИФФЕРЕНЦИРОВАНИЯ ТРИГОНОМЕТРИЧЕСКОГО РЯДА ФУРЬЕ 2. Простейшие условия абсолютной и равномерной сходимости тригонометрического ряда Фурье. 3. Простейшие условия почленного дифференцирования тригонометрического ряда Фурье. § 5. БОЛЕЕ ТОЧНЫЕ УСЛОВИЯ РАВНОМЕРНОЙ СХОДИМОСТИ И УСЛОВИЯ СХОДИМОСТИ В ДАННОЙ ТОЧКЕ 2. Выражение для частичной суммы тригонометрического ряда Фурье.  3. Вспомогательные предложения. 4. Принцип локализации. 5. Равномерная сходимость тригонометрического ряда Фурье для функции из класса Гёльдера. 6. О сходимости тригонометрического ряда Фурье кусочно гёльдеровой функции. 7. Суммируемость тригонометрического ряда Фурье непрерывной функции методом средних арифметических. 8. Заключительные замечания. § 6. КРАТНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ РЯДЫ ФУРЬЕ 2. Модуль непрерывности и классы Гёльдера для функции N переменных. 3. Условия абсолютной сходимости кратного тригонометрического ряда Фурье. Глава 9. ПРЕОБРАЗОВАНИЕ ФУРЬЕ § 1. ПРЕДСТАВЛЕНИЕ ФУНКЦИИ ИНТЕГРАЛОМ ФУРЬЕ 2. Основная теорема. Формула обращения. 3. Примеры. § 2. НЕКОТОРЫЕ СВОЙСТВА ПРЕОБРАЗОВАНИЯ ФУРЬЕ § 3. КРАТНЫЙ ИНТЕГРАЛ ФУРЬЕ |
Тема 3. Разложение функций в степенной ряд
3.1. Постановка задачи. Ряд Тейлора
В теории функциональных
рядов центральное место занимает раздел,
посвященный разложению функции в ряд.
Таким образом, ставится задача: по заданной функции требуется найти такой степенной ряд
,
который на некотором интервале сходился и его сумма была равна , т.е.
= ..
Эта задача называется задачей разложения функции в степенной ряд.
Необходимым условием разложимости функции в степенной ряд является её дифференцируемость бесконечное число раз – это следует из свойств сходящихся степенных рядов. Такое условие выполняется, как правило, для элементарных функций в их области определения.
Итак, предположим, что функция имеет производные любого порядка. Можно ли её разложить в степенной ряд, если можно, то как найти этот ряд? Проще решается вторая часть задачи, с неё и начнем.
Допустим, что функциюможно представить в виде суммы степенного ряда, сходящегося в интервале, содержащем точкух0:
= .
. (*)
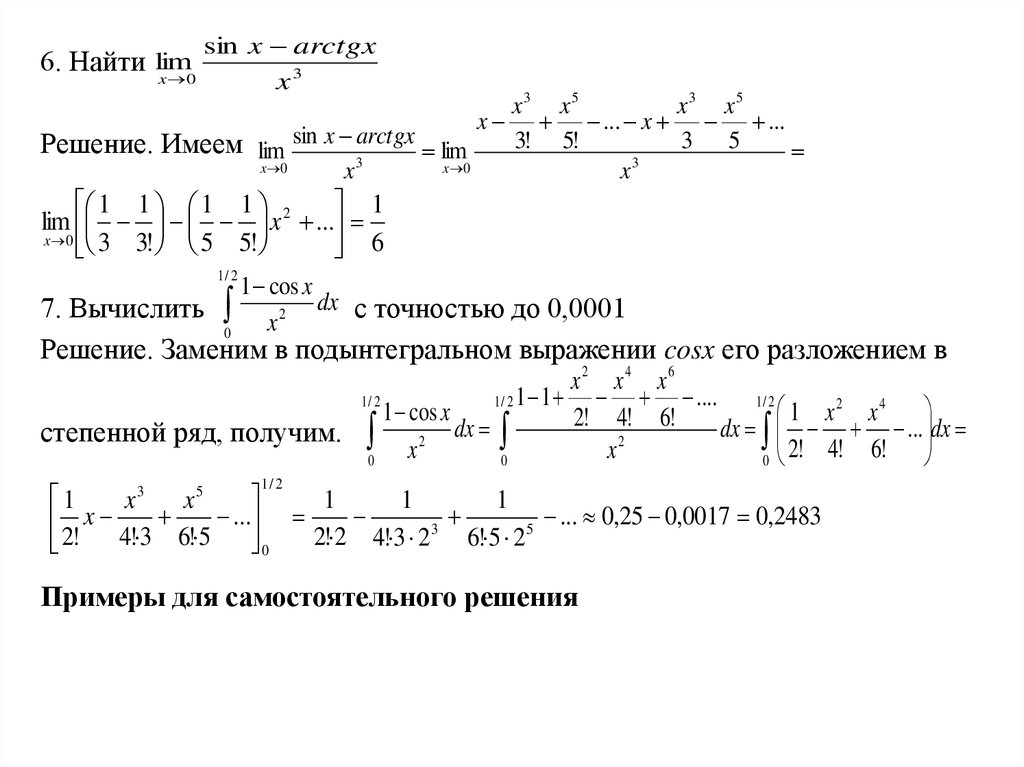где а0,а1,а2,,…,ап,… – неопределенные (пока) коэффициенты.
Положим в равенстве (*) значение х = х0, тогда получим
.
Продифференцируем степенной ряд (*) почленно
= ..
и полагая здесь х = х0, получим
.
При следующем дифференцировании получим ряд
= ..
полагая х = х0, получим, откуда .
После п -кратного дифференцирования получим
Полагая в последнем равенстве х = х0, получим , откуда
Итак, коэффициенты найдены
, ,
,
…,
,….
,
подставляя которые в ряд (*), получим
Полученный ряд называется рядом Тейлора для функции .
Таким образом, мы установили, что если функцию можно разложить в степенной ряд по степеням (х — х0), то это разложение единственно и полученный ряд обязательно является рядом Тейлора.
Заметим, что ряд Тейлора можно получить для любой функции, имеющей производные любого порядка в точке х = х0. Но это еще не означает, что между функцией и полученным рядом можно поставить знак равенства, т.е. что сумма ряда равна исходной функции. Во-первых, такое равенство может иметь смысл только в области сходимости, а полученный для функции ряд Тейлора может и расходиться, во-вторых, если ряд Тейлора будет сходиться, то его сумма может не совпадать с исходной функцией.
3.2. Достаточные условия разложимости функции в ряд Тейлора
Сформулируем
утверждение, с помощью которого будет
решена поставленная задача.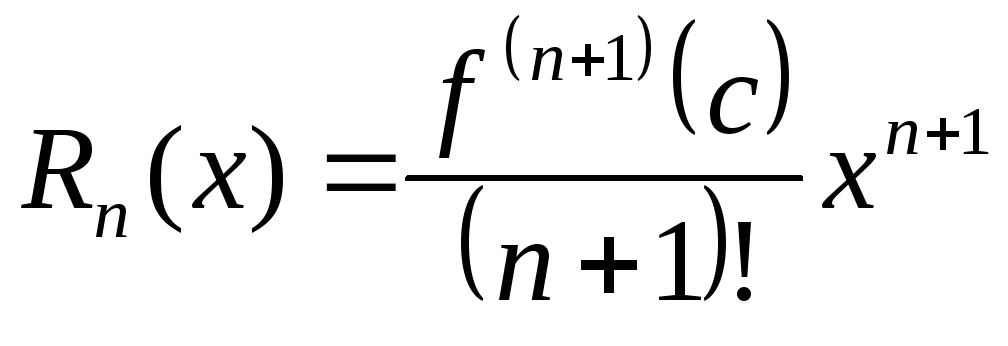
Если функция в некоторой окрестности точки х0 имеет производные до (n+1)-го порядка включительно, то в этой окрестности имеет место формула Тейлора
где Rn(х)-остаточный член формулы Тейлора – имеет вид (форма Лагранжа)
где точка ξ лежит между х и х0.
Отметим, что между рядом Тейлора и формулой Тейлора имеется различие: формула Тейлора представляет собой конечную сумму, т.е. п — фиксированное число.
Напомним, что сумма ряда S(x) может быть определена как предел функциональной последовательности частичных сумм Sп(x) на некотором промежутке Х:
.
Согласно этому, разложить функцию в ряд Тейлора означает найти такой ряд, что для любого х X
Запишем формулу Тейлора в виде, где
.
Заметим, что определяет ту ошибку, которую мы получаем, заменяй функцию f(x) многочленом Sn(x).
Если , то,т.е. функция разлагается в ряд Тейлора. И наоборот, если , то.
Тем самым мы доказали критерий разложимости функции в ряд Тейлора.
Для того, чтобы в некотором промежутке функция f(х) разлагалась в ряд Тейлора, необходимо и достаточно, чтобы на этом промежутке , где Rn(x) — остаточный член ряда Тейлора.
С помощью сформулированного критерия можно получить достаточные условия разложимости функции в ряд Тейлора.
Если в некоторой
окрестности точки х0 абсолютные величины всех производных
функции ограничены одним и тем же числом
М ≥ 0,
т.
е.
, то в этой окрестности функция разлагается в ряд Тейлора.
Из вышеизложенного следует алгоритм разложения функции f(x) в ряд Тейлора в окрестности точки х0:
1. Находим производные функции f(x):
f(x), f’(x), f”(x), f’”(x), f(n) (x),…
2. Вычисляем значение функции и значения её производных в точке х0
f(x0), f’(x0), f”(x0), f’”(x0), f(n) (x0),…
3. Формально записываем ряд Тейлора и находим область сходимости полученного степенного ряда.
4. Проверяем
выполнение достаточных условий, т.
е.
устанавливаем, для каких х из области
сходимости, остаточный член Rn(x) стремится
к нулю при
или .
Разложение функций в ряд Тейлора по данному алгоритму называют разложением функции в ряд Тейлора по определению или непосредственным разложением.
Силовая серия
Серия Power
Определение степенного ряда
Теперь исследуем обобщение многочленов. Полином ниже полином пятой степени
3x 5 — 2x 4 + 5x 3 + 4x — 1
если вместо многочлена пятой степени мы рассматриваем многочлен бесконечной степень.
Определение степенного ряда Пусть f(x) будет функцией, представленной рядом |
В более общем случае, если f(x) представлен рядом
Тогда мы называем f(x) степенным рядом с центром в точке x =
с .
Примеры
Серия мощности
является с центром в 0.
силовой ряд
является с центром в -2.
Радиус сходимости
Далее мы хотим исследовать область степенных рядов. Вспомнить, чтобы найти области, мы спрашиваем, какие значения x могут ручка функции? Это особенно важно для степенных рядов, поскольку бесконечные ряды часто не сходятся. Это была бы непреодолимая задача подставить каждое значение x и посмотреть, соответствует ли ряд сходится для этого значения. К счастью, у нас есть следующая теорема.
Теорема
Если
есть
степенной ряд с центром в точке c
тогда только следующие три являются возможными для области определения f.
домен — это значение c только.
Там домен — все действительные числа.
Там существует действительное число R такое, что все значения x которые удовлетворяют
| х — с | < Rнаходятся в домене и значения, которые удовлетворяют
| х — с | >
р.
не в домене.
Р
называется радиусом сходимости f.
Чтобы вычислить радиус сходимости, мы используем критерий отношения.
Пример: Найти радиус сходимости
Решение
Мы используем тест отношения:
Решаем
или
|x — 3| < 2
так что
1 < x < 5
Так как
1/2(5 — 1) = 2
радиус схождения 2
Упражнение:
Найдите радиус сходимости
Серия Тейлора и Маклорена
Поскольку степенные ряды являются функциями, возникает естественный вопрос: «Может ли наш повседневные функции могут быть представлены в виде степенных рядов?» Кроме того, «данные степенной ряд, можем ли мы найти повседневную функцию, эквивалентную степенной ряд?»
Следующее определение помогает ответить на эти вопросы.
| Определение Серия Тейлора для f (х) с центром в точке x = c равно Если с
= 0, то ряд называется
ряд Маклорена для ф. |
Мы используем обозначение f (n) для обозначения
n-я производная от f.
Пример:
Найти ряд Маклаурина для
f(x) = cos(x)
Решение
Вычисляем:
е (0) = 1 f ‘(0) = 0 f »(0) = -1 f (3) (0) = 0
f (4) (0) = 1 f (5) (0) = 0 f (6) (0) = -1 f (7) (0) = 0
f (8) (0) = 1 f (9) (0) = 0 ф (10) (0) = -1 f (11) (0) = 0
Отсюда имеем серию
1 — х 2 /2+ х 4 /4! — х 6 /6! +
х 8 /8! — х 8 /8! + .
..
Мы видим, что ряд
Упражнения Найти расширение ряда Тейлора для
sin(x) с центром в x = 0
ln(x) с центром в x = 0
Отличие и интеграция серии Power
Поскольку степенной ряд является функцией, естественно спросить, является ли функция
непрерывная, дифференцируемая или интегрируемая. Следующая теорема
отвечает на этот вопрос.
Теорема: Предположим, что функция задана степенным рядом f(x) =Sa n (x — c) n и что интервал сходимости равен , 9001 c + R) (плюс возможные конечные точки), то f(x) непрерывна, дифференцируема и интегрируема на этом интервале
(не обязательно включая конечные точки). и Кроме того, радиус сходимости производной и интеграла равен R. |
Чтобы получить производную или интеграл от f(x) мы можем передать производную или интеграл через S. В других
словаПример:
Рассмотрим серию
f(x) = Sx n
по ОТС этот ряд сходится при |x| < 1, поэтому центр сходимости равен 0, а радиус равен 1. По приведенной выше теореме
f ‘(x) = Snx n-1
имеет центр сходимости 0 и радиус сходимости
1 также. Мы также можем сказать, что
также имеет центр схождения 0 и радиус схождения
1.
Упражнение:
Покажите, что
удовлетворяет дифференциальному уравнению
у» + ху’ — у = 0
Мы также можем использовать подстановку, чтобы найти степенной ряд.
Пример
Найдите серию Maclaurin для
1
1 — х 2
Раствор
Замена x 2 вместо x в
у нас есть
Назад на главную страницу Math 117
Назад к математике Дом Департамента
электронная почта Вопросы и предложения
определение мощности+ряда+расширения по The Free Dictionary
Мощность+ряд+расширение — определение мощности+ряда+расширения по The Free DictionaryМощность+серия+расширение — определение степени+серия+расширение в The Free Dictionary
Слово, не найденное в Словаре и Энциклопедии.