91 решите уравнение: Решите уравнение: а) х + 3х + 5 = 17; в) 3,2у б) 3,5x + 2,2x = 4,56; г) 3,7z

Решите уравнение № 91 Математика 6 класс Виленкин. – Рамблер/класс

Решите уравнение № 91 Математика 6 класс Виленкин. – Рамблер/класс

Интересные вопросы

Школа

Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?

Новости

Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?

Школа

Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?

Школа

Когда в 2018 году намечено проведение основного периода ЕГЭ?

Новости

Будет ли как-то улучшаться система проверки и организации итоговых сочинений?

Вузы

Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания «Останкино»?

Хелп!
Решите уравнение:
а)    х + 3х + 5 = 17;                        в) 3,2у — 2,7у = 0,6;
б)     3,5x + 2,2x = 4,56;                  г) 3,7z — z = 0,54.

 

ответы

а) х + Зх + 5 = 17; 4х = 12; х = 3;
б) 3,5х + 2,2х = 4,56; 5,7х = 4,56; х = 0,8;
в) 3,2у — 2,7у = 0,6; 0,5у = 0,6; у = 1,2; 
г) 3,7z — z = 0,54; 2,7z = 0,54; z = 0,2.
 

ваш ответ

Можно ввести 4000 cимволов

отправить

дежурный

Нажимая кнопку «отправить», вы принимаете условия  пользовательского соглашения

похожие темы

Психология

3 класс

5 класс

Репетитор

похожие вопросы 5

Приветик! Кто решил? № 411 Математика 6 класс Виленкин.

Выполните вычисления с помощью микрокалькулятора и резуль-
тат округлите до тысячных:
3,281 ∙ 0,57 + 4,356 ∙ 0,278 — 13,758 (Подробнее…)

ГДЗМатематика6 классВиленкин Н.Я.

Помогите выбрать утверждения. Математика базовый уровень ЕГЭ — 2017. Вар. №1. Зад.№18. Под руководством Ященко И.В.

   Здравствуйте! Перед волейбольным турниром измерили рост игроков волейбольной команды города N. Оказалось, что рост каждого из (Подробнее…)

ЕГЭЭкзаменыМатематикаЯщенко И.В.

На каком расстоянии № 776 ГДЗ Математика 6 класс Дорофеев Г.В. Часть3.

Из города к озеру вышел турист со скоростью 5 км/ч, а через 15 мин вслед за
ним выехал велосипедист со скоростью 20 км/ч. Через (Подробнее…)

ГДЗМатематика6 классДорофеев Г. В.

16. Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)… Цыбулько И. П. Русский язык ЕГЭ-2017 ГДЗ. Вариант 13.

16.
Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)

в предложении должна(-ы) стоять запятая(-ые). (Подробнее…)

ГДЗЕГЭРусский языкЦыбулько И.П.

ЕГЭ-2017 Цыбулько И. П. Русский язык ГДЗ. Вариант 13. 18. Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых). {2}}=\sqrt{100}

Извлеките квадратный корень из обеих частей уравнения.

x+3=10 x+3=-10

Упростите.

x=7 x=-13

Вычтите 3 из обеих частей уравнения.

Квадратный корень из 91 — Как найти квадратный корень из 91?

LearnPracticeDownload

Квадратный корень из 91 выражается как √91 в радикальной форме и как (91) ^½ или (91) ^0,5 в экспоненциальной форме. Квадратный корень из 91, округленный до 10 знаков после запятой, равен 9,5393920142. Это положительное решение уравнения x ² = 91.

• Квадратный корень из 91: 9,539392014169456
• Квадратный корень из 91 в экспоненциальной форме:
  (91) ^½ или (91) ^0,5
• Квадратный корень из 91 в подкоренной форме: √91

1.	Что такое квадратный корень из 91?
2.	Является ли квадратный корень из 91 рациональным или иррациональным?
3.	Как найти квадратный корень из 91?
4.	Часто задаваемые вопросы о квадратном корне из 91

Что такое квадратный корень из 91?

• Квадратный корень числа — это число, которое при умножении само на себя дает исходное число как произведение.
• n × n = 91. Это показывает, что квадрат числа равен 91.
• n = √91 или n = 91 ^½
• Упрощенная форма квадратного корня из 91: √91
.

Является ли квадратный корень из 91 рациональным или иррациональным?

• Рациональное число определяется как число, которое может быть выражено в виде частного или деления двух целых чисел, т. е. p/q, где q не равно 0,
• Значение √91 вычисляется как 9,539392014169456
• Следовательно √91 иррационально.

Как найти квадратный корень из 91?

Квадратный корень из 91 можно вычислить с помощью различных методов, таких как разложение на простые множители, метод длинного деления или метод среднего.

Квадратный корень из 91 методом приближения

• Найдите 2 полных квадрата, ближайших к 91. Это 81 и 100. 81 < 91 < 100
• √81 < √91 < √100
• 9 < √91 < 10
• Разделите 91 на 9 или 10. Разделим на 9. 91 ÷ 9 = 10,11
• Найдите среднее значение этого частного и 9. (10,11 + 9) ÷ 2
• 19,11 ÷ 2 = 9,55
• Таким образом, √91 ≈ 9,55

Квадратный корень из 91 методом деления в длину

• Запишите 91 парами после запятой как 91. 00 00 00.
• Найдите (число × число), которое дает 91 или меньше. Находим 9 × 9 = 81. Вычитаем 81 из 91 и получить 10 в качестве остатка.
• Сбить следующую пару нулей. 10 00 становится новым дивидендом.
• Удвойте частное. Это 18. Теперь вместо нового делителя записывается 18
  0 .
• Найдите (число + 180) × число ≤ 10 00. Определяем, что 18 0 + 5 = 185 и 184 × 5 = 925. 
• Вычтите это из 1000. Это 75 и получите новый делитель, сведя следующую пару нулей. 7500 — это наш новый дивиденд.
• Повторяйте процесс, пока значение не приблизится к 3 знакам после запятой.
• Таким образом, √91 = 9,539

Изучение квадратного корня с помощью иллюстраций и интерактивных примеров

• Квадратный корень из 85
• Квадратный корень из 84
• Квадратный корень из 98
• Квадратный корень из 89
• Квадратный корень из 88

Советы и подсказки

• Знайте, что 91 лежит между полными квадратами 81 и 100, и, следовательно, квадратный корень из 91 лежит между 9и 10.
• Используйте метод усреднения, чтобы аппроксимировать квадратный корень из 91. 

Важные примечания

• Квадратный корень из 91 выражается как √91 в радикальной форме и как 91 ^½ в экспоненциальной форме.
• √91= ± 9,539392014169456

 

1. Пример 1: Джолли загадывает число. Одна седьмая часть квадрата числа равна 13. Какое число может быть округлено до сотых?

   Решение:

   Одна седьмая часть квадрата числа = 1/7 n ²  = 13
   n ²  = 7  × 13 = 91
   п = √91
   = ± 9,5393 = 9,54
   Число 9,54

2. Пример 2 : Какое число Рой должен добавить к 91, чтобы получить число в виде идеального квадрата? Найдите квадратный корень из результирующего числа и прибавления числа. Являются ли оба совершенными квадратами?

   Решение:

   Квадратный корень из 91 лежит между 9 и 10.
   Мы это знаем,
   Квадрат 9 = 81 90 193 Квадрат 10 = 100,90 193 91 лежит между 81 и 100.
   Прибавив число 9 к 91, мы получим
   . 91 + 9 = 100
   Квадратный корень из 100 равен 10.
   Квадратный корень из 9 равен 3.
   Да, 100 и 9 оба числа являются идеальными квадратами.

3. Пример: Если площадь поверхности куба равна 546 в ² . Найдите длину стороны куба.

   Решение:

   Пусть а будет длиной стороны куба.
   ⇒ Площадь куба = 6а ² = 546 в ²
   ⇒ а = ±√91 в
   Поскольку длина не может быть отрицательной,
   ⇒ а = √91
   Мы знаем, что квадратный корень из 91 равен 9,539.
   

   ⇒ а = 9,539 в

перейти к слайдуперейти к слайдуперейти к слайду

Разбивайте сложные концепции с помощью простых визуальных средств.

Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.

Запишитесь на бесплатный пробный урок

Часто задаваемые вопросы о квадратном корне из 91

Каково значение квадратного корня из 91?

Квадратный корень из 91 равен 9,53939.

Почему квадратный корень из 91 является иррациональным числом?

При простой факторизации 91, т. е. 7 ¹ × 13 ¹ , 7 находится в нечетной степени.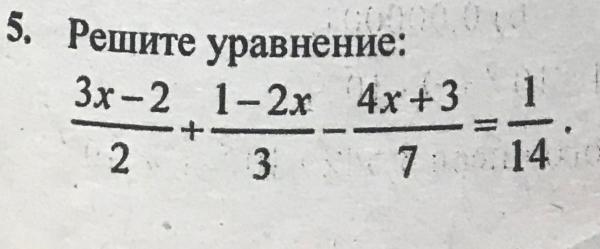 Следовательно, квадратный корень из 91 иррационален.

Чему равен квадрат квадратного корня из 91?

Квадрат квадратного корня из 91 — это само число 91, то есть (√91) ² = (91) ^2/2 = 91.

Является ли число 91 идеальным квадратом?

Разложение числа 91 на простые множители = 7 ¹ × 13 ¹ . Здесь простого множителя 7 нет в паре. Следовательно, 91 не является идеальным квадратом.

Что такое квадратный корень из -91?

Квадратный корень из -91 является мнимым числом. Его можно записать как √-91 = √-1 × √91 = i √91 = 9,539i
. где i = √-1 и называется мнимой единицей.

Вычислить 5 плюс 8 квадратный корень 91

Данное выражение равно 5 + 8 √91. Мы знаем, что квадратный корень из 91 равен 9,539. Таким образом, 5 + 8 √91 = 5 + 8 × 9,539 = 5 + 76,315 = 81,315

Рабочие листы по математике и
визуальные учебные программы

элементарная теория чисел — Найдите все неконгруэнтные решения для $21x \equiv 14 \pmod{91}$

спросил 6 лет, 11 месяцев назад

Изменено 3 года, 9несколько месяцев назад

Просмотрено 7к раз

$\begingroup$

Найдите все неконгруэнтные решения $21x \equiv 14 \pmod{91}$.

Я могу найти решение, используя приемы алгоритма Евклида, но знаки в выражении не совпадают с исходным выражением, когда я проверяю свою работу. Таким образом, по теореме о линейной конгруэнтности мое решение должно удовлетворять: $$21x — 91y = 14$$, но после прохождения процесса с $\gcd(21, 91)$ мое выражение заканчивается как $$91 — 21(4) = 7$$, которое я умножаю на $2$, чтобы получить: $$91(2) — 21(8) = 14$$ Что означало бы, что в моем решении должен быть где-то негатив. Я могу «присвоить» отрицательное значение одному из своих значений, и исходное выражение будет удовлетворено, но это не то, что я получил в результате своей работы. Путаница в знаках происходит намеренно или я что-то не так трактую?

• элементарная теория чисел
• модулярная арифметика
• сравнения

$\endgroup$

6

$\begingroup$

По определению соответствие $$21x \экв 14 \pmod{91} \tag{1}$$ эквивалентно уравнению $$21x = 14 + 91t, t \in \mathbb{Z} \tag{2}$$
Если каждый член уравнения 2 разделить на $7$, мы получим эквивалентное уравнение $$3x = 2 + 13t, t \in \mathbb{Z}$$ что эквивалентно сравнению $$3x \экв 2 \pmod{13} \tag{3}$$ 9{-1} \pmod{13}$$ Поэтому, если мы умножим обе части сравнения 3 на $-4$, мы получим $$x \экв -8 \pmod{13}$$ Чтобы найти все решения сравнения 1, мы должны найти все решения неравенства $$0 \leq -8 + 13t < 91$$ в целых числах. \начать{выравнивать*} 0 & \leq -8 + 13t < 91\\ 8 & \leq 13t < 99\\ \конец{выравнивание*} Следовательно, $1 \leq t \leq 7$. Поэтому решения сравнения $21x \equiv 14 \pmod{91}$ равны \начать{выравнивать*} х & \эквив 5 \pmod{91}\\ & \эквив 18 \pmod{91}\\ & \эквив 31 \pmod{91}\\ & \эквив 44 \pmod{91}\\ & \эквив 57 \pmod{91}\\ & \эквив 70 \pmod{91}\\ & \эквив 83 \pmod{91} \конец{выравнивание*} что можно проверить прямым вычислением.

$\endgroup$

0

$\begingroup$

Более простой способ решить задачу — сначала упростить ее, используя НОД $(21, 14, 91)$ в качестве делителя (НОД=7). Уравнение принимает вид $3x≡2 (mod 13)$. Используйте значения от 0 до 12, чтобы найти решение. Расширенный алгоритм Евклида будет полезен, когда делитель и делимое являются большими числами. Уравнение получает решение при $f(x) = f(5): (5*3)-2 = 13$; $13|13$.