Калькулятор научный Casio FX-85ES Plus 2nd edition
Научный калькулятор Casio FX-85ES Plus 2nd edition разрешен на ЕГЭ по физике, химии и географии. Он эргономичный, простой в использовании и имеет оптимальный набор функций для учебы.Второе поколение знаменитой серии Casio получило обновленный дизайн: теперь устройство еще удобнее лежит в руке, надписи на кнопках читаются легче, а корпус прошел многочисленные испытания на падения. Подтвердить подлинность калькулятора Casio FX-85ES Plus 2nd edition можно с помощью QR-кода: он указан на упаковке и выводится на дисплее устройства.
Важным достоинством Casio FX-85ES Plus 2nd edition является уникальная система Natural Display. Благодаря ей данные выводятся на экран в том же виде, как и в учебниках (естественный вывод математических выражений). Это упрощает вычисления с дробями, логарифмами, радикалами, модулями, корнями, степенями.
Калькулятор Casio FX-85ES Plus 2nd edition имеет 252 опции, в том числе расчеты с дробями, построение таблиц значений функций, разложение простых чисел на множители, тригонометрические, гиперболические, обратные, степенные, логарифмические функции.
У устройства 8 ячеек памяти, есть возможность редактирования и повторения вычислений.
Покупайте калькулятор FX-85ES Plus 2nd edition с официальной гарантией 36 месяцев у дилера Casio — в интернет-магазине Calculators-Online.ru. Доставка осуществляется во все регионы России.
Уроки и методические пособия для самостоятельной работы
- Повышение эффективности учебного процесса и результатов ЕГЭ по физике с использованием научных калькуляторов CASIO
Больше информации в руководстве пользователя
Инструкция к научному калькулятору Casio FX-85es plus 2nd edition на русском языке
Технические характеристики калькулятора
Дисплей с естественным вводом/выводом числовых и буквенных выражений: Natural Textbook Display, Natural-V.P.A.M.
Матричный дисплей
Разрядность: внутренняя — 15, вывод на дисплей (мантисса + экспонента) — (10 + 2) цифр
252 функции
Тригонометрические функции
Ячейки памяти переменных, количество: 8 (A, B, C, D, E, F, Y, X)
Двумерная статистика
Регрессионный анализ
Просмотр, редактирование и повторное вычисление выражений
Вывод ответа в максимально точном виде — в виде обыкновенной дроби
Построение таблиц значений функций
Разложение чисел на простые множители
Генерирование случайных чисел
Источник питания: солнечный элемент и батарея LR44
Чехол: сдвижная пластиковая крышка
Размеры (Ш х В х Т): 80,0 х 162,0 x 11,1 мм
Вес: 95 г
Функции калькулятора
Расчеты с дробями
Генерирование целых случайных чисел
Разложение чисел на простые множители
Просмотр, редактирование и повторное вычисление выражений
24 уровня вложенных скобок
Ячейки памяти переменных, количество: 8 (A, B, C, D, E, F, Y, X)
Кнопки сохранения/вызова чисел в ячейках памяти переменных (STO/RCL)
Научные функции
Тригонометрические и обратные тригонометрические функции
Гиперболические и обратные гиперболические функции
Показательные функции (10x, ex)
Обратная функция (x-1)
Степенные функции и радикалы (√, 3√, x√, x2, x3, xy)
Логарифмические функции (log, ln, logab)
Перестановки и сочетания
Генерирование случайных чисел
Преобразования между полярными и прямоугольными координатами
Два формата представления обыкновенной дроби (смешанная или неправильная дробь)
Преобразования между шестидесятеричными и десятичными величинами
Мера угла в градусах, радианах и градах
Клавиши для вывода на дисплей символов π, e, %
Представление чисел в стандартном виде (SCI) / Округление десятичных дробей до заданной точности (FIX)
Статистические расчеты
Табличный редактор статистических данных
Одномерная статистика
Стандартное отклонение
Двумерная статистика и регрессионный анализ
Линейная регрессия
Экспоненциальная регрессия
Экспоненциальная регрессия ab
Логарифмическая регрессия
Степенная регрессия
Обратная регрессия
Квадратичная регрессия
Вывод на дисплей в естественном виде
Обыкновенные дроби
Радикалы
Степенная регрессия
Скобки
Функция модуля
Логарифмы
Алгебраический формат ввода/ввывода (как в моделях серии fx-MS)
Вывод ответа в виде иррационального выражения, содержащего √
Вывод ответа в виде иррационального выражения, содержащего π
Построение таблиц значений функций
Разрешен для сдачи ЕГЭ по физике, химии и географии.
Добавить комментарий
Уведомлять меня о новых комментариях по E-mail
Наши покупатели уже неоднократно заказывали этот калькулятор и делились с нами информацией, зачем он им необходим, планируют ли они использовать его для учебы или работы.
Прочитайте комментарии — и, возможно, вы откроете для себя новые варианты использования калькулятора:
- ЕГЭ школа 1354
- Работа
- МБОУ «Гимназия 96»
- Университет
- Британская Школа на Крылатском
- ЕГЭ-2021
- Озерская средняя школа
- Школа № 1329
- Британская Школа на Крылатском
- ГБОУ Школа 1506
- МБОУ СШ #66
- Озерская средняя школа
- СОШ 17
- Школа 1502
- Школа РСО — Алания, г.Моздок
- Экзамен СИМА
- ГБОУ 192
- Досуг
- Лицей 23, сдача егэ
- ОГЭ
- Финансовый университет
- Школа / Сдача ЕГЭ
- Школа №7
- Школа имени Достоевского
- школа Летово
- школа, ЕГЭ
- Лицей Сизвова
- МГУ, химический факультет
- Метафизическая лаборатория
- РТУ МИРЭА
- Учеба(инженерный класс)
- Школа, уроки физики
- Школа Гимназия
- ФМЛ №30
- для ЕГЭ
- МАОУ СОШ № 104 г.
Челябинск (будем применять в школе) - егэ по физике
- Учёба, ЕГЭ
- Экзамен
- Гимназия
- Школа
- Сдача огэ по физике
- Институт
- ЕГЭ
- Учёба
- 1595 и для ЕГЭ по физике
- QE Collegiate
- Место работы
- School Integration 21 Century
Челябинск (будем применять в школе)| Производитель: | Casio, Япония |
| Категория: | Графические калькуляторы |
| Гарантийный срок: | 36 мес. |
| Особенности: | программируемый, цветной эран, построение графика по картинке, 3D графика, статистика, QR-код, русификатор меню, Casio, международный бакалавриат IB, экзамен Advanced Placement (AP), ФГОС Математика, SAT Математика, ACT Математика |
Алгоритм Евклида для многочленов. Алгоритм Евклида позволяет найти наибольший общий делитель двух многочленов, т.е. многочлен наибольшей степени, на который делятся без остатка оба данных многочлена. f (x ) = g (x )∙q (x ) + r (x ), (*) при этом степень остатка меньше степени делителя, многочлена g (x ), и, кроме того, по данным многочленам f (x ) и g (x ) частное и остаток находятся однозначно. f (x ) = g (x )∙q 1 (x ) + r 1 (x ), (1) затем, если r 1 (x ) ≠ 0, – второго данного многочлена, g (x ), на первый остаток – на многочлен r 1 (x ): g (x ) = r 1 (x )∙q 2 (x ) + r 2 (x ), (2) r 1 (x ) = r 2 (x )∙q 3 (x ) + r 3 (x ), (3) затем, если r 3 (x ) ≠ 0, – второго остатка на третий: r 2 (x ) = r 3 (x )∙q 4 (x ) + r 4 (x ), (4) и т.
Тогда последний не равный нулю остаток r n и будет наибольшим общим делителем исходной пары многочленов f (x ) и g (x ). |
Как решить уравнения многочлена по математике
Получившаяся в результате дробь
(2.2)
Можно было бы составить систему
уравнений, приравняв числители левой
и правой дробей, но в данном примере
вычисления будут слишком громоздки.
Упростить их поможет следующий прием:
подставим в числители по очереди корни
знаменателя.
Деление многочленов 
При этом, в записи делимого и последующих разностей желательно производить члены суммы по всем убывающим степеням аргумента без пропуска.
При этом последняя разность является остатком.
Поэтому, всякое неравное нулю число называется тривиальным общим делителем данных многочленов.
Тогда,
В итоге, частное и остаток, полученные при делении многочленов с целыми коэффициентами, в раз будут отличаться от искомых значений частного
Q
и остатка
R
, полученных при делении данных многочленов.
Как показано выше, умножение делимого и делителя приведет к соответствующему изменению частного остатка, но такому, что в итоге НОД данных многочленов умножится на некоторое равное нулю число, что допустимо.
0pt»>8х 2х +
Наибольший общий делитель многочленов f(x) и g(x) обозначают символами НОД, d(x), (f(x), g(x)). Заметим, что такое определение НОД имеет место и для целых чисел, хотя чаще используется другое, известное всем студентам.
Делим g(x) на первый остаток, предварительно умножив g(x) на 19:
Если многочлены, для которых находится НОД, имеют одинаковые степени, то делимое и делитель выбираются произвольно.
Таким образом, при умножении делимого на число 0, частное и остаток так же умножаются на, ч.т.д
Это обстоятельство дает возможность упрощать вычисления в алгоритме Евклида. А именно, перед очередным делением делимое или делитель можно умножать на числа, подобранные специальным образом так, чтобы коэффициент первого слагаемого в частном был числом целым. Как показано выше, умножение делимого и делителя приведет к соответствующему изменению частного остатка, но такому, что в итоге НОД данных многочленов умножится на некоторое равное нулю число, что допустимо.
Если в равенстве (*) остаток r (x ) равен нулевому многочлену (нулю), то говорят, что многочлен f (x ) делится на g (x ) без остатка.
д. Поскольку на каждом этапе степень очередного остатка уменьшается, процесс не может продолжаться бесконечно, так что на некотором этапе мы обязательно придем к ситуации, когда очередной, n + 1-й остаток r n + 1 равен нулю:
е. r n – 2 (x ) = r n (x )(q n + 1 (x ) q n (x ) + 1), и т.д. В равенстве (2) после подстановки получим, что g (x ) = r n (x )∙Q (x ), и, наконец, из равенства (1) – что f (x ) = r n (x )∙S (x ), где Q и S – некоторые многочлены. Таким образом, r n (x ) – общий делитель двух исходных многочленов, а то, что он наибольший (т.е. наибольшей возможной степени), следует из процедуры алгоритма.Наибольший общий делитель и наименьшее общее кратное. Онлайн калькулятор
Рассмотрим три способа нахождения наименьшего общего кратного.
Нахождение путём разложения на множители
Первый способ заключается в нахождении наименьшего общего кратного путём разложения данных чисел на простые множители.
Допустим, нам требуется найти НОК чисел: 99, 30 и 28. Для этого разложим каждое из этих чисел на простые множители:
Чтобы искомое число делилось на 99, на 30 и на 28, необходимо и достаточно, чтобы в него входили все простые множители этих делителей. Для этого нам необходимо взять все простые множители этих чисел в наибольшей встречающейся степени и перемножить их между собой:
2 2 · 3 2 · 5 · 7 · 11 = 13 860
Таким образом, НОК (99, 30, 28) = 13 860. Никакое другое число меньше 13 860 не делится нацело на 99, на 30 и на 28.
Чтобы найти наименьшее общее кратное данных чисел, нужно разложить их на простые множители, затем взять каждый простой множитель с наибольшим показателем степени, с каким он встречается, и перемножить эти множители между собой.
Так как взаимно простые числа не имеют общих простых множителей, то их наименьшее общее кратное равно произведению этих чисел. Например, три числа: 20, 49 и 33 — взаимно простые. Поэтому
НОК (20, 49, 33) = 20 · 49 · 33 = 32 340.
Таким же образом надо поступать, когда отыскивается наименьшее общее кратное различных простых чисел. Например, НОК (3, 7, 11) = 3 · 7 · 11 = 231.
Нахождение путём подбора
Второй способ заключается в нахождении наименьшего общего кратного путём подбора.
Пример 1. Когда наибольшее из данных чисел делится нацело на другие данные числа, то НОК этих чисел равно большему из них. Например, дано четыре числа: 60, 30, 10 и 6. Каждое из них делится нацело на 60, следовательно:
НОК (60, 30, 10, 6) = 60
В остальных случаях, чтобы найти наименьшее общее кратное используется следующий порядок действий:
- Определяем наибольшее число из данных чисел.
- Далее находим числа, кратные наибольшему числу, умножая его на натуральные числа в порядке их возрастания и проверяя делятся ли на полученное произведение остальные данные числа.
Пример 2. Дано три числа 24, 3 и 18. Определяем самое большое из них — это число 24. Далее находим числа кратные 24, проверяя делится ли каждое из них на 18 и на 3:
24 · 1 = 24 — делится на 3, но не делится на 18.
24 · 2 = 48 — делится на 3, но не делится на 18.
24 · 3 = 72 — делится на 3 и на 18.
Таким образом, НОК (24, 3, 18) = 72.
Нахождение путём последовательного нахождения НОК
Третий способ заключается в нахождении наименьшего общего кратного путём последовательного нахождения НОК.
НОК двух данных чисел равно произведению этих чисел, поделённого на их наибольший общий делитель.
Пример 1. Найдём НОК двух данных чисел: 12 и 8. Определяем их наибольший общий делитель: НОД (12, 8) = 4. Перемножаем данные числа:
Делим произведение на их НОД:
Таким образом, НОК (12, 8) = 24.
Чтобы найти НОК трёх и более чисел используется следующий порядок действий:
- Сначала находят НОК каких-нибудь двух из данных чисел.
- Потом, НОК найденного наименьшего общего кратного и третьего данного числа.
- Затем, НОК полученного наименьшего общего кратного и четвёртого числа и т. д.
- Таким образом поиск НОК продолжается до тех пор, пока есть числа.
Пример 2. Найдём НОК трёх данных чисел: 12, 8 и 9. НОК чисел 12 и 8 мы уже нашли в предыдущем примере (это число 24). Осталось найти наименьшее общее кратное числа 24 и третьего данного числа — 9. Определяем их наибольший общий делитель: НОД (24, 9) = 3. Перемножаем НОК с числом 9:
Делим произведение на их НОД:
Таким образом, НОК (12, 8, 9) = 72.
Представленный ниже материал является логическим продолжением теории из статьи под заголовком НОК — наименьшее общее кратное, определение, примеры, связь между НОК и НОД . Здесь мы поговорим про нахождение наименьшего общего кратного (НОК) , и особое внимание уделим решению примеров. Сначала покажем, как вычисляется НОК двух чисел через НОД этих чисел. Дальше рассмотрим нахождение наименьшего общего кратного с помощью разложения чисел на простые множители. После этого остановимся на нахождении НОК трех и большего количества чисел, а также уделим внимание вычислению НОК отрицательных чисел.
Навигация по странице.
Вычисление наименьшего общего кратного (НОК) через НОД
Один из способов нахождения наименьшего общего кратного основан на связи между НОК и НОД . Существующая связь между НОК и НОД позволяет вычислять наименьшее общее кратное двух целых положительных чисел через известный наибольший общий делитель. Соответствующая формула имеет вид НОК(a, b)=a·b:НОД(a, b) . Рассмотрим примеры нахождения НОК по приведенной формуле.
Пример.
Найдите наименьшее общее кратное двух чисел 126 и 70 .
Решение.
В этом примере a=126 , b=70 . Воспользуемся связью НОК с НОД, выражающуюся формулой НОК(a, b)=a·b:НОД(a, b) . То есть, сначала нам предстоит найти наибольший общий делитель чисел 70 и 126 , после чего мы сможем вычислить НОК этих чисел по записанной формуле.
Найдем НОД(126, 70) , используя алгоритм Евклида: 126=70·1+56 , 70=56·1+14 , 56=14·4 , следовательно, НОД(126, 70)=14 .
Теперь находим требуемое наименьшее общее кратное: НОК(126, 70)=126·70:НОД(126, 70)=
126·70:14=630
.
Ответ:
НОК(126, 70)=630 .
Пример.
Чему равно НОК(68, 34) ?
Решение.
Так как 68 делится нацело на 34 , то НОД(68, 34)=34 . Теперь вычисляем наименьшее общее кратное: НОК(68, 34)=68·34:НОД(68, 34)= 68·34:34=68 .
Ответ:
НОК(68, 34)=68 .
Заметим, что предыдущий пример подходит под следующее правило нахождения НОК для целых положительные чисел a и b : если число a делится на b , то наименьшее общее кратное этих чисел равно a .
Нахождение НОК с помощью разложения чисел на простые множители
Другой способ нахождения наименьшего общего кратного базируется на разложении чисел на простые множители . Если составить произведение из всех простых множителей данных чисел, после чего из этого произведения исключить все общие простые множители, присутствующие в разложениях данных чисел, то полученное произведение будет равно наименьшему общему кратному данных чисел .
Озвученное правило нахождения НОК следует из равенства НОК(a, b)=a·b:НОД(a, b)
.
Действительно, произведение чисел a
и b
равно произведению всех множителей, участвующих в разложениях чисел a
и b
. В свою очередь НОД(a, b)
равен произведению всех простых множителей, одновременно присутствующих в разложениях чисел a
и b
(о чем написано в разделе нахождение НОД с помощью разложения чисел на простые множители).
Приведем пример. Пусть мы знаем, что 75=3·5·5 и 210=2·3·5·7 . Составим произведение из всех множителей данных разложений: 2·3·3·5·5·5·7 . Теперь из этого произведения исключим все множители, присутствующие и в разложении числа 75 и в разложении числа 210 (такими множителями являются 3 и 5 ), тогда произведение примет вид 2·3·5·5·7 . Значение этого произведения равно наименьшему общему кратному чисел 75 и 210 , то есть, НОК(75, 210)= 2·3·5·5·7=1 050 .
Пример.
Разложив числа 441 и 700 на простые множители, найдите наименьшее общее кратное этих чисел.
Решение.
Разложим числа 441 и 700 на простые множители:
Получаем 441=3·3·7·7
и 700=2·2·5·5·7
.
Теперь составим произведение из всех множителей, участвующих в разложениях данных чисел: 2·2·3·3·5·5·7·7·7 . Исключим из этого произведения все множители, одновременно присутствующие в обоих разложениях (такой множитель только один – это число 7 ): 2·2·3·3·5·5·7·7 . Таким образом, НОК(441, 700)=2·2·3·3·5·5·7·7=44 100 .
Ответ:
НОК(441, 700)= 44 100 .
Правило нахождения НОК с использованием разложения чисел на простые множители можно сформулировать немного иначе. Если ко множителям из разложения числа a добавить недостающие множители из разложения числа b , то значение полученного произведения будет равно наименьшему общему кратному чисел a и b .
Для примера возьмем все те же числа 75
и 210
, их разложения на простые множители таковы: 75=3·5·5
и 210=2·3·5·7
. Ко множителям 3
, 5
и 5
из разложения числа 75
добавляем недостающие множители 2
и 7
из разложения числа 210
, получаем произведение 2·3·5·5·7
, значение которого равно НОК(75, 210)
.
Пример.
Найдите наименьшее общее кратное чисел 84 и 648 .
Решение.
Получаем сначала разложения чисел 84 и 648 на простые множители. Они имеют вид 84=2·2·3·7 и 648=2·2·2·3·3·3·3 . К множителям 2 , 2 , 3 и 7 из разложения числа 84 добавляем недостающие множители 2 , 3 , 3 и 3 из разложения числа 648 , получаем произведение 2·2·2·3·3·3·3·7 , которое равно 4 536 . Таким образом, искомое наименьшее общее кратное чисел 84 и 648 равно 4 536 .
Ответ:
НОК(84, 648)=4 536 .
Нахождение НОК трех и большего количества чисел
Наименьшее общее кратное трех и большего количества чисел может быть найдено через последовательное нахождение НОК двух чисел. Напомним соответствующую теорему, дающую способ нахождения НОК трех и большего количества чисел.
Теорема.
Пусть даны целые положительные числа a 1 , a 2 , …, a k
, наименьшее общее кратное m k
этих чисел находится при последовательном вычислении m 2 =НОК(a 1 , a 2)
, m 3 =НОК(m 2 , a 3)
, …, m k =НОК(m k−1 , a k)
.
Рассмотрим применение этой теоремы на примере нахождения наименьшего общего кратного четырех чисел.
Пример.
Найдите НОК четырех чисел 140 , 9 , 54 и 250 .
Решение.
В этом примере a 1 =140 , a 2 =9 , a 3 =54 , a 4 =250 .
Сначала находим m 2 =НОК(a 1 , a 2)=НОК(140, 9) . Для этого по алгоритму Евклида определяем НОД(140, 9) , имеем 140=9·15+5 , 9=5·1+4 , 5=4·1+1 , 4=1·4 , следовательно, НОД(140, 9)=1 , откуда НОК(140, 9)=140·9:НОД(140, 9)= 140·9:1=1 260 . То есть, m 2 =1 260 .
Теперь находим m 3 =НОК(m 2 , a 3)=НОК(1 260, 54) . Вычислим его через НОД(1 260, 54) , который также определим по алгоритму Евклида: 1 260=54·23+18 , 54=18·3 . Тогда НОД(1 260, 54)=18 , откуда НОК(1 260, 54)= 1 260·54:НОД(1 260, 54)= 1 260·54:18=3 780 . То есть, m 3 =3 780 .
Осталось найти m 4 =НОК(m 3 , a 4)=НОК(3 780, 250)
. Для этого находим НОД(3 780, 250)
по алгоритму Евклида: 3 780=250·15+30
, 250=30·8+10
, 30=10·3
. Следовательно, НОД(3 780, 250)=10
, откуда НОК(3 780, 250)=
3 780·250:НОД(3 780, 250)=
3 780·250:10=94 500
.
То есть, m 4 =94 500
.
Таким образом, наименьшее общее кратное исходных четырех чисел равно 94 500 .
Ответ:
НОК(140, 9, 54, 250)=94 500 .
Во многих случаях наименьшее общее кратное трех и большего количества чисел удобно находить с использованием разложений данных чисел на простые множители. При этом следует придерживаться следующего правила. Наименьшее общее кратное нескольких чисел равно произведению, которое составляется так: ко всем множителям из разложения первого числа добавляются недостающие множители из разложения второго числа, к полученным множителям добавляются недостающие множители из разложения третьего числа и так далее .
Рассмотрим пример нахождения наименьшего общего кратного с использованием разложения чисел на простые множители.
Пример.
Найдите наименьшее общее кратное пяти чисел 84 , 6 , 48 , 7 , 143 .
Решение.
Сначала получаем разложения данных чисел на простые множители: 84=2·2·3·7
, 6=2·3
, 48=2·2·2·2·3
, 7
(7
– простое число , оно совпадает со своим разложением на простые множители) и 143=11·13
.
Для нахождения НОК данных чисел к множителям первого числа 84 (ими являются 2 , 2 , 3 и 7 ) нужно добавить недостающие множители из разложения второго числа 6 . Разложение числа 6 не содержит недостающих множителей, так как и 2 и 3 уже присутствуют в разложении первого числа 84 . Дальше к множителям 2 , 2 , 3 и 7 добавляем недостающие множители 2 и 2 из разложения третьего числа 48 , получаем набор множителей 2 , 2 , 2 , 2 , 3 и 7 . К этому набору на следующем шаге не придется добавлять множителей, так как 7 уже содержится в нем. Наконец, к множителям 2 , 2 , 2 , 2 , 3 и 7 добавляем недостающие множители 11 и 13 из разложения числа 143 . Получаем произведение 2·2·2·2·3·7·11·13 , которое равно 48 048 .
Кратное число – это число, которое делится на данное число без остатка. Наименьшее общее кратное (НОК) группы чисел – это наименьшее число, которое делится без остатка на каждое число группы. Чтобы найти наименьшее общее кратное, нужно найти простые множители данных чисел.
Также НОК можно вычислить с помощью ряда других методов, которые применимы к группам из двух и более чисел.
Шаги
Ряд кратных чисел
Посмотрите на данные числа. Описанный здесь метод лучше применять, когда даны два числа, каждое из которых меньше 10. Если даны большие числа, воспользуйтесь другим методом.
- Например, найдите наименьшее общее кратное чисел 5 и 8. Это небольшие числа, поэтому можно использовать данный метод.
Кратное число – это число, которое делится на данное число без остатка. Кратные числа можно посмотреть в таблице умножения..
- Например, числами, которые кратны 5, являются: 5, 10, 15, 20, 25, 30, 35, 40.
Запишите ряд чисел, которые кратны первому числу. Сделайте это под кратными числами первого числа, чтобы сравнить два ряда чисел.
- Например, числами, которые кратны 8, являются: 8, 16, 24, 32, 40, 48, 56, и 64.
Найдите наименьшее число, которое присутствует в обоих рядах кратных чисел.
Возможно, вам придется написать длинные ряды кратных чисел, чтобы найти общее число. Наименьшее число, которое присутствует в обоих рядах кратных чисел, является наименьшим общим кратным.
- Например, наименьшим числом, которое присутствует в рядах кратных чисел 5 и 8, является число 40. Поэтому 40 – это наименьшее общее кратное чисел 5 и 8.
Разложение на простые множители
Посмотрите на данные числа. Описанный здесь метод лучше применять, когда даны два числа, каждое из которых больше 10. Если даны меньшие числа, воспользуйтесь другим методом.
- Например, найдите наименьшее общее кратное чисел 20 и 84. Каждое из чисел больше 10, поэтому можно использовать данный метод.
Разложите на простые множители первое число. То есть нужно найти такие простые числа, при перемножении которых получится данное число. Найдя простые множители, запишите их в виде равенства.
- Например, 2 × 10 = 20 {\displaystyle {\mathbf {2} }\times 10=20}
и 2 × 5 = 10 {\displaystyle {\mathbf {2} }\times {\mathbf {5} }=10}
. Таким образом, простыми множителями числа 20 являются числа 2, 2 и 5. Запишите их в виде выражения: .
- Например, 2 × 10 = 20 {\displaystyle {\mathbf {2} }\times 10=20}
и 2 × 5 = 10 {\displaystyle {\mathbf {2} }\times {\mathbf {5} }=10}
.
Разложите на простые множители второе число. Сделайте это так же, как вы раскладывали на множители первое число, то есть найдите такие простые числа, при перемножении которых получится данное число.
- Например, 2 × 42 = 84 {\displaystyle {\mathbf {2} }\times 42=84} , 7 × 6 = 42 {\displaystyle {\mathbf {7} }\times 6=42} и 3 × 2 = 6 {\displaystyle {\mathbf {3} }\times {\mathbf {2} }=6} . Таким образом, простыми множителями числа 84 являются числа 2, 7, 3 и 2. Запишите их в виде выражения: .
Запишите множители, общие для обоих чисел. Запишите такие множители в виде операции умножения. По мере записи каждого множителя зачеркивайте его в обоих выражениях (выражения, которые описывают разложения чисел на простые множители).
- Например, общим для обоих чисел является множитель 2, поэтому напишите 2 × {\displaystyle 2\times }
и зачеркните 2 в обоих выражениях.
- Общим для обоих чисел является еще один множитель 2, поэтому напишите 2 × 2 {\displaystyle 2\times 2} и зачеркните вторую 2 в обоих выражениях.
- Например, общим для обоих чисел является множитель 2, поэтому напишите 2 × {\displaystyle 2\times }
и зачеркните 2 в обоих выражениях.
К операции умножения добавьте оставшиеся множители. Это множители, которые не зачеркнуты в обоих выражениях, то есть множители, не являющиеся общими для обоих чисел.
- Например, в выражении 20 = 2 × 2 × 5 {\displaystyle 20=2\times 2\times 5} зачеркнуты обе двойки (2), потому что они являются общими множителями. Не зачеркнут множитель 5, поэтому операцию умножения запишите так: 2 × 2 × 5 {\displaystyle 2\times 2\times 5}
- В выражении 84 = 2 × 7 × 3 × 2 {\displaystyle 84=2\times 7\times 3\times 2} также зачеркнуты обе двойки (2). Не зачеркнуты множители 7 и 3, поэтому операцию умножения запишите так: 2 × 2 × 5 × 7 × 3 {\displaystyle 2\times 2\times 5\times 7\times 3} .
Вычислите наименьшее общее кратное. Для этого перемножьте числа в записанной операции умножения.
- Например, 2 × 2 × 5 × 7 × 3 = 420 {\displaystyle 2\times 2\times 5\times 7\times 3=420} . Таким образом, наименьшее общее кратное 20 и 84 равно 420.
Таким образом, простыми множителями числа 20 являются числа 2, 2 и 5. Запишите их в виде выражения: .
Нахождение общих делителей
Нарисуйте сетку как для игры в крестики-нолики. Такая сетка представляет собой две параллельные прямые, которые пересекаются (под прямым углом) с другими двумя параллельными прямыми. Таким образом, получатся три строки и три столбца (сетка очень похожа на значок #). Первое число напишите в первой строке и втором столбце. Второе число напишите в первой строке и третьем столбце.
- Например, найдите наименьшее общее кратное чисел 18 и 30. Число 18 напишите в первой строке и втором столбце, а число 30 напишите в первой строке и третьем столбце.
Найдите делитель, общий для обоих чисел. Запишите его в первой строке и первом столбце. Лучше искать простые делители, но это не является обязательным условием.
- Например, 18 и 30 – это четные числа, поэтому их общим делителем будет число 2. Таким образом, напишите 2 в первой строке и первом столбце.
- Например, 18 и 30 – это четные числа, поэтому их общим делителем будет число 2.
Разделите каждое число на первый делитель. Каждое частное запишите под соответствующим числом. Частное – это результат деления двух чисел.
- Например, 18 ÷ 2 = 9 {\displaystyle 18\div 2=9} , поэтому запишите 9 под 18.
- 30 ÷ 2 = 15 {\displaystyle 30\div 2=15} , поэтому запишите 15 под 30.
Найдите делитель, общий для обоих частных. Если такого делителя нет, пропустите два следующих шага. В противном случае делитель запишите во второй строке и первом столбце.
- Например, 9 и 15 делятся на 3, поэтому запишите 3 во второй строке и первом столбце.
Разделите каждое частное на второй делитель. Каждый результат деления запишите под соответствующим частным.
- Например, 9 ÷ 3 = 3 {\displaystyle 9\div 3=3} , поэтому запишите 3 под 9.
- 15 ÷ 3 = 5 {\displaystyle 15\div 3=5}
, поэтому запишите 5 под 15.
Если нужно, дополните сетку дополнительными ячейками. Повторяйте описанные действия до тех пор, пока у частных не будет общего делителя.
Обведите кружками числа в первом столбце и последней строке сетки. Затем выделенные числа запишите в виде операции умножения.
- Например, числа 2 и 3 находятся в первом столбце, а числа 3 и 5 находятся в последней строке, поэтому операцию умножения запишите так: 2 × 3 × 3 × 5 {\displaystyle 2\times 3\times 3\times 5} .
Найдите результат умножения чисел. Так вы вычислите наименьшее общее кратное двух данных чисел.
- Например, 2 × 3 × 3 × 5 = 90 {\displaystyle 2\times 3\times 3\times 5=90} . Таким образом, наименьшее общее кратное 18 и 30 равно 90.
Таким образом, напишите 2 в первой строке и первом столбце.
Алгоритм Евклида
Запомните терминологию, связанную с операцией деления. Делимое – это число, которое делят. Делитель – это число, на которое делят.
Частное – это результат деления двух чисел. Остаток – это число, оставшееся при делении двух чисел.- Например, в выражении 15 ÷ 6 = 2 {\displaystyle 15\div 6=2}
ост. 3:
15 – это делимое
6 – это делитель
2 – это частное
3 – это остаток.
- Например, в выражении 15 ÷ 6 = 2 {\displaystyle 15\div 6=2}
ост. 3:
Частное – это результат деления двух чисел. Остаток – это число, оставшееся при делении двух чисел.Онлайн калькулятор позволяет быстро находить наибольший общий делитель и наименьшее общее кратное как для двух, так и для любого другого количества чисел.
Калькулятор для нахождения НОД и НОК
Найти НОД и НОК
Найдено НОД и НОК: 5806
Как пользоваться калькулятором
- Введите числа в поле для ввода
- В случае ввода некорректных символов поле для ввода будет подсвечено красным
- нажмите кнопку «Найти НОД и НОК»
Как вводить числа
- Числа вводятся через пробел, точку или запятую
- Длина вводимых чисел не ограничена , так что найти НОД и НОК длинных чисел не составит никакого труда
Что такое НОД и НОК?
Наибольший общий делитель нескольких чисел – это наибольшее натуральное целое число, на которое все исходные числа делятся без остатка.
Наибольший общий делитель сокращённо записывается как НОД .
Наименьшее общее кратное нескольких чисел – это наименьшее число, которое делится на каждое из исходных чисел без остатка. Наименьшее общее кратное сокращённо записывается как НОК .
Как проверить, что число делится на другое число без остатка?
Чтобы узнать, делится ли одно число на другое без остатка, можно воспользоваться некоторыми свойствами делимости чисел. Тогда, комбинируя их, можно проверять делимость на некоторые их них и их комбинации.
Некоторые признаки делимости чисел
1. Признак делимости числа на 2
Чтобы определить, делится ли число на два (является ли оно чётным), достаточно посмотреть на последнююю цифру этого числа: если она равна 0, 2, 4, 6 или 8, то число чётно, а значит делится на 2.
Пример: определить, делится ли на 2 число 34938 .
Решение: смотрим на последнюю цифру: 8 — значит число делится на два.
2. Признак делимости числа на 3
Число делится на 3 тогда, когда сумма его цифр делится на три.
Таким образом, чтобы определить, делится ли число на 3, нужно посчитать сумму цифр и проверить, делится ли она на 3. Даже если сумма цифр получилась очень большой, можно повторить этот же процесс вновь.
Пример: определить, делится ли число 34938 на 3.
Решение: считаем сумму цифр: 3+4+9+3+8 = 27. 27 делится на 3, а значит и число делится на три.
3. Признак делимости числа на 5
Число делится на 5 тогда, когда его последняя цифра равна нулю или пяти.
Пример: определить, делится ли число 34938 на 5.
Решение: смотрим на последнюю цифру: 8 — значит число НЕ делится на пять.
4. Признак делимости числа на 9
Этот признак очень похож на признак делимости на тройку: число делится на 9 тогда, когда сумма его цифр делится на 9.
Пример: определить, делится ли число 34938 на 9.
Решение: считаем сумму цифр: 3+4+9+3+8 = 27. 27 делится на 9, а значит и число делится на девять.
Как найти НОД и НОК двух чисел
Как найти НОД двух чисел
Наиболее простым способом вычисления наибольшего общего делителя двух чисел является поиск всех возможных делителей этих чисел и выбор наибольшего из них.
Рассмотрим этот способ на примере нахождения НОД(28, 36) :
- Раскладываем оба числа на множители: 28 = 1·2·2·7 , 36 = 1·2·2·3·3
- Находим общие множители, то есть те, которые есть у обоих чисел: 1, 2 и 2.
- Вычисляем произведение этих множителей: 1·2·2 = 4 — это и есть наибольший общий делитель чисел 28 и 36.
Как найти НОК двух чисел
Наиболее распространены два способа нахождения наименьшего кратного двух чисел. Первый способ заключается в том, что можно выписать первые кратные двух чисел, а затем выбрать среди них такое число, которое будет общим для обоих чисел и при этом наименьшем. А второй заключается в нахождении НОД этих чисел. Рассмотрим только его.
Для вычисления НОК нужно вычислить произведение исходных чисел и затем разделить его на предварительно найденный НОД. Найдём НОК для тех же чисел 28 и 36:
- Находим произведение чисел 28 и 36: 28·36 = 1008
- НОД(28, 36), как уже известно, равен 4
- НОК(28, 36) = 1008 / 4 = 252 .
Нахождение НОД и НОК для нескольких чисел
Наибольший общий делитель можно находить и для нескольких чисел, а не только для двух. Для этого числа, подлежащие поиску наибольшего общего делителя, раскладывают на простые множители, затем находят произведение общих простых множителей этих чисел. Также для нахождение НОД нескольких чисел можно воспользоваться следующим соотношением: НОД(a, b, c) = НОД(НОД(a, b), c) .
Аналогичное соотношение действует и для наименьшего общего кратного чисел: НОК(a, b, c) = НОК(НОК(a, b), c)
Пример: найти НОД и НОК для чисел 12, 32 и 36.
- Cперва разложим числа на множители: 12 = 1·2·2·3 , 32 = 1·2·2·2·2·2 , 36 = 1·2·2·3·3 .
- Найдём обшие множители: 1, 2 и 2 .
- Их произведение даст НОД: 1·2·2 = 4
- Найдём теперь НОК: для этого найдём сначала НОК(12, 32): 12·32 / 4 = 96 .
- Чтобы найти НОК всех трёх чисел, нужно найти НОД(96, 36): 96 = 1·2·2·2·2·2·3 , 36 = 1·2·2·3·3 , НОД = 1·2·2·3 = 12 .
- НОК(12, 32, 36) = 96·36 / 12 = 288 .
Математические выражения и задачи требуют множества дополнительных знаний. НОК — это одно из основных, особенно часто применяемое в Тема изучается в средней школе, при этом не является особо сложным в понимании материалом, человеку знакомому со степенями и таблицей умножения не составит труда выделить необходимые числа и обнаружить результат.
Определение
Общее кратное — число, способное нацело разделиться на два числа одновременно (а и b). Чаще всего, это число получают методом перемножения исходных чисел a и b. Число обязано делиться сразу на оба числа, без отклонений.
НОК — это принятое для обозначения краткое название, собранной из первых букв.
Способы получения числа
Для нахождения НОК не всегда подходит способ перемножения чисел, он гораздо лучше подходит для простых однозначных или двухзначных чисел. принято разделять на множители, чем больше число, тем больше множителей будет.
Пример № 1
Для простейшего примера в школах обычно берутся простые, однозначные или двухзначные числа.
Например, необходимо решить следующее задание, найти наименьшее общее кратное от чисел 7 и 3, решение достаточно простое, просто их перемножить. В итоге имеется число 21, меньшего числа просто нет.
Пример № 2
Второй вариант задания гораздо сложнее. Даны числа 300 и 1260, нахождение НОК — обязательно. Для решения задания предполагаются следующие действия:
Разложение первого и второго чисел на простейшие множители. 300 = 2 2 * 3 * 5 2 ; 1260 = 2 2 * 3 2 *5 *7. Первый этап завершен.
Второй этап предполагает работу с уже полученными данными. Каждое из полученных чисел обязано участвовать в вычислении итогового результата. Для каждого множителя из состава исходных чисел берется самое большое число вхождений. НОК — это общее число, поэтому множители из чисел должны в нем повторятся все до единого, даже те, которые присутствуют в одном экземпляре. Оба изначальных числа имеют в своем составе числа 2, 3 и 5, в разных степенях, 7 есть только в одном случае.
Для вычисления итогового результата необходимо взять каждое число в наибольшей их представленных степеней, в уравнение. Остается только перемножить и получить ответ, при правильном заполнении задача укладывается в два действия без пояснений:
1) 300 = 2 2 * 3 * 5 2 ; 1260 = 2 2 * 3 2 *5 *7.
2) НОК = 6300.
Вот и вся задача, если попробовать вычислить нужное число посредством перемножения, то ответ однозначно не будет верным, так как 300 * 1260 = 378 000.
Проверка:
6300 / 300 = 21 — верно;
6300 / 1260 = 5 — верно.
Правильность полученного результата определяется посредством проверки — деления НОК на оба исходных числа, если число целое в обоих случаях, то ответ верен.
Что значит НОК в математике
Как известно, в математике нет ни одной бесполезной функции, эта — не исключение. Самым распространенным предназначением этого числа является приведение дробей к общему знаменателю. Что изучают обычно в 5-6 классах средней школы.
Также дополнительно является общим делителем для всех кратных чисел, если такие условия стоят в задаче. Подобное выражение может найти кратное не только к двум числам, но и к гораздо большему количестве — трем, пяти и так далее. Чем больше чисел — тем больше действий в задаче, но сложность от этого не увеличивается.
Например, даны числа 250, 600 и 1500, необходимо найти их общее НОК:
1) 250 = 25 * 10 = 5 2 *5 * 2 = 5 3 * 2 — на этом примере детально описано разложение на множители, без сокращения.
2) 600 = 60 * 10 = 3 * 2 3 *5 2 ;
3) 1500 = 15 * 100 = 33 * 5 3 *2 2 ;
Для того чтобы составить выражение, требуется упомянуть все множители, в этом случае даны 2, 5, 3, — для всех этих чисел требуется определить максимальную степень.
Внимание: все множители необходимо доводить до полного упрощения, по возможности, раскладывая до уровня однозначных.
Проверка:
1) 3000 / 250 = 12 — верно;
2) 3000 / 600 = 5 — верно;
3) 3000 / 1500 = 2 — верно.
Данный метод не требует каких-либо ухищрений или способностей уровня гения, все просто и понятно.
Еще один способ
В математике многое связано, многое можно решить двумя и более способами, то же самое касается поиска наименьшего общего кратного, НОК. Следующий способ можно использовать в случае с простыми двузначными и однозначными числами. Составляется таблица, в которую вносятся по вертикали множимое, по горизонтали множитель, а в пересекающихся клетках столбца указывается произведение. Можно отразить таблицу посредством строчки, берется число и в ряд записываются результаты умножения этого числа на целые числа, от 1 до бесконечности, иногда хватает и 3-5 пунктов, второе и последующие числа подвергаются тому же вычислительному процессу. Все происходит вплоть до того, как найдется общее кратное.
Даны числа 30, 35, 42 необходимо найти НОК, связывающий все числа:
1) Кратные 30: 60, 90, 120, 150, 180, 210, 250 и т. д.
2) Кратные 35: 70, 105, 140, 175, 210, 245 и т.
д.
3) Кратные 42: 84, 126, 168, 210, 252 и т. д.
Заметно, что все числа достаточно разные, единственное общее среди них число 210, вот оно и будет НОК. Среди связанных с этим вычислением процессов есть также наибольший общий делитель, вычисляющийся по похожим принципам и часто встречающийся в соседствующих задачах. Различие невелико, но достаточно значимо, НОК предполагает вычисление числа, которое делится на все данные исходные значения, а НОД предполагает под собой вычисление наибольшего значение на которое делятся исходные числа.
Калькулятор факторизации с шагами
В общем, первый шаг в факторизации любого алгебраического выражения состоит в том, чтобы определить, имеют ли термины общий множитель. Факторинг или факторизация — это процесс разбиения выражения на более простые выражения, произведение которых равно исходному выражению.
Наш калькулятор факторинговых полиномов может преобразовать любые алгебраические выражения в произведение простых множителей/простых множителей.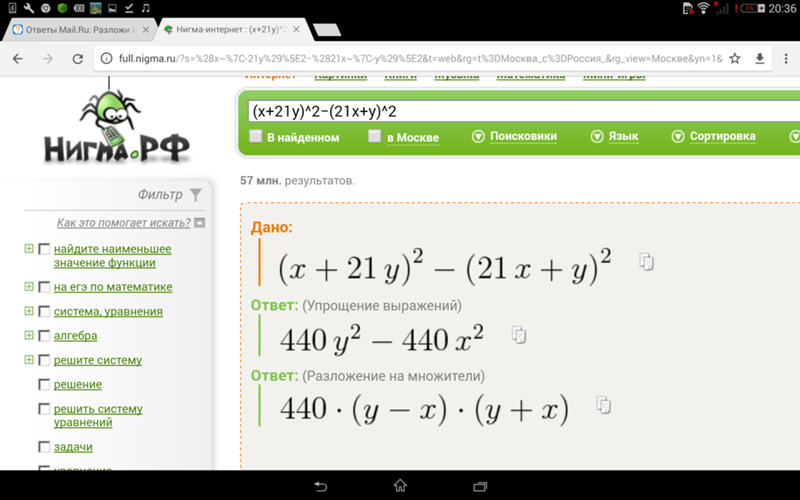
2-3x+3q \neq 0
Факторное выражение Калькулятор для биномов, квадратичных и полиномиальных выражений
Этот калькулятор поможет вам разложить любые алгебраические выражения на его множители. Калькулятор работает с любым алгебраическим выражением.
Бесплатный онлайн-калькулятор Factor Expression
Чтобы узнать, как работает калькулятор коэффициентов, нажмите кнопку «Попробовать», чтобы просмотреть решения с пошаговыми инструкциями. Вы также можете ввести выражение в поле ввода, указанное выше, и нажать кнопку «коэффициент», чтобы просмотреть решение. 92-9
Решение: (2x+3)(2x-3)
Как работает бесплатный калькулятор факторизации
Факторизация — это процесс разбиения сложного выражения на более простые элементы. Чтобы полностью разложить выражение на множители, нужно переписать выражение как произведение его неприводимых произведений. Таким образом, выражение факторизуемо тогда и только тогда, когда оно может быть записано как произведение двух или более множителей при умножении.
Например, 2x-2= 2(x-1) , в этом примере 2 и x-1 являются множителями 2x-2, множители являются простыми / неприводимыми, так как их нельзя разбить на более простые множители с рациональным числом 92-1)
Решение: (x-3)(x+1)(x-1)
Из приведенных выше примеров видно, что выражение называется полностью факторизованным, если оно может быть полностью выражено как произведение простых множителей. Кроме того, выражение может быть составлено из любой комбинации терминов и факторов.
Фактор числа в калькуляторе простых множителей
Наш калькулятор факторизации поможет вам переписать любое число как произведение его простых множителей. Любое число можно записать как произведение его простых множителей с помощью процесса факторизации. Процесс включает итерацию деления с наименьшим делителем заданного числа.
Разложить рациональное число на простые множители
Любое рациональное число можно разложить на простые множители. Учитывая рациональное число q, мы можем записать его как произведение его простых множителей e.
i q= p0 \times p_1 \times p_2….. \times pn, где p_0,p_1,p_2…. p_n — это конечное множество простых множителей или делителей числа q. Наш калькулятор множителей поможет вам разложить любое число на его простые множители. Чтобы разложить число, просто введите число в текстовую область, нажмите кнопку фактора, чтобы продолжить.
Как работает онлайн-калькулятор коэффициентов
Существует несколько методов, которые применяются при факторизации выражения. Применяемая техника зависит от данного выражения. Однако разложение выражения на множители не всегда очевидно, и не все выражения можно разложить на множители. Изучение того, как разложить выражение на множители, является полезным методом, который полезен при решении или нахождении корней многочленов.
Разложение выражения на множители с помощью калькулятора группировки
Это один из основных методов, применяемых при разложении выражений на множители. Метод группирует термины в выражении, находя общие факторы.
92-2x+y
Пример 3: множитель ax — ay — 2x + 2y
Решение: a(x-y)-2(x-y)=(a-2)(x-y)
Обратите внимание, что (a-2) и (x-y) являются множителями ax-ay-2x+2y
Разложение на множители трехчленного выражения
Трехчлен представляет собой алгебраическое выражение, состоящее из 3 членов, которые объединены сложением и вычитанием. Обычно трехчлен представляет собой произведение двух двучленов. Большинство задач факторинга связаны с трехчленами и могут быть решены с использованием нескольких методов.
Примеры трехчленных выражений и способы их разложения на множители 92-x-2 =(x+1)(x-1)(x+2) — полная факторизация выражения.
Калькулятор факторных полиномов
Полином — это алгебраическое выражение, включающее переменные, показатели степени и коэффициенты, а сложение и вычитание — единственные операции между членами. В то время как некоторые полиномы могут быть разложены на неприводимые/простые множители, другие нельзя разложить на множители.
Для многочленов степени выше 2 не существует общей процедуры факторизации. В таком случае применяется метод проб и ошибок. Наш калькулятор факторинговых полиномов дает вам мгновенное решение или коэффициенты для любого факторизуемого полинома. Это поможет вам избежать длительной процедуры проб и ошибок, которая может быть не лучшим подходом.
Чтобы разложить полином с помощью нашего калькулятора факторизации, просто введите алгебраическое выражение в соответствующее поле ввода, нажмите кнопку множителя для расчета.
Создание эквивалентных выражений с помощью калькулятора факторизации
Факторизация выражения означает создание эквивалентного выражения или коэффициентов исходного выражения таким образом, что при умножении/упрощении они приводят к исходному выражению. Создание эквивалентного выражения или разложение на множители может быть утомительным, особенно при работе с многочленами более высокой степени.
Наш факторинговый калькулятор позволяет; вы мгновенно находите факторы для данного алгебраического выражения.
Калькулятор полной факторизации трехчлена
Многочлен называется полностью факторизованным, если он записан в виде произведения простых множителей. При разложении полинома на множители результирующие множители не всегда неприводимы и нуждаются в дальнейшем факторинге. Наш калькулятор факторинга для полинома позволяет полностью факторизовать выражение, что приводит к простой факторизации. Калькулятор переписывает выражение путем факторизации калькулятора. 92 )+( 2y-xy)=x (2-x) +y(2-x)=(2-x)(x+y)
Gcf с калькулятором показателей степени
Ниже приведен ряд ключевых слов, которые сегодня вводили наши пользователи, чтобы попасть на сайт.
Чем это может быть вам полезно?
Найдите искомый термин (например, gcf с калькулятором показателей) в крайнем левом столбце ниже
Нажмите на соответствующую демонстрацию программы, которая находится в той же строке, что и ваша поисковая фраза gcf с калькулятором показателей
Если вы считаете, что демоверсия программы полезна, нажмите на кнопку покупки, чтобы купить программу по специальной цене, доступной только для посетителей сайта factoring-polynomials.
com
com| Родственная поисковая фраза | Алгебратор анимированный Flash Demo | Статическая демонстрация алгоритма | Купить сейчас |
| практика проблем жесткого факторинга | |||
| графический калькулятор решает системы уравнений с тремя переменными | |||
| Рабочий лист многошаговых уравнений | |||
| какие распечатки сделать с шестиклассником | |||
| сравнение листов с целыми числами | |||
| решатель умножения и деления подкоренных выражений | |||
| решить уравнение в кубе | |||
| Рабочий лист по построению графиков линейных уравнений | |||
| решатель нелинейных уравнений | |||
| ti-83 графический калькулятор финансовые коэффициенты | |||
| Бесплатные рабочие листы 6 класс естествознание | |||
| вычитание с миллиметровой бумагой | |||
| квадратный корень | |||
| нахождение уравнения по нелинейному графику | |||
| решение многочленов третьего порядка | |||
| матлаб решает квадратичную функцию | |||
| свойство квадратного корня для решения радикальных уравнений | |||
| БЕСПЛАТНЫЕ РАБОТЫ ПО ГЕОМЕТРИИ 8 КЛАСС | |||
| комплексное дифференциальное уравнение Matlab | |||
| онлайн-калькулятор построения таблиц | |||
| решить нелинейные алгебраические уравнения в MATlab | |||
| Glencoe алгебра 2 ответы в рабочей тетради |
| Предыдущий | Далее |
Калькулятор простой факторизации для нахождения простых делителей любых целых чисел
Онлайн-калькулятор простой факторизации вычисляет простые делители любого числа, создает список всех простых чисел до любого числа, а также создает решето Эратосфена.
Кроме того, этот калькулятор простых чисел говорит вам, является ли данное число простым числом или нет!
Просто прочитайте этот контент, чтобы узнать, как сделать простую факторизацию онлайн любого числа вручную или с помощью калькулятора для простой факторизации. Но перед этим мы собираемся начать с некоторых основных терминов! Читать дальше!
Что такое простая факторизация?Факторизация простых чисел — это метод, с помощью которого мы можем найти простые числа, которые дают нам исходное число при умножении. Например, если исходное число равно 12, то путем разложения на простые множители мы можем найти простое число, которое при умножении даст число 12. Мы должны выполнить несколько простых шагов ниже:
- 12 — исходный номер.
- На первом шаге мы должны разделить число 12 на наименьшее простое число.
- Наименьшее простое число равно 2, поэтому мы можем разделить 12 на 2 и получить 6.
- Теперь 6 не является простым числом, и по определению мы должны штрафовать простые числа, поэтому мы будем делить 6 дальше. Если разделить 6 на 2, получится 3, то есть простое число. Таким образом, у нас есть ответ: 2, умноженное на 2, равно 4, а 4, умноженное на 3, равно 12. Следовательно, мы можем сказать, что 2 2 3 являются множителями 12.
Если разделить 6 на 2, получится 3, то есть простое число. Таким образом, у нас есть ответ: 2, умноженное на 2, равно 4, а 4, умноженное на 3, равно 12. Следовательно, мы можем сказать, что 2 2 3 являются множителями 12.Это процесс ручного расчета, который может занять много времени. Чтобы сэкономить время и избежать ошибки, вы можете использовать калькулятор простых множителей, чтобы найти простые множители любого заданного числа.
Кроме того, вы можете попробовать этот простой и лучший онлайн-калькулятор для решения ваших математических задач, связанных с дробями!
Что такое простое число? Простое число — это целое число, которое больше 1 и не может быть получено путем умножения различных целых чисел. Простые числа — это числа, которые широко используются в теории чисел из-за основной теоремы арифметики. Теорема показывает, что натуральные числа больше 1 либо простые, либо даже могут быть просто разложены на множители как произведение простых чисел.
Помните, что простая факторизация — это разложение составного числа на произведение простых чисел, поэтому вы можете попробовать калькулятор произведения простых множителей, чтобы найти произведение простых чисел. Читать дальше!
Например, 2 — это первое простое число, которое не может быть получено путем умножения любых целых чисел. Точно так же 3, 11, 19 — некоторые другие простые числа. Принимая во внимание, что факторы относятся к числам, которые дают нам другое число путем умножения. Например, 2, умноженное на 3, дает 6, поэтому мы можем сказать, что 2 и 3 являются множителями 6.
В случае некоторых комплексных чисел может быть трудно найти множители, но калькулятор простых чисел — лучший способ решить такие задача и получить факторы любого числа сразу без какой-либо ошибки в мгновение ока.
Разница между простыми числами и составными числами: Простое число — это термин, который относится ко всем тем числам, которые не могут быть получены путем умножения различных целых чисел, таких как 11, 13, 17 и многих других, в то время как составные числа могут может быть получен путем умножения различных целых чисел, например, 4 — это составное число, являющееся результатом умножения 2 на 2.
Точно так же 9 — это другое составное число, являющееся результатом умножения 3 на 3. С другой стороны, 2 и 3 — простые числа.
Простой множитель — это простое число. Любое число имеет свои простые делители, которые дают нам исходное число при умножении. Например, 3 и 5 являются простыми делителями числа 15, потому что 3 и 5 являются простыми числами, а 3, умноженное на 5, равно 15. Просто вставьте целочисленное значение в указанное поле калькулятора простой факторизации, чтобы найти список всех простые числа, соответствующие данному целому числу.
Как найти простую факторизацию числа?Разложение простых чисел для нахождения простых множителей любого числа можно выполнить вручную с помощью следующих методов.
Деревья факторизации простых чисел или метод факторного дерева: Этот метод демонстрирует все простые делители любого составного числа в форме «дерева».
Создание деревьев факторов — это хороший способ факторизации простых чисел, который отображает все факторы в простой форме. Использование калькулятора дерева простых множителей может быть очень полезным и сэкономить время для этой цели.
Нахождение простых делителей любого числа также признается разложением простых чисел. Процедура аналогична описанной выше для простой факторизации. Однако в методе мы можем записать простые множители как показатели степени. Например, в случае 50 у нас есть 2 5 и 5. В виде показателей степени это будет 2, умноженное на 52. 2 на 5 известен как показатель степени. Калькулятор простой факторизации имеет возможность отображать показатели степени факторов, чтобы вы могли безошибочно выполнить расчет.
Факторизация простых чисел с помощью пробного деления или (тест на делимость или метод деления): В этом методе, если вам нужно найти простые делители числа 50, вам нужно начать с проверки каждого целого числа на то, как часто оно будет делиться на 50.
Последующий набор будет состоять из простых множителей, которые при умножении дадут нам 50. Однако вычисление таким образом может занять много времени, поэтому для вашего удобства вы можете использовать калькулятор факторизованной формы.
Пример:
2 умножить на 5 и 5, умножив снова на 5, получим 50, поэтому простые множители 50 равны 2, 5 и 5. Простейшим способом можно выполнить следующую процедуру:
- 50/2 = 25
- 25/5 = 5
- 5/5 = 1
Авторизованная платформа онлайн-калькулятора предоставляет простой, но очень точный калькулятор, который поможет вам преобразовать любое число в стандартную форму.
О калькуляторе простой факторизации:Этот калькулятор простой факторизации помогает разложить любое число на простые, создать список всех простых чисел до любого числа, создать решето Эратосфена, а также помогает вычислить, является ли данное число является простым или нет.
Как произвести разложение на простые множители с помощью этого Калькулятора разложения на простые множители: Этот онлайн-калькулятор для разложения на простые множители представляет собой 100% бесплатный и загруженный надежный интерфейс, с помощью которого вы можете легко разложить на множители любые целочисленные значения.
Кроме того, этот калькулятор представляет собой умный инструмент, который позволяет:
Ввод:
- Прежде всего, вам просто нужно выбрать опцию «найти простую факторизацию». из выпадающего списка этого калькулятора целочисленной факторизации
- Далее все, что вам нужно ввести число в специальное поле этого инструмента, и нажмите кнопку расчета
Вывод:
- Факторизация простых чисел, соответствующая заданному числу
- Экспоненциальная форма данного входа
- Формат значений, разделенных запятыми (CSV), для заданного значения
- Все факторы данного числа
- Кроме того, этот калькулятор дерева простых множителей показывает дерево простых множителей, соответствующее заданному числу 9.0012
Математические термины, обозначающие, что решето Эратосфена — это термин, относящийся к древнему алгоритму определения всех простых чисел до любого заданного предела.
Ввод:
- Во-первых, вы должны выбрать опцию «Создать сито Эратосфена» из назначенного раскрывающегося меню
- Теперь просто добавьте число в данное поле, нажмите кнопку расчета
Вывод:
- Создать решето Эратосфена (стол)
Ввод:
- Итак, все, что вам нужно выбрать «создать список простых чисел до» из раскрывающегося списка
- Затем просто добавьте число по вашему выбору и нажмите кнопку расчета
Вывод:
- Этот калькулятор разложения на простые множители предоставляет список всех положительных простых чисел, меньших выбранного вами числа
Ввод:
- Просто нужно выбрать опцию «найти количество простых чисел до» из выпадающего списка
- Далее необходимо ввести число в указанное поле, нажать кнопку расчета
Вывод:
- Калькулятор простой факторизации определит, сколько простых чисел меньше выбранного вами числа
Ввод:
- Просто выберите опцию «проверить, является ли введенное число простым» из раскрывающегося списка
- Сразу после этого просто добавьте число по вашему выбору в указанное поле, а затем просто нажмите кнопку расчета
Вывод:
Калькулятор подскажет, является ли выбранное вами число простым или нет
Найти ближайшие простые числа:Ввод:
- Просто вам нужно выбрать опцию «найти ближайшие простые числа» из выпадающего списка
- После этого вам нужно просто добавить число по вашему выбору и нажать кнопку расчета
Вывод:
Калькулятор показывает:
- Предыдущее ближайшее простое число, соответствующее заданному числу
- Следующее ближайшее простое число, соответствующее данному числу 92 × 5 × 101
Поскольку число 2020 состоит всего из 4 простых делителей, его называют составным числом.
Так как 5 — простое число, то простые делители 5 равны 1 и 5.
Каковы делители числа 2020?Ответ: Факторы 2020 представлены следующим образом: 1, 2, 4, 5, 10, 20, 101, 202, 404, 505, 1010.
Почему 9 не простое число?Когда дело доходит до 9Чтобы быть простым числом, вы можете видеть, что 9 имеет только два делителя i: само e и только 1. Однако 9 также называют полупростым числом (также называемым двупростым или 2-почти простым), поскольку оно является произведением двух не обязательно различных простых множителей. Действительно, 9 = 3 x 3, где 3 называется простым числом.
Какое пятое простое число? Помните, что если число имеет более двух делителей, то оно называется составным числом. Итак, давайте посмотрим на первые несколько простых чисел: 2, 3, 5, 7, 11, 13, 17, 19., 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113, 127, 131, 137 , 139, 149, 151, 157, 163, 167, 173, 179, 181, 191, 193, 197, 199 и т.
д.
Множитель — это число, которое делится на другое число точно и без остатка. Как правило, большинство чисел содержат четное число множителей; однако квадратное число состоит из нечетного числа множителей. Простое число имеет только два делителя: само число и 1,9.0003
Что такое наименьший делитель числа?Наименьшим простым делителем целого числа n называется наименьшее простое число, на которое оно делится.
Почему 1 не является простым числом?Согласно научно обоснованному исследованию, определение простого числа показывает, что простое число — это положительное целое число, имеющее ровно два положительных делителя. Однако число 1 содержит только один положительный делитель, т. е. само 1, поэтому его не называют простым числом.
Есть ли закономерность для простых чисел? Нет, даже в простых числах нет ни одного шаблона.
Проще говоря, набор простых чисел просто действует как случайная подпоследовательность целочисленной последовательности, но, очевидно, у него есть некий шаблон, который мы не можем описать.
Одиннадцать называется наименьшим четырехзначным простым числом в целочисленной системе счисления. Кроме того, вы можете воспользоваться онлайн-калькулятором простого факторинга, чтобы найти простое число до 11.9.0003
Разве 2 не простое число?Доказательство: 2 является простым числом, просто введите 2 в специальное поле, чтобы проверить, является ли это простым числом или нет. Кроме того, вы можете попробовать калькулятор простых чисел, чтобы узнать, является ли данное число простым или нет!
В чем смысл простых чисел? Простые числа имеют решающее значение для теоретиков чисел, поскольку они являются строительными блоками целых чисел, и чрезвычайно важны для мира, поскольку их странные математические свойства делают их идеальными для текущего использования.
Эксперты ответили, что существует бесконечное количество простых чисел, и все они являются целыми положительными числами, поэтому сумма всех простых чисел равна бесконечности.
Вывод:Этот калькулятор простой факторизации поддерживает вычисление списка простых чисел, дерева простых множителей и формы показателей. Этот простой калькулятор дерева простой факторизации может помочь в изучении простой факторизации в пошаговой процедуре, этот инструмент лучше всего подходит для студентов и профессионалов. Чтобы понять, что такое простая факторизация, он начинает вычисления с самых маленьких простых чисел и рассказывает нам, как простые множители используются для создания составного числа.
Ссылки:Из источника Википедии: О факторизации — Факторизация целых чисел и общие методы
Из источника исследования: как найти простую факторизацию числа (Глава 1 / Урок 2)
Из источника гениального: узнайте о решете Эратосфена (простой и древний алгоритм, используемый для нахождения простых чисел до любого заданного предела)
Из источника helpwithmath: Prime Factorization (создайте факторные деревья) — простой калькулятор дерева простой факторизации также поможет вам создать дерево факторов для числа по вашему выбору.