Разложение вектора по базису — онлайн калькулятор
- Справочник
- Онлайн-калькуляторы
- Тесты с ответами
В основе нашего сервиса лежит теорема о разложении вектора по базису. По ней любой вектор векторного пространства раскладывается по его базису. Способ разложения всегда только 1. Вы получаете точный ответ сразу после ввода данных.
Разложить вектор по базису онлайн потребуется студентам, ученикам школ старших классов. Вы сможете свериться с самостоятельно полученным ответом и увидеть пошаговые вычисления.
- Укажите размерность вектора. Для изменения размерности используйте кнопки «+», «-».
- Введите значения базисных векторов в соответствующие поля.
- Введите значение вектора, который нужно разложить по базису.

- Для решения задачи записывается векторное уравнение, находится определитель матрицы. Определитель матрицы не равен 0, поэтому система векторов является базисом. Смотрите подробное решение после нажатия кнопки.
- Решим уравнение методом Гаусса
- Подставляем полученное значение в уравнение и вычисляем ответ.
Материалы, которые помогут вам лучше разобраться в теме:
- Векторы на плоскости и в пространстве — основные определения
- Координаты вектора в декартовой системе координат (ДСК)
- Нахождение длины вектора, примеры и решения
- Нахождение координат вектора через координаты точек
Ответ:
Решение
Ответ:- list» :key=»`error-${eIdx}`» v-html=»e»/>
Похожие калькуляторы:
- Длина вектора. Модуль вектора
- Векторное произведение векторов
- Умножение вектора на число
- Угол между векторами
- Смешанное произведение векторов
- Сложение и вычитание двух векторов
- Скалярное произведение векторов
- Определение вектора по двум точкам
- Проверить являются ли вектора базисом
- Ортогональность векторов
- Компланарность векторов
- Коллинеарность векторов
- Проекция вектора на вектор
- Площадь треугольника, построенного на векторах
- Площадь параллелограмма, построенного на векторах
Как быстро разложить вектор по базису
Вам не придется искать нужные формулы и высчитывать результаты промежуточных действий. Разложение вектора по базису происходит автоматически. Zaochnik дает возможность учащимся осуществлять подготовку к занятиям по сложным темам, быстрее осваивать новый и непонятный материал. Сервисом пользуются, потому что:
Разложение вектора по базису происходит автоматически. Zaochnik дает возможность учащимся осуществлять подготовку к занятиям по сложным темам, быстрее осваивать новый и непонятный материал. Сервисом пользуются, потому что:
- Услуга предоставляется бесплатно. Не всегда есть возможность нанимать репетитора. Теперь повышать свой уровень образования можно без дополнительных трат.
- Не нужна регистрация. Ничто не мешает получить ответ максимально быстро. А это так важно учащимся во время урока, семинара, зачета.
- Количество вводимых примеров не ограничивается. Наша команда разработала сервис, чтобы учащимся было легче справляться с заданиями. Калькулятор позволяет осуществлять самопроверку столько раз, сколько необходимо.
- Широкий охват тем. Мы максимально учли запросы по вычислениям и создали программы по решению задач для школ и университетов.
Если у вас возникли вопросы по использованию калькулятора, напишите консультанту.
Понравился калькулятор? Поделись с друзьями!
Разделы калькуляторов
- Решение матриц
- Точка, прямая, плоскость
- Конвертеры
- Объем фигур
- Калькуляторы площади фигур
- Решение уравнений
- Операции над векторами
- Периметр фигур
Поможем с любой работой
- Дипломные работы
- Курсовые работы
- Рефераты
- Контрольные работы
- Решение задач
- Отчеты по практике
Не получается написать работу самому?
Доверь это кандидату наук!
Разложение вектора по базису | Онлайн калькулятор
org/ListItem»>Все калькуляторы /Вектор является элементом векторного пространства. Коллинеарные векторы принадлежат одной или двум параллельным прямым. Могут быть противо- и сонаправленными. Из произвольно выбранной точки в пространстве можно отложить любой вектор одним способом.
Базис плоскости – два неколлинеарных вектора, то есть – линейно независимых. Следует понимать, что любой вектор заданной плоскости представляет собой линейную комбинацию базисных векторов. Если есть два заданных на плоскости неколлинеарных вектора, то любой иной вектор, принадлежащий этой же плоскости, можно разложить по первым двум, то есть – по базису. Для осуществления операции можно воспользоваться онлайн-калькулятором. Это упростит задачу.
«,»className»,»ramka»,»
| A = | ‘,» | «,» | «,» |
«,»m1″,»»,»;»,» maxLength=8 class=mvect>»,»v1″,’
a‘,»
= {‘,» maxLength=8 class=mvect1> x«,» + «,» = «,» maxLength=8 class=mvect1>
| ‘,»showzn»,»m»,» | «,'»/>‘,»
| «,»«,» = «,»clear»,»
| B= | «,» | |
| ‘,» | ||
| «,» |
| X= |
«,»
|
Координаты вектора в базисе
Доказать, что векторы a, b, c образуют базис, и найти координаты вектора d в этом базисе.
Пусть в R3 относительно канонического базисы даны четыре вектора f1 = (1,2,3), f2 = (2,3,7), f3=(1,3,1), x = (2,3,4). Докажите, что векторы f1, f2, f3 можно принять за новый базис. Найдите координаты η1, η2, η3 вектора х относительно этого базиса.
Решение:
Записываем матрицу перехода А:
и находим ее определитель
<>0
Видим, что ранг матрицы С равен трем. Из теоремы о базисном миноре векторы f1, f2, f3 линейно независимы, а поэтому могут быть приняты в качестве базиса пространства R3.
Находим обратную матрицу А-1.
Транспонированная матрица:
Алгебраические дополнения:
Обратная матрица А-1
Находим координаты вектора х относительно нового базиса.
Перейти к онлайн решению своей задачи
Пример №1. Даны векторы a{1;2;1}, b{2;-2;1}, c{1;-2;0} и d {0;3;1}. Установить, что векторы a, b, c образуют базис, и найти координаты вектора d в этом базисе.
Решение:
Соотношение, записанное для векторов d = αa + βb + γc, справедливо для каждой из проекций:
α*1 + β*2 + γ*1 = 0
α*2 — β*2 — γ*2 = 3
α*1 + β*1 + γ0 = 1
т.е. получена алгебраическая система трёх уравнений с тремя неизвестными. Решение системы удобнее вычислять методом Крамера или методом обратной матрицы:
α = 1/2; β = 1/2; γ = -3/2
следовательно, и вектор d имеет разложение в базисе a, b, c:
d = 1/2a + 1/2b — 3/2c
Пример №2. Даны векторы . Показать, что векторы образуют базис трехмерного пространства и найти координаты вектора в этом базисе:
Решение. Данная задача состоит из двух частей. Сначала необходимо проверить образуют ли векторы базис.
Данная задача состоит из двух частей. Сначала необходимо проверить образуют ли векторы базис.
Векторы образуют базис, если определитель, составленный из координат этих векторов, отличен от нуля, в противном случае вектора не являются базисными и вектор нельзя разложить по данному базису. Так как определитель отличен от нуля, то векторы образуют базис, следовательно, вектор можно разложить по данному базису. Т.е. существуют такие числа α,β,γ что имеет место равенство:
Запишем данное равенство в координатной форме:
(-3;5;4)=α(5;1;2) + β(3;4;-1) + γ(-4;2;1)
Используя свойства векторов, получим следующее равенство:
(-3;5;4) = (5α;α;2α) + (3β;4β;-β) + (-4γ;2γ;γ)
(-3;5;4) = (5α+3β-4γ;α+4β+2γ;2α-β+γ)
По свойству равенства векторов имеем:
Решая полученную систему уравнений методом Гаусса (методом последовательного исключения неизвестных из уравнений системы), выберем в качестве ведущего уравнения второе уравнение системы:
Выразим из первого уравнения полученной системы α и подставим полученное выражение во второе и третье уравнения системы:
Разделим второе уравнение системы на -1 ,а третье уравнение системы на -3 и выразим из полученного равенства γ :
Подставим полученное выражение для γ в третье уравнение системы: Тогда:
В итоге получим разложение вектора в базисе :
Ответ:
Пример №3. Даны два линейных преобразования:
Даны два линейных преобразования:
х’1 = a11x1 + a12x2 + a13x3, х»1 = b11x’1 + b12x’2 + b13x’3,
х’2 = a21x1 + a22x2 + a23x3, х»2 = b21x’1 + b22x’2 + b23x’3,
х’3 = a31x1 + a32x2 + a33x3, х»3 = b31x’1 + b32x’2 + b33x’3,
Средствами матричного исчисления найти преобразование, выражающее х»1, x»2, x»3 через х1, х2, х3.
х’1 = 4x1 + 3x2 + 5x3, х»1 = — x’1 + 3x’2 — 2x’3,
х’2 = 6x1 + 7x2 + x3, х»2 = — 4x’1 + x’2 + 2x’3,
х’3 = 9x1 + x2 + 8x3, х»3 = 3x’1 — 4x’2 + 5x’3,
Решение. Используя калькулятор, получаем:
Используя калькулятор, получаем:
Обозначим:
| A = |
|
| B = |
|
Вычислим определитель матрицы А:
∆ = 4*(7*8 — 1*1) — 6*(3*8 — 1*5) + 9*(3*1 — 7*5) = -182
Определитель матрицы А равен detA=-182
Так как A невырожденная матрица, то существует обратная матрица A-1. Умножим слева обе части уравнения на A-1: A-1·A·X = A-1·B, тогда получим E·X = A-1·B, или X = A-1·B.
Найдем обратную матрицу A-1.
| A-1 = -1/182 |
|
Матрицу Х ищем по формуле:
| X = A-1·B = -1/182 |
| * |
| = |
|
x’1 = 75/182x1 -146/91x2 + 19/13
x’2 = -13/14x1 + 12/7 -x3
x’3 = 5/182x1 + 13/91x2 -12/13x3
Пример №4.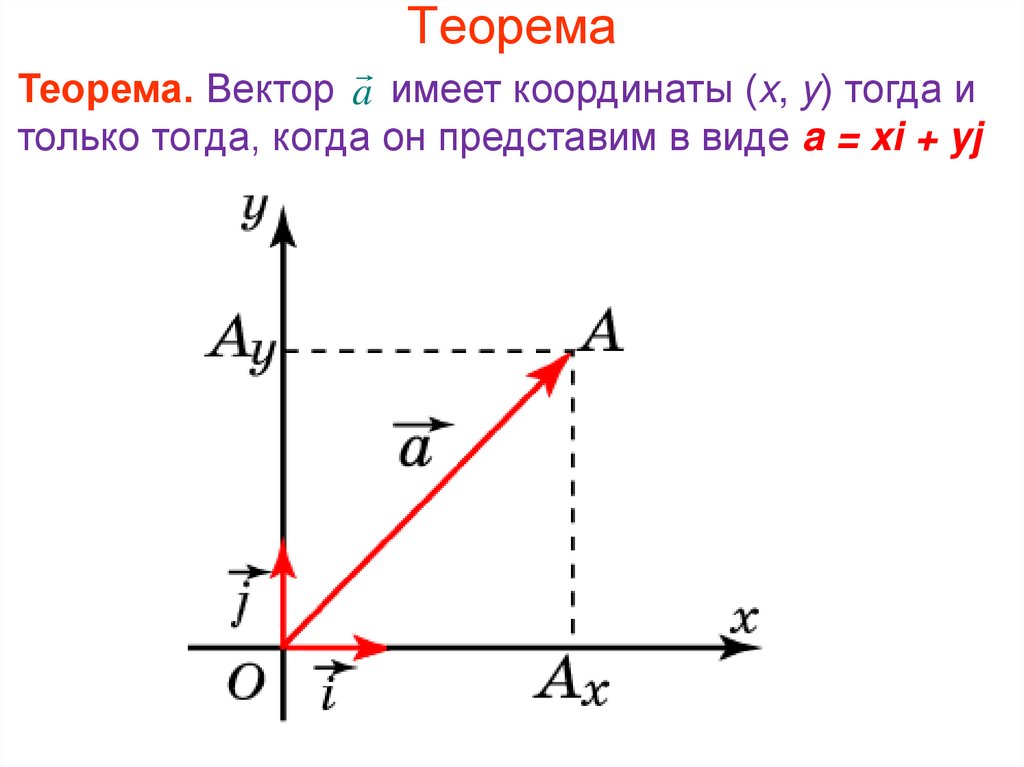 В декартовой прямой системе координат даны вершины пирамиды A(3,0,-1), B(-1,-2,-4), C(-1,2,4), D(7,-3,1). Найдите:
В декартовой прямой системе координат даны вершины пирамиды A(3,0,-1), B(-1,-2,-4), C(-1,2,4), D(7,-3,1). Найдите:
а) длину ребра AB;
б) косинус угла между векторами AB и AC;
в) уравнение ребра AB;
г) уравнение грани ABC;
д) уравнение высоты, опущенной из вершины D на грань ABC;
е) координаты векторов e1=AB, e2=AC, e3=AD и докажите, что они образуют линейную независимую систему;
ж) координаты вектора MN, где M и N – середины ребер AD и DC соответственно;
з) разложение вектора MN по базису (e1, e2, e3)
Решение. Пункты (а-д) решаются через онлайн калькулятор.
Скачать решение
Скачать
Задание 1. Разложить вектор d=(8;-5) по векторам a=(1;-2) и b=(2;3).
Решение. Векторы a и b образуют базис на плоскости, так как они не коллинеарны (, то есть соответствующие координаты этих векторов не пропорциональны).
Следовательно, вектор d = αa+βb, где α и β – коэффициенты, которые надо найти.
Таким образом, имеем равенство
8i-5j=α(i-2j)+β(2i+3j)=(α+2β)i+ (-2α+3β)j.
В координатной форме это равенство примет вид
Решим полученную систему уравнений.
Перейти к онлайн решению своей задачи
Пример №2. Разложите вектор v = (36; -6) по базису e1=(-5;3),e2=(-2;-4).
Решение. Даны векторы ε1(-5;3), ε2(-2;-4), X(36;-6). Показать, что векторы образуют базис двухмерного пространства и найти координаты вектора X в этом базисе.
Данная задача состоит из двух частей. Сначала необходимо проверить образуют ли векторы базис. Векторы образуют базис, если определитель, составленный из координат этих векторов, отличен от нуля, в противном случае вектора не являются базисными и вектор X нельзя разложить по данному базису.
Вычислим определитель матрицы:
| E = |
|
∆ = (-5)*(-4) — (-2)*3 = 26
Определитель матрицы равен ∆ =26
Так как определитель отличен от нуля, то векторы образуют базис, следовательно, вектор X можно разложить по данному базису.
 Т.е. существуют такие числа α1, α2, что имеет место равенство:
Т.е. существуют такие числа α1, α2, что имеет место равенство:X = α1ε1 + α2ε2
Запишем данное равенство в координатной форме:
(36;-6) = α(-5;3) + α(-2;-4)
Используя свойства векторов, получим следующее равенство:
(36;-6) = (-5α1;3α1😉 + (-2α2;-4α2😉
(36;-6) = (-5α1 -2α2;3α1 -4α2)
По свойству равенства векторов имеем:
-5α1 -2α2 = 36
3α1 -4α2 = -6
Решаем полученную систему уравнений методом Гаусса или методом Крамера.
Ответ:
X = -6ε1 -3ε2
Разложить вектор d по векторам a,b,c
Коэффициент — разложение — вектор
Cтраница 1
Коэффициенты разложения вектора по базису ( т.е. числа, фигурирующие в этом разложении), называются координатами вектора в этом базисе. [1]
Коэффициенты разложения векторов с началом в точке О по указанному базису называются декартовыми координатами элементов пространства. Прямые, проходящие через точку О параллельно базисным векторам, называются декартовыми осями координат с началом в точке О.
[2]
Прямые, проходящие через точку О параллельно базисным векторам, называются декартовыми осями координат с началом в точке О.
[2]
Для нахождения коэффициентов разложения вектора b по векторам — а и oj составлена система из трех линейных уравнений с двумя неизвестными. Установить, что теорема Фредгольма для этой системы равносильна следующему ( геометрически очевидному) утверждению: вектор b раскладывается по — а и — о / 2 тогда и только тогда, когда он ортогонален каждому вектору у, ортогональному этим векторам. [3]
Итак, коэффициентами разложения вектора R no координатным ортам прямоугольной системы являются его проекции Rx, Rv, Rz на соответствующие координатные оси. [4]
Видим, что коэффициенты разложений векторов RI и R2 оказываются постоянными. [5]
Числа х и у, являющиеся коэффициентами разложения вектора а по векторам базиса, называются координатами этого вектора в данном базисе. При этом х называется его абсциссой, ay — ординатой.
[6]
При этом х называется его абсциссой, ay — ординатой.
[6]
Если базисные векторы даны, то определение коэффициентов разложения вектора приводит к системе линейных уравнений, так как данный вектор надо получить в виде линейной комбинации столбцов, представляющих базисные векторы. [7]
Однако можно избежать необходимости запоминания всей матрицы коэффициентов разложения небазисных векторов, если объединить выполнение этапов 2 — 5 ЦИКЛИЧЕСКОЙ программы. Этот вариант требует для хранения коэффициентов разложения небазисных векторов только двух массивов ( рабочего и эталонного) по т ячеек в каждом. Основная идея заключается в сравнении приращения критерия оптимальности только для двух небазисных векторов, в результате чего находится вектор, дающий наибольшее приращение, который размещается в эталонном массиве. В дальнейшем каждый следующий — небазисный вектор сравнивается с эталонным, и если он дает большее приращение критерия оптимальности, то его коэффициенты разложения располагаются в эталонном массиве. [8]
[8]
Выше было установлено, что, если хотя бы один из коэффициентов разложения вектора PJ по векторам базиса положителен, может бцть получен новый опорный план, соответствующий введению в базис нового вектора PJ. Случай, когда все коэффициенты разложения для всех векторов Р, отрицательны, здесь не рассматривается. Следует, однако, иметь в виду, что как можно показать, этой ситуации соответствует неограниченность линейной формы снизу. Сравнение (10.28) и (10.29) показывает, что если в этом случае разность Zj — Cj0, то новому опорному плану соответствует значение линейной формы меньшее, чем это значение z0 для исходного опорного плана. [9]
После выделения направляющей строки и направляющего столбца находят новый опорный план и коэффициенты разложения векторов Р, через векторы нового базиса, соответствующего новому опорному плану. Это легко реализовать, если воспользоваться методом Жордана-Гаусса. [10]
Соотношение (2. 6.23) означает, что уклонения истинной диаграммы направленности от оптимальной представляют собой коэффициенты разложения вектора А по векторам Fp. Таким образом, квадрат длины вектора А может быть представлен в виде суммы квадратов его разложения векторам Fp или в виде суммы квадратов его собственных компонентов.
[11]
6.23) означает, что уклонения истинной диаграммы направленности от оптимальной представляют собой коэффициенты разложения вектора А по векторам Fp. Таким образом, квадрат длины вектора А может быть представлен в виде суммы квадратов его разложения векторам Fp или в виде суммы квадратов его собственных компонентов.
[11]
Соотношения ( VIII185) обычно и используются при выполнении этого этапа расчета, причем, если найдены коэффициенты разложения небазисного вектора Ak, вводимого в исходный базис вместо вектора Ап р, то формулы ( VIII, 185) позволяют сразу же определить и обратную матрицу нового базиса. [12]
Это и позволяет производить ортонормирование базиса ( получать новый базис) с одним условием: будут определяться коэффициенты разложения векторов нового базиса в старом. [13]
Соотношения ( VIII, 185) обычно и используются при выполнении этого этапа расчета, причем, если найдены коэффициенты разложения небазисного вектора Дй, вводимого в исходный базис вместо вектора Ап Р, то формулы ( VIII, 185) позволяют сразу же определить и обратную матрицу нового базиса. [14]
[14]
Общий объем памяти, требуемый для размещения числовой информации при решении задачи линейного программирования с п — — т переменными и т ограничениями типа ( VIII, 195), исключая память, необходимую для размещения программы вычислений, складывается из массивов: 1) для размещения матрицы обобщенных векторов Ys: ( п т) ( т 3) ячеек; 2) для размещения обратной матрицы исходного базида: т2 ячеек; 3) для размещения коэффициентов разложения небазисных векторов: 2т или т2 ячеек, если матрица коэффициентов разложения небазисных векторов запоминается полностью. [15]
Страницы: 1 2
§ 2. Разложение векторов состояний . Том 3. Квантовая механика
Посмотрим на уравнение (6.8) еще раз; его можно рассматривать следующим образом. Любой вектор состояния |?> может быть представлен в виде линейной комбинации совокупности базисных «векторов» с подходящими коэффициентами, или, если угодно, в виде суперпозиции «единичных векторов» в подходящих пропорциях. Чтобы подчеркнуть, что коэффициенты <i|?> — это просто обычные (комплексные) числа, напишем
Чтобы подчеркнуть, что коэффициенты <i|?> — это просто обычные (комплексные) числа, напишем
Тогда (6.8) совпадает с
(6.10)
Такое же уравнение можно написать и для всякого другого вектора состояния, скажем для |?>, но, конечно, с другими коэффициентами, скажем с Di. Тогда будем иметь
(6.11)
где Di — это просто амплитуды <i|?>.
Представим, что мы начали бы с того, что в (6.1) абстрагировались бы от ?. Тогда мы бы имели
(6.12)
Вспоминая, что <?|i>=<i|?>*, можно записать это в виде
(6.13)
А теперь интересно вот что: чтобы обратно получить <?|?>, можно просто перемножить (6.13) и (6.10). Только, делая это, надо быть внимательным к индексам суммирования, потому что они в разных уравнениях разные. Перепишем сперва (6.13):
Это ничего не меняет. Объединяя с (6. 10), получаем
10), получаем
(6.14)
Вспомните, однако, что <j|i>=?ij, так что в сумме останутся только члены с j=i. Выйдет
(6.15)
где, как вы помните, Di*=<i|?>*=<?|i>, а Ci=<i|?>. Опять мы являемся свидетелями тесной аналогии со скалярным произведением
Единственная разница — что Di нужно комплексно сопрягать. Значит, (6.15) утверждает, что если разложить векторы состояний <?| и |?> по базисным векторам <i| или |i>, то амплитуда перехода из ? в ? дается своего рода скалярным произведением (6.15). А это просто (6.1), записанное в других символах. Мы ходим по кругу, привыкая к новым символам.
Может быть, стоит подчеркнуть, что в то время, как пространственные трехмерные векторы выражаются через три ортогональных единичных вектора, базисные векторы |i> квантовомеханических состояний должны пробегать всю совокупность, отвечающую данной задаче. В зависимости от положения вещей в нее может входить два или три, пять или бесконечно много базисных состояний.
В зависимости от положения вещей в нее может входить два или три, пять или бесконечно много базисных состояний.
Мы говорили также о том, что происходит, когда частицы проходят через прибор. Если мы выпустим частицы в определенном состоянии ?, затем проведем их через прибор, а после проделаем измерение, чтобы посмотреть, находятся ли они в состоянии ?, то результат будет описываться амплитудой
(6.16)
Такой символ не имеет близкого аналога в векторной алгебре. (Он ближе к тензорной алгебре, но эта аналогия не так уж полезна.) Мы видели в гл. 3 [формула (3.32)], что (6.16) можно переписать так:
(6.17)
Это пример двукратного применения основного правила (6.9).
Мы обнаружили также, что если вслед за прибором А по ставить другой прибор B, то можно написать
(6.18)
Это опять-таки следует прямо из предложенного Дираком метода записи уравнения (6.9). Вспомните, что между В и A всегда можно поставить черту (|), которая ведет себя совсем как множитель единица.
Кстати говоря, об уравнении (6.17) можно рассуждать и иначе. Предположим, что мы рассуждаем о частице, попадающей в прибор А в состоянии ? и выходящей из него в состоянии ?. Мы можем задать себе такой вопрос: можно ли найти такое состояние ?, чтобы амплитуда перехода от ? к ? тождественно совпадала с амплитудой <?|A|?>? Ответ гласит: да. Мы хотим, чтобы (6.17) заменилось уравнением
(6.19)
Конечно, этого можно достичь, если взять
(6.20)
что и определяет собой ?. «Но оно не определяет собой ?, — скажете вы, — оно определяет только <i|?>». Однако <i|?> все же определяет ?; ведь если у вас есть все коэффициенты, связывающие ? с базисными состояниями i, то ? определяется однозначно. И действительно, можно поупражняться с нашими обозначениями и записать (6.20) в виде
(6.21)
А раз это уравнение справедливо при всех i, то можно просто писать
(6.22)
Теперь мы вправе сказать: «Состояние ? — это то, что получается, если начать с ? и пройти сквозь аппарат A».
Еще один, последний пример полезных уловок. Начинаем опять с (6.17). Раз это уравнение соблюдается при любых ? и ?, то их обоих можно сократить! Получаем[19]
(6.23)
Что это значит? Только то, что получится, если вернуть на свои места ? и ?. В таком виде это уравнение «недокончено» и неполно. Если умножить его «справа» на |?>, то оно превращается в
(6.24)
а это снова то же уравнение (6.22). В самом деле, мы бы могли просто убрать из (6.22) все j и написать
(6.25)
Символ А — это не амплитуда и не вектор; это вещь особого рода, именуемая оператором. Он — нечто, что «оперирует» над состоянием, чтобы создать новое состояние; уравнение (6.25) говорит, что |?> — это то, что получается, если А действует на |?>. Это уравнение тоже нужно считать недоконченным, открытым, пока слева оно не умножится на какое-то «брэ», скажем на <?|, и не обратится в
(6.26)
Оператор А, разумеется, полностью описывается тем, что за дается матрица амплитуд <i|A|j>; ее также пишут в виде Аij— через любую совокупность базисных векторов.
Все эти математические обозначения на самом деле ничего нового не вносят. Единственный резон, почему мы их ввели, — мы хотели показать, как пишутся обрывки уравнений, потому что во многих книжках вы встретите уравнения, написанные в неполном виде, и нет причин вам пугаться, увидев их. Если вы захотите, вы всегда сможете дописать те части, которых не хватает, и получить уравнение, связывающее числа. Оно будет выглядеть более привычно.
Кроме того, как вы увидите, обозначения «брэ» и «кет» очень удобны. Прежде всего мы теперь сможем указывать состояния, задавая их вектор состояния. Когда мы захотим вести речь о состоянии с определенным импульсом р, то скажем: «состояние |р>». Или будем говорить о некотором произвольном состоянии |?>. Для единообразия мы всегда, говоря о состоянии, будем употреблять «кет» и писать |?>. (Конечно, этот выбор совершенно произволен; в равной мере мы могли бы остановиться и на «брэ» <?|.)
Базис системы векторов.
 Аффинные координаты
Аффинные координаты- Понятие базиса системы векторов
- Разложение вектора по базису
- Аффинные координаты
Тема базиса системы векторов связана с понятием линейной независимости векторов и линейной комбинации.
Определение 1. Три линейно независимых вектора (система векторов) , и образуют в пространстве базис, если любой вектор может быть представлен в виде некоторой линейной комбинации векторов , и , т.е. если для любого вектора найдутся такие вещественные числа , и , что справедливо равенство
. (2)
Аналогично определяется базис на некоторой плоскости.
Определение 2.. Два лежащих в плоскости линейно независимых вектора (система векторов) и образуют на этой плоскости базис, если любой лежащий в этой же плоскости вектор
может быть представлен в виде некоторой линейной комбинации векторов и ,
т. е. если для любого лежащего в этой плоскости вектора
найдутся такие вещественные числа и ,
что справедливо равенство
е. если для любого лежащего в этой плоскости вектора
найдутся такие вещественные числа и ,
что справедливо равенство
. (3)
Справедливы следующие утверждения:
1) любая тройка некомпланарных векторов , и образует базис в пространстве,
2) любая пара лежащих в данной плоскости неколлинеарных векторов и образует базис на этой плоскости.
Определение 3. Векторное пространство называется n-мерным, если в нём существует в точности n линейно независимых векторов.
Базисом n-мерного пространства называется любая система из n независимых векторов этого пространства.
Пример 1. Доказать, что векторы
образуют базис в четырёхмерном пространстве.
Решение. Система векторов образует базис, если: 1) количество векторов равно размерности пространства; 2) эти векторы линейно независимы. Первое требование выполнено, остаётся доказать, что эти векторы линейно независимы. Попытаемся составить из них линейную нулевую комбинацию:
Первое требование выполнено, остаётся доказать, что эти векторы линейно независимы. Попытаемся составить из них линейную нулевую комбинацию:
Подставим в это равенство вместо данных векторов их выражения в координатах и преобразуем левую часть:
или
Но вектор является нулевым, когда все его проекции равны нулю, т.е.
Таким образом, из данных векторов невозможно составить нулевую линейную комбинацию, у которой хотя бы один коэффициент был отличен от нуля. Поэтому векторы
линейно независимы и, следовательно, образуют базис в четырёхмерном пространстве.
Итак, пусть , и — произвольный базис в пространстве, т.е. произвольная тройка некомпланарных векторов. Тогда для любого вектора найдутся такие вещественные числа , и , что будет справедливо равенство
. (2)
(2)
Принято называть равенство (2) разложением вектора по базису , , , а числа , и — координатами вектора относительно базиса , , .
Аналогичным образом определяется разложение вектора по базису на плоскости: базис образуется двумя векторами, а координат разложенного по базису вектора также две.
Теорема 6. При сложении двух векторов и их координаты (относительно любого базиса , , ) складываются:
.
При умножении вектора на любое число все его координаты умножаются на это число:
.
Основное значение базиса состоит в том, что линейные операции над векторами при задании базиса становятся обычными линейными операциями над числами — координатами этих векторов.
Пример 2 Разложить вектор
по базису где
Решение. Рассматриваемые векторы принадлежат двумерному пространству: базис в этом пространстве должен состоять из двух векторов. В примере 7 установлено, что векторы
Рассматриваемые векторы принадлежат двумерному пространству: базис в этом пространстве должен состоять из двух векторов. В примере 7 установлено, что векторы
и
линейно независимы и, следовательно, образуют базис. Запишем разложение вектора по этому базису:
Чтобы найти значения и , подставим в это разложение выражения векторов , и через координаты:
Выполнив преобразования в правой части равенства, получим
или
Равенство векторов означает равенство их соответствующих координат, т.е.
откуда
Следовательно, разложение вектора по базису , имеет вид
Замечание. В каждом векторном пространстве существует бесконечное множество различных базисов и в различных базисах один и тот же вектор имеет различные разложения (подобно тому, как точка имеет различные координаты в различных системах коорднат).
Аффинные координаты в пространстве определяются заданием базиса , , и некоторой точки O, называемой началом координат.
Аффинными координатами любой точки M называются координаты вектора (относительно базиса , , .)
Так как каждый вектор может быть, и притом единственным способом, разложен по базису , , , то каждой точке пространства M однозначно соответствует тройка аффинных координат , , .
Декартовы прямоугольные координаты являются частным случаем аффинных координат, соответствующим тройке взаимно ортогональных и единичных базисных векторов.
| Назад | Листать | Вперёд>>> |
Поделиться с друзьями
Начало темы «Векторы»
Векторы: определения и действия над векторами
Сложение векторов: длина суммы векторов и теорема косинусов
Скалярное произведение векторов
Линейная зависимость векторов. Линейные комбинации векторов
Линейные комбинации векторов
Продолжение темы «Векторы»
Векторное и смешанное произведение векторов
15.9: Расширения ортонормированного базиса — Инженерные тексты LibreTexts
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 23199
- Richard Baraniuk et al.
- Университет Райса
Основная идея
При работе с сигналами часто полезно разбивать сигнал на более мелкие, более управляемые части. Надеюсь, вы уже познакомились с концепцией собственных векторов (раздел 14.2) и использовали ее для разложения сигнала на одну из его возможных базисов. Делая это, мы можем упростить наши расчеты сигналов и систем с помощью собственных функций систем LTI (раздел 14. 5).
5).
Теперь мы хотели бы рассмотреть альтернативный способ представления сигналов с помощью 9{j \omega_{0} n t}\), \(\left\{c_{n}\right\}\) являются просто другим представлением \(f(t)\).
Примечание
Для сигналов/векторов в гильбертовом пространстве легко найти коэффициенты разложения.
Альтернативное представление
Напомним наше определение базиса : Набор векторов \(\left\{b_{i}\right\}\) в векторном пространстве \(S\) является базисом, если
- \(b_i\) линейно независимы.
- Промежуток \(b_i\) \(S\). То есть мы можем найти \(\left\{\alpha_{i}\right\}\), где \(\alpha_{i} \in \mathbb{C}\) (скаляры) такие, что
\[\boldsymbol{x}=\sum_{i} \alpha_{i} b_{i}, x \in S \nonumber \]
где \(\boldsymbol{x}\) — вектор в \(S\), \(\alpha\) — скаляр в \(\mathbb{C}\) и \(\boldsymbol{b}\) является вектором в \(S\).
Условие 2 в приведенном выше определении говорит, что мы можем разложить любой вектор в терминах \(\left\{b_{i}\right\}\). Условие 1 гарантирует, что разложение уникально (подумайте об этом дома).
Условие 1 гарантирует, что разложение уникально (подумайте об этом дома).
Примечание
Символ \(\left\{\alpha_{i}\right\}\) представляет собой альтернативное представление \(\boldsymbol{x}\). 92\). Начнем с того, что перепишем уравнение \ref{15.48}, чтобы мы могли сложить наши \(b_i\) в виде столбцов в матрице \(2 \times 2\).
\[(x)=\alpha_{0}\left(b_{0}\right)+\alpha_{1}\left(b_{1}\right) \label{15.49} \]
\[ (x)=\left(\begin{array}{ccc}
\vdots & \vdots \\
b_{0} & b_{1} \\
\vdots & \vdots
\end{массив}\right) \left(\begin{array}{l}
a_{0} \\
a_{1}
\end{array}\right) \label{15.50} \]
Пример \(\PageIndex{3}\ )
Вот простой пример, который немного подробнее показывает приведенные выше уравнения.
\[\begin{align}
\left(\begin{array}{c}
x[0] \\
x[1]
\end{массив}\right) &=\alpha_{0}\ left(\begin{array}{c}
b_{0}[0] \\
b_{0}[1]
\end{array}\right)+\alpha_{1}\left(\begin{array }{c}
b_{1}[0] \\
b_{1}[1]
\end{массив}\right) \nonumber \\
&=\left(\begin{array}{c}
\alpha_{0} b_{0}[0]+\alpha_{1} b_{1}[0] \\
\alpha_{0} b_{0}[1]+\alpha_{1} b_{1} [1]
\end{массив}\right)
\end{align} \nonumber \]
\[\left(\begin{array}{l}
x[0] \\
x[1]
\end{ array}\right)=\left(\begin{array}{ll}
b_{0}[0] & b_{1}[0] \\
b_{0}[1] & b_{1}[1 ]
\end{массив}\right)\left(\begin{array}{l}
\alpha_{0} \\
\alpha_{1}
\end{массив}\right) \nonumber \]
Упрощение нашего уравнения
Чтобы упростить запись, мы определяем следующие два элемента из приведенных выше уравнений:
- Базовая матрица :
\[B=\left(\begin{array}{cc}
\vdots & \vdots \\
b_{0} & b_{1} \\
\vdots & \vdots
\end{array}\right ) \номер\] - Вектор коэффициентов :
\[\boldsymbol{\alpha}=\left(\begin{array}{l}
\alpha_{0} \\
\alpha_{1}
\end{array}\right) \nonumber \]
Это дает нам следующее краткое уравнение:
\[\boldsymbol{x}=B \boldsymbol{\alpha} \label{15. 53} \] 9{1} \alpha_{i} b_{i}\).
53} \] 9{1} \alpha_{i} b_{i}\).
Пример \(\PageIndex{4}\)
При стандартной основе \(\left\{\left(\begin{array}{l}
1 \\
0
\end{array}\right ),\left(\begin{array}{l}
0 \\
1
\end{array}\right)\right\}\), то имеем следующую базисную матрицу:
\[B=\ left(\begin{array}{ll}
0 & 1 \\
1 & 0
\end{array}\right)\nonumber \]
Чтобы получить \(\alpha_i\)s, мы находим вектор коэффициентов в уравнении \ref{15.53} 9{-1}\) — обратная матрица \(B\).
Примеры
Пример \(\PageIndex{5}\)
Давайте сначала посмотрим на стандартный базис и попробуем вычислить \(\boldsymbol{\alpha}\) из него.
\[B=\left(\begin{array}{ll}
1 & 0 \\
0 & 1
\end{массив}\right)=I \nonnumber \]
Где \(I\) является единичной матрицей . Чтобы решить для \(\boldsymbol{\alpha}\), давайте сначала найдем обратное \(B\) (что, очевидно, очень тривиально в этом случае): 9{-1} \boldsymbol{x}=\boldsymbol{x} \nonumber \]
Пример \(\PageIndex{6}\)
Давайте посмотрим на немного более сложную основу \(\ left\{\left(\begin{array}{l}
1 \\
1
\end{array}\right),\left(\begin{array}{c}
1 \\
-1
\ end{array}\right)\right\}=\left\{h_{0}, h_{1}\right\}\) Тогда наша базовая матрица и обратная базовая матрица примут вид:
\[\begin{aligned}
B &=\left(\begin{array}{cc}
1 & 1 \\
1 & -1 9{-1} \boldsymbol{x}=\left(\begin{array}{cc}
\frac{1}{2} & \frac{1}{2} \\
\frac{1}{2} & \frac{-1}{2}
\end{массив}\right)\left(\begin{array}{l}
3 \\
2
\end{массив}\right)=\left(\ begin{array}{l}
2. 5 \\
5 \\
0.5
\end{array}\right) \nonumber \]
и мы получаем
\[\boldsymbol{x}=2.5 h_{0}+0.5 h_{ 1} \номер \]
Упражнение \(\PageIndex{1}\)
Теперь у нас есть следующая базисная матрица и \(\boldsymbol{x}\):
\[\begin{array}{c}
\left\{b_{0}, b_{1}\right\}=\left\{\left(\begin{array}{l}
1 \\
2
\end{массив}\right),\left(\begin{array}{l}
3 \\
0
\end{массив}\right)\right\} \\
\boldsymbol{x}= \left(\begin{array}{l}
3 \\
2
\end{массив}\right)
\end{массив} \nonumber \]
Для этой задачи сделайте набросок оснований, а затем представьте \(\boldsymbol{x}\) через \(b_0\) и \(b_1\).
- Ответ 9{-1} \boldsymbol{x}=\left(\begin{array}{c}
1 \\
\frac{2}{3}
\end{массив}\right)
\end{массив} \ не число \] Теперь мы можем написать \(\boldsymbol{x}\) через \(b_0\) и \(b_1\).- \[\boldsymbol{x}=b_{0}+\frac{2}{3} b_{1} \nonumber \]
- И мы можем легко заменить наши известные значения \(b_0\) и \(b_1\), чтобы проверить наши результаты.
). = ½ ( а — б ). {-1}\) 9n\), мы хотим найти \(\left\{\alpha_{0}, \alpha_{1}, \ldots, \alpha_{n-1}\right\}\) такие, что
{-1}\) 9n\), мы хотим найти \(\left\{\alpha_{0}, \alpha_{1}, \ldots, \alpha_{n-1}\right\}\) такие, что\[\boldsymbol {x}=\alpha_{0} b_{0}+\alpha_{1} b_{1}+\ldots+\alpha_{n-1} b_{n-1} \label{15.55} \]
Опять же, мы создадим базовую матрицу
\[B=\left(\begin{array}{lllll}
b_{0} & b_{1} & b_{2} & \dots & b_{n-1}
\end{array}\right) \nonumber \], где столбцы равны базисным векторам, и это всегда будет матрица \(n \times n\) (хотя приведенная выше матрица не кажется квадратной, поскольку мы оставили термины в векторной записи). Затем мы можем приступить к переписыванию уравнения \ref{15.53} 9{-1} \boldsymbol{x} \номер\]
Эта страница под названием 15.9: Orthonormal Basis Expansions распространяется по лицензии CC BY, автором, ремиксом и/или куратором выступили Richard Baraniuk et al.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- Ричард Баранюк и др.

- Лицензия
- СС BY
- Программа OER или Publisher
- OpenStax CNX
- Теги
- основа
- базовая матрица
- вектор коэффициентов
- тождественная матрица
- ортонормированный базис
Изменение основы линейной алгебры
Теги МатематикаЗнание того, как преобразовать вектор в другой базис, имеет много практических Приложения. У Гилберта Стрэнга есть хорошая цитата о важности базиса. изменений в его книге [1] (выделено мной):
Стандартные базисные векторы для и это столбцы I .
 Этот выбор приводит к стандартной матрице, и
обычным способом. Но у этих пространств есть и другие основания,
так тот же Т представлен другими матрицами. Основная тема линейного
алгебра состоит в том, чтобы выбрать основания, дающие наилучшую матрицу для T .
Этот выбор приводит к стандартной матрице, и
обычным способом. Но у этих пространств есть и другие основания,
так тот же Т представлен другими матрицами. Основная тема линейного
алгебра состоит в том, чтобы выбрать основания, дающие наилучшую матрицу для T .Это должно послужить хорошей мотивацией, но я оставлю заявки на будущие посты; в этом я сосредоточусь на механике изменения базиса, начиная с первых принципов.
Компоненты базиса и вектора
Базис векторного пространства представляет собой набор векторов, т.е. линейно независимы и пролетны. Упорядоченный базис — это список, а не чем набор, что означает, что порядок векторов в упорядоченном базисе имеет значение. Это важно в отношении тем, обсуждаемых в этом посте.
Теперь определим компонентов . Если это заказанный основой для и является вектором в , то есть уникальный [2] список скаляров таких, что:
Они называются компонентами относительно заказанной основы .
 Здесь мы введем полезную нотацию: соберите
компоненты в вектор-столбец и назовите его
: это вектор компонентов относительно основы.
Здесь мы введем полезную нотацию: соберите
компоненты в вектор-столбец и назовите его
: это вектор компонентов относительно основы.Пример: нахождение вектора компонентов
Используем в качестве примера. является упорядоченный базис для (поскольку два вектора в нем равны независимый). Скажем, у нас есть. Что такое ? Нам нужно решить систему уравнения:
В двумерном случае это тривиально — решение есть и . Поэтому:
В более общем случае это сродни решению линейная система из n уравнений с n переменными. Поскольку базисные векторы определение, линейно независимое, решение системы просто инвертирует матрица [3].
Изменение базовой матрицы
Теперь ключевая часть поста. Скажем, у нас есть две разные упорядоченные базы для то же векторное пространство: и . Для некоторых мы можем найти и . Как эти двое связаны?
Конечно, учитывая, что мы можем найти его коэффициенты в базе так же, как мы это сделали в примере выше [4]. Он включает в себя решение линейная система уравнений.
 Нам придется повторить эту операцию для
каждый вектор, который мы хотим преобразовать. Есть ли более простой способ?
Нам придется повторить эту операцию для
каждый вектор, который мы хотим преобразовать. Есть ли более простой способ?К счастью для науки, да. Ключевым моментом здесь является нахождение того, как базисные векторы смотреть в базе. Другими словами, мы должны найти и так далее .
Допустим, мы делаем это и находим коэффициенты такими, что:
Теперь, если задан некоторый вектор , предположим, что его компоненты находятся в базисе are:
Попробуем разобраться, как это выглядит в базисе. Приведенное выше уравнение (по определения компонентов) эквивалентно:
Подставляя разложение s в базис, мы получаем:
Переупорядочивая бит, чтобы найти множители каждого:
По нашему определению компонентов вектора, это уравнение эквивалентно:
Теперь мы снова в векторном представлении, так что мы можем разложить вектор-столбец на правая сторона до:
Это матрица, умноженная на вектор. Вектор справа . Матрица тоже должна выглядеть знакомо, потому что она состоит из тех коэффициентов, которые мы определили выше.
 На самом деле это
матрица просто представляет базисные векторы выраженных в базисе
. Назовем эту матрицу — изменение базовой матрицы с на . Это
должен выложить
в его столбцах:
На самом деле это
матрица просто представляет базисные векторы выраженных в базисе
. Назовем эту матрицу — изменение базовой матрицы с на . Это
должен выложить
в его столбцах:Таким образом, мы имеем:
Подводя итог, учитывая два основания и , мы можем приложить некоторые усилия, чтобы вычислить матрицу «изменения базиса», но тогда мы можем легко преобразовать любой вектор в базис в основу, если мы просто умножим ее влево на эту матрицу.
Разумный вопрос, который можно задать в этот момент: как насчет преобразования из к ? Ну, так как приведенные выше вычисления полностью общий и не является особым случаем ни для одной базы, мы можем просто поменять местами роли и и получить еще одно изменение основы матрица, — она преобразует векторов в базе к векторам в базе следующим образом:
И эта матрица:
Вскоре мы увидим, что две замены базисных матриц тесно связаны; но сначала пример.
Пример: замена баз с матрицами
Давайте рассмотрим еще один конкретный пример в формате .
 У нас есть
использовали основу раньше; воспользуемся им снова, а также добавим
основа . Мы уже видели это для
у нас есть:
У нас есть
использовали основу раньше; воспользуемся им снова, а также добавим
основа . Мы уже видели это для
у нас есть:Точно так же мы можем решить набор из двух уравнений, чтобы найти:
Хорошо, давайте посмотрим, как изменение базовой матрицы может быть использовано для легкого вычисления одного учитывая другое. Во-первых, для нахождения нам понадобятся и . Мы знаем, как это сделать. Результат:
Теперь мы можем проверить, что задано и , мы можем легко найти :
Действительно, это подтверждается! Давайте также проверим другое направление. Найти нам понадобится и:
А теперь, чтобы найти:
Проверяет снова! Если у вас острый глаз или вы недавно провели некоторое время решая задачи линейной алгебры, вы заметите кое-что интересное в две матрицы изменения базиса, используемые в этом примере. Одно противоположно другому! Это какое-то совпадение? Нет — на самом деле это всегда так, и мы можем Докажите это.
Обратное изменение базовой матрицы
Мы получили изменение базисной матрицы с на на выполнение преобразование:
Умножение этого уравнения влево на :
Но левая часть теперь, по нашему предыдущему определению, равна , так что мы получаем:
Поскольку это верно для каждого вектора , должно быть что:
Из этого мы можем сделать вывод, что и наоборот [5].

Переход на стандартную основу и обратно
Вы могли заметить, что в приведенных выше примерах мы немного замкнули строгости путем составления вектора (например, ) без явного указание основы, к которой относятся его компоненты. Это потому что мы такие привыкшие работать со «стандартной основой» мы часто забываем, что она есть.
Стандартный базис (назовем его ) состоит из единичных векторов, указывающих в направлениях осей декартовой системы координат. За у нас есть базисные векторы:
И вообще у нас есть упорядоченный список векторы, где 1 в й позиции и нули в другом месте.
Итак, когда мы говорим , на самом деле мы имеем в виду:
Стандартная основа настолько укоренилась в нашем интуитивном понимании векторов, что мы обычно пренебрегают упоминанием об этом. Это нормально, пока мы имеем дело только с стандартная основа. Раз требуется смена базы, стоит придерживаться к более последовательному обозначению, чтобы избежать путаницы. Кроме того, часто полезно изменить базис вектора на стандартный или наоборот.
 Давайте посмотрим, как это работает.
Вспомните, как мы используем замену базовой матрицы:
Давайте посмотрим, как это работает.
Вспомните, как мы используем замену базовой матрицы:Замена произвольного базиса стандартным базисом в этом уравнения, получаем:
А есть матрица с в его столбцы. Но подождите, это всего лишь базовые векторы ! Итак, нахождение матрица для любого заданного основа тривиальна — просто выровняйте базисные векторы в виде столбцов чтобы получить матрицу. Это означает, что любая квадратная обратимая матрица можно рассматривать как изменение базисной матрицы по сравнению с базисом, изложенным в ее колонны к стандартной основе. Это естественное следствие того, как умножается матрица по вектору работает путем линейного объединения столбцов матрицы.
Итак, мы знаем, как найти данный . А как насчет наоборот? Для этого нам понадобится, и мы это знаем:
Следовательно:
Сцепление изменений базиса
Что произойдет, если мы изменим вектор из одного базиса в другой, а затем изменим результирующий вектор в еще один базис? Я имею в виду, для баз, и и некоторый произвольный вектор, мы сделаем:
Это просто применение замены базиса уравнением умножения матриц, дважды:
Это означает, что изменения базиса могут быть связаны цепочкой, что неудивительно учитывая их линейный характер.
 Это также означает, что мы только что нашли
, так как мы нашли, как
преобразовать в (используя
посредническая база).
Это также означает, что мы только что нашли
, так как мы нашли, как
преобразовать в (используя
посредническая база).Наконец, скажем, что посредническим базисом является не какой-то произвольный , а стандартная основа . Итак, мы имеем:
. Мы предпочитаем последнюю форму, поскольку нахождение для любого базиса, как мы видели выше, тривиально.
Пример: стандартная основа и цепочка
Пришло время закрепить идеи двух последних разделов конкретным пример. Мы будем использовать наши знакомые базы и из предыдущего примера, наряду со стандартным основанием за . Ранее мы преобразовали вектор из в и наоборот, используя замену базисных матриц между эти базы. На этот раз давайте сделаем это, цепляя через стандартный базис.
Мы выберем . Формально компоненты относительно стандартная база:
В последнем примере мы уже вычислили компоненты относительного to и :
Раньше одно вычислялось из другого с использованием «прямого» изменения базиса матрицы из в и наоборот.
 Теперь мы можем использовать цепочку через
стандартная основа для достижения того же результата. Например, мы знаем, что:
Теперь мы можем использовать цепочку через
стандартная основа для достижения того же результата. Например, мы знаем, что:Нахождение замены базисных матриц с какого-то базиса на просто наложение из базисных векторов в виде столбцов, так что мы сразу знаем, что:
Замена базисной матрицы с на некоторый базис обратна, поэтому инвертируя приведенные выше матрицы, мы находим:
Теперь у нас есть все, что нам нужно найти из :
Другое направление можно сделать аналогично.
[1] Introduction to Linear Algebra , 4th edition, section 7.2 [2] Why is this list unique? Поскольку при заданной основе вектора пробел, каждый может быть выражен однозначно как линейная комбинация векторов в .  Доказательством этого является
очень просто — просто предположим, что есть два разных способа выразить
— два альтернативных набора компонентов. Вычесть единицу из
другой и использовать линейную независимость базисных векторов, чтобы заключить, что
два пути должны быть одинаковыми.
Доказательством этого является
очень просто — просто предположим, что есть два разных способа выразить
— два альтернативных набора компонентов. Вычесть единицу из
другой и использовать линейную независимость базисных векторов, чтобы заключить, что
два пути должны быть одинаковыми.[3] Здесь базисные векторы размещены в столбцах матрицы. Поскольку базисные векторы независимы, матрица обратима. В нашем маленьком Например, матричное уравнение, которое мы хотим решить: [4] Пример преобразует стандартный базис в какой-либо другой базис, но переход с нестандартной основы на другую требует именно те же шаги: мы пытаемся найти такие коэффициенты, что комбинация некоторый набор базисных векторов суммируется с некоторыми компонентами другого основа. 
[5] Для квадратных матриц и , если то также . Для комментариев, пожалуйста, пришлите мне письмо.
Ортонормированный базис
Марко Табога, доктор философии
Базис ортонормирован если его векторы:
иметь единичную норму;
ортогональны друг другу (т. внутренний продукт равен нулю).
Представление вектора в виде линейной комбинации ортонормированного базиса называется разложением Фурье. Это особенно важно в приложениях.
СОДЕРЖАНИЕ
Ортонормальные наборы
Ортонормальные наборы являются линейными независимыми
Основные ортонормальные векторы
- 333333 3 -й ортонормальные векторы
- 333333 3 Фортонормальные векторы
- 3333333 3 Fourder.
 9003
9003 - 33333333 3 Fourder.0034
Упражнение 1
Упражнение 2
Ортонормированные множества
Начнем с определения ортонормированности набора векторов (не обязательно основу).
Определение Позволять быть векторным пространством, снабженным внутренний продукт . Набор векторы называется ортонормированным набором если и только если
Таким образом, все векторы в ортонормированном множестве ортогональны друг другу и имеют Ед. изм норма:
Давайте сделаем простой пример.
Пример Рассмотрите пространство из всех векторы-столбцы, имеющие действительные записи вместе с внутренней продуктгде а также обозначает транспонирование . Рассмотрим набор из двух векторов внутренний продукт сам с собой это внутренний продукт сам с собой это внутренний продукт а также следовательно является, а также образуют ортонормированное множество.

Ортонормированные множества линейно независимы
Следующее предложение показывает ключевое свойство ортонормированных множеств.
Предложение Позволять быть векторным пространством, снабженным внутренним произведением . Векторы ортонормированного множества линейно независимы.
Доказательство
Доказательство от противного. Предположим, что векторы линейно зависимы. Тогда существуют скаляры , не все равны нулю, так что Таким образом, для любого ,куда: в ногу мы использовали аддитивность и однородность скалярного продукта в его первом аргумент; в ногу мы воспользовались тем, что имеем дело с ортонормированным множеством, так что если ; в ногу мы воспользовались тем, что векторы имеют единичную норму. Поэтому все коэффициенты должен быть равен нулю. Мы пришли к противоречию и, как следствие, гипотеза о том, что линейно зависимы неверно.
 Следовательно, они линейно независимы.
Следовательно, они линейно независимы.Базис ортонормированных векторов
Если ортонормированное множество является базисом своего пространства, то оно называется ортонормированный базис.
Определение Позволять быть векторным пространством, снабженным внутренним произведением . Набор векторы называются ортонормированным базисом тогда и только тогда, когда они являются основа для и они образуют ортонормированный набор.
В следующем примере мы покажем, что каноническим базисом координатного пространства является ортонормированный базис.
Пример Как и в предыдущем примере, рассмотрим пространство из всех векторы-столбцы, имеющие реальные записи, вместе с внутренним продуктдля . Рассмотрим три векторыкоторые составляют каноническую основу из .
 Мы можем ясно видеть
что для
пример и, таким образом,
канонический базис является ортонормированным базисом.
Мы можем ясно видеть
что для
пример и, таким образом,
канонический базис является ортонормированным базисом.Расширение Фурье
Невероятно легко получить представление данного вектора в виде линейная комбинация ортонормированного базиса.
Предложение Позволять быть векторным пространством, снабженным внутренним произведением . Позволять быть ортонормированным базисом . Тогда для любого , мы have
Proof
Предположим, что единственное представление с точки зрения основы это здесь являются скалярами. Тогда для , у нас есть это где: в ногу мы использовали аддитивность и однородность скалярного продукта в его первом аргумент; в ногу мы воспользовались тем, что имеем дело с ортонормированным базисом, так что если ; в ногу мы воспользовались тем, что векторы имеют единичную норму.
 Таким образом, мы обнаружили, что
для любого
,
что доказывает предложение.
Таким образом, мы обнаружили, что
для любого
,
что доказывает предложение.Линейная комбинация выше называется разложением Фурье, а коэффициенты называются коэффициентами Фурье.
Другими словами, мы можем найти коэффициент путем простого вычисления внутреннего продукта с .
Пример Позволять быть пространством всех векторы-столбцы с сложные записи вместе с внутренними продуктгде а также является сопряженным транспонированием из . Рассмотрим ортонормированный основаУчитывать в векторЗатем, первый коэффициент Фурье остров второй коэффициент Фурье мы можете проверить это действительно может быть записана как линейная комбинация базиса с коэффициенты просто производное:
Решенные упражнения
Ниже вы можете найти несколько упражнений с поясненными решениями.

Упражнение 1
Используйте ортонормированный базис двух комплексных векторов, введенный в предыдущем Пример для получения коэффициентов Фурье вектор
Решение
Выведен первый коэффициент Фурье путем вычисления внутреннего продукта а также : второй коэффициент Фурье находится путем вычисления внутреннего произведения а также :
Упражнение 2
Убедитесь, что коэффициенты Фурье, найденные в предыдущем упражнении, равны правильный.
В частности, проверьте, что с их помощью можно линейно комбинировать два вектора основа дает как результат.
Решение
Фурье-представление который является желаемым результатом.
Как цитировать
Пожалуйста, указывайте как:
Taboga, Marco (2021). «Ортонормированный базис», Лекции по матричной алгебре. https://www.statlect.com/matrix-алгебра/ортонормал-базис.
Линейно-независимый набор можно разложить в базис
Зависимости:
- Основа векторного пространства
- Линейно независимое множество не больше размаха
- Увеличение линейно независимого набора
Пусть $S = \{v_1, v_2, \ldots, v_k\}$ — линейно независимое подмножество векторного пространства $V$.
 Пусть $V$ имеет базис размера $n$.
Тогда $k \le n$ и $\существует S’ = \{v_{k+1}, \ldots, v_n\} \subset V$ такое, что $S \cup S’$ является базисом $V$.
Пусть $V$ имеет базис размера $n$.
Тогда $k \le n$ и $\существует S’ = \{v_{k+1}, \ldots, v_n\} \subset V$ такое, что $S \cup S’$ является базисом $V$.Доказательство
Пусть $B$ — базис $V$. Поскольку $B$ охватывает $V$ и $S$ линейно зависима, $|С| \le |B| \Rightarrow k \le n$.
Определите $S_k = S$. $|S_k| = к$.
Если $S_i$ не охватывает $V$, $\существует v \in V$, что не может быть выражено в виде линейной комбинации $S_i$. Определите $S_{i+1} = S_i \cup \{v\}$. Если $S_i$ линейно независима, $S_{i+1}$ линейно независима. $|S_{я+1}| = |S_i| + 1$.
Следовательно, из $S_k$ мы можем сгенерировать $S_{k+1}$, если $S_k$ не охватывает $V$, из $S_{k+1}$ мы можем сгенерировать $S_{k+2}$, если $S_{k+1}$ не охватывает $V$, и так далее. В конце концов мы либо получим множество $S_m$, охватывающее $V$, или $S_i$ не охватывает $V$ для всех $i \ge k$.
Используя математическую индукцию, можно доказать, что для всех $i \ge k$:
- $S_i$ линейно независима.

- $|S_i| = я$.
- $S \подмножество S_i$.
Случай 1: $S_i$ не порождает $V$ для всех $i \ge k$
Поскольку $S_{n+1}$ линейно независима, а $B$ порождает $V$, $|S_{n+1}| \le |B| \Стрелка вправо n+1 \le n \Стрелка вправо \bot$.
Следовательно, такого случая быть не может.
Случай 2: Существует множество $S_m$, которое охватывает $V$
Это делает $S_m$ основой $V$.
Поскольку $S_m$ покрывает $V$ и $B$ линейно независима, $|B| \le |S_m|$. Поскольку $S_m$ линейно независима и $B$ порождает $V$, $|S_m| \le |B|$. Следовательно, $|S_m| = м = |В| = п$.
Следовательно, можно расширить $S$, чтобы получить базис $V$ размера $n$.
Зависимость для:
- База диапазона линейного преобразования
- Симметрический оператор на V имеет базис ортонормированных собственных векторов
Информация:
- Глубина: 6
- Количество транзитивных зависимостей: 38
Переходные зависимости:
- /линейная-алгебра/векторные-пространства/условие-для-подпространства
- /линейная-алгебра/матрицы/гаусс-джордан-алго
- /множества-и-отношения/эквивалентность-отношение
- Группа
- Звенеть
- Полиномиальный
- Интегральный домен
- Сравнение коэффициентов многочлена с непересекающимися переменными
- Поле
- Векторное пространство
- Линейная независимость
- Охватывать
- Увеличение линейно независимого набора
- полукольцо
- Матрица
- Укладка
- Система линейных уравнений
- Произведение сложенных матриц
- Умножение матриц ассоциативно
- Уменьшенная форма эшелона строк (RREF)
- Матрицы над полем образуют векторное пространство
- Пространство строки
- Элементарная операция строки
- Каждая элементарная операция строки имеет уникальную обратную
- Эквивалентность строк матриц
- Матрицы, эквивалентные строкам, имеют одинаковое пространство строк.

- RREF уникален
- Единичная матрица
- Обратная матрица
- Инверсия продукта
- Элементарная операция со строками — предварительное умножение матриц.
- Матрица эквивалентности строк
- Уравнения с матрицами, эквивалентными строкам, имеют один и тот же набор решений.
- Основа векторного пространства
- Линейно независимое множество не больше размаха
- Однородные линейные уравнения с большим количеством переменных, чем уравнения
- Ранг однородной системы линейных уравнений
- Ранг матрицы
Основа векторного пространства
Пусть V будет подпространством R n для некоторого n .
 A collection B = { v 1 , v 2 , …, v r } of vectors from V is said to be a basis for V если B линейно независима и охватывает V . Если хотя бы один из этих критериев не выполняется, то коллекция не является основой для В . Если набор векторов охватывает V , то он содержит столько векторов, что каждый вектор из V может быть записан как линейная комбинация векторов в наборе. Если набор линейно независим, то он не содержит столько векторов, чтобы одни становились зависимыми от других. Таким образом, интуитивно понятно, что базис имеет правильный размер: он достаточно велик, чтобы охватывать пространство, но не настолько велик, чтобы быть зависимым.
A collection B = { v 1 , v 2 , …, v r } of vectors from V is said to be a basis for V если B линейно независима и охватывает V . Если хотя бы один из этих критериев не выполняется, то коллекция не является основой для В . Если набор векторов охватывает V , то он содержит столько векторов, что каждый вектор из V может быть записан как линейная комбинация векторов в наборе. Если набор линейно независим, то он не содержит столько векторов, чтобы одни становились зависимыми от других. Таким образом, интуитивно понятно, что базис имеет правильный размер: он достаточно велик, чтобы охватывать пространство, но не настолько велик, чтобы быть зависимым.Пример 1 : Коллекция { i, j } является базисом для R 2 , поскольку он охватывает R 2 , а векторы i и j линейно независимы (поскольку ни один из них не кратен другому).
 Это называется стандартной базой для R 2 . Аналогично набор { i, j, k } называется стандартным базисом для R 3 и вообще
Это называется стандартной базой для R 2 . Аналогично набор { i, j, k } называется стандартным базисом для R 3 и вообщеявляется стандартной основой для R n .
Пример 2 : Набор { i, i+j , 2 j } не является основой для R 2 . Хотя он охватывает R 2 , он не является линейно независимым. Никакая коллекция из 3 или более векторов из R 2 не может быть независимой.
Пример 3 : Коллекция { i+j, j+k } не является основой для R 3 . Хотя он линейно независим, он не охватывает все R 3 . Например, не существует линейной комбинации i + j и j + k , равной i + j + k .

Пример 4 : Набор { i + j, i − j } является основой для R 2 . Во-первых, оно линейно независимо, поскольку ни i + j , ни i − j не кратны другим. Во-вторых, он охватывает все R 2 , потому что каждый вектор в R 2 может быть выражен как линейная комбинация i + j и i − j . В частности, если A I + B J — любой вектор в R 2 , тогда IF K 1 = ½ ( A + B ) и и ) и
Пространство может иметь много разных оснований. Например, оба { i, j } и { i + j, i − j } являются базами для R 2 . Фактически, любой набор , содержащий ровно два линейно независимых вектора из R 2 , является основой для R 2 .
 Точно так же любой набор, содержащий ровно три линейно независимых вектора из R 3 , является основой для R 3 и так далее. Хотя нет нетривиального подпространства R n имеет уникальную основу, там есть то, что должно быть общим для всех основ данного пространства.
Точно так же любой набор, содержащий ровно три линейно независимых вектора из R 3 , является основой для R 3 и так далее. Хотя нет нетривиального подпространства R n имеет уникальную основу, там есть то, что должно быть общим для всех основ данного пространства.Пусть V будет подпространством R n для некоторого n . Если V имеет базис, содержащий ровно r векторов, то каждый базис для V содержит ровно r векторов. То есть выбор базисных векторов для данного пространства не уникален, а число базисных векторов является уникальным. Этот факт позволяет четко определить следующее понятие: число векторов в базисе векторного пространства V ⊆ R n называется размерностью V , обозначаемой dim V .

Пример 5 : Поскольку стандартный базис для R 2 , { i, j } содержит ровно 2 вектора, каждый базис для R 2 содержит ровно 2 вектора, поэтому dim R 2 = 2. Точно так же, поскольку { i, j, k } является основой для R 3 , которое содержит ровно 3 вектора, Каждое основание для R 3 содержит ровно 3 вектора, так что DIM R 3 = 3. В целом, DIM R N = N для каждого натурального номера .
Пример 6 : В R 3 векторы i и k охватывают подпространство размерности 2. Это плоскость x−z , как показано на рисунке .
Рисунок 1Пример 7: Одноэлементный набор { i + j = (1, 1)} является базой для одномерного подпространства V из R 2 , состоящего из строки y = х .
 См. рис.
См. рис.Рисунок 2
Пример 8 : Тривиальное подпространство { 0 } в R n имеет размерность 0. Таким образом, чтобы соответствовать определению размерности, можно получить основу для { 0 } должна быть коллекцией, не содержащей элементов; это пустой набор, ø.
Подпространства R 1 , R 2 и R 3 , некоторые из которых были проиллюстрированы в предыдущих примерах, можно резюмировать следующим образом:0034
Пример 9 : Найдите размерность подпространства V из R 4 , натянутого на векторы
Коллекция { V 1 , V 2 , V 3 , V 4 } не является основой для V — и DIM — и DIM — и DIM — и DIM — и DIM — и DIM — и DIM — и DIM .
 потому что { v 1 , v 2 , v 3 , v 4 } не является линейно независимым; см. расчет, предшествующий приведенному выше примеру. Сброс V 3 и V 4 из этой коллекции не уменьшает пролет { V 1 , V 2 , V 9037 2 , V 9037 9037 9037 9037 9037 9037 9037 9037 9037 9037 9037 9. 9037 9. 9. . }, но результирующий набор { v 1 , v 2 } линейно независим. Таким образом, { v 1 , v 2 } является основой для V , поэтому тусклый V = 2.
потому что { v 1 , v 2 , v 3 , v 4 } не является линейно независимым; см. расчет, предшествующий приведенному выше примеру. Сброс V 3 и V 4 из этой коллекции не уменьшает пролет { V 1 , V 2 , V 9037 2 , V 9037 9037 9037 9037 9037 9037 9037 9037 9037 9037 9037 9. 9037 9. 9. . }, но результирующий набор { v 1 , v 2 } линейно независим. Таким образом, { v 1 , v 2 } является основой для V , поэтому тусклый V = 2.
Пример 10 : Найдите размер промежутка векторов
Поскольку эти векторы находятся в R 5 , их диапазон, S , является подпространством R 5 . Однако это не трехмерное подпространство R 5 , поскольку три вектора w 1 , w 2 и w 3 не являются линейно независимыми. Фактически, поскольку w 3 = 3w 1 + 2w 2 , вектор w 3 можно исключить из набора, не уменьшая его. Поскольку векторы w 1 и w 2 независимы — ни один из них не является скалярным кратным другого — набор { w 1 , w 2 } служит основой для S , поэтому его размерность равна 2.

Наиболее важным атрибутом базиса является возможность записать каждый вектор в пространстве уникальным способом в терминах базисных векторов. Чтобы понять, почему это так, пусть B = { v 1 , v 2 , …, v r } пространство будет базисом a 9 . Поскольку базис должен охватывать V , каждый вектор v в V может быть записан по крайней мере одним способом как линейная комбинация векторов в B . То есть существуют скаляры k 1 , k 2 , …, k r такие, что
Чтобы показать, что никакой другой выбор скалярных множителей не может дать v , предположим, что
также является линейной комбинацией базисных векторов, равной против .
Вычитание (*) из (**) дает
Это выражение представляет собой линейную комбинацию базисных векторов, которая дает нулевой вектор.
 Поскольку базисные векторы должны быть линейно независимыми, каждый из скаляров в (***) должен быть равен нулю:
Поскольку базисные векторы должны быть линейно независимыми, каждый из скаляров в (***) должен быть равен нулю:Следовательно, K ′ 1 = K 1 , K ′ 2 = K 2 ,… и K R = K , K , K , K , K = K , K . *) действительно уникален. Когда V написан в виде линейной комбинации (*) базисных векторов V 1 , V 2 ,…, V R , определение UNIQUENININININED R , UNIQUELINININED R . 1 , k 2 , …, k r называются компонентами v относительно основы B . Вектор-строка ( k 1 , k 2 , …, k r ) называется компонентным вектором v относительно B и обозначается ( v ) B 9.
 Иногда удобно записать вектор компонентов как вектор столбцов ; в этом случае компонентный вектор ( k 1 , k 2 , …, k r ) T обозначается [6 1 7 B 1
Иногда удобно записать вектор компонентов как вектор столбцов ; в этом случае компонентный вектор ( k 1 , k 2 , …, k r ) T обозначается [6 1 7 B 1]
0418
.Пример 11 : Рассмотрим набор C = { i, i + j , 2 j } векторов в R 2 . Заметим, что вектор v = 3 i + 4 j можно записать в виде линейной комбинации векторов C следующим образом:
и
Тот факт, что существует более одного способа выразить вектор v в R 2 как линейная комбинация векторов в C дает еще одно указание на то, что C не может быть основой для R 2 . Если бы C были базисом, вектор v можно было бы записать как линейную комбинацию векторов из C одним и только одним способом.

Пример 12 : Рассмотрим базис B = { i + j , 2 i − j } из R 2 . Определить компоненты вектора v = 2 i − 7 j относительно B .
Компоненты v относительно B представляют собой скалярные коэффициенты k 1 и k 2 , которые удовлетворяют уравнению
Это уравнение эквивалентно системе
Решение этой системы равно k 1 = −4 и k 2 = 3, поэтому
Example 13 : Relative to the standard basis { i, j, k } = { ê 1 , ê 2 , ê 3 } for R 3 , компонентный вектор любого вектора v в R 3 равен самому v : ( v ) B = v .
 Тот же самый результат справедлив для стандартного базиса { ê 1 , ê 2 ,…, ê n } для каждого R
Тот же самый результат справедлив для стандартного базиса { ê 1 , ê 2 ,…, ê n } для каждого Rn 9 04926 } .
Ортонормированные базисы . Если B = { V 1 , V 2 ,…, V N } является основанием для пространства Execter V }.0417 V можно записать как линейную комбинацию базисных векторов одним и только одним способом:
Нахождение компонент v относительно базиса B — скалярных коэффициентов k 1 , k 2 , …, k 7 n 90 система уравнений. Однако, если базисные векторы являются ортонормированными , то есть взаимно ортогональными единичными векторами, то вычисление компонентов особенно легко. Вот почему.
 Предположим, что B = {vˆ 1 ,vˆ 2 ,…,vˆ n } является ортонормированным базисом. Начиная с приведенного выше уравнения — с Vˆ 1 , Vˆ 2 ,…, Vˆ N Замена V 1 , V 2 ,…, V 2 ,…, V 99936 2 ,…, V 2 ,…, V 2 ,…, V 2 ,…, V 9037 2 . что базисные векторы теперь считаются единичными — возьмем скалярное произведение обеих сторон с vˆ 1 :
Предположим, что B = {vˆ 1 ,vˆ 2 ,…,vˆ n } является ортонормированным базисом. Начиная с приведенного выше уравнения — с Vˆ 1 , Vˆ 2 ,…, Vˆ N Замена V 1 , V 2 ,…, V 2 ,…, V 99936 2 ,…, V 2 ,…, V 2 ,…, V 2 ,…, V 9037 2 . что базисные векторы теперь считаются единичными — возьмем скалярное произведение обеих сторон с vˆ 1 :В силу линейности скалярного произведения левая часть становится равной
Теперь, в силу ортогональности базисных векторов, vˆ i · vˆ 1 = 0 для i = 2 через n . Кроме того, поскольку vˆ является единичным вектором, vˆ 1 · vˆ 1 = ‖vˆ 1 ‖1 2 = 1 2 = 1.
 Следовательно, приведенное выше уравнение упрощается до утверждения
Следовательно, приведенное выше уравнение упрощается до утвержденияВ общем, если B = { vˆ 1 , vˆ 2 ,…, vˆ n } является ортонормированным базисом векторного пространства V , то компоненты k i любого вектора v относительно B находятся по простой формуле
Пример 14 : Рассмотрим векторы
из Р 3 . Эти векторы взаимно ортогональны, в чем легко убедиться, проверив, что v 1 · v 2 = V 1 · V 3 = V 2 · V 3 = 0,0937. , а затем найти компоненты вектора v = (1, 2, 3) относительно этого базиса.
Ненулевой вектор нормализуется — преобразуется в единичный вектор — путем деления его на длину.
 Следовательно,
Следовательно,С B = { Vˆ 1 , Vˆ 2 , Vˆ 3 } — это ортономерное основание для R } — это ортономерное основание для r }. v
относительно B можно найти, просто взяв следующие скалярные произведения:Следовательно, ( v ) B = (5/3, 11/(3√2),3/√2), что означает, что единственное представление v как линейная комбинация базисных векторов читается как v = 5/3 vˆ 1 + 11/(3√2) vˆ 2 + 3/√9093 vˆ26 , как вы можете убедиться.
Пример 15 : Докажите, что набор взаимно ортогональных ненулевых векторов линейно независим.
Доказательство . Пусть { v 1 , v 2 , …, v r } be a set of nonzero vectors from some R n which are mutually orthogonal, which means that no v i = 0 and v i · v j = 0 для i ≠ j .
 Пусть
Пусть— линейная комбинация векторов в этом наборе, дающая нулевой вектор. Цель состоит в том, чтобы показать, что k 1 = k 2 = … = k r = 0. Для этого возьмем скалярное произведение обеих частей уравнения с v 1 :
Второе уравнение следует из первого в силу линейности скалярного произведения, третье уравнение следует из второго в силу ортогональности векторов, а итоговое уравнение является следствием того, что ‖ v 1 ‖ 2 ≠ 0 (поскольку v 1 ≠ 0 ). Теперь легко видеть, что скалярное произведение обеих сторон (*) с v i дает k i = 0, устанавливая, что каждый скалярный коэффициент в (*) должен быть нулю, тем самым подтверждая, что векторы v 1 , v 2 , …, v r действительно независимы.

Базовое представление — документация scikit-fda 0.7.1
В этом разделе мы познакомимся с базовым представлением функциональные данные. Это очень полезное представление для функций, которые принадлежат (или могут быть разумно спроектированы) пространству, натянутому на конечное множество базисных функций.
# Автор: Карлос Рамос Карреньо # Лицензия: Массачусетский технологический институт # # sphinx_gallery_thumbnail_number = 7
Функции и векторные пространства
Функции, являющиеся объектом изучения FDA, могут быть добавлены и умножается на скаляры, и эти операции проверяют необходимые свойства рассматривать эти функции как векторы в векторном пространстве.
Объекты
FDataGrid, используемые для представляют функциональные наблюдения в scikit-fda, также поддерживают эти операции.Чтобы показать векторные операции, мы создаем два FDatagrid с две функции каждая, \(\mathbf{X}_1 = \{x_{1i}: \mathbb{R} \to \mathbb{R}\}, i=1,2\) и \(\mathbf{X}_2 = \{x_{2i}: \mathbb{R} \to \mathbb{R}\}, i=1,2\), и зарисуйте их.

импортировать numpy как np импорт скфда импортировать matplotlib.pyplot как plt рис, оси = plt.subplots(1, 2, figsize=(8, 3)) т = np.linspace (0, 1, 100) fd = skfda.FDataGrid( data_matrix=[ np.sin(6 * t), # Первая функция 2 * t, # Вторая функция ], grid_points=t, ) fd.plot (оси = оси [0]) оси [0].set_title(r"$\mathbf{X}_1$") fd2 = skfda.FDataGrid( data_matrix=[ 3 * t**2, # Первая функция np.log(t + 0.1), # Вторая функция ], grid_points=t, ) fd2.plot (оси = оси [1]) оси[1].set_title(r"$\mathbf{X}_2$") plt.show()Функции можно умножать на скаляр. Это только меняет масштаб функции, но не их форму. Обратите внимание, что все функции в набор данных затронут.
Также можно сложить две функции вместе. Если вы сделаете это с два объекта
FDataGridс одинаковыми длина, будут добавлены соответствующие функции.рис, оси = plt.subplots(1, 2, figsize=(8, 3)) скалярное_множество = 3 * ПД scalar_mul.
 plot (оси = оси [0])
оси[0].set_title(r"$3\mathbf{X}_1$")
fd_sum = fd + fd2
fd_sum.plot (оси = оси [1])
оси[1].set_title(r"$\mathbf{X}_1 + \mathbf{X}_2$")
plt.show()
9{\infty} a_i \phi_i(t)\]
plot (оси = оси [0])
оси[0].set_title(r"$3\mathbf{X}_1$")
fd_sum = fd + fd2
fd_sum.plot (оси = оси [1])
оси[1].set_title(r"$\mathbf{X}_1 + \mathbf{X}_2$")
plt.show()
9{\infty} a_i \phi_i(t)\]
где сходимость этого ряда относительно векторного пространства топология.
Если вы знаете, что интересующие вас функции относятся к одному из этих векторов пространства, может быть интересно выразить ваши функции в базисе. Поскольку компьютеры имеют ограниченную память и вычислительные ресурсы, это не можно получить бесконечное расширение базиса. Вместо этого обычно сокращает расширение до нескольких базовых функций, которых достаточно для аппроксимируйте свои наблюдения с определенной степенью точности. Этот усечение также имеет эффект сглаживания данных, как менее важный изменения, такие как шум, устраняются в процессе. Более того, в качестве основы усечены, векторное пространство, порожденное усеченным набором базиса функций отличается от исходного пространства, а также отличается между разные базисные семейства.
 Таким образом, выбор базиса имеет значение, даже если
изначально они должны были генерировать одно и то же пространство.
Таким образом, выбор базиса имеет значение, даже если
изначально они должны были генерировать одно и то же пространство. В scikit-fda функции, выраженные в виде базового расширения, могут быть представлены используя класс
FDataBasis. Главный атрибутами объектов этого класса являютсяосновы, объект, представляющий собой базисное семейство функций икоэффициентов, матрица со скаляром коэффициенты функций в базисе.В качестве примера мы можем создать следующую функцию, которая выражается в усеченный мономиальный базис (и, следовательно, полином): 93\]
основа = skfda.representation.basis.Monomial( n_базис=4, диапазон_домена=(-10, 10), ) fd_basis = skfda.FDataBasis( основа=основа, коэффициенты=[ [3, 2, -4, 1], # Первое (и единственное) наблюдение ], ) fd_basis.plot() plt.show()Преобразование между FDataGrid и FDataBasis
Возможно преобразование между функциями в дискретной форме (класс
FDataGrid) и форма расширения базы ( классFDataBasis). Чтобы преобразовать
Чтобы преобразовать FDataGridобъектов к основе представления вам нужно будет вызвать методto_basis, передав желаемое основание в качестве аргумента. Затем функции будут проецироваться на функциональный базис, решая задачу наименьших квадратов, чтобы найти оптимальные коэффициенты расширения. Чтобы преобразоватьFDataBasisв дискретизированный представления вы должны вызвать методto_grid. Этот метод оценивает функции в сетке, которые могут быть предоставлены в качестве аргумента для получить значения дискретизированного представления.Теперь мы можем видеть, как количество базисных функций влияет на расширение базиса представление нескольких наблюдений, взятых из реального набора данных. Ты можно видеть, что чем больше базисных функций используется, тем базисное представление обеспечивает лучшее представление реальных данных.
макс_базис = 9 X, y = skfda.datasets.fetch_phoneme(return_X_y=True) # Выбрать только первые 5 образцов Х = Х[:5] X.
 сюжет()
рис., оси = plt.subplots(nrows=3, ncols=3)
для n_basis в диапазоне (1, max_basis + 1):
base = skfda.representation.basis.Monomial(n_basis=n_basis)
X_basis = X.to_basis(основа)
топор = axes.ravel()[n_basis - 1]
рис = X_basis.plot (оси = топор)
ax.set_title(f"{n_basis} базовые функции")
fig.tight_layout()
plt.show()
сюжет()
рис., оси = plt.subplots(nrows=3, ncols=3)
для n_basis в диапазоне (1, max_basis + 1):
base = skfda.representation.basis.Monomial(n_basis=n_basis)
X_basis = X.to_basis(основа)
топор = axes.ravel()[n_basis - 1]
рис = X_basis.plot (оси = топор)
ax.set_title(f"{n_basis} базовые функции")
fig.tight_layout()
plt.show()
Список доступных базовых функций
В этом разделе мы предоставим список доступных баз в scikit-fda. Как объяснялось ранее, базисное семейство важно при расширении базиса. усекается (что всегда происходит, чтобы представить его в компьютере). Таким образом, рекомендуется взглянуть на доступную основу, чтобы выберите тот, который обеспечивает наилучшее представление исходных данных.
Сначала мы загрузим набор данных для проверки базовых представлений.
X, y = skfda.datasets.fetch_phoneme(return_X_y=True) # Выбрать только первые 5 образцов Х = Х[:5] X.сюжет() plt.show()
Мономиальный базис
Мономиальный базис (класс
Мономиал) наверное один из самых простых и известных базисов функций. Часто ряды Тейлора и МакЛорина объясняются в самом
первые курсы научных и инженерных степеней, и студенты знакомы
с полиномами намного раньше. Таким образом, мономиальный базис полезен для
учебных целях (именно поэтому мы использовали его в примерах). это
также очень полезно для целей тестирования, так как легко вручную получить
ожидаемые результаты операций с участием этого базиса. 92\), то есть \(\langle x_1, x_2 \rangle =
\ int _ {\ mathcal {T}} x_1 (t) x_2 (t) dt \). Это тормозит некоторые
оптимизация производительности, доступная для операций, требующих
внутренние продукты. Можно найти ортогональный базис многочленов,
но его будет не так просто понять, потеряв многие свои преимущества.
Еще одна проблема с этой базой – необходимость большого
количество базовых функций для выражения локальных особенностей, плохое поведение в
экстремумы функции и тот факт, что производные базиса
расширения не являются хорошими приближениями производных от оригинала
данных, так как полиномы высокого порядка имеют тенденцию к очень большим колебаниям.
Часто ряды Тейлора и МакЛорина объясняются в самом
первые курсы научных и инженерных степеней, и студенты знакомы
с полиномами намного раньше. Таким образом, мономиальный базис полезен для
учебных целях (именно поэтому мы использовали его в примерах). это
также очень полезно для целей тестирования, так как легко вручную получить
ожидаемые результаты операций с участием этого базиса. 92\), то есть \(\langle x_1, x_2 \rangle =
\ int _ {\ mathcal {T}} x_1 (t) x_2 (t) dt \). Это тормозит некоторые
оптимизация производительности, доступная для операций, требующих
внутренние продукты. Можно найти ортогональный базис многочленов,
но его будет не так просто понять, потеряв многие свои преимущества.
Еще одна проблема с этой базой – необходимость большого
количество базовых функций для выражения локальных особенностей, плохое поведение в
экстремумы функции и тот факт, что производные базиса
расширения не являются хорошими приближениями производных от оригинала
данных, так как полиномы высокого порядка имеют тенденцию к очень большим колебаниям.
Здесь показаны первые пять элементов мономиального базиса.
основа = skfda.representation.basis.Monomial(n_basis=5) базис.участок() plt.show()
Теперь мы покажем, как предыдущие наблюдения представлены с помощью первого пять элементов этого основания.
X_basis = X.to_basis(база) X_basis.plot() plt.show()
Базис Фурье
Вероятно, второе по известности расширение серии для статиков. инженеров, физиков и математиков — это ряд Фурье. Фурье основа (класс 92\)) норма. Этот базис является хорошим выбором для периодических функций (как функция выраженная в этом основании, имеет одинаковое значение в начале и в конце своего доменного интервала, если он имеет ту же длину, что и период \(\омега\). Более того, в этом случае функции ортонормированы (т.е. поэтому используемая база нормализована).
Этот базис специально указан для функций без сильных локальных особенности и с почти таким же порядком кривизны везде, как в противном случае расширение потребует снова большого количества базиса для представления эти детали.

Здесь показаны первые пять элементов базиса Фурье.
базис = skfda.representation.basis.Fourier(n_basis=5) базис.участок() plt.show()
Теперь мы покажем, как предыдущие наблюдения представлены с помощью первого пять элементов этого основания.
X_basis = X.to_basis(база) X_basis.plot() plt.show()
B-шлицевая основа
Сплайны — это семейство функций, важность которых возросла с появлением современных компьютеров, и в настоящее время хорошо известны многим инженерам и дизайнеры. По существу, это кусочно-полиномы, которые гладко соединяются в точках разделения (обычно называемых узлами). Таким образом, оба полинома и кусочно-линейные функции входят в это семейство. Учитывая набор узлы, базис B-сплайн (класс
BСплайн) заданного порядка можно использовать для выражения каждого сплайна того же порядка, что использует одни и те же узлы.Эта основа очень мощная, так как узлы можно регулировать, чтобы иметь возможность для выражения местных особенностей, и даже возможно создать точки, где функции не обязательно должны быть гладкими или непрерывными, если разместить несколько узлы вместе.
 Также элементы основания имеют компактную опору
свойство, позволяющее повысить эффективность вычислений. Таким образом, это основание
указывается для непериодических функций или функций с локальными особенностями или с
различных порядков кривизны вдоль их домена.
Также элементы основания имеют компактную опору
свойство, позволяющее повысить эффективность вычислений. Таким образом, это основание
указывается для непериодических функций или функций с локальными особенностями или с
различных порядков кривизны вдоль их домена.Здесь показаны первые пять элементов базиса B-сплайна.
базис = skfda.representation.basis.BSpline(n_basis=5) базис.участок() plt.show()
Теперь мы покажем, как предыдущие наблюдения представлены с помощью первого пять элементов этого основания.
X_basis = X.to_basis(база) X_basis.plot() plt.show()
Постоянная основа
Иногда полезно рассмотреть базис, единственной функцией которого является постоянная. В частности, используя этот базис, мы можем просматривать скалярные значения как функциональные наблюдения, которые можно использовать для объединения многомерных и функциональные данные в той же модели. 9Н\). Однако scikit-fda также допускает представление поверхностей или функций в более высоких измерениях.
 В этом случае еще больше
полезно иметь возможность представлять их, используя базисные расширения, как число
параметров в дискретном представлении растет как произведение
точки сетки в каждом измерении домена.
В этом случае еще больше
полезно иметь возможность представлять их, используя базисные расширения, как число
параметров в дискретном представлении растет как произведение
точки сетки в каждом измерении домена.Основа тензорного произведения (класс
Тензор) позволяет построить базис для этих функций более высокой размерности как тензорные произведения базиса \(\mathbb{R} \to \mathbb{R}\).В качестве примера мы можем импортировать наборы данных scikit-learn, которые поверхностей и преобразовать его в базисное расширение. Обратите внимание, что мы используем разные основе различных непрерывных параметров функции, чтобы показать, как это работает, хотя, вероятно, это не имеет смысла в данном конкретном случае пример.
из sklearn.datasets импортирует load_digits X, y = load_digits (return_X_y = True) X = X. изменить форму (-1, 8, 8) fd = skfda.FDataGrid(X) базис = skfda.representation.basis.Tensor([ skfda.representation.basis.Fourier( # ось X n_базис=5, domain_range=fd. domain_range[0],
),
skfda.representation.basis.BSpline( # ось Y
n_базис=6,
диапазон_домена=fd.диапазон_домена[1],
),
])
fd_basis = fd.to_basis(основа)
# Мы строим только первую функцию
fd_basis[0].plot()
plt.show()
domain_range[0],
),
skfda.representation.basis.BSpline( # ось Y
n_базис=6,
диапазон_домена=fd.диапазон_домена[1],
),
])
fd_basis = fd.to_basis(основа)
# Мы строим только первую функцию
fd_basis[0].plot()
plt.show()
Базис конечных элементов
Базис конечных элементов (класс
FiniteElement) является основой, используемой в метод конечных элементов (МКЭ). Для создания экземпляра базы необходимо необходимо пройти множество вершин и множество симплексов или ячеек, которые присоединяйтесь к ним, соблюдая сетку. Тогда базисными элементами являются функции, которые равны единице ровно в одной из этих вершин и нулю в остальных.Преимущество этого базиса для многомерных функций состоит в том, что можно иметь больший контроль над базисом, размещая больше вершин в областях с интересное поведение, такое как местные особенности и меньше в других местах.
Здесь мы показываем пример, в котором набор цифр scikit-learn выражается в базисе конечных элементов.
 Сначала мы создаем вершины и
симплексы, которые мы будем использовать, и мы построим их.
Сначала мы создаем вершины и
симплексы, которые мы будем использовать, и мы построим их.вершин = np.array([ (0, 0), (0, 1), (1, 0), (1, 1), (0,25, 0,5), (0,5, 0,25), (0,5, 0,75), (0,75, 0,5), (0,5, 0,5), ]) ячейки = np.массив([ (0, 1, 4), (0, 2, 5), (1, 3, 6), (2, 3, 7), (0, 4, 5), (1, 4, 6), (2, 5, 7), (3, 6, 7), (4, 5, 8), (4, 6, 8), (5, 7, 8), (6, 7, 8), ]) plt.triplot (вершины [:, 0], вершины [:, 1], ячейки) plt.show() 9p \to \mathbb{R}\) функций. Чтобы выразить вектор оценочные функции в качестве расширения базы, нужно просто выразить каждую координатную функцию как базисное разложение и умножить на соответствующий унитарный вектор в направлении координат, добавляя, наконец, все из них вместе.Векторнозначный базис (
VectorValued) позволяет представлять векторные функции, делающие именно это.В качестве примера рассмотрим канадский набор данных Weather, включающий как данные о температуре и осадках в виде функций координат и нанесены на график ниже.



 «,»ch»,»inv»,»r»,»>A-1 =
«,»ch»,»inv»,»r»,»>A-1 = «,»search»,»,»,»replace»,»split»,»length»,»t»,»add»,»add1″,»
«,»search»,»,»,»replace»,»split»,»length»,»t»,»add»,»add1″,» {-1}\) 9n\), мы хотим найти \(\left\{\alpha_{0}, \alpha_{1}, \ldots, \alpha_{n-1}\right\}\) такие, что
{-1}\) 9n\), мы хотим найти \(\left\{\alpha_{0}, \alpha_{1}, \ldots, \alpha_{n-1}\right\}\) такие, что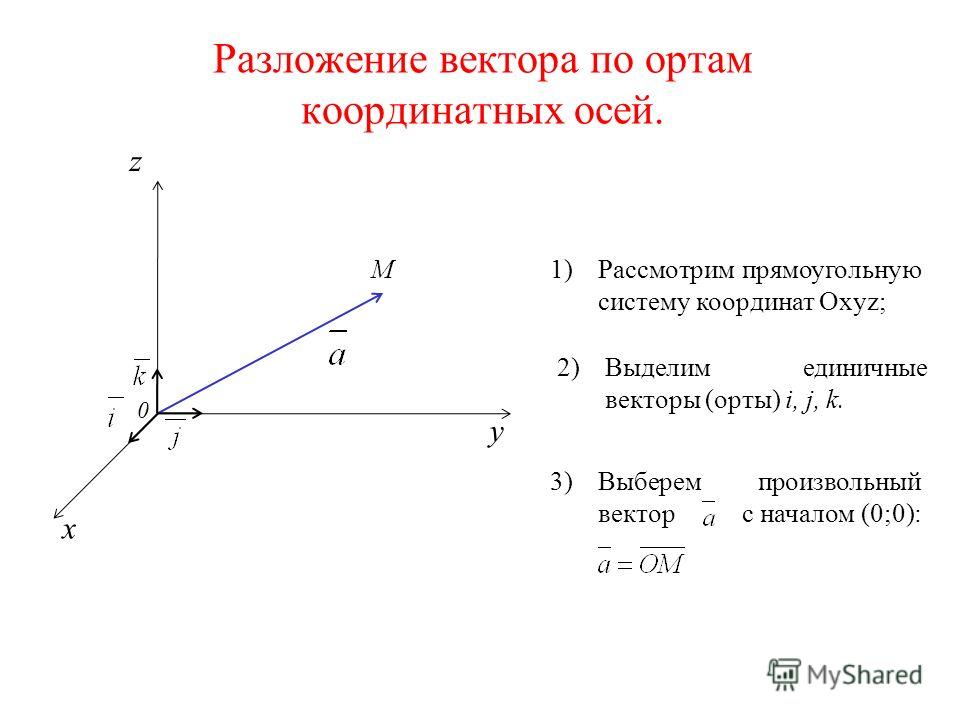
 Этот выбор приводит к стандартной матрице, и
обычным способом. Но у этих пространств есть и другие основания,
так тот же Т представлен другими матрицами. Основная тема линейного
алгебра состоит в том, чтобы выбрать основания, дающие наилучшую матрицу для T .
Этот выбор приводит к стандартной матрице, и
обычным способом. Но у этих пространств есть и другие основания,
так тот же Т представлен другими матрицами. Основная тема линейного
алгебра состоит в том, чтобы выбрать основания, дающие наилучшую матрицу для T . Здесь мы введем полезную нотацию: соберите
компоненты в вектор-столбец и назовите его
: это вектор компонентов относительно основы.
Здесь мы введем полезную нотацию: соберите
компоненты в вектор-столбец и назовите его
: это вектор компонентов относительно основы. Нам придется повторить эту операцию для
каждый вектор, который мы хотим преобразовать. Есть ли более простой способ?
Нам придется повторить эту операцию для
каждый вектор, который мы хотим преобразовать. Есть ли более простой способ? На самом деле это
матрица просто представляет базисные векторы выраженных в базисе
. Назовем эту матрицу — изменение базовой матрицы с на . Это
должен выложить
в его столбцах:
На самом деле это
матрица просто представляет базисные векторы выраженных в базисе
. Назовем эту матрицу — изменение базовой матрицы с на . Это
должен выложить
в его столбцах: У нас есть
использовали основу раньше; воспользуемся им снова, а также добавим
основа . Мы уже видели это для
у нас есть:
У нас есть
использовали основу раньше; воспользуемся им снова, а также добавим
основа . Мы уже видели это для
у нас есть:
 Давайте посмотрим, как это работает.
Вспомните, как мы используем замену базовой матрицы:
Давайте посмотрим, как это работает.
Вспомните, как мы используем замену базовой матрицы: Это также означает, что мы только что нашли
, так как мы нашли, как
преобразовать в (используя
посредническая база).
Это также означает, что мы только что нашли
, так как мы нашли, как
преобразовать в (используя
посредническая база).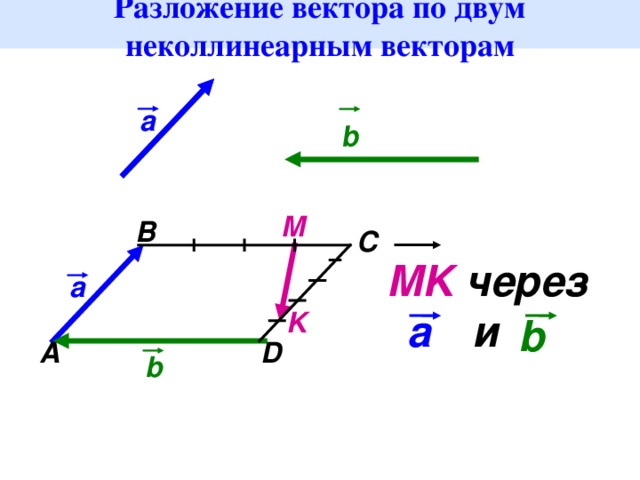 Теперь мы можем использовать цепочку через
стандартная основа для достижения того же результата. Например, мы знаем, что:
Теперь мы можем использовать цепочку через
стандартная основа для достижения того же результата. Например, мы знаем, что: Доказательством этого является
очень просто — просто предположим, что есть два разных способа выразить
— два альтернативных набора компонентов. Вычесть единицу из
другой и использовать линейную независимость базисных векторов, чтобы заключить, что
два пути должны быть одинаковыми.
Доказательством этого является
очень просто — просто предположим, что есть два разных способа выразить
— два альтернативных набора компонентов. Вычесть единицу из
другой и использовать линейную независимость базисных векторов, чтобы заключить, что
два пути должны быть одинаковыми.
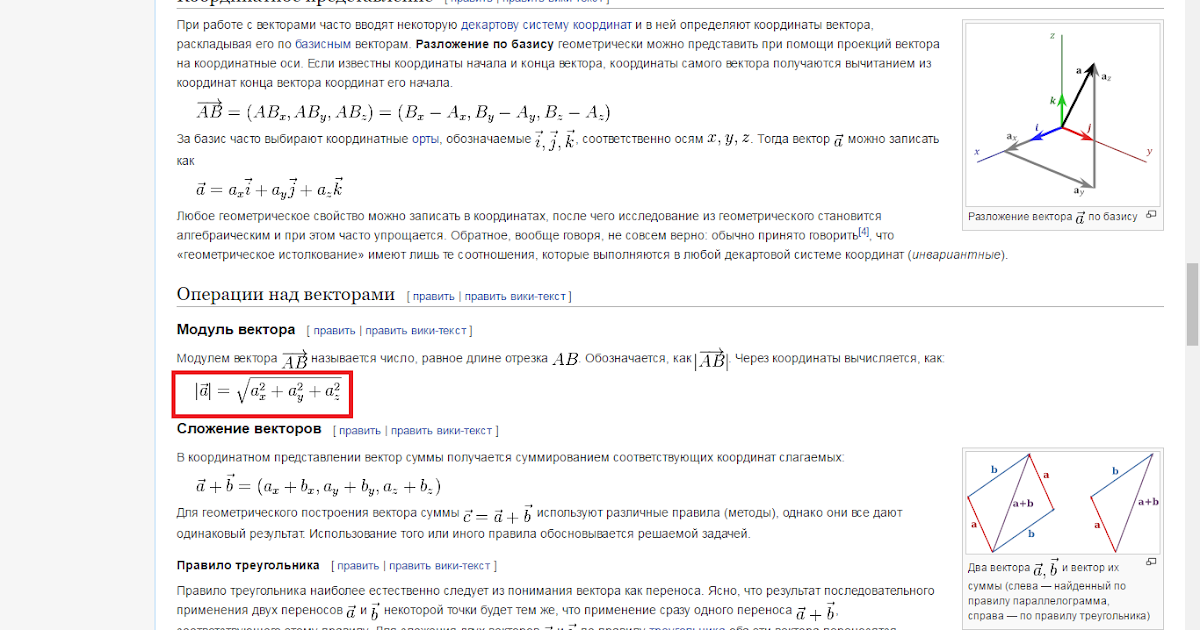 9003
9003
 Следовательно, они линейно независимы.
Следовательно, они линейно независимы. Мы можем ясно видеть
что для
пример и, таким образом,
канонический базис является ортонормированным базисом.
Мы можем ясно видеть
что для
пример и, таким образом,
канонический базис является ортонормированным базисом. Таким образом, мы обнаружили, что
для любого
,
что доказывает предложение.
Таким образом, мы обнаружили, что
для любого
,
что доказывает предложение.
 Пусть $V$ имеет базис размера $n$.
Тогда $k \le n$ и $\существует S’ = \{v_{k+1}, \ldots, v_n\} \subset V$ такое, что $S \cup S’$ является базисом $V$.
Пусть $V$ имеет базис размера $n$.
Тогда $k \le n$ и $\существует S’ = \{v_{k+1}, \ldots, v_n\} \subset V$ такое, что $S \cup S’$ является базисом $V$.

 A collection B = { v 1 , v 2 , …, v r } of vectors from V is said to be a basis for V если B линейно независима и охватывает V . Если хотя бы один из этих критериев не выполняется, то коллекция не является основой для В . Если набор векторов охватывает V , то он содержит столько векторов, что каждый вектор из V может быть записан как линейная комбинация векторов в наборе. Если набор линейно независим, то он не содержит столько векторов, чтобы одни становились зависимыми от других. Таким образом, интуитивно понятно, что базис имеет правильный размер: он достаточно велик, чтобы охватывать пространство, но не настолько велик, чтобы быть зависимым.
A collection B = { v 1 , v 2 , …, v r } of vectors from V is said to be a basis for V если B линейно независима и охватывает V . Если хотя бы один из этих критериев не выполняется, то коллекция не является основой для В . Если набор векторов охватывает V , то он содержит столько векторов, что каждый вектор из V может быть записан как линейная комбинация векторов в наборе. Если набор линейно независим, то он не содержит столько векторов, чтобы одни становились зависимыми от других. Таким образом, интуитивно понятно, что базис имеет правильный размер: он достаточно велик, чтобы охватывать пространство, но не настолько велик, чтобы быть зависимым.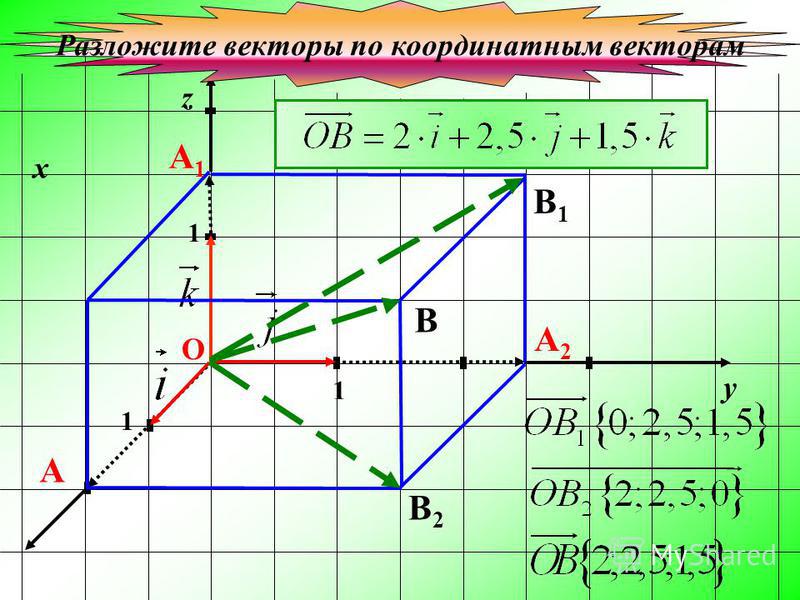 Это называется стандартной базой для R 2 . Аналогично набор { i, j, k } называется стандартным базисом для R 3 и вообще
Это называется стандартной базой для R 2 . Аналогично набор { i, j, k } называется стандартным базисом для R 3 и вообще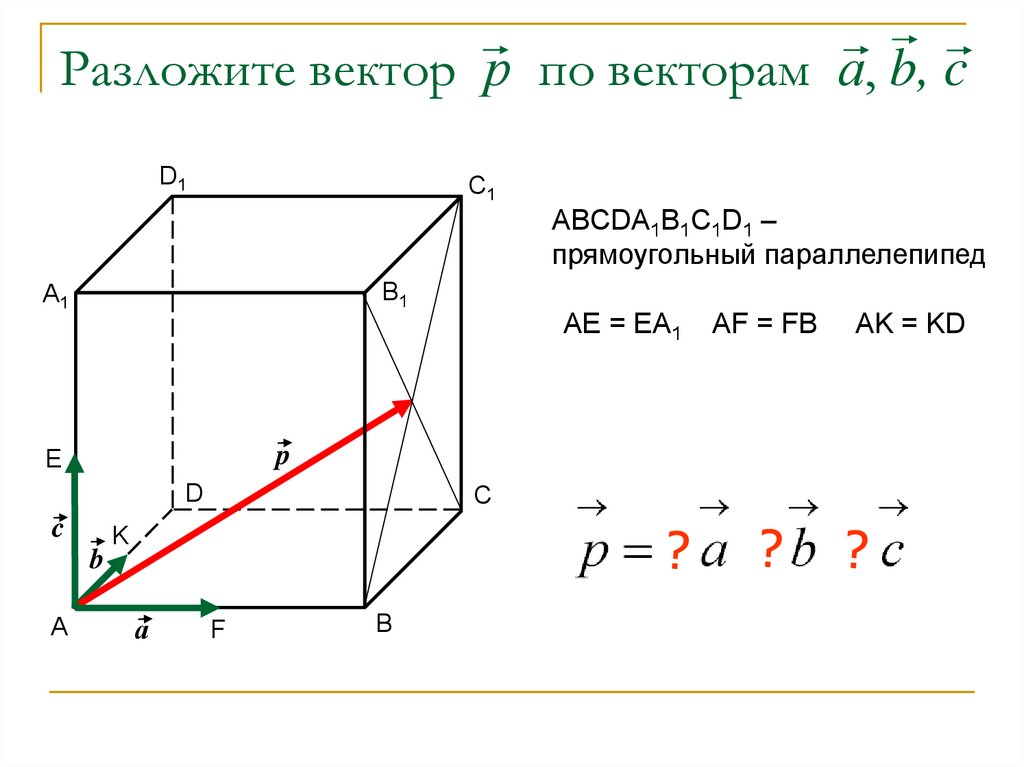
 Точно так же любой набор, содержащий ровно три линейно независимых вектора из R 3 , является основой для R 3 и так далее. Хотя нет нетривиального подпространства R n имеет уникальную основу, там есть то, что должно быть общим для всех основ данного пространства.
Точно так же любой набор, содержащий ровно три линейно независимых вектора из R 3 , является основой для R 3 и так далее. Хотя нет нетривиального подпространства R n имеет уникальную основу, там есть то, что должно быть общим для всех основ данного пространства.
 См. рис.
См. рис. потому что { v 1 , v 2 , v 3 , v 4 } не является линейно независимым; см. расчет, предшествующий приведенному выше примеру. Сброс V 3 и V 4 из этой коллекции не уменьшает пролет { V 1 , V 2 , V 9037 2 , V 9037 9037 9037 9037 9037 9037 9037 9037 9037 9037 9037 9. 9037 9. 9. . }, но результирующий набор { v 1 , v 2 } линейно независим. Таким образом, { v 1 , v 2 } является основой для V , поэтому тусклый V = 2.
потому что { v 1 , v 2 , v 3 , v 4 } не является линейно независимым; см. расчет, предшествующий приведенному выше примеру. Сброс V 3 и V 4 из этой коллекции не уменьшает пролет { V 1 , V 2 , V 9037 2 , V 9037 9037 9037 9037 9037 9037 9037 9037 9037 9037 9037 9. 9037 9. 9. . }, но результирующий набор { v 1 , v 2 } линейно независим. Таким образом, { v 1 , v 2 } является основой для V , поэтому тусклый V = 2.

 Поскольку базисные векторы должны быть линейно независимыми, каждый из скаляров в (***) должен быть равен нулю:
Поскольку базисные векторы должны быть линейно независимыми, каждый из скаляров в (***) должен быть равен нулю: Иногда удобно записать вектор компонентов как вектор столбцов ; в этом случае компонентный вектор ( k 1 , k 2 , …, k r ) T обозначается [6 1 7 B 1
Иногда удобно записать вектор компонентов как вектор столбцов ; в этом случае компонентный вектор ( k 1 , k 2 , …, k r ) T обозначается [6 1 7 B 1
 Тот же самый результат справедлив для стандартного базиса { ê 1 , ê 2 ,…, ê n } для каждого R
Тот же самый результат справедлив для стандартного базиса { ê 1 , ê 2 ,…, ê n } для каждого R Предположим, что B = {vˆ 1 ,vˆ 2 ,…,vˆ n } является ортонормированным базисом. Начиная с приведенного выше уравнения — с Vˆ 1 , Vˆ 2 ,…, Vˆ N Замена V 1 , V 2 ,…, V 2 ,…, V 99936 2 ,…, V 2 ,…, V 2 ,…, V 2 ,…, V 9037 2 . что базисные векторы теперь считаются единичными — возьмем скалярное произведение обеих сторон с vˆ 1 :
Предположим, что B = {vˆ 1 ,vˆ 2 ,…,vˆ n } является ортонормированным базисом. Начиная с приведенного выше уравнения — с Vˆ 1 , Vˆ 2 ,…, Vˆ N Замена V 1 , V 2 ,…, V 2 ,…, V 99936 2 ,…, V 2 ,…, V 2 ,…, V 2 ,…, V 9037 2 . что базисные векторы теперь считаются единичными — возьмем скалярное произведение обеих сторон с vˆ 1 : Следовательно, приведенное выше уравнение упрощается до утверждения
Следовательно, приведенное выше уравнение упрощается до утверждения Следовательно,
Следовательно,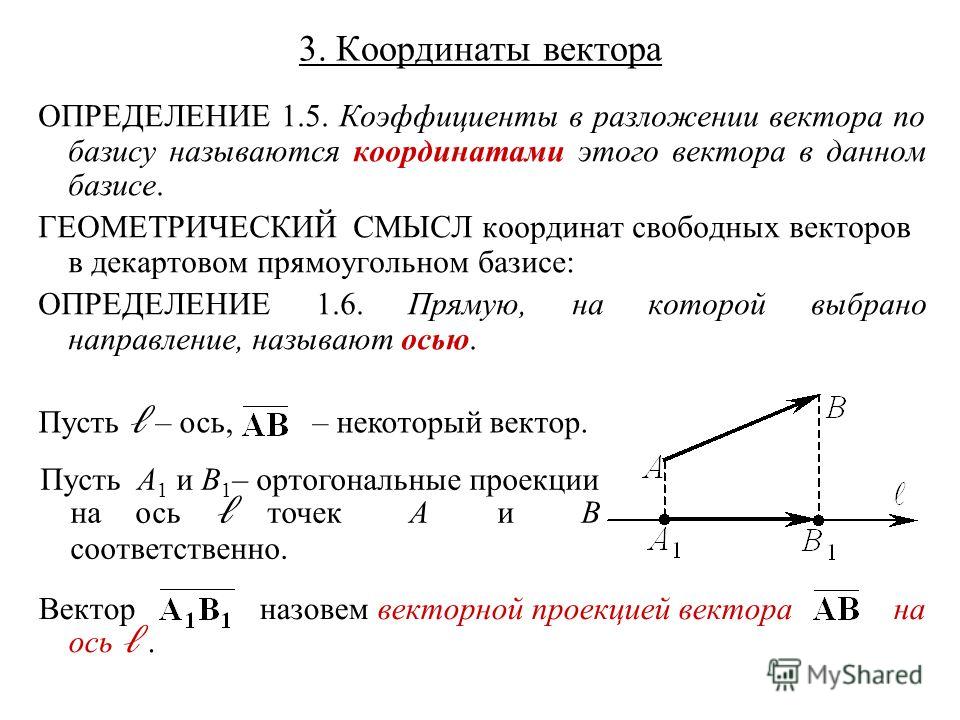 Пусть
Пусть

 plot (оси = оси [0])
оси[0].set_title(r"$3\mathbf{X}_1$")
fd_sum = fd + fd2
fd_sum.plot (оси = оси [1])
оси[1].set_title(r"$\mathbf{X}_1 + \mathbf{X}_2$")
plt.show()
9{\infty} a_i \phi_i(t)\]
plot (оси = оси [0])
оси[0].set_title(r"$3\mathbf{X}_1$")
fd_sum = fd + fd2
fd_sum.plot (оси = оси [1])
оси[1].set_title(r"$\mathbf{X}_1 + \mathbf{X}_2$")
plt.show()
9{\infty} a_i \phi_i(t)\]
 Таким образом, выбор базиса имеет значение, даже если
изначально они должны были генерировать одно и то же пространство.
Таким образом, выбор базиса имеет значение, даже если
изначально они должны были генерировать одно и то же пространство.  Чтобы преобразовать
Чтобы преобразовать 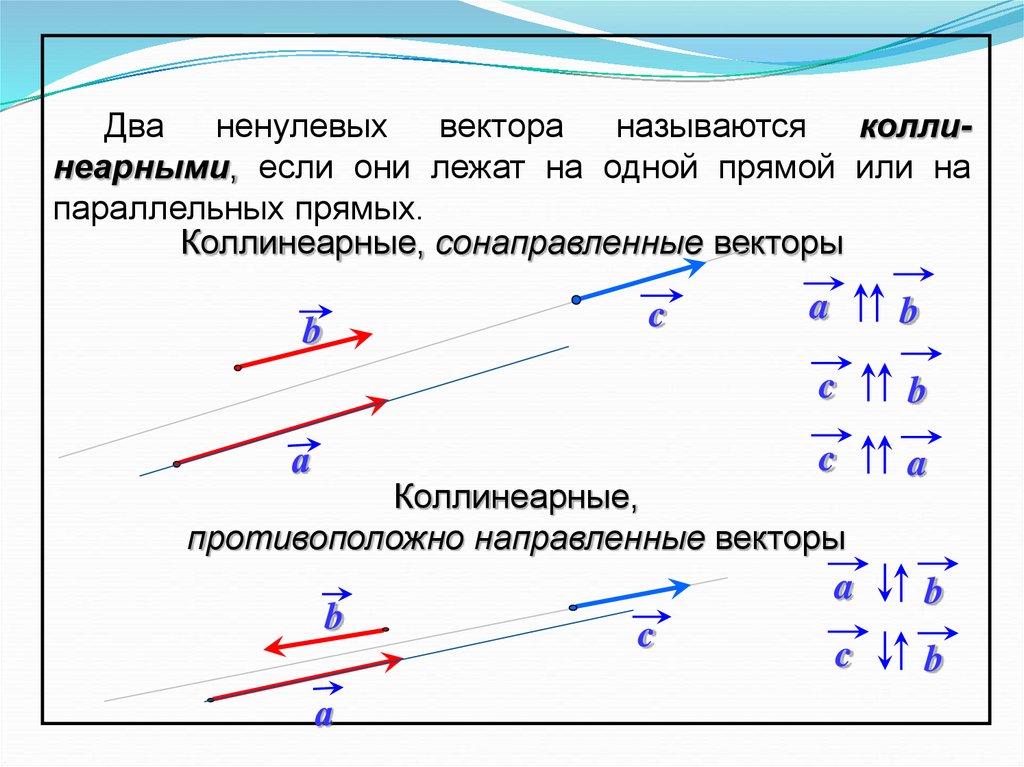 сюжет()
рис., оси = plt.subplots(nrows=3, ncols=3)
для n_basis в диапазоне (1, max_basis + 1):
base = skfda.representation.basis.Monomial(n_basis=n_basis)
X_basis = X.to_basis(основа)
топор = axes.ravel()[n_basis - 1]
рис = X_basis.plot (оси = топор)
ax.set_title(f"{n_basis} базовые функции")
fig.tight_layout()
plt.show()
сюжет()
рис., оси = plt.subplots(nrows=3, ncols=3)
для n_basis в диапазоне (1, max_basis + 1):
base = skfda.representation.basis.Monomial(n_basis=n_basis)
X_basis = X.to_basis(основа)
топор = axes.ravel()[n_basis - 1]
рис = X_basis.plot (оси = топор)
ax.set_title(f"{n_basis} базовые функции")
fig.tight_layout()
plt.show()
 Часто ряды Тейлора и МакЛорина объясняются в самом
первые курсы научных и инженерных степеней, и студенты знакомы
с полиномами намного раньше. Таким образом, мономиальный базис полезен для
учебных целях (именно поэтому мы использовали его в примерах). это
также очень полезно для целей тестирования, так как легко вручную получить
ожидаемые результаты операций с участием этого базиса. 92\), то есть \(\langle x_1, x_2 \rangle =
\ int _ {\ mathcal {T}} x_1 (t) x_2 (t) dt \). Это тормозит некоторые
оптимизация производительности, доступная для операций, требующих
внутренние продукты. Можно найти ортогональный базис многочленов,
но его будет не так просто понять, потеряв многие свои преимущества.
Еще одна проблема с этой базой – необходимость большого
количество базовых функций для выражения локальных особенностей, плохое поведение в
экстремумы функции и тот факт, что производные базиса
расширения не являются хорошими приближениями производных от оригинала
данных, так как полиномы высокого порядка имеют тенденцию к очень большим колебаниям.
Часто ряды Тейлора и МакЛорина объясняются в самом
первые курсы научных и инженерных степеней, и студенты знакомы
с полиномами намного раньше. Таким образом, мономиальный базис полезен для
учебных целях (именно поэтому мы использовали его в примерах). это
также очень полезно для целей тестирования, так как легко вручную получить
ожидаемые результаты операций с участием этого базиса. 92\), то есть \(\langle x_1, x_2 \rangle =
\ int _ {\ mathcal {T}} x_1 (t) x_2 (t) dt \). Это тормозит некоторые
оптимизация производительности, доступная для операций, требующих
внутренние продукты. Можно найти ортогональный базис многочленов,
но его будет не так просто понять, потеряв многие свои преимущества.
Еще одна проблема с этой базой – необходимость большого
количество базовых функций для выражения локальных особенностей, плохое поведение в
экстремумы функции и тот факт, что производные базиса
расширения не являются хорошими приближениями производных от оригинала
данных, так как полиномы высокого порядка имеют тенденцию к очень большим колебаниям.

 Также элементы основания имеют компактную опору
свойство, позволяющее повысить эффективность вычислений. Таким образом, это основание
указывается для непериодических функций или функций с локальными особенностями или с
различных порядков кривизны вдоль их домена.
Также элементы основания имеют компактную опору
свойство, позволяющее повысить эффективность вычислений. Таким образом, это основание
указывается для непериодических функций или функций с локальными особенностями или с
различных порядков кривизны вдоль их домена. В этом случае еще больше
полезно иметь возможность представлять их, используя базисные расширения, как число
параметров в дискретном представлении растет как произведение
точки сетки в каждом измерении домена.
В этом случае еще больше
полезно иметь возможность представлять их, используя базисные расширения, как число
параметров в дискретном представлении растет как произведение
точки сетки в каждом измерении домена. domain_range[0],
),
skfda.representation.basis.BSpline( # ось Y
n_базис=6,
диапазон_домена=fd.диапазон_домена[1],
),
])
fd_basis = fd.to_basis(основа)
# Мы строим только первую функцию
fd_basis[0].plot()
plt.show()
domain_range[0],
),
skfda.representation.basis.BSpline( # ось Y
n_базис=6,
диапазон_домена=fd.диапазон_домена[1],
),
])
fd_basis = fd.to_basis(основа)
# Мы строим только первую функцию
fd_basis[0].plot()
plt.show()
 Сначала мы создаем вершины и
симплексы, которые мы будем использовать, и мы построим их.
Сначала мы создаем вершины и
симплексы, которые мы будем использовать, и мы построим их.