§3. Разложение вектора на составляющие
Теорема 1. Если векторы илинейно независимы (неколлинеарны), то любой вектор , лежащий в плоскости векторов и , единственным образом представляется в виде .
Выражение называется разложением вектора на составляющие по направлениям векторови .
Доказательство. Дано: векторы и независимы, векторы компланарны. Так как векторыкомпланарны, то существуют числа такие, что и . Коэффициент , так как в противном случае получим, что векторы линейно зависимы, поэтому из последнего равенства имеем:или , где .
Докажем
единственность такого разложения.
Предположим, что существует два разных
разложения вектора
по
направлениям векторови
:
и
.
Вычитая из одного равенства другое,
получим
.
Так как векторы
илинейно независимы, то последнее
равенство возможно только прии
,
т.е. разложение вектора
по направлениям векторовиединственно.
Теорема 2. Если три вектора линейно независимы (некомпланарны), то любой четвертый вектор единственным образом представляется в виде(разложение вектора на составляющие по направлениям векторов ).
D
C
A B
Рис. 12.
Доказательство. Дано: Некомпланарные векторы и вектор. Все векторы приводим к общему началу и строим параллелепипед со сторонами, параллельными векторам , и с диагональю, совпадающей с вектором (рис.12). Имеем .
Так как , то существует число
, такое, что , аналогично, , откуда.
Единственность разложения доказывается аналогично плоскому случаю.
Следствие. В пространстве любые четыре вектора линейно зависимы.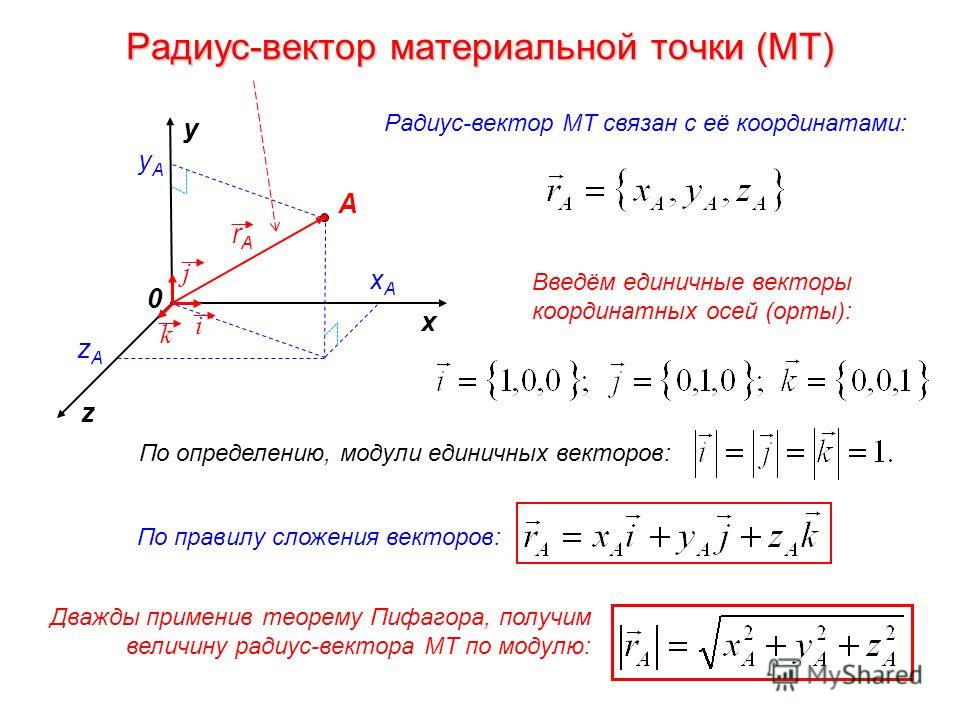
КОНТРОЛЬНЫЕ ВОПРОСЫ
Докажите теоремы о разложении вектора на две, на три составляющие.
Любая упорядоченная тройка некомпланарных векторов образует базис трехмерного пространства; упорядоченная пара неколлинеарных векторов образует базис на плоскости.
Пусть в пространстве выбран базис: ; тогда любой векторединственным образом можно разложить на составляющие по базисным векторам:Таким образом, базис устанавливает взаимно однозначное соответствие между векторами пространства и упорядоченными тройками чисел , которые называются координатами вектора в заданном базисе. Вместо записи используется так же символическая запись или.
Если
базисные векторы – единичные (орты) и
попарно ортогональны, то базис называется
ортонормированным, а базисные векторы
обозначаются
.
Пусть некоторый вектор
имеет в этом базисе координаты
,
тогда
или используется символическая запись
.
Базисные векторы в пространстве образуют правую тройку, если поворот на наименьший угол от первого вектора ко второму происходит против часовой стрелки, если смотреть с конца третьего вектора (рис. 13). В противном случае тройка векторов называется левой.
Рис. 13.
В дальнейшем используются только правые тройки.
Основное значение базиса состоит в том, что линейные операции над векторами при задании базиса становятся обычными операциями над числами (координатами этих векторов).
РАВЕНСТВО ВЕКТОРОВ ПРИ ЗАДАННОМ БАЗИСЕ
Два
вектора в любом базисе равны тогда и
только тогда, когда равны их одноименные
координаты. Это следует из взаимно
однозначного соответствия между
вектором и его координатами.
Ортогональная составляющая вектора : Высшая алгебра
Правила форума
В этом разделе нельзя создавать новые темы.
Если Вы хотите задать новый вопрос, то не дописывайте его в существующую тему, а создайте новую в корневом разделе «Помогите решить/разобраться (М)».
Если Вы зададите новый вопрос в существующей теме, то в случае нарушения оформления или других правил форума Ваше сообщение и все ответы на него могут быть удалены без предупреждения.
Не ищите на этом форуме халяву, правила запрещают участникам публиковать готовые решения стандартных учебных задач. Автор вопроса обязан привести свои попытки решения и указать конкретные затруднения.
Обязательно просмотрите тему Правила данного раздела, иначе Ваша тема может быть удалена или перемещена в Карантин, а Вы так и не узнаете, почему.
| 64gl |
| ||
2 |
| ||
| |||
| AV_77 |
| |||
11/11/07 |
| |||
| ||||
| ewert |
| |||
11/05/08 |
| |||
| ||||
| Joker_vD |
| |||
09/09/10 |
| |||
| ||||
| ewert |
| |||
11/05/08 |
| |||
| ||||
| Joker_vD |
| |||
09/09/10 |
| |||
| ||||
| ewert |
| |||
11/05/08 |
| |||
| ||||
| Shtorm |
| ||
14/02/10 |
| ||
| |||
| mihailm |
| ||
19/05/10 |
| ||
| |||
| ewert |
| |||
11/05/08 |
| |||
| ||||
| _hum_ |
| ||
23/12/07 |
| ||
| |||
| Joker_vD |
| |||
09/09/10 |
| |||
| ||||
| ewert |
| |||
11/05/08 |
| |||
| ||||
| svv |
| |||
23/07/08 |
| |||
| ||||
| ewert |
| |||
11/05/08 |
| |||
| ||||
| Показать сообщения за: Все сообщения1 день7 дней2 недели1 месяц3 месяца6 месяцев1 год Поле сортировки АвторВремя размещенияЗаголовокпо возрастаниюпо убыванию |
| Страница 1 из 1 | [ Сообщений: 15 ] |
Модераторы: Модераторы Математики, Супермодераторы
Как разложить силу на компоненты x и y
Часто бывает полезно разложить силу на компоненты x и y, т. е. найти две силы, одна из которых направлена в направлении x, другая — в направлении y, а векторная сумма двух сил равна исходной силе.
е. найти две силы, одна из которых направлена в направлении x, другая — в направлении y, а векторная сумма двух сил равна исходной силе.
Давайте посмотрим, как мы можем это сделать.
Предположим, у нас есть сила F, образующая угол 30° с положительной осью x, как показано ниже:
Сила F, образующая угол 30 градусов с положительной осью x Fx30°yИ мы хотим разложить F на компоненты x и y.
Первое, что нам нужно сделать, это представить два компонента на плоскости xy . Сделаем это, опустив из головы F два перпендикуляра: один на ось x, другой на ось y.
Вот так:
Представление двух перпендикуляров, которые идут от головы F к осям x и y Fx30°yИ мы соединяем начало координат плоскости xy с точкой пересечения x, составляющая F:
Представление x-компоненты FFx30°yxFИ снова мы соединяем начало координат с y-пересечением , чтобы представить y-компоненту F:
Обе x- и y-компоненты F представлены Fx30°yxFyF F x и F y — это два вектора, т. е. они оба имеют величину и направление . Однако, поскольку F x и F y расположены в направлениях осей x и y, они обычно выражаются только звездной величиной 9.0010 , которым предшествует положительный или отрицательный знак: положительный, когда они указывают в положительном направлении, и отрицательный, когда они указывают в отрицательном направлении осей x и y.
е. они оба имеют величину и направление . Однако, поскольку F x и F y расположены в направлениях осей x и y, они обычно выражаются только звездной величиной 9.0010 , которым предшествует положительный или отрицательный знак: положительный, когда они указывают в положительном направлении, и отрицательный, когда они указывают в отрицательном направлении осей x и y.
В нашем примере F x и F y положительны, потому что оба указывают в положительном направлении осей x и y.
Положительные значения F x и F y можно найти с помощью тригонометрии:0005
Для простоты помните, что , если компонент примыкает к углу , то это cos, иначе sin.
Часто F x будет составляющей, примыкающей к углу, так что это будет cos, а F y будет sin.
Теперь рассмотрим силу, одна из составляющих которой отрицательна:
Сила F, имеющая отрицательную x-компоненту Fx15°yxFyF В этом случае F x отрицательна, поскольку направлена в отрицательном направлении оси x.
Следовательно:
F x = −F cos 15°
F y = F sin 15°
Обратите внимание на знак минус перед F cos 15°, который мы добавили, чтобы сделать F x 9003 отрицательным.
Вы должны быть очень осторожны, если ваш угол равен , а не между 0° и 90°, потому что sin или (и) cos этого угла может быть уже минус , поэтому произведение также минус и вам не нужно добавлять знак минус.
На всякий случай мы рекомендуем всегда работать с углами от 0° до 9°.0°, так что sin и cos всегда положительны, а значит, и произведение всегда положительно.
Резюме
Процесс разложения силы F можно обобщить следующим образом: по осям x и y, а затем соединить начало плоскости xy с двумя точками пересечения ( цель графического представления компонентов состоит в том, чтобы помочь вам увидеть, какой компонент примыкает к углу и каковы знаки двух компонентов ).
 Компоненты, которые указывают в отрицательных направлениях осей x и y, являются отрицательными, поэтому вам нужно будет добавить знак минус (учитывая, что вы работаете с θ между 0 ° и 90 °, так что F cos θ и F sin θ равны всегда позитивный).
Компоненты, которые указывают в отрицательных направлениях осей x и y, являются отрицательными, поэтому вам нужно будет добавить знак минус (учитывая, что вы работаете с θ между 0 ° и 90 °, так что F cos θ и F sin θ равны всегда позитивный).Силы с хвостом не в начале координат
Иногда силы не имеют хвоста в начале координат плоскости xy.
Например:
Сила с хвостом в 3-м квадранте Fx30°yВ подобных случаях мы проводим две прямые, параллельные осям x и y, которые проходят через хвост силы, а затем опускаем две перпендикуляры от головы силы к прямым:
Разложение на компоненты x y силы с хвостом в 3-м квадранте Fx30°yxFyFF x = F cos 30°
F y = F sin 30°
Силы, которые уже действуют в направлении x или y
Часто мы имеем дело с силами, которые уже находятся в направлении x или y. В этом случае мы можем определить компоненты x и y более простым и интуитивно понятным способом, не прибегая к тригонометрии.
Если, например, у нас есть сила F, направленная в сторону положительной оси x:
Сила F, направленная в сторону положительной оси x, FxyОчевидно, что Y-компонент F равен 0, а компонент x равен положительным с величиной, равной величине F:
Компонент x силы F в положительном направлении x xFxyF x = F
F y = 0
С другой стороны, если у нас есть сила F в отрицательном направлении оси x:
Сила F, направленная в отрицательном направлении оси xFxyТогда компонент y снова равен 0, а компонент x равен отрицательному (поскольку он указывает в отрицательном направлении оси x) и имеет ту же величину, что и F:
Компонент x силы F в отрицательном направлении xxFxyF x = −F
F y = 0
То же самое можно показать для сил в направлении y: они всегда будут иметь компонент x, равный 0, а компонент y, положительный или отрицательный, с величиной, равной величина силы.
Чтобы проверить свое понимание концепции, выполните приведенные ниже упражнения.
Упражнения
#1
Сила 19 Н действует в направлении отрицательной оси x. Найдите компоненты x и y силы.
Решение
Компонент x силы указывает в отрицательном направлении, компонент y равен нулюxFxyF x является отрицательным и имеет ту же величину, что и сила (19 Н). F y равно нулю.
F x = −19 Н
F y = 0 Н
#2
Сила 114 Н образует угол 67° с положительной осью x. Разложите силу на компоненты x и y.
Решение
Сила, образующая угол 67 градусов с положительным x, и ее компоненты Fx67°yxFyFОба компонента положительные.
F x = F cos 67° = 44,5 Н
F y = F sin 67° = 105 Н
#3
Сила образует угол 221° с положительной осью x. Предполагая, что сила имеет величину 3,1 × 10 3 Н, найдите компоненты x и y.
Решение
Сила, образующая угол 221 градус с положительной осью x, и ее компоненты Fx221°yxFyFВместо того, чтобы иметь дело с углом 221°, мы хотим иметь дело с углом 41° (221° − 180°), под которым сила делает с отрицательной осью x:
Теперь мы рассматриваем угол 41 градус, который сила образует с отрицательной осью x41°FxyxFyFКак вы можете видеть, как F x , так и F y отрицательны:
F x = −F cos 41° = −2,3 × 10 3 Н
F y = −F sin 41° = −2,0 × 10 3 Н
#4
Сила 4,5 × 10 5 положительная ось Y. Определите его составляющие.
Решение
Y-компонент силы имеет положительное y-направление. Компонент x равен 0.yFxyЭто просто. F x равно нулю. F y положительно и имеет ту же величину, что и сила.
F x = 0 Н
F y = F = 4,5 × 10 5 Н
#5
Сила 90,0 Н образует угол y с положительным направлением 33°. Вычислите компоненты x и y силы.
Вычислите компоненты x и y силы.
Подсказка: Поскольку угол равен +33°, он идет против часовой стрелки от положительной оси y.
Решение
Сила, образующая угол 33 градуса с положительным y. Его компоненты x и y также представлены 33°FxyxFyFВ этом случае F y находится рядом с углом, поэтому его величина равна силе, умноженной на cos угла, а величина F x равна силе, умноженной на sin.
Также обратите внимание, что F x отрицательно:
F x = −F sin 33° = −49,0 N
F y = F cos 33° = 75,5 N
Угол 57° (90° − 33°), который F составляет с F x . Таким образом, F x был бы смежным с углом.
#6
Сила, имеющая величину 3,21 × 10 4 Н, образует угол −50° с положительной осью x. Определите компоненты.
Совет: Угол отрицательный, то есть он идет по часовой стрелке от положительной оси x.
Решение
Сила образует угол 50 градусов по часовой стрелке от оси x. Компоненты силы x и y также представлены 50°FxyxFyF
Компоненты силы x и y также представлены 50°FxyxFyFF x = F cos 50° = 2,06 × 10 4 Н
F y = −F sin 50° = −2,46 × 10 4 N
Задачи с решениями
объекты, которые движутся горизонтально, поднимаются по склону и висят на веревках. Для каждой проблемы мы предоставляем пошаговое руководство по ее решению.
Вы также можете прочитать:
- Как найти величину и направление силы, зная компоненты x и y
- Что такое результирующая сила и как ее найти (с примерами)
- Что такое диаграмма свободного тела и как ее нарисовать (с примерами)
Разложить вектор AC как сумму векторов, параллельных и перпендикулярных AB
спросил
Изменено 1 год, 5 месяцев назад
Просмотрено 8к раз
$\begingroup$
У меня есть два вектора AB = (0,-2,1) и AC = (2,-1,0)
Скалярное произведение AB и AC = 2 и длина каждого из них равны $\sqrt{5}$ .

 07.2012, 21:43
07.2012, 21:43 
 07.2012, 22:27
07.2012, 22:27 

 Чего еще уточнять-то?
Чего еще уточнять-то? Чего еще уточнять-то?
Чего еще уточнять-то?
 07.2012, 20:33
07.2012, 20:33  07.2012, 21:17
07.2012, 21:17  07.2012, 08:00
07.2012, 08:00  07.2012, 12:06
07.2012, 12:06