Нужно разложить на простые множители число 56
Математика
56 = 2³*7
Пошаговое объяснение:
56 | 2
28 | 2
14 | 2
7 | 7
1
Запишем результат разложения числа 56 на простые множители:
56 = 2*2*2*7 = 2³*7
1 — написать число как произведение простых чисел, 2 — нет, любое составное делится на простое, то есть можно разложить всегда, 3 — порядком простых множитель, это основная теорема арифметики, что число можно разложить на множители единственным
1)2240= 2000+200+40
2)1782=1000+700+80+2
3)4900=4000=900
1) Простое число делится без остатка только на 1 и на само себя, а составные делятся на себя и на какое-нибудь еще число(числа)
Например, простые числа это:2,3,5,7
Составные числа: 4,6,8,10,12
2) Это число 1
3) Да любое составное число можно разложить на простые множители.
1)
48:2
24:2
12:2
6:2
3
2) 47:47
3)
56:2
28:2
14:2
7
4)
59:59
1. 5544 = 2 * 2 * 2 * 3 * 3 * 7 * 112. 504 = 2 * 2 * 2 * 3 * 3 * 7 756 = 2 * 2 * 3 * 3 * 3 * 7НОД (504; 756) = 2 * 2 * 3 * 3 * 7 = 252 — наибольший общий делительНОК (504; 756) = 2 * 2 * 2 * 3 * 3 * 3 * 7 = 1512 — наименьшее общее кратное3. а) 255 = 3 * 5 * 17 238 = 2 * 7 * 17НОД (255; 238) = 17 — наибольший общий делительЧисла 255 и 238 не взаимно простые, так как у них есть общий делительб) 392 = 2 * 2 * 2 * 7 * 7 675 = 3 * 3 * 3 * 5 * 5Числа 392 и 675 не взаимно простые, так как у них нет общих делителей, кроме единицы.4. Разность двух простых чисел может быть простым числом. Например:7 — 5 = 219 — 17 = 243 — 41 = 2
1) 5*3*3*13
2)а)3 б)6 в)3 г)7
3) Простые множители числа 98 это 2, 7, 7. А простые множители числа 665 это 5, 7, 19. Ни одни из них не совпадают
1)2*2*3*3*7*11
2)4)=30; 5)=60; 6)=182; 1)=315; 2)=46; 3)=24
1)2*3*3*3*1; 2*2*2*2*7*1; 2*5*3*7*13*1
2)105 = 3*5*7
286 = 2*11*13
НОД (105;286) = 1, значит они взаимно простые
3)Разложим на простые множители 36
36 =2*2*3*3
Разложим на простые множители 45
45=3*3*5
Найдем произведение одинаковых простых множителей 3*3
НОД (36; 45) = 3*3=9
4)14 = 2 * 7 — простые множители числа
12 = (2*2) * 3 — простые множители числа
НОК (14 и 12) = (2*2) * 3 * 7 = 84 — наименьшее общее кратное
84 + 84 = 168 — общее кратное 14 и 12
168 + 84 = 252 — общее кратное 14 и 12
и т. д. + 84 … — общее кратное 14 и 12
д. + 84 … — общее кратное 14 и 12
84 и 168 не превышают 170
84 + 168 = 252 — сумма общих кратных, не превышающих 170.
ответ: 252.
Подробнее — на —
Пошаговое объяснение:
1) 5544 2
2772 2
1386 2
693 3
231 3
77 11
7 7
1
1. 5544 = 2 * 2 * 2 * 3 * 3 * 7 * 11
2. 504 = 2 * 2 * 2 * 3 * 3 * 7 756 = 2 * 2 * 3 * 3 * 3 * 7
НОД (504; 756) = 2 * 2 * 3 * 3 * 7 = 252 — наибольший общий делитель
НОК (504; 756) = 2 * 2 * 2 * 3 * 3 * 3 * 7 = 1512 — наименьшее общее кратное
3. а) 255 = 3 * 5 * 17 238 = 2 * 7 * 17
НОД (255; 238) = 17 — наибольший общий делитель
Числа 255 и 238 не взаимно простые, так как у них есть общий делитель
б) 392 = 2 * 2 * 2 * 7 * 7 675 = 3 * 3 * 3 * 5 * 5
Числа 392 и 675 не взаимно простые, так как у них нет общих делителей, кроме единицы.
4. Разность двух простых чисел может быть простым числом
Подробнее — на —
14=2*7, 26=2*13, 35=5*7, 38=2*19, 52=2*2*13, 87=3*29
4=2*2, 9=3*3, 25=5*5, 32=2*2*2*2*2, 49=7*7, 92=2*2*23
12=2*2*3, 18=2*3*3, 36=2*2*3*3, 51=3*17, 58=2*29, 78=2*3*13, 105=3*5*7
30, 84, 90, 40, 770, 198
88=2*2*2*11, 136=2*2*2*17, 222=2*3*37, 246=2*3*41, 385=5*7*11, 435=3*5*29, 530=2*5*53, 555=3*5*37
396=2*2*3*3*11, 456=2*2*2*3*19, 504=2*2*2*3*3*7, 700=2*2*5*5*7, 594=2*3*3*3*11, 1170=2*3*3*5*13, 2310=2*3*5*7*11, 3100=2*2*5*5*31
17, 19, 23, 29, 31, 37
Математика: новые вопросы
Математика, 27. 02.2019 12:20, КаролинаКим
02.2019 12:20, КаролинаКим
Определите , пропорциональны ли пары отрезков(ab; cd) и (mn; pq),если: а)ab=0.9см; cd=0.4см; mn=3.6см; pq=1.6см;
Ответы:
Показать ответы
Математика, 02.03.2019 03:40, andreymikilov
Медвежонок поймал 17 маленьких рыбок. несколько рыбок медвежонок выпустил в реку, и у него осталось на 5 рыбок больше, чем он выпустил. сколько рыбок осталось у медвежонка?
Ответы:
Показать ответы
Математика, 03.03.2019 19:10, eremenko6kirov
Вкубе abcda1b1c1d1 найдите тангенс угла между диагональю куба ac1 и плоскости проходящей через вершины a1b1cd )
Ответы:
Показать ответы
Математика, 04.03.2019 01:20, manechka2007
Одна бригада рабочих изготавливает за 12 дней 1512 деталей, другая-1260. сколько дней потребуется для изготовления 1617деталей, если обе бригады будут работать вместе с той же производительностью
Ответы:
Показать ответы
Алгебра, 04.10.2022 00:04
-х/7=2 знайти корень ривняня. ..
..
Русский язык, 03.10.2022 20:23
А. К какому классу относятся зёрна определяется прежде всего их всхожестью и чистотой. Б. Урожай зависит от погоды, от искусства земледельца, от уровня агротехники,
Математика, 03.10.2022 19:15
5 рабочих работали 10 дней, 10 рабочих эту работу сколько дней…
Биология, 03.10.2022 19:01
Помогите пожалуйста по биологии заполнить пропуски в схеме…
Математика, 03.10.2022 16:13
помогите решить 5.6.7.8. 8 класс… геометрия…
Алгебра, 24.11.2020 20:52
с решением Найти область сходимости ряда
Английский язык, 24.11.2020 20:52
составить сочинение по английскому на 180-200 слов на тему «Идеальное общество» принимаются и по русскому сочинения)…
Қазақ тiлi, 24.11.2020 20:52
Куля масою 30г після пружного зіткнення з нерухомими тілом змінила напрямок ркху на 90°,а модуль її швидкість зменшився в 2 раза .Визначте масу тіла яким зіткнулась куля . …
Английский язык, 24. 11.2020 20:52
11.2020 20:52
быстро и просто…
Литература, 24.11.2020 20:52
Как звали маму, папу, и бабушку толстого?…
Lebih banyak pertanyaan tentang hal ini: Математика Вопросы без ответов
На что можно разделить 56? – Обзоры Вики
Разделите 56 на каждое из чисел от 1 в 28 и посмотрим, какой из них даст в остатке 0. Делителями всех таких делений являются множители. Кроме того, 56 является фактором сам по себе. Таким образом, 1,2,4,7,8,14,28 и 56 являются делителями числа 56.
Аналогично, 56 делится на 2 Да или нет? Поскольку ответом на наше деление является целое число, мы знаем, что 56 делится на 2.
56 делится на 6 да или нет? Мы видим, что 56 НЕ делится ни на 3, ни на 2, а это значит, что 56 IS делится на 6.
56 делится на 3 да или нет? Поскольку деление не дает целого числа, это показывает нам, что 56 не делится на 3.
Во-вторых, как найти множители числа 56? Таким образом, множители 56 равны 1, 2, 4, 7, 8, 14, 28 и 56. Факторы числа 56: 1, 2, 4, 7, 8, 14, 28 и 56. Факторизация числа 56: 2×2×2×7 или 2.3 × 7.
Факторы числа 56: 1, 2, 4, 7, 8, 14, 28 и 56. Факторизация числа 56: 2×2×2×7 или 2.3 × 7.
Сколько факторов у 56?
Факторы 56: 1, 2, 4, 7, 8, 14, 28, 56.
тогда что такое LCM 56? Чтобы найти НОК чисел 56 и 96 с помощью простой факторизации, мы найдем простые множители (56 = 2 × 2 × 2 × 7) и (96 = 2 × 2 × 2 × 2 × 2 × 3). НОК, равный 56 и 96, является произведением простых множителей, возведенных в соответствующую наивысшую степень среди чисел 56 и 96. ⇒ НОК, равный 56, 96 = 2.5 × 31 × 71 = 672.
Что такое таблица 56? Повторное сложение 56 — это таблица умножения 56. Например, 56 + 56 + 56 = 3 × 56 = 168 .
…
Таблица от 56 до 10.
| 56 1 × 56 = XNUMX XNUMX | 56 × 6 = 336 |
|---|---|
| 56 2 × 112 = XNUMX XNUMX | 56 7 × 392 = XNUMX XNUMX |
| 56 3 × 168 = XNUMX XNUMX | 56 8 × 448 = XNUMX XNUMX |
| 56 4 × 224 = XNUMX XNUMX | 56 9 × 504 = XNUMX XNUMX |
| 56 5 × 280 = XNUMX XNUMX | 56 10 × 560 = XNUMX XNUMX |
Как разложить на множители дерево 56?
56 = 1 х 56, 2 х 28, 4 x 14 или 7 x 8. Факторы числа 56: 1, 2, 4, 7, 8, 14, 28, 56. Простая факторизация: 56 = 2 x 2 x 2 x 7, что также может быть записано как 56 = 2³ х 7.
Факторы числа 56: 1, 2, 4, 7, 8, 14, 28, 56. Простая факторизация: 56 = 2 x 2 x 2 x 7, что также может быть записано как 56 = 2³ х 7.
Что такое GCF 56? GCF 56 и 64 составляет 8. Чтобы вычислить наибольший общий множитель 56 и 64, нам нужно разложить каждое число на множители (множители 56 = 1, 2, 4, 7, 8, 14, 28, 56; множители 64 = 1, 2, 4, 8, 16, 32, 64) и выберите наибольший множитель, который точно делит и 56, и 64, т. е. 8.
Что такое НОК 56 и 8?
Ответ: LCM 8 и 56 — это 56.
Что такое GCF 56 и 84 с использованием простой факторизации? GCF 56 и 84 с помощью простой факторизации
Следовательно, GCF 56 и 84 равен 2×2×7 = 28.
Что такое стол на 8?
Таблица 8 обозначает результат умножения числа 8 на другие целые числа. … Забавный факт о числе 8 заключается в том, что при переворачивании оно становится символом бесконечности (∞).
Какое число при умножении на 56 дает произведение 9688?
173 это число, которое при умножении на 56 дает результат 9688.
Что такое 13 стол? Результаты, полученные в таблице 13, называются кратными 13.
…
| Таблица умножения 13 до 10 | |
|---|---|
| 13 1 × 13 = XNUMX XNUMX | 13 |
| 13 7 × 91 = XNUMX XNUMX | 13 + 13 + 13 + 13 + 13 + 13 + 13 = 91 |
| 13 8 × 104 = XNUMX XNUMX | 13 + 13 + 13 + 13 + 13 + 13 + 13 + 13 = 104 |
| 13 9 × 117 = XNUMX XNUMX | 13 + 13 + 13 + 13 + 13 + 13 + 13 + 13 + 13 = 117 |
Каковы простые делители числа 56? Следовательно, простые множители числа 56 записываются как 2x2x2x7 или 23×2 где 2 и 7 — простые числа.
Что такое факторное дерево?
Факторные деревья способ выражения делителей числа, в частности, простая факторизация числа. Каждая ветвь дерева разбита на факторы. Как только множитель в конце ветви является простым числом, остаются только два множителя — он сам и один, поэтому ветвь останавливается, и мы обводим число.
Что такое Факторное дерево 16? В случае простой факторизации дерева 16 также будет выражаться как 16=2×2×2×2=24.
Что такое GCF для 56 и 6?
Как вы можете видеть, когда перечисляете факторы каждого числа, 2 — это наибольшее число, на которое делятся 6 и 56.
Как найти общие делители 56 и 120? Общие делители 56 и 120 равны = 1, 2, 4, 8.
Что такое НОК 70 и 56?
Ответ: LCM 56 и 70 — это 280.
Каков наибольший общий делитель восьми и 56? Как вы видите, когда вы перечисляете множители каждого числа, 8 — это наибольшее число, на которое делятся 8 и 56.
Что такое GCF для 16 и 24?
Ответ: GCF 16 и 24 составляет 8.
Как вы показываете 56 разделить на 8? Используя калькулятор, если вы наберете 56, разделенное на 8, вы получите 7. Вы также можете выразить 56/8 в виде смешанной дроби: 7 0/8.
Что такое LCM для 56 и 84?
Ответ: LCM 56 и 84 — это 168.
Что такое GCF для 56 и 8?
Как вы можете видеть, когда перечисляете факторы каждого числа, 8 — это наибольшее число, на которое делятся 8 и 56.
Как решить проблему с LCM? Найдите НОК, используя метод простых множителей
- Найдите разложение на простые множители каждого числа.
- Запишите каждое число как произведение простых чисел, сопоставляя простые числа по вертикали, если это возможно.
- Уберите простые числа в каждом столбце.
- Умножьте множители, чтобы получить НОК.
Множители выписать разложение чисел. Разложение числа на множители
Встречали такой термин, как «простые числа» или «простые множители», но не знаете, что это такое? Также простые числа очень популярны в киноиндустрии, поэтому не редко их можно встретить в фильмах и сериалах. Давайте разберёмся, что такое простые числа в данной статье!
Простые числа – это целое положительное (натуральное) число, которое может быть разделено лишь на единицу и самого себя. Числа, которые имеют более двух натуральных делителей являются составными.
- Пример 1: простое число 7 может быть разделено лишь на 1 и на 7.

- Пример 2: составное число 6 может быть разделено на 1, 2, 3, 6.
Простые числа до 100: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97
Простые числа – очень популярная тема в математике, с ней связано огромное множество задач, теорем и т.д.
Простые множители
– это множители (элементы произведения), являющиеся простыми числами. С простыми множителями связано несколько школьных заданий, которые могут вызвать проблемы даже у старшего поколения.Разложите на простые множители числа…
Довольно популярная в математике задача. Наиболее распространённые примеры:
Разложите не простые множители числа 27, 54, 56, 65, 99, 162, 625, 1000. В первую очередь следует сказать, что самая распространённая ошибка при решении данной задачи – количество множителей не указано, их не обязательно именно 2! Если Вы совершили данную ошибку – можете попробовать решить задание самостоятельно.
Ответы:
- 27 = 3 х 3 х 3
- 54 = 2 х 3 х 3 х 3
- 56 = 2 х 2 х 2 х7
- 65 = 5 х 13
- 99 = 3 х 3 х 11
- 162 = 2 х 3 х 3 х 3 х 3
- 625 = 5 х 5 х 5 х 5
- 1000 = 2 х 2 х 2 х 5 х 5 х 5
Каждое натуральное число, кроме единицы, имеет два или более делителей. Например, число 7, делится без остатка только на 1 и на 7, то есть имеет два делителя. А у числа 8, делители 1, 2, 4, 8, то есть аж 4 делителя сразу.
Чем отличаются простые и составные числа
Числа, которые имеют более двух делителей, называются составными. Числа, которые имеют только два делителя: единица и само это число, называются простыми числами.
Число 1 имеет только один делить, а именно само это число. Единица не относится ни к простым, ни к составным числам.
- Например, число 7 простое, а число 8 составное.
Первые 10 простых чисел: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29. Число 2 единственное четное простое число, все остальные простые числа нечетные.
Число 78 составное, так как помимо 1 и самого себя, оно делится еще и на 2. При делении на 2 получим 39. То есть 78= 2*39. В таких случаях говорят, что число разложили на множители 2 и 39.
Любое составное число можно разложить на два множителя, каждый из которых больше 1. С простым числом такой фокус не прокатит. Такие дела.
Разложение числа на простые множители
Как уже отмечалось выше, любое составное число, можно разложить на два множителя. Возьмем, к примеру, число 210. Это число можно разложить на два множителя 21 и 10. Но числа 21 и 10 тоже составные, разложим и их на два множителя. Получим 10 = 2*5, 21=3*7. И в итоге число 210 разложилось уже на 4 множителя: 2,3,5,7. Эти числа уже простые и их разложить нельзя. То есть мы разложили число 210 на простые множители.
При разложении составных чисел на простые множители, их обычно, записывают в порядке возрастания.
Следует запомнить, что любое составное число можно разложить на простые множители и причем единственным образом, с точностью до перестановки.
- Обычно, при разложении числа на простые множители пользуются признаками делимости.
Разложим число 378 на простые множители
Будем записывать числа, разделяя их вертикальной чертой. Число 378 делится на 2, так как оканчивается на 8. При делении получим число 189. Сумма цифр числа 189 делится на 3, значит и само число 189 делится на 3. В результате получим 63.
Число 63 тоже делится на 3, по признаку делимости. Получаем 21, число 21 снова можно разделить на 3, получим 7. Семерка делится только на себя, получаем единицу. На этом закончено деление. Справа после черты получились простые множители, на которые раскладывается число 378.
378|2
189|3
63|3
21|3
Что значит разложить на простые множители? Как это сделать? Что можно узнать по разложению числа на простые множители? Ответы на эти вопросы иллюстрируются конкретными примерами.
Определения:
Простым называют число, которое имеет ровно два различных делителя.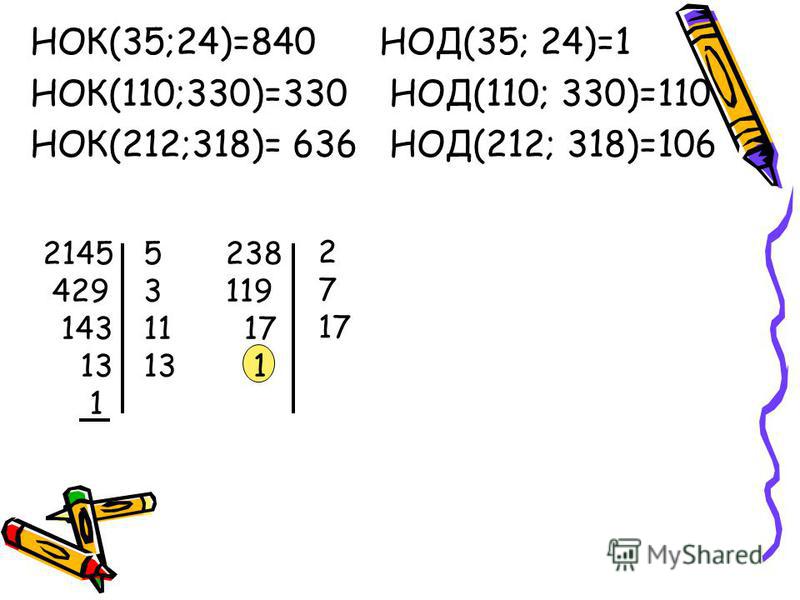
Составным называют число, которое имеет более двух делителей.
Разложить натуральное число на множители — значит представить его в виде произведения натуральных чисел.
Разложить натуральное число на простые множители — значит представить его в виде произведения простых чисел.
Замечания:
- В разложении простого числа один из множителей равен единице, а другой — самому этому числу.
- Говорить о разложении единицы на множители не имеет смысла.
- Составное число можно разложить на множители, каждый из которых отличен от 1.
Разложим число 150 на множители. Например, 150 — это 15 умножить на 10. 15 — это составное число. Его можно разложить на простые множители 5 и 3. 10 — это составное число. Его можно разложить на простые множители 5 и 2. Записав вместо 15 и 10 их разложения на простые множители, мы получили разложение числа 150. | |
Число 150 можно по-другому разложить на множители. Например, 150 — это произведение чисел 5 и 30. 5 — число простое. 30 — это число составное. Его можно представить как произведение 10 и 3. 10 — число составное. Его можно разложить на простые множители 5 и 2. Мы получили разложение числа 150 на простые множители другим способом. | |
Заметим, что первое и второе разложение одинаковы. Они отличаются только порядком следования множителей. Принято записывать множители в порядке возрастания. | |
Всякое составное число можно разложить на простые множители единственным образом с точностью до порядка множителей. | |
При разложении больших чисел на простые множители используют запись в столбик:
Наименьшее простое число, на которое делится 216 — это 2. Разделим 216 на 2. Получим 108. | |
Полученное число 108 делится на 2. Выполним деление. Получим в результате 54. | |
Согласно признаку делимости на 2 число 54 делится на 2. Выполнив деление, получим 27. | |
Число 27 заканчивается на нечетную цифру 7 . Оно Не делится на 2. Следующее простое число — это 3. Разделим 27 на 3. Получим 9. Наименьшее простое Число, на которое делится 9, — это 3. Три — само является простым числом, оно делится на себя и на единицу. Разделим 3 на себя. В итоге мы получили 1. | |
- Число делится лишь на те простые числа, которые входят в состав его разложения.
- Число делится лишь на те составные числа, разложение которых на простые множители полностью в нем содержится.
Рассмотрим примеры:
4900 делится на простые числа 2, 5 и 7. | |
11 550 75. Это так, потому что разложение числа 75 полностью содержится в разложении числа 11550. В результате деления будет произведение множителей 2, 7 и 11. 11550 не делится на 4 потому, что в разложении четырех есть лишняя двойка. |
Найти частное от деления числа a на число b, если эти числа раскладываются на простые множители следующим образом a=2∙2∙2∙3∙3∙3∙5∙5∙19; b=2∙2∙3∙3∙5∙19
Разложение числа b полностью содержится в разложении числа a. | |
Результат деления a на b — это произведение оставшихся в разложении числа a трех чисел. Итак, ответ: 30. |
Список литературы
- Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И. Математика 6.
 — М.: Мнемозина, 2012.
— М.: Мнемозина, 2012. - Мерзляк А.Г., Полонский В.В., Якир М.С. Математика 6 класс. — Гимназия. 2006.
- Депман И.Я., Виленкин Н.Я. За страницами учебника математики. — М.: Просвещение, 1989.
- Рурукин А.Н., Чайковский И.В. Задания по курсу математика 5-6 класс. — М.: ЗШ МИФИ, 2011.
- Рурукин А.Н., Сочилов С.В., Чайковский К.Г. Математика 5-6. Пособие для учащихся 6-х классов заочной школы МИФИ. — М.: ЗШ МИФИ, 2011.
- Шеврин Л.Н., Гейн А.Г., Коряков И.О., Волков М.В. Математика: Учебник-собеседник для 5-6 классов средней школы. — М.: Просвещение, Библиотека учителя математики, 1989.
- Интернет-портал Matematika-na.ru ().
- Интернет-портал Math-portal.ru ().
Домашнее задание
- Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И. Математика 6. — М.: Мнемозина, 2012. № 127, № 129, № 141.
- Другие задания: № 133, № 144.
Любое натуральное число можно разложить на произведение простых множителей. Если вы не любите иметь дело с большими числами, такими как 5733, научитесь раскладывать их на простые множители (в данном случае это 3 x 3 x 7 x 7 x 13). Подобная задача часто встречается в криптографии, которая занимается проблемами информационной безопасности. Если вы еще не готовы создать собственную систему безопасной электронной почты, для начала научитесь раскладывать числа на простые множители.
Если вы не любите иметь дело с большими числами, такими как 5733, научитесь раскладывать их на простые множители (в данном случае это 3 x 3 x 7 x 7 x 13). Подобная задача часто встречается в криптографии, которая занимается проблемами информационной безопасности. Если вы еще не готовы создать собственную систему безопасной электронной почты, для начала научитесь раскладывать числа на простые множители.
Шаги
Часть 1
Нахождение простых множителейНачните с исходного числа. Выберите составное число больше 3. Нет смысла брать простое число, так как оно делится лишь на само себя и единицу.
- Пример: разложим на произведение простых чисел число 24.
Разложим данное число на произведение двух множителей. Найдем два меньших числа, произведение которых равно исходному числу. Можно использовать любые множители, но проще взять простые числа. Один из хороших способов состоит в том, чтобы попробовать поделить исходное число сначала на 2, затем на 3, потом на 5 и проверить, на какие из этих простых чисел оно делится без остатка.

- Пример: если вы не знаете множителей для числа 24, попробуйте поделить его на малые простые числа. Так вы обнаружите, что данное число делится на 2: 24 = 2 x 12 . Это хорошее начало.
- Поскольку 2 является простым числом, его хорошо использовать при разложении четных чисел.
Начните строить дерево множителей. Эта простая процедура поможет вам разложить число на простые множители. Для начала проведите от исходного числа две «ветки» вниз. На конце каждой ветки напишите найденные множители.
- Пример:
Разложите на множители следующую строку чисел. Взгляните на два новых числа (вторая строка дерева множителей). Оба ли они относятся к простым числам? Если одно из них не является простым, также разложите его на два множителя. Проведите еще две ветки и напишите два новых множителя в третьей строке дерева.
- Пример:
12 не является простым числом, поэтому его следует разложить на множители.
 Используем разложение 12 = 2 x 6 и запишем его в третьей строке дерева:
Используем разложение 12 = 2 x 6 и запишем его в третьей строке дерева: - 2 x 6
- Пример:
12 не является простым числом, поэтому его следует разложить на множители.
Продолжайте двигаться вниз по дереву. Если один из новых множителей окажется простым числом, проводите от него одну «ветку» и пишите на ее конце это же число. Простые числа не раскладываются на меньшие множители, поэтому просто переносите их на уровень ниже.
- Пример: 2 является простым числом. Просто перенесите 2 из второй в третью строку:
- 2 2 6
Продолжайте раскладывать числа на множители, пока у вас не останутся одни простые числа. Проверяйте каждую новую строку дерева. Если хоть один из новых множителей не является простым числом, разложите его на множители и запишите новую строку. В конце концов у вас останутся одни простые числа.
- Пример: 6 не является простым числом, поэтому его также следует разложить на множители. В то же время 2 представляет собой простое число, и мы переносим две двойки на следующий уровень:
- 2 2 6
- / / /\
- 2 2 2 3
Запишите последнюю строку в виде произведения простых множителей.
 В конце концов у вас останутся одни простые числа. Когда это случится, разложение на простые множители завершено. Последняя строка представляет собой набор простых чисел, произведение которых дает исходное число.
В конце концов у вас останутся одни простые числа. Когда это случится, разложение на простые множители завершено. Последняя строка представляет собой набор простых чисел, произведение которых дает исходное число.- Проверьте ответ: перемножьте стоящие в последней строке числа. В результате должно получиться исходное число.
- Пример: в последней строке дерева множителей содержатся числа 2 и 3. Оба этих числа являются простыми, поэтому разложение завершено. Таким образом, разложение числа 24 на простые множители имеет следующий вид: 24 = 2 x 2 x 2 x 3 .
- Порядок множителей не имеет значения. Разложение можно записать также в виде 2 x 3 x 2 x 2.
При желании упростите ответ с помощью степенной записи. Если вы знакомы с возведением чисел в степень, можно записать полученный ответ в более простом виде. Помните, что внизу записывается основание, а надстрочное число показывает, сколько раз это основание следует умножить на само себя.

- Пример: сколько раз встречается число 2 в найденном разложении 2 x 2 x 2 x 3? Три раза, поэтому выражение 2 x 2 x 2 можно записать в виде 2 3 . В упрощенной записи получаем 2 3 x 3.
Часть 2
Использование разложения на простые множителиНайдите наибольший общий делитель двух чисел. Наибольшим общим делителем (НОД) двух чисел называется максимальное число, на которое оба числа делятся без остатка. В приведенном ниже примере показано, как с помощью разложения на простые множители найти наибольший общий делитель чисел 30 и 36.
- Разложим оба числа на простые множители. Для числа 30 разложение имеет вид 2 x 3 x 5. Число 36 раскладывается на простые множители следующим образом: 2 x 2 x 3 x 3.
- Найдем число, которое встречается в обоих разложениях. Перечеркнем это число в обоих списках и напишем его с новой строки. Например, 2 встречается в двух разложениях, поэтому запишем 2 в новой строке. После этого у нас остается 30 = 2
x 3 x 5 и 36 = 2
x 2 x 3 x 3.

- Повторяйте это действие, пока в разложениях не останется общих множителей. В оба списка входит также число 3, поэтому в новой строке можно записать 2 и 3 . После этого вновь сравните разложения: 30 = 2 x 3 x 5 и 36 = 2 x 2 x 3 x 3. Как видно, в них не осталось общих множителей.
- Чтобы найти наибольший общий делитель, следует найти произведение всех общих множителей. В нашем примере это 2 и 3, поэтому НОД равен 2 x 3 = 6 . Это наибольшее число, на которое делятся без остатка числа 30 и 36.
С помощью НОД можно упрощать дроби. Если вы подозреваете, что какую-то дробь можно сократить, используйте наибольший общий делитель. По описанной выше процедуре найдите НОД числителя и знаменателя. После этого поделите числитель и знаменатель дроби на это число. В результате вы получите ту же дробь в более простом виде.
- К примеру, упростим дробь 30 / 36 . Как мы установили выше, для 30 и 36 НОД равен 6, поэтому поделим числитель и знаменатель на 6:
- 30 ÷ 6 = 5
- 36 ÷ 6 = 6
- 30 / 36 = 5 / 6
Найдем наименьшее общее кратное двух чисел.
 Наименьшее общее кратное (НОК) двух чисел — это наименьшее число, которое делится без остатка на оба данных числа. Например, НОК 2 и 3 является 6, поскольку это наименьшее число, которое делится на 2 и 3. Ниже приведен пример нахождения НОК с помощью разложения на простые множители:
Наименьшее общее кратное (НОК) двух чисел — это наименьшее число, которое делится без остатка на оба данных числа. Например, НОК 2 и 3 является 6, поскольку это наименьшее число, которое делится на 2 и 3. Ниже приведен пример нахождения НОК с помощью разложения на простые множители:- Начнем с двух разложений на простые множители. Например, для числа 126 разложение можно записать как 2 x 3 x 3 x 7. Число 84 раскладывается на простые множители в виде 2 x 2 x 3 x 7.
- Сравним, сколько раз каждый множитель встречается в разложениях. Выберите тот список, где множитель встречается максимальное число раз, и обведите это место. Например, число 2 встречается один раз в разложении для числа 126 и дважды в списке для 84, поэтому следует обвести 2 x 2 во втором списке множителей.
- Повторите это действие для каждого множителя. Например, 3 встречается чаще в первом разложении, поэтому следует обвести в нем 3 x 3 . Число 7 встречается по одному разу в обоих списках, так что обводим 7 (неважно в каком списке, если данный множитель встречается в обоих списках одинаковое число раз).

- Чтобы найти НОК, перемножьте все обведенные числа. В нашем примере наименьшим общим кратным чисел 126 и 84 является 2 x 2 x 3 x 3 x 7 = 252 . Это наименьшее число, которое делится на 126 и 84 без остатка.
Используйте НОК для сложения дробей. При сложении двух дробей необходимо привести их к общему знаменателю. Для этого найдите НОК двух знаменателей. Затем умножьте числитель и знаменатель каждой дроби на такое число, чтобы знаменатели дробей стали равны НОК. После этого можно сложить дроби.
- Например, необходимо найти сумму 1 / 6 + 4 / 21 .
- С помощью приведенного выше метода можно найти НОК для 6 и 21. Оно равно 42.
- Преобразуем дробь 1 / 6 так, чтобы ее знаменатель равнялся 42. Для этого необходимо поделить 42 на 6: 42 ÷ 6 = 7. Теперь умножим числитель и знаменатель дроби на 7: 1 / 6 x 7 / 7 = 7 / 42 .
- Чтобы привести вторую дробь к знаменателю 42, поделим 42 на 21: 42 ÷ 21 = 2. Умножим числитель и знаменатель дроби на 2: 4 / 21 x 2 / 2 = 8 / 42 .

- После того как дроби приведены к одинаковому знаменателю, их можно легко сложить: 7 / 42 + 8 / 42 = 15 / 42 .
Что значит разложить на простые множители? Как это сделать? Что можно узнать по разложению числа на простые множители? Ответы на эти вопросы иллюстрируются конкретными примерами.
Определения:
Простым называют число, которое имеет ровно два различных делителя.
Составным называют число, которое имеет более двух делителей.
Разложить натуральное число на множители — значит представить его в виде произведения натуральных чисел.
Разложить натуральное число на простые множители — значит представить его в виде произведения простых чисел.
Замечания:
- В разложении простого числа один из множителей равен единице, а другой — самому этому числу.
- Говорить о разложении единицы на множители не имеет смысла.
- Составное число можно разложить на множители, каждый из которых отличен от 1.

Разложим число 150 на множители. Например, 150 — это 15 умножить на 10. 15 — это составное число. Его можно разложить на простые множители 5 и 3. 10 — это составное число. Его можно разложить на простые множители 5 и 2. Записав вместо 15 и 10 их разложения на простые множители, мы получили разложение числа 150. | |
Число 150 можно по-другому разложить на множители. Например, 150 — это произведение чисел 5 и 30. 5 — число простое. 30 — это число составное. Его можно представить как произведение 10 и 3. 10 — число составное. Его можно разложить на простые множители 5 и 2. Мы получили разложение числа 150 на простые множители другим способом. | |
Заметим, что первое и второе разложение одинаковы. Они отличаются только порядком следования множителей. Принято записывать множители в порядке возрастания. | |
Всякое составное число можно разложить на простые множители единственным образом с точностью до порядка множителей. | |
При разложении больших чисел на простые множители используют запись в столбик:
Наименьшее простое число, на которое делится 216 — это 2. Разделим 216 на 2. Получим 108. | |
Полученное число 108 делится на 2. Выполним деление. Получим в результате 54. | |
Согласно признаку делимости на 2 число 54 делится на 2. Выполнив деление, получим 27. | |
Число 27 заканчивается на нечетную цифру 7 . Оно Не делится на 2. Следующее простое число — это 3. Разделим 27 на 3. Получим 9. Наименьшее простое Число, на которое делится 9, — это 3. Три — само является простым числом, оно делится на себя и на единицу. | |
- Число делится лишь на те простые числа, которые входят в состав его разложения.
- Число делится лишь на те составные числа, разложение которых на простые множители полностью в нем содержится.
Рассмотрим примеры:
4900 делится на простые числа 2, 5 и 7. (они входят в разложение числа 4900), но не делится, например, на 13. | |
11 550 75. Это так, потому что разложение числа 75 полностью содержится в разложении числа 11550. В результате деления будет произведение множителей 2, 7 и 11. 11550 не делится на 4 потому, что в разложении четырех есть лишняя двойка. |
Найти частное от деления числа a на число b, если эти числа раскладываются на простые множители следующим образом a=2∙2∙2∙3∙3∙3∙5∙5∙19; b=2∙2∙3∙3∙5∙19
Разложение числа b полностью содержится в разложении числа a. | |
Результат деления a на b — это произведение оставшихся в разложении числа a трех чисел. Итак, ответ: 30. |
Список литературы
- Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И. Математика 6. — М.: Мнемозина, 2012.
- Мерзляк А.Г., Полонский В.В., Якир М.С. Математика 6 класс. — Гимназия. 2006.
- Депман И.Я., Виленкин Н.Я. За страницами учебника математики. — М.: Просвещение, 1989.
- Рурукин А.Н., Чайковский И.В. Задания по курсу математика 5-6 класс. — М.: ЗШ МИФИ, 2011.
- Рурукин А.Н., Сочилов С.В., Чайковский К.Г. Математика 5-6. Пособие для учащихся 6-х классов заочной школы МИФИ. — М.: ЗШ МИФИ, 2011.
- Шеврин Л.Н., Гейн А.Г., Коряков И.О., Волков М.В. Математика: Учебник-собеседник для 5-6 классов средней школы. — М.: Просвещение, Библиотека учителя математики, 1989.
- Интернет-портал Matematika-na.ru ().
- Интернет-портал Math-portal.
 ru ().
ru ().
Домашнее задание
- Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И. Математика 6. — М.: Мнемозина, 2012. № 127, № 129, № 141.
- Другие задания: № 133, № 144.
Делители 56 — Найти простые факторизации/Множители 56
Факторы 56 — это числа, которые полностью делят число 56 и при парном умножении дают произведение, равное 56. Эти множители 56 являются положительными числами, но могут быть и отрицательными, как Что ж. Число 56 — четное составное число, а значит, оно имеет несколько делителей. На этом уроке мы вычислим множители 56, простые множители 56 и множители 56 попарно вместе с решенными примерами для лучшего понимания.
- Коэффициенты 56: 1, 2, 4, 7, 8, 14, 28 и 56
- Факторизация числа 56: 56 = 2 3 × 7
| 1. | Каковы делители числа 56? |
2. | Как рассчитать коэффициенты числа 56? |
| 3. | Коэффициенты 56 с помощью простой факторизации |
| 4. | Коэффициенты 56 в парах |
| 5. | Часто задаваемые вопросы о факторах 56 |
Каковы делители числа 56?
Делители 56 — это целые числа, которые делят 56 без остатка. Например, 8 — это коэффициент 56, потому что 8 делит 56 без остатка. Интересно, что 7, являющееся частным от приведенного выше деления, также является коэффициентом 56. Проверьте, получите ли вы 0 в остатке, разделив 56 на 8 с помощью деления в длинное число.
Чтобы лучше понять концепцию поиска факторов с помощью простой факторизации, давайте рассмотрим еще несколько примеров.
- Множители числа 256 — Множители числа 256 равны 1, 2, 4, 8, 16, 32, 64, 128, 256
- Коэффициенты 54 – множители 54 равны 1, 2, 3, 6, 9, 18, 24 и 56
- Коэффициенты 55 – множители 55 равны 1, 5, 11 и 55
- Коэффициенты 58 – множители 58 равны 1, 2 и 29
- Коэффициенты 48 – множители 148 2, 3, 4, 6, 8, 12, 16, 24, 48
Как рассчитать коэффициенты числа 56?
Шаги для нахождения множителей любого числа:
- Разделите число на 2 и получите другое число.
 Если полученное число не является целым числом, то округлить его до ближайшего целого числа.
Если полученное число не является целым числом, то округлить его до ближайшего целого числа. - Разделите данное число на каждое из чисел от 1 до полученного числа (из шага 1) и посмотрите, какое из них дает в остатке 0. Мы делим только на эти числа как любое число, которое больше половины заданного числа не может быть его фактором.
- Делитель каждого такого деления (с остатком 0) — это множители этого числа. Кроме того, данное число также является фактором само по себе.
Нахождение множителей числа 56
Разделив 56 на 2, мы получим 28. Разделите 56 на каждое из чисел от 1 до 28 и посмотрите, какое из них даст в остатке 0. Делители всех таких делений являются множителями. Кроме того, 56 является фактором сам по себе. Таким образом, 1,2,4,7,8,14,28 и 56 являются делителями числа 56.
Важные примечания
- Дроби и десятичные дроби, не являющиеся целыми числами, не могут быть делителями любого числа
- Если число является множителем данного числа, то его аддитивная инверсия также является множителем данного числа.

Например, поскольку 8 — это коэффициент 56, -8 также является коэффициентом 56.
Разложение числа 56 на простые множители
Найдем разложение числа 56 на простые множители, представив его как произведение простых чисел.
Таким образом, простая факторизация числа 56 равна 2 × 2 × 2 × 7 .
Из разложения числа 56 на простые множители ясно, что 2 и 7 являются делителями числа 56. Фактически, 2 и 7 являются простыми делителями числа 56. Кроме того, мы знаем, что 1 является делителем каждого числа. Таким образом, множители числа 56 при простой факторизации равны 1, 2, 4, 7, 8, 14, 28 и 56.
Советы и подсказки
При нахождении делителей числа помните следующее:
- 1 и само число всегда являются делителями числа.
- Чтобы найти другие делители числа, мы сначала найдем его простую факторизацию. Тогда множители простой факторизации являются простыми множителями числа.

- Перемножая некоторые или все множимые в различных комбинациях, мы получаем составные множители числа.
Множители 56 в парах
Парные множители 56 получаются путем записи 56 как произведения двух чисел всеми возможными способами.
В каждом произведении оба множимых являются множителями 56.
Продукт, результатом которого является 56 | Пара факторов 56 |
|---|---|
1 х 56 | (1, 56) |
2 х 28 | (2, 28) |
4 х 14 | (4, 14) |
7 х 8 | (7, 8) |
Отрицательные парные множители числа 56: (-1, -56), (-2, -28), (-4, -14) и (-7, -8).
Пример 1 Эвелин — классный руководитель, в ее классе 56 учеников.
 Она хочет разделить свой класс на группы и дать им групповую математическую практику. Сколькими способами она может сгруппировать 56 учеников так, чтобы:
Она хочет разделить свой класс на группы и дать им групповую математическую практику. Сколькими способами она может сгруппировать 56 учеников так, чтобы:В группе не может быть 1 или все ученики класса.
В каждой группе одинаковое количество студентов.
Решение
Мы уже узнали, что делители числа 56 равны 1, 2, 4, 7, 8, 14, 28 и 56. Но в группах не может быть одного или всех учащихся. Поэтому мы игнорируем 1 и 56. Другие делители 56 – это 2, 4, 7, 8, 14 и 28 (число которых равно 6).
Таким образом, необходимое количество путей = 6Пример 2 Когда на экзамене Джейми попросили найти разложение числа 56 на простые множители, он сделал это следующим образом и ответил, что разложение числа 56 на простые множители равно 2 × 7. Однако его учитель отметил это неправильно. Можем ли мы помочь Джейми, показав ему правильный способ вычисления простой факторизации?
Решение
Разложение на простые множители, данное Джейми, равно 2 × 7
Это неправильно. Давайте попробуем метод факторного дерева, чтобы найти простую факторизацию числа 56.
Давайте попробуем метод факторного дерева, чтобы найти простую факторизацию числа 56.Таким образом, простая факторизация числа 56 равна 2 3 × 7,
.
перейти к слайдуперейти к слайду
Разбивайте сложные концепции с помощью простых визуальных средств.
Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.
Записаться на бесплатный пробный урок
перейти к слайдуперейти к слайдуперейти к слайду
Часто задаваемые вопросы о коэффициентах 56.
1. Что такое все множители 56?
Делители числа 56: 1, 2, 4, 7, 8, 14, 28 и 56
2. Какие общие делители чисел 56 и 96?
Общие делители чисел 56 и 96: 1, 2, 4, 6 и 8.
3. Сколько делителей в числе 56?
8 Коэффициенты 56 равны 1, 2, 4, 7, 8, 14, 28, 56.
4. Каковы делители чисел 56 и 21?
Коэффициенты 56: 1, 2, 4, 7, 8, 14, 28, 56.
Множители 21: 1, 3, 7, 21.
Наивысшие общие делители: 7.
5. Каковы делители 56 и 120?
Коэффициенты 56: 1, 2, 4, 7, 8, 14, 28, 56.
Факторы 120: 1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 20, 24, 30, 40, 120.
Наивысшие общие множители: 8
Факторы 56
В математике факторизация — это разбиение числа на более мелкие числа. Меньшие числа при умножении вместе дают исходное число. Процесс разложения числа на делители и делители называется факторизацией. Таким образом, делители 56 будут некоторыми простыми числами, которые при умножении дают результат, равный 56. Это известно как простая факторизация числа 56. Факторы числа — это те, которые без остатка делятся на другое число. Это имеет огромное значение в элементарной арифметике. Его можно использовать по-разному, например, для определения наименьшего общего кратного или наибольшего общего делителя. Как правило, мы факторизуем число до тех пор, пока не достигнем точки, в которой оно больше не может делиться. Это обычно известно как первичная факторизация.
Это обычно известно как первичная факторизация.
Определение
Когда два числа умножаются вместе и в результате получается заданное число, то эти два числа называются факторами этого конкретного числа. Например, 5 х 3 равно 15; следовательно, числа 5 и 3 являются множителями числа 15. Числа, которые перемножаются вместе, называются парами множителей.
Каковы множители 56 в парах?
Каждое число делится само на себя и на единицу. Например, 56/1 = 56. Поскольку умножение — это обратная сторона деления, мы можем сказать, что 56 x 1 = 56, поэтому делители 56 — это 1 и 56. 1 и 56 также известны как пары множителей. Точно так же существуют другие множители и пары множителей числа 56, например 9.0003
7 x 8 = 56 или 56/7 = 8 и 56/8 = 7
2 x 28 = 56 или 56/2 = 28
4 x 14 = 56 или 56/4 = 14 и 56/14 = 4.
Таким образом, парами множителей числа 56 являются 1 и 56, 7 и 8, 2 и 28 и 4 и 14. , 28 и 56 должны быть различными множителями числа 56. Факторы и различные множители одинаковы. Факторы положительны и делятся без остатка.
, 28 и 56 должны быть различными множителями числа 56. Факторы и различные множители одинаковы. Факторы положительны и делятся без остатка.
Однако факторы могут быть и отрицательными. Например, это -56, тогда множители -56 равны 9.0003
-1 х 56 или 1 х -56 = -56
-2 х 28 или 2 х -28 = -56
-7 х 8 или 7 х -8 = -56
-4 х -14 или 4 x -14 = -56
Проще говоря, отрицательные факторы — это факторы с отрицательным знаком (-). Аналогично,
-1 x -56 = 56
-2 x -28 = 56
-7 x -8 = 56
-4 x -14 = 56
Расчет коэффициентов
Только целые числа и целые числа можно преобразовать в множители. Чтобы 56 было целым числом, вы должны иметь возможность писать 56 без дроби или десятичных частей, например. 56/3, 23/56 или 56.01. Чтобы 56 было целым числом, оно должно быть целым числом, а не дробью. Таким образом, 56 является целым числом, а также целым числом.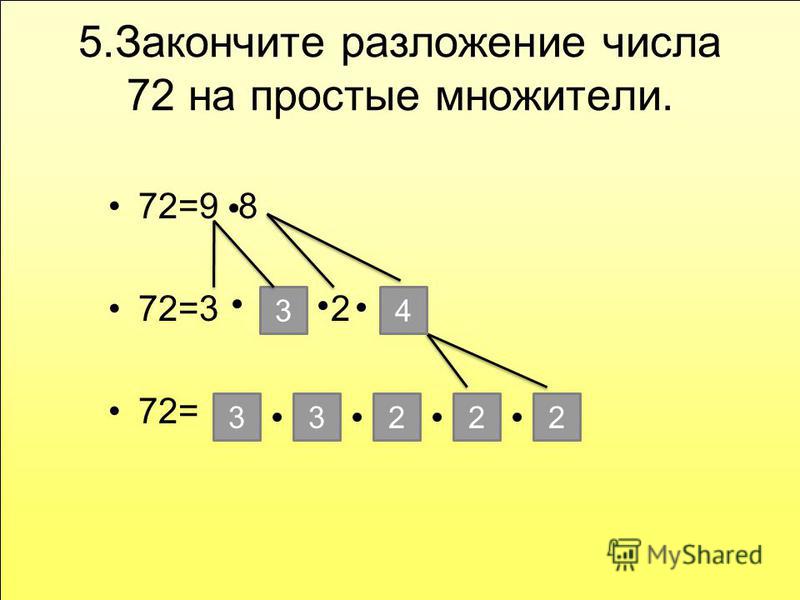 Когда вы делите 56 на его множители, остаток всегда равен нулю. Например,
Когда вы делите 56 на его множители, остаток всегда равен нулю. Например,
56/1 = 56, дает ноль и делится на 1
56/2 = 28, дает ноль и делится на 2
56/4 = 14, дает ноль и делится на 4
56/7 = 8 дает ноль и делится на 8.
56/56 = 1 дает ноль и делится на 1
56/28 = 2 дает ноль и делится на 28 /8 = 7, дает ноль и делится на 8
56/14 = 4, дает ноль и делится на 14.
Как записать множители 56
Начнем с того, что сначала напишем число 56. Теперь у нас достаточно знаний о факторе и паре факторов числа 56, так что давайте начнем с любой пары. Например, 7 х 56
= 7 х 8 = 56
= 7 х 2 х 2 х 2 = 56
Итак, 7 — простое число, и его нельзя разложить дальше, как число 8. 7 можно записать только как 7 x 1. Таким образом, мы записываем множители 56 как = 7 x 2 x 2 x 2 x 1.
Возьмем другую пару множителей, 2 и 28
= 2 x 28 = 56
= 2 x 14 x 2 = 56
= 2 x 7 x 2 x 2 = 56
= 2 x 2 x 2 x 7 = 56
= 2 x 2 x 2 x 7 = 56 2 x 2 x 7 x 1 = 56
Следовательно, множители 56 можно записать как 7 x 2 x 2 x 2 x 1. Вы получите тот же ответ с любой другой парой множителей, которую вы используете. Вывод состоит в том, что множители числа 56 всегда записываются как 7 x 2 x 2 x 2 x 1.
Вы получите тот же ответ с любой другой парой множителей, которую вы используете. Вывод состоит в том, что множители числа 56 всегда записываются как 7 x 2 x 2 x 2 x 1.
Разложение числа 56 на простые множители
Во-первых, знайте, что 56 — составное число. Вы уже знаете, что 56 — это целое число, а также целое число (не дробь и не десятичная дробь). Умножение может занимать 7 х 8 или 2 х 28, поэтому 56 — составное число. Составное число также состоит из простых множителей. Как вы знаете, простые числа — это 1, 2, 3, 5, 7, 11, 13, 17 и 31, так как они не имеют других делителей, кроме 1.
Для начала разделите число 56 на 2, один из его простых множителей.
56/2 = 28
28/2 = 14
14/2 = 7
7/2 = 3,5, дробь. Итак, следующий вариант
7/7 = 1
ставит точку в дальнейшем делении. Следовательно, простые множители числа 56 записываются как 2 х 2 х 2 х 7 или 23 х 2, где 2 и 7 — простые числа. Это простая факторизация числа 56.
Это простая факторизация числа 56.
Забавные факты о множителях
Факторы — это целые числа, а не десятичные числа или дроби.
Все четные числа всегда имеют множитель два.
Все числа, оканчивающиеся на пять, имеют делитель пять.
Все числа, оканчивающиеся на ноль, имеют делители 2, 5 и 10.
Коэффициенты 56
При умножении двух чисел получается 56, а множители 56 — это числа, которые дают этот результат. Полные числа, положительные или отрицательные, но не дроби или десятичные числа, являются парами множителей числа 56. Рассмотрим пару множителей числа 56, которая записывается (1, 56) и (-1, -56). В результате можно рассматривать как положительные, так и отрицательные пары факторов из 11. Метод факторизации будет использоваться для определения множителей целого числа 56. Используя метод факторизации простых чисел и несколько решенных случаев, в этой статье мы обнаружим множители числа 56, парные множители и простые множители числа 56.
Метод факторизации будет использоваться для определения множителей целого числа 56. Используя метод факторизации простых чисел и несколько решенных случаев, в этой статье мы обнаружим множители числа 56, парные множители и простые множители числа 56.
1,2,4,7,8,14,28,56
Pair Factors | Prime Factorization |
1 x 56 2 x 28 4 x 14 7 x 8 | 2 x 2 x 2 x 7 23 x 7 |
9 Какие коэффициенты?
Делители 56 — это числа, на которые 56 точно делится. Другими словами, делители 56 — это целые числа, попарно перемноженные для получения 56. Число 56 имеет несколько делителей, отличных от 1 и 56, поскольку это четное составное число. В результате 56 множителей равны 1, 2, 4, 7, 8, 14, 28 и 56.
1, 2, 4, 7, 8, 14, 28 и 56 являются делителями числа 56.
Факторизация числа 56: 2×2×2×7 или 23 × 7.
Парные коэффициенты числа 56
Умножьте два числа в паре, чтобы получить исходное число 56; examples of such numbers are as follows:
Positive Pair Factors | Negative Pair Factor |
1 x 56 = 56 => (1, 56) | -1 x -56 = 56 => (-1, -56) |
2 x 28 = 56 => (2, 28) | -2 x -28 = 56 => ( -2, -28) |
4 x 14 = 56 => (4, 14) | -4 x -14 = 56 => (-4, -14) 6 70093 | -7 x -8 = 56 => (-7, -8) |
В результате положительные парные множители числа 56 равны ( 1, 56), (2, 28), (4, 14) и (5, 14) соответственно (7, 8).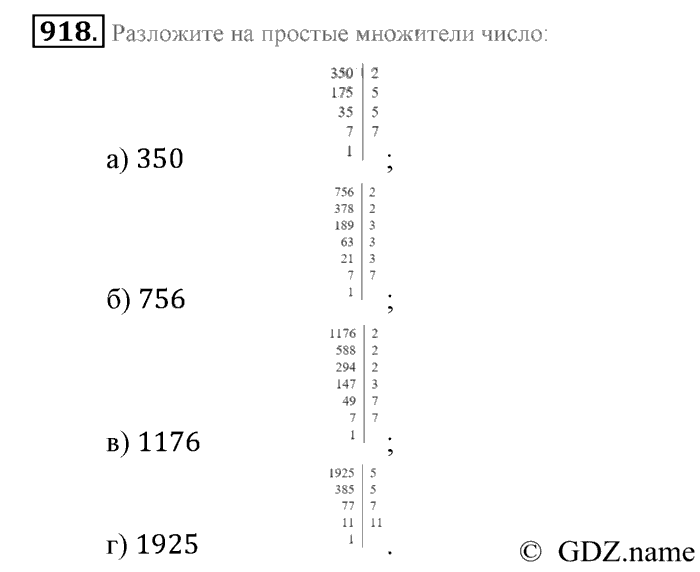 (-1, -56), (-2, -28), (-4, -14) и (-1, -56) — отрицательные парные множители числа 56 соответственно (-7, -8).
(-1, -56), (-2, -28), (-4, -14) и (-1, -56) — отрицательные парные множители числа 56 соответственно (-7, -8).
56 Множители с использованием метода деления
Множители 56 можно вычислить с помощью метода деления путем деления 56 на различные последовательные целые числа. Если целые числа идеально делят 56, то это 56 множителей. Начнем с деления 56 на единицу, а затем перейдем к другим целочисленным значениям.
(Коэффициент = 1 и остаток = 0) 56/1 = 56
(Коэффициент = 2 и остаток = 0) 56/2 = 28
(Коэффициент = 4 и остаток = 0) 56/4 = 14
(Коэффициент = 7 и остаток = 0) 56/7 = 8
(Коэффициент = 8 и остаток = 0) 56/8 = 7
(Коэффициент = 14 и остаток = 0) 56/14 = 4
(Коэффициент = 28 и остаток = 0) 56/28 = 2
(Коэффициент = 56, остаток = 0) 56/56 = 1
В результате 56 множителей равны 1, 2, 4, 7, 8, 14, 28 и 56.
Коэффициенты 56 и как найти Их · Материя математики
Есть много удивительных фактов о числе 56!
Согласно Аристотелю, 56 — это число слоев Вселенной. Он считал, что Земля — это первый слой с 55 кристаллическими сферами над ним.
Этот урок проведет вас через все факторы 56, как найти факторы и другие интересные факты о факторах!
Если вам нужен краткий справочник по факторам, эта таблица факторов и множителей будет более полезной.
Множитель — это число, которое идеально переходит в другое число. Например, 2 — это коэффициент 10, потому что он идеально входит в 10, не оставляя остатка.
Если умножить 2 на 5, получится 10, а это значит, что и 2, и 5 являются делителями 10.
В этом уроке вы узнаете, что такое множители числа 56, как найти пары множителей и все о простой факторизации.
Как только вы это поймете, вы сможете находить множители любого числа!
Содержание
Множители 56
Пары
Простые числа
Факторизация 56
Как найти множители 56
Факторизация простых чисел
Разве 56 не интересно?
Подводя итог (каламбур!)
Все множители 56
youtube.com/embed/NehxR6y81iM» frameborder=»0″ allow=»accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture» allowfullscreen=»»>Делители 56 равны 1, 2, 4, 7, 8, 14, 28 и 56 .
56 можно разделить само на себя и на единицу, но оно также делится и на другие числа, так что составное число , а множителей больше двух!
Как вы только что узнали, делит на одно число, которое делится на другое без остатка.
Вы можете записать число в терминах его пар множителей или произведения его простых множителей.
Пары множителей из 56
Самый простой способ найти все множители числа — вычислить пары множителей.
Пары множителей — это наборы из двух чисел, которые перемножаются вместе, чтобы получить другое число.
Итак, вам нужно выяснить, какие два числа, X и Y , умножить вместе, чтобы получить 56. 56)
56)
(2, 28)
(4, 14)
(7, 8)
Иногда в качестве множителя можно использовать отрицательные числа, потому что при умножении двух отрицательных чисел получается положительное число!
Важно помнить, что оба числа должны быть отрицательными, чтобы получилось положительное число. Если один из них отрицательный, а другой положительный, они будут отрицательными.
(-1, -56)
(-2, -28)
(-4, -14)
(-7, -8)
Вы, наверное, замечали, что отрицательные факторы такие же, как и положительные. , только они отрицательные!
Однако упоминаются только положительные, если не указано иное, когда речь идет о парах факторов.
Много ли 56?
Если сумма положительных множителей более чем в два раза превышает само число, оно называется избыточным числом .
Сумма положительных множителей:
120 = 1+2+4+7+8+14+28+56
Двойное число 56 равно 112, а сумма всех его множителей равна 120. Получается 56 обильное число: сумма его множителей больше, чем удвоенная.
Простые делители числа 56
Простое число — это число, которое не делится ни на что, кроме 1 или на себя. Например, 3.
3 ÷ 1 = 3
3 ÷ 3 = 1
3 нельзя разделить ни на что другое, поэтому это простое число.
56 имеет только два простых делителя: 2 и 7.
Вы можете использовать эти простые делители, чтобы записать число 56 как произведение его простых делителей.
56=2 × 2 × 2 × 7
Вы можете решить это, используя любые две пары множителей и продолжая делить их в меньшую сторону, пока не получите простые числа.
Это дерево факторов . Он начинается с исходного числа вверху, которое разбито на пары факторов.
Когда найдено простое число, оно обводится кружком, а другое число разбивается дальше.
Простое число 2 встречается трижды, поэтому его можно записать проще, используя степень или показатель степени.
56 = 2 3 × 7
У числа 56 есть и другие простые числа. Вы можете выразить 56 как сумму последовательных простых чисел.
Вы можете выразить 56 как сумму последовательных простых чисел.
56 = 3 + 5 + 7 + 11 + 13 + 17
Нахождение всех простых делителей числа может быть полезно при нахождении наибольшего общего делителя ( GCF ) двух чисел, а также наименьшее общее кратное ( LCM ) двух чисел.
Факторизация простых чисел также полезна в реальном мире в криптографии. Нахождение простой факторизации большого числа может занять исключительно много времени, даже для компьютеров!
Разложение на множители 56
Как найти делители числа 56
Чтобы найти все делители, вам нужно начать с 1 и работать с каждым числом одно за другим до 56, проверяя, есть ли остаток при делении 56 по каждому номеру. Если остатка нет, число является множителем.
Если остатка нет, число является множителем.
Каждый раз, когда вы находите пару факторов, вы уменьшаете интервал искомых факторов до чисел в пределах таких интервалов пар факторов.
Мы поделимся с вами несколькими хитростями, которые сделают эту работу быстрой.
Начиная с 1…
56 ÷ 1 = 56
Остаток отсутствует, поэтому вы подтвердили, что 1 и 56 являются парой множителей. Теперь вам нужно найти множители от 1 до 56.
56 ÷ 2 = 28
Итак, 2 и 28 — это пара множителей. Теперь вам нужно найти множители от 2 до 28.
56 ÷ 3 = 18,67
Итак, 3 не является фактором. Продолжите этот процесс с 4, 5 и 6.
Вы увидите, что до 6 множителей нет.
56 ÷ 7 = 56
7 и 8 являются парой множителей. Между 7 и 8 нет целых чисел, поэтому вы нашли все пары множителей числа 56.
Итак, всего у вас есть следующие множители:
1, 2, 7, 8, 14, 28, 56
Здесь Вот несколько приемов определения множителей:
- Все целые числа имеют множитель 1
- Любое четное число имеет коэффициент 2
- Если сумма цифр числа кратна 3, то 3 является коэффициентом
- Числа с коэффициентом 4 должны быть четными и если последние две цифры равны 00 или делится на 4, то 4 является коэффициентом
- Любое число с последней цифрой 0 или 5 имеет коэффициент 5
- Любое четное число, сумма цифр которого кратна 3, будет иметь коэффициент 6
- Не существует простого трюка для определения множителей 7!
- Если последние 3 цифры числа делятся на 8, оно будет иметь коэффициент 8
- Если сумма цифр числа кратна 9, то оно имеет коэффициент 9
- Числа с последней цифрой 0 будет иметь коэффициент 10
На самом деле они настолько полезны, что мы сделали распечатанную таблицу правил делимости от 2 до 15, а также рабочий лист для практики, который вы можете держать при себе — для собственного использования. Просто нажмите или коснитесь изображений ниже!
Просто нажмите или коснитесь изображений ниже!
Теперь немного практики.
а) 1, 2, 3, 4, 6, 8, 12, 24
б) 37 — простое число, поэтому единственными делителями являются 1, 37
в) 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, 72
Факторизация простых чисел
Факторизация простых чисел заключается в нахождении всех простых чисел, которые перемножаются, чтобы получить исходное число.
Самый простой способ найти все простые числа — использовать дерево простых множителей.
В начале дерева у вас 56.
Начните с выбора двух пар множителей, которые перемножаются, чтобы получить число.
Выберите пару множителей с наименьшим простым числом в ней, например, 2 и 28, и добавьте их как ветви к дереву.
Поскольку 2 — простое число, вы можете обвести его кружком, чтобы показать, что это последний множитель в этой ветви, и его нельзя больше делить.
Теперь вам нужно продолжить разложение числа 28 на его множители, найдя наименьшее простое число, на которое делится 28.
Оно снова делится на 2, поэтому…
Снова 2 можно обвести. Вам еще нужно разбить 14, которое, как оказалось, снова делится на 2!
И 2, и 7 — простые числа, поэтому вы можете обвести их оба.
Точно так же, как в дереве множителей, которое вам показывали ранее, конец каждой ветви обведен кружком, так что вы завершили свое собственное дерево множителей!
Теперь вы можете выразить 56 как произведение обведенных простых множителей.
56 = 2 × 2 × 2 × 7
Это можно уточнить, используя форму степени или экспоненты:
56 = 2 3 × 7
a) 2×2×2×2×3=2 4 ×3
b) 2 ×3×3×5=2×3 2 ×5
в) 2×2×2×13=2 3 ×13
Не правда ли 56 Интересно?
Существует несколько способов выражения числа 56, помимо его множителей, поскольку число 56 обладает некоторыми интересными свойствами.
56 — это сумма первых 6 треугольных чисел.
56 = 1+3+6+10+15+21
Треугольное число подсчитывает объекты, расположенные в виде равностороннего треугольника.
Это делает 56 6-м тетраэдрическим числом, поскольку оно является суммой первых 6 треугольных чисел, что делает его треугольным пирамидальным числом.
Вы также можете выразить 56 как сумму последовательных четных или нечетных чисел.
Для четных чисел…
56 = 2+4+6+8+10+12+14
Для нечетных чисел…
56 = 11+13+15+17
и
56 = 27+27
56 также является частью пифагорейской тройки. Пифагоровы тройки — это наборы из 3 чисел, которые удовлетворяют:
a 2 + B 2 = C 2
В этом случае…
33 2 + 56 2 = 65 2
Это представленное значение. , 56 и 65, где самая длинная сторона или гипотенуза равна 65.
Знаете ли вы?
56 — атомный номер элемента бария.
Пифагорейцы связывали многоугольник из 56 сторон с Тифоном, греческим мифическим существом, описанным как чудовищный змеевидный гигант.
Совершенный правильный 56-угольник невозможно построить без помощи компьютера; однако близкое приближение было обнаружено в Стоунхендже под названием Обри Хоулс.
В 56 году нашей эры началась война между Римом и Парфией из-за вторжения в Армению.
И странно… В Арканзасе есть город под названием Пятьдесят Шесть!
Чтобы подвести итог (каламбур!)
Множители делятся точно на число, не оставляя остатка. Вы можете выразить множители числа 56 через его пары множителей или его простые множители.
Пары множителей числа 56 задаются в виде:
( X , Y )
Это потому, что X и Y
— это два числа, которые вместе составляют 5 597 Y. Чтобы найти все пары множителей, вам нужно проверить каждую пару чисел от 1 до 56, которые умножаются вместе, чтобы получить 56. Перейдите по этой ссылке, чтобы ознакомиться с нашими правилами делимости, которые можно распечатать.
Вы обнаружили, что делители числа 56 равны 1, 2, 4, 7, 8, 14, 28 и 56 .
Пожалуйста, оставьте комментарий ниже, если у вас есть какие-либо вопросы, и сообщите нам, как вы справились с испытаниями!
Ознакомьтесь с другими уроками со множителями:
Факторы числа 42
Факторы числа 100
Экспресс 56 как произведение его простых множителей?
Обогатите свои знания с помощью наших информативных блогов
- Забронируйте демонстрационный класс
Прежде чем найти простые делители числа 56, мы должны знать, что означает термин «множители». Когда два числа перемножаются вместе, и результатом является заданное число, то два числа называются факторами этого числа.
Делители 56 — это все такие числа, которые полностью делят число 56 и при парном умножении дают произведение равное 56.
Эти делители 56 являются положительными числами, но могут быть и отрицательными.
Все такие числа, которые делят 56 без остатка, являются делителями 56. Только целые числа могут быть делителями числа.
Таким образом, делители числа 56 равны 1 , 2 , 4 , 7 , 8 , 14 , 28 и 56. Это означает, что все эти числа полностью делят 56.
Важные моменты, которые следует помнить
- Десятичные числа и дроби (все, что не является целым числом) не могут быть делителями любого числа.
- Когда число является множителем данного числа, то его аддитивная инверсия также является множителем данного числа. Например, поскольку 4 — это коэффициент 56, – 4 также является коэффициентом 56.
Теперь, прежде чем найти простые делители числа 56, мы должны знать, что мы подразумеваем под простыми числами.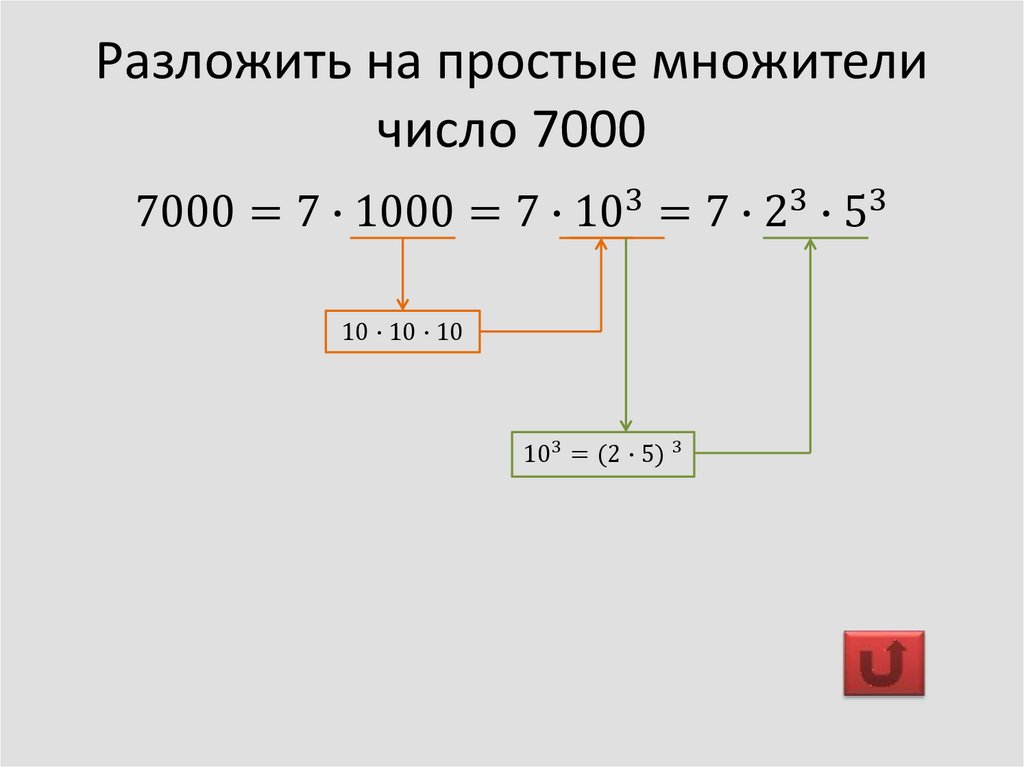
Простые числа — это основные строительные блоки всех чисел. Их нельзя разделить ни на какое число, кроме 1 или самих себя.
Это означает, что простое число — это число, имеющее ровно два делителя: 1 и само число.
Разложение на простые множители означает представление любого данного числа в виде произведения простых чисел.
Существуют различные методы нахождения простых множителей числа.
- Метод деления
- Метод факторного дерева
- Метод деления
Разложение числа 56 на простые множители с помощью метода деления
Мы знаем, что 56 — составное число, и у него будут делители, которые можно разбить на простые числа. Теперь дайте нам знать, как узнать простые делители числа 56.
Теперь дайте нам знать, как узнать простые делители числа 56.
Шаг 1: Давайте разделим число 56 на наименьшее простое число, т. е. 2
Следовательно, 56 / 2 = 28
Шаг 2: Снова разделим 28 на 2, и процесс продолжится.
28 / 2 = 14
14 / 2 = 7
Шаг 3: Теперь, если мы разделим 7 на 2, мы получим дробное число, которое не может быть множителем. Итак, мы переходим к следующему простому числу, которое полностью делит 7, что само по себе является 7.
7 / 7 = 1
Шаг 4: Мы получили 1 в конце процесса деления и поэтому не можем двигаться дальше.
Таким образом, простые делители числа 56 – это 2 x 2 x 2 x 7
56 как произведение его простых делителей методом деления = 2 x 2 x 2 x 7, где 2 и 7 являются простыми числами.
Факторизация простых чисел
Это похоже на метод деления. Единственная разница в том, что представление.
| 2 | 56 |
| 2 | 28 |
| 2 | 14 |
| 7 | 7 |
| 1 |
Таким образом, простая факторизация становится равной 56 = 2 * 2 * 2 * 7.
Простая факторизация числа 56 с помощью метода дерева факторов Здесь нам нужно подсчитать последние узлы или листья дерева.
Таким образом, простые множители числа 56 равны 2 x 2 x 2 x 7 по дереву множителей.
Из двух приведенных выше методов мы можем сделать вывод, что 56 как произведение его простых множителей = 2 x 2 x 2 x 7 .
Вид спереди
Подробнее – Вопросы по математике
Подробнее – Полезные ссылки для развития вашего ребенка Откройте для себя новый способ изучения концепций с помощью реальных методов визуализации и мгновенного разрешения сомнений.
Забронировать демонстрационный класс
Как изменить подлежащее в формуле?
Когда я использую цепное правило и когда я использую правило произведения при дифференциации?
Забронируйте 60-минутный БЕСПЛАТНЫЙ урок сегодня! Зарегистрируйтесь сейчас
Откройте для себя новый способ обучения с TEL Gurus. 93% детей уже продемонстрировали невероятный прогресс в учебе и чувствуют себя более уверенно благодаря веселым и интерактивным онлайн-классам TEL Gurus.
93% детей уже продемонстрировали невероятный прогресс в учебе и чувствуют себя более уверенно благодаря веселым и интерактивным онлайн-классам TEL Gurus.
Book A Demo Class
Найдите разложение числа 56 на простые множители, используя показатели степени
| Введите целое число, которое вы хотите получить, его простые делители: Пример: 2, 3, 4, 11, 10225 и т. д. |
Результат разложения на простые множители: Число 56 является составным числом, поэтому его можно разложить на множители. Другими словами, 56 можно разделить на 1, само по себе и по крайней мере на 2 и 7. Составное число — это натуральное число, имеющее хотя бы один положительный делитель, отличный от единицы или самого числа. Другими словами, составное число — это любое целое число, большее единицы, которое не является простым числом. Факторизация числа 56 = 2 3 •7. Простые делители числа 56 равны 2 и 7. Факторное дерево или простое разложение для 56Поскольку 56 является составным числом, мы можем нарисовать его факторное дерево: |
Вот ответ на такие вопросы, как: Найдите разложение 56 на простые множители с использованием показателей степени или является ли 56 простым или составным числом?
Используйте приведенный выше инструмент факторизации простых чисел, чтобы определить, является ли данное число простым или составным, и в этом случае вычислите его простые множители. См. также на этой веб-странице диаграмму факторизации простых чисел со всеми простыми числами от 1 до 1000.
Что такое первичная факторизация?
Определение простой факторизации
Простой факторизации — это разложение составного числа на произведение простых множителей, которые при умножении воссоздают исходное число. Факторы по определению — это числа, которые умножаются, чтобы создать другое число. Простое число — это целое число больше единицы, которое делится только на единицу и само на себя. Например, единственные делители 7 — это 1 и 7, поэтому 7 — простое число, а число 72 имеет делители, полученные из 2·9.0012 3 •3 2 подобно 2, 3, 4, 6, 8, 12, 24 … и самому 72, что делает 72 не простым числом. Обратите внимание, что единственными «простыми» делителями числа 72 являются 2 и 3, которые являются простыми числами.
Факторы по определению — это числа, которые умножаются, чтобы создать другое число. Простое число — это целое число больше единицы, которое делится только на единицу и само на себя. Например, единственные делители 7 — это 1 и 7, поэтому 7 — простое число, а число 72 имеет делители, полученные из 2·9.0012 3 •3 2 подобно 2, 3, 4, 6, 8, 12, 24 … и самому 72, что делает 72 не простым числом. Обратите внимание, что единственными «простыми» делителями числа 72 являются 2 и 3, которые являются простыми числами.
Пример 1 простой факторизации
Давайте найдем простую факторизацию числа 72.
Решение 1
Начните с наименьшего простого числа, которое делится на 72, в данном случае 2. Мы можем записать 72 как:
72 = 2 x 36
Теперь найдите наименьшее простое число, которое делится на 36. Снова мы можем использовать 2 и записать 36 как 2 х 18, чтобы дать.
72 = 2 x 2 x 18
18 также делится на 2 (18 = 2 x 9), поэтому мы имеем:
72 = 2 x 2 x 2 x 9
9 делится на 3 (9 = 3 x 3), поэтому у нас есть:
72 = 2 x 2 x 2 x 3 x 3
2, 2, 2, 3 и 3 — все простые числа, поэтому у нас есть ответ.
Короче говоря, решение можно записать так:
72 = 2 x 36
72 = 2 x 2 x 18
72 = 2 x 2 x 2 x 9
72 = 2 x 2 x 2 x 3 x 3
72 = 2 3 x 3 2 (экспоненциальная форма простой факторизации)
Раствор 2
Использование дерева факторов:
- Процедура:
- Найти 2 множителя числа;
- Посмотрите на 2 множителя и определите, не является ли хотя бы один из них простым;
- Если это не простой множитель это;
- Повторяйте этот процесс, пока все множители не станут простыми.
Посмотрите, как разложить число 72 на множители:
| 72 / \ 2 36 / \ 2 18 / \ 2 9 / \ 3 3 | 72 не простое —> разделить на 2 36 не простое —> разделить на 2 18 не простое —> разделить на 2 9 не простое —> разделить на 3 3 и 3 простые —> стоп |
Умножив левые числа и крайнее правое число последней строки (делителей), мы получим
72 = 2 x 2 x 2 x 3 x 3
72 = 2 3 x 3 2 (экспоненциальная форма простой факторизации)
Обратите внимание, что эти делители являются простыми множителями. Их также называют листьями факторного дерева.
Их также называют листьями факторного дерева.
Пример факторизации простых чисел 2
Посмотрите, как разложить число 588 на множители:
| 588 /\ 2 294 /\ 2 147 /\ 3 49 /\ 7 7 | 588 не простое —> разделить на 2 294 не простое —> разделить на 2 147 не простое —> разделить на 3 49 не простое —> разделить на 7 7 и 7 простые —> стоп |
Взяв левые числа и крайнее правое число последней строки (делители), умножив их, мы получим
588 = 2 x 2 x 3 x 7 x 7
588 = 2 2 x 3 x 7 2 (экспоненциальная форма простой факторизации)
Таблица факторизации простых чисел 1-1000
| n | Prime Factorization | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2 = | 2 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3 = | 3 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 4 = | 2•2 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 5 = | 5 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 6 = | 2•3 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 7 = | 7 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 8 = | 2•2•2 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 9 = | 3•3 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 10 = | 2 • 5 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
. •7 •7 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 15 = | 3•5 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 16 = | 2•2•2•2 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 17 = | 17 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 18 = | 2•3•3 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 19 = | 19 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 20 = | 2•2•5 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 21 = | 3•7 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 22 = | 2•11 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 23 = | 23 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 24 = | 2 • 2 • 2 • 3 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 25 = | 5 • 5 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 26 = | 2 • 13 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 27 = | 3 • 3 • 3 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 28 282012019 2 | 019 2019 22 | 019 22 | 019 22 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 019 2 =3 • 3. 2•2•7 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 29 = | 29 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 30 = | 2•3•5 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 31 = | 31 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 32 = | 2•2•2•2•2 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 33 = | 3•11 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 34 = | 2 • 17 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 35 = | 5 • 7 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 36 = | 2 • 2 • 3 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 37 = | 37 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 37 = | 37 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 37 = | 37 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 37 = | 37 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
. | 2•19 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 39 = | 3•13 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 40 = | 2 • 2 • 2 • 5 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 41 = | 41 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 42 = | 2 • 3 • 7 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 43 = | 43 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 43 = | 43 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 43 = | 43 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 43 = | 43 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 43 = | 43 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 43. | 2•2•11 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 45 = | 3•3•5 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 46 = | 2•23 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 47 = | 47 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 48 = | 2•2 •2•2•3 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 49 = | 7•7 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 50 = | 2 • 5 • 5 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 51 = | 3 • 17 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 52 = | 2 • 2 • 13 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 53 = | 53 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 53 = | 53 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| . | 2•3•3•3 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 55 = | 5•11 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 56 = | 2•2•2•7 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 57 = | 3•19 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 58 = | 2•29 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 59 = | 59 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 60 = | 2 • 2 • 3 • 5 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 61 = | . = = | 2 • 2 • 2 • 2 • 2 • 2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 65 = | 5 • 13 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 66 = | 2 • 3 • 11 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 67 = | 67 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 67 = | 67 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 67 = | 67 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 67. | 68 = | 2•2•17 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 69 = | 3•23 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 70 = | 2•5•7 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 71 = | 71 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 72 = | 2•2•2•3•3 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 73 = | 73 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 74 = | 2•37 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 75 = | 3•5•5 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 76 = | 2•2•19 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 77 = | 7•11 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 78 = | 2•3•13 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 79 = | 79 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 80 = | 2 • 2 • 2 • 2 • 5 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 81 = | 3 • 3 • 3 • 3 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 82 = | 2 • 41 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 83 = | 2 • 41 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 83 = | 201 | 201 | 2019 2 | 293012 | 293012 | 2 2.2 | 2 | 2 | 2 | 2 | 2. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 84 = | 2•2•3•7 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 85 = | 5•17 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 86 = | 2•43 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 87 = | 3•29 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 88 = | 2•2•2•11 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 89 = | 89 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 90 = | 2 • 3 • 3 • 5 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 91 = | 7 • 13 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 92 = | 2 • 2 • 23 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| = | . | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 94 = | 2 • 47 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 95 = | 5 • 19 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 96 = | 2 • 2 • 2 • 2 • 3 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2 • 2 • 2. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 98 = | 2•7•7 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 99 = | 3•3•11 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 100 = | 2•2•5•5 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 101 = | 101 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 102 = | 2•3•17 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 103 = | 103 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 104 = | 2 • 2 • 2 • 13 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 105 = | 3 • 5 • 7 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 106 = | 2 • 53 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 107 = | 107 | 202023||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 107 = | 107 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 107 = | 107 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
107. | 2•2•3•3•3 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 109 = | 109 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 110 = | 2 • 5 • 11 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 111 = | 3 • 37 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 112 = | 2 • 2 • 2 • 7 | 2020112019 | 2 • 2 • 2 • 7 | 2020= | 2 • 2 • 2 • 7 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| = | 2 = 2 • 2 • 7 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
0| 2). | 113 | | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 114 = | 2•3•19 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 115 = | 5•23 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 116 = | 2•2•29 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 117 = | 3• 3•13 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 118 = | 2•59 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 119 = | 7 • 17 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 120 = | 2 • 2 • 2 • 3 • 5 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 121 = | 11 • 11 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 121 = | 9 2920 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
121 = | 9 2920 2 | 121 = | 99 2923 | 121 = | 2923 | . | 123 = | 3•41 | 124 = | 2•2•31 | 125 = | 5•5•5 | 126 = | 2•3•3•7 | 127 = | 127 | 128 = | 2•2•2•2•2•2•2 | 129 = | 3•43 | 130 = | 2•5•13 | 131 = | 131 | 132 = | 2•2•3•11 | 133 = | 7 • 19 | 134 = | 2 • 67 | 135 = | 3 • 3 • 3 • 5 | 136 = | 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 5 | 136 = | 2 • 2 • 2 • 5 | 136 = | 2 • 2 • 5 | 136 = | 2 • 2 • 5 | . |  137 = | 137 | 138 = | 2•3•23 | 139 = | 139 | 140 = | 2•2•5•7 | 141 = | 3•47 | 142 = | 2 • 71 | 143 = | 11 • 13 | 144 = | 2 • 2 • 2 • 3 • 3 | 145 = | 5 • 2 | = | 5 • 2 | 5. | 2•73 | 147 = | 3•7•7 | 148 = | 2•2•37 | 149 = | 149 | 150 = | 2•3•5•5 | 151 = | 151 | 152 = | 2•2•2•19 | 153 = | 3•3•17 | 154 = | 2•7•11 | 155 = | 5•31 | 156 = | 2•2•3•13 | 157 = | 157 | 158 = | 2•79 | 159 = | 3•53 | 160 = | 2•2•2•2•2•5 | 161 = | 7•23 | 162 = | 2•3•3•3•3 | 163 = | 163 | 164 = | 2•2•41 | 165 = | 3•5•11 | 166 = | 2•83 | 167 = | 167 | 168 = | 2 • 2) | 171 = | 3 • 3 • 19 | 172 = | 2 • 2 • 43 | 173 = | 173 | 174 = | 174 = | 2 • 3 | 174 = | 2 • 3 | 174 = | 2 • 3 2 | 174 = | 2 • 3 | 174 = | 2. |  3 3 174 = | 174. = | 5•5•7 | 176 = | 2•2•2•2•11 | 177 = | 3•59 | 178 = | 2•89 | 179 = | 179 | 180 = | 2•2•3•3•5 | 181 = | 181 | 182 = | 2 • 7 • 13 | 183 = | 3 • 61 | 184 = | 2 • 2. 2900 2900 2900 2900 2900 2900 2900 2900 2900 2900 2900 2900 2900 2900 2 2 | 1 | 1. 2 | 2900 2900 2 2 | 184 = | 2 | . 185 = | 5•37 | 186 = | 2 • 3 • 31 | 187 = | 11 • 17 | 188 = | 2 • 2 • 47 | 189 = | 3 • 3 • 7 | 2020202018 3 • 3 • 7 | 202020202018 3 • 3 • 7 | 2020202018 3 • 3 • 700202020202018 | 3. |  190 = 190 = 2•5•19 | 191 = | 191 | 192 = | 2•2•2•2•2•2•3 | 193 = | 193 | 194 = | 2•97 | 195 = | 3•5•13 | 196 = | 2•2•7•7 | 197 = | 197 | 198 = | 2•3•3•11 | 199 = | 199 | 200 = | 2•2•2•5•5 | 201 = | 3•67 | 202 = | 2•101 | 203 = | 7•29 | 204 = | 2•2•3•17 | 205 = | 5 • 41 | 206 = | 2 • 103 | 207 = | 3 • 3 • 23 | 208 = | 2 • 2 • 2 • • 13 | 201919 2 • 2 • 2 • 13 | 2 • 2 • 2 • 13 | = | 2 • 2 • 2 • 13 | = | 2 • 2 • 2 • 13 | 208 = | 2 • 2 • 2 • 13 | 208 = | 2. |  = = 11 • 19 | 210 = | 2 • 3 • 5 • 7 | 211 = | 211 | 212 = | 2 • 2 • 53 | 2 • 53 | 210020 | 212 = | 210020 | 212 = | 2 210020 | 212. | 3•71 | 214 = | 2•107 | 215 = | 5•43 | 216 = | 2•2•2•3•3•3 | 217 = | 7•31 | 218 = | 2•109 | 219 = | 3•73 | 220 = | 2•2•5•11 | 221 = | 13•17 | 222 = | 2•3•37 | 223 = | 223 | 224 = | 2•2•2•2•2•7 | 225 = | 3•3•5•5 | 226 = | 2•113 | 227 = | 227 | 228 = | 2•2•3•19 | 229 = | 229 | 230 = | 2 • 5 • 23 | 231 = | 3 • 7 • 110020 | 232 = | 3 • 7 • 210020 | 232 = | 3 • | 232 = | . |  233 = | 233 | 234 = | 2 • 3 • 3 • 13 | 235 = | 5 • 47 | 236 = | 2 • 2 • 59 | 237 = | 3 • 79 | 2020 237 = | 3 • 79 | 202020 237 = | 3 • 7 | 20202020 237 = | 3 | 237 = | 3 | 237. | 2•7•17 | 239 = | 239 | 240 = | 2•2•2•2•3•5 | 241 = | 241 | 242 = | 2•11•11 | 243 = | 3•3•3•3•3 | 244 = | 2 • 2 • 61 | 245 = | 5 • 7 • 7 | 246 = | 2 • 3 • 41 | 247 = 9 2918 = 9 2918 = 9 2918 = 9 2 | 2918 = 9 29 2 | . | 248 = | 2 • 2 • 2 • 31 | 249 = | 3 • 83 | 250 = | 2 • 5 • 5 | |
| n | Простое число Факторизация | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 251 = | 251 | ||||||||||||||
| 252 = | 2•2•3•3•7 | ||||||||||||||
| 253 = | 11•23 | ||||||||||||||
| 254 = | 2•127 | ||||||||||||||
| 255 = | 3 • 5 • 17 | ||||||||||||||
| 256 = | 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 | ||||||||||||||
| 257 = | 257 | ||||||||||||||
| 258 = | 2 • 3 • 43 | 202020202020202020202020202020202020202||||||||||||||
| 259 = | 7•37 | ||||||||||||||
| 260 = | 2•2•5•13 | ||||||||||||||
| 261 = | 3•3•29 | ||||||||||||||
| 262 = | 2•131 | ||||||||||||||
| 263 = | 263 | ||||||||||||||
| 264 = | 2•2•2•3•11 | ||||||||||||||
| 265 = | 5 • 53 | ||||||||||||||
| 266 = | 2 • 7 • 19 | ||||||||||||||
| 267 = | 3 • 89 | ||||||||||||||
| 268 = | 3 • 89 | ||||||||||||||
| 268 = | 2019 21 | 201 | 201 | 2 | 201 | 2019 2 | 201 | 2019 2 | 1201 | 2 | 12019 2672020202019 261 | 2019 2 | 19 26720202019 2 2 267 = 3. | 269 = | 269 |
| 270 = | 2 • 3 • 3 • 3 • 5 | ||||||||||||||
| 271 = | 271 | ||||||||||||||
| 272 = | 2 • 2 • 2 • 2 • 17 | ||||||||||||||
| 273 = | 3 • 13 | ||||||||||||||
| 273 = | 3 • | ||||||||||||||
| 274 = | 2•137 | ||||||||||||||
| 275 = | 5•5•11 | ||||||||||||||
| 276 = | 2•2•3•23 | ||||||||||||||
| 277 = | 277 | ||||||||||||||
| 278 = | 2•139 | ||||||||||||||
| 279 = | 3•3•31 | ||||||||||||||
| 280 = | 2•2•2•5•7 | ||||||||||||||
| 281 = | 281 | ||||||||||||||
| 282 = | 2•3•47 | ||||||||||||||
| 283 = | 283 | ||||||||||||||
| 284 = | 2•2•71 | ||||||||||||||
| 285 = | 3•5•19 | ||||||||||||||
| 286 = | 2•11•13 | ||||||||||||||
| 287 = | 7•41 | ||||||||||||||
| 288 = | 2•2•2•2•2•3•3 | ||||||||||||||
| 289 = | 17•17 | ||||||||||||||
| 290 = | 2•5•29 | ||||||||||||||
| 291 = | 3•97 | ||||||||||||||
| 292 = | 2•2•73 | ||||||||||||||
| 293 = | 293 | ||||||||||||||
| 294 = | 2 • 3 • 7 • 7 | ||||||||||||||
| 295 = | 5 • 59 | ||||||||||||||
| 296 = | 2. •3•3•11 •3•3•11 | ||||||||||||||
| 298 = | 2•149 | ||||||||||||||
| 299 = | 13•23 | ||||||||||||||
| 300 = | 2•2•3•5•5 | ||||||||||||||
| 301 = | 7•43 | ||||||||||||||
| 302 = | 2•151 | ||||||||||||||
| 303 = | 3•101 | ||||||||||||||
| 304 = | 2•2•2•2•19 | ||||||||||||||
| 305 = | 5•61 | ||||||||||||||
| 306 = | 2•3•3• 17 | ||||||||||||||
| 307 = | 307 | ||||||||||||||
| 308 = | 2•2•7•11 | ||||||||||||||
| 309 = | 3•103 | ||||||||||||||
| 310 = | 2•5•31 | ||||||||||||||
| 311 = | 311 | ||||||||||||||
| 312 = | 2•2•2•3•13 | ||||||||||||||
| 313 = | 313 | ||||||||||||||
| 314 = | 2•157 | ||||||||||||||
| 315 = | 3•3•5•7 | ||||||||||||||
| 316 = | 2•2•79 | ||||||||||||||
| 317 = | 317 | ||||||||||||||
| 318 = | 2 • 3 • 53 | ||||||||||||||
| 319 = | 11 • 29 | ||||||||||||||
| 320 = | 2 • 2 • 2 • 2 • 2 • 5 | ||||||||||||||
| 321 = | 3 | ||||||||||||||
| 321 = | 3 • 107 • 107 • 107 • 107 • 107 • 107 • 107 • 107 • 107 • 107 • 107 • 107 • 107 • 107 • 107 • 107 • 107 • 107 • 107 • 107 • 107. 107. 100023 107. 100023 | ||||||||||||||
| 321 = | 3 | ||||||||||||||
| 321. | |||||||||||||||
| 322 = | 2•7•23 | ||||||||||||||
| 323 = | 17•19 | ||||||||||||||
| 324 = | 2•2•3•3•3•3 | ||||||||||||||
| 325 = | 5•5•13 | ||||||||||||||
| 326 = | 2•163 | ||||||||||||||
| 327 = | 3•109 | ||||||||||||||
| 328 = | 2•2•2•41 | ||||||||||||||
| 329 = | 7•47 | ||||||||||||||
| 330 = | 2•3•5•11 | ||||||||||||||
| 331 = | 331 | ||||||||||||||
| 332 = | 2•2•83 | ||||||||||||||
| 333 = | 3•3•37 | ||||||||||||||
| 334 = | 2•167 | ||||||||||||||
| 335 = | 5•67 | ||||||||||||||
| 336 = | 2•2•2•2•3•7 | ||||||||||||||
| 337 = | 337 | ||||||||||||||
| 338 = | 2•13•13 | ||||||||||||||
| 339 = | 3•113 | ||||||||||||||
| 340 = | 2•2•5•17 | ||||||||||||||
| 341 = | 11 • 31 | ||||||||||||||
| 342 = | 2 • 3 • 3 • 19 | ||||||||||||||
| 343 = | 7 • 7 • 7 | ||||||||||||||
| 344 = | 2 • 2 • 2 • 2 • 43 | ||||||||||||||
| 344 = | 2 • 2 • 2 • 43 | ||||||||||||||
| 344 = | 2 • 2 • 2 • 43 | ||||||||||||||
| 344 = | 2 • 40023 | ||||||||||||||
| 344 = | 2 • 40023 | ||||||||||||||
344. | |||||||||||||||
| 345 = | 3•5•23 | ||||||||||||||
| 346 = | 2•173 | ||||||||||||||
| 347 = | 347 | ||||||||||||||
| 348 = | 2•2•3•29 | ||||||||||||||
| 349 = | 349 | ||||||||||||||
| 350 = | 2•5•5• 7 | ||||||||||||||
| 351 = | 3•3•3•13 | ||||||||||||||
| 352 = | 2•2•2•2•2•11 | ||||||||||||||
| 353 = | 353 | ||||||||||||||
| 354 = | 2•3•59 | ||||||||||||||
| 355 = | 5•71 | ||||||||||||||
| 356 = | 2•2•89 | ||||||||||||||
| 357 = | 3•7•17 | ||||||||||||||
| 358 = | 2•179 | ||||||||||||||
| 359 = | 359 | ||||||||||||||
| 360 = | 2 • 2 • 2 • 3 • 3 • 5 | ||||||||||||||
| 361 = | 19 • 19 | ||||||||||||||
| 362 = | 2 • 181 | ||||||||||||||
| 363 = | 3 • 11002020920 | ||||||||||||||
| 363 = | 3 • 11002020 | ||||||||||||||
| 363 = | 3 • 110020 | ||||||||||||||
| 363 = | 3 • 110020 | ||||||||||||||
| 363 = | 3 • 110020 | ||||||||||||||
| 363 = | 3 • | 364 = | 2•2•7•13 | ||||||||||||
| 365 = | 5•73 | ||||||||||||||
| 366 = | 2•3•61 | ||||||||||||||
| 367 = | 367 | ||||||||||||||
| 368 = | 2•2•2•2•23 | ||||||||||||||
| 369 = | 3 • 3 • 41 | ||||||||||||||
| 370 = | 2 • 5 • 37 | ||||||||||||||
| 371 = | 7 • 53 | ||||||||||||||
| 372 = | 2 • 2 • 310020 | . | 373 | ||||||||||||
| 374 = | 2•11•17 | ||||||||||||||
| 375 = | 3 • 5 • 5 • 5 | ||||||||||||||
| 376 = | 2 • 2 • 2 • 47 | ||||||||||||||
| 377 = | 13 • 29 | ||||||||||||||
| 378 = | 13 • 2 | ||||||||||||||
| 378 = | • | 1 | |||||||||||||
| 378 = | • 2 | ||||||||||||||
| 378 = | . 3 • 3 • 7 | ||||||||||||||
| 379 = | 379 | ||||||||||||||
| 380 = | 2 • 2 • 5 • 1 | ||||||||||||||
| 381 = | 3 • 127 | ||||||||||||||
| 381 = | . 191 | ||||||||||||||
| 383 = | 383 | ||||||||||||||
| 384 = | 2•2•2•2•2•2•2•3 | ||||||||||||||
| 385 = | 5•7•11 | ||||||||||||||
| 386 = | 2•193 | ||||||||||||||
| 387 = | 3•3•43 | ||||||||||||||
| 388 = | 2•2•97 | ||||||||||||||
| 389 = | 389 | ||||||||||||||
| 390 = | 2•3•5•13 | ||||||||||||||
| 391 = | 17•23 | ||||||||||||||
| 392 = | 2•2•2•7 •7 | ||||||||||||||
| 393 = | 3•131 | ||||||||||||||
| 394 = | 2•197 | ||||||||||||||
| 395 = | 5•79 | ||||||||||||||
| 396 = | 2•2•3•3•11 | ||||||||||||||
| 397 = | 397 | ||||||||||||||
| 398 = | 2 • 199 | ||||||||||||||
| 399 = | 3 • 7 • 19 | ||||||||||||||
| 400 = | 2 • 2 • 2 • 5 • 5 | ||||||||||||||
| 401 = | 401020202023 | ||||||||||||||
| 401 = | 40102020202018 | ||||||||||||||
| 401 = | 40102020202018 | ||||||||||||||
| 401 = | 40102020 2 | ||||||||||||||
| 401 = | 401020202023 | ||||||||||||||
| 401 = | 402020 | ||||||||||||||
401. 402 = 402 = | 2•3•67 | ||||||||||||||
| 403 = | 13•31 | ||||||||||||||
| 404 = | 2•2•101 | ||||||||||||||
| 405 = | 3•3•3•3•5 | ||||||||||||||
| 406 = | 2•7•29 | ||||||||||||||
| 407 = | 11 • 37 | ||||||||||||||
| 408 = | 2 • 2 • 2 • 3 • 17 | ||||||||||||||
| 409 = | 409 | ||||||||||||||
| 410 = | 2 • 5 • 410020 | ||||||||||||||
| 410 = | 2 • 510020 | | 2 • 510020 | 410 = | 2 • 510020 | 410 = | 2 • 410020 | 410 = | 2 • 410020 | 410 = | 2. | 3•137 | 412 = | 2•2•103 | 413 = | 7•59 | 414 = | 2•3•3•23 | 415 = | 5•83 | 416 = | 2•2•2•2• 2 • 13 | 417 = | 3 • 139 | 418 = | 2. |  5•7 5•7 421 = | 421 | 422 = | 2 • 211 | 423 = | 3 • 3 • 47 | 424 = | 2 • 2 • 2 • 53 | 425 = | 5 • 17 | 5. • 17 | 53 | 425 = | 53 | 425 = | . | 2 • 3 • 71 | 427 = | 7 • 61 | 428 = | 2 • 2 • 107 | 429 = | 3 • 13 | 429 = | 3 • 13 | 429. | 2•5•43 | 431 = | 431 | 432 = | 2 • 2 • 2 • 2 • 3 • 3 • 3 | 433 = | 433 | 434 = | 2 • 7 • 31 | 435 = | = 01201201201201201201 | 201 | 201 | 201 | 21.1 | 435 = | . 5•29 | 436 = | 2•2•109 | 437 = | 19•23 | 438 = | 2•3•73 | 439 = | 439 | 440 = | 2•2•2•5•11 | 441 = | 3 • 3 • 7 • 7 | 442 = | 2 • 13 • 17 | 443 = | 443 | 444 = | 2 • 2 • 37 | 444 = | . |  = = 5 • 89 | 446 = | 2 • 223 | 447 = | 3 • 149 | 448 = | 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2. | 449 = | 449 | 450 = | 2•3•3•5•5 | 451 = | 11•41 | 452 = | 2•2•113 | 453 = | 3•151 | 454 = | 2•227 | 455 = | 5•7•13 | 456 = | 2•2•2•3•19 | 457 = | 457 | 458 = | 2•229 | 459 = | 3•3•3•17 | 460 = | 2 • 2 • 5 • 23 | 461 = | 461 | 462 = | 2 • 3 • 7 • 11 | 463 = | 463 | 463 = | 463 | 463 = | 463 | 463 = | 463 | 463. |  2•2•2•2•29 2•2•2•2•29 465 = | 3•5•31 | 466 = | 2•233 | 467 = | 467 | 468 = | 2•2•3•3•13 | 469 = | 7•67 | 470 = | 2•5•47 | 471 = | 3•157 | 472 = | 2•2•2•59 | 473 = | 11•43 | 474 = | 2•3•79 | 475 = | 5•5•19 | 476 = | 2•2•7•17 | 477 = | 3• 3•53 | 478 = | 2•239 | 479 = | 479 | 480 = | 2•2•2•2•2•3•5 | 481 = | 13•37 | 482 = | 2•241 | 483 = | 3 • 7 • 23 | 484 = | 2 • 2 • 11 • 11 | 485 = | 5 • 97 | 486 = | 2 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3. |  •3•3 •3•3 487 = | 487 | 488 = | 2•2•2•61 | 489 = | 3•163 | 490 = | 2•5•7•7 | 491 = | 491 | 492 = | 2•2•3•41 | 493 = | 17•29 | 494 = | 2•13•19 | 495 = | 3•3•5•11 | 496 = | 2•2 •2•2•31 | 497 = | 7•71 | 498 = | 2 • 3 • 83 | 499 = | 499 | 500 = | 2 • 2 • 5 • 5 • 5 | |
| n | Prime Factorization | |||||
|---|---|---|---|---|---|---|
| 501 = | 3•167 | |||||
| 502 = | 2•251 | |||||
| 503 = | 503 | |||||
| 504 = | 2 •2•2•3•3•7 | |||||
| 505 = | 5•101 | |||||
| 506 = | 2•11•23 | |||||
| 507 = | 3•13•13 | |||||
| 508 = | 2•2•127 | |||||
| 509 = | 509 | |||||
| 510 = | 2 • 3 • 5 • 17 | |||||
| 511 = | 7 • 73 | |||||
| 512 = | 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 | |||||
| 513 = | 3•3•3•19 | |||||
| 514 = | 2•257 | |||||
| 515 = | 5•103 | |||||
| 516 = | 2•2•3•43 | |||||
| 517 = | 11•47 | |||||
| 518 = | 2•7•37 | |||||
| 519 = | 3 • 173 | |||||
| 520 = | 2. | |||||
| 523 = | 523 | |||||
| 524 = | 2•2•131 | |||||
| 525 = | 3•5•5•7 | |||||
| 526 = | 2•263 | |||||
| 527 = | 17•31 | |||||
| 528 = | 2•2•2 •2•3•11 | |||||
| 529 = | 23•23 | |||||
| 530 = | 2•5•53 | |||||
| 531 = | 3•3•59 | |||||
| 532 = | 2•2•7•19 | |||||
| 533 = | 13•41 | |||||
| 534 = | 2•3•89 | |||||
| 535 = | 5•107 | |||||
| 536 = | 2•2•2•67 | |||||
| 537 = | 3•179 | |||||
| 538 = | 2 • 269 | |||||
| 539 = | 7 • 7 • 11 | |||||
| 540 = | 2 • 2 • 3 • 3 • 5 | |||||
| 541 = 0 0 0 0 0 0 0 0 | ||||||
| 542 = | 2•271 | |||||
| 543 = | 3•181 | |||||
| 544 = | 2 • 2 • 2 • 2 • 2 • 17 | |||||
| 545 = | 5 • 109 | |||||
| 546 = | 2 • 3 • 7 • 13 | |||||
| 2 • 3 • 13 | 18546 = | 2 • 3 • 13 | ||||
| 546 = | 2. = = | 547 | ||||
| 548 = | 2•2•137 | |||||
| 549 = | 3•3•61 | |||||
| 550 = | 2•5•5•11 | |||||
| 551 = | 19•29 | |||||
| 552 = | 2•2•2•3•23 | |||||
| 553 = | 7•79 | |||||
| 554 = | 2•277 | |||||
| 555 = | 3•5•37 | |||||
| 556 = | 2•2•139 | |||||
| 557 = | 557 | |||||
| 558 = | 2 • 3 • 3) | |||||
| 561 = | 3•11•17 | |||||
| 562 = | 2•281 | |||||
| 563 = | 563 | |||||
| 564 = | 2•2•3•47 | |||||
| 565 = | 5•113 | |||||
| 566 = | 2•283 | |||||
| 567 = | 3•3•3•3•7 | |||||
| 568 = | 2•2•2•71 | |||||
| 569 = | 569 | |||||
| 570 = | 2 •3•5•19 | |||||
| 571 = | 571 | |||||
| 572 = | 2 • 2 • 11 • 13 | |||||
| 573 = | 3 • 191 | |||||
| 574 = | 2 • 7 • 41 | |||||
| 575 = | = | 201223|||||
| 575 = | = | 20201230123018 == 30123012019201 | 30120 22019201 9 2 | 201920 2 | 2019 2 | 012019.2 • |
| 576 = | 2•2•2•2•2•2•3•3 | |||||
| 577 = | 577 | |||||
| 578 = | 2•17•17 | |||||
| 579 = | 3•193 | |||||
| 580 = | 2•2•5•29 | |||||
| 581 = | 7•83 | |||||
| 582 = | 2•3•97 | |||||
| 583 = | 11•53 | |||||
| 584 = | 2•2•2•73 | |||||
| 585 = | 3 • 3 • 5 • 13 | |||||
| 586 = | 2. 589 = | 19•31 | ||||
| 590 = | 2•5•59 | |||||
| 591 = | 3 • 197 | |||||
| 592 = | 2 • 2 • 2 • 2 • 37 | |||||
| 593 = | 593 | |||||
| 593 = | 593 | |||||
| 594 594 394 394 394 594 594 594 594 594 594 594 594 594 594 594 594 594 594 = | 19. 39419 594 = = 2||||||
| 593 = | 593 | |||||
| 593 = | . 3•11 3•11 | |||||
| 595 = | 5•7•17 | |||||
| 596 = | 2•2•149 | |||||
| 597 = | 3•199 | |||||
| 598 = | 2• 13•23 | |||||
| 599 = | 599 | |||||
| 600 = | 2 • 2 • 2 • 3 • 5 • 5 | |||||
| 601 = | 601 | |||||
| 602 = | 2 • 7 • 43 | |||||
| 603 = | 3 • 67 | |||||
| 603 = | 3 • 67 | 603 = | 3 • 67 | |||
| 603 = | 3 • 67 | |||||
| . | ||||||
| 604 = | 2•2•151 | |||||
| 605 = | 5•11•11 | |||||
| 606 = | 2•3•101 | |||||
| 607 = | 607 | |||||
| 608 = | 2•2•2•2•2•19 | |||||
| 609 = | 3•7•29 | |||||
| 610 = | 2•5•61 | |||||
| 611 = | 13•47 | |||||
| 612 = | 2•2•3•3•17 | |||||
| 613 = | 613 | |||||
| 614 = | 2•307 | |||||
| 615 = | 3•5•41 | |||||
| 616 = | 2•2•2•7•11 | |||||
| 617 = | 617 | |||||
| 618 = | 2•3•103 | |||||
| 619 = | 619 | |||||
| 620 = | 2•2•5•31 | |||||
| 621 = | 3•3•3•23 | |||||
| 622 = | 2•311 | |||||
| 623 = | 7•89 | |||||
| 624 = | 2•2•2•2•3•13 | |||||
| 625 = | 5•5•5•5 | |||||
| 626 = | 2•313 | |||||
| 627 = | 3•11•19 | |||||
| 628 = | 2•2•157 | |||||
| 629 = | 17•37 | |||||
| 630 = | 2•3•3•5•7 | |||||
| 631 = | 631 | |||||
| 632 = | 2•2•2•79 | |||||
| 633 = | 3•211 | |||||
| 634 = | 2•317 | |||||
| 635 = | 5•127 | |||||
| 636 = | 2 •2•3•53 | |||||
| 637 = | 7•7•13 | |||||
| 638 = | 2 • 11 • 29 | |||||
| 639 = | 3 • 3 • 71 | |||||
| 640 = | 2 • 2 • 2 • 2 • 2 • 2 • 5 | |||||
| 641 = | 641 | |||||
| 642 = | 2 • 3 • 107 | |||||
| 643 = | 643 | |||||
| 644 = | 2. 29002. 2900 2900 2900 2900 2900 2900 2900 2900 2900 2 29002. 29002. 2 29002. 2900 2900 2900 2900 2900 2900 2900 2900 2900 2 29002. 29002. 2 | |||||
| 644. | 3•5•43 | |||||
| 646 = | 2•17•19 | |||||
| 647 = | 647 | |||||
| 648 = | 2•2•2•3•3•3•3 | |||||
| 649 = | 11•59 | |||||
| 650 = | 2•5•5•13 | |||||
| 651 = | 3•7•31 | |||||
| 652 = | 2•2•163 | |||||
| 653 = | 653 | |||||
| 654 = | 2•3•109 | |||||
| 655 = | 5•131 | |||||
| 656 = | 2•2•2•2•41 | |||||
| 657 = | 3•3•73 | |||||
| 658 = | 2•7•47 | |||||
| 659 = | 659 | |||||
| 660 = | 2•2•3•5 •11 | |||||
| 661 = | 661 | |||||
| 662 = | 2•331 | |||||
| 663 = | 3•13•17 | |||||
| 664 = | 2•2•2•83 | |||||
| 665 = | 5•7•19 | |||||
| 666 = | 2•3•3•37 | |||||
| 667 = | 23•29 | |||||
| 668 = | 2•2•167 | |||||
| 669 = | 3•223 | |||||
| 670 = | 2•5•67 | |||||
| 671 = | 11•61 | |||||
| 672 = | 2•2•2•2•2•3•7 | |||||
| 673 = | 673 | |||||
| 674 = | 2•337 | |||||
| 675 = | 3•3•3•5•5 | |||||
| 676 = | 2 • 2 • 13 • 13 | |||||
| 677 = | 677 | |||||
| 678 = | 2. | |||||
| 680 = | 2 • 2 • 2 • 5 • 17 | |||||
| 681 = | 3 • 227 | |||||
| 682 = | 2 • 11. 31920 | |||||
| 683 = | ||||||
| 684 = | 2•2•3•3•19 | |||||
| 685 = | 5 • 137 | |||||
| 686 = | 2 • 7 • 7 • 7 | |||||
| 687 = | 3 • 229 | |||||
| 688 = | 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 229 | |||||
| 688 = | 2 229 | |||||
| . 43 | ||||||
| 689 = | 13•53 | |||||
| 690 = | 2•3•5•23 | |||||
| 691 = | 691 | |||||
| 692 = | 2•2•173 | |||||
| 693 = | 3•3•7•11 | |||||
| 694 = | 2 • 347 | |||||
| 695 = | 5 • 139 | |||||
| 696 = | 2 • 2 • 2 • 3 • 29 | |||||
| 697 = | 17. • 410020 • 410020 | |||||
| . 2•349 | ||||||
| 699 = | 3•233 | |||||
| 700 = | 2•2•5•5•7 | |||||
| 701 = | 701 | |||||
| 702 = | 2• 3•3•3•13 | |||||
| 703 = | 19•37 | |||||
| 704 = | 2•2•2•2•2•2•11 | |||||
| 705 = | 3•5•47 | |||||
| 706 = | 2•353 | |||||
| 707 = | 7•101 | |||||
| 708 = | 2•2•3•59 | |||||
| 709 = | 709 | |||||
| 710 = | 2•5•71 | |||||
| 711 = | 3 •3•79 | |||||
| 712 = | 2•2•2•89 | |||||
| 713 = | 23•31 | |||||
| 714 = | 2•3•7•17 | |||||
| 715 = | 5•11•13 | |||||
| 716 = | 2•2•179 | |||||
| 717 = | 3•239 | |||||
| 718 = | 2•359 | |||||
| 719 = | 719 | |||||
| 720 = | 2•2•2•2•3•3•5 | |||||
| 721 = | 7•103 | |||||
| 722 = | 2•19•19 | |||||
| 723 = | 3•241 | |||||
| 724 = | 2•2•181 | |||||
| 725 = | 5•5•29 | |||||
| 726 = | 2•3•11 • 11 | |||||
| 727 = | 727 | |||||
| 728 = | 2 • 2 • 7 • 13 | |||||
| 729 = | 3 • 3 • 3 • 3 | 202018|||||
3. | 730 = | 2•5•73 | ||||
| 731 = | 17•43 | |||||
| 732 = | 2•2•3•61 | |||||
| 733 = | 733 | |||||
| 734 = | 2•367 | |||||
| 735 = | 3•5•7•7 | |||||
| 736 = | 2 • 2 • 2 • 2 • 2 • 23 | |||||
| 737 = | 11 • 67 | |||||
| 738 = | 2 • 3 • 3 • 41 | |||||
| . 739 | ||||||
| 740 = | 2•2•5•37 | |||||
| 741 = | 3•13•19 | |||||
| 742 = | 2•7•53 | |||||
| 743 = | 743 | |||||
| 744 = | 2•2•2•3•31 | |||||
| 745 = | 5 • 149 | |||||
| 746 = | 2 • 373 | |||||
| 747 = | 3 • 3 • 83 | |||||
| 748 = | 2 • | |||||
| 748 = | 2 • | |||||
| 748 = | 2 • | |||||
| 748 = | 2 • | |||||
| 748 = | 2 • | |||||
| 748 = | 2 • | |||||
| 748 = | 2 • | |||||
| 748 = | . = = | 7•107 | ||||
| 750 = | 2•3•5•5•5 |
| N | PRIME ФУКТРИЗАЦИЯ | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 751 = | 751 | ||||||||||
| 752 = | 2 • 2 • 2 • • 47 | 202020202020192020 | 2 • 2 • 2 • 47 | 202020202020192 • 2 • 2 • 47 | 20202020192 • 2 • 2 • 47 | 2020192. | 754 = | 2 • 13 • 29 | |||
| 755 = | 5 • 151 | ||||||||||
| 756 = | 2 • 2 • 3 • 3 • 3 • 70020 | ||||||||||
| 757 = 0 0 0 0 0 0 0 0 | |||||||||||
| 758 = | 2•379 | ||||||||||
| 759 = | 3•11•23 | ||||||||||
| 760 = | 2•2•2•5•19 | ||||||||||
| 761 = | 761 | ||||||||||
| 762 = | 2•3•127 | ||||||||||
| 763 = | 7•109 | ||||||||||
| 764 = | 2•2•191 | ||||||||||
| 765 = | 3•3•5•17 | ||||||||||
| 766 = | 2•383 | ||||||||||
| 767 = | 13•59 | ||||||||||
| 768 = | 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 3 | ||||||||||
| 769 = | 769 | ||||||||||
| 770 = | 2 • 5 • 7 • | ||||||||||
| 2 • 5 • 7 • | |||||||||||
2 • 5 • 7. | |||||||||||
| 2 • 5 • 700202023 | 970 = | 2 • 5 • 7002018 | 770 = | 2 • | 771 = | 3•257 | |||||
| 772 = | 2•2•193 | ||||||||||
| 773 = | 773 | ||||||||||
| 774 = | 2•3•3•43 | ||||||||||
| 775 = | 5•5•31 | ||||||||||
| 776 = | 2•2•2•97 | ||||||||||
| 777 = | 3•7•37 | ||||||||||
| 778 = | 2•389 | ||||||||||
| 779 = | 19•41 | ||||||||||
| 780 = | 2•2•3•5•13 | ||||||||||
| 781 = | 11 • 71 | ||||||||||
| 782 = | 2 • 17 • 23 | ||||||||||
| 783 = | 3 • 3 • 3 • 29 | ||||||||||
| 784 = | 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2. •7•7 •7•7 | ||||||||||
| 785 = | 5•157 | ||||||||||
| 786 = | 2•3•131 | ||||||||||
| 787 = | 787 | ||||||||||
| 788 = | 2•2•197 | ||||||||||
| 789 = | 3•263 | ||||||||||
| 790 = | 2•5•79 | ||||||||||
| 791 = | 7•113 | ||||||||||
| 792 = | 2•2•2•3•3•11 | ||||||||||
| 793 = | 13•61 | ||||||||||
| 794 = | 2•397 | ||||||||||
| 795 = | 3•5•53 | ||||||||||
| 796 = | 2•2•199 | ||||||||||
| 797 = | 797 | ||||||||||
| 798 = | 2•3•7•19 | ||||||||||
| 799 = | 17•47 | ||||||||||
| 800 = | 2 • 2 • 2 • 2 • 2 • 5 • 5 | ||||||||||
| 801 = | 3 • 3 • 89 | ||||||||||
| 802 = | 2 • 401 | ||||||||||
| 803 = | 2 | ||||||||||
| 803 = | |||||||||||
. | |||||||||||
| 804 = | 2•2•3•67 | ||||||||||
| 805 = | 5 • 7 • 23 | ||||||||||
| 806 = | 2 • 13 • 31 | ||||||||||
| 807 = | 3 • 269 | ||||||||||
| 808 = | 2 • 2 • 2 • 101 | ||||||||||
| = 2 • 2 • 2 • 101 | |||||||||||
| = 2 • 2 • 2 • 101 | |||||||||||
| 2 • 2. | 809 | ||||||||||
| 810 = | 2 • 3 • 3 • 3 • 3 • 5 | ||||||||||
| 811 = | |||||||||||
| 812 = | 21 • 70023 | ||||||||||
| 2 • 70023 | |||||||||||
| 21 • 70023 | |||||||||||
| 21123 | |||||||||||
| 2123 | |||||||||||
| 2112 813 = | 3•271 | ||||||||||
| 814 = | 2•11•37 | ||||||||||
| 815 = | 5•163 | ||||||||||
| 816 = | 2•2•2•2•3•17 | ||||||||||
| 817 = | 19•43 | ||||||||||
| 818 = | 2•409 | ||||||||||
| 819 = | 3•3•7•13 | ||||||||||
| 820 = | 2•2•5•41 | ||||||||||
| 821 = | 821 | ||||||||||
| 822 = | 2•3 •137 | ||||||||||
| 823 = | 823 | ||||||||||
| 824 = | 2 • 2 • 2 • 103 | ||||||||||
| 825 = | 3 • 5 • 5 • 11 | ||||||||||
| 826 = | 2 • 7 • 59 | ||||||||||
| 827 = | 82777 | ||||||||||
| 827 = | |||||||||||
827. = = | 2•2•3•3•23 | ||||||||||
| 829 = | 829 | ||||||||||
| 830 = | 2•5•83 | ||||||||||
| 831 = | 3•277 | ||||||||||
| 832 = | 2•2•2•2•2•2•13 | ||||||||||
| 833 = | 7•7•17 | ||||||||||
| 834 = | 2 • 3 • 139 | ||||||||||
| 835 = | 5 • 167 | ||||||||||
| 836 = | 2 • 2 • 11 • 1 | ||||||||||
| 2 • 2 • 11.112020 | |||||||||||
| 8377777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777. | 2 | 2 | . 3•31|||||||||
| 838 = | 2•419 | ||||||||||
| 839 = | 839 | ||||||||||
| 840 = | 2•2•2•3•5•7 | ||||||||||
| 841 = | 29•29 | ||||||||||
| 842 = | 2•421 | ||||||||||
| 843 = | 3 • 281 | ||||||||||
| 844 = | 2 • 2 • 211 | ||||||||||
| 845 = | 5 • 13 • 13 | ||||||||||
| 846 = | 2 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 847 = | 7 • 11 • 11 | |||||||||
| 848 = | 2 • 2 • 2 • 2 • 53 | ||||||||||
| 849 = | 3 • 283 | ||||||||||
| 850 = | 2 283 | ||||||||||
| 850 = | 219 2. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. •17 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. •17 | ||||||||||
| 851 = | 23•37 | ||||||||||
| 852 = | 2•2•3•71 | ||||||||||
| 853 = | 853 | ||||||||||
| 854 = | 2•7•61 | ||||||||||
| 855 = | 3•3•5•19 | ||||||||||
| 856 = | 2•2•2 • 107 | ||||||||||
| 857 = | 857 | ||||||||||
| 858 = | 2. | ||||||||||
| 861 = | 3•7•41 | ||||||||||
| 862 = | 2•431 | ||||||||||
| 863 = | 863 | ||||||||||
| 864 = | 2•2•2•2•2•3•3•3 | ||||||||||
| 865 = | 5•173 | ||||||||||
| 866 = | 2•433 | ||||||||||
| 867 = | 3•17•17 | ||||||||||
| 868 = | 2•2•7•31 | ||||||||||
| 869 = | 11•79 | ||||||||||
| 870 = | 2•3•5•29 | ||||||||||
| 871 = | 13 • 67 | ||||||||||
| 872 = | 2 • 2 • 2 • 109 | ||||||||||
| 873 = | 3 • 3 • 97 | ||||||||||
| 874 = | 2 • 1 | ||||||||||
| 2 • 1 | |||||||||||
. | 5•5•5•7 | ||||||||||
| 876 = | 2•2•3•73 | ||||||||||
| 877 = | 877 | ||||||||||
| 878 = | 2•439 | ||||||||||
| 879 = | 3•293 | ||||||||||
| 880 = | 2•2•2•2•5•11 | ||||||||||
| 881 = | 881 | ||||||||||
| 882 = | 2•3•3•7•7 | ||||||||||
| 883 = | 883 | ||||||||||
| 884 = | 2•2•13•17 | ||||||||||
| 885 = | 3•5•59 | ||||||||||
| 886 = | 2•443 | ||||||||||
| 887 = | 887 | ||||||||||
| 888 = | 2•2•2•3•37 | ||||||||||
| 889 = | 7•127 | ||||||||||
| 890 = | 2•5•89 | ||||||||||
| 891 = | 3•3•3•3•11 | ||||||||||
| 892 = | 2•2•223 | ||||||||||
| 893 = | 19•47 | ||||||||||
| 894 = | 2 • 3 • 149 | ||||||||||
| 895 = | 5 • 179 | ||||||||||
| 896 = | 2 • 2 • 2 • 2 • 2 • 2 • 7 | ||||||||||
797 897 = 2 • 2. | 3•13•23 | ||||||||||
| 898 = | 2•449 | ||||||||||
| 899 = | 29•31 | ||||||||||
| 900 = | 2 • 2 • 3 • 3 • 5 • 5 | ||||||||||
| 901 = | 17 • 53 | ||||||||||
| 902 = | 2 • 11. 41 | ||||||||||
| 2 • 110020202018 | |||||||||||
| 2 • 110020202018 | 902 = | 2 • 110020 | |||||||||
| 902 = | 2 • 110020 | ||||||||||
| 902 = | 2. | 3•7•43 | |||||||||
| 904 = | 2•2•2•113 | ||||||||||
| 905 = | 5•181 | ||||||||||
| 906 = | 2•3•151 | ||||||||||
| 907 = | 907 | ||||||||||
| 908 = | 2•2•227 | ||||||||||
| 909 = | 3 • 3 • 101 | ||||||||||
| 910 = | 2 • 5 • 7 • 13 | ||||||||||
| 911 = | 911 | ||||||||||
| 912 = | 919|||||||||||
| 912 = | |||||||||||
| 912 = | |||||||||||
| 912 = | |||||||||||
. 3•19 3•19 | |||||||||||
| 913 = | 11•83 | ||||||||||
| 914 = | 2•457 | ||||||||||
| 915 = | 3•5•61 | ||||||||||
| 916 = | 2•2• 229 | ||||||||||
| 917 = | 7•131 | ||||||||||
| 918 = | 2•3•3•3•17 | ||||||||||
| 919 = | 919 | ||||||||||
| 920 = | 2•2•2•5•23 | ||||||||||
| 921 = | 3•307 | ||||||||||
| 922 = | 2 • 461 | ||||||||||
| 923 = | 13 • 71 | ||||||||||
| 924 = | 2 • 2 • 3 • 7 • 11 | ||||||||||
| 925 = | |||||||||||
| 925 = | • 3777. 377. | ||||||||||
| . | |||||||||||
| 926 = | 2•463 | ||||||||||
| 927 = | 3•3•103 | ||||||||||
| 928 = | 2•2•2•2•2•29 | ||||||||||
| 929 = | 929 | ||||||||||
| 930 = | 2•3•5•31 | ||||||||||
| 931 = | 7 • 7 • 19 | ||||||||||
| 932 = | 2 • 2 • 233 | ||||||||||
| 933 = | 3 • 311 | ||||||||||
| 934 = | 2 • 467 | 934 = | 2 • 467 | 934 = | 2 • 467 | 934 = | 2 • 467 | 934 = | 2 • 467 | 934 = | 2 • 467 |
| 934 = | 2. •17 •17 | ||||||||||
| 936 = | 2•2•2•3•3•13 | ||||||||||
| 937 = | 937 | ||||||||||
| 938 = | 2•7•67 | ||||||||||
| 939 = | 3•313 | ||||||||||
| 940 = | 2•2•5•47 | ||||||||||
| 941 = | 941 | ||||||||||
| 942 = | 2•3•157 | ||||||||||
| 943 = | 23•41 | ||||||||||
| 944 = | 2•2•2•2•59 | ||||||||||
| 945 = | 3•3•3•5•7 | ||||||||||
| 946 = | 2•11•43 | ||||||||||
| 947 = | 947 | ||||||||||
| 948 = | 2 • 2 • 3 • 79 | ||||||||||
| 949 = | 13 • 73 | ||||||||||
| 13. • 73 | |||||||||||
| . | |||||||||||
| 951 = | 3•317 | ||||||||||
| 952 = | 2•2•2•7•17 | ||||||||||
| 953 = | 953 | ||||||||||
| 954 = | 2•3•3 •53 | ||||||||||
| 955 = | 5•191 | ||||||||||
| 956 = | 2 • 2 • 239 | ||||||||||
| 957 = | 3 • 11 • 29 | ||||||||||
| 958 = | 2 • 479 | ||||||||||
| 959 = | |||||||||||
| 959 = | |||||||||||
| 959 = | |||||||||||
| 959 = | |||||||||||
| | |||||||||||
| | |||||||||||
| | |||||||||||
. | 2 • 2 • 2 • 2 • 2 • 2 • 3 • 5 | ||||||||||
| 961 = | 31 • 31 | ||||||||||
| 962 = | 2 • 13 • 37 | ||||||||||
| 963 = | 202020202020202020202019 37|||||||||||
| 9003 = | 20202020202020202019 37|||||||||||
| . •3•107 | |||||||||||
| 964 = | 2•2•241 | ||||||||||
| 965 = | 5•193 | ||||||||||
| 966 = | 2•3•7•23 | ||||||||||
| 967 = | 967 | ||||||||||
| 968 = | 2•2•2•11•11 | ||||||||||
| 969 = | 3 • 17 • 19 | ||||||||||
| 970 = | 2 • 5 • 97 | ||||||||||
| 971 = | 971 | ||||||||||
| 972 = | 2 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3. 3 | ||||||||||
| 973 = | 7•139 | ||||||||||
| 974 = | 2•487 | ||||||||||
| 975 = | 3•5•5•13 | ||||||||||
| 976 = | 2•2•2•2•61 | ||||||||||
| 977 = | 977 | ||||||||||
| 978 = | 2• 3•163 | ||||||||||
| 979 = | 11•89 | ||||||||||
| 980 = | 2•2•5•7•7 | ||||||||||
| 981 = | 3•3•109 | ||||||||||
| 982 = | 2•491 | ||||||||||
| 983 = | 983 | ||||||||||
| 984 = | 2 • 2 • 2 • 3 • 41 | ||||||||||
| 985 = | 5 • 197 | ||||||||||
| 986 = | 2 • 17 • 29 | ||||||||||
| 987 = | 3 • 70023 | ||||||||||
| 987 = | 3 • 47. 70023 70023 | ||||||||||
| 987 = | 3 • 47. 70023 | ||||||||||
| 987 = | 3 • 47. 70023 | ||||||||||
| 987 = | 3. 70020 | ||||||||||
| 987. | |||||||||||
| 988 = | 2•2•13•19 | ||||||||||
| 989 = | 23•43 | ||||||||||
| 990 = | 2•3•3•5•11 | ||||||||||
| 991 = | 991 | ||||||||||
| 992 = | 2•2•2•2•2•31 | ||||||||||
| 993 = | 3•331 | ||||||||||
| 994 = | 2•7•71 | ||||||||||
| 995 = | 5•199 | ||||||||||
| 996 = | 2•2•3•83 | ||||||||||
| 997 = | 997 | ||||||||||
| 998 = | 2•499 | ||||||||||
| 999 = | 3•3•3•37 | ||||||||||
| 1000 = | 2•2•2•5•5•5 |
Калькулятор факторизации простых чисел
Пожалуйста, дайте ссылку на эту страницу! Просто щелкните правой кнопкой мыши на изображении выше, выберите «Скопировать адрес ссылки», а затем вставьте его в HTML-код.
Факторизация числа образцов.
- Прайскую факторизацию 1401
- Прайскую факторизацию 1697
- Прайскую факторизацию 80650
- Прайвизация 1
- Прайскую фактор. Факторизация 701408733
- Разложение на простые множители 40040
3.3: Факторизация натуральных чисел на простые множители
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 48845
- Денни Бурзински и Уэйд Эллис-младший
- Колледж Южной Невады 9050 08X через OpenStax
Цели обучения
- уметь определять множители целого числа
- уметь различать простые и составные числа
- быть знакомым с фундаментальным принципом арифметики
- уметь находить разложение целого числа на простые множители
Коэффициенты
Из наблюдений, сделанных в процессе умножения, мы увидели, что
\((\text{фактор}) \cdot (\text{фактор}) = \text{продукт}\)
Коэффициенты, Произведение
Два числа, которые нужно умножить, представляют собой множителей , а результат умножения — произведение . Теперь, используя наши знания о делении, мы можем видеть, что первое число является делителем второго числа, если первое число делится на второе целое число раз (без остатка).
Теперь, используя наши знания о делении, мы можем видеть, что первое число является делителем второго числа, если первое число делится на второе целое число раз (без остатка).Одно число как множитель Другое
Первое число является множителем второго числа, если первое число делится на второе целое число раз (без остатка).Мы покажем это на следующих примерах:
Пример \(\PageIndex{1}\)
3 является коэффициентом 27, так как \(27 \div 3 = 9\), или \(3 \cdot 9 = 27\).
Пример \(\PageIndex{2}\)
7 является коэффициентом 56, поскольку \(56 \div 7 = 8\) или \(7 \cdot 8 = 56\).
Пример \(\PageIndex{3}\)
4 равно , а не в 10 раз, поскольку \(10 \div 4 = \text{2R2}\). (Есть остаток.)
Определение делителей целого числа
Мы можем использовать тесты на делимость от [ссылка] для определения всех делителей целого числа.

Набор образцов A
Найдите все множители числа 24.
Решение
\(\begin{array} {lll} {\text{Try 1:}} & {24 \div 1 = 24} & {\text{1 и 24 — множители}} \\ {\text{Попробуйте 2:}} & {\text{24 четно, поэтому 24 делится на 2.}} & {} \\ {} & {24 \div 2 = 12} & {\text{2 и 12 — множители}} \\ {\text{Попробуйте 3:}} & {2 + 4 = 6 \text{и 6 делится на 3, поэтому 24 делится на 3.}} & {} \\ {} & {24 \div 3 = 8} & {\text{3 и 8 являются множителями}} \\ {\text{Попробуйте 4:}} & {24 \div 4 = 6} & {\text{4 и 6 являются множителями}} \\ {\text{Попробуйте 5:}} & {24 \div 5 = \text{4R4}} & {\text{5 не является множителем} } \end{массив}\)
Следующее число, которое нужно попробовать, — 6, но мы уже знаем, что 6 — это множитель. Как только мы сталкиваемся с фактором, который мы уже обнаружили, мы можем остановиться.
Все множители целого числа 24 равны 1, 2, 3, 4, 6, 8, 12 и 24.
Практический набор A
Найдите все множители каждого из следующих чисел.

6
- Ответить
1, 2, 3, 6
Тренировочный набор A
12
- Ответить
1, 2, 3, 4, 6, 12
Тренировочный набор A
18
- Ответить
1, 2, 3, 6, 9, 18
Тренировочный набор A
5
- Ответить
1, 5
Тренировочный набор A
10
- Ответить
1, 2, 5, 10
Тренировочный набор A
33
- Ответить
1, 3, 11, 33
Тренировочный набор A
19
- Ответить
1, 19
Простые и составные числа
Обратите внимание, что единственными делителями числа 7 являются 1 и само 7, а единственными делителями числа 3 являются 1 и само 3.
 Однако у числа 8 есть делители 1, 2, 4 и 8, а у числа 10 есть делители 1, 2, 5 и 10. Таким образом, мы видим, что целое число может иметь только два делителя (само себя и 1) и другое целое число может иметь несколько делителей.
Однако у числа 8 есть делители 1, 2, 4 и 8, а у числа 10 есть делители 1, 2, 5 и 10. Таким образом, мы видим, что целое число может иметь только два делителя (само себя и 1) и другое целое число может иметь несколько делителей.Мы можем использовать это наблюдение, чтобы провести полезную классификацию целых чисел: простые и составные числа.
Определение: Простое число
Целое число (больше единицы), единственными делителями которого являются само себя и 1, называется простым числом .
Число 1 — это Не простое число
Первые семь простых чисел — это 2, 3, 5, 7, 11, 13 и 17. Обратите внимание, что целое число 1 равно , а не считается простым числом, а целое число 2 — это первое простое число , а — только четное простое число .
Определение: составное число
Целое число, состоящее из множителей, отличных от самого себя и 1, называется составным числом . Составные числа не являются простыми числами.
Некоторые составные числа: 4, 6, 8, 9, 10, 12 и 15.
Набор образцов B
Определите, какие целые числа простые, а какие составные.
39. Так как 3 делится на 39, число 39 составное: \(39 \div 3 = 13\)
Sample Set B
47. Несколько проб деления убеждают нас, что 47 делится только на 1 и 47. Следовательно, 47 — простое число.
Тренировочный набор B
Определите, какие из следующих целых чисел простые, а какие составные.
3
- Ответить
прайм
Практический набор B
16
- Ответить
композитный
Практический набор B
21
- Ответить
композитный
Практический набор B
35
- Ответить
композитный
Практический набор B
47
- Ответить
прайм
Практический набор B
29
- Ответить
прайм
Практический набор B
101
- Ответить
прайм
Практический набор B
51
- Ответить
композитный
Основной принцип арифметики
Простые числа очень полезны при изучении математики.
 Мы увидим, как они используются в следующих разделах. Теперь сформулируем основной принцип арифметики.
Мы увидим, как они используются в следующих разделах. Теперь сформулируем основной принцип арифметики.Фундаментальный принцип арифметики
За исключением порядка множителей, каждое натуральное число, отличное от 1, можно разложить на множители одним и только одним способом как произведение простых чисел.Определение: Факторизация простых чисел
Когда число разлагается на множители так, что все его делители являются простыми числами. факторизация называется простая факторизация числа.
Метод простой факторизации проиллюстрирован в следующих трех примерах.
\(10 = 5 \cdot 2\). И 2, и 5 — простые числа. Следовательно, \(2 \cdot 5\) — это простая факторизация числа 10.
11. Число 11 — простое число. Факторизация простых чисел применяется только к составным числам. Таким образом, число 11 не имеет простых факторизаций без простых чисел.
\(60 = 2 \cdot 30\). Число 30 не простое: \(30 = 2 \cdot 15\).
\(60 = 2 \cdot 2 \cdot 15\) 92 \cdot 3 \cdot 5\) является разложением на простые множители числа 60.
Разложение натурального числа на простые множители
Следующий метод позволяет найти разложение натурального числа на простые множители.
Метод нахождения разложения натурального числа на простые множители
- Несколько раз разделить число на наименьшее простое число, которое будет делиться на него целое число раз (без остатка).
- Когда простое число, использованное в шаге 1, больше не делится на данное число без остатка, повторите процесс деления со следующим наибольшим простым числом, на которое делится данное число.
- Продолжайте этот процесс, пока частное не станет меньше делителя.
- Разложение данного числа на простые множители — это произведение всех этих простых делителей. Если число не имеет простых делителей, оно является простым числом.
Мы можем использовать некоторые тесты на делимость, которые мы изучили в [ссылка] , чтобы помочь найти простые числа, которые делят данное число.

Sample Set C
Найдите простую факторизацию числа 60.
Решение
Так как последняя цифра 60 0, то есть четная, 60 делится на 2. Мы будем многократно делить на 2, пока не перестанем. Разделим так:
\(\begin{array} {l} {\text{30 снова делится на 2}} \\ {\text{15 не делится на 2, но делится на 3, следующее простое число}} \\ {\text{5 не делится на 3, но делится на 5, следующее простое число.}} \end{массив}\)
Наконец, частное 1 меньше, чем делитель 5, а простая факторизация числа 60 есть произведение этих простых делителей. 92 \cdot 3 \cdot 5\)
Sample Set C
Найдите простую факторизацию числа 441.
Решение
441 не делится на 2, так как его последняя цифра не делится на 2.
3 4 делится на 3, так как \(4 + 4 + 1 = 9\) и 9 делится на 3. + 7 = 12).} \\ {\text{49 не делится ни на 3, ни на 5. Оно делится на 7.}} \end{массив}\)
92\)Sample Set C
Найдите простую факторизацию числа 31.

Решение
\(\begin{array} {ll} {\text{31 не делится на 2}} & {\text {Его последняя цифра не четная}} \\ {} & {31 \div 2 = \text{15R1}} \\ {} & {\text{Частное 15 больше делителя 3. Продолжаем. }} \\ {\text{31 не делится на 3}} & {\text{Цифры} 3 + 1 = 4, \text{и 4 не делится на 3.}} \\ {} & {31 \div 3 = \text{10R1}} \\ {} & {\text{Частное 10 больше делителя 3. Продолжайте.}} \\ {\text{31 не делится на 5}} & {\text{Последняя цифра числа 31 не 0 и не 5.}} \\ {} & {31 \div 5 = \text{6R1}} \\ {} & {\text{Частное 6 равно больше делителя 5. Продолжайте.}} \\ {\text{31 не делится на 7.}} & {\text{Разделить на 7.}} \\ {} & {31 \div 7 = \text {4R1}} \\ {} & {\text{Частное 4 меньше делителя 7.}} \\ {} & {\text{Мы можем остановить процесс и сделать вывод, что 31 — простое число. }} \end{массив}\) 92 \cdot 11\)
Тренировочный набор C
17
- Ответить
17 простое число
Тренировочный набор C
61
- Ответить
61 простое число
Упражнения
Для следующих задач определите отсутствующие факторы.

Упражнение \(\PageIndex{1}\)
\(14 = 7 \cdot\)
- Ответить
2
Упражнение \(\PageIndex{2}\)
\(20 = 4 \cdot\)
Упражнение \(\PageIndex{3}\)
\(36 = 9 \cdot\)
- Ответить
4
Упражнение \(\PageIndex{4}\)
\(42 = 21 \cdot\)
Упражнение \(\PageIndex{5}\)
\(44 = 4 \cdot\)
- Ответить
11
Упражнение \(\PageIndex{6}\)
\(38 = 2 \cdot\)
Упражнение \(\PageIndex{7}\)
\(18 = 3 \cdot\).
- Ответить
\(3 \cdot 2\)
Упражнение \(\PageIndex{8}\)
\(28 = 2 \cdot\).
Упражнение \(\PageIndex{9}\)
\(300 = 2 \cdot 5 \cdot \).
- Ответить
\(2 \cточка 3 \cточка 5\)
Упражнение \(\PageIndex{10}\)
\(840 = 2 \cdot\).

Для следующих задач найдите все множители каждого из чисел.
Упражнение \(\PageIndex{11}\)
16
- Ответить
1, 2, 4, 8, 16
Упражнение \(\PageIndex{12}\)
22
Упражнение \(\PageIndex{13}\)
56
- Ответить
1, 2, 4, 7, 8, 14, 28, 56
Упражнение \(\PageIndex{14}\)
105
Упражнение \(\PageIndex{15}\)
220
- Ответить
1, 2, 4, 5, 10, 11, 20, 22, 44, 55, 110, 220
Упражнение \(\PageIndex{16}\)
15
Упражнение \(\PageIndex{17}\)
32
- Ответить
1, 2, 4, 8, 16, 32
Упражнение \(\PageIndex{18}\)
80
Упражнение \(\PageIndex{19}\)
142
- Ответить
1, 2, 71, 142
Упражнение \(\PageIndex{20}\)
218
В следующих задачах определите, какие из целых чисел простые, а какие составные.

Упражнение \(\PageIndex{21}\)
23
- Ответить
прайм
Упражнение \(\PageIndex{22}\)
25
Упражнение \(\PageIndex{23}\)
27
- Ответить
композитный
Упражнение \(\PageIndex{24}\)
2
Упражнение \(\PageIndex{25}\)
3
- Ответить
прайм
Упражнение \(\PageIndex{26}\)
5
Упражнение \(\PageIndex{27}\)
7
- Ответить
прайм
Упражнение \(\PageIndex{28}\)
9
Упражнение \(\PageIndex{29}\)
11
- Ответить
прайм
Упражнение \(\PageIndex{30}\)
34
Упражнение \(\PageIndex{31}\)
55
- Ответить
составной (\(5 \cdot 11\))
Упражнение \(\PageIndex{32}\)
63
Упражнение \(\PageIndex{33}\)
1 044
- Ответить
композитный
Упражнение \(\PageIndex{34}\)
924
Упражнение \(\PageIndex{35}\)
339
- Ответить
композитный
Упражнение \(\PageIndex{36}\)
103
Упражнение \(\PageIndex{37}\)
209
- Ответить
составной \((11 \cdot 19)\)
Упражнение \(\PageIndex{38}\)
667
Упражнение \(\PageIndex{39}\)
4 575
- Ответить
композитный
Упражнение \(\PageIndex{40}\)
119
Для следующих задач найдите простую факторизацию каждого из целых чисел.

Упражнение \(\PageIndex{41}\)
26
- Ответить
\(2 \cdot 13\)
Упражнение \(\PageIndex{42}\)
92\)Упражнение \(\PageIndex{50}\)
148 225
Упражнения для обзора
Упражнение \(\PageIndex{51}\)
Округлите 26 584 до ближайших десяти.
- Ответить
26 580
Упражнение \(\PageIndex{52}\)
Насколько 106 больше 79?
Упражнение \(\PageIndex{53}\)
Правда или ложь? Ноль, деленный на любое ненулевое целое число, равен нулю. 92 \дел 3\).
- Ответить
14
Эта страница под названием 3.3: Факторизация натуральных чисел с простыми числами распространяется по лицензии CC BY, ее автор, ремикширование и/или куратор — Денни Бурзински и Уэйд Эллис-младший (OpenStax CNX).





 (они входят в разложение числа 4900), но не делится, например, на 13.
(они входят в разложение числа 4900), но не делится, например, на 13. — М.: Мнемозина, 2012.
— М.: Мнемозина, 2012.
 Используем разложение 12 = 2 x 6 и запишем его в третьей строке дерева:
Используем разложение 12 = 2 x 6 и запишем его в третьей строке дерева: В конце концов у вас останутся одни простые числа. Когда это случится, разложение на простые множители завершено. Последняя строка представляет собой набор простых чисел, произведение которых дает исходное число.
В конце концов у вас останутся одни простые числа. Когда это случится, разложение на простые множители завершено. Последняя строка представляет собой набор простых чисел, произведение которых дает исходное число.

 Наименьшее общее кратное (НОК) двух чисел — это наименьшее число, которое делится без остатка на оба данных числа. Например, НОК 2 и 3 является 6, поскольку это наименьшее число, которое делится на 2 и 3. Ниже приведен пример нахождения НОК с помощью разложения на простые множители:
Наименьшее общее кратное (НОК) двух чисел — это наименьшее число, которое делится без остатка на оба данных числа. Например, НОК 2 и 3 является 6, поскольку это наименьшее число, которое делится на 2 и 3. Ниже приведен пример нахождения НОК с помощью разложения на простые множители:



 Разделим 3 на себя. В итоге мы получили 1.
Разделим 3 на себя. В итоге мы получили 1.
 ru ().
ru (). Если полученное число не является целым числом, то округлить его до ближайшего целого числа.
Если полученное число не является целым числом, то округлить его до ближайшего целого числа. 

 Она хочет разделить свой класс на группы и дать им групповую математическую практику. Сколькими способами она может сгруппировать 56 учеников так, чтобы:
Она хочет разделить свой класс на группы и дать им групповую математическую практику. Сколькими способами она может сгруппировать 56 учеников так, чтобы: Давайте попробуем метод факторного дерева, чтобы найти простую факторизацию числа 56.
Давайте попробуем метод факторного дерева, чтобы найти простую факторизацию числа 56.