Разложить число 72 на простые множители: Разложите на простые множители число 72 210 1820

Содержание

разложить на простые множители, онлайн калькулятор CALC.WS

В теории чисел, простые множители (простые делители) положительного целого числа — это простые числа, которые делят это число нацело (без остатка). Выделить простые множители положительного целого числа означает перечислить эти простые множители вместе с их кратностями. Процесс определения простых множителей называется факторизацией целых чисел. Основная теорема арифметики утверждает, что любое натуральное число можно представить в виде единственного (с точностью до порядка следования) произведения простых множителей

Решение

Число 50 по признакам делимости делится на 2

Делим, получаем число 36, которое так же делится на 2:

72	2
36	2
18

Делим, получаем число 18, которое так же делится на 2:

72	2
36	2
18	2
9

Получили число 9, которое на два уже не делится, зато делится на 3:

72	2
36	2
18	2
9	3
3

Ну и остаётся простое число 3, которое делится только на само себя:

72	2
36	2
18	2
9	3
3	3
1

Ответ

Простые множители числа 72:

Число — простое

Подробно:

2 * 2 * 2 * 3 * 3

Кратко (со степенями):

2³ * 3²

В столбик:

72	2
36	2
18	2
9	3
3	3
1

Разложить любое число с помощью калькулятора:

Результат

Простые множители числа :

Число — простое

Подробно:

Кратко (со степенями):

В столбик:

Видео

Подробно про разложение на простые множители можно узнать из видео:

Нахождение нод с помощью разложения чисел на простые множители

Рассмотрим еще один способ нахождения НОД. Наибольший общий делитель может быть найден по разложениям чисел на простые множители. Сформулируем правило:

НОД двух целых положительных чисел a и b равен произведению всех общих простых множителей, находящихся в разложениях чисел a и b на простые множители.

Приведем пример для пояснения правила нахождения НОД. Пусть нам известны разложения чисел 220 и 600 на простые множители, они имеют вид 220=2·2·5·11 и 600=2·2·2·3·5·5. Общими простыми множителями, участвующими в разложении чисел 220 и 600, являются 2, 2 и5. Следовательно, НОД(220, 600)=2·2·5=20.

Таким образом, если разложить числа a и b на простые множители и найти произведение всех их общих множителей, то этим будет найден наибольший общий делитель чисел a и b.

Рассмотрим пример нахождения НОД по озвученному правилу.

Пример.

Найдите наибольший общий делитель чисел 72 и 96.

Решение.

Разложим на простые множители числа 72 и 96:

То есть, 72=2·2·2·3·3 и 96=2·2·2·2·2·3. Общими простыми множителями являются 2, 2, 2и 3. Таким образом, НОД(72, 96)=2·2·2·3=24.

Ответ:

НОД(72, 96)=24.

В заключение этого пункта заметим, что справедливость приведенного правила нахождения НОД следует из свойства наибольшего общего делителя, которое утверждает, чтоНОД(m·a₁, m·b₁)=m·НОД(a₁, b₁), где m – любое целое положительное число.

К началу страницы

Нахождение наибольшего общего делителя трех и большего количества чисел может быть сведено к последовательному нахождению НОД двух чисел. Мы об этом упоминали, при изучении свойств НОД.

Там мы сформулировали и доказали теорему: наибольший общий делитель нескольких чисел a₁, a₂, …, a_k равен числу d_k, которое находится при последовательном вычислении НОД(a₁, a₂)=d₂, НОД(d₂, a₃)=d₃, НОД(d₃, a₄)=d₄, …,НОД(d_k-1, a_k)=d_k.

Давайте разберемся, как выглядит процесс нахождения НОД нескольких чисел, рассмотрев решение примера.

Пример.

Найдите наибольший общий делитель четырех чисел 78, 294, 570 и 36.

Решение.

В этом примере a₁=78, a₂=294, a₃=570, a₄=36.

Сначала по алгоритму Евклида определим наибольший общий делитель d₂ двух первых чисел 78 и 294. При делении получаем равенства 294=78·3+60; 78=60·1+18;60=18·3+6 и 18=6·3. Таким образом, d₂=НОД(78, 294)=6.

Теперь вычислим d₃=НОД(d₂, a₃)=НОД(6, 570). Опять применим алгоритм Евклида:570=6·95, следовательно, d₃=НОД(6, 570)=6.

Осталось вычислить

d₄=НОД(d₃, a₄)=НОД(6, 36). Так как 36 делится на 6, тоd₄=НОД(6, 36)=6.

Таким образом, наибольший общий делитель четырех данных чисел равен d₄=6, то есть,НОД(78, 294, 570, 36)=6.

Ответ:

НОД(78, 294, 570, 36)=6.

Разложение чисел на простые множители также позволяет вычислять НОД трех и большего количества чисел. В этом случае наибольший общий делитель находится как произведение всех общих простых множителей данных чисел.

Пример.

Вычислите НОД чисел из предыдущего примера, используя их разложения на простые множители.

Решение.

Разложим числа 78, 294, 570 и 36 на простые множители, получаем

78=2·3·13,294=2·3·7·7, 570=2·3·5·19, 36=2·2·3·3. Общими простыми множителями всех данных четырех чисел являются числа 2 и 3. Следовательно, НОД(78, 294, 570, 36)=2·3=6.

Ответ:

НОД(78, 294, 570, 36)=6.

К началу страницы

Каковы простые делители числа 72?

Например, мы можем записать число 72 как произведение простых множителей: 72 = 2 3 ⋅ 3 2 . Выражение 2 3 ⋅ 3 2 называется простой факторизацией числа 72.

Запрос на удаление

| Посмотреть полный ответ на hmhco. com

Каковы делители числа 72?

Решение: делители числа 72 равны 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36 и 72. Делители числа 71 равны 1 и 71. Таким образом, общий делитель чисел 72 и 71 равен 1.

Запрос на удаление

| Посмотреть полный ответ на byjus.com

Что такое факторное дерево числа 72?

Ответ и объяснение: Простые множители числа 72 с использованием дерева множителей. Из дерева множителей простые множители числа 72 равны 2×2×2×3×3 2 × 2 × 2 × 3 × 3 или 23 × 32 2 3 × 3. 2 .

Запрос на удаление

| Посмотреть полный ответ на homework.study.com

Является ли 3 коэффициентом 72 и почему?

3 является коэффициентом 72. Вы можете сказать это, потому что 72 можно без остатка разделить на 3. Когда вы разделите 72 на 3, вы получите 24. Это означает, что 24 x 3 = 72.

Запрос на удаление

| Посмотреть полный ответ на homework.study.com

Как найти простой множитель?

Самый простой алгоритм для нахождения простых множителей числа состоит в том, чтобы продолжать делить исходное число на простые множители, пока мы не получим остаток, равный 1. Например, разлагая полученное число 30 на простые множители, 30/2 = 15, 15/ 3 = 5, 5/5 = 1.

Запрос на удаление

| Посмотреть полный ответ на byjus.com

Простая факторизация числа 72

Сколько кратно 72?

Итак, первые 10 кратных 72: 72, 144, 216, 288, 360, 432, 504, 576, 648 и 720. Число кратных 72 бесконечно.

Запрос на удаление

| Посмотреть полный ответ на hellothinkster.com

Каковы квадратные множители числа 72?

Упрощенная радикальная форма квадратного корня из 72

Следовательно, множители числа 72 равны 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36 и 72.

Запрос на удаление

| Посмотреть полный ответ на cuemath.com

Почему 2 равно 72?

Поскольку 72 — четное число, оно по определению делится на 2. Любое четное число будет иметь множитель 2. Делителями числа 72 являются: 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36 и 72.

Запрос на удаление

| Посмотреть полный ответ на homework.study.com

Является ли число 72 полным квадратом?

Нет, 72 не является совершенным квадратным числом, так как квадратный корень из 72 — это не целое число, а дробь (содержит десятичную точку в упрощенном значении).

Запрос на удаление

| Посмотреть полный ответ на byjus.com

Как решить проблему с Root 72?

Следовательно, мы можем написать √72=2×3×√2=6√2. Следовательно, упрощенная форма квадратного корня из 72 равна 6√2.

Запрос на удаление

| Посмотреть полный ответ на vedantu.com

Чему равен квадратный коэффициент 72?

Разложение числа 72 на множители равно 2 × 2 × 2 × 3 × 3, в котором есть 1 пара одинаковых чисел. Таким образом, простейшая радикальная форма √72 — это 6√2.

Запрос на удаление

| Посмотреть полный ответ на cuemath.com

Что такое произведение 72?

72 = 2*2*2*3*3.

Запрос на удаление

| Посмотреть полный ответ на quora.com

Что такое совершенный корень из 72?

Значение квадратного корня из 72 равно 8,48528137424… или мы можем записать квадратный корень из 72 как √72 = 6√2 = 8,485.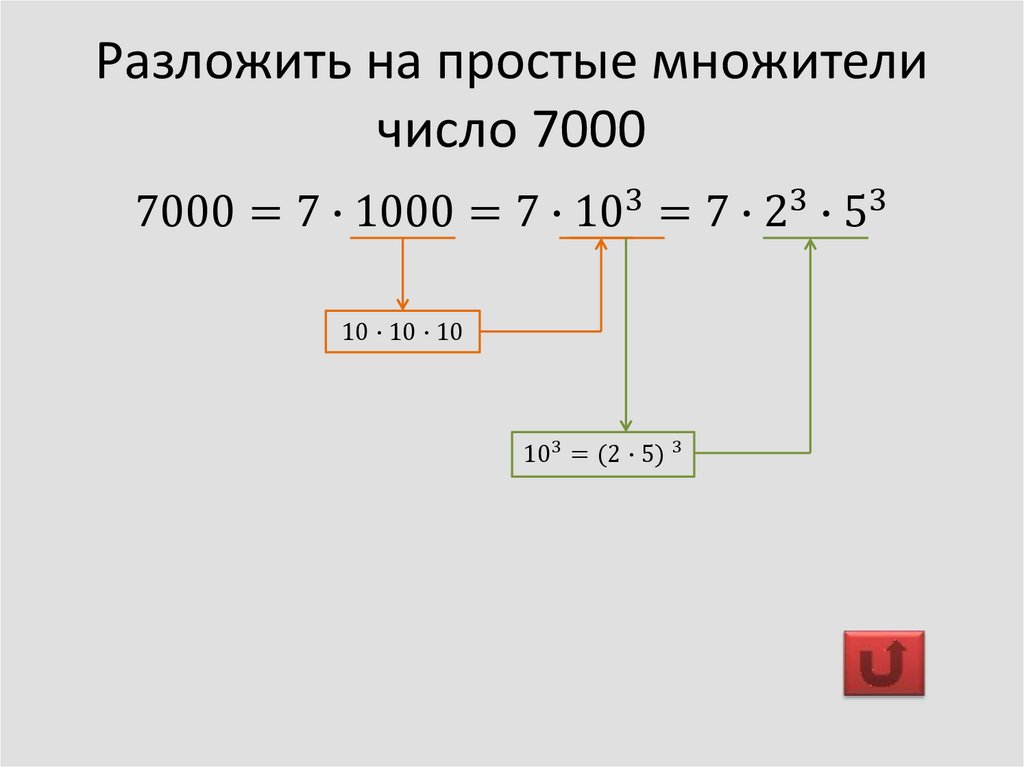

Запрос на удаление

| Посмотреть полный ответ на byjus.com

Каковы простые произведения чисел 72 и 32?

Первичная факторизация 32 и 72 равна (2 × 2 × 2 × 2 × 2) и (2 × 2 × 2 × 3 × 3) соответственно.

Запрос на удаление

| Посмотреть полный ответ на cuemath.com

Каково число, кратное 72?

Итак, первые 10 кратных 72: 72, 144, 216, 288, 360, 432, 504, 576, 648 и 720.

Запрос на удаление

| Посмотреть полный ответ на hellothinkster.com

Является ли 2 коэффициентом 72 и почему?

Любое четное число будет иметь множитель 2. Факторы 72: 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36 и 72. Вы можете получить 72, умножив 2 x 36. Так что да, 2 — это коэффициент 72. !

Запрос на удаление

| Посмотреть полный ответ на homework. study.com

Является ли 72 реальным числом?

72 (семьдесят два) — натуральное число, стоящее между 71 и 73. Это половина брутто или 6 дюжин (т. е. 60 в двенадцатеричном формате).

Запрос на удаление

| Посмотреть полный ответ на en.wikipedia.org

Что такое коэффициент радуги?

Факторная радуга — это красивая идея, которая заслуживает того, чтобы быть частью математического словаря каждого ребенка. Вот множитель радуги для 6: множители 6 — это числа, которые точно делятся на 6: 1, 2, 3 и 6. В радуге они идут в порядке размера, и каждый связан луком со своим партнером.

Запрос на удаление

| Посмотреть полный ответ на mathsweeklondon.org

Почему 2 — простое число?

2 — простое число, потому что его делителями являются только 1 и оно само.

Запрос на удаление

| Посмотреть полный ответ на сайте Thirdspacelearning. com

Что такое простое число в математике?

Простое число — это целое число больше 1, единственными делителями которого являются 1 и само себя. Множитель – это целое число, которое можно без остатка разделить на другое число. Первые несколько простых чисел — это 2, 3, 5, 7, 11, 13, 17, 19, 23 и 29. Числа, имеющие более двух делителей, называются составными числами.

Запрос на удаление

| Посмотреть полный ответ на techtarget.com

Что такое LCM 72?

2: Найдите НОК 72 и 96, используя метод простой факторизации. Следовательно, наименьшее общее кратное 72 и 96 при простой факторизации равно 288.

Запрос на удаление

| Посмотреть полный ответ на byjus.com

Можно ли упростить root 72?

Запрос на удаление

| Посмотреть полный ответ на vedantu.com

← Предыдущий вопрос
Какой фрукт согревает тело?

Следующий вопрос →
Как перейти от желтого блонда к ледяному блонду?

Факторы 72 | Определение, примеры, способы нахождения, положительное, отрицательное

Введение

Можно ли разделить целое число 72 на 6 без остатка?

Да, 72÷6=12

Можно ли разделить целое число 72 на 7 без остатка?

Нет, 72÷7=10 р.2

Можно ли определить все числа, на которые можно разделить целое число 72 ?

Да, об этом пойдет речь в этой статье.

Эти номера особенные?

Эти числа называются факторами.

Определение множителей

Множитель числа — это число, на которое данное число делится без остатка. Обычно, когда мы говорим о числовых факторах, мы говорим только о положительных целых факторах.

Например, множители 10 равны 1, 2, 5 и 10. Если 10 разделить на любое из чисел 1, 2, 5, 10, ответ будет целым числом:

10÷1=10

10÷2=5

10÷5=2

10÷10=1

Делителями числа являются любые числа, которые делятся на него точно, включая 1 и само число. Число 1 всегда является наименьшим целым делителем числа, само число всегда является наибольшим целым делителем числа. Таким образом, каждое число всегда имеет не менее двух делителей.

Если число имеет ровно два делителя, 1 и само число, то это число называется простым числом. Число 1 не является простым числом. Наименьшим простым числом является число 2 (делится без остатка и на 1, и на 2). Для записи последовательных простых чисел, начиная с наименьшего, можно использовать алгоритм решета Эратосфена, известный еще до нашей эры. Рассмотрим работу этого алгоритма на следующем примере.

ПРИМЕР: Запишите все простые числа до 72.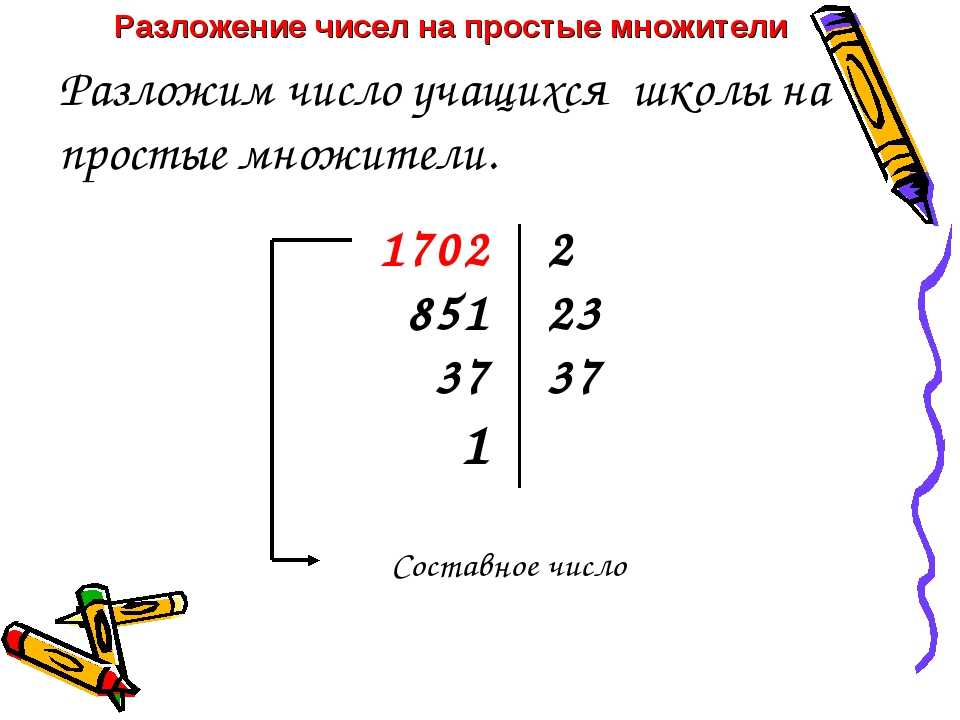

РЕШЕНИЕ: Напишите список целых чисел, начиная с наименьшего простого числа от 2 до 72.

Обведите число 2 и вычеркните все числа, которые делятся на 2.

Обведите следующее число 3 и вычеркните все числа, которые делятся на 2. 3.

Обведите следующее число 5 и зачеркните все числа, которые делятся на 5.

Обведите следующее число 7 и вычеркните все числа, которые делятся на 2.

И так далее, обведите следующие числа и зачеркните из всех чисел, делящихся без остатка на это число. Все обведенные числа — простые числа от 2 до 72.

Число, имеющее более двух делителей, называется составным числом.

Способы нахождения делителей числа

Существуют три метода нахождения делителей числа:

метод деления;
метод умножения;
метод простой факторизации.

МЕТОД ДЕЛЕНИЯ: метод деления состоит в том, чтобы найти все делители от 1 до самого числа, которые делят число без остатка.

МЕТОД УМНОЖЕНИЯ: метод умножения заключается в записи числа как произведения двух чисел различными возможными способами.

МЕТОД ПРОСТОЙ ФАКТОРИЗАЦИИ: метод простой факторизации состоит в том, чтобы представить составное число как произведение его простых множителей.

Метод деления для нахождения множителей 72

Поскольку число 72 не обведено в приведенном выше примере (алгоритм решета Эратосфена), число 72 является составным числом, поэтому оно имеет более двух множителей.

Мы можем использовать деление, чтобы найти все положительные делители числа 72 (начать с 1, затем проверить 2, 3, 4, 5, 6, 7, 8, 9и т.д. до 36 (число 36 ровно половина 72) и само число 72):

72÷1=72

72÷2=36

72÷3=24

72÷4=18

72÷5=14 r.2

72÷6=12

72÷7=14 r.2

72÷8=9

72÷9=8

72÷10=7 72÷10=7 2

72÷11=6 к.6

72÷12=6

72÷13=5 к.7

72÷14=5 к. 2

72÷15=4 к.12

5

5 72÷16=4 r.8

72÷17=4 r.5

72÷18=4

72÷19=3 r.15

72÷20=3 r.12

72÷21=3 r.9

72÷22=3 r.6

72÷23=3 r.3

72÷24 =3

72÷25=2 r.22

72÷26=2 r.20

72÷27=2 r.18

72÷28=2 r.16

72÷29=2 r .14

72÷30=2 r.12

72÷31=2 r.10

72÷32=2 r.8

72÷33=2 r.6

72÷34=2 r .4

72÷35=2 r.2

72÷36=2

72÷72=1

Таким образом, 72 имеет всего 12 положительных факторов: 1, 2, 3, 4, 6, 8 , 912, 18, 24, 36 и 72.

Метод умножения для нахождения множителей числа 72

Представьте число 72 как произведение двух чисел всеми возможными способами:

72 = 1 × 72

72 = 2 × 36

72 = 3 × 24

72 = 4 × 18

72 = 6 × 12

72 = 8 × 9

Все числа, которые используются в этих произведениях 72. Таким образом, положительные делители числа 72 равны 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36 и 72.

Метод простой факторизации для нахождения делителей числа 72

Основная факторизация — это способ представления числа как произведения его простых делителей. Например,

72=6×6×2

не является простой факторизацией числа 72, поскольку число 6 не является простым числом.

Произведение

72=2×2×2×3×3

– это простая факторизация числа 72, поскольку числа 2 и 3 являются простыми числами.

Есть два возможных способа выразить число как произведение простых множителей:

метод деления;
метод факторного дерева.

ФАКТОРИЗАЦИЯ НА ПРОСТЫЕ С ПОМОЩЬЮ МЕТОДА ДЕЛЕНИЯ

Метод деления можно использовать для нахождения простых множителей числа путем деления числа на простые числа. Чтобы найти простые множители числа с помощью метода деления, выполните следующие действия:

ШАГ 1. Разделите число на наименьшее возможное простое число.

ШАГ 2. Разделите частное из шага 1 на наименьшее возможное простое число.

ШАГ 3: Повторяйте шаг 2, пока частное не станет равным 1.

ПОСЛЕДНИЙ ШАГ: Умножьте все простые множители, являющиеся делителями.

ПРИМЕР: Напишите разложение числа 72 на простые множители, используя метод деления.

РЕШЕНИЕ:

ШАГ 1. Наименьшее возможное простое число, на которое 72 делится без остатка, равно числу 2. Разделите 72 на 2:

72÷2=36

. частное 36 равно числу 2. Разделите 36 на 2:

36÷2=18

ШАГ 3. Наименьшее возможное простое число, на которое делится частное 18, равно числу 2. Разделите 18 на 2:

18÷2=9

ШАГ 4. Наименьшее возможное простое число, которое делит частное 9 без остатка на 3. Разделите 9 на 3:

9÷3=3

ШАГ 5: Наименьшее возможное простое число, на которое частное 3 делится без остатка, равно числу 3. Разделите 3 на 3:

3÷ 3=1

ПОСЛЕДНИЙ ШАГ: Умножьте все простые множители, которые являются делителями:

72=2×2×2×3×3

Вы можете переписать эту простую факторизацию в виде экспоненты:

72=2232

ЗАМЕЧАНИЕ : Обычно этот процесс не описывается так долго, но изображается в форме столбца, как показано ниже.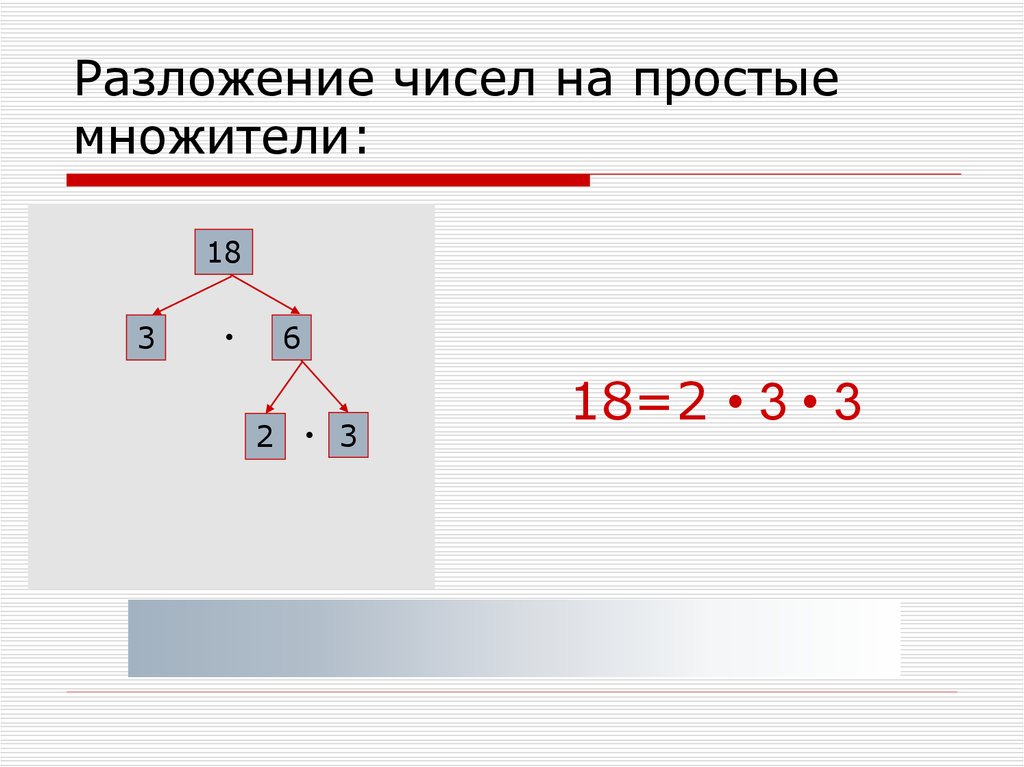

2	72
2	36
2	18
3	9
3	3
	1

Прайскую факторизацию 72 = 22233

= 2332

Прайвизация. множители этих множителей и так далее, пока не получим только простые множители.
ПРИМЕР : Нарисуйте дерево множителей для числа 72.
РЕШЕНИЕ : Из таблицы умножения мы знаем, что 72=8×9. Таким образом,
Каждое из этих чисел мы можем представить как произведение простых чисел:
8=2×2×2
9=3×3
Таким образом, окончательное дерево факторов равно
, а простая факторизация числа 72 равно 2×2×2×3×3 или 2332,
, и убедитесь, что простые факторизации для всех деревьев факторов одинаковы. Это обеспечивается Фундаментальной теоремой арифметики, которая утверждает, что
каждое натуральное число, большее 1 , может быть записано как произведение простых чисел, и что с точностью до перестановки множителей это произведение единственно.
Чтобы найти простые множители числа с помощью метода дерева множителей, выполните следующие шаги:
   ШАГ 1: Нарисуйте дерево множителей, начиная с произвольных чисел с произведением, равным заданному числу, и заканчивая только простыми числами.
   ШАГ 2. Перемножьте все простые множители, встречающиеся в этом дереве множителей.
Метод нахождения множителей числа с помощью разложения числа на простые множители заключается в умножении произвольных комбинаций простых множителей.
ПРИМЕР : Разложение числа 72 на простые множители равно 2332. Запишите все положительные делители числа 72, используя метод разложения на простые множители.
РЕШЕНИЕ : Чтобы записать все множители и не потерять ни одного, воспользуйтесь следующим руководством по написанию комбинаций:
сначала запишите все возможные степени первого простого множителя (начиная с показателя степени 0 и заканчивая максимально возможный показатель, определенный при простой факторизации числа):
20=1, 21=2, 22=4, 23=8
затем запишите все возможные степени второго простого множителя (начиная с показателя степени 0 и заканчивая максимально возможным показателем, определенным в простой факторизации числа):
30=1, 31=3, 32=9
и далее все возможные произведения степеней обоих множителей
2131=6, 2132=18,
2231=322, 2231=322 =36,
2331=24, 2332=72
Следовательно, список всех 12 положительных множителей числа 72, записанных в порядке возрастания, равен
1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, 72
Обратите внимание, что только 2 и 3 являются простыми делителями числа 72.
Используя простую факторизацию числа, мы можем найти количество множителей этого числа. Для этого выполните следующие шаги:
ШАГ 1: Запишите простую факторизацию числа в форме экспоненты.
ШАГ 2: Добавьте по единице к каждому показателю степени.
ШАГ 3: Перемножьте все полученные числа. Это произведение обозначает количество множителей числа.
ПРИМЕР : Найдите количество делителей числа 72.
РЕШЕНИЕ : Из предыдущей темы разложение числа 72 на простые множители в виде экспоненты равно 2332.
Добавьте 1 к каждому показателю степени:
3
+1=4
2+1=3
и умножить полученные суммы:
4×3=12
Следовательно, число множителей 72 равно 12.
Положительные пары множителей
Факторная пара числа представляет собой набор двух множителей, произведение которых при умножении дает это число. Например, факторы 5 и 8 образуют пару факторов 40, потому что
40=5×8
ПРИМЕР: Перечислите все пары множителей числа 72.
РЕШЕНИЕ: Начните с 1. Поскольку 72=1×72, поместите 1 в начало списка и 72 в конец списка. Множители 1 и 72 образуют первую пару множителей числа 72.
Теперь попробуйте 2. Поскольку 72=2×36, поместите 2 в начало списка (после 1) и 36 в конец списка (перед 72). . Множители 2 и 36 образуют вторую пару множителей числа 72.
1 2 36 72
Затем попробуйте 3. Поскольку 72=3×24, поставьте 2 в конец списка из 4 (после 4 в конец списка 2) и (до 36). Factors 3 and 24 form the third factor pair of 72.
1 2 3 24 36 72
Continue with 4. Since 72 =4×18, поставить 4 в начало списка (после 3) и 18 в конец списка (до 24). Множители 4 и 18 образуют четвертую пару множителей числа 72.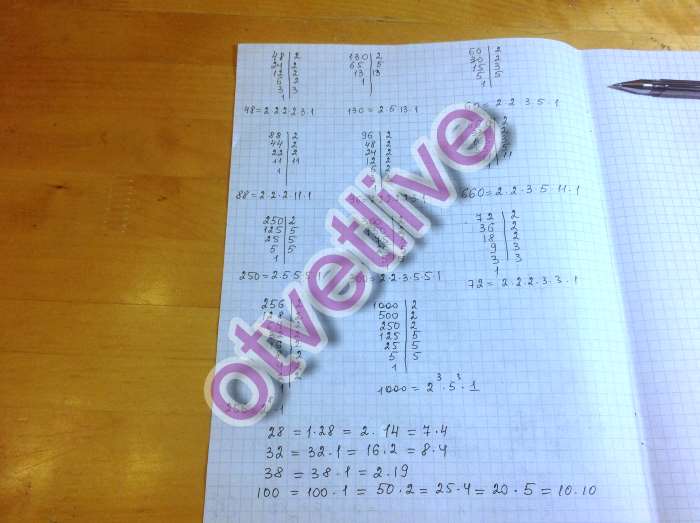
1 2 3 4 18 24 36 72
Check the next factor 6. Since 72=6×12, put 6 в начале списка (после 4) и 12 в конце списка (до 18). Множители 6 и 12 образуют пятую пару множителей числа 72.0463 12 18 24 36 72
Наконец, 72=8×9. Два средних фактора — 8 и 9. Эти два фактора образуют последнюю пару факторов 72.
1 2 3 4 6 6 6 6 6 6 . 24 36 72
Больше нет целых чисел между 8 и 9, так что мы закончили!
Мы можем графически представить пары положительных факторов, как показано ниже.
Отрицательные множители 72
Из предыдущей темы видно, что существует 6 пар множителей по 72. Все эти пары состоят из положительных целых чисел.
Если мы заметим, что произведение двух отрицательных чисел дает положительное число, то те же самые пары отрицательных чисел будут также парами множителей.
Таким образом, отрицательные пары множителей
-1 и -72
-2 и -36
-3 и -24
-4 и -18
-6 и -12
-8 и -9
и список пар отрицательных коэффициентов:
940461 1
-2 -3 -4 -6 -8 -9 -12 -18 -24 -36 -72
Здесь два числа, окрашенные в один цвет, образуют отрицательную пару множителей.
Викторина
Каково произведение всех простых множителей числа 72?
РЕШЕНИЕ : Число 72 имеет только два простых делителя: 2 и 3. Произведение этих двух чисел равно 2×3=6.
ОТВЕТ: 6
Каково среднее значение всех составных делителей числа 72?
РЕШЕНИЕ : Число 72 имеет 12 положительных делителей: 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36 и 72. простое и не составное число, поэтому их 9составные множители 72:
4, 6, 8, 9, 12, 18, 24, 36, 72
Среднее число равно сумме всех чисел, деленной на количество чисел. Следовательно, среднее значение всех составных множителей числа 72 равно
4+6+8+9+12+18+24+ 36+729=1899=21
ОТВЕТ: 21
Какова сумма всех положительные факторы 72?
РЕШЕНИЕ : Число 72 имеет 12 положительных факторов: 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36 и 72. Сумма этих факторов 1+2+3+4 +6+8+9+12+18+24+36+72=195.
ОТВЕТ: 195
Какое из следующих утверждений верно?
а) Сумма всех делителей числа 72 равна 0.
б) Произведение всех делителей числа 72 равно 0,
в) Число 72 имеет 24 делителя.
d) Число 72 имеет 6 пар факторов.
РЕШЕНИЕ : Число 72 имеет 24 фактора: 12 положительных и 12 отрицательных. Итак, утверждение в) верно.
Положительные факторы числа 72: 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, 72.
Отрицательные факторы числа 72: -1, -2, -3, -4, -6, -8, -9, -12, -18, -24, -36, -72.
Сумма всех этих множителей равна 0, потому что сумма положительного и соответствующего отрицательного множителей равна 0, а сумма двенадцати нулей тоже равна нулю. Следовательно, утверждение а) верно.
Утверждение b) неверно. Произведение чисел равно 0, когда одно из этих чисел равно 0. Число 0 не является делителем числа 72, поэтому произведение делителей числа 72 не может быть равно 0.
Утверждение d) также неверно, потому что число 72 имеет 6 положительных пар множителей и 6 отрицательных пар множителей, всего 12 пар множителей.
ОТВЕТ : а) Верно
б) Ложно
в) Верно
г) Ложно
Почему числа -12 и -4 не образуют пару множителей 72?
РЕШЕНИЕ: Факторная пара числа — это набор двух чисел, произведение которых равно этому числу.
Так как -12-4=48≠72, числа -12 и -4 не образуют пару множителей 72, хотя оба эти числа являются делителями 72.
Выводы
Чаще всего нас интересуют только положительные множители числа.
Иногда отрицательные факторы имеют математический интерес.
Мы никогда не говорим о дробных множителях числа.
Количество делителей числа равно количеству простых делителей этого числа, только если данное число является простым числом.
Количество делителей составного числа всегда больше 2.
Все натуральные числа являются произведением хотя бы одной пары множителей.
Число 1 является делителем каждого натурального числа.
No related posts.