Разложить множетели на множетели: 5 способов разложения многочлена на множители

Немного теории

Разложение  многочлена  на  множители

        Для преобразования выражений, при решении уравнений, в вычислениях и ряде других задач бывает полезно заменить многочлен произведением нескольких многочленов.

Разложением многочлена на множители называется представление        многочлена  в виде произведения двух или нескольких многочленов.

       Существует несколько способов разложения многочлена на множители:

*   вынесение общего множителя за скобки;

*   способ группировки;

*   с помощью формул сокращенного умножения.

                                         Вынесение общего множителя за скобки

      Рассмотрим несколько примеров. Вынесем за скобки общий множитель на основе распределительного свойства умножения:

                                                 4х — 4у = 4( х-у )

                                                 ab + ac = a( b+c )

      Теперь рассмотрим такой многочлен:

                                        8х²— 12xy = 4х·2х — 4х·3у = 4х( 2х-3у )

       Каждый член многочлена мы заменили произведением двух множителей, один из которых — общий множитель

4х, и вынесли этот множитель за скобки.

        Разложим на множители многочлен:      -10х²у + 2х³у² — 6х⁴       

*    Найдем наибольший общий делитель коэффициентов -10, 2 и 6. Он равен 2.

*    Переменная х входит во все члены многочлена с показателями 2, 3 и 4; следовательно, можно вынести за скобки х².

*    Переменная у входит не во все члены многочлена, значит, ее нельзя вынести за скобки.

Поэтому за скобки можно вынести 2х²

. Правда, в данном случае целесообразнее вынести —2х².Теперь разделим каждый член многочлена на -2х².Получим:

                                         -10х²у + 2х³у²— 6х⁴= -2х²( 5у — ху²+ 3х²)

                                               Способ  группировки

      Чтобы уяснить суть способа группировки, рассмотрим следующий пример:                    

                  Разложите на множители многочлен:       ху + 3х — 2у — 6          

      Сгруппируем его члены так, чтобы слагаемые в каждой группе имели общий множитель, и вынесем его за скобки:

              ху + 3х — 2у — 6 = ( ху + 3х ) + ( -2у — 6 ) = х( у + 3 ) — 2( у + 3 ) = ( у + 3 )( х — 2 )

      Этот же многочлен можно разложить на множители, группируя его члены иначе:

              ху + 3х — 2у — 6 = ( ху — 2у ) + ( 3х — 6 ) = у( х — 2 ) + 3( х — 2 ) = ( х — 2 )( у + 3 )

                       Разложим на множители трехчлен:       х²— 6х + 5

      Представим -6х в виде суммы -х — 5х, а затем применим способ группировки:

              х²— 6х + 5 = х²— х — 5х + 5 = ( х²— х ) + (-5х + 5 ) = х( х — 1 ) — 5( х — 1 ) = ( х — 1 )( х — 5 )         

                   Разложение многочлена на множители с помощью формул сокращенного умножения  

      Вот эти формулы:  а²— b²= (a-b)(a+b) — формула разности квадратов;

                                    a³— b³= (a-b)(a²+ab+b²) — формула разности кубов;   

                                    a³+ b³= (a+b)(a²-ab+b²) — формула суммы кубов;

                                    a²+2ab+b²= (a+b)² — квадрат суммы;

                                    a²-2ab+b²= (a-b)² — квадрат разности.

                   Рассмотрим примеры:

4х

2-у²= (2х)²-у²= (2х-у)(2х+у)                                      9х⁴-х⁶= (3х²)²-(х³)²= (3х²-х³)(3х²+х³)

8а³+b³= (2a)³+b³=(2a+b)(4a²-2ab+b²)                          27x⁶— 64y³= (3x²)³-(4y)³= (3x²-4y)(9x⁴+12x²y+16y²)

4x²-4xy+y²=(2x)²-2·2x·y+y²=(2x-y)²                              25a²+40a+16=(5a)²+2·5a·4+4²=(5a+4)²

         В математике не так часто бывает, что при разложении многочлена на множители применяется только один способ.

Чаще встречаются комбинированные примеры, где сначала используется один способ, затем другой и т. д. Например:

                   Разложите на множители многочлен:  27x³-18x²y+3xy²

         Сначала вынесем за скобки общий множитель, затем рассмотрим трехчлен в скобках, не является ли он квадратом суммы или квадратом разности.

                                       27x³-18x²y+3xy²=3x(9x²-6xy+y²)=3x(3x-y)²

                    Разложите на множители многочлен:  a⁴

+a²b²+b⁴

          Представим  a²b² в виде  2a²b²— a²b²

           a⁴+a²b²+b⁴=a⁴+2a²b²-a²b²+b⁴=(a⁴+2a²b²+b⁴)-a²b²=(a²+b²)²-(ab)²=(a²+b²-ab)(a²+b²+ab)

                                                                                                                                            вверх            

2.

3.4. Разложение на множители MathCAD 12 руководство

RADIOMASTER

Лучшие смартфоны на Android в 2022 году

Серия iPhone от Apple редко чем удивляет. Когда вы получаете новый iPhone, общее впечатление, скорее всего, будет очень похожим на ваше предыдущее устройство. Однако всё совсем не так в лагере владельцев устройств на Android. Существуют телефоны Android всех форм и размеров, не говоря уже о разных ценовых категориях. Другими словами, Android-телефон может подойти многим. Однако поиск лучших телефонов на Android может быть сложной задачей.

Документация Схемотехника CAD / CAM Статьи

MathCAD 12 MatLab OrCAD P CAD AutoCAD MathCAD 8 — 11

• Главная
/
• База знаний
/
• CAD / CAM
/
• org/Breadcrumb»>MathCAD 12

• Алгебраические вычисления
• 2.1. Операторы
  • 2.1.1. Арифметические операторы
  • 2.1.2. Вычислительные операторы
  • 2.1.3. Логические операторы
  • 2.1.4. Матричные операторы
  • 2.1.5. Операторы выражения
• 2.2. Функции
  • 2.2.1. Элементарные функции
  • 2.2.2. Вспомогательные функции
  • 2.2.3. Функция вывода текущего времени
  • 2.2.4. Спецфункции
• 2.3. Алгебраические преобразования
  • 2.3.1. О способах символьных вычислений
  • 2.3.2. Разложение выражений
  • 2.3.3. Упрощение выражений
  • 2.3.4. Разложение на множители
  • 2.3.5. Приведение подобных слагаемых
  • 2.3.6. Вычисление коэффициентов полинома
  • 2.3.7. Разложение на простые дроби
  • 2.3.8. Вычисление рядов и произведений
  • 2. 3.9. Подстановка переменной
  • 2.3.10. Получение численного значения выражения
  • 2.3.11. Вычисление предела
  • 2.3.12. О специфике аналитических вычислений

Разложение выражений на простые множители производится при помощи команды Symbolics/ Factor (Символика/ Разложить на множители) (рис. 2.18) либо использованием вместе с оператором символьного вывода ключевого слова factor (листинг 2.15). Эта операция позволяет разложить полиномы на произведение более простых полиномов, а целые числа — на простые сомножители. Применяя команду меню, не забывайте перед ее вызовом выделить все выражение или его часть, которую планируете разложить на множители.

Листинг 2.15. Примеры разложения на множители

Рис. 2.18. Разложение выражения на множители

Теги MathCad САПР

Сюжеты MathCad

Глава 1 Основы работы с системой Mathcad 11

9938 0

Глава 10 Работа с информационными ресурсами Mathcad 11

6960 0

Глава 2 Работа с файлами Mathcad 11

12453 0

Комментарии (0)

Вы должны авторизоваться, чтобы оставлять комментарии.

Вход

О проекте Использование материалов Контакты

Новости Статьи База знаний

Радиомастер
© 2005–2022 radiomaster.ru

При использовании материалов данного сайта прямая и явная ссылка на сайт radiomaster.ru обязательна. 0.2457 s

Фактор – элементарная математика

Термины фактор и множитель иногда путают друг с другом. Факторы 15 включают 3 и 5; числа, кратные 15, включают 30, 45, 60 (и более). Подробнее см. ниже и в нескольких местах.

Значение

Factor может использоваться как глагол или существительное.

• Глагол: Разложить число на множители означает выразить его как произведение (других) целых чисел, называемых его множителями. Например, мы можем разложить 12 как 3 × 4, или как 2 × 6, или как 2 × 2 × 3. Таким образом, 2, 3, 4 и 6 являются делителями 12.
• Существительное: Множитель числа — назовем это число N — это число, которое можно умножить на что-то, чтобы получить N как произведение. Другими словами: делители числа — это его делители; то есть они могут разделить это число, не оставляя остатка.

Итак, например, 3 — это коэффициент 12, потому что 3 — счетное число, и его можно умножить на 4, чтобы получить 12. Опять же, 3 — это коэффициент 12, потому что 3 делит 12 без остатка. Делителями 12 являются 1, 2, 3, 4, 6 и 12, потому что каждый из них делит 12 без остатка (или, альтернативно, каждый из них является счетным числом, которое можно умножить на другое счетное число, чтобы получить 12).

Некоторые тонкости

• Делители числа включают число, само себя и 1. Но это довольно тривиальные множители, и поэтому, когда мы говорим о разложении числа на множители, мы обычно не включаем факторизации, которые включают 1 или сам номер.
• В контексте чисел термины множитель (а также кратность и делимость) используются только в связи с целыми числами. Так, например, хотя 12 можно выразить в виде произведения с помощью дробей, например, 8 × 1 или 24 ×, это не факторизация 12.
• Простые числа имеют два множителя, само себя и 1, но это тривиальные множители, которые есть у каждого числа. Поскольку они не могут быть факторизованы каким-либо другим способом, мы говорим, что они не могут быть факторизованы. Например, число 7 «нельзя разложить на множители» (даже несмотря на то, что оно имеет два делителя 1 и 7 или может быть выражено как произведение нецелых чисел различными способами).
• Составные числа (подсчет чисел, которые не являются ни простыми, ни единицами) часто можно разложить на множители (выразить в виде произведения целых чисел) более чем одним способом. Например, 12 можно разложить как 3 × 4, или как 2 × 6, или как 2 × 2 × 3. Однако не все составные числа можно разложить более чем одним способом. Например, 25 можно разложить только как 5 × 5,9.0010
• Порядок, в котором числа перечислены в факторизации, не имеет значения: 3 × 4 и 4 × 3 — это одна и та же факторизация 12.

Дополнительные сведения о математике

Простой множитель числа — это просто множитель этого числа, который также является простым. Итак, число 12 имеет шесть делителей — 1, 2, 3, 4, 6 и 12, — но только два из них (2 и 3) простые, поэтому оно имеет только два простых делителя.

Разложение числа на простые множители — это факторизация — способ представления этого числа в виде произведения — состоящая только из простых чисел. Таким образом, число 12 может быть выражено в виде произведения многими способами — 1 × 2 × 2 × 3, или 3 × 4, 2 × 2 × 3 или 2 × 6, — но только один из них состоит исключительно из простых чисел: 2 × 2 × 3. (Число 1 не является простым. См. «Простые», чтобы узнать, почему.) Числа 2 и 3 — единственные простые делители числа 12, но простая факторизация числа 12 должна содержать двойку дважды — 2 × 2 × 3 (или 22 × 3), потому что 2 × 3 само по себе не дает 12,

Хотя многие числа можно разложить на множители более чем одним способом, их простая факторизация уникальна! Помимо порядка, есть только один способ разложить любое число на простые!

Что в слове?

Фактор относится к заводу.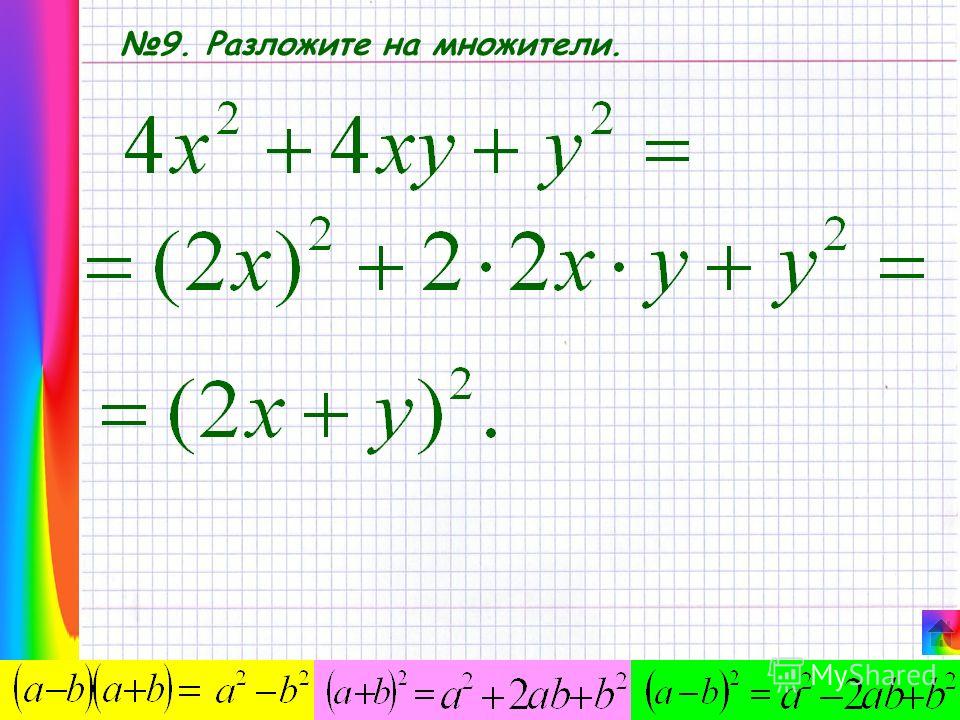 Точно так же, как фабрика — это место, производящее различные продукты, фактор — это число, которое производит другие числа как продукты. Слова фактор и фабрика происходят от латинского корня, означающего «делать» или «делать». Факт слова также связан; изначально «дело», что-то, что мы знаем, как истинное, потому что это было сделано.

Факторинг. Факторы и множители

Факторинг. Факторы и множители. Первый взгляд

Дом | Учитель | Родители | Глоссарий | О нас

В задача 3 х 4 = 12, 3 и 4 множители а 12 это произведение.

Факторинг это как разобрать число. Это значит представить число в виде произведения из его факторов.