Разложение многочленов на множители в комбинации с формулами сокращённого умножения 7 класс онлайн-подготовка на
Вводная информация
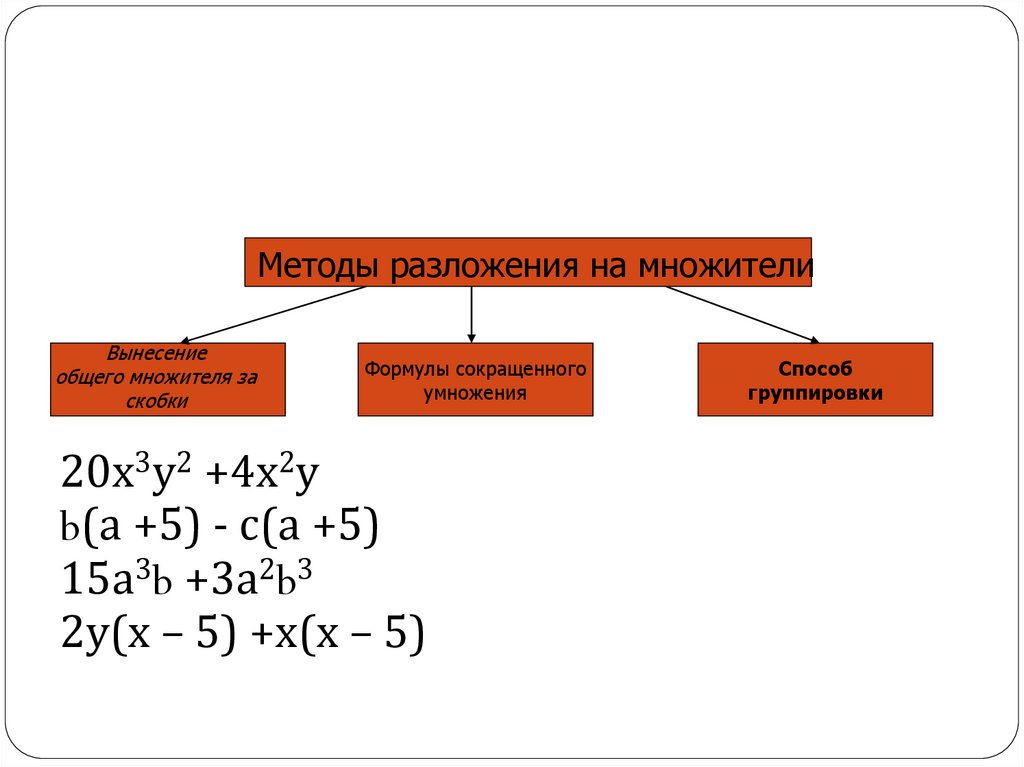
На предыдущих уроках мы изучили два способа разложения многочлена на множители – способ вынесения общего множителя и способ группировки. Кроме того, мы изучили формулы сокращенного умножения и говорили, что их также можно использовать для разложения многочлена на множители.
Теперь для начала рассмотрим простейшие способы комбинирования вышеуказанных методов разложения.
Пример 1:
;
Теперь усложним выражение, умножив заданный многочлен на три:
;
Данная формула очень похожа на полный квадрат, но в таком виде свернуть ее мы не можем, но мы видим, что у всех членов есть общий множитель и можем вынести его за скобку. Получаем:
;
Итак, первая комбинация это формулы сокращенного умножения плюс вынесение общего множителя за скобки.
Примеры на комбинацию вынесения общего множителя и формулы квадрата разности
Пример 2:
;
Определим, что можно вынести за скобки.
Для этого для начала найдем НОД:
;
Вынесем найденный общий множитель:
;
Определим, какие буквенные множители можно вынести. Обе переменные a и b есть во всех членах многочлена, значит, их можно выносить. Осталось определить только, в какой степени. Для этого найдем минимальную степень каждой из переменных. Это и . Вынесем найденную буквенную часть:
;
Распишем полученную скобку более подробно, для этого определим, квадратами каких выражений являются первое и третье выражение, а затем проверим удвоенное произведение:
;
Очевидно, что в скобке стоит полный квадрат разности, так как мы помним его формулу: . Свернем его:
;
Комбинирование способа группировки и формулы разности квадратов
Пример 3:
;
Сгруппируем первый, третий и четвертый член, получим:
;
В скобках мы видим квадрат суммы. Свернем его:
;
Теперь мы видим разность квадратов. Вспомним формулу: .
На основании этой формулы распишем наше выражение:
;
Итак, мы рассмотрели комбинацию способа группировки и формул сокращенного умножения.
Пример 4:
Поступаем аналогично предыдущему примеру: сначала группируем члены по схеме «3+1», после этого применяем формулы сокращенного умножения:
;
Комбинация вынесения множителя и формулы суммы кубов
Пример 5:
Очевидно, что нужно вынести за скобки:
В скобках мы получили формулу суммы кубов. Распишем ее:
В данном примере мы применили комбинацию вынесения общего множителя за скобки и формулы куба суммы.
Решение объемных примеров на комбинацию многих способов
Пример 6:
;
Распишем разность квадратов:
;
Пример 7:
;
Вынесем общий множитель за скобки:
;
Во второй скобке мы видим квадрат разности, можем свернуть его:
;
Выводы по уроку
Вывод: в данном уроке мы рассмотрели простейшие комбинации способов разложения многочлена на множители и формул сокращенного умножения и решили много различных примеров на разные варианты этих комбинаций.
Список рекомендованной литературы
1) Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. и др. Алгебра 7. 6 издание. М.: Просвещение. 2010 г.
2) Мерзляк А.Г., Полонский В.Б., Якир М.С. Алгебра 7. М.: ВЕНТАНА-ГРАФ
3) Колягин Ю.М., Ткачёва М.В., Фёдорова Н.Е. и др. Алгебра 7 .М.: Просвещение. 2006 г.
Рекомендованные ссылки на ресурсы интернет:
1. Школьный помощник (Источник).
2. Математика для чайников (Источник).
3. ЕГЭ по математике (Источник).
Рекомендованное домашнее задание:
Задание 1: Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. и др. Алгебра 7, № 890, ст.224;
Задание 2: Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. и др. Алгебра 7, № 897, ст.225
Задание 3: Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. и др. Алгебра 7, №899, ст. 225;
Разложение многочленов на множители по формулам суммы кубов и разности кубов.
Часть 1012+
4 месяца назад
Математика от Баканчиковой255 подписчиков
Алгебра 7 класс. Как разложить многочлен на множители с помощью формул сокращенного умножения суммы кубов и разности кубов? Сегодня, продолжая говорить о разложении многочленов на множители, мы ответим на этот вопрос. А чтобы Вы легко поняли и запомнили новый материал, вначале мы напомним Вам, как получаются формулы суммы кубов и разности кубов. Обратим Ваше внимание на то, чем отличаются формулы суммы и разности кубов. Дадим подсказки, которые помогут Вам находить в упражнениях формулы суммы кубов и разности кубов. На примере 6 упражнений мы подробно объясним Вам все нюансы разложения многочленов на множители по формулам суммы кубов и разности кубов. План урока и ссылки на предыдущие уроки Вы можете найти в описании под видео.
00:00 Начало видео.
00:32 Вспомним, как получаются формулы суммы кубов и разности кубов.
03:41 Как применять формулы суммы кубов и разности кубов при разложении многочленов на множители?
05:39 Как искать формулы суммы кубов и разности кубов?
09:20 Упражнение 1.
https://rutube.ru/video/fb2b71b55629739c9fcfe3dd41f51c0c/
Разложение многочленов на множители по формулам сокращенного умножения (разности квадратов). Часть 5. Алгебра 7 класс. https://rutube.ru/video/97a3410dd67f08691a3b148db5470edc/
Что такое разложение многочленов на множители. Как разложить одночлен на множители. Алгебра 7 класс. https://rutube.ru/video/e8012f424fccab7e8fc5e2506d4c7043/
Как вынести общий множитель (одночлен) за скобки. Разложение многочленов на множители. Часть 2. Алгебра 7 класс. https://rutube.ru/video/6d0a0ce6953e9a62a7dc0150ad3c1592/
Как вынести общий множитель (многочлен) за скобки. Разложение многочленов на множители. Часть 3. Алгебра 7 класс. https://rutube.ru/video/0e8aff292a37999c69c4a5831d4db654/
Разложение многочленов на множители. Способ группировки. Часть 4. Алгебра 7 класс. https://rutube.ru/video/614f1f9034150f4a7d271256ec96f6c7/
Алгебра 7 класс. Формулы сокращенного умножения. Разность квадратов двух выражений. Примеры упражнений. Урок 2 из 5. https://rutube.
Factorizing Expressions: Examples & Algebra
На широко известном университетском мероприятии под названием «день тряпок» я и мой друг Биодун оделись в разные костюмы.
Однако люди, видевшие нас, говорили, что мы братья, потому что, хотя мы были одеты в разные костюмы, они оба были костюмами для боевых искусств. Здесь вы узнаете о выражениях факторизации, понятиях, которые подсознательно использовались нашими наблюдателями.
Что такое факторизация выражений?
Факторизация выражений — это процесс упрощения выражений, при котором наибольший общий делитель (НОД) находится вне скобок, а результат — внутри скобок.
Расширение между НОД и результатом воспроизведет исходное выражение.
Вспомните, в начале этого исследования я и мой друг Биодун были одеты в костюмы и считались родственниками. На самом деле нас разложили на множители, потому что наблюдатели увидели, что между нами общего.
В выражениях, подобных обсуждаемым здесь, сходство определяется путем нахождения наибольшего общего делителя. Например, числа 6 и 4 имеют общее число. Это число должно делиться без остатка и на 6, и на 4, это число равно 2.
Точно так же 12 и 8 имеют 2 в качестве делителя, однако 4 также является делителем. В этом случае мы выбираем 4, потому что это число больше, чем 2, и сведет 8 и 12 к наименьшим результатам.
Когда 2 делится на 12 и 8, получается 6 и 4 соответственно. Между тем, 4 разделит 12 и 8 на 3 и 2 соответственно.
Как рассчитывается факторизация простых выражений?
Для факторизации простых выражений необходимо выполнить следующие шаги:
При необходимости изменить порядок выражений — это делается путем приведения одинаковых терминов.
Найдите наибольший общий делитель (НОД) среди слагаемых в выражении.
Разделите члены на НОД.
Откройте скобу.
Поместите НОД за скобку, а результат деления внутрь скобки.
Следовательно, ваше факторизованное выражение должно иметь вид:
a(x±y)
Где
a — НОД
, а x±y — результат.
Я часто называю то, что находится в скобках, макронимом, означающим математический акроним, потому что большинство акронимов находятся внутри скобок
Разложите на множители следующие выражения.
a) 15x+25y
b) 2x+4xy
c) 7pq+2ab-21bq+4AP
Решение:
A)
15x+25y
В этом случае нет необходимости. чтобы изменить выражение, чтобы найти НОД. На какое наибольшее число или выражение можно разделить без остатка и 15x, и 25y? НОД равен 5,9.0005
Затем разделите каждое из выражений на 5, чтобы получить результат (макроним). Таким образом,
(15x+25y)5=15×5+25y5(15x+25y)5=3x+5y
Теперь откройте скобку, поместите НОД вне скобки, а результат (макроним) внутри скобки. Вы должны получить
5(3x+5y)
Это означает, что при разложении на множители: нет необходимости переставлять выражение, чтобы найти НОД. Какое наибольшее число или выражение может делить без остатка как 2x, так и 4xy? НОД равен 2x.
Затем разделите каждое выражение на 2, чтобы получить результат (макроним). Таким образом,
(2x+4xy)2x=2x2x+4xy2x(2x+4xy)2x=1+2y
Теперь откройте скобку, поместите НОД вне скобки, а результат (макроним) внутри скобки.
Вы должны получить
2x(1+2y)
Это означает, что при факторизации:
2x+4xy=2x(1+2y)
c)
7pq+2ab-21bq+4ap
Первый что нужно сделать, это изменить выражение, приведя подобные термины. Используйте наилучший маршрут для достижения этой цели. Например, 2ab и -21bq могут быть сгруппированы, но только b является НОД между терминами в этой паре по сравнению с группировкой 2ab и 4ap, что можно сделать, как показано ниже,
7pq+2ab-21bq+4ap=7pq-21bq+2ab+4ap
Следующее, что нужно сделать, это разделить пары скобками, чтобы легко видеть, какие группы вы факторизуете, убедитесь, что у вас есть знак плюс между скобками.
7pq-21bq+2ab+4ap=(7pq-21bq)+(2ab+4ap)
Теперь разложите то, что у вас есть в скобках, отдельно, следуя ранее описанным шагам. Итак,
(7pq-21bq)7q=7pq7q-21bq7q(7pq-21bq)7q=p-3b7pq-21bq=7q(p-3b)
Аналогично, для другой пары имеем
(2ab+4ap)2a=2ab2a+4ap2a(2ab+4ap)2a=b+2p2ab+4ap=2a(b+2p)
Теперь вы успешно факторизовали пары, соедините их вместе, но на этот раз в их факторизованных формах.
. Таким образом,
7q(p-3b)+2a(b+2p)
Отсюда следует, что:
7pq+2ab-21bq+4ap=7q(p-3b)+2a(b+2p)
вы факторизуете и расширяете линейные выражения?
Линейные выражения представляют собой алгебраические представления, в которых константы и переменные находятся в первой степени. Они в форме:
3x+y-6
однако выражение
3x+y2-6
не является линейным выражением, поскольку y находится во второй степени.
При разложении на множители линейных выражений по-прежнему применяются ранее описанные шаги.
Факторизируйте следующее.
a) 4x+2y-10
b) 3x+y-9
Решение:
a)
4x+2y-10
Найдите НОД2, разделите на 2 здесь используя те же шаги, описанные в предыдущих примерах, и вы получите
4x+2y-10=2(2x+y-5)
b)
3x+y-9
Здесь нет общего множителя между всеми тремя терминами, однако есть общий множитель между двумя условий. Это означает, что вы можете сгруппировать их вместе, чтобы получить
3x+y-9=3x-9+y
Теперь поставьте скобки, отделяющие члены, которые вы должны разложить на множители, от тех, которые не могут быть разделены на общий фактор.
3x-9+y=(3x-9)+y
Теперь вы можете разложить на множители то, что находится в скобках, по НОД, равному 3. Избегайте вмешательства в другие члены вне скобок.
(3x-9)3=3×3-933×3-93=x-3
Итак, вы разложили на множители, чтобы получить
3x-9=3(x-3)
Теперь вы можете добавить обратно другой член( s) вне скобок, чтобы завершить выражение.
3x+y-9=3(x-3)+y
Обратите внимание, что при расширении факторизованного выражения будет получено исходное выражение. Если вы пытаетесь расширить и не можете прийти к исходному выражению, это указывает на то, что вы, должно быть, сделали один или несколько шагов неправильно. Следовательно, вам рекомендуется реорганизовать выражение, пока вы не получите его правильно.
Как разложить на множители квадратные выражения?
Квадратные выражения представляют собой выражения в форме:
ax2+bx+c
где a, b и c — числа, не равные нулю.
Вы факторизуете квадратные выражения, используя правило суммы и произведения.
Правило суммы и произведения факторизации квадратных выражений
Правило сумм квадратных выражений утверждает, что сумма двух множителей квадратного уравнения равна коэффициенту bx в уравнении,
ax2+bx+c
что b. Если факторами квадратного уравнения являются α и β, то:
α+β=b
Между тем правило произведения гласит, что когда эти два фактора умножаются, произведение равно коэффициенту acx 2 . Таким образом,
αβ=ac
Следовательно, при нахождении множителей квадратного уравнения вы должны убедиться, что найденные множители соответствуют правилу суммы и произведения.
Разложите на множители следующие выражения.
а) х2-5х+6
б) 2х2+9х+4
Решение:
а)
х2-5х+6
Первое, что нужно сделать, это умножить константу 6 на х 2 , чтобы получить 6x 2 . Напомним, что правило произведения гласит:
αβ=ac
ac — это коэффициент при x 2 , и в данном случае он равен 6.
Теперь выпишите произведение множителей 6, учитывая как положительные, так и отрицательные числа. Сюда входят:
2×3=6,
-2×(-3)=6,
1×6=6
и
-1×(-6)=6
Теперь у вас есть возможные факторы, вам нужно знать, какая пара будет соответствовать правило суммы. Напомним, что:
α+β=b
Итак, мы ищем сумму факторов, которые дали бы коэффициент x, который равен -5 из этого вопроса. Посмотрим на сумму пар.
2+3=5-2+(-3)=-51+6=7-1+(-6)=-7
Это означает, что наша правая пара множителей равна -2 и -3.
Следующее, что нужно сделать, это заменить -5x на наши множители, зная, что
-5x=-2x+(-3x)-5x=-2x-3x
Таким образом,
x2-5x+6=x2-2x-3x+6
Теперь просто следуйте описанным выше шагам и разложите сначала размещение скобок и наличие знака плюс, чтобы разделить обе скобки.
x2-2x-3x+6=(x2-2x)+(-3x+6)
Затем разложите на множители НОД каждого выражения в скобках.
(x2-2x)+(-3x+6)=x(x-2)-3(x-2)
При факторизации квадратных уравнений необходимо убедиться, что результаты (макронимы) одинаковы в обоих кронштейны.
В этом случае у нас есть (x-2) в обеих скобках.
Следующий шаг весьма интересен, добавьте множители вне скобок и поместите их в скобки, и удалите одну из похожих скобок, чтобы у вас было две скобки, разделенные без знака между скобками. Сделайте это, и вы получите:
(x-3)(x-2)
Следовательно,
x2-5x+6=(x-3)(x-2)
b)
2×2+9x +4
Первое, что нужно сделать, это умножить константу 4 на 2x 2 , чтобы получить 8x 2 . Напомним, что правило произведения гласит:
αβ=ac
ac — это коэффициент при x 2 , и в данном случае он равен 8.
Теперь выпишите произведение 8, учитывая как положительные, так и отрицательные числа. Сюда входят:
2×4=8,
-2×(-4)=8,
1×8=8
и
-1×(-8)=8
Теперь у вас есть возможность факторов, вам нужно знать, какая пара будет соответствовать правилу сумм. Напомним, что:
α+β=b
Итак, мы ищем сумму множителей, которая дает коэффициент x, равный 9от этого вопроса.
Посмотрим на сумму пар.
2+4=6-2+(-4)=-61+8=9-1+(-8)=-9
Это означает, что наша правильная пара множителей равна 1 и 8.
Следующее состоит в том, чтобы заменить 9x на наши множители, зная, что
9x=x+8x
Следовательно,
2×2+9x+4=2×2+x+8x+4
ваши скобки и знак плюс, чтобы разделить обе скобки.
2×2+x+8x+4=(2×2+x)+(8x+4)
Затем разложите на множители НОД каждого выражения в скобках.
(2×2+x)+(8x+4)=x(2x+1)+4(2x+1)
При факторизации квадратных уравнений необходимо убедиться, что результаты (макронимы) одинаковы в обеих скобках . В этом случае у нас есть (2x+1) в обеих скобках.
Следующий шаг весьма интересен, добавьте множители вне скобок и поместите их в скобки, и удалите одну из похожих скобок, чтобы у вас было две скобки, разделенные без знака между скобками. Сделайте это, и у вас будет:
(x+4)(2x+1)
Следовательно,
2×2+9x+4=(x+4)(2x+1)
Следует отметить, что коэффициенты квадратного выражения можно получить используя другие методы, такие как метод завершения квадрата, всемогущая формула и графический метод.
Другие примеры разложения выражений на множители
Лучшего понимания выражений можно достичь, решая как можно больше задач.
Решите следующее.
14(к+1)2+21(к+1)
Решение:
Чтобы разложить на множители:
14(k+1)2+21(k+1)
вы должны расширить выражение. Таким образом,
14(k+1)2+21(k+1)=14(k+1)(k+1)+21k+21(k+1)(k+1)=k2+2k+114 (k+1)(k+1)+21k+21=14(k2+2k+1)+21k+2114(k2+2k+1)+21k+21=14k2+28k+14+21k+21
Соедините похожие термины.
14k2+28k+14+21k+21=14k2+28k+21k+14+2114k2+28k+21k+14+21=14k2+49k+35
Глядя на выражение 14k2+49k+35, вы можете сказать, что общий коэффициент равен 7. Примените шаги, описанные ранее, и получите:
14k2+49k+35=7(2k2+7k+5)
Теперь выражение7(2k2+7k+5) может быть дополнительно разложено на множители (2k2+7k+5), которое является квадратным выражением. Попробуйте то, что вы уже узнали, разложив на множители выражение 2k2+7k+5, и вы должны получить:
2k2+7k+5=(2k+5)(k+1)
Не забывайте, что у вас есть 7 умножение на выражение, поэтому факторизованное выражение будет
7(2k2+7k+5)=7(2k+5)(k+1)14(k+1)2+21(k+1)=7( 2k+5)(k+1)
Финики получили 7 апельсинов и 4 груши, а Индодо — 3 апельсина и 11 груш.
Выразите сумму их плодов в факторизованном выражении.
Решение:
Пусть апельсинов будет x, а груш — y. Таким образом, полученные плоды Финики могут быть выражены как
7x+4y
, а полученные плоды Индодо могут быть выражены как
3x+11y
Сумма плодов Финики и Индодо будет:
(7x+4y)+ (3x+11y)=7x+3x+4y+11y7x+3x+4y+11y=10x+15y
Теперь у вас есть сумма, разложите выражение на множители.
10x+15y=5(2x+3y)
Выражения на множители. Ключевые выводы
- Факторизация выражений — это процесс упрощения выражений, который дает наибольший общий делитель (НОД) вне скобок и результат внутри скобок.
- Чтобы разложить на множители простые выражения, необходимо выполнить несколько шагов.
- Линейные выражения — это алгебраические представления, в которых константы и переменные находятся в первой степени.
- Квадратные выражения факторизуются с применением правила суммы и произведения.
Факторизация полиномов — Факторизация полиномов с примерами
Факторизация полиномов требуется для решения различных задач по алгебре. Множители — это числа или алгебраические выражения, которые делят другое число или выражение нацело, т. е. их деление дает в остатке 0, (или) множители считаются небольшими числами или выражениями, которые при умножении дают другие числа.
Пример: 1, 2, 4, 7, 14 и 28 являются множителями числа 28.
Аналогично, многочлен разлагается на множители, чтобы записать его как произведение двух или более многочленов. Это называется факторизацией многочлена. любое число или полином является простой факторизацией. В этом методе мы записываем число в виде произведения его простых множителей.
Пример. Найдите простые делители числа 70
70 = 2 × 5 × 7
(здесь 2, 5, 7 — множители 70; их также называют простыми множителями, поскольку эти 2, 5, 7 — простые числа)
Аналогично можно выразить алгебраическую выражения как произведение их множителей.
Если алгебраическое выражение нельзя сократить дальше, то его множители называются простыми множителями.
Пример:
Типы факторинговых полиномов8xy = 2 × 2 × 2 × x × y
(здесь 8xy образуется путем умножения чисел (2, 2, 2, x, y) они являются множителями 8xy)
Факторизация — это не что иное, как запись числа как произведения меньших чисел. Это разложение ряда (или) математических объектов на меньшие или более простые числа/объекты. Факторизация различных типов алгебраических выражений очень полезна для различных целей, используемых в математике. Существуют различные методы факторизации:0028
Наибольший общий делительНаибольший общий делитель между двумя числами называется GCF (Greatest Common Factor). Это полезно для разложения многочленов на множители
Шаги для нахождения GCF:
- Шаг 1: Сначала разделите каждый член алгебраического выражения на неприводимые множители
- Шаг 2: Затем найдите среди них общие члены.
- Шаг 3: Теперь произведение общих членов и оставшихся членов дает требуемую форму множителя.
Пример: Факторизация 3x + 18
Решение:
ПерегруппировкаШаг 1: Сначала разобьем каждый член на несократимые множители.
3x = 3 × x
18 = 2 × 3 × 3Шаг 2: Следующий шаг, чтобы найти общий термин
3 является единственным общим термином
Шаг 3: Теперь произведение общих терминов а оставшиеся члены равны 3(x + 6)
Итак, 3(x + 6) искомая форма.
Иногда члены данного выражения следует расположить в подходящие группы таким образом, чтобы все группы имели общий делитель, и тогда общий делитель выносится. Таким образом производится факторизация многочлена.
Пример: разложить на множители x 2 + yz + xy + xz
Решение:
Факторизация с использованием тождеств) как одну группу и (yz + xz) как другую группу.
Факторы (x 2 + xy) = (x × x) + (x × y)
= x(x + y) × z)
= z(x + y)После их объединения
x 2 + yz + xy + xz = x(x + y) + 2 (x + 0y) 900 ) как обычно получаем,
x 2 + yz + xy + xz = (x + y) (x + z)
Существует множество стандартных алгебраических тождеств, которые используются для факторизации различных многочленов. Некоторые из них приведены ниже:
- (a + b) 2 = a 2 + 2ab + b 2
- (a – b) 2 = a 2 2
- a 2 – b 2 = (a + b) (a – b)
Example 1: Factorise x 2 + 8x + 16
Solution:
Это в виде (a + b) 2 = A 2 + 2AB + B 2
x 2 + 8x + 16 = x 2 + 2 × x × 4 + 4 2
= (x + 4) 2 (x + 4) 2
= (x + 4) 2 .
= (x + 4) (x + 4)
Пример 2: Фактор x 2 — 6x +
Решение:
Это в форме (a — b. ) 2 = а 2 – 2аб + б 2
х 2 — 6x + 9 = x 2 — 2 × x × 3 + 3 2
= (x — 3) 2
= (x — 3) (x — 3) 9058 = (x — 3) (x — 3) 3
3
3
3
3
9033
3
3
3
3.
= . Факторы с использованием терминов SplitigФакторирование многочленов в основном используется для решения квадратных уравнений. Квадратное уравнение факторизуется, чтобы свести его к линейным множителям. Используемое квадратное уравнение имеет вид x 2 + (a + b)x + ab = 0, которое разбивается на два множителя (x + a)(x + b) = 0. Рассмотрим квадратичный полином вида
х 2 + (а + б)х + аб.
= x.x + ax + bx + ab
= x(x + a) + b(x + a)
= (x + a)(x + b)В приведенном выше многочлене средний член разбивается как сумма или разность двух членов, а постоянный член является произведением этих двух факторов.
Например: х 2 + 5х + 6
Решение:
= х 2 + 5х + 6
= х.х + (3 + 2)х + 3.2
= х.х + х5 = 4х3 + 2х 0 + 3) + 4(x + 3)
= (x + 3)(x + 4)Таким образом, разложение многочленов на множители осуществляется путем разделения средних членов квадратного многочлена.
Решенные примеры факторизации
Пример 1. Факторизация a 2 – 20a + 100
Решение:
Это в виде (a – b) 2 = a 2 – 2ab + b 2
a 2 – 20a + 100 = a 2 – 2 × a1 +
2
= (a — 10) 2
= (A — 10) (A — 10)
Пример 2: Фактор 25x 2 — 49
Solution: 9
5669929292962:
666992962.
25x 2 — 49 = (5x) 2 — 7 2
= (5x + 7) (5x — 7)
Затем общие факторы берутся путем группировки первого и второго членов, а также третьего и четвертого членов. Таким образом, квадратичный многочлен выражается как произведение двух множителей.
Это форма a 2 – b 2 = (a + b) (a – b)Пример 3: Фактор 2x + 3 + 2Y + 3X
Решение:
2xy + 2y + 3x + 3 [ перестановка членов для получения общих членов]
= 2y (x + 1) + 3(x + 1)
920003 = ( x + 1)
Часто задаваемые вопросы по факторизации
Вопрос 1: Что такое факторизация и напишите ее пример?
Ответ:
Факторизация — это разбиение большего числа на меньшие числа, так что при умножении они дают исходное число. Например, факторизация 15 достигается путем умножения 3 на 5.
т. е. 15 = 5 × 3
Вопрос 2: Каковы основные 4 типа методов факторизации?
Ответ:
Четыре основных типа методов факторинга:
- Наибольший общий множитель (GCF),
- Метод группировки,
- Разность в двух квадратах,
- Сумма или разность в кубах.
