Теория рядов
Теория рядов
ОглавлениеПРЕДИСЛОВИЕ К ПЕРВОМУ ИЗДАНИЮГЛАВА 1.  ПРОГРЕССИИ§ 2. Геометрические прогрессии § 3. Бесконечные прогрессии; их сходимость и расходимость § 4. Элементарные преобразования прогрессий § 5. Функциональные прогрессии: область сходимости; равномерная сходимость § 6. Почленное интегрирование прогрессий § 7. Почленное дифференцирование прогрессий § 8. Прогрессии с комплексными членами ГЛАВА 2. ЧИСЛОВЫЕ РЯДЫ. ОСНОВНЫЕ ПОНЯТИЯ. ОСНОВНЫЕ ТЕОРЕМЫ О СХОДИМОСТИ § 2. Определение числового ряда и его сходимости § 3. Остаток ряда § 4. Принцип сходимости Коши § 5. Критерий Коши сходимости рядов § 6. Необходимый признак сходимости ряда § 7. Желательность систематической теории § 8. Свойства сходящихся рядов, подобные свойствам сумм § 9. Дальнейшие свойства рядов ГЛАВА 3. РЯДЫ С ПОЛОЖИТЕЛЬНЫМИ ЧЛЕНАМИ § 1. Признаки сходимости рядов § 2. Признаки сравнения § 3. Интегральный признак сходимости Маклорена — Коши § 4. Применения интегрального признака сходимости § 5.  Сравнительная оценка различных признаков сходимости§ 6. Признак сходимости Даламбера § 7. Признак сходимости Коши § 8. Чувствительность признаков сходимости Даламбера и Коши ГЛАВА 4. ЗНАКОПЕРЕМЕННЫЕ РЯДЫ § 2. Абсолютная сходимость и расходимость § 3. Возможность переставлять члены в абсолютно сходящихся рядах § 4. Условно сходящиеся знакопеременные ряды § 5. Умножение абсолютно сходящихся рядов § 6. Признак сходимости Лейбница § 7. Существенность условий признака сходимости Лейбница ГЛАВА 5. ФУНКЦИОНАЛЬНЫЕ РЯДЫ § 2. Область сходимости функционального ряда § 3. Сходимость последовательности функций. Основные определения § 4. Предел последовательности непрерывных функций § 5. Переход к пределу под знаком интеграла § 6. Переход к пределу под знаком производной § 8. Непрерывность суммы равномерно сходящегося ряда с непрерывными членами § 9. 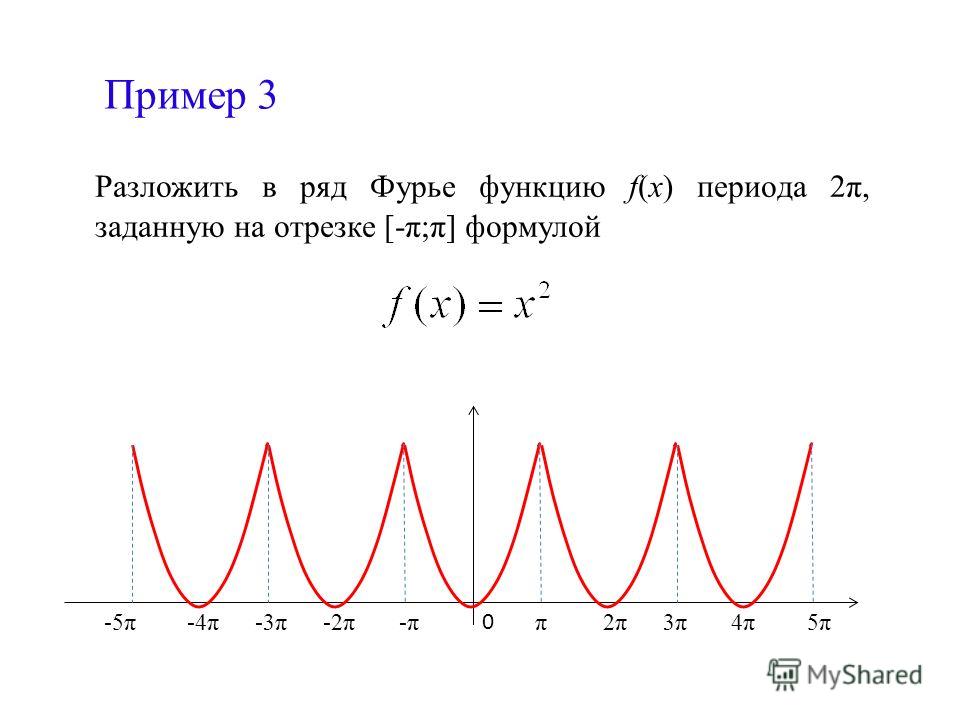 Почленное интегрирование функциональных рядов§ 10. Почленное дифференцирование функциональных рядов ГЛАВА 6. СТЕПЕННЫЕ РЯДЫ. ОБЩИЕ ВОПРОСЫ § 2. Теорема Абеля § 3. Круг сходимости ряда § 4. Вещественный степенной ряд и его интервал сходимости § 5. Равномерная сходимость ряда в круге его сходимости § 6. Вещественные ряды § 7. Комплексные ряды § 8. Разложение функций в степенные ряды § 9. Формула Тейлора § 10. Ряды Тейлора и Маклорена ГЛАВА 7. СТЕПЕННЫЕ РЯДЫ. ПРИМЕРЫ И ПРИЛОЖЕНИЯ § 2. Разложения в ряды Маклорена гиперболических функций ch x и sh x § 3. Разложения в ряды Маклорена тригонометрических функций cos x и sin x § 4. Показательная функция с комплексным значением показателя § 5. Формулы Эйлера § 6. Тригонометрические функции от комплексного значения аргумента § 7. Гиперболические функции от комплексного значения аргумента § 8. Вычисление значений функций при помощи ряда Маклорена § 9. Биномиальный ряд § 10.  Приложения биномиального ряда§ 11. Разложение в ряд Маклорена логарифмической функции § 12. Приближенное вычисление определенных интегралов при помощи степенных рядов § 13. Приближенное интегрирование дифференциальных уравнений при помощи степенных рядов ГЛАВА 8. ОРТОГОНАЛЬНЫЕ И ОРТОНОРМАЛЬНЫЕ СИСТЕМЫ ФУНКЦИЙ § 2. Векторы и функции § 3. Нормированные и ортогональные функции § 4. Нормированные и ортогональные системы функций § 5. Нормировка систем функций § 6. Разложение по системам функций ГЛАВА 9. РЯДЫ ФУРЬЕ § 1. Ряды и коэффициенты Фурье § 2. Условия Дирихле и теорема о разложении функции в ряд Фурье § 4. Физическое истолкование разложения функции в тригонометрический ряд Фурье § 5. Разложение функции f(x) = x § 6. Сдвиг сегмента разложения § 7. Изменение длины сегмента разложения § 8. Четные и нечетные функции § 9. Разложение четной функции в ряд Фурье § 10.  Разложение нечетной функции в ряд Фурье§ 11. Разложение ряд Фурье функций на сегменте от 0 до пи § 12. Комплексная форма записи ряда Фурье § 13. Разложение в комплексный ряд Фурье § 14. Характер сходимости рядов Фурье ГЛАВА 10. УРАВНЕНИЕ СВОБОДНЫХ МАЛЫХ КОЛЕБАНИЙ СТРУНЫ С ЗАКРЕПЛЕННЫМИ КОНЦАМИ § 2. Начальные и граничные условия § 3. Метод разделения переменных § 4. Использование граничных условий. Собственные функции и собственные значения § 5. Использование начальных условий ГЛАВА 11. ИНТЕГРАЛ ФУРЬЕ § 1. Представление функций интегралом Фурье § 2. Простейшие достаточные условия представимости функции интегралом Фурье § 3. Интеграл Фурье для четных функций § 4. Интеграл Фурье для нечетных функций § 5. Комплексная форма интеграла Фурье § 6. Понятие о преобразовании Фурье § 7. Косинус-преобразование Фурье § 8. Синус-преобразование Фурье § 9. Спектральная функция Часть II § 1. Признак сходимости Куммера § 2.  Признак сходимости Раабе§ 3. Признак сходимости Бертрана § 4. Признак сходимости Гаусса § 5. Сходимость знакопеременных рядов § 6. Признак сходимости Дирихле ГЛАВА 13. ДВОЙНЫЕ РЯДЫ § 1. Определение двойного ряда § 2. Сходимость двойных рядов § 3. Критерии сходимости двойных рядов. Теорема Маркова § 4. Свойства двойных рядов и признаки сходимости § 6. Двойные функциональные ряды § 7. Двойные степенные ряды § 8. Разложение функций двух переменных в двойные ряды Тейлора и Маклорена § 9. Ортогональные и ортонормальные системы функций от двух переменных § 10. Двойные ряды Фурье ГЛАВА 14. СУММИРОВАНИЕ СХОДЯЩИХСЯ РЯДОВ § 2. Линейные преобразования рядов § 3. Теорема Абеля и почленное дифференцирование и интегрирование рядов § 4. Последовательности разностей § 5. Преобразование рядов по Эйлеру § 6. Преобразование рядов по Куммеру ГЛАВА 15. СУММИРОВАНИЕ РАСХОДЯЩИХСЯ РЯДОВ § 1.  Расходящиеся геометрические прогрессии§ 2. Суммирующие функции § 3. Суммирование по Пуассону — Абелю § 4. Линейность и регулярность суммирования по Пуассону — Абелю § 5. Суммируемость рядов по Пуассону — Абелю и их абсолютная сходимость § 6. Теорема Таубера § 7. Суммирование по Чезаро § 8. Соотношение между сходимостью по Чезаро и по Пуассону — Абелю § 9. Суммирование по Эйлеру ГЛАВА 16. СХОДИМОСТЬ РЯДОВ ФУРЬЕ § 2. Исследование двух интегралов § 3. Исследование одного класса интегралов § 4. Доказательство теоремы Дирихле § 5. Теорема Фурье § 6. Коэффициенты Фурье разрывных функций § 7. Скорость сходимости рядов Фурье § 8. Улучшение сходимости рядов Фурье по методу выделения особенностей § 9. О равномерной сходимости рядов Фурье § 10. Неравномерная сходимость последовательностей непрерывных функций § 11. Поведение рядов Фурье функций в точках их разрыва. Явление Гиббса § 12. Экстремальное свойство сумм Фурье § 13.  Суммирование рядов Фурье по Чезаро. Теорема Фейера§ 14. Равенство Парсеваля ГЛАВА 17. ПРИМЕНЕНИЕ РЯДОВ ФУРЬЕ В ТЕОРИИ ИЗГИБА БАЛОК § 2. Изгиб балки § 3. Свободно опертая балка § 4. Первая возможность ограничиться двукратным дифференцированием § 5. Случай сосредоточенной нагрузки § 6. Прогиб балки от распределенной нагрузки § 7. Прогиб от сосредоточенного момента § 8. Статически неопределимая балка § 9. Сложный изгиб балки § 10. Балка на упругом основании § 11. Вторая возможность ограничиться двукратным дифференцированием. Потенциальная энергия изгиба балки § 12. Потенциальная энергия изгиба балки в случае нескольких нагрузок § 13. Функции прогиба с ортогональными вторыми производными § 14. Свободно опертая нагруженная балка § 15. Работа продольных сил при сложном изгибе балки § 16. Общий случай изгиба балки § 17. Общий случай изгиба свободно опертой балки § 18. Изгиб симметрично нагруженной балки, жестко заделанной по концам § 19.  Функция прогиба симметрично загруженной балки с жестко заделанными концами |
Вариант 25
1. Разложить в ряд Фурье функцию , заданную с помощью графика или в явном виде. Построить график суммы полученного ряда Фурье и записать 4 первых ненулевых члена этого ряда.
Разложим функцию в ряд Фурье с периодом
,
Где:
Сумма ряда : 1) в точках непрерывности:
2) в точках разрыва:
2. Разложить функцию, представленную графиком, в ряд Фурье по косинусам. Построить график суммы полученного ряда Фурье и записать 4 ненулевых члена ряда
Функцию можно представить в виде
,
Продолжаем функцию четным образом до периода
Сумма ряда : 1) в точках непрерывности:
2) в точках разрыва:
3. Решить задачу Штурма – Лиувилля . Найти собственные функции, проверить их ортогональность.
Разложить функцию в ряд по собственным функциям.
Решение задачи Штурма – Лиувилля ищем в виде: .
Характеристическое уравнение
1) — кратный корень.
Общее решение имеет вид: ,
Граничные условия:
2)
Общее решение имеет вид:
Граничные условия:
Т. к. — тривиальное решение.
3)
Общее решение имеет вид:
Граничные условия:
Система собственных функций при .
Проверка на ортогональность собственных функций Система собственных функций ортогональна.
Разложим в ряд по собственным функциям .
Согласно теореме Стеклова функцию можно разложить в ряд Фурье: ,
Где
Значит:
4. Решить задачу о свободном колебании струны длины м с заданными краевыми условиями ; . Вычислить приближённое отклонение середины струны при сек, используя для этого первые три ненулевых слагаемых в разложении в ряд функции . Положить .
Решение
Будем искать решение уравнения свободных колебаний струны , удовлетворяющее однородным граничным условиям: и начальным условиям И представимое в виде произведения.
Подставляем его в исходное уравнение
Отсюда
Следовательно: Граничные условия
При получили задачу Штурма – Лиувилля для X(x): .
Решение ищем в виде:
Характеристическое уравнение
1) — кратный корень.
Общее решение имеет вид:
Граничные условия: — тривиальное решение
2) , где — действительное число
Общее решение имеет вид:
Граничные условия:
Т. к. — тривиальное решение.
3), — действительное число
Общее решение имеет вид:
Граничные условия:
Если
При этом пусть С2=1, тогда , при .
Этим же значениям соответствуют решения уравнения , имеющие вид:
Частное решение уравнения свободных колебаний струны:
Общее решение имеет вид:
Начальные условия Значит
Разлагаем в ряд Фурье по синусам на промежутке : Сравнивая ряды, видим:
Общее решение представится в виде:
Приближенное отклонение середины струны ( ) в момент времени :
; ;
| < Предыдущая | Следующая > |
|---|
(2): серия Фурье Расширение серии
(2): серия ФурьеРасширение серии 5.
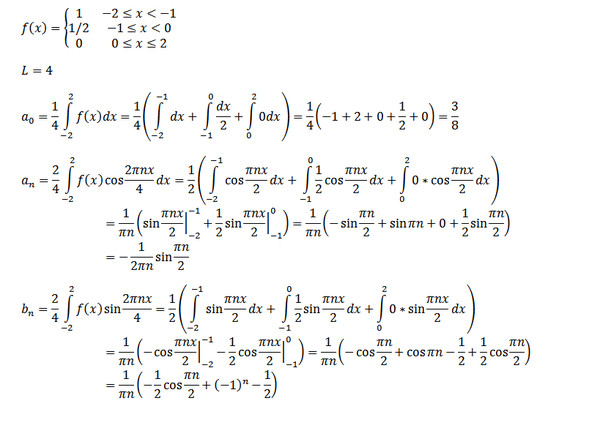10 (2): серия Фурье5.10.1 Ряды Тейлора и ряды Фурье
Частичные суммы ряда Тейлора, приближающие функцию f(x) в окрестности расчетная точка x0 через частичные суммы степенного ряда. Если кто-то хочет аппроксимировать функцию над Для большего интервала потребуются члены очень высокого порядка. Полином, полученный усечение ряда Тейлора должно иметь как минимум столько поворотных точек, сколько функция. Для периодических функций это было бы очень утомительно для больших интервалов. чем период.
Периодические функции имеют большое практическое значение в телекоммуникациях и электротехника. Для таких функций аппроксимация через суперпозиция периодических стандартных функций (синуса и косинуса0 гораздо лучше подходит. On расширяет функцию в ряд, который состоит из основного тона и обертонов, т. е. из функций грех и cosnx с целым числом значения н.
Сразу очевидна аналогия с анализом колеблющейся струны:
sinx описывает вибрацию
основного тона, sin2x
что у октавы, sin3x
что из квинты выше октавы и так далее.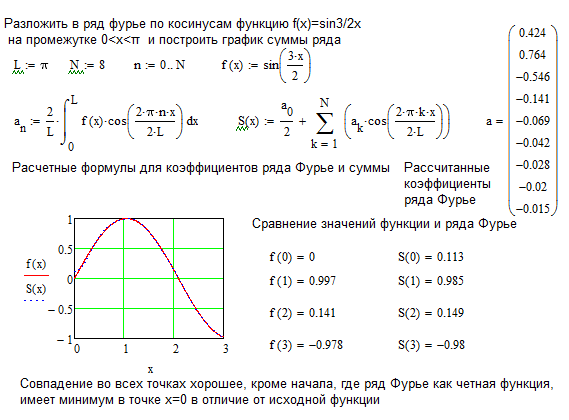
Для струны, закрепленной на обоих концах; переменная
х теперь
произведение ωt
угловая частота ω
и время т.
x=ωt=2πνt=2πtT;νчастота колебаний;T продолжительность одного периода
Фурье
В зависимости от формы f(t) накладывают большее или меньшее количество этих синусоидальных/косинусоидальных колебаний с определенной силы и выражается в виде числа, определяющего амплитуду. Набор амплитуды обертонов, т.е. коэффициенты разложения ряда представляют собой спектр периодических колебаний. Спектр и форма колебаний соответствующие представления об одном и том же явлении. Это представление в терминах функций синусов и косинусов называется рядом Фурье ф(т).
В то время как частичные суммы ряда Тейлора аппроксимируют функцию в
близости точки , частичные суммы ряда Фурье являются приближениями для
весь интервал основного периода и, следовательно, также — из-за
периодичность рассматриваемых функций — для неограниченной области переменной
Икс.
Ряд Фурье не обязательно должен совпадать с функцией ни в одной точке, а это
случай для ряда Тейлора в точке вычисления.
Зависит от свойств f(t), сколько обертонов нужно наложить, чтобы аппроксимировать функцию почти все точки. Если трактовать понятие сходимости не строго, то ряды Фурье сходятся для всех функций, даже для непрерывных. Конвергенция тогда не обязательно монотонно, т.е. может быть лучше для некоторых значений т и хуже для некоторых другие значения t и даже потерпеть неудачу для некоторых значений! На разрывах наблюдаются перерегулирования даже для высших порядков ряда. В телекоммуникациях это называется звонком.
Поскольку периодические явления, которые мы здесь рассматриваем, в основном представляют собой колебания во времени, переменной обычно является x=ωt. Чтобы также смоделировать фазы отдельных обертонов, мы используем сумму членов с грех и cosnx. Затем сумма представляет собой сдвинутую по фазе функцию синуса или косинуса. Таким образом, общий Фурье серия читает
f(t)=a02+ ∑n=1∞an cos(nωt)+bn sin(nωt).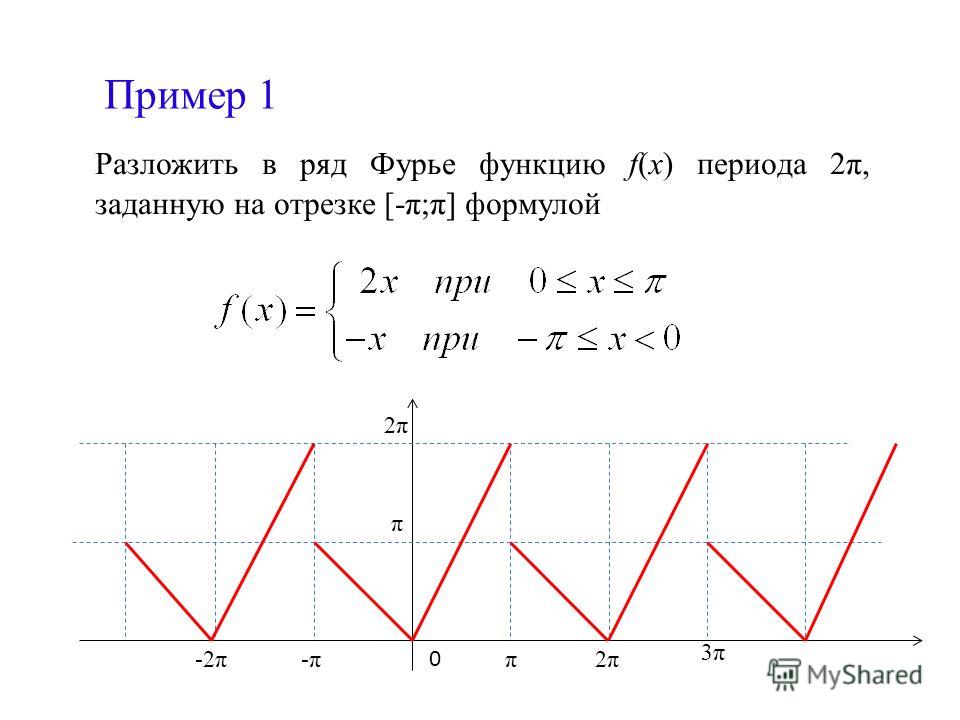
Для заданного спектра a0,ai,bi,i=1,2,⋯ можно вычислить f(t). Для заданной функции f(t) все коэффициенты могут быть определены и, таким образом, известен спектр.
5.10.2 Определение коэффициентов Фурье
Как нам теперь получить коэффициенты а бн?
Для ряда Тейлора мы использовали тот факт, что после дифференцирования все члены, которые еще содержат расстояние х к моменту вычисления, становятся равными нулю, так что коэффициент соответствующий постоянный член дает множителю соответствующую производную a пункт расчета.
Вместо этого для ряда Фурье мы начинаем с интегрирования произведения функции и обертонов cos(mωt)or.sin(mωt);m=1,2,3… за один период T фундаментальной частота (м=1)
∫ 0Tcos(mωt)f(t)dt= ∫ 0Tcos(mωt)(a02+ ∑n=1∞an cos(nωt)+bn sin(nωt))dt∫ 0Tsin(mωt)f(t)dt= ∫ 0Tsin(mωt)(a02+ ∑n=1∞an cos(nωt)+bn sin(nωt))dt
Сначала это выглядит немного сложно; однако оказывается, что интеграл
над константой, т.
е. первый член перед символом суммы почти всегда
обращается в нуль, так как интеграл по периоду косинуса или синуса равен нулю. Только для
m=0 получается
вклад, поскольку имеем cos0=1=
константа Поэтому применяется следующее:
а02=1Т∫ 0Tf(t)dt.
Кроме того, интеграл по произведению обертона м и секунда обертон сущ. ноль, если м и n не равный. Это также применимо, когда функция косинуса и синуса умножается, потому что функции синуса нечетны, а функция косинуса четна относительно х=0. Поэтому нам осталось только с интегралами cos2nx или sin2nx который обе равны T/2. Таким образом, коэффициенты легко выписываются, но для этого требуется определение интегралов, что требует численных расчетов.
ан=2Т∫ cos(nωt)f(t)dt;bn=2T∫ sin(nωt)f(t)dt
Моделирование на рис.5.15 визуализирует эти обстоятельства, которые упрощают
расчет коэффициентов Фурье.
Из поля выбора продукт
периодических функций интересующего нас общего вида есть
выбрано: cos(mx)(acos(nx)+bsin(nx)). Красная кривая
представляет произведение в cosmx
и регулируемый обертон acosnx+bsinnx,
на рисунке имеем m=10
и n=8.
синяя кривая показывает интеграл, конечное значение которого (определенный интеграл за один период
f(t)) обращается в нуль
для m≠n. Для
m=n получаем, когда
интегрирование по acosmxcosmx
результат aπ, а интеграл
над смешанным термином bcosmxsinmx
исчезает. Интеграция запускается выбором соответствующей опции
коробка.
С слайдами параметры a и б и целые числа м и н может быть выбранным. Функция обведена красным. После активации поля под названием Интеграл интегральная функция синего цвета вычисляется по периоду основного колебания от 0 до 2π. Окончательное значение представляет собой интересующий нас определенный интеграл.
В качестве первого шага убеждаемся, что интегралы по синусу и
косинус обращается в нуль и что сложение функций синуса и косинуса приводит к
сдвинутая по фазе функция синуса или косинуса, интеграл которой также равен нулю.
вычисление интеграла от произведения определенной выше функции на
обертона изначально неизвестного порядка показывает, что действительно все вклады
исчезают, за исключением того, где обертоны идентичны, а функция
тип (синус или косинус) одинаков. Понятно, что симметрия
различные функции относительно середины периода на
ось x
является причиной этого конкретного результата. Таким образом, мы имеем.
∫ 0Tcos(mωt)dt=0;∫ 0Tcos(mωt)sin(nωt)dt=0;
∫ 0Tcos(mωt)cos(nωt)dt=0 для m≠nT∕2form=n
Это свойство функций синуса и косинуса означает, что они являются примером ортогональная система функций. Две функции называются ортогональными, если применяется следующее:
∫ 0Tf1(t)f2(t)dt=0forf1(t)≠f2(t)
Рисунок 5.15: Моделирование визуализирует ортогональность тригонометрического функции.
На страницах описания симуляции более подробные инструкции и подсказки для
предусмотрены эксперименты.
После открытия симуляции вы выбираете тип функции
и нажмите клавишу ввода. Процесс интеграции анимирован для вас
легче увидеть разницу между интегралами при изменении
функции.
5.10.3 Визуализация расчета коэффициентов и спектра
Моделирование на рис.5.16 визуализирует вычисление коэффициентов Фурье для
основной тон и первые девять обертонов для следующего типичного периодического издания
функции: пилообразная, прямоугольная волна, прямоугольный импульс и импульс Гаусса. С этой целью
произведение функций под знаком интеграла определяется и рисуется красным цветом
а определенный интеграл показан синим цветом. Окончательное значение интеграла равно, за исключением
фактор π
который был подавлен, чтобы получить более легко читаемые значения, равные коэффициенту
выбранный порядок. Функции предоставляются с тремя параметрами
группа
с этим
контролировать амплитуду, точку симметрии и ширину импульса.
Из
моделирования спектры показанных функций могут быть получены в численном и
экспериментальным способом.
Рисунок 5.16: Расчет коэффициентов Фурье для выбора функций F(t)для колебание зуба пилы.
Интерактивный рисунок моделирования показывает ситуацию для синуса коэффициенты десятого порядка симметричного зуба пилы. Моделирование начинается с выбор функции и нажатие на клавишу ввода. Страницы с описанием и инструкции для экспериментов содержат дополнительные подробности.
5.10.4 Примеры разложения Фурье
В следующих интерактивных примерах (рис. 5.17 — рис. 5.19) вычисление
коэффициенты происходят в фоновом режиме. В окне функция
показан красным, а частичная сумма желаемого порядка показана синим цветом.
Окно функций является интерактивным, так что можно использовать гораздо больше функций.
введены и несколько предложены в описании. В текстовом окне
порядок анализа можно регулировать; с ползунком порядок приближения
н быть
используется для частичной суммы.
Моделирование позволяет использовать очень высокие
заказы.
Вычисление разложения Фурье n-й заказ следует сразу после входа в функцию. Диаграмма выходит за рамки интеграции область 2π чтобы увидеть периодическое продолжение в обе стороны.
На рис.5.17 разложение Фурье порядка 43 это показано как приближение для симметричного и периодического прямоугольного импульса. Для прямоугольная волна очень четко распознает типичный выброс на разрывах, которая не обращается в нуль даже для очень высоких порядков.
Рисунок 5.17: Периодический прямоугольный импульс (красный) и его приближение Фурье (синий) 43-го порядка. Расчетный заказ н можно выбрать.
На рис.5.18 с использованием того же моделирования показано приближение 17-го порядка
для пилообразных колебаний, которые были модулированы нелинейным образом с
синусоидальная функция высокой частоты.
Рисунок 5.18: Периодическая пилообразная форма, модулированная из середины периода с помощью высокочастотной синусоидальной функции (красный) и приближения Фурье 17-го порядок (синий). Частоту модуляции можно выбрать с помощью ползунка. Похожий сложные формы волны используются в синтезаторах для получения интересных звуков.
Во втором окне симуляции (рис.5.19) показан спектр. Это можно изменить между синусом (а)-, косинус (bn) и спектр мощности (sn2+bn2). На этом рисунке показан спектр модулированной пилообразной формы, богатый обертонами. и имеет ярко выраженную форманту на шестом и седьмом обертоне. В акустике форманты определяются как ограниченные области обертонов с большой амплитудой; они в значительной степени определяют качество тона.
.
Рисунок 5.19: частотный спектр для Фурье-разложения
модулированная пилообразная форма на рис.5.18. По оси абсцисс показан порядок
н
обертона (основной тон n=1),
по ординате можно выбирать между отображением отдельных коэффициентов
или полная мощность в заданном порядке.
Описание симуляции содержит дальнейшие инструкции.
5.10.5 Комплексный ряд Фурье
В пространстве комплексных чисел ряд Фурье можно сформулировать очень просто. элегантный способ:
f(t)= ∑n=-∞∞cneinωtcn=1T ∫ 0Tf(t)einωtdt.
Связь с реальным представлением получается путем переупорядочения суммы и объединения, начиная с n=1 термины с -n и н. Принимая во внимание cos(-x)=cos(x);sin(-x)=-sin(x) мы получаем
f(t)= ∑p=-∞∞cneinωt= ∑p=-∞∞cn(cosnωt+isinnωt)=c0+(c1+c-1)cosωt+i(c1-c-1)sinωt+…f (t)=c0+ ∑p=1∞(cn+c-n)(cosnωt+i(cn-c-n)sinnωt)
В качестве связи между вещественными и комплексными коэффициентами получаем
a0=2c0;an=cn+c-n;bn=i(cn-c-n).
Комплексный состав особенно используется в электротехнике. Он имеет
Преимущество в том, что вычисления с экспонентами в целом проще и удобнее.
прозрачными, чем те, у которых есть тригонометрическая функция.
Для быстрого численного расчета компонентов ряда Фурье a был разработан специальный алгоритм, известный как FFT (Fast Fourier Трансформация). БПФ
5.10.6 Численное решение уравнений и итерационные методы
В математике и физике часто требуется определить значения переменная, для которой функция, зависящая от этой переменной, имеет определенное значение Может такая же проблема
Итерация в том, что касается вычислений, заключается в том, чтобы найти значение переменная, у которой две функции одной переменной имеют одинаковое значение. Один решает эти задачи через поиск нулей функции.
f мы определяем y1=f(x);y2=g(x), для которого x равен y1=C? ответ: f(x)-C=0, для которого x равен y1=y2? ответ: h(x)≡ f(x)-g(x)=0
Аналитическое решение для нахождения нулей функции может быть найдено только для очень
простые функции, поэтому это исключение.
Поэтому нужен числовой
метод решения, который предпочтительно работает для всех функций и всех параметров
ценности.
Это достигается с помощью итерационных методов, которые представляют собой обращение вопроса.
Сначала берется значение переменной, которое, вероятно, меньше, чем
оценивает первый нуль в интересующем интервале и вычисляет абсолютное значение
значения функции и ее знака. Затем увеличивают переменную на заданный интервал
(конечно, можно начать справа и уменьшить шаг переменной на
шаг). Является ли новое абсолютное значение для того же знака одним переходом к следующему
точка. Если знак меняется, очевидно, что вы пересекли ноль. Теперь направление
движения инвертируется, а ширина шага умножается на коэффициент <1. Таким образом
находятся ящики уменьшающегося размера, содержащие нуль до тех пор, пока отклонение
значение функции от нуля становится меньше заданного допуска. Затем
процесс продолжается в исходном направлении, пока не исчезнут все нули.
были найдены или до определенного порога для значения переменной или
сама функция была превышена, и, таким образом, человек находится за пределами области
интерес.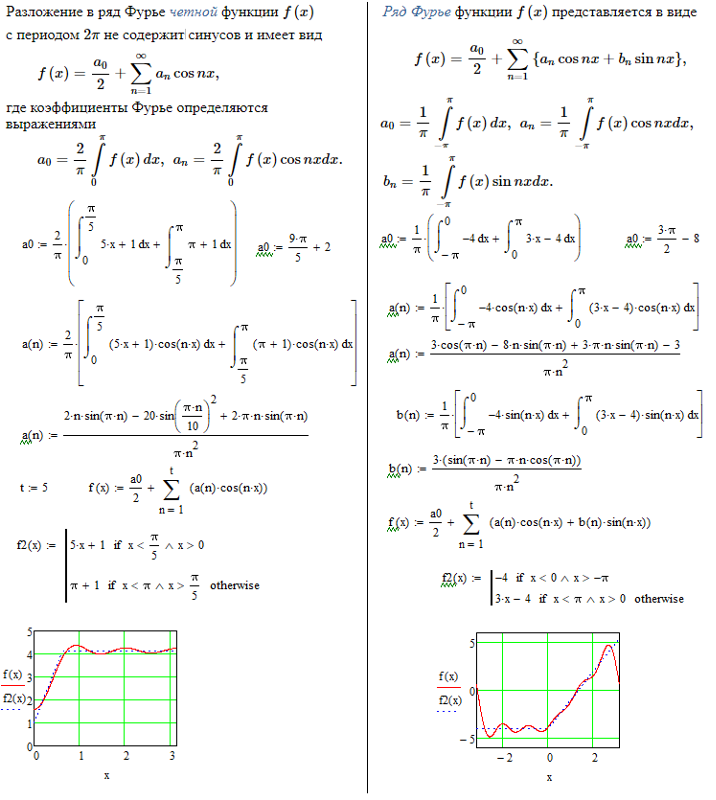
Для этого итерационного процесса доступны готовые алгоритмы в стандартном числовые компьютерные коды, которые включают дальнейшие уточнения. Таким образом, можно, для например, варьировать ширину интервалов итераций так, чтобы характер учитывается функция. Например, в методе Ньютона используется его наклоните первую производную, чтобы скорректировать эти интервалы. Учитывая скорость сегодняшнего компьютеры эти усовершенствования не играют роли для простых задач. Следующее интерактивный пример на рис. 5.17 определяет нули функции, которые могут быть вошел по желанию. Эта функция задается как многочлен четвертой степени с иррациональные корни.
Последовательность показывает ход выполнения очень простого алгоритма итерации.
скорость можно регулировать. Начальную точку итерации (пурпурный) можно перетаскивать
с мышью. Итерация продолжается с постоянной шириной шага к большему
x-значения
пока знак функции не изменится.
Начальное значение сбрасывается до последнего
значение до смены знака, а ширина шага уменьшается в
10 и прогресс
к большим значениям x
возобновляется. Это повторяется до тех пор, пока не произойдет отклонение
y-значение
от нуля падает ниже заданного допуска. В моделировании можно выбрать, будет ли
останавливается после достижения определенной точности, или все нули в переменном интервале
определяются последовательно. В одном вычислении пурпурная точка перескакивает на
расчетное значение. в то время как синяя точка показывает значение первой итерации при определении
несколько нулей.
Для того, чтобы иметь возможность следовать прогрессивной итерации также для высокой точности уже достигнуто хорошо, часть окна подробно показана в увеличительном стекле, и шкала подстраивается под возрастающую точность.
Из окна масштабирования на Рис. 5.20 видно, что кривая всегда почти
linear закрывает корень кривой. Regula Falsi использует в качестве следующего значения итерации для
х
пересечение секущей, образованной двумя предыдущими точками итерации, с
ось х.
Поэтому он быстро приводит к окончательному решению. Однако мы выбрали константу
ширину шага, чтобы было легче наблюдать за процессом.
Рисунок 5.20: Анимированное итеративное вычисление нулей функции,
многочлен четвертой степени на рисунке. Левое окно показывает
весь расчетный интервал, правый участок, шкала которого
соответствует достигнутому разрешению. Показана последняя точка итерации
синего цвета в обоих окнах, а три предшественника показаны в
красный цвет в «зазеркалье». на картинке для возврата после
деления интервала на 10. Пурпурная точка является начальной точкой
итерация. Его можно нарисовать мышкой. Желаемая точность
дельта
, количество временных шагов в секунду (скорость) и диапазон абсцисс
хмакс
можно выбрать. В числовых полях координаты текущей точки итерации
х, у
и начальная точка
х0, у0
показаны итерации. В окне формулы можно вводить любые функции
нули которого необходимо вычислить.