Разложить в ряд фурье по синусам: Ряд Фурье. Разложение функции в ряд Фурье.Разложение функции в ряд синусов и косинусов.

Ряд Фурье. Разложение функции в ряд Фурье.Разложение функции в ряд синусов и косинусов.

Ряд Фурье периодических функций с периодом 2π. Четные и нечетные функции. Разложение в ряд Фурье по синусам. Ряд Фурье для произвольного интервала.

Ряд Фурье непериодических функций с периодом 2π. Разложение в ряд Фурье по косинусам. Ряд Фурье на полупериоде. Ряд Фурье на полупериоде для функций, заданных на интервале L≠2π.

Ряд Фурье периодических функций с периодом 2π.

Ряд Фурье позволяет изучать периодические (непериодические) функции, разлагая их на компоненты. Переменные токи и напряжения, смещения, скорость и ускорение кривошипно-шатунных механизмов и акустические волны — это типичные практические примеры применения периодических функций в инженерных расчетах.

Разложение в ряд Фурье основывается на предположении, что все имеющие практическое значение функции в интервале -π ≤x≤ π можно выразить в виде сходящихся тригонометрических рядов (ряд считается сходящимся, если сходится последовательность частичных сумм, составленных из его членов):

Стандартная (=обычная) запись через сумму sinx и cosx

f(x)=a_o+ a₁cosx+a₂cos2x+a₃cos3x+…+b₁sinx+b₂sin2x+b₃sin3x+…,

где a_o, a₁,a₂,…,b₁,b₂,.. — действительные константы, т.е.

(1)

Где для диапазона от -π до π коэффициенты ряда Фурье рассчитываются по формулам:

Коэффициенты a_o,a_n и b_n называются коэффициентами Фурье, и если их можно найти, то ряд (1) называется рядом Фурье, соответствующим функции f(x).

Для ряда (1) член (a₁cosx+b₁sinx) называется первой или основной гармоникой,

Другой способ записи ряда — использование соотношения acosx+bsinx=csin(x+α)

f(x)=a_o+c₁sin(x+α₁)+c₂sin(2x+α₂)+…+c_nsin(nx+α_n)

Где a_o — константа, с ₁=(a₁²+b₁²)^1/2 , с _n=(a_n²+b_n²)^1/2— амплитуды различных компонент, а фазовый угол равен a_n=arctg a_n/b_n.

Для ряда (1) член (a₁cosx+b₁sinx) или c₁sin(x+α₁) называется первой или основной гармоникой, (a₂cos2x+b₂sin2x) или c₂sin(2x+α

2) называется второй гармоникой и так далее.

Для точного представления сложного сигнала обычно требуется бесконечное количество членов. Однако во многих практических задачах достаточно рассмотреть только несколько первых членов.

Ряд Фурье непериодических функций с периодом 2π.

Разложение непериодических функций в ряд Фурье.

Если функция f(x) непериодическая, значит, она не может быть разложена в ряд Фурье для всех значений х. Однако можно определить ряд Фурье, представляющий функцию в любом диапазоне шириной 2π.

Если задана непериодическая функция, можно составить новую функцию, выбирая значения f(x) в определенном диапазоне и повторяя их вне этого диапазона с интервалом 2π. Поскольку новая функция является периодической с периодом 2π, ее можно разложить в ряд Фурье для всех значений х. Например, функция f(x)=x не является периодической. Однако, если необходимо разложить ее в ряд Фурье на интервале от о до 2π, тогда вне этого интервала строится периодическая функция с периодом 2π (как показано на рис.

ниже) .

Для непериодических функций, таких как f(x)=х, сумма ряда Фурье равна значению f(x) во всех точках заданного диапазона, но она не равна f(x) для точек вне диапазона. Для нахождения ряда Фурье непериодической функции в диапазоне 2π используется все таже формула коэффициентов Фурье.

Четные и нечетные функции.

Говорят, функция y=f(x) четная, если f(-x)=f(x) для всех значений х. Графики четных функций всегда симметричны относительно оси у (т.е. являются зеркально отраженными). Два примера четных функций: у=х² и у=cosx.

Говорят, что функция y=f(x) нечетная, если f(-x)=-f(x) для всех значений х. Графики нечетных функций всегда симметричны относительно начала координат.

Многие функции не являются ни четными, ни нечетными.

Разложение в ряд Фурье по косинусам.

Ряд Фурье четной периодической функции f(x) с периодом 2π содержит только члены с косинусами (т.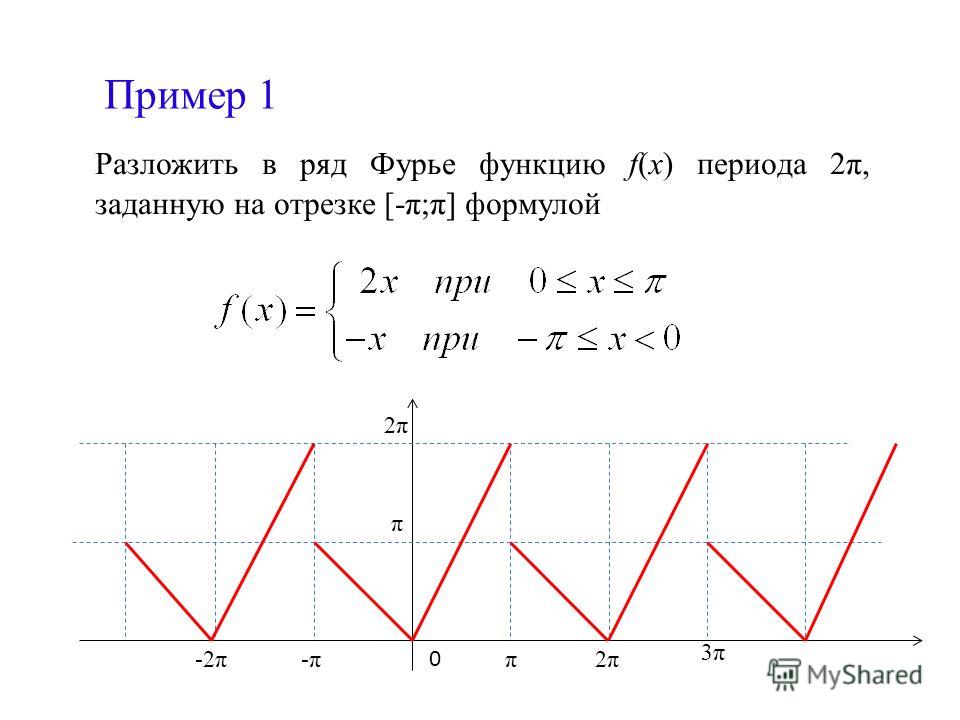 е. не содержит членов с синусами) и может включать постоянный член. Следовательно,

где коэффициенты ряда Фурье,

Разложение в ряд Фурье по синусам.

Ряд Фурье нечетной периодической функции f(x) с периодом 2π содержит только члены с синусами (т.е. не содержит членов с косинусами).

Следовательно,

где коэффициенты ряда Фурье,

Ряд Фурье на полупериоде.

Если функция определена для диапазона, скажем от 0 до π, а не только от 0 до 2π, ее можно разложить в ряд только по синусам или тольо по косинусам. Полученный ряд Фурье называется рядом Фурье на полупериоде.

Если требуется получить разложение Фурье на полупериоде по косинусам функции f(x) в диапазоне от 0 до π, то необходимо составить четную периодическую функцию.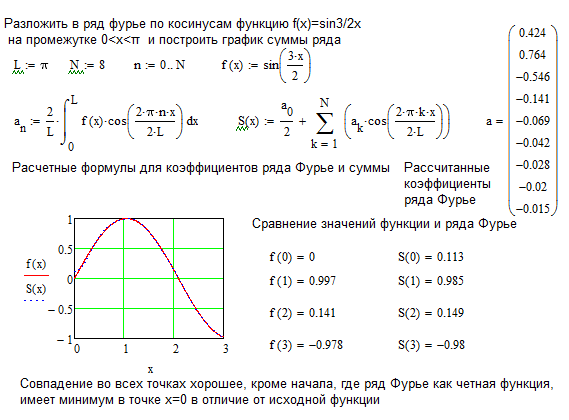 На рис. ниже показана функция f(x)=х, построенная на интервале от х=0 до х=π. Поскольку четная функция симметрична относительно оси f(x), проводим линию АВ, как показано на рис. ниже. Если предположить, что за пределами рассмотренного интервала полученная треугольная форма является периодической с периодом 2π, то итоговый график имеет вид, показ. на рис. ниже. Поскольку требуется получить разложение Фурье по косинусам, как и ранее, вычисляем коэффициенты Фурье a_o и a_n

Если требуется получить разложение Фурье на полупериоде по синусам функции f(x) в диапазоне от 0 до π, то необходимо составить нечетную периодическую функцию. На рис. ниже показана функция f(x)=x, построенная на интервале от от х=0 до х=π. Поскольку нечетная функция симметрична относительно начала координат, строим линию CD, как показано на рис. Если предположить, что за пределами рассмотренного интервала полученный пилообразный сигнал является периодическим с периодом 2π, то итоговый график имеет вид, показанный на рис.

Поскольку требуется получить разложение Фурие на полупериоде по синусам, как и ранее, вычисляем коэффициент Фурье. b

Ряд Фурье для произвольного интервала.

Разложение периодической функции с периодом L.

Периодическая функция f(x) повторяется при увеличении х на L, т.е. f(x+L)=f(x). Переход от рассмотренных ранее функций с периодом 2π к функциям с периодом L довольно прост, поскольку его можно осуществить с помощью замены переменной.

Чтобы найти ряд Фурье функции f(x) в диапазоне -L/2≤x≤L/2, введем новую переменную u таким образом, чтобы функция f(x) имела период 2π относительно u. Если u=2πх/L, то х=-L/2 при u=-π и х=L/2 при u=π. Также пусть f(x)=f(Lu/2π)=F(u). Ряд Фурье F(u) имеет вид

Где коэффициенты ряда Фурье, 

Однако чаще приведенную выше формулу приводят к зависимости от х. Поскольку u=2πх/L, значит, du=(2π/L)dx, а пределы интегрирования — от -L/2 до L/2 вместо — π до π. Следовательно, ряд Фурье для зависимости от х имеет вид

где в диапазоне от -L/2 до L/2 коэффициенты ряда Фурье,

(Пределы интегрирования могут быть заменены на любой интервал длиной L, например, от 0 до L)

Ряд Фурье на полупериоде для функций, заданных в интервале L≠2π.

Для подстановки u=πх/L интервал от х=0 до х=L соответствует интервалу от u=0 до u=π. Следовательно, функцию можно разложить в ряд только по косинусам или только по синусам, т.е. в

ряд Фурье на полупериоде.

Разложение по косинусам в диапазоне от 0 до L имеет вид

Ряд Фурье. Разложение функции в ряд Фурье.Разложение функции в ряд синусов и косинусов.

Ряд Фурье периодических функций с периодом 2π. Четные и нечетные функции. Разложение в ряд Фурье по синусам. Ряд Фурье для произвольного интервала.

Ряд Фурье непериодических функций с периодом 2π. Разложение в ряд Фурье по косинусам. Ряд Фурье на полупериоде. Ряд Фурье на полупериоде для функций, заданных на интервале L≠2π.

Ряд Фурье периодических функций с периодом 2π.

Ряд Фурье позволяет изучать периодические (непериодические) функции, разлагая их на компоненты. Переменные токи и напряжения, смещения, скорость и ускорение кривошипно-шатунных механизмов и акустические волны — это типичные практические примеры применения периодических функций в инженерных расчетах.

Разложение в ряд Фурье основывается на предположении, что все имеющие практическое значение функции в интервале -π ≤x≤ π можно выразить в виде сходящихся тригонометрических рядов (ряд считается сходящимся, если сходится последовательность частичных сумм, составленных из его членов):

Стандартная (=обычная) запись через сумму sinx и cosx

f(x)=a_o+ a₁cosx+a₂

cos2x+a₃cos3x+…+b₁sinx+b₂sin2x+b₃sin3x+…,

где a_o, a₁,a₂,…,b₁,b₂,.. — действительные константы, т.е.

(1)

Где для диапазона от -π до π коэффициенты ряда Фурье рассчитываются по формулам:

Коэффициенты a_o,a_n и b_n называются коэффициентами Фурье, и если их можно найти, то ряд (1) называется рядом Фурье, соответствующим функции f(x). Для ряда (1) член (a₁cosx+b₁sinx) называется первой или основной гармоникой,

Другой способ записи ряда — использование соотношения acosx+bsinx=csin(x+α)

f(x)=a_o+c₁sin(x+α₁)+c₂sin(2x+α₂)+…+c_nsin(nx+α_n)

Где a_o — константа, с ₁=(a₁²+b₁²)^1/2 , с _n=(a_n²+b_n²)^1/2— амплитуды различных компонент, а фазовый угол равен a_n=arctg a_n/b_n.

Для ряда (1) член (a₁cosx+b₁sinx) или c₁sin(x+α₁) называется первой или основной гармоникой, (a₂cos2x+b₂sin2x) или c₂sin(2x+α₂) называется второй гармоникой и так далее.

Для точного представления сложного сигнала обычно требуется бесконечное количество членов. Однако во многих практических задачах достаточно рассмотреть только несколько первых членов.

Ряд Фурье непериодических функций с периодом 2π.

Разложение непериодических функций в ряд Фурье.

Если функция f(x) непериодическая, значит, она не может быть разложена в ряд Фурье для всех значений х. Однако можно определить ряд Фурье, представляющий функцию в любом диапазоне шириной 2π.

Если задана непериодическая функция, можно составить новую функцию, выбирая значения f(x) в определенном диапазоне и повторяя их вне этого диапазона с интервалом 2π. Поскольку новая функция является периодической с периодом 2π, ее можно разложить в ряд Фурье для всех значений х. Например, функция f(x)=x не является периодической. Однако, если необходимо разложить ее в ряд Фурье на интервале от о до 2π, тогда вне этого интервала строится периодическая функция с периодом 2π (как показано на рис. ниже) .

Для непериодических функций, таких как f(x)=х, сумма ряда Фурье равна значению f(x) во всех точках заданного диапазона, но она не равна f(x) для точек вне диапазона. Для нахождения ряда Фурье непериодической функции в диапазоне 2π используется все таже формула коэффициентов Фурье.

Четные и нечетные функции.

Говорят, функция y=f(x) четная, если f(-x)=f(x) для всех значений х. Графики четных функций всегда симметричны относительно оси у (т.е. являются зеркально отраженными). Два примера четных функций: у=х² и у=cosx.

Говорят, что функция y=f(x) нечетная, если f(-x)=-f(x) для всех значений х. Графики нечетных функций всегда симметричны относительно начала координат.

Многие функции не являются ни четными, ни нечетными.

Разложение в ряд Фурье по косинусам.

Ряд Фурье четной периодической функции f(x) с периодом 2π содержит только члены с косинусами (т.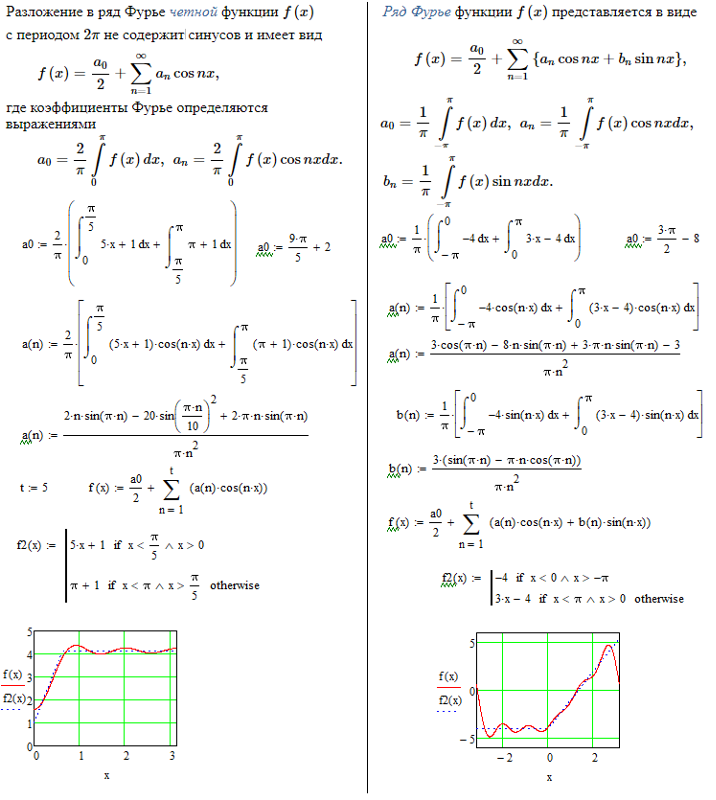 е. не содержит членов с синусами) и может включать постоянный член. Следовательно,

где коэффициенты ряда Фурье,

Разложение в ряд Фурье по синусам.

Ряд Фурье нечетной периодической функции f(x) с периодом 2π содержит только члены с синусами (т.е. не содержит членов с косинусами).

Следовательно,

где коэффициенты ряда Фурье,

Ряд Фурье на полупериоде.

Если функция определена для диапазона, скажем от 0 до π, а не только от 0 до 2π, ее можно разложить в ряд только по синусам или тольо по косинусам. Полученный ряд Фурье называется рядом Фурье на полупериоде.

Если требуется получить разложение Фурье на полупериоде по косинусам функции f(x) в диапазоне от 0 до π, то необходимо составить четную периодическую функцию.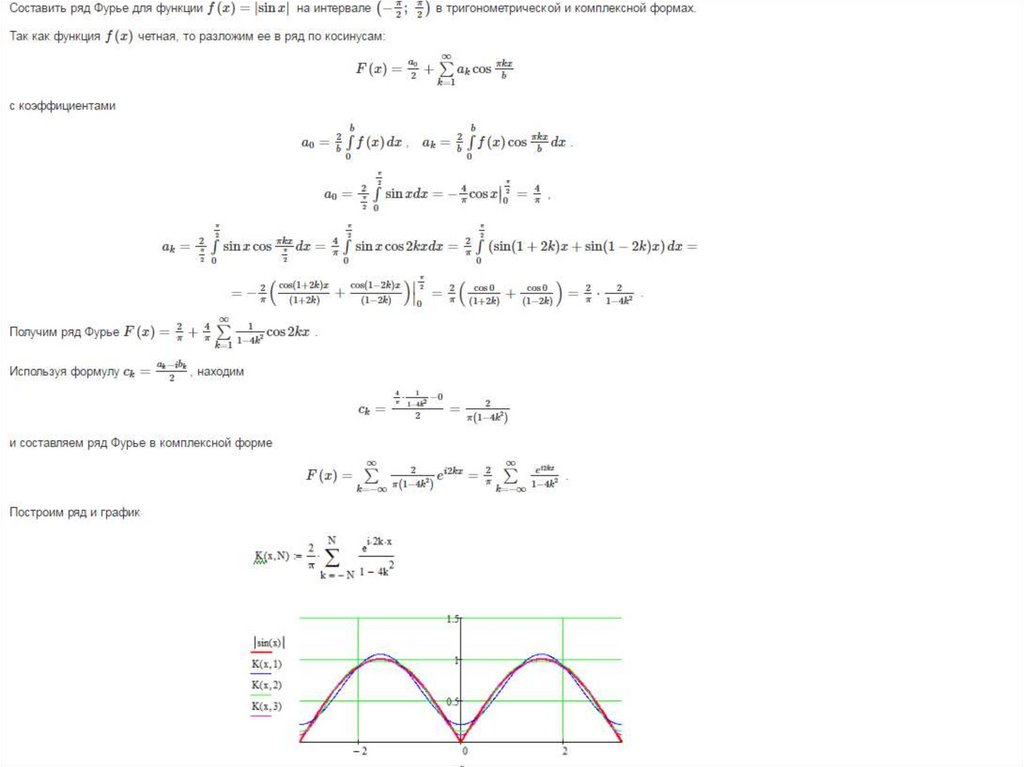 На рис. ниже показана функция f(x)=х, построенная на интервале от х=0 до х=π. Поскольку четная функция симметрична относительно оси f(x), проводим линию АВ, как показано на рис. ниже. Если предположить, что за пределами рассмотренного интервала полученная треугольная форма является периодической с периодом 2π, то итоговый график имеет вид, показ. на рис. ниже. Поскольку требуется получить разложение Фурье по косинусам, как и ранее, вычисляем коэффициенты Фурье a_o и a_n

Если требуется получить разложение Фурье на полупериоде по синусам функции f(x) в диапазоне от 0 до π, то необходимо составить нечетную периодическую функцию. На рис. ниже показана функция f(x)=x, построенная на интервале от от х=0 до х=π. Поскольку нечетная функция симметрична относительно начала координат, строим линию CD, как показано на рис. Если предположить, что за пределами рассмотренного интервала полученный пилообразный сигнал является периодическим с периодом 2π, то итоговый график имеет вид, показанный на рис. Поскольку требуется получить разложение Фурие на полупериоде по синусам, как и ранее, вычисляем коэффициент Фурье. b

Ряд Фурье для произвольного интервала.

Разложение периодической функции с периодом L.

Периодическая функция f(x) повторяется при увеличении х на L, т.е. f(x+L)=f(x). Переход от рассмотренных ранее функций с периодом 2π к функциям с периодом L довольно прост, поскольку его можно осуществить с помощью замены переменной.

Чтобы найти ряд Фурье функции f(x) в диапазоне -L/2≤x≤L/2, введем новую переменную u таким образом, чтобы функция f(x) имела период 2π относительно u. Если u=2πх/L, то х=-L/2 при u=-π и х=L/2 при u=π. Также пусть f(x)=f(Lu/2π)=F(u). Ряд Фурье F(u) имеет вид

Где коэффициенты ряда Фурье, 

Однако чаще приведенную выше формулу приводят к зависимости от х. Поскольку u=2πх/L, значит, du=(2π/L)dx, а пределы интегрирования — от -L/2 до L/2 вместо — π до π. Следовательно, ряд Фурье для зависимости от х имеет вид

где в диапазоне от -L/2 до L/2 коэффициенты ряда Фурье,

(Пределы интегрирования могут быть заменены на любой интервал длиной L, например, от 0 до L)

Ряд Фурье на полупериоде для функций, заданных в интервале L≠2π.

Для подстановки u=πх/L интервал от х=0 до х=L соответствует интервалу от u=0 до u=π. Следовательно, функцию можно разложить в ряд только по косинусам или только по синусам, т.е. в ряд Фурье на полупериоде.

Разложение по косинусам в диапазоне от 0 до L имеет вид

11.3: Серия Фурье II — Mathematics LibreTexts

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

9462

• Уильям Ф. Тренч
• Университет Тринити

В этом разделе мы обсуждаем разложения Фурье по собственным функциям задач 1-4 раздела 11.1.

Косинусный ряд Фурье

Из Упражнение 11.1.20 собственные функции

\[1,\, \cos{\pi x\over L}, \, \cos{2\pi x\over L},\ точки, \, \cos{n\pi x\over L},\dots\nonumber \]

краевой задачи

\[\label{eq:11.3.1} y»+\lambda y= 0,\quad y'(0)=0,\quad y'(L)=0\]

(задача 2) ортогональны на \([0,L]\). Если \(f\) интегрируема на \([0,L]\), то разложение Фурье \(f\) по этим функциям называется 9Lf(x)\cos{n\pi x\over L}\,dx,\quad n=1,2,3,\dots.\nonumber \]

Сравнение этого определения с теоремой 11.2.6a показывает, что функция Фурье Косинусный ряд \(f\) на \([0,L]\) — это ряд Фурье функции

\[f_{1}(x)=\left\{\begin{array}{cc}{ f(-x),}&{-L

получается расширением \(f\) на \([-L,L]\) как четная функция (рис. 11.3.1). ).

Рисунок 11.3.1

Применение теоремы 11.2.4 к \(f_1\) дает следующую теорему. 9Lf(x)\cos{n\pi x\over L}\,dx,\quad n=1,2,3,\dots,\nonumber \]

сходится для всех \(x\) в \([0,L];\), причем

\[C(x)=\left\{\begin{array}{cl}{f(0+),}&{\text{if}x=0}\\[5pt]{f(x), } & {\ text {если} 0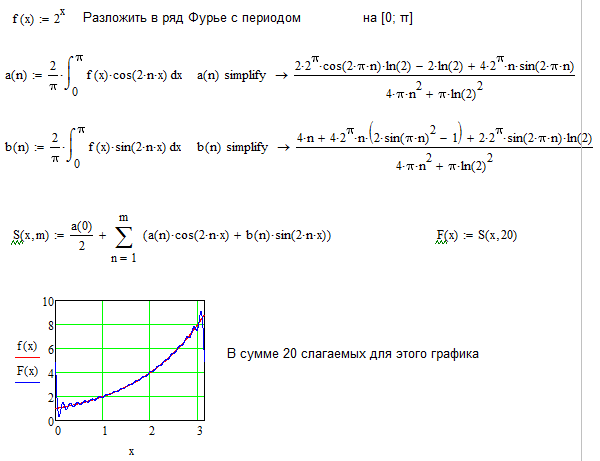

Пример 11.3.1

9{2}}\cos\frac{(2n-1)\pi x}{L}\номер\]

Теорема 11.3.1 подразумевает, что

\[C(x)=x,\quad 0\le x\le L.\nonnumber \]

Ряд синусов Фурье

Из Упражнение 11.1.19 , собственные функции

\[\sin{\pi x\over L}, \, \sin{2\pi x\over L},\dots, \, \sin{n\pi x\over L},\dots\nonumber \]

краевой задачи

\[y»+\lambda y=0,\quad y(0)=0,\quad y(L)=0\nonumber \]

(задача 1) ортогональны на \([0,L]\). Если \(f\) интегрируема на \([0,L]\), то разложение Фурье \(f\) по этим функциям называется 9Lf(x)\sin{n\pi x\over L}\,dx,\quad n=1,2,3,\dots.\nonumber \]

Сравнение этого определения с теоремой 11.2.6b показывает, что функция Фурье ряд синусов \(f\) на \([0,L]\) — это ряд Фурье функции

\[f_{2}(x)=\left\{\begin{array}{cc}{ -f(-x),}&{-L

, полученное расширением \(f\) над \([-L,L]\) как нечетной функцией (рис. 11.3.2). ).

Рисунок 11.3.2

Применение теоремы 11.2.4 к \(f_2\) дает следующую теорему. 9Lf(x)\sin{n\pi x\over L}\,dx,\nonumber \]

сходится для всех \(x\) в \([0,L];\), причем

\[S (x) = \ left \ {\ begin {array} {cl} {0} & {\ text {if} x = 0} \\ [5pt] {f (x),} & {\ text {если}0

Пример 11.

3.2

Найдите ряд Фурье по синусу \(f(x)=x\) на \([0,L]\). 9n\over n} \sin{n\pi x\over L}.\nonumber \]

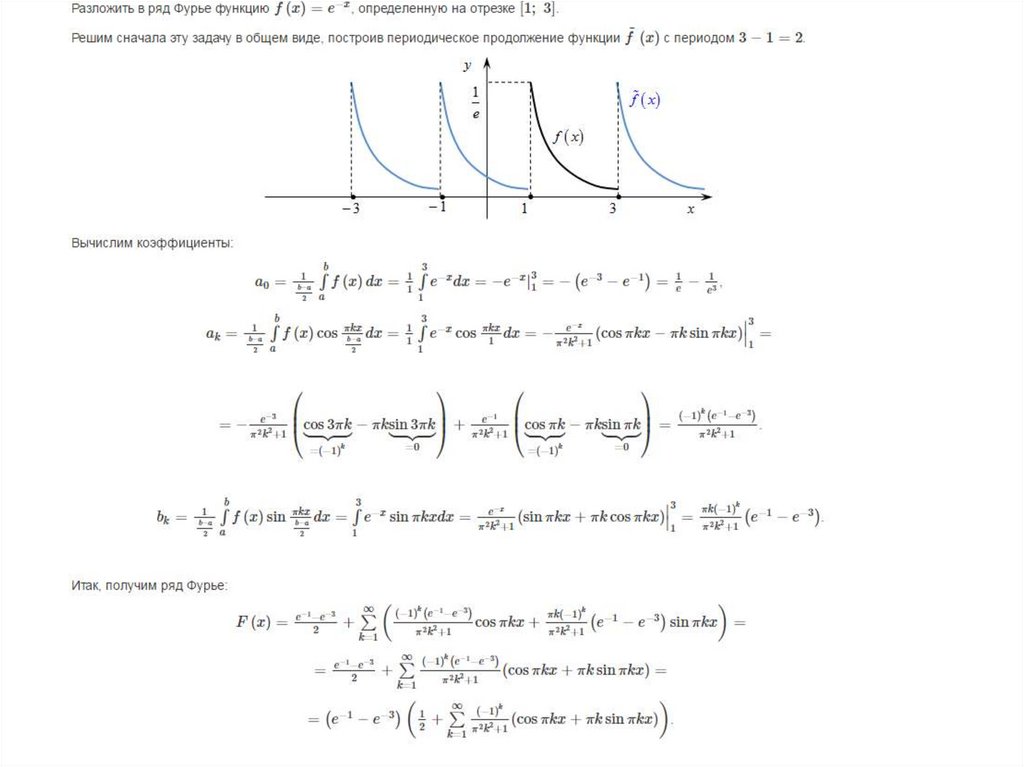
Теорема 11.3.2 следует, что

\[S(x)= \left\{\begin{array}{cl} x,&0\le x< L,\\0,& x=L. \end{array}\right.\nonumber \]

Смешанный ряд косинусов Фурье

Из Упражнение 11.1.22 собственные функции

\[\cos{\pi x\over 2L}, \, \cos{ 3\pi x\over 2L},\dots, \, \cos{(2n-1)\pi x\over 2L},\dots\nonumber \]

краевой задачи

\[\label{ eq:11.3.2} y»+\lambda y=0,\quad y'(0)=0,\quad y(L)=0\] 9Lf(x)\cos{(2n-1)\pi x\over2L}\,dx.\nonumber \]

Мы будем называть это разложение смешанным косинусным рядом Фурье функции \(f\) на \( [0,L]\), потому что граничные условия (Уравнение \ref{eq:11.3.2}) «смешанные» в том смысле, что они требуют, чтобы \(y\) было равно нулю в одной граничной точке и \(y’ \) быть равным нулю на другом. Напротив, «обычный» ряд косинусов Фурье связан с ( Уравнение \ref{eq:11.3.1}), где граничные условия требуют, чтобы \(y’\) было равно нулю в обеих конечных точках.

Можно показать ( Упражнение 11.3.57 ), что смешанный ряд косинусов Фурье \(f\) на \([0,L]\) является просто ограничением на \([0,L]\) ряда косинусов Фурье

\[f_3(x)=\left\{\begin{array}{cl} f(x),&0\le x\le L,\\-f(2L-x), &L< x\le 2L \end{array}\right.\nonumber \]

on \([0,2L]\) (рис. 11.3.3). ).

Рисунок 11.3.3

Применение теоремы 11.3.1 с заменой \(f\) на \(f_3\) и \(L\) на \(2L\) получается следующая теорема. 9Lf(x)\cos{(2n-1)\pi x\over2L}\,dx,\nonumber \]

сходится для всех \(x\) в \([0,L];\), причем

\[C_{M}(x)=\left\{\begin{array}{cl}{f(0+),}&{\text{if}x=0}\\[5pt]{f( x),} & {\ text {если} 0

Пример 11.3.3

Найдите смешанный ряд косинусов Фурье для \(f(x)=x-L\) на \([0,L]\). 92} \cos{(2n-1)\pi x\over2L}. \nonumber \]

Теорема 11.3.3 следует, что

\[C_M(x)= x-L,\quad 0\le x\le L.\nonumber \]

Смешанный ряд по синусу Фурье

Из Упражнение 11.1.21 собственные функции

\[\ sin{\pi x\over 2L}, \, \sin{3\pi x\over 2L},\dots, \, \sin{(2n-1)\pi x\over 2L},\dots\nonumber \ ]

краевой задачи

\[y»+\lambda y=0,\quad y(0)=0,\quad y'(L)=0\nonnumber \]

(задача 3) ортогональны на \([0,L]\). Если \(f\) интегрируема на \([0,L]\), то Фурье-разложение \(f\) по этим функциям равно 9Lf(x)\sin{(2n-1)\pi x\over2L}\,dx.\nonumber \]

Мы назовем это разложение смешанным рядом синусов Фурье функции \(f\) на \( [0,L]\).

Можно показать ( Упражнение 11.3.58 ), что смешанный ряд Фурье по синусам \(f\) на \([0,L]\) является просто ограничением на \([0,L]\) ряда синусов Фурье

\[f_4(x)=\left\{\begin{array}{cl} f(x),&0\le x\le L,\\f(2L-x),&L < x\le 2L, \end{array}\right.\nonumber \]

on \([0,2L]\) (рис. 11.3.4 ). 9Lf(x)\sin{(2n-1)\pi x\over2L}\,dx,\nonumber \]

сходится для всех \(x\) в \([0,L];\), причем

\[S{M}(x)=\left\{\begin{array}{cl}{0,}&{\text{if}x=0}\\[5pt]{f(x),} &{\ text{if}0

Пример 11.3.4

Найдите смешанный ряд Фурье по синусам \(f(x)=x\) на \([0,L]\). 92} \sin{(2n-1)\pi x\over2L}.\nonumber \]

Теорема 11.3.4 следует, что

\[S_M(x)=x,\quad 0\le x\le L.\nonumber \]

Полезное наблюдение

В приложениях, включающих разложение по собственным функциям задач 1-4, разлагаемые функции часто являются полиномами, удовлетворяющими граничным условиям рассматриваемой задачи. В этом случае следующая теорема предлагает эффективный способ получения коэффициентов в разложении.

9L f»(x)\sin{(2n-1)\pi x\over2L} \,dx.\]

Доказательство

Мы докажем (а), а остальное предоставим вам ( Упражнения 11. 2(3L-2x)\) на \([0,L]\). 9{n}\frac{4}{(2n-1)\pi } \right]\sin\frac{(2n-1)\pi x}{2L}\nonumber\]

---

Эта страница под названием 11.3: Серия Фурье II распространяется под лицензией CC BY-NC-SA 3.0 и была создана, изменена и/или курирована Уильямом Ф. Тренчем посредством исходного контента, который был отредактирован в соответствии со стилем и стандартами Платформа LibreTexts; подробная история редактирования доступна по запросу.

1. Наверх

• Была ли эта статья полезной?

1. Тип изделия

   Раздел или Страница

   Автор

   Уильям Ф. Тренч

   Лицензия

   CC BY-NC-SA

   Версия лицензии

   3,0

   Показать страницу TOC

   нет

2. Теги

   1. косинус серии
   2. Серия косинусов Фурье
   3. Синусоида Фурье серии
   4. синусоидальная серия
   5. источник@https://digitalcommons. trinity.edu/mono/9

Формула ряда Фурье. Что такое формула ряда Фурье?

Формула ряда Фурье дает разложение периодической функции f(x) через бесконечную сумму синусов и косинусов. Он используется для разложения любой периодической функции или периодического сигнала на сумму набора простых осциллирующих функций, а именно синусов и косинусов. Давайте разберемся с формулой ряда Фурье на решенных примерах.

Что такое формулы ряда Фурье?

В рядах Фурье используются ортогональные соотношения функций косинуса и синуса. Формула ряда Фурье для функции имеет вид 9{\pi}f(x)sin\;nx\;dx\)

n = 1, 2, 3…..

Есть вопросы по основным математическим понятиям?

Станьте чемпионом по решению проблем, используя логику, а не правила. Узнайте, почему математика стоит за нашими сертифицированными экспертами.

Примеры формул ряда Фурье

9{2}}\)

Часто задаваемые вопросы о формулах ряда Фурье

Что подразумевается под рядом Фурье?

Ряд Фурье представляет собой разложение периодической функции f(x) по бесконечной сумме синусов и косинусов.

No related posts.