Координаты вектора. Разложение вектора по двум неколлинеарным векторам 9 класс онлайн-подготовка на Ростелеком Лицей |
Тема 5: Метод координат
- Видео
- Тренажер
- Теория
Заметили ошибку?
Координаты вектора. Разложение вектора по двум неколлинеарным векторам.
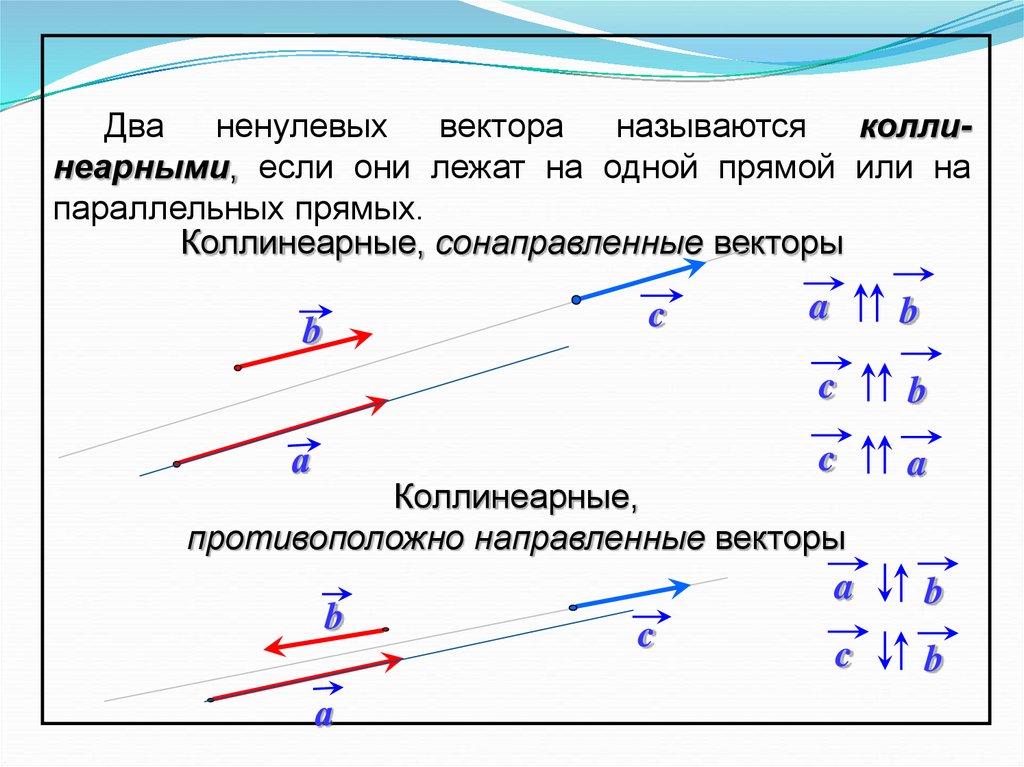
Если векторы a⃗ и b⃗ коллинеарны и a⃗≠0⃗, то существует такое число k, что b⃗=ka⃗.
Пусть a⃗ и b⃗ – два данных вектора. Если вектор p представлен в виде p⃗=xa⃗+yb⃗, где x и y – некоторые числа, то говорят, что вектор p⃗ разложен по векторам a⃗ и b⃗. Числа x и y называются коэффициентами разложения.
Теорема
На плоскости любой вектор можно разложить по двум данным неколлинеарным векторам, причем коэффициенты разложения определяются единственным образом.
Напомню, что для задания прямоугольной системы координат нужно провести две взаимно перпендикулярные прямые, на каждой из них выбрать направление (оно обозначается стрелкой) и выбрать единицу измерения отрезков.
В дальнейшем под длиной отрезка мы будем понимать это число.
Отложим от начала координат O единичные векторы (т.е. векторы, длины которых равны единице) i⃗ и j⃗ так, чтобы направление вектора i⃗совпало с напралением оси Ox, а направление вектора j⃗ – с направлением оси Oy. Векторы i⃗ и j⃗ назовем координатными векторами.
Координатные векторы не коллинеарны, поэтому любой вектор p⃗ можно разложить по координатным векторам, т.е. представить в виде p⃗=xi⃗+yj⃗, причем коэффициенты разложения (числа x и y) определяются единственным образом. Коэффициенты разложения вектора p⃗ по координатным векторамназываются координатными векторами
p⃗ в данной системе координат. Координаты вектора будем записывать в фигурных скобках после обозначения вектора: p⃗{x;y}.Так как нулевой вектор можно представить в виде 0⃗=0. i⃗+0.j⃗, то его координаты равны нулю: 0⃗{0;0}. Если векторы a⃗=x1i⃗+y1j⃗ и b⃗=x2i⃗+y2j⃗ равны, то x1 = x2 и y1 = y3. Таким образом, координаты равных векторов соответственно равны.
i⃗+0.j⃗, то его координаты равны нулю: 0⃗{0;0}. Если векторы a⃗=x1i⃗+y1j⃗ и b⃗=x2i⃗+y2j⃗ равны, то x1 = x2 и y1 = y3. Таким образом, координаты равных векторов соответственно равны.
Рассмотрим правила, позволяющие по координатам векторов находить координаты их суммы, разности и произведения вектора на число.
-
Каждая координата суммы двух или более векторов равна сумме соответствующих координат этих векторов.
Докажем это утверждение для двух векторов. Рассмотрим векторы a{x1;y1} и b{x2;y2}. Так как a⃗=x1i⃗+y1j⃗ и b ⃗=x2i⃗ +y2j⃗ ,то, пользуясь свойствами сложения векторов и умножения вектора на число, получим:
a⃗+b⃗=x1i⃗+y1j⃗+x2i⃗+y2j⃗=(x1+x2)i⃗+(y1+y2)j⃗ .
Следовательно, что координаты вектора a⃗+b⃗ равны {x1+x2;y1+y2}.

Аналогично доказывается следующее утверждение:
-
Каждая координата разности двух или более векторов равна разности соответствующих координат этих векторов.
Иными словами, если a⃗{x1;y1} и b⃗{x2;y2} – данные векторы, то вектор a⃗–b⃗ имеет координаты {x1-x2;y1-y2}.
-
Каждая координата произведения вектора на число равна произведению соответствующей координаты вектора на это число.
В самом деле, пусть вектор a⃗ имеет координаты {x;y}. Найдем координаты вектора ka⃗, гдеk – произвольное число. Так как a⃗=xi⃗+yj⃗, то kxi⃗+kyj⃗. Отсюда следует, что координаты вектора ka⃗ равны {kx;ky}.
Рассмотренные правила позволяют определить координаты любого вектора, представленного в виде алгебраической суммы данных векторов с известными координатами.
Найти координаты вектора a⃗+b⃗,если a⃗{3;2},b⃗{2;5}
Чтобы найти координаты вектора суммы, надо сложить соответствующие координаты данных векторов, получим:
a⃗+b⃗ имеет координаты {3 + 2; 2 + 5}, то есть {5; 7}
Найти координаты вектора 2a⃗, если a⃗{3;2}
Значит, вектор 2a⃗ имеет координаты {2 ⋅ 3; 2 ⋅ 2}, то есть {6;4}
Итак, сегодня мы узнали, что любой вектор можно разложить по двум неколлинеарным векторам, ввели понятие координат вектора и рассмотрели правила, позволяющие находить координаты суммы, разности векторов, и произведения вектора на число.
Заметили ошибку?
Расскажите нам об ошибке, и мы ее исправим.Разложение вектора по трем некомпланарным векторам
Теорема. Любой вектор m может быть представлен, и притом единственным образом, в виде линейной комбинации трех любых некомпланарных векторов а, b и с:
m = xa + yb + zc. (1)
Прежде всего отметим, что никакие два вектора из векторов а, b, с не коллинеарны; в противном случае векторы а, b, с были бы компланарны. Поэтому, если вектор m компланарен с какими-нибудь двумя векторами (например, с а и b), то m = ха + уb и, следовательно,
m = ха + уb + 0 • с,
т.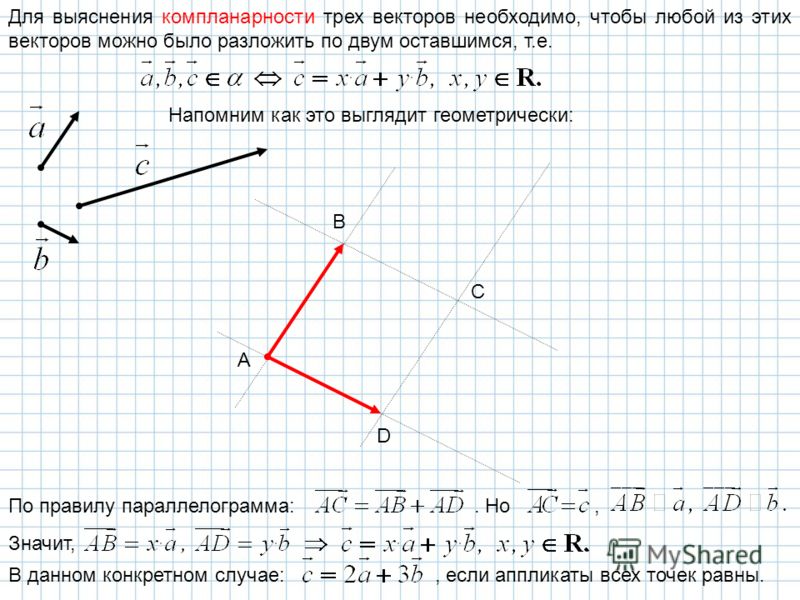 е. в этом случае теорема доказана.
е. в этом случае теорема доказана.
Пусть вектор m не компланарен ни с какими двумя векторами из векторов а, b, с (рис. 30).
Приведем все векторы к общему началу О и проведем через точку М (конец направленного отрезка, изображающего вектор \(\overrightarrow{OM}\) = т) прямую, параллельную вектору с. Эта прямая пересечет плоскость ОАВ в некоторой точке N. Ясно, что
\(\overrightarrow{OM}\) = \(\overrightarrow{ON}\) + \(\overrightarrow{NM}\).
По свойству коллинеарных векторов \(\overrightarrow{NM}\) = zc.
По теореме о разложении вектора по двум неколлинеарным векторам существуют числа х, у такие, что \(\overrightarrow{ON}\) = ха + уb.
Таким образом,
\(\overrightarrow{OM}\) = \(\overrightarrow{ON}\) + \(\overrightarrow{NM}\) = xa + yb + zc.
Единственность разложения вектора т по векторам а, b и с: доказывается аналогично тому, как это было сделано в теореме о разложении вектора по двум неколлинеарным векторам.
Базисом пространства называются любые три некомпланарных вектора, взятые в определенном порядке.
Пусть e1, e2 и e3 — некоторый базис, и a — произвольный вектор. Тогда, по только что доказанной теореме, существуют три числа х, у, z таких, что
а = хe1 + уe2 + ze3.
Числа х, у и z называются координатами вектора а в данном базисе. В этом случае пишут а = (х; у; z).
Задача 1. Дан куб ABCDA1B1C1D1. Разложить вектор \(\overrightarrow{AK}\), где K — центр грани ВСС1В1 по векторам а = \(\overrightarrow{AB}\), b = \(\overrightarrow{AC}\), с = \(\overrightarrow{AA}\) (рис. 31).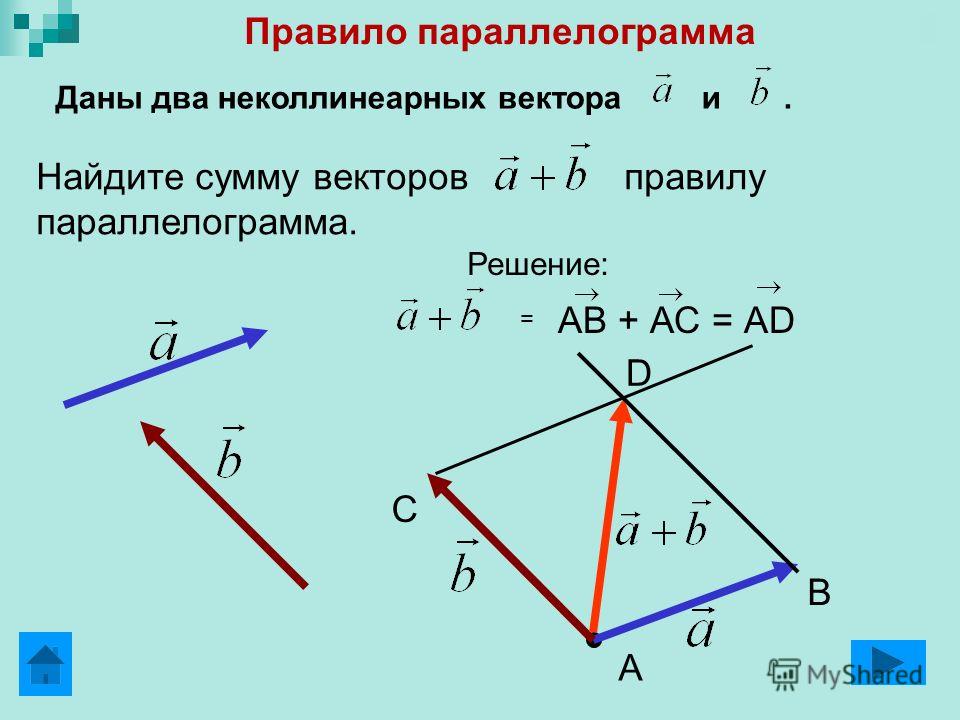
Из \(\Delta\)AKL имеем \(\overrightarrow{AK}\) = \(\overrightarrow{AL}\) + \(\overrightarrow{LK}\), но
$$ \overrightarrow{AL} = \frac{\overrightarrow{AB}+\overrightarrow{AC}}{2} = \frac{a+b}{2} $$
$$ а \;\; \overrightarrow{LK} = \frac{\overrightarrow{AA_1}}{2} = \frac{c}{2} $$
Следовательно,
$$ \overrightarrow{AK} = \frac{a+b}{2} + \frac{c}{2} = \frac{1}{2}a + \frac{1}{2}b + \frac{1}{2}c $$
Задача 2. Пусть векторы \(\overrightarrow{DA}\), \(\overrightarrow{DB}\), \(\overrightarrow{DC}\), изображенные соответствующими направленными ребрами треугольной пирамиды ABCD, образуют базис. Найти координаты вектора \(\overrightarrow{AB}\) в этом базисе.
Воспользуемся рис. 29a.
Обозначив \(\overrightarrow{DA}\) = e1, \(\overrightarrow{DB}\) = e2, \(\overrightarrow{DC}\) = e3, получим \(\overrightarrow{AB}\) = \(\overrightarrow{DB}\) — \(\overrightarrow{DA}\) = — e1 + e2 или \(\overrightarrow{AB}\) = — 1•e1 + 1•e2 + 0•e3,
откуда \(\overrightarrow{AB}\) = (- 1; 1; 0).
Векторная декомпозиция | Brilliant Math & Science Wiki
Каждый вектор можно рассматривать как сумму двух или более других векторов.
Рассмотрим три вектора на рисунке выше. Поскольку AC→ \overrightarrow{AC} AC состоит из AB→ \overrightarrow{AB}AB и BC→, \overrightarrow{BC} ,BC, получается следующее выражение:
AC→=AB→+BC→. \overrightarrow{AC} = \overrightarrow{AB} + \overrightarrow{BC} .AC=AB+BC.
Разложение вектора — это общий процесс разбиения одного вектора на два или более векторов, которые в сумме составляют исходный вектор. Векторы компонентов
, на которые разлагается исходный вектор, выбираются на основе конкретных деталей рассматриваемой проблемы.Учитывая точки O=(0,0,0),A=(1,0,0),B=(0,1,0),C=(0,0,1),O=(0,0, 0), А=(1,0,0), В=(0,1,0), С=(0,0,1), О=(0,0,0),А=(1,0, 0),B=(0,1,0),C=(0,0,1) и D=(3,4,5),D=(3,4,5),D=(3,4 ,5), каково значение a+b+c,a+b+c,a+b+c, где a,b, a, b, a,b и c c c удовлетворяют следующему уравнению:
OD→=a⋅OA→+b⋅OB→+c⋅OC→? \overrightarrow{OD} = a\cdot\overrightarrow{OA}+b\cdot\overrightarrow{OB}+c\cdot\overrightarrow{OC}? OD=a⋅OA+b⋅OB+c⋅OC?
У нас есть
OD→=(3,4,5),OA→=(1,0,0),OB→=(0,1,0),OC→=(0,0,1).
\begin{array}{c}&\overrightarrow {OD} = (3,4,5), &\overrightarrow {OA} = (1,0,0), &\overrightarrow {OB} = (0,1, 0), &\overrightarrow {OC} = (0,0,1).\end{массив} OD=(3,4,5),OA=(1,0,0),OB=(0 ,1,0),OC=(0,0,1).
Затем
OD→=a⋅OA→+b⋅OB→+c⋅OC→(3,4,5)=a(1,0,0)+b(0,1,0)+c(0,0, 1)=(а,0,0)+(0,б,0)+(0,0,в)=(а,б,в)⇒а=3,б=4,в=5. \begin{выровнено} \overrightarrow{OD} &= a\cdot\overrightarrow{OA}+b\cdot\overrightarrow{OB}+c\cdot\overrightarrow{OC} \\ (3,4,5) &= а(1,0,0) + б(0,1,0) + с(0,0,1) \\ &= (а,0,0) + (0,b,0) + (0,0,с) \\ &= (а,б,в) \\\\ \Стрелка вправо a &= 3, b = 4, c = 5. \end{выровнено} OD(3,4,5)⇒a=a⋅OA+b⋅OB+c⋅OC=a(1,0,0)+b(0,1,0)+c(0 ,0,1)=(a,0,0)+(0,b,0)+(0,0,c)=(a,b,c)=3,b=4,c=5.
Следовательно, a+b+c=3+4+5=12.a+b+c = 3+4+5 = 12.a+b+c=3+4+5=12. □_\квадрат □
Обратите внимание, что OD→\overrightarrow{OD}OD был разложен на три вектора, параллельных трем координатным осям. Также обратите внимание, что векторы OA→,OB→,\overrightarrow{OA},\overrightarrow{OB},OA,OB и OC→\overrightarrow{OC}OC являются единичными векторами координатного пространства.
Если a⃗=(1,1,0),b⃗=(1,0,1) \vec{a} = (1,1,0), \vec{b} = (1,0,1)a=( 1,1,0),b=(1,0,1) и c⃗=(0,1,1),\vec{c} = (0,1,1),c=(0,1,1) , как можно выразить d⃗=(5,6,7) \vec{d} = (5,6,7) d=(5,6,7) с помощью a⃗,b⃗ \vec{a}, \vec{b }а,б и в⃗? \vec{с}? с?
Пусть d⃗=xa⃗+yb⃗+zc⃗. \vec{d}= x \vec{a} + y \vec{b} + z \vec{c} .d=xa+yb+zc. Тогда у нас есть
d⃗=xa⃗+yb⃗+zc⃗(5,6,7)=x(1,1,0)+y(1,0,1)+z(0,1,1)=(x+y,x+ г, у+г), \begin{выровнено} \vec{d} &= x \vec{a} + y \vec{b} + z\vec{c} \\ (5,6,7) &= х(1,1,0) + у(1,0,1) + z(0,1,1) \\ &= (х+у, х+z, у+z), \end{выровнено} d(5,6,7)=xa+yb+zc=x(1,1,0)+y(1,0,1)+z(0,1,1)=(x +y,x+z,y+z),
что подразумевает
х+у=5х+г=6у+г=7⇒х=2,у=3,г=4. \begin{выровнено} х+у &= 5 \\ х+г &= 6 \\ у+г &= 7 \\\\ \Стрелка вправо x=2, y&=3, z=4. \end{выровнено} x+yx+zy+z⇒x=2,y=5=6=7=3,z=4.
Следовательно,
d⃗=2a⃗+3b⃗+4c⃗. □ \vec{d} = 2 \vec{a} + 3 \vec{b} + 4 \vec{c}.\ _\squared=2a+3b+4c. □
Если векторы a⃗=(3,−2,−4) \vec{a} = (3,-2,-4) a=(3,−2,−4) и b⃗=(x+1,8, 2y) \vec{b} = (x+1,8,2y) b=(x+1,8,2y) параллельны, каково значение x+y?x+y?x+y?
Поскольку a⃗ \vec{a}a и b⃗ \vec{b} b параллельны, существует некоторое действительное число mmm, удовлетворяющее условию b⃗=ma⃗ \vec{b} = m \vec{a} b=ma.
Таким образом,
b⃗=ma⃗(x+1,8,2y)=m(3,−2,−4)=(3m,−2m,−4m), \begin{align} \vec{b} &= m\vec{a} \\ (x+1, 8, 2y) &= m(3,-2,-4) \\ &= (3м, -2м, -4м), \end{выровнено} b(x+1,8,2y)=ma=m(3,−2,−4)=(3m,−2m,−4m),
что подразумевает
х+1=3m8=-2m2y=-4m⇒m=-4,x=-13,y=8. \begin{выровнено} х+1 &= 3м\\ 8&=-2м\\ 2г&= -4м \\\\ \Стрелка вправо m&= -4, x=-13, y=8. \end{выровнено} x+182y⇒m=3m=−2m=−4m=−4,x=−13,y=8.
Следовательно, x+y=−13+8=−5. □ х+у = -13+8=-5. \ _ \квадрат х+у=-13+8=-5. □
Координаты точек A,B,A,B,A,B и CCC равны (1,3),(4,1), (1,3), (4,1),(1,3),( 4,1) и (7,5),(7,5),(7,5) соответственно. Если PA→+PB→+PC→=0→,\overrightarrow{PA} + \overrightarrow{PB} + \overrightarrow{PC}=\overrightarrow{0}, PA+PB+PC=0, каковы координаты точка P?P?P?
Пусть вектор положения точки PPP равен OP→=(x,y).\overrightarrow{OP}=(x,y).OP=(x,y). Тогда у нас есть
PA→=(1−x,3−y)PB→=(4−x,1−y)PC→=(7−x,5−y). \begin{выровнено} \overrightarrow{PA} &= (1-x,3-y) \\ \overrightarrow{PB} &= (4-x,1-y) \\ \overrightarrow{PC} &= (7-x, 5-y).
\end{выровнено} PAPBPC=(1−x,3−y)=(4−x,1−y)=(7−x,5−y).
Так как нам дано PA→+PB→+PC→=0→, \overrightarrow{PA} + \overrightarrow{PB} + \overrightarrow{PC} = \overrightarrow{0} ,PA+PB+PC=0, мы есть
PA→+PB→+PC→=0→(1−x,3−y)+(4−x,1−y)+(7−x,5−y)=(0,0)(12− 3x,9−3y)=(0,0)⇒x=4,y=3. \begin{выровнено} \overrightarrow{PA} + \overrightarrow{PB} + \overrightarrow{PC} &= \overrightarrow{0} \\ (1-x,3-y)+ (4-x,1-y)+(7-x, 5-y) &= (0,0) \\ (12-3x, 9-3y) &= (0,0) \\\\ \Стрелка вправо x&= 4, y= 3. \end{выровнено} PA+PB+PC(1−x,3−y)+(4−x,1−y)+(7−x,5−y)(12−3x,9−3y)⇒x =0=(0,0)=(0,0)=4,y=3.
Таким образом, координаты точки PPP равны P=(4,3). Р=(4,3). Р=(4,3). □_\квадрат□
Если векторы a⃗=(1,−2) \vec{a} = (1,-2)a=(1,−2) и b⃗=(4,−5) \vec{b} = (4,- 5)b=(4,−5) удовлетворяют a⃗=x⃗+y⃗ \vec{a}=\vec{x} + \vec{y}a=x+y и b⃗=x⃗−2y⃗,\vec{b }= \vec{x} -2\vec{y},b=x−2y, что такое x⃗−y⃗?\vec{x}-\vec{y}?x−y?
У нас есть
х⃗+у⃗=а⃗х⃗−2y⃗=b⃗⇒x⃗=13(2a⃗+b⃗),y⃗=13(a⃗−b⃗).
\begin{выровнено} \vec{x} + \vec{y} &= \vec{a} \\ \vec{x} -2\vec{y} &= \vec{b} \\ \стрелка вправо \vec{x} &= \frac{1}{3} \big(2 \vec{a} + \vec{b} \big), \\ \vec{y} &= \frac{1}{3} \big( \vec{a} — \vec{b}\big). \end{выровнено} x+yx−2y⇒xy=a=b=31(2a+b),=31(a−b).
Следовательно, x⃗−y⃗ \vec{x} — \vec{y} x−y равно
x⃗−y⃗=13(2a⃗+b⃗)−13(a⃗−b⃗)=13(a⃗+2b⃗)=13a⃗+23b⃗=(13,−23)+(83,−103)=(3,−4) . □ \begin{выровнено} \vec{x} — \vec{y} &= \frac{1}{3} \big(2 \vec{a} + \vec{b}\big) — \frac{1}{3} \big ( \vec{a} — \vec{b}\big) \\ &= \frac{1}{3} \big( \vec{a}+2\vec{b} \big) \\ &= \frac{1}{3} \vec{a} + \frac{2}{3} \vec{b} \\ &= \left( \frac{1}{3}, -\frac{2}{3} \right) + \left( \frac{8}{3}, -\frac{10}{3}\right ) \\ &= (3, -4).\ _\квадрат \end{выровнено} x−y=31(2a+b)−31(a−b)=31(a+2b)=31a+32b=(31,−32 )+(38,−310)=(3,−4). □
Одно обычно полезное разложение — с компонентами, которые лежат параллельно каждой из осей координат.
На рисунке выше показано разложение вектора в трехмерном пространстве.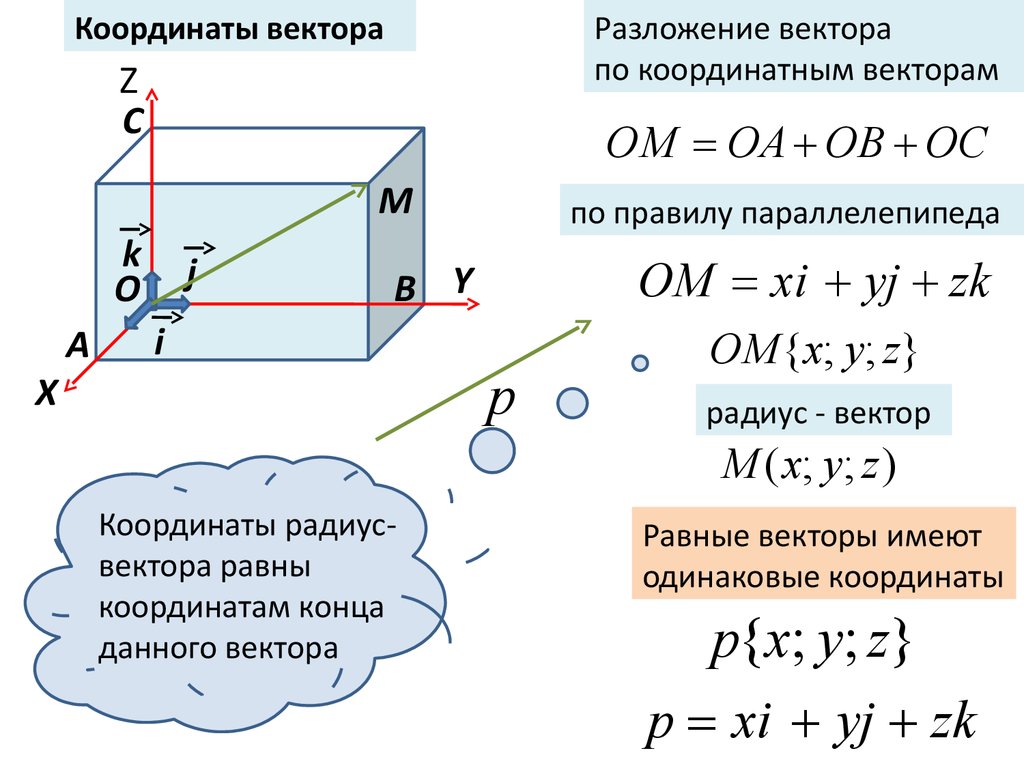 Обратите внимание, что красный вектор можно разложить на три зеленых вектора, которые параллельны трем осям координат. Таким образом, OD→ \overrightarrow{OD} OD состоит из трех векторов OA→,OB→ \overrightarrow{OA}, \overrightarrow{OB} OA,OB и OC→. \overrightarrow{OC}.OC. Поэтому соответствует следующее выражение: 9=vxwx+vywy+vzwz,
Обратите внимание, что красный вектор можно разложить на три зеленых вектора, которые параллельны трем осям координат. Таким образом, OD→ \overrightarrow{OD} OD состоит из трех векторов OA→,OB→ \overrightarrow{OA}, \overrightarrow{OB} OA,OB и OC→. \overrightarrow{OC}.OC. Поэтому соответствует следующее выражение: 9=vxwx+vywy+vzwz,
как и ожидалось.
Разложение вектора на компоненты
Главная > Математика > Предварительное исчисление > Разложение вектора на компоненты
Во многих приложениях необходимо разложить вектор на сумму двух перпендикулярных компонент вектора. Это верно для многих физических приложений, связанных с силой, работой и другими векторными величинами. Перпендикулярные векторы имеют скалярное произведение нуля и называются ортогональными векторами .
На рис. 1 показаны векторы u и v с вектором u , разложенным на ортогональные компоненты w 1 и w 2 .
Вектор u теперь можно записать как u = w 1 + w 2 , где w 1 параллелен вектору v , а w 1 перпендикулярен/ортогонален вектору w 2 9 0904 Компонента вектора w 1 также называется проекцией вектора u на вектор v , proj v u .
Proj V U можно рассчитать следующим образом:
Проекция U на V:
LET U и V BE NONZER VECTORS: и V BE NONZERO: и V . vv2]v
Как только компонент вектора proj v u найден, поскольку u = w 1 + w 2 , компонент вектора w 2 может быть найден путем вычитания w 1 от до .
w 2 = u — w 1
Рассмотрим несколько примеров.
Для работы этих примеров требуется использование различных векторных правил.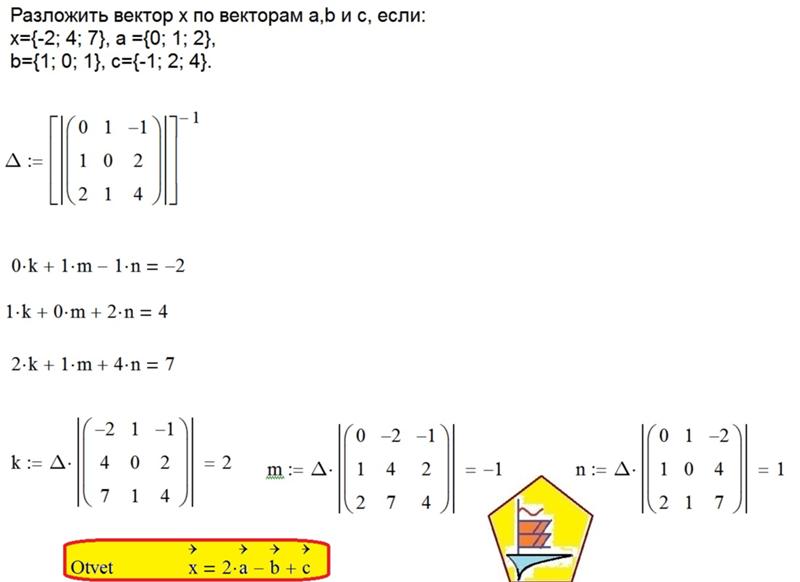 Если вы не знакомы с правилом, перейдите в соответствующую тему для ознакомления.
Если вы не знакомы с правилом, перейдите в соответствующую тему для ознакомления.
Пример 1: Пусть u=〈-2,2〉 и v=〈3,5〉. Запишите вектор u как сумму двух ортогональных векторов, один из которых является проекцией u на v.
Шаг 1: Найдите проект v u . projvu=[u·v∥v∥2]v=w1 | projvu=[u·v∥v∥2]v projvu=[(−2·3)+(2·5)32+522]〈3,5〉 projvu=[−6+10342]〈3,5〉 projvu=[434]〈3,5〉=[217]〈3,5〉 projvu=〈617,1017〉 |
Шаг 2: Найдите ортогональный компонент. ш 2 = и — ш 1 | ш 2 = и — ш 1 w2=〈−2,2〉−〈617,1017〉 w2=〈(−2−617), (2−1017)〉 w2=〈−4017,2417〉 |
Шаг 3: Запишите вектор как сумму двух ортогональных векторов. и = ш 1 + ш 2 | ты = ш 1 + ш 2 и=〈617,1017〉+〈−4017,2417〉 |
Пример 2. Для заданных векторов u=〈1,3〉 и v=〈-4,5〉 запишите u как сумму двух ортогональных векторов, один из которых является проекцией u на v.
Для заданных векторов u=〈1,3〉 и v=〈-4,5〉 запишите u как сумму двух ортогональных векторов, один из которых является проекцией u на v.
Шаг 1: Найдите проект v u . projvu=[u·v∥v∥2]v=w1 | projvu=[u·v∥v∥2]v projvu=[(1·−4)+(3·5)(−4)2+522]〈−4,5〉 projvu=[−4+15412]〈−4,5〉 projvu=[1141]〈−4,5〉 projvu=〈−4441,5541〉 |
Шаг 2: Найдите ортогональный компонент. ш 2 = и — ш 1 | ш 2 = и — ш 1 w2=〈1,3〉−〈−4441,5541〉 w2=〈(1+4441), (3−5541)〉 w2=〈8541,6841〉 |
Шаг 3: Запишите вектор как сумму двух ортогональных векторов. |


 \begin{array}{c}&\overrightarrow {OD} = (3,4,5), &\overrightarrow {OA} = (1,0,0), &\overrightarrow {OB} = (0,1, 0), &\overrightarrow {OC} = (0,0,1).\end{массив} OD=(3,4,5),OA=(1,0,0),OB=(0 ,1,0),OC=(0,0,1).
\begin{array}{c}&\overrightarrow {OD} = (3,4,5), &\overrightarrow {OA} = (1,0,0), &\overrightarrow {OB} = (0,1, 0), &\overrightarrow {OC} = (0,0,1).\end{массив} OD=(3,4,5),OA=(1,0,0),OB=(0 ,1,0),OC=(0,0,1).
 Таким образом,
Таким образом, \end{выровнено} PAPBPC=(1−x,3−y)=(4−x,1−y)=(7−x,5−y).
\end{выровнено} PAPBPC=(1−x,3−y)=(4−x,1−y)=(7−x,5−y).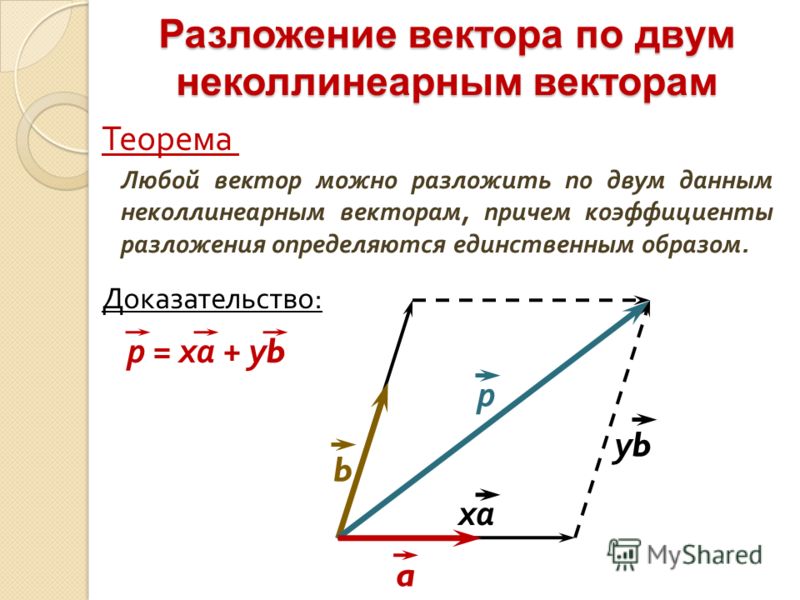 \begin{выровнено}
\vec{x} + \vec{y} &= \vec{a} \\
\vec{x} -2\vec{y} &= \vec{b} \\
\стрелка вправо \vec{x} &= \frac{1}{3} \big(2 \vec{a} + \vec{b} \big), \\
\vec{y} &= \frac{1}{3} \big( \vec{a} — \vec{b}\big).
\end{выровнено} x+yx−2y⇒xy=a=b=31(2a+b),=31(a−b).
\begin{выровнено}
\vec{x} + \vec{y} &= \vec{a} \\
\vec{x} -2\vec{y} &= \vec{b} \\
\стрелка вправо \vec{x} &= \frac{1}{3} \big(2 \vec{a} + \vec{b} \big), \\
\vec{y} &= \frac{1}{3} \big( \vec{a} — \vec{b}\big).
\end{выровнено} x+yx−2y⇒xy=a=b=31(2a+b),=31(a−b).
