Решите двойное неравенство: Двойные неравенства. 2 способа решения

Двойные неравенства. 2 способа решения

Например:

\(5<11<17\)
\(-2\leq3x+5\leq2\)
\(2x-5\leq3x+7\leq8x\)

Двойное неравенство по своей сути – это система из двух неравенств, записанных в одну строку. Поэтому  их всегда можно представить в виде системы.

Например:

\(-2\leq3x+5\leq2\Leftrightarrow\begin{cases}-2\leq3x+5\\3x+5\leq2\end{cases}\)
\(2x-5\leq3x+7\leq8x\Leftrightarrow\begin{cases}2x-5\leq3x+7\\3x+7\leq8x\end{cases}\)

Но делать это нужно не всегда.

1) Если в крайней левой и крайней правой частях двойного неравенства нет неизвестных, то удобнее оставить его как есть. При этом в процессе решения стремится равносильными преобразованиями привести неравенство к виду \([число]\)\(<\)\(x\)\(<\)\([число]\).

Пример: Решите двойное неравенство:

\(-2\leq3x+5\leq2\)    \(|-5\)		Здесь нет неизвестных по краям, поэтому к системе переходить не будем. Вместо этого делаем такие преобразования, чтоб в центре остался голый икс, а по краям — числа. Для того чтобы «оголить» икс нужно избавиться от пятерки и тройки. Вычтем \(5\) из всего неравенства.
\(-7≤3x≤-3\)   \(|:3\)		Теперь нам мешает \(3\). Поделим все три части неравенства на \(3\).
\(-\)\(\frac{7}{3}\)\(\leq x \leq-1\)		Готово, наш икс «голый». Можно записывать ответ.

Ответ: \([-\)\(\frac{7}{3}\)\(;-1]\)

2) Если в крайних частях двойного неравенства есть неизвестные лучше перевести неравенство в систему и решать его как обычную систему неравенств.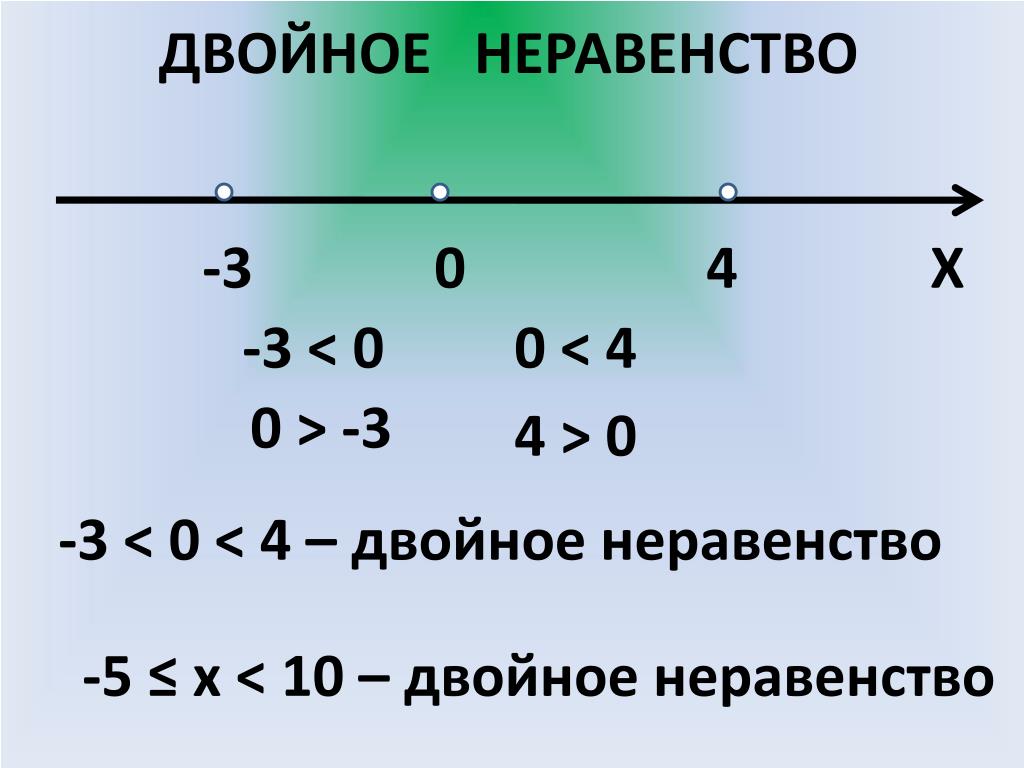

Пример: Решите двойное неравенство:

\(2x-5<3x+7≤8x\)	В крайней левой и крайней правой частях есть неизвестные –значит переходим к системе.
\(\begin{cases}2x-5<3x+7\\3x+7\leq8x\end{cases}\)	Решаем обычные линейные неравенства: все, что с иксами переносим в левую сторону, все что без иксов — в правую.
\(\begin{cases}2x-3x<7+5\\3x-8x\leq-7\end{cases}\)	Приводим подобные слагаемые
\(\begin{cases}-x<12   \\-5x\leq-7   \end{cases}\)	«Оголим» иксы, поделив верхнее неравенство на \((-1)\), нижнее на \((-5)\). Не забываем при этом перевернуть знаки сравнения, так как мы делим на отрицательное число.
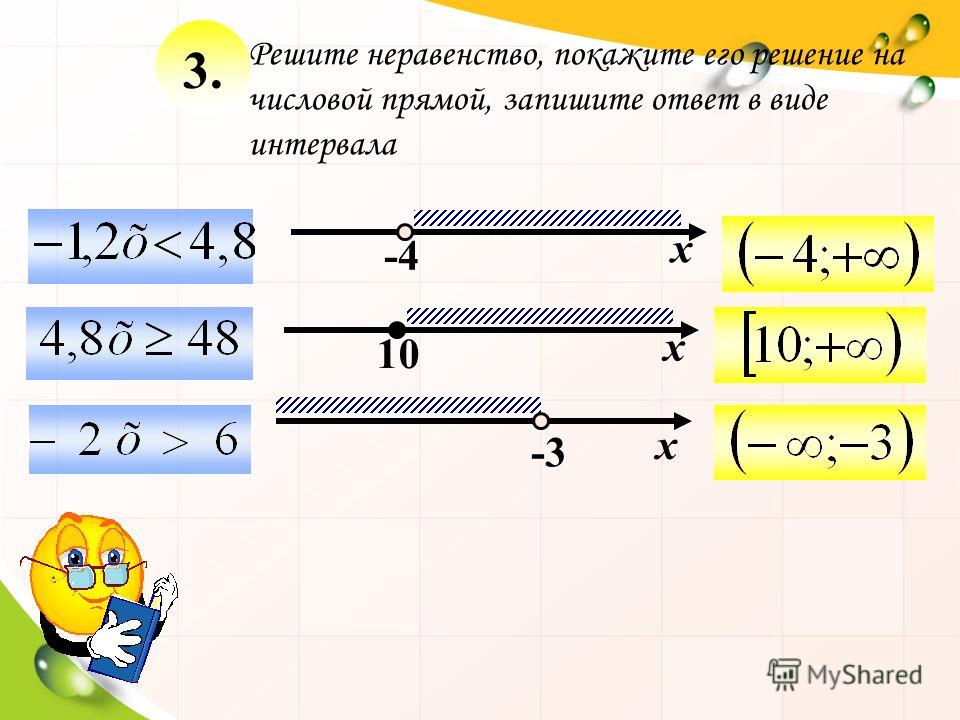
\(\begin{cases}x>-12   \\x\geq \frac{7}{5}\end{cases}\)	Отметим на числовой оси оба решения
	Так как у нас система, то мы ищем значения иксов, которые подойдут обоим неравенствам, т.е. интервал, где есть двойная штриховка: и сверху, и снизу. Его и запишем ответ.

Ответ: \([\)\(\frac{7}{5}\)\(;\infty)\)

Решите двойное неравенство » задачи

неравенства »

• Решите двойное неравенство -3<2-5x<1 и ещё одно такое -4<2-4x<-2

  
  Решение: Все двойные неравенства решаются системой 
  1 неравенство: 
  -3<2-5x<1 
  составлю систему: 
  {2-5x>-3 {-5x>-3-2 {-5x>-5 {x<1 
  {2-5x<1 {-5x<1-2 {-5x<-1 {x>0. 2 
  Ответ: (0,2;1) или 0,2<x<1 

  2 неравенство: 
  {2-4x>-4 {-4x>-4-2 {-4x>-6 {x<1.5 
  {2-4x<-2 {-4x<-2-2 {-4x<-4 {x>1
  Ответ: (1;1,5) или 1<x<1.5 

• Решите двойное неравенство и укажите,если возможно,наибольшее и наименьшее целое решение неравенства $$ -5

  
  Решение: $$ -5Умножим все части неравенства на 7:
  -35 Прибавим (-4)
  -39Разделим на  (-3) и поменяем знаки
  13>x≥-10/3
  запишем в привычном виде
  -10/3≤хнаименьшее целое решение неравенства ( -3)
  Наибольшее целое решение неравенства  10
  

• Решите двойное неравенство 3<4-2/3x<=5

  
  Решение: 1. Избавимся от 4. Для этого прибавим противоположное число во все части неравенства.
  3-4<4-4-2/3х<=5-4
  -1<-2/3х<=1
  2. Избавимся от дроби. Для этого умножим на обратное число с таким же знаком все части.
  -1*(-3/2)<-2/3х*(-3/2)<=1*(-3/2)
  1,5>х>=-1,5
  3. Теперь, так как знаки измннились из-за умножения на отрицательное число, мы перевернем неравенство.
  -1,5<=х<1,5
  4. Ответ [-1,5;1,5)

• Решите двойное неравенство :-3≤2x-1≤5 2)-2≤1-3x≤7

  
  Решение: Двойное неравенство переводим в систему неравенств:
  $$ \left \{ {{2x-1 \leq 5} \atop {2x-1 \geq -3}} \right. \\ \left \{ {{2x \leq 4} \atop {2x \geq -2}} \right. \\ \left \{ {{x \leq 2} \atop {x \geq -1}} \right. \\ -1 \leq x \leq 2 $$

  Таким же путем решаем второе:
  1 — 3х ≤ 7
  1 — 3х ≥ -2

  -3х ≤ 6
  -3х ≥ — 3

  х ≥ -2
  х ≤ 1

  -2 ≤ х ≤ 1

• Решите двойное неравенство:1) 0 меньше или равно 1-2х/3 меньше 3

  
  2) 2 меньше х/3-1/2 меньше или равно 10
  3) -3 меньше 1- 2-х/3 меньше 3
  Решение: 1)0 <= 1-2x/3 <3

  0 <= (3-2x)/3 <3 

  0 <= 3-2x <9

  3 <= -2x <12

  -1,5 => x > -6

  2) 2< x/3-1/2 <= 0

    2< (2x-3)/6 <= 0

    12< 2x-3 <= 0

    15< 2x <= 3

    30< x <= 6

  3) -3 < 1 -(2-x)/3<3

    -3 < (1-x)/3<3

    -9 < 1-x <9

    -10 < -x <8

    -10 > -x >8

   

• Решите двойное неравенство а) 3 б) 4 в)-1

  
  Решение: Суть того чтобы решить неравенство в первом примере заключается в том чтобы (х) остался один.  
  для этого разделим все на 3
  1

  аналогично только уже на -2
  при этом меняем знак!
  -2≥у≥-5

  делим на 3

  -1/3

• решите двойное неравенство -2(меньше или равно)3 — 4х(меньше или равно) 5

  
  Решение: -2=

  -2-3=

  -5=

  -5/-4=>-4x/-4=>2/-4

  -1/2=

  знаки развернули так как делили на отрицательное число 

  -2

  Вычтем из неравности 3

  -2-3

   -5

  Поделим неравенство на -4 и изменим знаки на противоположные, потому -4 — отрицательное число

  1,25>=x>=-0,5

  -0,5

  Неравенство решено 

• Решите двойное неравенство и укажите, если возможно, наибольшее и наименьшее целое решение неравенства : -5 =

  
  Решение: Умножаем все нравенство на 7
  $$ -5*7 \leq \frac{4-3x}{7} *7 \leq 2*7 $$, получим
  $$ -35 \leq 4-3 x \leq 14 $$, теперь отнимем 4 от каждой части неравенства, получим:
  $$ -35-4 \leq 4-3 x-4 \leq 14-4 $$
  $$ -39 \leq -3 x \leq 10 $$, разделим все неравенство на -3 (минус три), знаки поменяются на противоположные:
  $$ \frac{-39}{-3} \geq x \geq \frac{10}{-3} $$
  $$ 13 \geq x \geq -3 \frac{1}{3} $$
  тогда наибольшее целое решение 13, наименьшее -3 (минус три). {2} \)
  Решение: 1)  $$ |x| \leq b $$ можно найти из двойного неравенства $$ -b \leq x \leq b $$, которое записывается в виде системы 
   $$ \left \{ {{x \leq b} \atop {x \geq -b}} \right. $$.
  Действительно,
   $$ |x| \leq b\\a)\; x \geq 0\;,\; x \leq b\\b)\; xПересечением первого и второго множеств является промежуток между (-b) и (b).
   А вот, если бы неравенство было обратное, то есть
  |x|>b, то здесь не было бы пересечения множеств, а было бы объединение:
   $$ |x|>b\\a)\; x \geq 0\;,\; x>b\\b)\; xb\;,\; xb \; \; ili\; \; x    В этой задаче неравенство получается более сложное, но принцип тот же: если |A| система {A>-B, A2) При решении неравенства х(х-2)Тогда решением будет интервал 0прямые, перпендикулярные оси ОХ, а значит, это двойное неравенство — часть плоскости, заключённая между двумя прямыми х=0 и х=2 ( пересечение множеств х>=0 и x

Вопрос Видео: Решение двойных неравенств с переменными по трем сторонам

Стенограмма видео

Найдите все значения 𝑥, удовлетворяющие неравенству минус 20 минус 𝑥 меньше или равно трем 𝑥 плюс два, что меньше 18 минус два 𝑥 . Запишите ответ в виде интервала.

Для начала мы решим эту задачу, разделив ее на две части: первое неравенство слева, а затем второе неравенство справа. Итак, мы можем приступить к решению нашего первого неравенства. Итак, у нас есть минус 20 минус 𝑥 меньше или равно трем 𝑥 плюс два. Итак, мы собираемся решить это неравенство, но помня так же, как мы решаем уравнение. Итак, первое, что мы собираемся сделать, это на самом деле мы собираемся вычесть два с каждой стороны, что дает нам минус 22 минус 𝑥 меньше или равно трем 𝑥.

Хорошо, теперь наш следующий шаг, мы на самом деле собираемся добавить 𝑥 к каждой стороне, что дает нам минус 22 меньше или равно четырем 𝑥. Хорошо, теперь мы можем решить это неравенство, потому что мы собираемся разделить три на четыре, что дает минус 22, если четыре меньше или равны 𝑥. Просто чтобы привести это в порядок, мы упростим эту дробь в левой части. Таким образом, мы можем сказать, что минус 11 больше двух меньше или равно 𝑥. Большой! Итак, наше первое неравенство решено.

Теперь мы продолжим и решим правую часть, наше второе неравенство. И это второе неравенство говорит нам, что три 𝑥 плюс два меньше, чем 18 минус два 𝑥. Хорошо, снова решим это так, как мы решаем уравнение, поэтому первое, что мы собираемся сделать, это на самом деле мы собираемся вычесть два из каждой стороны, что дает нам три 𝑥 меньше, чем 16 минус два 𝑥. Итак, теперь мы добавим по две 𝑥 с каждой стороны. Таким образом, мы получаем пять 𝑥 меньше 16.

И затем, наконец, чтобы решить наше неравенство, мы делим обе части на пять, что дает нам, что 𝑥 меньше 16 на пять. Так здорово! Мы решили оба неравенства. Итак, давайте теперь соберем их вместе, чтобы увидеть, какими могут быть наши возможные значения 𝑥.

Если мы объединим наши решения, мы увидим, что 𝑥 больше или равно минус 11 для двух и меньше 16 для пяти. Хорошо, давайте покажем, что это на самом деле означает. Итак, если мы посмотрим на это на числовой прямой, мы увидим это вот так, где мы фактически получили заполненную точку над нашим минусом 11 над двумя. И это потому, что он меньше или равен. И тогда у нас фактически есть открытый круг над нашими 16 против пяти. И это потому, что он просто говорит, что это больше, чем 𝑥.

Итак, мы решили эту проблему. И мы знаем, где лежат наши ценности. Но мы закончили? Ну, нет, потому что на самом деле наш вопрос просит нас записать наш ответ в виде интервала. Таким образом, в интервальной записи это будет наше решение со скобкой слева. И это потому, что он меньше или равен. И снова это то же самое, что когда мы показываем на числовой строке. У нас там другое обозначение и у нас есть цветной кружок.

Но когда мы используем обозначение интервала, мы фактически используем для этого скобки. А справа у нас скобки. И мы используем эту скобку в правой части, потому что, как мы видим, здесь просто 𝑥 меньше 16 на пять, не меньше или равно. И снова мы получили обозначение открытого круга. Итак, мы подошли к окончательному ответу. И это написано как интервал.

Составные неравенства: Составные неравенства | SparkNotes

Чтобы решить составное неравенство, сначала разделите его на два неравенства. Определите, должен ли ответ быть объединением множеств («или») или пересечением множеств («и»). Затем решите оба неравенства и график.

Если неясно, является ли неравенство объединением множеств или пересечением множеств, то ##проверьте каждую область##, чтобы убедиться, что она удовлетворяет составному неравенству.

Пример 1 : Решить и построить график: 4≤2 x ≤8

4≤2 x и 2 x ≤8 (пересечение множеств)
4≤2 x

≤
2≤ x
х ≥2

2 x ≤8

≤82
х ≤4

2≤ х и х ≤4.
График:

Пример 1

Пример 2 : Решите и постройте график: { x : 5≤ +5 < 6}

5≤ + 5 и +5 < 6 (пересечение множеств)
5≤ + 5

0≤
0≤ x

+5 < 6

< 1
х < 3

0≤ x и x < 3.
График:

Пример 2

Пример 3 : Решить и построить график: 3( x — 2) < 9 или 3( x — 2) > 15 (объединение наборов)

3( x — 2) < 2)

х

— 2 < 3
х < 5

3( х — 2) > 15

х — 2 > 5
х > 7

x < 5 или x > 7.
График:

Пример 3

Пример 4 : Решите и постройте график: { x : 2 x ≤ x — 3}∪{ x : x < 3 x 94029 -}

2 х ≤ x — 3 или x < 3 x — 4 (объединение наборов)
2 x ≤ x — 3

х ≤ — 3

х < 3 х — 4

-2 x < - 4
х >2

x ≤ — 3 или x > 2.

No related posts.