$=\frac{-3-i}{1-(-1)}=\frac{-3-i}{2}=-\frac{3}{2}-\frac{i}{2}$
Ответ. $\frac{-2+i}{1-i}=-\frac{3}{2}-\frac{i}{2}$
Деление комплексных чисел в геометрической форме
Если надо поделить комплексные числа $z_{1}$ и $z_{2}$ в геометрической форме: $\frac{z_{1}}{z_{2}}=\frac{\left|z_{1}\right|\left(\cos \phi_{1}+i \sin \phi_{1}\right)}{\left|z_{2}\right|\left(\cos \phi_{2}+i \sin \phi_{2}\right)}$ , то искомое число
$z=\frac{z_{1}}{z_{2}}=\frac{\left|z_{1}\right|}{\left|z_{2}\right|}\left[\cos \left(\phi_{1}-\phi_{2}\right)+i \sin \left(\phi_{1}-\phi_{2}\right)\right]$
То есть модуль частного двух комплексных чисел равен частному модулей, а аргумент — разности аргументов делимого и делителя.
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание.
Решение. Искомое частное
$\frac{z_{1}}{z_{2}}=\frac{2 \cdot\left(\cos \frac{3 \pi}{4}+i \sin \frac{3 \pi}{4}\right)}{\cos \frac{\pi}{4}+i \sin \frac{\pi}{4}}=$
$=\frac{2}{1} \cdot\left[\cos \left(\frac{3 \pi}{4}-\frac{\pi}{4}\right)+i \sin \left(\frac{3 \pi}{4}-\frac{\pi}{4}\right)\right]=$
$=2 \cdot\left[\cos \frac{\pi}{2}+i \sin \frac{\pi}{2}\right]=2 \cdot(0+i)=2 i$
Ответ. $\frac{z_{1}}{z_{2}}=2 \cdot\left(\cos \frac{\pi}{2}+i \sin \frac{\pi}{2}\right)=2 i$
Читать дальше: возведение комплексного числа в степень.
Как найти частное двух комплексных чисел: формула, примеры
Sign in
Password recovery
Восстановите свой пароль
Ваш адрес электронной почты
MicroExcel.ru Математика Алгебра Деление комплексных чисел
В данной публикации мы рассмотрим формулы, с помощью которых можно найти частное двух комплексных чисел, представленных в алгебраической или тригонометрической форме. Также приведены примеры для лучшего понимания теоретического материала.
Также приведены примеры для лучшего понимания теоретического материала.
- Деление в алгебраической форме
- Деление в геометрической форме
Деление в алгебраической форме
Результатом деления (т.е. частное) двух комплексных чисел x = a1 + b1i и y = a2 + b2i также является комплексное число z:
Порядок действий следующий:
- Делимое и делитель умножаем на число, комплексно сопряженное делителю. Не забываем, что i2 = -1.
Примечание: Для (a + bi) комплексно сопряженным будет число (a – bi), т.е. действительная часть остается той же, а у мнимой знак меняется на противоположный. - В результате выполнения умножения в знаменателе получается обычное действительное число.
(a2 + b2i)(a2 – b2i) = a2 ⋅ a2 – a2 ⋅ b2i + b2i ⋅ a2 – b2i ⋅ b2i = a22 – b22 ⋅ i2 = a22 + b22.
- Теперь выполним аналогичное действие в числителе:
(a1 + b1i)(a2 – b2i) = a1 ⋅ a2 – a1 ⋅ b2i + b1i ⋅ a2 – b1i ⋅ b2i = a1a2 – b1b2i2 – a1b2i + b1a2i = (a1a2 + b1b2) + (a2b1 – a1b2) ⋅ i. - Делим полученный числитель на знаменатель:
Пример 1:
Разделим комплексное число (3 – i) на (-5 + 2i).
Решение:
Руководствуемся планом действий, описанным выше, и получаем:
Деление в геометрической форме
Если комплексные числа заданы в тригонометрической форме, например, x = |x| ⋅ (cos φ1 + i ⋅ sin φ1) и y = |y| ⋅ (cos φ2 + i ⋅ sin φ2), то разделить их можно по формуле ниже:
Пример 2
Найдем частное комплексных чисел: x = 4 ⋅ (cos 60° + i ⋅ sin 60°) и y = 2 ⋅ (cos 25° + i ⋅ sin 25°).
Решение:
|x| : |y| = 4 : 2 = 2
φ1 – φ2 = 60° – 25° = 35°
x : y = 2 ⋅ (cos 35° + i ⋅ sin 35°)
ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ
Таблица знаков зодиака
Нахождение площади трапеции: формула и примеры
Нахождение длины окружности: формула и задачи
Римские цифры: таблицы
Таблица синусов
Тригонометрическая функция: Тангенс угла (tg)
Нахождение площади ромба: формула и примеры
Нахождение объема цилиндра: формула и задачи
Тригонометрическая функция: Синус угла (sin)
Геометрическая фигура: треугольник
Нахождение объема шара: формула и задачи
Тригонометрическая функция: Косинус угла (cos)
Нахождение объема конуса: формула и задачи
Таблица сложения чисел
Нахождение площади квадрата: формула и примеры
Что такое тетраэдр: определение, виды, формулы площади и объема
Нахождение объема пирамиды: формула и задачи
Признаки подобия треугольников
Нахождение периметра прямоугольника: формула и задачи
Формула Герона для треугольника
Что такое средняя линия треугольника
Нахождение площади треугольника: формула и примеры
Нахождение площади поверхности конуса: формула и задачи
Что такое прямоугольник: определение, свойства, признаки, формулы
Разность кубов: формула и примеры
Степени натуральных чисел
Нахождение площади правильного шестиугольника: формула и примеры
Тригонометрические значения углов: sin, cos, tg, ctg
Нахождение периметра квадрата: формула и задачи
Теорема Фалеса: формулировка и пример решения задачи
Сумма кубов: формула и примеры
Нахождение объема куба: формула и задачи
Куб разности: формула и примеры
Нахождение площади шарового сегмента
Что такое окружность: определение, свойства, формулы
комплексных чисел
комплексных чиселУмножение комплексных чисел в декартовой форме является биномиальным умножением и c + jd = + j затем (a + jb)(c + jd) = + j немного больше связано с декартовой формой и требует процесса, называемого рационализацией комплексного числа. | Индекс Комплексные числа | ||||||||||||||||||||
|





 Чтобы вычесть комплексные числа, вычтите каждый элемент отдельно.
Чтобы вычесть комплексные числа, вычтите каждый элемент отдельно.

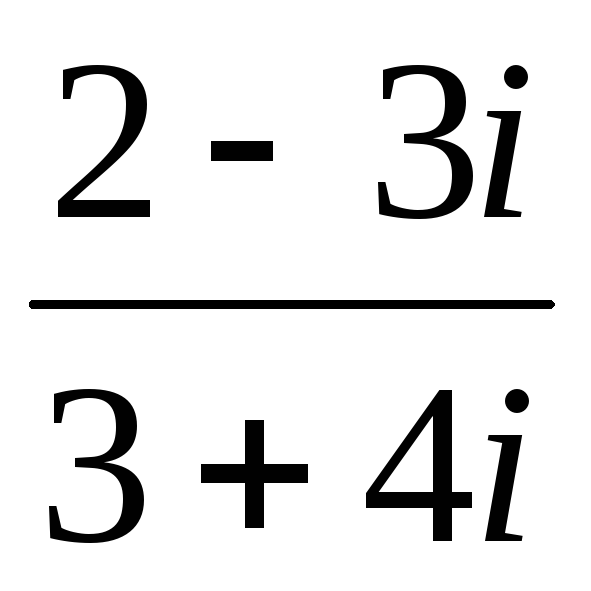 Чтобы добавить комплексные числа, добавьте каждый элемент отдельно.
Чтобы добавить комплексные числа, добавьте каждый элемент отдельно.
