Калькулятор сложения векторов: сложение и вычитание векторов
Этот бесплатный калькулятор сложения векторов позволяет вычислять сумму двух векторов (с кратными или без кратных) в двухмерной и трехмерной системе координат.
Что такое вектор? «Величина, представленная величиной и направлением, называется вектором»0022 Векторы представлены в виде координат или кратных координат. Ниже приведены формулы векторной суммы, которые используются для отображения комбинации векторов в целом. Давайте пройдем через это! (a,b) + (d,e) = (a + d, b + e) (a,b,c) + (d,e,f) = (a + d, b + e, c + f) Наш бесплатный калькулятор сложения векторов также учитывает формулы для сложения или вычитания векторов соответственно . Теперь представьте, что вы столкнулись с кратными, которые помогают вам составить сумму векторов более чем в два раза. Просто возьмем пример: Предположим, у вас есть следующее выражение: a+b*2 Приведенное выше выражение означает, что вы, вероятно, добавите 2 копии изображения b к a. С нашим бесплатным калькулятором суммы векторов вы можете легко решать задачи сложения или вычитания векторов с кратными или без них. Это еще одно правило сложения векторов, позволяющее считать сумму векторов без координат вообще. Давайте сначала прольем свет на правило: » Предположим, что у вас есть два вектора a и b. Чтобы добавить их, соедините хвост вектора b с головой вектора a. Теперь возьмем результирующий вектор c так, чтобы его хвост совпадал с хвостом вектора a, а голова с головой вектора b. Этот вектор c представляет собой сумму двух векторов, которые вы также можете определить с помощью этого бесплатного онлайн-вектора 9.
0005 ”
Помимо правила сложения векторов «голова к хвосту», это еще одно правило, которое считается более надежным, чем все остальные. Теперь давайте поясним, что какой бы метод или правило вы ни выбрали для расчетов, этот бесплатный калькулятор сложения векторов сделает это за вас за пару секунд, сохраняя при этом точность. Кроме того, вы также можете использовать наш лучший калькулятор цифр, чтобы получить максимальную точность для любого расчета или числа.
Заявление: “ Если вы хотите сложить два вектора a и b, соедините их оба так, чтобы их хвосты совпадали друг с другом. Теперь создайте пунктирную линию напротив объединенных векторов. Наконец, диагональ параллелограмма будет представлять собой сумму векторов, которые вы также можете определить с помощью этого бесплатного 2D-калькулятора сложения векторов.
”
Без сомнения, вы можете использовать бесплатный калькулятор вычитания векторов, чтобы вычесть один вектор из другого, но здесь мы также познакомим вас с краткой концепцией.
Посмотрите на картинку выше! Что ты видишь? Давайте объясним!
У нас есть два вектора a и -a , где a — положительный вектор, а -a — отрицательный вектор.
«Отрицательный вектор — это вектор, имеющий ту же величину, что и исходный вектор, но направление, противоположное ему»
Теперь, когда вы хотите вычесть два вектора, это означает, что вам нужно добавить исходный вектор к его противоположному вектору. Для векторов a и -a имеем:
a-a = a+(a-)
Вы также можете легко сложить два вектора с помощью этого калькулятора вычитания векторов.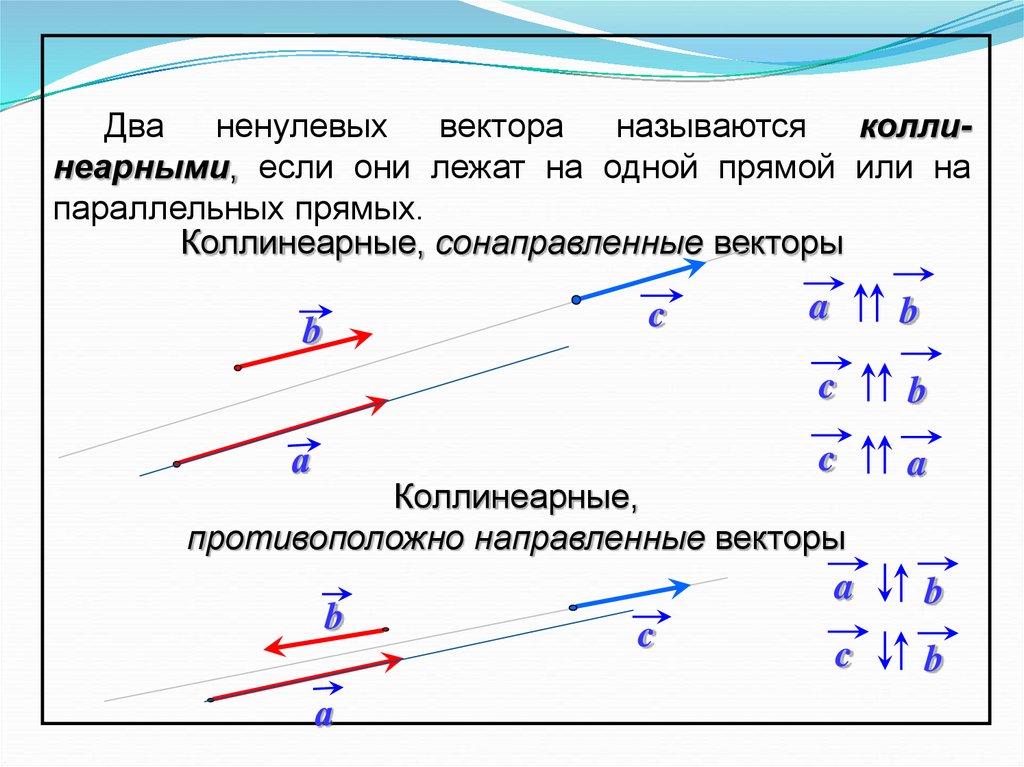
Давайте разберем пример, чтобы лучше понять концепцию векторной суммы или минус!
Пример № 01:
Как сложить векторы, указанные ниже:
Вектор A = (1, 4)
Вектор B = (6, 8)
Решение: 3 Сложение вектора Вектор А + Вектор В = (1, 4) + (6, 8) Вектор А + Вектор В = (1+6, 4+8) Вектор А + Вектор В = (7, 14) Для мгновенной проверки вы можете доверять расчетам нашего бесплатного векторного сумматора. Давайте узнаем, как можно использовать этот калькулятор сложения векторов для сложения и вычитания двух векторов с кратными или без них. Ввод: Вывод: Бесплатный графический калькулятор сложения векторов выполняет следующие вычисления: В реальной жизни существует огромное количество векторных приложений. В области инженерных наук у вектора действительно есть важная теория. Это помогает найти векторную сумму и вычитание для большинства физических или механических величин, таких как сила, работа, крутящий момент и т. д., и теперь вы также можете использовать этот бесплатный калькулятор векторной суммы для анализа добавления таких векторных параметров в кратчайшие сроки без снижение точности результатов. Проще говоря, величина вектора — это длина вектора от начальной до конечной точки. Если v — произвольный вектор, то его величина обозначается следующей формулой: Величина вектора = |v| Кроме того, у нас есть еще один калькулятор величины вектора для определения нормы вектора в интервале моментов. Кроме того, если вы хотите сложить величины векторов, вы также можете сделать это с помощью этого простого онлайн-калькулятора. Концепция сложения и вычитания векторов очень важна и находит применение практически во всех областях науки и техники. Принимая во внимание фактическую важность этой концепции, мы разработали этот лучший онлайн-калькулятор сложения 2D-векторов. Просто прекратите свои исследования и начните использовать этот калькулятор добавления векторов, чтобы насладиться точными и быстрыми вычислениями, касающимися вашей векторной арифметики. Из источника Википедии: Евклидов вектор, История, Декартово пространство, Аффинные векторы, Обобщения, Разложение или разрешение, Основные свойства, Скалярное умножение, Скалярное тройное произведение, Преобразование между несколькими декартовыми основаниями Из источника Академии Хана: Добавить векторы, вычитание векторов из конца в конец, величина Из источника Lumen Обучение: графические методы, векторы в двух измерениях, метод «голова к хвосту», вычитание векторов, разложение вектора на компоненты Если вы собираетесь заниматься 3D, вам необходимо понимать линейную алгебру и матричные обозначения.
Часто задаваемые вопросы: Как векторы используются в повседневной жизни? 
Просто рассмотрим пример лодки и ее двигателя. Когда двигатель прикладывает силу в одном конкретном направлении для движения лодки, приливы будут прилагать силу, противоположную направлению движения лодки. И чтобы понять фактическое направление этих сил, вы можете использовать другой калькулятор векторной проекции, чтобы получить точные результаты.
Вычислить трехмерный угол Эйлера между двумя трехмерными векторами?
Причина, по которой матричная запись полезна, заключается в следующем: становится возможным манипулировать такими вещами, как обычные математические символы. Если вы помните из школы решение x от:
a * x = b
Разделите обе части на a, и вы получите
a/a * x = b /a -> х = б / а
Теперь, если у вас есть 2 пробела с 3 векторами в каждом, вы, по сути, имеете 2 полностью сформированных пробела в начале координат.
Предполагая, что векторы охватывают трехмерное пространство (другими словами, не указывайте все в одной плоскости, еще лучше, если они ортогональны друг другу, и в этом случае вы можете просто использовать функции преобразования напрямую). Это означает, что у вас есть 3 места. Итак, ваша проблема заключается в том, что вы знаете 2 пробела. Вам нужно знать преобразование пространства из пространства A в пространство B (обычно матрицы пишутся большими буквами, чтобы обозначить, что они более сложны). Это математически: 9-1 * В
X — пространство вращения. В коде единства это выглядит так:
X = A.inverse * B
Как составить А и Б из векторов? Просто поместите вектор для начального пространства в столбцы A 0-2 и места назначения соответственно в столбцы B [2].