Наименьшее общее кратное простых чисел » задачи
НОД и НОК »
Числа а и б разложили на простые множители : а= 2*3(2)*5(3)*11 ; б=2(3)*3*5(2)*7. Найдите их наименьшее общее кратное. В скобках написана степень
Решение: 126 = 2*3*3* НОД = 2*3*7 = 42
84 = 2*2*3*7 НОК = 2²*3²* = 4*9*7 = 252
84/126 = 2/3
105= 3*5*7 НОК = 3*7 =21
924 = 2*2*3*7*11 НОД = 3*5*7*2²*11 =46205/44
105/924 = 5/44Наименьшее общее кратное так же можно понять рассматривая определение общее кратное. Общим кратным нескольких чисел называется число, которое делится на каждое из этих чисел. Например, числа 9, 18 и 45 имеют общее кратное 180. Но 90 и 360 – тоже их общие кратные. Среди всех общих кратных всегда есть наименьшее, в данном случае это 90. Это число и называется наименьшим общим кратным. Наименьшее общее кратное двух или нескольких натуральных чисел — наименьшее, делящееся на каждое из них, положительное число.
Разложите числа на простые множители и найдите их наименьшее общее кратное 1)180 и 300 2)42,60и 70 3) 18,63 и 35.
Решение: Наименьшим общим кратным (НОК) двух и более натуральных чисел называется наименьшее натуральное число, которое само делится нацело на каждое из этих чисел.
Разлагаем числа на простые множители.
Находим в разложении меньшего числа (меньших чисел) множители, которые не вошли в разложение бóльшего числа. и добавляем эти множители в разложение бóльшего числа.
1) 300=2*2*3*5*5
180=2*2*3*3*5
В разложение 180 две тройки, а в разложение 300 — одна тройка. Значит добавляем тройку в разложение 300. Получается, что 300 умножаем на 3.
НОК (180, 300) = 2*2*3*3*5*5=900
2) 70=2*5*7
60=2*2*3*5
42=2*3*7
Из разложения 42 берём 3 (её нет в разложение 70; 2 и 7 есть). Из разложения 60 берём одну двойку, всё остальное в разложение 70 уже есть.
НОК (42, 60, 70)=2*2*3*5*7=420
3) 63=3*3*7
35=5*7
18=2*3*3
НОК (18, 35, 65)=2*3*3*5*7=630Разложите числа на простые множители.
 Найдите их наименьшее общее кратное 54 и 135
Найдите их наименьшее общее кратное 54 и 135
Решение: Раскладываем числа 54 и 135
раскладываем число 135
135 3
45 3
15 3
5 5
1
получаем 135=3×3×3×5
раскладываем число 54
54 2
27 3
9 3
3 3
1
получаем 54=2×3×3×3
чтобы найти Наименьшее обшее кратное надо выписать разложение этих чисел и вычеркнуть не совпадающие
135=3×3×3×5
54=2×3×3×3
в 1 разложении вычеркиваем 5 во 2 вычеркиваем 2
перемножаем получаем НОК(54;135)=27Разложите числа на простые множители и найдите их наименьшее общее кратное 54и135: 38и114: 150и400: 180и300: 42,60и70: 18,63и35:
Решение: НОК(54,135)=54*5=270
54:2 135:5
27:3 27:3
9:3 9:3
3:3 3:3
1 1
НОК(38,114)=38*3=114
38:2 114:2
19:19 57:3
1 19:19 1
НОК(150,400)=150*2*2*2=1200
150:2 400:2
75:5 200:2
15:3 100:2
5:5 50:2
1 25:5
5:5
1
Ух больше не могу(((54 и 135= 270, 38 и 114=114, 150 и 400=400,180 и 300=300, 42,60 и 70= 420,18, 63 и 35=126.

Разложите числа на простые множители и найдите их наименьшее общее кратное 1) 54 и 135 2) 38 и 114 3) 150 и 400 4) 180 и 300 5) 42,60 и 70 6) 18,63 и 35
Решение: 1)54=2*3*3*3
135= 5*3*3*3
Наименьшее общее кратное — 3
2) 38= 2*19
114 = 2*3*19
Наименьшее общее кратное — 2
3) 150=5*3*2*5
400=2*2*2*2*5*5
Наименьшее общее кратное — 2
4) 180=2*2*5*3*3
300=2*2*5*5*3
Наименьшее общее кратное — 2
5) 42,60=2*3*7,1
70=2*5*7
Наименьшее общее кратное — 2
6)18,63=2*3*3*1,035
35=2*17,5
Наименьшее общее кратное — 2Разложите числа на простые множители и найдите их наименьшее общее кратное: НОД; НОК: 1)54и135; 2)38и114; 3)150и400;4)180и300;5)42,60и70;6)18,63и35.
Решение: 1. НОД 54 = 9 3*3*3*2=54 НСК=270 270/54=5
135= 9 3*3*3*5=135 270/135=2
2. НОД 38=
114=
3. НОД 150=50 2*5*5*3 НСК=25 150/25=6
400=50 2*2*5*5*4 400/25=16
4. НОД 180= 60 2*3*3*5*2 НСК=30 180/30=6
НОД 180= 60 2*3*3*5*2 НСК=30 180/30=6
300= 60 2*3*5*5*2 300/30=10 и т. дРазложите числа на простые множители найдите их наименьшее общее кратное 180
и 300
Решение: 180 ДЕЛИМ НА 2 300 ДЕЛИМ НА 2
90 ДЕЛИМ НА 3 150 ДЕЛИМ НА 3
30 ДЕЛИМ НА 2 50 ДЕЛИМ НА 2
15 ДЕЛИМ НА 3 25 ДЕЛИМ НА 5
5 ДЕЛИМ НА 5 5 ДЕЛИМ НА 5
1 1
НАХОДИМ НОК-наименьшее общее кратное
180=2*3*2*3*5
300=2*3*2*5*5
НОК=2*2*3*3*5*5Разложите числа на простые множители и найдите их наименьшее общее кратное 150 и 400; 180 и 300
Решение: На всякий случай, объясню, как раскладывать на простые множители) Берёшь таблицу простых чисел и по порядку делите данное число на простые от 2 и далее, их можно повторять. Например,3 раза поделить на 2. Таким образом у 150 простые множители это 2,5,5 и 3 (две 5-ки, а не одна), у 180: 2,2,3,3,5, у 400:2,2,2,5,5 Наименьшее общее кратное я, если честно, уже не помню, как находить через множители, но я делаю так: беру наибольшее число, сначала проверяют кратно ли оно остальным, если да, то оно наименьшое кратное, если нет, то умножают его на 2 и опять проверяют, потом на 3 и т. д. пока не найдётся оно) А здесь наименьшее общее кратное это 3600. Я надеюсь, я довольно доступно объяснила и больше у тебя проблем с этим не будет)
Таким образом у 150 простые множители это 2,5,5 и 3 (две 5-ки, а не одна), у 180: 2,2,3,3,5, у 400:2,2,2,5,5 Наименьшее общее кратное я, если честно, уже не помню, как находить через множители, но я делаю так: беру наибольшее число, сначала проверяют кратно ли оно остальным, если да, то оно наименьшое кратное, если нет, то умножают его на 2 и опять проверяют, потом на 3 и т. д. пока не найдётся оно) А здесь наименьшее общее кратное это 3600. Я надеюсь, я довольно доступно объяснила и больше у тебя проблем с этим не будет)Разложите числа на простые множителии найдите их наименьшее общее кратное 60 и найдите его нок
Решение: Наибольший общий делитель:: Разложим числа на простые множители:42 = 2 · 3 · 760 = 2 · 2 · 3 · 570 = 2 · 5 · 7Общие множители чисел: 2НОД (42; 60; 70) = 2Наименьшее общее кратное:: Разложим числа на простые множители. 70 = 2 · 5 · 742 = 2 · 3 · 760 = 2 · 2 · 3 · 5Чтобы определить НОК, необходимо недостающие множители добавить к множителям большего числа и перемножить их: НОК (42; 60; 70) = 2 · 5 · 7 · 3 · 2 = 420Ответ: Наибольший общий делитель НОД (42; 60; 70) = 2Наименьшее общее кратное НОК (42; 60; 70) = 420Взаимно простые числа.
 признак делимости на произведение. наименьшее общее кратное
признак делимости на произведение. наименьшее общее кратное
Решение: Признаки делимости чиселНа 2 делятся числа, оканчивающиеся нулем или четной цифрой. Например, 526, 1002, 600. На 5 делятся числа, оканчивающиеся нулем или цифрой 5. Например, 1005, 200. На 4 (или 25) делятся только те числа, у которых две последние цифры — нули или выражают число, делящееся на 4 (или 25). Например, 700, 216, 4325. На 3 (на 9) делятся только те числа, сумма цифр которых делится на 3 (на 9). Например, 171 (1+7+1=9), 837 (8+3+7=18) На 10 делятся числа, оканчивающиеся нулем. Например, 1020, 50, 400. Признак делимости суммы: если каждое из слагаемых a и b делится на некоторое число c, то и сумма a+bделится на это число c. Наибольший общий делительНаибольшее из натуральных чисел, на которое делятся числа a и b. Чтобы найти НОД нескольких чисел, можно:
1) разложить эти числа на простые множители;
2) подчеркнуть в этих разложениях все общие множители;
3) вычислить подчеркнутое произведениеНапример, найти НОД(385; 1694) Два числа, НОД которых равен 1, называют взаимно простыми.
1) Разложить эти числа на простые множители;
2) выписать разложение первого числа;
3) дополнить его недостающими множителями второго числа, третьего и т. д.;
4) вычислить полученное произведение. Например, найти НОК(24; 180; 14) НОК двух простых чисел равно их произведению. Например, НОК(3;7)=21
1 2 > >>
Навигация по странице: |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Разложение числа на простые множители
Разложение числа на простые множители — МАТВОКСПерейти к содержанию
ПОИСК
Страница Вконтакте открывается в новом окне
Вы здесь:
Определение разложения числа на простые множители
Представление числа в виде произведения степеней простых чисел называют
разложением числа на простые множители.
Любое натуральное число (n>1) можно представить в виде простых множителей.
При разложении числа на простые множители используют признаки делимости и применяют запись столбиком, при которой делитель располагают справа от вертикальной черты, а частное записывают под делением.
Когда простые множители располагаются в порядке возрастания, называют
каноническим разложением.Как разложить число на простые множители
Разложение на множители обычно записывают столбиком (в две колонки).
Записать число и провести черту.
Шаг 2
Берем число 2 и, используя признаки делимости на 2, проверяем, делится ли исходное число на 2. Если делится, то справа от черты записываем 2, а под исходным числом, слева от черты, записываем результат от деления числа на 2.
Если же число на 2 не делится, то берем число 3. Используя признаки деления на 3, проверяем, делится ли число на 3. Если не делится, то берем следующее простое число.
Повторяем эти шаги, записывая справа числа, на которые делится число, записанное слева, а слева – результат от деления. Заканчиваем разложение, когда в левой колонке будет записано число «1».
Пример 1
Разложить число 224 на простые множители.
РешениеЗаписываем число 224 и проводим вертикальную черту.
Проверяем, делится ли 224 на 2. Так как 224 заканчивается на четное число, то, значит 224 делится на 2. Записываем 2 справа. Результат от деления 224 на 2 (224:2=112) записываем слева под 224.
Записываем 2 справа. Результат от деления 224 на 2 (224:2=112) записываем слева под 224.
Проверяем, делится ли 112 на 2. Так как 112 заканчивается на четное число, то, значит 112 делится на 2. Записываем 2 справа. Результат от деления 112 на 2 (112:2=56) записываем слева под 112.
56 делится на 2. Записываем 2 справа. Результат от деления 56 на 2 (56:2=28) записываем слева под 56.
28 делится на 2. Записываем 2 справа. Результат от деления 28 на 2 (28:2=14) записываем слева под 28.
14 делится на 2. Записываем 2 справа. Результат от деления 14 на 2 (14:2=7) записываем слева под 14.
7 делится на 7. Записываем 7 справа. Результат от деления 7на 7 (7:7=1) записываем слева под 7.
Итак, мы разложили 224 на простые множители:
224 = 2∙2∙2∙2∙2∙7
Пример 2
Найдем наибольший общий множитель и наименьшее общее кратное чисел 648 и 432.
Разложим числа на простые множители:
Можем записать:
Найдем НОД:
Найдем НОК:
Пример 3
Найдем наибольший общий делитель и наименьшее общее кратное чисел 180 и 120.
Разложим числа на простые множители:
Можем записать:
Найдем НОД:
Найдем НОК:
Ссылки по теме:
Делимость целых чисел. Понятие делимости
Свойства делимости
Кратные числа и делители числа
Совершенное число
Дружественные числа
Простые и составные числа
Взаимно простые числа
Свойства взаимно простых чисел
Разложение числа на простые множители
Наибольший общий делитель НОД. Как найти НОД
Алгоритм Евклида, чтобы найти НОД
Как найти НОД трех и более чисел
Наименьшее общее кратное. Как найти наименьшее общее кратное
Теорема о разложении на множители. Основная теорема арифметики
Признаки делимости на 2, на 3 и на 4
Признаки делимости на 5 и на 6
Признаки делимости на 7
Признаки делимости на 8
Признаки делимости на 9
Признаки делимости на 10, 100, 1000 и т. д.
Признаки делимости на 11
Признаки делимости на 12
Признаки делимости на 13
Признаки делимости на 14
Признаки делимости на 15
Признаки делимости на 17
Признаки делимости на 19
Признаки делимости на 20 и на 23
Признаки делимости на 25, на 27 и на 29
Признаки делимости на 99
Признаки делимости на 101
9E09BEAE0A118E93DED3D74128EA2C147A65428915829EB11235F7758F7B38C3
MATHVOX
Вверх
Этот сайт использует файлы cookies для более комфортной работы пользователя. Продолжая просмотр страниц сайта, вы соглашаетесь с использованием файлов cookies. Если вам нужна дополнительная информация , пожалуйста, посетите страницу Политика Конфиденциальности Принять
Продолжая просмотр страниц сайта, вы соглашаетесь с использованием файлов cookies. Если вам нужна дополнительная информация , пожалуйста, посетите страницу Политика Конфиденциальности Принять
Privacy & Cookies Policy
Don`t copy text!
Разложение квадратного корня на множители: внесение и вынесение. Извлечение корней: способы, примеры, решения
На первый взгляд может показаться, что процедура разложения квадратного корня на множители сложная и неприступная. Но это не так. В этой статье мы расскажем вам, как подступиться к квадратному корню и множителям, а также легко и просто разложить квадратный корень, воспользовавшись двумя проверенными методами.
Yandex.RTB R-A-339285-1
Разложение корня на множители
Для начала определим цель процедуры разложения квадратного корня на множители.
Определение 1
Разложение квадратного корня на множители — нахождение двух или нескольких чисел, которые, при условии перемножения их друг на друга, дадут число равное исходному. Например: 4×4 = 16.
Например: 4×4 = 16.
Если вы найдете множители, то сможете легко упростить выражение с квадратным корнем или вовсе его упразднить:
Пример 1
Разделите подкоренное число на 2, если оно четное.
Подкоренное число всегда следует делить на простые числа, поскольку любое значение простого числа можно разложить на простые множители. Если у вас нечетное число, то попробуйте разделить его на 3. Не делится на 3? Делите дальше на 5, 7, 9 и т.д.
Запишите выражение в виде корня произведения двух чисел.
Например, можно упростить таким способом 98: = 98 ÷ 2 = 49 . Из этого следует, что 2 × 49 = 98 , поэтому можно переписать задачу следующим образом: 98 = (2 × 49) .
Продолжите раскладывать числа, пока под корнем не останется произведение двух одинаковых чисел и других чисел.
Возьмем наш пример (2 × 49) :
Поскольку 2 уже и так максимально упрощено, необходимо упростить 49 . Ищем простое число, на которое можно разделить 49 . Очевидно, что ни 3 , ни 5 не подходят. Остается 7: 49 ÷ 7 = 7 , поэтому 7 × 7 = 49 .
Остается 7: 49 ÷ 7 = 7 , поэтому 7 × 7 = 49 .
Записываем пример в следующем виде: (2 × 49) = (2 × 7 × 7) .
Упростите выражение с квадратным корнем.
Поскольку в скобках у нас произведение 2 и двух одинаковых чисел (7) , то мы можем вынести за знак корня число 7 .
Пример 2
(2 × 7 × 7) = (2) × (7 × 7) = (2) × 7 = 7 (2) .
В тот момент, когда под корнем оказалось два одинаковых числа, останавливайтесь с разложением чисел на множители. Конечно, если вы использовали все возможности по максимуму.
Запомните: существуют корни, которые можно упрощать многократно.
В таком случае, числа, которые мы выносим из-под корня, и числа, которые стоят перед ним, перемножаются.
Пример 3
180 = (2 × 90) 180 = (2 × 2 × 45) 180 = 2 45
но 45 можно разложить на множители и еще раз упростить корень.
180 = 2 (3 × 15) 180 = 2 (3 × 3 × 5) 180 = 2 × 3 5 180 = 6 5
Когда невозможно получить два одинаковых числа под знаком корня, это значит, что упростить такой корень нельзя.
Если после разложения подкоренного выражения на произведение простых чисел, у вас не получилось получить два одинаковых числа, то такой корень упростить нельзя.
Пример 4
70 = 35 × 2 , поэтому 70 = (35 × 2)
35 = 7 × 5 , поэтому (35 × 2) = (7 × 5 × 2)
Как видим, все три множителя — простые числа, которые нельзя разложить на множители. Среди них нет одинаковых чисел, поэтому не представляется возможным вынести целое число из-под корня. Упростить 70 нельзя.
Полный квадрат
Запомните несколько квадратов простых чисел.
Квадрат числа получается, если умножить его на самого себя, т.е. при возведении в квадрат. Если вы запомните десяток квадратов простых чисел, то это очень упростить вам жизнь в дальнейшем упрощении корней.
Пример 5
1 2 = 1 2 2 = 4 3 2 = 9 4 2 = 16 5 2 = 25 6 2 = 36 7 2 = 49 8 2 = 64 9 2 = 81 10 2 = 100
В случае если под знаком корня квадратного корня находится полный квадрат, то стоит убрать знак корня и записать квадратный корень данного полного квадрата.
Сложно? Нет:
Пример 6
1 = 1 4 = 2 9 = 3 16 = 4 25 = 5 36 = 6 49 = 7 64 = 8 81 = 9 100 = 10
Попробуйте разложить число под знаком корня на произведения полного квадрата и другого числа.
Если вы видите, что подкоренное выражение раскладывается на произведение полного квадрата и какого-либо числа, то, запомнив несколько примеров, вы существенно сэкономите время и нервы:
Пример 7
50 = (25 × 2) = 5 2 . Если подкоренное число оканчивается на 25, 50 или 75, вы всегда можете разложить его на произведение 25 и какого-то числа.
1700 = (100 × 17) = 10 17 . Если подкоренное число оканчивается на 00, вы всегда можете разложить его на произведение 100 и какого-то числа.
72 = (9 × 8) = 3 8 . Если сумма цифр подкоренного числа равна 9, вы всегда можете разложить его на произведение 9 и какого-то числа.
Попробуйте разложить подкоренное число на произведение нескольких полных квадратов: вынесите их из-под знака корня и перемножьте.
Пример 8
72 = (9 × 8) 72 = (9 × 4 × 2) 72 = 9 × 4 × 2 72 = 3 × 2 × 2 72 = 6 2
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Формулы корней.
 Свойства квадратных корней.
Свойства квадратных корней.Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно «не очень…»
И для тех, кто «очень даже…»)
В предыдущем уроке мы разобрались, что такое квадратный корень . Пришла пора разобраться, какие существуют формулы для корней , каковы свойства корней , и что со всем этим можно делать.
Формулы корней, свойства корней и правила действий с корнями — это, по сути, одно и то же. Формул для квадратных корней на удивление немного. Что, безусловно, радует! Вернее, понаписать всяких формул можно много, но для практической и уверенной работы с корнями достаточно всего трёх. Все остальное из этих трёх проистекает. Хотя и в трех формулах корней многие плутают, да…
Начнём с самой простой. Вот она:
Если Вам нравится этот сайт…Кстати, у меня есть ещё парочка интересных сайтов для Вас.)
Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)
Тестирование с мгновенной проверкой. Учимся — с интересом!)
можно познакомиться с функциями и производными.
Для вычисления квадратного корня без калькулятора существует несколько методов.
Как найти корень из числа – 1 способ
- Один из методов заключается в разложении на множители того числа, которое находится под корнем. Эти составляющие в результате умножения образуют подкоренное значение. Точность полученного результата зависит от числа под корнем.
- Например, если взять число 1 600 и начать раскладывать его на множители, то рассуждение построится таким образом: данное число кратно 100, значит, его можно разделить на 25; так как корень из числа 25 извлекается, то число является квадратным и подходит для дальнейших вычислений; при делении получаем еще одно число – 64. Это число тоже квадратное, поэтому корень извлекается хорошо; после этих расчетов под корнем можно записать число 1600 в виде произведения 25 и 64.
- Одно из правил извлечения корня гласит, что корень из произведения множителей равен числу, которое получается при умножении корней из каждого множителя.
 Это значит, что: √(25*64) = √25 * √64. Если из 25 и 64 извлечь корни, то получим такое выражение: 5 * 8 = 40. То есть, квадратный корень из числа 1600 равен 40.
Это значит, что: √(25*64) = √25 * √64. Если из 25 и 64 извлечь корни, то получим такое выражение: 5 * 8 = 40. То есть, квадратный корень из числа 1600 равен 40. - Но бывает так, что число, находящееся под корнем, не раскладывается на два множителя, из которых извлекается целый корень. Обычно такое можно осуществить только для одного из множителей. Поэтому чаще всего найти абсолютно точный ответ в таком уравнении не получается.
- В таком случае можно высчитать только приблизительное значение. Поэтому нужно извлечь корень из множителя, который является квадратным числом. Это значение затем умножить на корень из второго числа, которое не является квадратным членом уравнения.
- Выглядит это таким образом, например, возьмем число 320. Его можно разложить на 64 и 5. Из 64 целый корень извлечь можно, а из 5 – нет. Поэтому, выражение будет выглядеть так: √320 = √(64*5) = √64*√5 = 8√5.
- Если есть необходимость, то можно найти приблизительное значение этого результата, вычислив
√5 ≈ 2,236, следовательно, √320 = 8 * 2,236 = 17,88 ≈ 18.
- Также число под корнем можно разложить на несколько простых множителей, а одинаковые можно вынести из-под него. Пример: √75 = √(5*5*3) = 5√3 ≈ 8,66 ≈ 9.
Как найти корень из числа – 2 способ
- Другой способ заключается в делении в столбик. Деление происходит аналогично, но только искать нужно квадратные числа, из которых потом извлекать корень.
- В этом случае квадратное число пишем сверху и отнимаем его в левой части, а извлеченный корень снизу.
- Теперь второе значение нужно удвоить и записать снизу справа в виде: число_х_=. Пропуски необходимо заполнить числом, которое будет меньше или равно необходимому значению слева – все как в обычном делении.
- При необходимости этот результат снова вычитается слева. Такие вычисления продолжаются до тех пор, пока результат не будет достигнут. Нули также можно добавлять, пока не получите нужное количество знаков после запятой.
Цель упрощения квадратного корня – это переписать его в такой форме, которую проще использовать в вычислениях.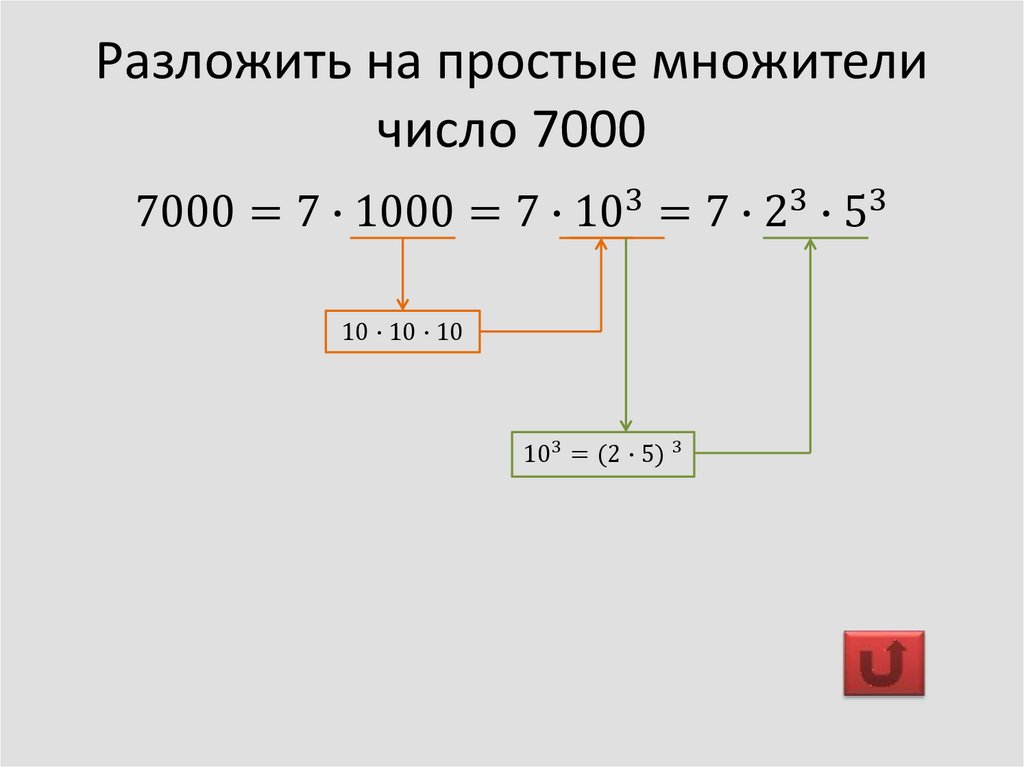 Разложение числа на множители – это нахождение двух или нескольких чисел, которые при перемножении дадут исходное число, например, 3 х 3 = 9. Найдя множители, вы сможете упростить квадратный корень или вообще избавиться от него. Например, √9 = √(3×3) = 3.
Разложение числа на множители – это нахождение двух или нескольких чисел, которые при перемножении дадут исходное число, например, 3 х 3 = 9. Найдя множители, вы сможете упростить квадратный корень или вообще избавиться от него. Например, √9 = √(3×3) = 3.
Если подкоренное число четное, разделите его на 2. Если подкоренное число нечетное, попробуйте разделить его на 3 (если число на 3 не делится, делите его на 5, 7 и так далее по списку простых чисел). Делите подкоренное число исключительно на простые числа, так как любое число можно разложить на простые множители. Например, вам не нужно делить подкоренное число на 4, так как 4 делится на 2, а вы уже разделили подкоренное число на 2.
Перепишите задачу как корень из произведения двух чисел. Например, упростим √98: 98 ÷ 2 = 49, поэтому 98 = 2 x 49. Перепишите задачу так: √98 = √(2 x 49).
Продолжите разложение чисел до тех пор, пока под корнем не останется произведение двух одинаковых чисел и других чисел. Это имеет смысл, если задуматься о смысле квадратного корня: √(2 х 2) равен числу, которое, будучи умноженным само на себя, будет равно 2 х 2. Очевидно, что это число 2! Повторите описанные выше действия для нашего примера: √(2 х 49).
Это имеет смысл, если задуматься о смысле квадратного корня: √(2 х 2) равен числу, которое, будучи умноженным само на себя, будет равно 2 х 2. Очевидно, что это число 2! Повторите описанные выше действия для нашего примера: √(2 х 49).
- 2 уже максимально упрощено, так как это простое число (см. список простых чисел выше). Поэтому разложите на множители число 49.
- 49 на 2, 3, 5 не делится. Поэтому переходите к следующему простому числу – 7.
- 49 ÷ 7 = 7, поэтому 49 = 7 x 7.
- Перепишите задачу так: √(2 x 49) = √(2 x 7 x 7).
Упростите квадратный корень. Так как под корнем находится произведение 2 и двух одинаковых чисел (7), вы можете вынести такое число за знак корня. В нашем примере: √(2 x 7 x 7) = √(2)√(7 x 7) = √(2) x 7 = 7√(2).
- Как только под корнем вы получили два одинаковых числа, вы можете остановиться с разложением чисел на множители (если их все еще можно разложить). Например, √(16) = √(4 х 4) = 4. Если вы продолжите разложение чисел на множители, вы получите тот же ответ, но проделаете больше вычислений: √(16) = √(4 х 4) = √(2 х 2 х 2 х 2) = √(2 х 2) √(2 х 2) = 2 х 2 = 4.

Некоторые корни можно упрощать многократно. В этом случае числа, выносимые из-под знака корня, и числа, стоящие перед корнем, перемножаются. Например:
- √180 = √(2 x 90)
- √180 = √(2 x 2 x 45)
- √180 = 2√45, но 45 можно разложить на множители и еще раз упростить корень.
- √180 = 2√(3 x 15)
- √180 = 2√(3 x 3 x 5)
- √180 = (2)(3√5)
- √180 = 6√5
Если вы не можете получить два одинаковых числа под знаком корня, то такой корень упростить нельзя. Если вы разложили подкоренное выражение на произведение простых множителей, и среди них нет двух одинаковых чисел, то такой корень упростить нельзя. Например, попробуем упростить √70:
- 70 = 35 x 2, поэтому √70 = √(35 x 2)
- 35 = 7 x 5, поэтому √(35 x 2) = √(7 x 5 x 2)
- Все три множителя являются простыми, поэтому их больше нельзя разложить на множители. Все три множителя разные, поэтому вы не сможете вынести целое число из-под знака корня.
 Следовательно, √70 упростить нельзя.
Следовательно, √70 упростить нельзя.
внесение и вынесение. Как упростить квадратный корень
Для вычисления квадратного корня без калькулятора существует несколько методов.
Как найти корень из числа – 1 способ
- Один из методов заключается в разложении на множители того числа, которое находится под корнем. Эти составляющие в результате умножения образуют подкоренное значение. Точность полученного результата зависит от числа под корнем.
- Например, если взять число 1 600 и начать раскладывать его на множители, то рассуждение построится таким образом: данное число кратно 100, значит, его можно разделить на 25; так как корень из числа 25 извлекается, то число является квадратным и подходит для дальнейших вычислений; при делении получаем еще одно число – 64. Это число тоже квадратное, поэтому корень извлекается хорошо; после этих расчетов под корнем можно записать число 1600 в виде произведения 25 и 64.

- Одно из правил извлечения корня гласит, что корень из произведения множителей равен числу, которое получается при умножении корней из каждого множителя. Это значит, что: √(25*64) = √25 * √64. Если из 25 и 64 извлечь корни, то получим такое выражение: 5 * 8 = 40. То есть, квадратный корень из числа 1600 равен 40.
- Но бывает так, что число, находящееся под корнем, не раскладывается на два множителя, из которых извлекается целый корень. Обычно такое можно осуществить только для одного из множителей. Поэтому чаще всего найти абсолютно точный ответ в таком уравнении не получается.
- В таком случае можно высчитать только приблизительное значение. Поэтому нужно извлечь корень из множителя, который является квадратным числом. Это значение затем умножить на корень из второго числа, которое не является квадратным членом уравнения.
- Выглядит это таким образом, например, возьмем число 320. Его можно разложить на 64 и 5. Из 64 целый корень извлечь можно, а из 5 – нет.
 Поэтому, выражение будет выглядеть так: √320 = √(64*5) = √64*√5 = 8√5.
Поэтому, выражение будет выглядеть так: √320 = √(64*5) = √64*√5 = 8√5. - Если есть необходимость, то можно найти приблизительное значение этого результата, вычислив
√5 ≈ 2,236, следовательно, √320 = 8 * 2,236 = 17,88 ≈ 18. - Также число под корнем можно разложить на несколько простых множителей, а одинаковые можно вынести из-под него. Пример: √75 = √(5*5*3) = 5√3 ≈ 8,66 ≈ 9.
Как найти корень из числа – 2 способ
- Другой способ заключается в делении в столбик. Деление происходит аналогично, но только искать нужно квадратные числа, из которых потом извлекать корень.
- В этом случае квадратное число пишем сверху и отнимаем его в левой части, а извлеченный корень снизу.
- Теперь второе значение нужно удвоить и записать снизу справа в виде: число_х_=. Пропуски необходимо заполнить числом, которое будет меньше или равно необходимому значению слева – все как в обычном делении.
- При необходимости этот результат снова вычитается слева.
 Такие вычисления продолжаются до тех пор, пока результат не будет достигнут. Нули также можно добавлять, пока не получите нужное количество знаков после запятой.
Такие вычисления продолжаются до тех пор, пока результат не будет достигнут. Нули также можно добавлять, пока не получите нужное количество знаков после запятой.
Формулы корней. Свойства квадратных корней.
Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно «не очень…»
И для тех, кто «очень даже…»)
В предыдущем уроке мы разобрались, что такое квадратный корень . Пришла пора разобраться, какие существуют формулы для корней , каковы свойства корней , и что со всем этим можно делать.
Формулы корней, свойства корней и правила действий с корнями — это, по сути, одно и то же. Формул для квадратных корней на удивление немного. Что, безусловно, радует! Вернее, понаписать всяких формул можно много, но для практической и уверенной работы с корнями достаточно всего трёх. Все остальное из этих трёх проистекает. Хотя и в трех формулах корней многие плутают, да…
Начнём с самой простой. Вот она:
Вот она:
Кстати, у меня есть ещё парочка интересных сайтов для Вас.)
Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)
можно познакомиться с функциями и производными.
Цель упрощения квадратного корня – это переписать его в такой форме, которую проще использовать в вычислениях. Разложение числа на множители – это нахождение двух или нескольких чисел, которые при перемножении дадут исходное число, например, 3 х 3 = 9. Найдя множители, вы сможете упростить квадратный корень или вообще избавиться от него. Например, √9 = √(3×3) = 3.
Если подкоренное число четное, разделите его на 2. Если подкоренное число нечетное, попробуйте разделить его на 3 (если число на 3 не делится, делите его на 5, 7 и так далее по списку простых чисел). Делите подкоренное число исключительно на простые числа, так как любое число можно разложить на простые множители. Например, вам не нужно делить подкоренное число на 4, так как 4 делится на 2, а вы уже разделили подкоренное число на 2.
Например, вам не нужно делить подкоренное число на 4, так как 4 делится на 2, а вы уже разделили подкоренное число на 2.
Перепишите задачу как корень из произведения двух чисел. Например, упростим √98: 98 ÷ 2 = 49, поэтому 98 = 2 x 49. Перепишите задачу так: √98 = √(2 x 49).
Продолжите разложение чисел до тех пор, пока под корнем не останется произведение двух одинаковых чисел и других чисел. Это имеет смысл, если задуматься о смысле квадратного корня: √(2 х 2) равен числу, которое, будучи умноженным само на себя, будет равно 2 х 2. Очевидно, что это число 2! Повторите описанные выше действия для нашего примера: √(2 х 49).
- 2 уже максимально упрощено, так как это простое число (см. список простых чисел выше). Поэтому разложите на множители число 49.
- 49 на 2, 3, 5 не делится. Поэтому переходите к следующему простому числу – 7.
- 49 ÷ 7 = 7, поэтому 49 = 7 x 7.
- Перепишите задачу так: √(2 x 49) = √(2 x 7 x 7).
Упростите квадратный корень. Так как под корнем находится произведение 2 и двух одинаковых чисел (7), вы можете вынести такое число за знак корня. В нашем примере: √(2 x 7 x 7) = √(2)√(7 x 7) = √(2) x 7 = 7√(2).
Так как под корнем находится произведение 2 и двух одинаковых чисел (7), вы можете вынести такое число за знак корня. В нашем примере: √(2 x 7 x 7) = √(2)√(7 x 7) = √(2) x 7 = 7√(2).
- Как только под корнем вы получили два одинаковых числа, вы можете остановиться с разложением чисел на множители (если их все еще можно разложить). Например, √(16) = √(4 х 4) = 4. Если вы продолжите разложение чисел на множители, вы получите тот же ответ, но проделаете больше вычислений: √(16) = √(4 х 4) = √(2 х 2 х 2 х 2) = √(2 х 2) √(2 х 2) = 2 х 2 = 4.
Некоторые корни можно упрощать многократно. В этом случае числа, выносимые из-под знака корня, и числа, стоящие перед корнем, перемножаются. Например:
- √180 = √(2 x 90)
- √180 = √(2 x 2 x 45)
- √180 = 2√45, но 45 можно разложить на множители и еще раз упростить корень.
- √180 = 2√(3 x 15)
- √180 = 2√(3 x 3 x 5)
- √180 = (2)(3√5)
- √180 = 6√5
Если вы не можете получить два одинаковых числа под знаком корня, то такой корень упростить нельзя. Если вы разложили подкоренное выражение на произведение простых множителей, и среди них нет двух одинаковых чисел, то такой корень упростить нельзя. Например, попробуем упростить √70:
Если вы разложили подкоренное выражение на произведение простых множителей, и среди них нет двух одинаковых чисел, то такой корень упростить нельзя. Например, попробуем упростить √70:
- 70 = 35 x 2, поэтому √70 = √(35 x 2)
- 35 = 7 x 5, поэтому √(35 x 2) = √(7 x 5 x 2)
- Все три множителя являются простыми, поэтому их больше нельзя разложить на множители. Все три множителя разные, поэтому вы не сможете вынести целое число из-под знака корня. Следовательно, √70 упростить нельзя.
На первый взгляд может показаться, что процедура разложения квадратного корня на множители сложная и неприступная. Но это не так. В этой статье мы расскажем вам, как подступиться к квадратному корню и множителям, а также легко и просто разложить квадратный корень, воспользовавшись двумя проверенными методами.
Yandex.RTB R-A-339285-1
Разложение корня на множители
Для начала определим цель процедуры разложения квадратного корня на множители. Цель — упростить квадратный корень и записать его в удобном для вычислений виде.
Определение 1
Разложение квадратного корня на множители — нахождение двух или нескольких чисел, которые, при условии перемножения их друг на друга, дадут число равное исходному. Например: 4×4 = 16.
Если вы найдете множители, то сможете легко упростить выражение с квадратным корнем или вовсе его упразднить:
Пример 1
Разделите подкоренное число на 2, если оно четное.
Подкоренное число всегда следует делить на простые числа, поскольку любое значение простого числа можно разложить на простые множители. Если у вас нечетное число, то попробуйте разделить его на 3. Не делится на 3? Делите дальше на 5, 7, 9 и т.д.
Запишите выражение в виде корня произведения двух чисел.
Например, можно упростить таким способом 98: = 98 ÷ 2 = 49 . Из этого следует, что 2 × 49 = 98 , поэтому можно переписать задачу следующим образом: 98 = (2 × 49) .
Продолжите раскладывать числа, пока под корнем не останется произведение двух одинаковых чисел и других чисел.
Возьмем наш пример (2 × 49) :
Поскольку 2 уже и так максимально упрощено, необходимо упростить 49 . Ищем простое число, на которое можно разделить 49 . Очевидно, что ни 3 , ни 5 не подходят. Остается 7: 49 ÷ 7 = 7 , поэтому 7 × 7 = 49 .
Записываем пример в следующем виде: (2 × 49) = (2 × 7 × 7) .
Упростите выражение с квадратным корнем.
Поскольку в скобках у нас произведение 2 и двух одинаковых чисел (7) , то мы можем вынести за знак корня число 7 .
Пример 2
(2 × 7 × 7) = (2) × (7 × 7) = (2) × 7 = 7 (2) .
В тот момент, когда под корнем оказалось два одинаковых числа, останавливайтесь с разложением чисел на множители. Конечно, если вы использовали все возможности по максимуму.
Запомните: существуют корни, которые можно упрощать многократно.
В таком случае, числа, которые мы выносим из-под корня, и числа, которые стоят перед ним, перемножаются.
Пример 3
180 = (2 × 90) 180 = (2 × 2 × 45) 180 = 2 45
но 45 можно разложить на множители и еще раз упростить корень.
180 = 2 (3 × 15) 180 = 2 (3 × 3 × 5) 180 = 2 × 3 5 180 = 6 5
Когда невозможно получить два одинаковых числа под знаком корня, это значит, что упростить такой корень нельзя.
Если после разложения подкоренного выражения на произведение простых чисел, у вас не получилось получить два одинаковых числа, то такой корень упростить нельзя.
Пример 4
70 = 35 × 2 , поэтому 70 = (35 × 2)
35 = 7 × 5 , поэтому (35 × 2) = (7 × 5 × 2)
Как видим, все три множителя — простые числа, которые нельзя разложить на множители. Среди них нет одинаковых чисел, поэтому не представляется возможным вынести целое число из-под корня. Упростить 70 нельзя.
Полный квадрат
Запомните несколько квадратов простых чисел.
Квадрат числа получается, если умножить его на самого себя, т.е. при возведении в квадрат. Если вы запомните десяток квадратов простых чисел, то это очень упростить вам жизнь в дальнейшем упрощении корней.
Пример 5
1 2 = 1 2 2 = 4 3 2 = 9 4 2 = 16 5 2 = 25 6 2 = 36 7 2 = 49 8 2 = 64 9 2 = 81 10 2 = 100
В случае если под знаком корня квадратного корня находится полный квадрат, то стоит убрать знак корня и записать квадратный корень данного полного квадрата.
Сложно? Нет:
Пример 6
1 = 1 4 = 2 9 = 3 16 = 4 25 = 5 36 = 6 49 = 7 64 = 8 81 = 9 100 = 10
Попробуйте разложить число под знаком корня на произведения полного квадрата и другого числа.
Если вы видите, что подкоренное выражение раскладывается на произведение полного квадрата и какого-либо числа, то, запомнив несколько примеров, вы существенно сэкономите время и нервы:
Пример 7
50 = (25 × 2) = 5 2 . Если подкоренное число оканчивается на 25, 50 или 75, вы всегда можете разложить его на произведение 25 и какого-то числа.
1700 = (100 × 17) = 10 17 . Если подкоренное число оканчивается на 00, вы всегда можете разложить его на произведение 100 и какого-то числа.
72 = (9 × 8) = 3 8 . Если сумма цифр подкоренного числа равна 9, вы всегда можете разложить его на произведение 9 и какого-то числа.
Попробуйте разложить подкоренное число на произведение нескольких полных квадратов: вынесите их из-под знака корня и перемножьте.
Пример 8
72 = (9 × 8) 72 = (9 × 4 × 2) 72 = 9 × 4 × 2 72 = 3 × 2 × 2 72 = 6 2
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
множителей 180 и как их найти · Математика
180 — отличное число для изучения. Мало того, что он обладает множеством приятных математических свойств, так еще и весело кричать, если вы играете в дартс!
В этом уроке мы разобьем число 180 на множители, посмотрим на их свойства, а затем научимся использовать приемы разложения любого числа на множители.
Прежде чем вы застрянете, давайте кое-что проясним. Что означает фактор ?
Факторы — это числа, которые точно делят другое число, без остатка .
Возможно, было бы проще думать об этом определении наоборот — можно умножить два множителя, чтобы получить точное исходное число.
Если вам нужен краткий справочник, вот все множители и куча множителей от 1 до 100!
Содержание
Факторы числа 180
Пары
Простые числа
Правильные
Разложение на множители 180
Правила делимости
Как найти множители числа 180
Факторизация числа 180
180 — это математически специальное число
Для суммирования (каламбур!)
Все делители числа 180
youtube.com/embed/ZJnpsEZ1RU4″ frameborder=»0″ allow=»accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture» allowfullscreen=»»>Делители числа 180 равны 1, 2, 3, 4, 5, 6, 9, 10 12, 15, 18, 20, 30, 36, 45, 60, 90 и 180 .
Думая о факторах, следует исходить из того, что они положительны, однако иногда они могут быть и отрицательными. Мы рассмотрим это позже.
Пары множителей по 180
У каждого множителя есть пара, на которую он умножается, чтобы получить исходное число.
Второй множитель в каждой паре можно найти, разделив исходное число на первый множитель пары. Это означает, что когда вы умножаете пару вместе, вы всегда получаете исходное число.
Мы знаем, что 10 — это коэффициент 180, поэтому, чтобы вычислить другое число в паре, вам нужно разделить 180 на 10, что равно 18!
Таким образом, и 10, и 18 составляют пару множителей числа 180.
Вы можете сказать, что 180 не является квадратным числом, потому что оно имеет четное число множителей. Это означает, что все его множители могут быть объединены в пары, которые умножаются на 180.
Это означает, что все его множители могут быть объединены в пары, которые умножаются на 180.
Пары множителей числа 180:
(1,180)
(2,90)
(3,60)
(4,45)
(5,36)
(6,30)
(9,20)
(10,18)
(12,15)
Но что произойдет, если мы нарушим правила?
Если вы также подумаете об отрицательных числах, количество возможных множителей удвоится! Вы можете сделать каждый фактор отрицательным, и эти уравнения все равно будут иметь смысл.
Не забывайте, что при умножении двух отрицательных чисел получается положительное число, но положительное, умноженное на отрицательное, будет отрицательным! Факторы в каждой паре должен иметь тот же знак.
(-180,-1)
(-90,-2)
(-60,-3)
(-45,-4)
(-36,-5)
(-30,-6)
(-20,-9)
(-18,-10)
(-15,-12)
Простые множители числа 180
Простые множители, как следует из их названия, являются множителями, являющимися простыми числами.
Чтобы число было простым, в него могут входить только оно само и 1 без остатка.
11 является простым, потому что делится только на 11 и 1.
Нет других чисел, которые входят в 11 без остатка.
Число, не являющееся простым, называется составным числом .
4 можно разделить на 2, так что это составное число.
Для числа 180, которое мы рассматриваем в этом уроке, существуют простые делители 5, 3 и 2.
Важно помнить, что каждое число может быть записано как произведение его простых делителей .
Это известно как простая факторизация, которую мы рассмотрим позже в этом уроке.
Правильные коэффициенты
Собственными делителями числа являются все его делители, кроме 1 или самого себя. Они являются подкатегорией «обычных» факторов, определенных выше.
Собственные делители числа 180: 2, 3, 4, 5, 6, 9, 10, 12, 15, 18, 20, 30, 36, 45, 60 и 90 .
24 имеет 8 делителей: 1, 2, 3, 4, 6, 8, 12, 24. У него 6 собственных делителей: 2, 3, 4, 6, 8, 12.
У него 6 собственных делителей: 2, 3, 4, 6, 8, 12.
27 имеет 4 делителя: 1, 3, 9, 27. У него 2 собственных делителя: 3, 9.
89 имеет 2 делителя: 1, 89. У него нет собственных делителей.
Вы видите закономерность?
Каждое число имеет на два собственных делителя меньше, чем «обычные» делители. Простые числа, включая 89, всегда имеют два делителя, поэтому у них никогда не бывает правильных делителей.
Факторизация 180
Если вы предпочитаете читать, продолжайте здесь.
У вас есть список 180-х множителей и простых множителей. Теперь, когда вы знаете пункт назначения, отправляйтесь в путешествие по факторизации, чтобы добраться туда!
Мы также рассмотрим более сложный пример, чтобы дать вам уверенность в решении проблем в одиночку.
Самый простой способ найти делители числа — использовать следующие правила делимости или калькулятор.
Чтобы не пропустить какие-либо факторы, вам может быть проще начать с 1 и двигаться вверх.
Правила делимости
Правила делимости — это удобный набор приемов или сокращений, которые позволяют нам быстро и легко увидеть, можно ли разделить большое число на меньшее.
На самом деле они настолько полезны, что мы сделали для вас распечатанную таблицу и рабочий лист для правил делимости от 2 до 15. Просто нажмите или коснитесь изображений ниже, чтобы получить их для себя!
Если у вас есть калькулятор, вы можете просто разделить число на 1, 2, 3 и т. д., чтобы увидеть, получится ли целое число!
Каждый раз, когда вы найдете число, входящее в основное число, записывайте его — это множитель. Вам нужно найти пару, разделив основное число на новый множитель, который вы только что нашли.
Как только число, которое вы проверяете, становится больше, чем квадратный корень, вы можете прекратить поиск.
Все множители после этой точки уже найдены — это пары меньших множителей, которые у вас уже есть!
Как найти множители числа 180
Давайте применим правила делимости к 180.
Даже если вы сможете найти множители в уме, важно попрактиковаться в этом методе на меньших числах, чтобы вы могли его использовать. уверенно на более сложных номерах!
1 : 1 является первым делителем, потому что все целые числа делятся на 1
2 : 180 четно, поэтому оно делится на 2.
3 : Сложение 9 цифр дает 1800011 1+8+0=9 и 9÷3=3 , поэтому 180 делится на 3 4
5 : Последняя цифра числа 180 равна 0, поэтому оно делится на 5
6 : 180 делится на 6, потому что делится и на 2, и на 3
1 7 9: 180.
8 : И не делится на 8, потому что половина 180 равна 90, а 90 не делится на 4.
9 : добавление цифр 180 -х годов равны 9, и 9 ÷ 9 = 1 , так что 180 делится на 9.
10 : 180’s Последняя цифра равенства 0, поэтому она делится на 10
11 : Оно не делится на 11
12 : 180 делится на 3 и 4, поэтому делится на 12
13 : 13 не входит в число 180. Не нужно больше проверять номера.
Теперь вы нашли, что 1, 2, 3, 4, 5, 6, 9, 10 и 12 — все это делители 180, вам нужно найти пары каждого из этих чисел.
Для этого разделите 180 на каждый коэффициент!
180 ÷ 1 = 180
180 ÷ 2 = 90
180 ÷ 3 = 60
180 ÷ 4 = 45
180 ÷ 5 = 36
180 ÷ 6 = 30
180 ÷ 9 = 20
180 ÷ 10 = 18
180 ÷ 12 = 15
Ответами на эти суммы являются остальные множители!
Таким образом, полный список факторов 180: 1, 2, 3, 4, 5, 6, 9, 10, 12, 15, 18, 20, 30, 36, 45, 60, 90, 180 .
Разложение числа 180 на простые множители
Самый простой способ найти разложение числа на простые множители — это разделить его на наименьший простой множитель. Затем повторите этот процесс, разбивая множители до тех пор, пока не останется составных чисел!
Затем повторите этот процесс, разбивая множители до тех пор, пока не останется составных чисел!
Составное число — это число, которое можно разделить на что-то другое или на 1 без остатка. Это означает, что это НЕ простое число.
Полезно представить процесс в виде перевернутого дерева, потому что, в конце концов, мы собираем обведенные простые множители с концов ветвей.
Начните с деления 180 на его наименьший простой делитель, 2.
2 простое число, поэтому оно обведено кружком и останется таким, какое оно есть. 90 не является простым числом, поэтому оно разбивается дальше.
Найдите его наименьший простой множитель. Для 90 легко увидеть, что это тоже 2, потому что 90 четно.
90 ÷ 2 = 45
45 наименьший простой делитель не может быть равен 2, поэтому вам нужно проверить делимость на каждое простое число. Следующее наименьшее число равно 3. Используйте правило делимости на 3, сложив цифры 45 вместе.
4 + 5 = 9
9 делится на 3, поэтому 45 тоже делится на 3.
45 ÷ 3 = 15
15 не простое число, так что вы еще не закончили. Оно не делится на 2, поэтому снова проверьте следующее наименьшее простое число, 3. Да! Легко видеть, что 3 делит 15.
15 ÷ 3 = 5
5 также является простым числом, так что вы закончили! Вот окончательное дерево факторов.
Соберите все простые числа и запишите их как умножение:
180 = 2 × 2 × 3 × 3 × 5
Это проще записать с помощью показателей или степеней:
180 = 2 2 × 3 2 × 5 2
Это простое число факторизация 180!
Принять вызов? Давайте посмотрим на большее число, 288. Вы можете использовать тот же метод, что и раньше, чтобы найти его множители. С калькулятором намного проще, когда нужно проверить так много чисел!
Посмотри, сможешь ли ты найти ответ, а затем проверь, прав ли ты!
Делители числа 288: 1, 2, 3, 4, 6, 8, 9, 12, 16, 18, 24, 32, 36, 48, 72, 96, 144 и 288.
Теперь это у вас есть его факторы, используя описанный выше метод дерева факторов, вы можете решить это…
288 = 2 × 2 × 2 × 2 × 2 × 3 × 3
:
288 = 2 5 × 3 2
180 — это математически специальное число
Помимо огромного списка множителей, число 180 обладает рядом особых свойств. Они полезны в теории чисел — области математики, которая может вас заинтересовать.0003
180 — это номер Харшада. Это означает, что сумма его цифр является одним из его множителей:
1 + 8 + 0 = 9
, а 9 — множитель.
180 имеет больше делителей, чем любые меньшие положительные целые числа, поэтому это число называется очень составным.
Это сумма двух квадратов: 180=6 2 +12 2 . Это означает, что прямоугольный треугольник с короткими сторонами 6 и 12 будет иметь гипотенузу той же длины, что и квадратный корень из 180.
180 можно записать в виде суммы последовательных простых чисел двумя способами:
Первый:
180 = 11+13+17+19+23+29+31+37
Второй способ:
180 = 19+23+29+31+37+41
Подводя итог (каламбур!)
В этом уроке мы определили множители, правильные множители и простые множители.
Мы определили множители числа 180, изучили надежный метод нахождения множителей любого числа, а затем применили его для нахождения множителей числа 180 и факторизации простых чисел.
Факторинг может быть длительным процессом, когда число большое. Начиная с 1 и считая вверх, проверьте, делится ли число, и найдите пару множителей, если это так. Вы можете прекратить поиск множителей, когда доберетесь до квадратного корня из числа!
Чтобы найти разложение числа на простые множители, вы разложите его на множители. Если его факторы не являются простыми, вы факторизуете факторы! Этот процесс продолжается до тех пор, пока вы не достигнете простых множителей.
Мы надеемся, что вы уверенно разбираете сложные числа и понимаете определения различных типов факторов. Следующий шаг – больше практиковаться! Если у вас есть какие-либо вопросы или хороший факт о 180, пожалуйста, оставьте комментарий.
См. другие наши уроки с факторами:
Факторы 42
Факторы 56
Найдите простую факторизацию числа 180 с использованием показателей
| Введите целое число, которое вы хотите получить, его простые делители: Пример: 2, 3, 4, 11, 10225 и т.  д. д. |
| Котировки |
Результат разложения на простые множители:Число 180 является составным числом, поэтому его можно разложить на множители. Другими словами, 180 можно разделить на 1, само по себе и по крайней мере на 2, 3 и 5. Составное число — это натуральное число, имеющее хотя бы один положительный делитель, отличный от единицы или самого числа. Другими словами, составное число — это любое целое число, большее единицы, которое не является простым числом. Факторизация числа 180 = 2 2 • 3 2 • 5. Простые делители числа 180 равны 2, 3 и 5. Факторное дерево или простое разложение числа 180Поскольку 180 является составным числом, мы можем нарисовать его факторное дерево: |
Вот ответ на такие вопросы, как: Найдите разложение числа 180 на простые множители с использованием показателей степени или является ли 180 простым или составным числом?
Используйте приведенный выше инструмент факторизации простых чисел, чтобы определить, является ли данное число простым или составным, и в этом случае вычислите его простые множители. См. также на этой веб-странице диаграмму факторизации простых чисел со всеми простыми числами от 1 до 1000.
См. также на этой веб-странице диаграмму факторизации простых чисел со всеми простыми числами от 1 до 1000.
Что такое первичная факторизация?
Определение простой факторизации
Простой факторизации — это разложение составного числа на произведение простых множителей, которые при умножении воссоздают исходное число. Факторы по определению — это числа, которые умножаются, чтобы создать другое число. Простое число — это целое число больше единицы, которое делится только на единицу и само на себя. Например, единственные делители 7 — это 1 и 7, поэтому 7 — простое число, а число 72 имеет делители, полученные из 2·9.0292 3 •3 2 подобно 2, 3, 4, 6, 8, 12, 24 … и самому 72, что делает 72 не простым числом. Обратите внимание, что единственными «простыми» делителями числа 72 являются 2 и 3, которые являются простыми числами.
Пример 1 простой факторизации
Давайте найдем простую факторизацию числа 72.
Решение 1
Начните с наименьшего простого числа, которое делится на 72, в данном случае 2. Мы можем записать 72 как:
Мы можем записать 72 как:
72 = 2 x 36
Теперь найдите наименьшее простое число, которое делится на 36. Снова мы можем использовать 2 и записать 36 как 2 х 18, чтобы дать.
72 = 2 x 2 x 18
18 также делится на 2 (18 = 2 x 9), поэтому мы имеем:
72 = 2 x 2 x 2 x 9
9 делится на 3 (9 = 3 x 3), поэтому у нас есть:
72 = 2 x 2 x 2 x 3 x 3
2, 2, 2, 3 и 3 — все простые числа, поэтому у нас есть ответ.
Короче говоря, решение можно записать так:
72 = 2 x 36
72 = 2 x 2 x 18
72 = 2 x 2 x 2 x 9
72 = 2 x 2 x 2 x 3 x 3
72 = 2 3 x 3 2 (экспоненциальная форма простой факторизации)
Раствор 2
Использование дерева факторов:
- Процедура:
- Найти 2 множителя числа;
- Посмотрите на 2 множителя и определите, не является ли хотя бы один из них простым;
- Если это не простой множитель это;
- Повторяйте этот процесс, пока все делители не станут простыми.

Посмотрите, как разложить число 72 на множители:
| 72 / \ 2 36 / \ 2 18 / \ 2 9 / \ 3 3 | 72 не простое —> разделить на 2 36 не простое —> разделить на 2 18 не простое —> разделить на 2 9 не простое —> разделить на 3 3 и 3 простые —> стоп |
Умножив левые числа и крайнее правое число последней строки (делители), мы получим
72 = 2 x 2 x 2 x 3 x 3
72 = 2 3 x 3 2 (экспоненциальная форма простой факторизации)
Обратите внимание, что эти делители являются простыми множителями. Их также называют листьями факторного дерева.
Пример факторизации простых чисел 2
Посмотрите, как разложить число 588 на множители:
| 588 /\ 2 294 /\ 2 147 /\ 3 49 /\ 7 7 | 588 не простое —> разделить на 2 294 не простое —> разделить на 2 147 не простое —> разделить на 3 49 не простое —> разделить на 7 7 и 7 простые —> стоп |
Взяв левые числа и крайнее правое число последней строки (делителей), умножив их, мы получим
588 = 2 x 2 x 3 x 7 x 7
588 = 2 2 x 3 x 7 2 (экспоненциальная форма простой факторизации)
Таблица факторизации простых чисел 1-1000
| n | Prime Factorization | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2 = | 2 | ||||||||||||||
| 3 = | 3 | ||||||||||||||
| 4 = | 2•2 | ||||||||||||||
| 5 = | 5 | ||||||||||||||
| 6 = | 2•3 | ||||||||||||||
| 7 = | 7 | ||||||||||||||
| 8 = | 2•2•2 | ||||||||||||||
| 9 = | 3•3 | ||||||||||||||
| 10 = | 2•5 | ||||||||||||||
| 11 = | 11 | ||||||||||||||
| 12 = | 2•2•3 | ||||||||||||||
| 13 = | 13 | ||||||||||||||
| 14 = | 2 • 7 | ||||||||||||||
| 15 = | 3 • 5 | ||||||||||||||
| 16 = | 2 • 2 • 2 • 2 | ||||||||||||||
| 17 = | |||||||||||||||
| 17 = | |||||||||||||||
| 17 = | |||||||||||||||
| 17 = | |||||||||||||||
| 17 = | |||||||||||||||
| 17 = | |||||||||||||||
17. | |||||||||||||||
| 19 = | 19 | ||||||||||||||
| 20 = | 2•2•5 | ||||||||||||||
| 21 = | 3•7 | ||||||||||||||
| 22 = | 2•11 | ||||||||||||||
| 23 = | 23 | ||||||||||||||
| 24 = | 2 • 2 • 2 • 3 | ||||||||||||||
| . 2•2•7 | |||||||||||||||
| 29 = | 29 | ||||||||||||||
| 30 = | 2•3•5 | ||||||||||||||
| 31 = | 31 | ||||||||||||||
| 32 = | 2•2•2•2•2 | ||||||||||||||
| 33 = | 3•11 | ||||||||||||||
| 34 = | 2•17 | ||||||||||||||
| 35 = | 5•7 | ||||||||||||||
| 36 = | 2•2•3•3 | ||||||||||||||
| 37 = | 37 | ||||||||||||||
| 38 = | 2•19 | ||||||||||||||
| 39 = | 3•13 | ||||||||||||||
| 40 = | 2•2•2•5 | ||||||||||||||
| 41 = | 41 | ||||||||||||||
| 42 = | 2•3•7 | ||||||||||||||
| 43 = | 43 | ||||||||||||||
| 44 = | 2•2•11 | ||||||||||||||
| 45 = | 3•3•5 | ||||||||||||||
| 46 = | 2•23 | ||||||||||||||
| 47 = | 47 | ||||||||||||||
| 48 = | 2•2 •2•2•3 | ||||||||||||||
| 49 = | 7•7 | ||||||||||||||
| 50 = | 2•5•5 | ||||||||||||||
| 51 = | 3•17 | ||||||||||||||
| 52 = | 2•2•13 | ||||||||||||||
| 53 = | 53 | ||||||||||||||
| 54 = | 2•3•3•3 | ||||||||||||||
| 55 = | 5•11 | ||||||||||||||
| 56 = | 2•2•2•7 | ||||||||||||||
| 57 = | 3•19 | ||||||||||||||
| 58 = | 2•29 | ||||||||||||||
| 59 = | 59 | ||||||||||||||
| 60 = | 2•2•3•5 | ||||||||||||||
| 61 = | 61 | ||||||||||||||
| 62 = | 2•31 | ||||||||||||||
| 63 = | 3•3•7 | ||||||||||||||
| 64 = | 2•2•2•2•2•2 | ||||||||||||||
| 65 = | 5•13 | ||||||||||||||
| 66 = | 2•3•11 | ||||||||||||||
| 67 = | 67 | ||||||||||||||
| 68 = | 2•2•17 | ||||||||||||||
| 69 = | 3•23 | ||||||||||||||
| 70 = | 2•5•7 | ||||||||||||||
| 71 = | 71 | ||||||||||||||
| 72 = | 2•2•2•3•3 | ||||||||||||||
| 73 = | 73 | ||||||||||||||
| 74 = | 2•37 | ||||||||||||||
| 75 = | 3•5•5 | ||||||||||||||
| 76 = | 2•2•19 | ||||||||||||||
| 77 = | 7•11 | ||||||||||||||
| 78 = | 2•3•13 | ||||||||||||||
| 79 = | 79 | ||||||||||||||
| 80 = | 2 • 2 • 2 • 2 • 5 | ||||||||||||||
| 81 = | 3 • 3 • 3 • 3 | ||||||||||||||
| 82 = | 2 • 410373 | 82 = | 2 • 40373 | 82 = | 2 • 40373 | 82 = | 2 • 40373 | 82 = | 2 • 40373 | 82 = | 2 • 40373 | 82 = | |||
. | |||||||||||||||
| 84 = | 2•2•3•7 | ||||||||||||||
| 85 = | 5•17 | ||||||||||||||
| 86 = | 2•43 | ||||||||||||||
| 87 = | 3•29 | ||||||||||||||
| 88 = | 2•2•2•11 | ||||||||||||||
| 89 = | 89 | ||||||||||||||
| 90 = | 2 • 3 • 3 • 5 | ||||||||||||||
| 91 = | 7 • 13 | ||||||||||||||
| 92 = | 92 = | 2 • 2 237373 | 92 = | 2 • 237773 | |||||||||||
| 92 = | 2 • 237373 | ||||||||||||||
| 92. | |||||||||||||||
| 94 = | 2•47 | ||||||||||||||
| 95 = | 5•19 | ||||||||||||||
| 96 = | 2•2•2•2•2•3 | ||||||||||||||
| 97 = | 97 | ||||||||||||||
| 98 = | 2•7•7 | ||||||||||||||
| 99 = | 3•3•11 | ||||||||||||||
| 100 = | 2•2•5•5 | ||||||||||||||
| 101 = | 101 | ||||||||||||||
| 102 = | 2•3•17 | ||||||||||||||
| 103 = | 103 | ||||||||||||||
| 104 = | 2•2•2•13 | ||||||||||||||
| 105 = | 3•5•7 | ||||||||||||||
| 106 = | 2•53 | ||||||||||||||
| 107 = | 107 | ||||||||||||||
| 108 = | 2•2•3•3•3 | ||||||||||||||
| 109 = | 109 | ||||||||||||||
| 110 = | 2•5•11 | ||||||||||||||
| 111 = | 3•37 | ||||||||||||||
| 112 = | 2•2•2•2•7 | ||||||||||||||
| 113 = | 113 | ||||||||||||||
| 114 = | 2•3•19 | ||||||||||||||
| 115 = | 5•23 | ||||||||||||||
| 116 = | 2•2•29 | ||||||||||||||
| 117 = | 3• 3•13 | ||||||||||||||
| 118 = | 2•59 | ||||||||||||||
| 119 = | 7•17 | ||||||||||||||
| 120 = | 2•2•2•3•5 | ||||||||||||||
| 121 = | 11•11 | ||||||||||||||
| 122 = | 2•61 | ||||||||||||||
| 123 = | 3 • 41 | ||||||||||||||
. | |||||||||||||||
| 127 = | 127 | ||||||||||||||
| 128 = | 2•2•2•2•2•2•2 | ||||||||||||||
| 129 = | 3•43 | ||||||||||||||
| 130 = | 2•5•13 | ||||||||||||||
| 131 = | 131 | ||||||||||||||
| 132 = | 2•2•3•11 | ||||||||||||||
| 133 = | 7 • 19 | ||||||||||||||
| 134 = | 2 • 67 | ||||||||||||||
| 135 = | 3 • 3 • 5 | 135 = | 3 • 3 • 5 | = | 3 • 3 • 5 | 135 = | 3 • 3 • 5 | 135 = | 3 • 3 70376 | = | 3 • 3 70376 | 135 = | 3. | ||
| 137 = | 137 | ||||||||||||||
| 138 = | 2•3•23 | ||||||||||||||
| 139 = | 139 | ||||||||||||||
| 140 = | 2•2•5•7 | ||||||||||||||
| 141 = | 3•47 | ||||||||||||||
| 142 = | 2 • 71 | ||||||||||||||
| 143 = | 11 • 13 | ||||||||||||||
| 144 = | 2 • 2 • 2 • 3 • 3 | ||||||||||||||
4 14 14 4. | |||||||||||||||
| 4 14 14 4. | |||||||||||||||
| 14 14 14 4. | |||||||||||||||
| 14 14 14 4. | |||||||||||||||
| 14 14 14 4. 9037 | 2•73 | ||||||||||||||
| 147 = | 3•7•7 | ||||||||||||||
| 148 = | 2•2•37 | ||||||||||||||
| 149 = | 149 | ||||||||||||||
| 150 = | 2•3•5•5 | ||||||||||||||
| 151 = | 151 | ||||||||||||||
| 152 = | 2 • 2 • 2 • 19 | ||||||||||||||
| 153 = | 3 • 3 • 17 | ||||||||||||||
| 154 = | 2 • 7 • 1103779 | 2 • 7 • 11037797777779 | 2. 156 = | 2•2•3•13 | |||||||||||
| 157 = | 157 | ||||||||||||||
| 158 = | 2•79 | ||||||||||||||
| 159 = | 3•53 | ||||||||||||||
| 160 = | 2•2•2•2•2•5 | ||||||||||||||
| 161 = | 7 •23 | ||||||||||||||
| 162 = | 2•3•3•3•3 | ||||||||||||||
| 163 = | 163 | ||||||||||||||
| 164 = | 2•2•41 | ||||||||||||||
| 165 = | 3 •5•11 | ||||||||||||||
| 166 = | 2•83 | ||||||||||||||
| 167 = | 167 | ||||||||||||||
| 168 = | 2•2•2•3•7 | ||||||||||||||
| 169 = | 13•13 | ||||||||||||||
| 170 = | 2•5•17 | ||||||||||||||
| 171 = | 3•3•19 | ||||||||||||||
| 172 = | 2•2•43 | ||||||||||||||
| 173 = | 173 | ||||||||||||||
| 174 = | 2•3•29 | ||||||||||||||
| 175 = | 5•5•7 | ||||||||||||||
| 176 = | 2•2•2•2•11 | ||||||||||||||
| 177 = | 3•59 | ||||||||||||||
| 178 = | 2•89 | ||||||||||||||
| 179 = | 179 | ||||||||||||||
| 180 = | 2•2•3•3•5 | ||||||||||||||
| 181 = | 181 | ||||||||||||||
| 182 = | 2•7•13 | ||||||||||||||
| 183 = | 3•61 | ||||||||||||||
| 184 = | 2•2•2•23 | ||||||||||||||
| 185 = | 5•37 | ||||||||||||||
| 186 = | 2 • 3 • 31 | ||||||||||||||
| 187 = | 11 • 17 | ||||||||||||||
| 188 = | 2 • 2 • 47 | ||||||||||||||
| 189 189 = | |||||||||||||||
| 189 189 = | |||||||||||||||
| 189374 18 | 373737373737373737373737377. 19377.19377.19377. 19377.19377.19377. | ||||||||||||||
| 189374. = | 2•5•19 | ||||||||||||||
| 191 = | 191 | ||||||||||||||
| 192 = | 2•2•2•2•2•2•3 | ||||||||||||||
| 193 = | 193 | ||||||||||||||
| 194 = | 2•97 | ||||||||||||||
| 195 = | 3•5•13 | ||||||||||||||
| 196 = | 2•2•7•7 | ||||||||||||||
| 197 = | 197 | ||||||||||||||
| 198 = | 2•3•3•11 | ||||||||||||||
| 199 = | 199 | ||||||||||||||
| 200 = | 2•2•2•5•5 | ||||||||||||||
| 201 = | 3•67 | ||||||||||||||
| 202 = | 2•101 | ||||||||||||||
| 203 = | 7•29 | ||||||||||||||
| 204 = | 2•2•3•17 | ||||||||||||||
| 205 = | 5•41 | ||||||||||||||
| 206 = | 2•103 | ||||||||||||||
| 207 = | 3•3•23 | ||||||||||||||
| 208 = | 2•2•2•2•13 | ||||||||||||||
| 209 = | 11 •19 | ||||||||||||||
| 210 = | 2•3•5•7 | ||||||||||||||
| 211 = | 211 | ||||||||||||||
| 212 = | 2•2•53 | ||||||||||||||
| 213 = | 3•71 | ||||||||||||||
| 214 = | 2•107 | ||||||||||||||
| 215 = | 5•43 | ||||||||||||||
| 216 = | 2•2•2•3•3•3 | ||||||||||||||
| 217 = | 7•31 | ||||||||||||||
| 218 = | 2•109 | ||||||||||||||
| 219 = | 3•73 | ||||||||||||||
| 220 = | 2•2•5•11 | ||||||||||||||
| 221 = | 13•17 | ||||||||||||||
| 222 = | 2•3•37 | ||||||||||||||
| 223 = | 223 | ||||||||||||||
| 224 = | 2•2•2•2•2•7 | ||||||||||||||
| 225 = | 3•3•5•5 | ||||||||||||||
| 226 = | 2•113 | ||||||||||||||
| 227 = | 227 | ||||||||||||||
| 228 = | 2•2•3•19 | ||||||||||||||
| 229 = | 229 | ||||||||||||||
| 230 = | 2•5•23 | ||||||||||||||
| 231 = | 3•7•11 | ||||||||||||||
| 232 = | 2•2•2•29 | ||||||||||||||
| 233 = | 233 | ||||||||||||||
| 234 = | 2•3•3•13 | ||||||||||||||
| 235 = | 5•47 | ||||||||||||||
| 236 = | 2•2•59 | ||||||||||||||
| 237 = | 3•79 | ||||||||||||||
| 238 = | 2•7•17 | ||||||||||||||
| 239 = | 239 | ||||||||||||||
| 240 = | 2•2•2•2•3•5 | ||||||||||||||
| 241 = | 241 | ||||||||||||||
| 242 = | 2•11•11 | ||||||||||||||
| 243 = | 3•3•3•3•3 | ||||||||||||||
| 244 = | 2•2•61 | ||||||||||||||
| 245 = | 5•7•7 | ||||||||||||||
| 246 = | 2•3•41 | ||||||||||||||
| 247 = | 13•19 | ||||||||||||||
| 248 = | 2 • 2 • 2 • 31 | ||||||||||||||
| 249 = | 3 • 83 | ||||||||||||||
| 250 = | 2 • 5 • 5,5. 5 5 | 250 = | 2 • 5,5. 5,5 | 2 • 5,5. 5 | 250 = | 2 • 5,54 250 = | 2 • 5,54 250 = | 2 • 5,54 250 = | 2 • 5,54 250 = | 2 • 5,5 | 250.
Калькулятор факторизации простых чиселПожалуйста, дайте ссылку на эту страницу! Просто щелкните правой кнопкой мыши на изображении выше, выберите «Скопировать адрес ссылки», а затем вставьте его в HTML-код. Факторизация числа образцов.
Факторизация простых чисел. Калькулятор | Определение Калькулятор | ОпределениеОбратите внимание на приведенный ниже список простых факторизаций, который можно проверить с помощью нашего калькулятора простых факторизаций. Разложение 2 на простые множители: это простое число! Разложение 3 на простые множители: это простое число! Разложение числа 4 на простые множители: 2 * 2 Разложение 5 на простые множители: это простое число! Разложение числа 6 на простые множители: 2 * 3 Разложение 7 на простые множители: это простое число! Разложение числа 8 на простые множители: 2 * 2 * 2 Разложение числа 9 на простые множители: 3 * 3 Разложение числа 10 на простые множители: 2 * 5 Разложение 11 на простые множители: это простое число! Разложение числа 12 на простые множители: 2 * 2 * 3 Разложение числа 13 на простые множители: это простое число! Простая факторизация 14: 2 * 7 Разложение числа 15 на простые множители: 3 * 5 Разложение числа 16 на простые множители: 2 * 2 * 2 * 2 Разложение 17 на простые множители: это простое число! Разложение числа 18 на простые множители: 2 * 3 * 3 Разложение 19 на простые множители: это простое число! Разложение числа 20 на простые множители: 2 * 2 * 5 Разложение числа 21 на простые множители: 3 * 7 Разложение числа 22 на простые множители: 2 * 11 Разложение 23 на простые множители: это простое число! Разложение числа 24 на простые множители: 2 * 2 * 2 * 3 Разложение числа 25 на простые множители: 5 * 5 Разложение числа 26 на простые множители: 2 * 13 Разложение числа 27 на простые множители: 3 * 3 * 3 Разложение числа 28 на простые множители: 2 * 2 * 7 Разложение 29 на простые множители: это простое число! Разложение числа 30 на простые множители: 2 * 3 * 5 Разложение числа 31 на простые множители: это простое число! Разложение числа 32 на простые множители: 2 * 2 * 2 * 2 * 2 Разложение числа 33 на простые множители: 3 * 11 Разложение числа 34 на простые множители: 2 * 17 Разложение числа 35 на простые множители: 5 * 7 Разложение числа 36 на простые множители: 2 * 2 * 3 * 3 Разложение числа 37 на простые множители: это простое число! Разложение числа 38 на простые множители: 2 * 19 Разложение числа 39 на простые множители: 3 * 13 Разложение числа 40 на простые множители: 2 * 2 * 2 * 5 Разложение числа 41 на простые множители: это простое число! Разложение числа 42 на простые множители: 2 * 3 * 7 Разложение числа 43 на простые множители: это простое число! Разложение числа 44 на простые множители: 2 * 2 * 11 Разложение числа 45 на простые множители: 3 * 3 * 5 Разложение числа 46 на простые множители: 2 * 23 Разложение числа 47 на простые множители: это простое число! Разложение числа 48 на простые множители: 2 * 2 * 2 * 2 * 3 Разложение числа 49 на простые множители: 7 * 7 Разложение числа 50 на простые множители: 2 * 5 * 5 Разложение числа 51 на простые множители: 3 * 17 Разложение числа 52 на простые множители: 2 * 2 * 13 Разложение 53 на простые множители: это простое число! Разложение числа 54 на простые множители: 2 * 3 * 3 * 3 Разложение числа 55 на простые множители: 5 * 11 Разложение числа 56 на простые множители: 2 * 2 * 2 * 7 Разложение числа 57 на простые множители: 3 * 19 Разложение числа 58 на простые множители: 2 * 29 Разложение числа 59 на простые множители: это простое число! Разложение числа 60 на простые множители: 2 * 2 * 3 * 5 Разложение 61 на простые множители: это простое число! Разложение числа 62 на простые множители: 2 * 31 Разложение числа 63 на простые множители: 3 * 3 * 7 Разложение числа 64 на простые множители: 2 * 2 * 2 * 2 * 2 * 2 Разложение числа 65 на простые множители: 5 * 13 Разложение числа 66 на простые множители: 2 * 3 * 11 Разложение 67 на простые множители: это простое число! Разложение числа 68 на простые множители: 2 * 2 * 17 Разложение числа 69 на простые множители: 3 * 23 Разложение числа 70 на простые множители: 2 * 5 * 7 Разложение 71 на простые множители: это простое число! Разложение числа 72 на простые множители: 2 * 2 * 2 * 3 * 3 Разложение 73 на простые множители: это простое число! Разложение числа 74 на простые множители: 2 * 37 Разложение числа 75 на простые множители: 3 * 5 * 5 Разложение числа 76 на простые множители: 2 * 2 * 19 Разложение числа 77 на простые множители: 7 * 11 Разложение числа 78 на простые множители: 2 * 3 * 13 Разложение 79 на простые множители: это простое число! Разложение числа 80 на простые множители: 2 * 2 * 2 * 2 * 5 Разложение числа 81 на простые множители: 3 * 3 * 3 * 3 Разложение числа 82 на простые множители: 2 * 41 Разложение числа 83 на простые множители: это простое число! Разложение числа 84 на простые множители: 2 * 2 * 3 * 7 Разложение числа 85 на простые множители: 5 * 17 Разложение числа 86 на простые множители: 2 * 43 Разложение числа 87 на простые множители: 3 * 29 Разложение числа 88 на простые множители: 2 * 2 * 2 * 11 Простая факторизация числа 89: это простое число! Разложение числа 90 на простые множители: 2 * 3 * 3 * 5 Разложение числа 91 на простые множители: 7 * 13 Разложение числа 92 на простые множители: 2 * 2 * 23 Разложение числа 93 на простые множители: 3 * 31 Разложение числа 94 на простые множители: 2 * 47 Разложение числа 95 на простые множители: 5 * 19 Разложение числа 96 на простые множители: 2 * 2 * 2 * 2 * 2 * 3 Разложение числа 97 на простые множители: это простое число! Разложение числа 98 на простые множители: 2 * 7 * 7 Разложение числа 99 на простые множители: 3 * 3 * 11 Разложение числа 100 на простые множители: 2 * 2 * 5 * 5 Разложение числа 104 на простые множители: 2 * 2 * 2 * 13 Разложение числа 105 на простые множители: 3 * 5 * 7 Разложение числа 108 на простые множители: 2 * 2 * 3 * 3 * 3 Разложение числа 117 на простые множители: 3 * 3 * 13 Разложение числа 120 на простые множители: 2 * 2 * 2 * 3 * 5 Разложение числа 121 на простые множители: 11 * 11 Разложение числа 125 на простые множители: 5 * 5 * 5 Разложение числа 126 на простые множители: 2 * 3 * 3 * 7 Разложение числа 130 на простые множители: 2 * 5 * 13 Разложение числа 132 на простые множители: 2 * 2 * 3 * 11 Разложение числа 135 на простые множители: 3 * 3 * 3 * 5 Разложение числа 140 на простые множители: 2 * 2 * 5 * 7 Разложение числа 144 на простые множители: 2 * 2 * 2 * 2 * 3 * 3 Разложение числа 147 на простые множители: 3 * 7 * 7 Разложение числа 150 на простые множители: 2 * 3 * 5 * 5 Разложение числа 162 на простые множители: 2 * 3 * 3 * 3 * 3 Разложение числа 175 на простые множители: 5 * 5 * 7 Разложение числа 180 на простые множители: 2 * 2 * 3 * 3 * 5 Разложение числа 196 на простые множители: 2 * 2 * 7 * 7 Разложение числа 200 на простые множители: 2 * 2 * 2 * 5 * 5 Разложение числа 210 на простые множители: 2 * 3 * 5 * 7 Разложение числа 216 на простые множители: 2 * 2 * 2 * 3 * 3 * 3 Разложение числа 225 на простые множители: 3 * 3 * 5 * 5 Разложение числа 245 на простые множители: 5 * 7 * 7 Разложение числа 250 на простые множители: 2 * 5 * 5 * 5 Разложение числа 256 на простые множители: 2 * 2 * 2 * 2 * 2 * 2 * 2 * 2 Разложение числа 300 на простые множители: 2 * 2 * 3 * 5 * 5 Разложение числа 375 на простые множители: 3 * 5 * 5 * 5 Разложение числа 400 на простые множители: 2 * 2 * 2 * 2 * 5 * 5 Разложение числа 500 на простые множители: 2 * 2 * 5 * 5 * 5 Разложение числа 625 на простые множители: 5 * 5 * 5 * 5 Сначала 1 считалось простым числом. 180 (номер)180 ( сто восемьдесят ) — четное трехзначное составное число, расположенное между числами 179 и 181. В научной записи оно записывается как 1,8 × 10 9029.2 2 . Сумма его цифр равна 9. Всего у него 5 простых множителей и 18 положительных делителей. Существует 48 положительных целых чисел (до 180), которые взаимно просты со 180.
Простые множители 2 2 × 3 2 × 5 Составное число
Разложение числа 180 на простые множители равно 2 2 × 3 2 × 5. 1, 2, 3, 4, 5, 6, 9, 10, 12, 15, 18, 20, 30, 36, 45, 60, 90, 180 18 делителей
Число 180 делится на 18 положительных делителей (из них 12 четных и 6 нечетных). Сумма этих делителей (считая 180) равна 546, среднее число равно 30,333. 1 ф (п) п
Существует 48 натуральных чисел (меньше 180), взаимно простых с 180.
Число 180 делится на 2, 3, 4, 5, 6 и 9. Арифметическими функциями
Выражается через конкретные суммы
Другие номера
Умножениеп × у
Отделn÷y
Возведение в степеньп г
N-й кореньг √n
КругРадиус = n
СфераРадиус = n
КвадратДлина = n
КубДлина = n
Равносторонний треугольникДлина = n
Треугольная пирамидаДлина = n
Что такое множители числа 180Что такое множитель в математике? Факторы — это числа, которые нужно перемножить, чтобы получить другое число. Делители числа могут быть положительными или отрицательными, но не могут быть равны нулю. С помощью множителей числа можно определить, является ли число простым или нет. Простое число — это число, имеющее только два делителя: само себя и 1. Например, число 7 простое, потому что его делителями являются только 7 и 1. Перечислите все множители числа 180 ?Для расчета коэффициентов 180 можно использовать метод деления. 1. Начните с деления 180 на наименьшее возможное число, равное 2. 2. Если деление четное, то 2 равно 180. 3. Продолжайте делить 180 на большие числа, пока не найдете нечетное число, которое не делится без остатка на 180 . 4. Числа, которые без остатка делятся на 180 являются коэффициентами 180 . Теперь давайте найдем, как рассчитать все коэффициенты Сто восемьдесят: 180 ÷ 1 = 180 | 1 | 1 | 1 | 1921 980 2 | 1921 980 2 | 1921 980 2 | 1 980 2 | 1 980 2 | 1 980 2 | 1 980 2921 980 2921 980 2921 . . 36 = 5 Как вы можете видеть, факторами 180 являются 1, 3, 4, 5, 5 . , 6 , 9 , 10 , 12 , 15 , 18 , 20 , 30 , 36 , 45 , 60 , 90 и 180 . Как писать цифры по-французски, похожие на180 ?Сколько делителей у числа 180?Коэффициенты 180 числа, которые могут без остатка делить 180. Это числа 1, 2, 3, 4, 5, 6, 9., 10 , 12 , 15 , 18 , 20 , 30 , 36 , 45 , 60 , 90 и 180. Таким образом, всего имеется 18 множителей числа 180 Какие пары множителей числа 180 ?Пара факторов 180 представляют собой комбинации двух множителей, которые при умножении дают 180. Есть много способов вычислить пары множителей числа 180 . Один из простых способов — перечислить множители числа 180: 180 Затем объедините множители в пары: Простая факторизация числа 180Существует несколько различных методов, которые можно использовать для вычисления простой факторизации числа. Ниже перечислены два наиболее распространенных метода. 1) Используйте дерево факторов: 1. Возьмите число, для которого вы хотите найти простую факторизацию, и запишите его вверху страницы 2. Найдите наименьшее число, входящее в число, которое вы находите простым разложением на четные числа, и запишите его рядом с числом, которое вы находите простым разложением на 3. Нарисуйте линию под только что написанным числом и число, которое вы находите разложением на простые множители4. Повторяйте шаг 2 с числом, которое вы только что написали, до тех пор, пока это число больше нельзя будет разделить без остатка 5. Числа, записанные в строках, будут простыми множителями числа, которое вы начали с Например, чтобы вычислить простую факторизацию числа 180
используя факторное дерево,
мы бы начали с написания 180
на листе бумаги. Окончательная простая факторизация числа 180 будет 2 x 2 x 3 x 3 x 5. 2) Используйте метод факторизации: Существует несколько различных методов факторизации, которые можно использовать для вычисления простой факторизации количество. Один из распространенных методов — начать с деления числа на наименьшее простое число, которое разделить на него поровну. Затем продолжайте делить число на последовательно большие простые числа, пока число не будет полностью факторизован. Например, чтобы вычислить простую факторизацию числа 180 с помощью этого метода, мы продолжаем делить, пока не получим ненулевой остаток. 180 ÷ 2 = 90 Таким образом 3 x 3 x 5. Часто задаваемые вопросы о факторахКаковы все делители числа 180? Коэффициенты 180
1 , 2 , 3 , 4 , 5 , 6 , 9 , 10 , 12 , 15 , 18 , 20 , 30 , 36 , 45 , 60 , 90 и 180 . Какова простая факторизация числа 180 ?Разложение числа 180 на простые множители равно 2 х 2 х 3 х 3 х 5 или же 2 2 x 3 2 x 5 1 , куда 2 , 3 , 5 простые числа . Каковы простые делители числа 180?Простые множители числа 180 равны 2 , 3 , 5 . Является ли 180 простым числом? Простое число — это число, имеющее только два делителя: 1 и само себя. Другие преобразования числа 180180 на французском языке 180 на английском языке Наибольший общий делитель чисел 180 и 192Существует множество методов, которые мы можем применить для вычисления НОД чисел 180 и 192. В нашем первом методе мы найдем простое число. факторизация 180 и 192 числа. Во втором методе мы создадим список всех множителей чисел 180 и 192. Это числа, на которые числа 180 и 192 делятся без остатка. Когда они у нас есть, все, что нам нужно сделать, это найти тот, который является самым большим общим числом из 2 списков. Теперь давайте рассмотрим каждый метод и рассчитаем GCF для чисел 180 и 192.
Метод 1 — Факторизация простых чиселПри использовании метода факторизации простых чисел все, что нам нужно сделать, это найти общие простые делители чисел 180 и 192, а затем умножить их. Очень просто: Шаг 1: Давайте создадим список всех простых делителей чисел 180 и 192:Простые делители числа 180:Как вы можете видеть ниже, простые делители числа 180 равны 3, 3 и 5 . Давайте проиллюстрируем простую факторизацию 180 в экспоненциальной форме: 180 = 2 2 x3 2 x5 1 Простые множители числа 192: 2 и 3 . Давайте проиллюстрируем простую факторизацию 192 в экспоненциальной форме: 192 = 2 6 x3 1 Шаг 2: Запишите список всех общих простых множителей чисел 180 и 19.2:Как видно из рамок выше, общие простые делители чисел 180 и 192 равны 2, 2 и 3 . Шаг 3: Все, что нам нужно сделать сейчас, это перемножить эти общие простые множители:Найти произведение всех общих простых множителей путем их умножения: 2 2 x3 1 = 12 Готово!Согласно нашим вычислениям выше, наибольший общий делитель 180 и 192 равен 12 Метод 2. Список множителейС помощью этого простого метода нам нужно найти все множители 180 и 192, Факторы — это числа, которые делят другое число без остатка и просто определяют общие, а затем выбирают, какое из них больше. Шаг 1: Создайте список всех чисел, которые делят 180 и 192 без остатка:Список факторов, которые делят 180 без остатка: 1, 2, 3, 4, 5, 6, 9, 10, 12, 15, 18, 20, 30, 36, 45, 60, 90 и 180 . Список множителей, которые делят 192 без остатка: 1, 2, 3, 4, 6, 8, 12, 16, 24, 32, 48, 64, 96 и 192 . Шаг 2: Определите наибольшее общее число из двух приведенных выше списков:Как видно в списках множителей сверху, для чисел 180 и 192 мы выделили число 12 , а это значит, что мы нашли Наибольший Общий Делитель, или НОД. Согласно нашим расчетам выше, Наибольший общий делитель 180 и 192 равен 12 Метод 3 — алгоритм ЕвклидаАлгоритм Евклида говорит, что если число k является GCM 180 и 192, тогда число k также является НОД остатка от деления чисел 180 и 192. Мы выполняем эту процедуру до тех пор, пока напоминание не станет равным 0. Наибольший общий делитель — это последнее ненулевое число. Шаг 1: Рассортируйте числа в порядке возрастания:180, 192 Шаг 2Выньте из набора меньшее число как делитель: 180 Оставшийся набор: 192 Найдите напоминание о делении числа на делитель 192 по модулю 180 = 12 Соберите делитель и все остатки и отсортируйте их в порядке возрастания. 12, 180 Повторяйте процесс, пока в наборе не останется только одно число. Выньте из набора меньшее число как делитель: 12 Оставшийся набор: 180 Найдите напоминание о делении между числом и делителем 180 по модулю 12 = 0 Соберите делитель и все остатки и отсортируйте их в порядке возрастания. Удалите все дубликаты и 0. Наш набор: 12 Шаг 3: Возьмите оставшееся число из нашего набораНаибольший общий делитель 180 и 192 равно 12 Метод 4. Двоичный алгоритм наибольшего общего делителя Двоичный алгоритм НОД, также известный как алгоритм Штейна или двоичный алгоритм Евклида, представляет собой алгоритм, вычисляющий наибольший общий делитель двух неотрицательных целых чисел. Алгоритм Штейна использует более простые арифметические операции, чем обычный алгоритм Евклида; он заменяет деление арифметическими сдвигами, сравнениями и вычитанием. Хотя алгоритм в его современном виде был впервые опубликован израильским физиком и программистом Йозефом Штейном в 1967, он мог быть известен ко II веку до нашей эры в древнем Китае. Шаг 1: Отсортируйте числа и установите начальный GCF равным 1Список: 180, 192 Шаг 2: Все числа четные.Разделите их все на 2 и умножьте ваш GCF на 2. Удалите дубликаты и отсортируйте. Повторите процесс, если все числа четные: Результирующий список: 90, 96 GCF = 1*2 = 2 Результирующий список: 45, 48 GCF = 2*2 = 4 Шаг 3: Разделите все оставшиеся четные значения на 2, удалите дубликаты и отсортируйте.Повторите процесс, если в списке есть четные номера: 48/2 = 24 Итоговый список: 24, 45 24/2 = 12 Итоговый список: 12, 45 12/2 = 6 Итоговый список: 6, 45 6/2 = 3 Полученный список: 3, 45 Шаг 4: Выберите первое число, 3. |

 Найдите их наименьшее общее кратное 54 и 135
Найдите их наименьшее общее кратное 54 и 135
 НОД 180= 60 2*3*3*5*2 НСК=30 180/30=6
НОД 180= 60 2*3*3*5*2 НСК=30 180/30=6  Таким образом у 150 простые множители это 2,5,5 и 3 (две 5-ки, а не одна), у 180: 2,2,3,3,5, у 400:2,2,2,5,5 Наименьшее общее кратное я, если честно, уже не помню, как находить через множители, но я делаю так: беру наибольшее число, сначала проверяют кратно ли оно остальным, если да, то оно наименьшое кратное, если нет, то умножают его на 2 и опять проверяют, потом на 3 и т. д. пока не найдётся оно) А здесь наименьшее общее кратное это 3600. Я надеюсь, я довольно доступно объяснила и больше у тебя проблем с этим не будет)
Таким образом у 150 простые множители это 2,5,5 и 3 (две 5-ки, а не одна), у 180: 2,2,3,3,5, у 400:2,2,2,5,5 Наименьшее общее кратное я, если честно, уже не помню, как находить через множители, но я делаю так: беру наибольшее число, сначала проверяют кратно ли оно остальным, если да, то оно наименьшое кратное, если нет, то умножают его на 2 и опять проверяют, потом на 3 и т. д. пока не найдётся оно) А здесь наименьшее общее кратное это 3600. Я надеюсь, я довольно доступно объяснила и больше у тебя проблем с этим не будет) признак делимости на произведение. наименьшее общее кратное
признак делимости на произведение. наименьшее общее кратное 
 41 Mb.
41 Mb.

 .. 14
.. 14 Это значит, что: √(25*64) = √25 * √64. Если из 25 и 64 извлечь корни, то получим такое выражение: 5 * 8 = 40. То есть, квадратный корень из числа 1600 равен 40.
Это значит, что: √(25*64) = √25 * √64. Если из 25 и 64 извлечь корни, то получим такое выражение: 5 * 8 = 40. То есть, квадратный корень из числа 1600 равен 40.
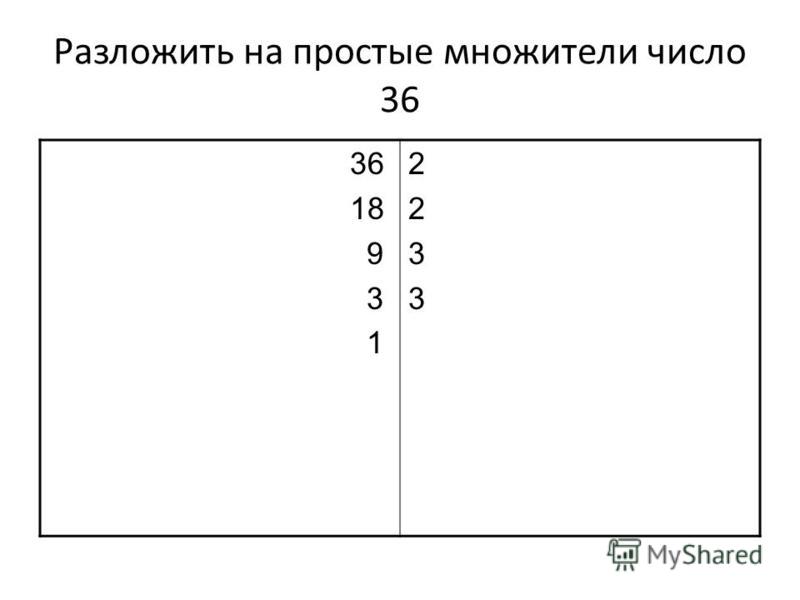
 Следовательно, √70 упростить нельзя.
Следовательно, √70 упростить нельзя.
 Поэтому, выражение будет выглядеть так: √320 = √(64*5) = √64*√5 = 8√5.
Поэтому, выражение будет выглядеть так: √320 = √(64*5) = √64*√5 = 8√5. Такие вычисления продолжаются до тех пор, пока результат не будет достигнут. Нули также можно добавлять, пока не получите нужное количество знаков после запятой.
Такие вычисления продолжаются до тех пор, пока результат не будет достигнут. Нули также можно добавлять, пока не получите нужное количество знаков после запятой.