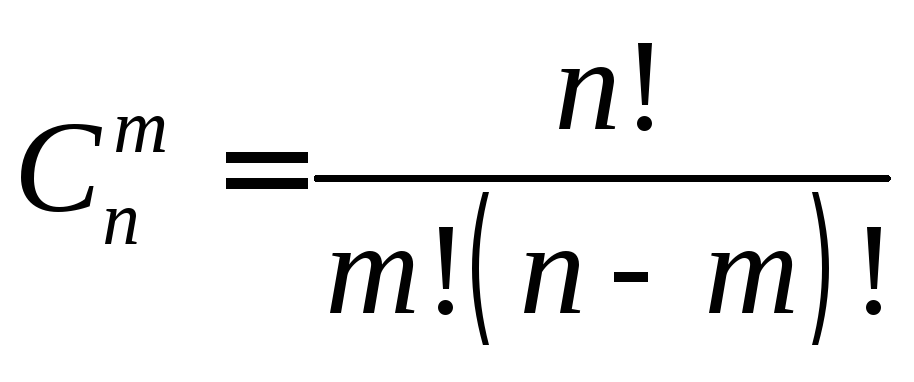Перестановки. Размещения. Сочетания. Урок решения комбинаторных задач
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
Перестановки.
Размещения.
Сочетания.
Урок решения
комбинаторных задач
9 класс
Пусть имеются три кубика с буквами А, В и С.
Составьте всевозможные комбинации из этих
букв.
В
А
ABC
ВСА
CAB
С
АСВ
ВАС
CBA
Эти комбинации отличаются друг от друга только
расположением букв (перестановка букв).
Перестановки
Перестановки — это комбинации, составленные из одних и тех же
элементов и отличающиеся порядком их следования.
Число всех возможных перестановок элементов обозначается Pn, и
может быть вычислено по формуле:
Формула перестановки:
Рn=n!
При перестановке число объектов остается неизменными,
меняется только их порядок
С ростом числа объектов количество перестановок очень
быстро растет и изображать их наглядно становится
затруднительно.
3 объекта
Рn=n!
Р3=3!=1∙2∙3=6
количество перестановок 6
Задача 1. В турнире участвуют семь команд. Сколько
вариантов распределения мест между ними возможно?
Р7=7!=1*2*3*4*5*6*7=5040
Ответ: 5040
Задача 2. Сколькими способами могут разместиться за круглым
столом 10 человек?
Р10 =10! = = 1*2*3*4*5*6*7*8*9*10 = 3628800
Ответ: 3628800
1. Вычислить:
а) 5!
7!
б)
3!
11!
в)
8!
2. В среду в 9 классе 6 уроков: алгебра, русский язык, черчение, биология,
химия, обществознание.
 Сколько вариантов расписания можно составить на
Сколько вариантов расписания можно составить насреду?
Размещения
Пусть имеется n различных объектов.
Будем выбирать из них m объектов и переставлять всеми
возможными способами между собой .
Получившиеся комбинации называются размещениями из
n объектов по m, а их число равно:
Формула размещения:
n!
А
n m !
m
n
При размещениях меняется и состав выбранных объектов, и их порядок.
n!
А
n m !
m
n
3 объекта
n=3 — всего объектов (различных фигур)
m= 2 – выбор и перестановка объектов
Размещение по 2 фигуры
А
2
3
3!
6
6
3 2 ! 1
Сколькими способами можно расставить 5 томов на книжной полке, если
выбирать их из имеющихся в наличии семи книг?
n!
А
n m !
n
А
5
7
7!
7! 2! 3 4 5 6 7
2520
7 5 ! 2!
2!
Ответ: 2520 способов
1. Вычислить:
а) А
2
6
А А
б)
3
А10
4
12
4
11
2.
 Найти количество трехзначных чисел с неповторяющимися
Найти количество трехзначных чисел с неповторяющимисяцифрами, которые можно составить из цифр: 1, 2, 3, 4, 5.
Ответ: 60 чисел
Сочетания
3 объекта
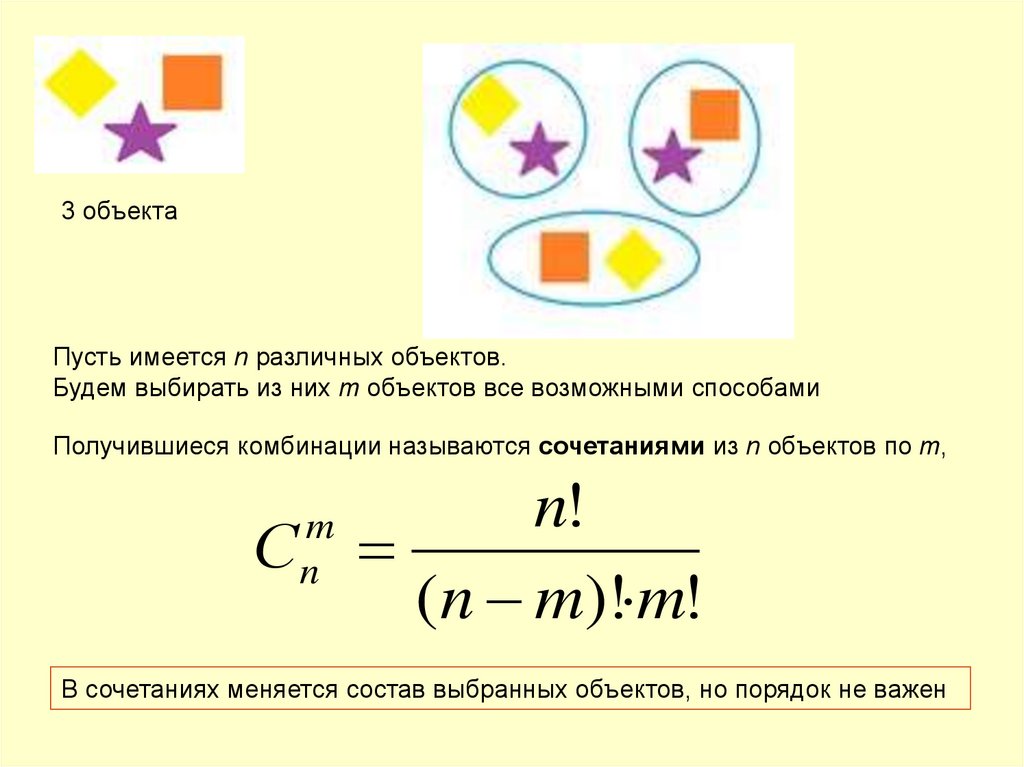
Пусть имеется n различных объектов.
Будем выбирать из них m объектов все возможными способами
Получившиеся комбинации называются сочетаниями из n объектов по m,
n!
С
(n m)! m!
m
n
В сочетаниях меняется состав выбранных объектов, но порядок не важен
Задача: Сколькими способами можно распределить три путевки в
один санаторий между пятью желающими?
Так как путевки предоставлены в один санаторий, то
варианты распределения отличаются друг от друга хотя бы
одним желающим. Поэтому число способов распределения
n!
С
(n m)! m!
m
n
Ответ: 10 способов.
Задача:
Группу из 20 студентов следует рассадить в аудитории по 2 человека за каждой
партой. Порядок их размещения не имеет значения. Определить количество
возможных вариантов сочетаний.
Ответ: 190
Задача: В цехе работают 12 человек: 5 женщин и 7 мужчин.
 Сколькими
Сколькимиспособами можно сформировать бригаду из 7 человек, чтобы в ней было
3 женщины?
Из пяти женщин необходимо выбирать по три, поэтому число способов отбора
Так как требуется отобрать четырех мужчин из семи,
то число способов отбора мужчин
Ответ: 350
.
English Русский Правила
Комбинаторика — перестановки, сочетания, размещения
Элементы комбинаторики–перестановки, размещения, сочетания– как термины, известные нам сегодня, впервые встречаются в трудах Якоба Бернулли («перестановка» и «размещение») и Блеза Паскаля («сочетание»). В то же время термин «комбинаторика» придуман Готфридом Вильгельмом Лейбницем (к слову, учителем Бернулли), рассуждавшим о данной области математики как об искусстве. Кроме указанных элементов, существуют и другие комбинаторные конфигурации: «композиция» (разложение) и «разбиение числа».
.
Поделиться расчетом:
Вычислить
Размещения
Пускай количество размещений(при выборе элементов без повторения) из n по k будет . Тогда для определения искомого значения служит следующее равенство:
Тогда для определения искомого значения служит следующее равенство:
При выборе же с повторением (т.е. при таковом размещении элементов) задействуют формулу
nk
ПРИМЕР №1
Дано 10 чисел: 1,2,…,10. Найти, сколько 4–значных чисел можно составить из предложенного ряда.
Для размещения с повторениями:
m=nk=104=10000
Для размещения без повторений:
Перестановки
Частный случай размещения при n=k– это перестановка из n элементов. Количество всех перестановок определяется следующим образом:
Ann=Pn=n!
ПРИМЕР №2
На книжной полке находится 20 книг, 5 из которых написаны в жанре детектива. Определить количество способов расстановки книг на полке, чтобы детективные произведения при этом всегда располагались рядом.
Если 5 детективов посчитать за 1 книгу, то количество перестановок выйдет следующим: P16
при этом все 5 произведений в жанре детектива можно переставлять следующим числом способов: P5
Тогда (следуя правилу произведения)
N=P5⋅P16=5!⋅16!
Сочетания
Сочетания из n элементов по k– это подмножества из k элементов, которые разнятся друг от друга хотя бы одним элементом (причём, в отличие от числа сочетаний, порядок элементов не важен, т. е., например,варианты 12 и 21 будут считаться одним и тем же).Пускай общее число сочетаний будет , и тогда для определения искомого значения служит следующее равенство:
е., например,варианты 12 и 21 будут считаться одним и тем же).Пускай общее число сочетаний будет , и тогда для определения искомого значения служит следующее равенство:
ПРИМЕР №3
В футбольной команде из 30 человек необходимо выбрать 10 полевых игроков и 1 вратаря (т.е. 11 игроков основного состава). Найти, каким количеством способов возможно сделать это.
Отталкиваясь от того, что порядок футболистов не важен, найдём:
Введём в соответствующие поля нашего калькулятора известные значения n и k и получим искомые ответы, отражающие нахождение числа перестановок, размещений и сочетаний.
Формулы комбинаций перестановок, трюки с примерами
В математике понятие перестановки используется в нескольких немного различающихся значениях, связанных с действием перестановки (перестановки) объектов или значений. Неформально перестановка набора объектов представляет собой расположение этих объектов в определенном порядке. Например, существует шесть перестановок множества {1,2,3}, а именно (1,2,3) , (1,3,2) , (2,1,3) , (2,3,1) , (3,1,2) и (3,2,1) . Можно определить анаграмму слова как перестановку его букв. Изучение перестановок в этом смысле вообще относится к области комбинаторики.
Например, существует шесть перестановок множества {1,2,3}, а именно (1,2,3) , (1,3,2) , (2,1,3) , (2,3,1) , (3,1,2) и (3,2,1) . Можно определить анаграмму слова как перестановку его букв. Изучение перестановок в этом смысле вообще относится к области комбинаторики.
Количество перестановок n различных объектов равно:
n×(n – 1) ×(n – 2) ×… ×2×1, это число называется «n факториал» и пишется «n!» .
В элементарной комбинаторике название «перестановки и комбинации» относится к двум связанным проблемам, обе из которых подсчитывают возможности выбора k различных элементов из множества n элементов, где для k-перестановок учитывается порядок выбора, но для k-сочетания игнорируется. Однако k-перестановки не соответствуют перестановкам, обсуждаемым в этой статье (если только k = n).
Факториал
Факториал — это когда после числа стоит восклицательный знак, поэтому оно представляет все положительные целые числа, предшествующие этому числу, после чего вы умножаете, чтобы решить факториал.
Обозначается n!. Следовательно, н! = 1 × 2 × 3 × … × (n – 1) × n
Например:
- 6! = 6 × 5 × 4 × 3 × 2 × 1 = 720
- 5! = 5 × 4 × 3 × 2 × 1 = 120
Формулы
Перестановка = n P r = n!/(n-r)!
Комбинация = n C r = n P r /r!
где n , r неотрицательные целые числа и r ≤ n .
- r — размер каждой перестановки.
- n — размер множества, из которого переставляются элементы.
- ! — оператор факториала.
Пример 1: Найдите количество перестановок и комбинаций:
н =6; r = 4.
Решение:
Шаг 1: Найдите факториал числа 6.
6! = 6 × 5 × 4 × 3 × 2 × 1 = 720
Шаг 2: Найдите факториал 6-4.
(6-4) ! = 2! = 2
Шаг 3: Разделите 720 на 2.
Перестановка = 720/2 = 360
Шаг 4: Найдите факториал числа 4.
4! = 4 × 3 × 2 × 1 = 24
Шаг 5: Разделите 360 на 24.
Комбинация = 360/24 = 15
Основные принципы счета
Если есть m способов сделать одно и n способов сделать другое, то существует m × n способов сделать и то, и другое. Фундаментальный принцип подсчета — это руководящее правило для определения количества способов выполнения двух задач.
Например:
- Допустим, вы хотите подбросить монетку и бросить кубик. Есть 2 способа подбросить монету и 6 способов бросить кубик. Тогда есть 2 × 6 = 12 способов, которыми вы можете подбросить монету и бросить кубик.
- Если вы хотите взять одну ноту на пианино и сыграть на одной струне на банджо, то есть 88 × 5 = 440 способов сделать и то, и другое.
- Если вы хотите вытянуть 2 карты из стандартной колоды из 52 карт, не заменяя их, то существует 52 способа вытянуть первую и 51 способ вытянуть вторую, так что всего 52 × 51 = 2652 способа вытяните две карты.

Принцип сложения
Если одно событие может произойти «m» способами, а другое событие может произойти «n» способами независимо от первого события, то любое из двух событий может произойти (m + n) способами .
Пример 2: В классе 10 мальчиков и 8 девочек. Классный руководитель хочет выбрать ученика для наблюдения за классом. Сколькими способами классный руководитель может сделать этот выбор?
Решение: Учитель может выбрать ученика для наблюдения двумя исключительными способами
- Выбрать мальчика среди 10 мальчиков, что можно сделать 10 способами ИЛИ
- Выбрать девочку среди 8 девочек, что можно сделать 8 способами.
Следовательно, согласно основному принципу сложения, мальчика или девочку можно выбрать 10 + 8 = 18 способами.
Принцип умножения
Если операцию можно выполнить «m» способами и после того, как она была выполнена любым из этих способов, вторую операцию можно выполнить «n» способами, то две операции последовательно можно выполнить (m × n) способами.
Пример 3: В классе 10 мальчиков и 8 девочек. Учитель хочет выбрать мальчика и девочку, которые будут представлять класс в функции. Сколькими способами учитель может сделать этот выбор?
Решение: Учитель должен выполнить два задания:
- Выбрать мальчика среди 10 мальчиков, что можно сделать 10 способами.
- Выбрать девушку среди 8 девушек, что можно сделать 8 способами.
Следовательно, необходимое количество способов = 10 × 8 = 80.
Методы выборки
- Процесс выборки можно разделить на следующие формы: ПОСЛЕДОВАТЕЛЬНОСТЬ.
- Порядок ВАЖЕН, и повторение НЕ РАЗРЕШЕНО, тогда каждый образец является ПЕРЕСТАВКОЙ.
- Порядок НЕ ВАЖЕН, и повторение РАЗРЕШЕНО, каждый образец является МНОЖЕСТВЕННЫМ.
- Порядок НЕ ВАЖЕН и повторение НЕ РАЗРЕШЕНО, каждый образец является КОМБИНАЦИЕЙ.
Перестановка
Перестановка — это расположение объектов без повторения, причем важен порядок. Другое определение перестановки — это количество возможных таких расположений.
Другое определение перестановки — это количество возможных таких расположений.
Количество перестановок «n» вещей, взятых «r» одновременно, обозначается как n P r Оно определяется как n P r
вы можете расположить объекты, это всегда будет целое число. Знаменатель в формуле всегда будет делиться на числитель без остатка.
Это также дает нам другое определение перестановок. n P n = n!
Пример 4: Список всех перестановок букв ABCD
Решение:
| ABCD | ABDC | ACBD | ACDB | ADBC | 4 235 |
| BACD | BADC | BCAD | BCDA | BDAC | BDCA |
| CABD | CADB | CBAD | CBDA | CDAB | CDBA |
| DABC | 2CB 4DB 9022 DA 3ДБКА | DCAB | DCBA |
Теперь, если вам на самом деле не нужен список всех перестановок, вы можете использовать формулу для количества перестановок. Есть 4 объекта, и вы берете 4 за раз.
Есть 4 объекта, и вы берете 4 за раз.
4 P 4 = 4!/(4 – 4) ! = 4!/0! = 24/1 = 24.
Пример 5. Перечислите все три перестановки букв в слове РУКА
Решение:
| HAN | HNA | HAD | HDA | HND | HDN |
| AHN | ANH | ||||
| И | ADN | ||||
| NHD | NDH | NAH | NHA | NAD | NDA |
| DHA | DAH | DAN | ДНК | DHN 70235 | DNH |
Теперь, если вам на самом деле не нужен список всех перестановок, вы можно использовать формулу числа перестановок. Есть 4 объекта, и вы берете 3 за раз.
⁴ P ³ = 4!/(4-3) ! = 4!/1! = 24/1 = 24.
Циклические перестановки
Это перестановка вокруг круглого объекта, следует отметить, что у круглого объекта нет ни начала, ни конца, мы фиксируем один объект (или человека) и переставляем оставшийся.
Расположение вокруг круглого стола
Предположим, что пять человек A, B, C, D и E сидят по окружности круглого стола по порядку (у которого нет головы) . Теперь, сдвинув A, B, C, D и E на одну позицию против часовой стрелки, мы получим следующие расположения:
мы видим, что расположение на всех рисунках одинаковое.
∴ Количество круговых перестановок n разных вещей, взятых одновременно, равно (n – 1) !, если порядок по часовой стрелке и против часовой стрелки считать разными.
Пример 6. Сколькими способами можно рассадить 6 школьников вокруг круглого стола?
Решение: Задача представляет собой циклическую перестановку
Количество способов рассадить 6 студентов
= 1 × (6 – 1) ! = 5! = 5 × 4 × 3 × 2 × 1 = 120
Бусины или цветы (все разные) вокруг круглого ожерелья или гирлянды
Рассмотрим пять бусин A, B, C, D и E в ожерелье или пять цветы A, B, C и D, E в гирлянде и т. д. Если ожерелье или гирлянду слева перевернуть, мы получим расположение справа, т. е. против и по часовой стрелке порядок расположения не отличается.
д. Если ожерелье или гирлянду слева перевернуть, мы получим расположение справа, т. е. против и по часовой стрелке порядок расположения не отличается.
Таким образом, количество циклических перестановок «n» разных вещей взято.
все сразу равно:
1/2 (n–1)!, если порядок по часовой и против часовой стрелки считается некоторым.
Пример 7: Количество способов, которыми 10 человек могут сесть вокруг круглого стола так, чтобы ни у одного из них не было одинаковых соседей в любых двух расстановках.
Решение: 10 человек могут сидеть за круглым столом за 9! способы. Но вот приказы по часовой и против часовой стрелки будут давать одни и те же соседи. Следовательно, искомое количество способов = 1/2 × 9!
Условные перестановки
Когда условия применяются к тому, как устроены вещи, тогда случается, что перестановки называются условными.
Количество перестановок n вещей, использующих r за раз, в которых всегда встречается конкретная вещь = .
Пример 8. Сколько 4-значных чисел (повторение не допускается) можно составить, используя цифры 1-7, если в числе всегда будет 4?
Решение: Всего цифр (n) = 7
Всего способов составить число, если всегда присутствует 4
= r × n-1 P r-1 = 4 × ⁶P³ = 480. имеет n₁ объектов одного вида, n₂ второго рода, n₃ третьего рода и т. д., где n = n₁ + n₂ + n₃ + . . . + n k , Тогда число различимых перестановок n объектов равно
Пример 9. Сколькими различимыми способами можно написать буквы в BANANA?
Решение: В этом слове шесть букв, из которых три буквы А, две буквы Н и одна буква В. Таким образом, количество различных способов записи букв равно:
Количество перестановок n вещи, занимающие r за раз, в которых конкретная вещь никогда не происходит = .
Пример 10. Сколько различных слов из 3 букв можно составить из 5 гласных, если гласная «А» никогда не будет включена?
Решение: Всего букв (n) = 5
Итак, общее количество способов = n-1 P r = 5-1 P 3 = 4 P 3 = 24.
время, в течение которого m указанных вещей всегда собираются вместе = m!(n-m+1).
Пример 11. Сколькими способами можно расположить пять гласных a, e, i, o и u, если:
- две гласные e и i всегда вместе.
- две гласные e и i никогда не стоят вместе.
Решение: 1. По формуле m!(n – m + 1)!
Здесь n = 5, m = 2(e и i)
⇒ Требуемый номер. способов = 2!(5 – 2 + 1) ! = 2 × 4! = 48
2. Количество способов, когда e и i никогда не встречаются вместе
= общее количество. способов расположения 5 гласных
– нет. способов, когда e & i вместе = 5! – 48 = 72
Или используйте n! – м!(п – м + 1) ! = 5! – 48 = 72
Количество перестановок n различных вещей, взятых одновременно, при которых m указанных вещей никогда не сойдутся вместе = n!-m!(n-m+1)!
Число перестановок «n» вещей, взятых одновременно, когда «p» одинаковы одного вида, «q» одинаковы второго, «r» одинаково третьего и т. д.
д.
Пример 12: Сколько разных слов можно составить из букв мира МИССИСИППИ.
Решение: В слове MISSISSIPPI 4 I, 4S и 2P.
Таким образом, требуемое количество слов =
Количество перестановок «n» разных вещей, берущих «r» за раз, когда каждая вещь может быть повторена «r» раз = nr
Пример 13. Сколькими способами можно раздать 5 призов 4 мальчикам, если каждый мальчик имеет право на получение всех призов?
Решение: Любой из призов можно получить 4 способами; то любой из оставшихся 4 призов можно снова дать 4 способами, так как его может получить даже тот мальчик, который уже получил приз.
Следовательно, 5 призов можно раздать 4 × 4 × 4 × 4 × 4 = 4⁵ способами.
Комбинация
Комбинация — это расположение объектов без повторения и порядка, не имеющего значения. Другим определением комбинации является количество возможных таких схем.
Количество комбинаций «n» разнородных вещей, взятых «r» одновременно, обозначается как n C r или C(n, r) . Он определяется как n C r
Ключевым моментом для комбинации является то, что не допускается повторение объектов, и порядок не важен.
Пример 14. Перечислите все комбинации букв ABCD группами по 3.
Решение: Всего четыре комбинации (ABC, ABD, ACD и BCD). Ниже каждой из этих комбинаций перечислены шесть перестановок, которые эквивалентны как комбинации.
| ABC | ABD | ACD | BCD | ||||
| ACD | BCD | ||||||
| ACB | ADB | ADC | BDC | ||||
| BAC | BAD | CAD | CBD | ||||
| BCA | BDA | CDA | CD | 9022 0222CAB | DAB | DAC | DBC |
| CBA | DBA | DCA | DCB |
Решение: Общее количество способов
=
= = 4368.
Условные комбинации
Количество комбинаций n различных объектов, взятых одновременно, когда k конкретных объектов никогда не встречаются =
Количество выборов r объектов из n объектов, когда p отдельных объектов не находятся вместе ни в одном выборе = n C r – n-p C r-p
Количество выбранных r последовательных вещей из n вещей подряд = n – r + 1
Количество выбранных r последовательных вещей из n вещей по кругу =
количество комбинаций «n» разных вещей, использующих некоторые или все сразу =
Количество способов разделить m + n вещей на две группы, содержащие соответственно m и n вещей = m+n C n . n C n
Количество способов разделить ‘m + n + p’ вещей на три группы, содержащие соответственно ‘m’, ‘n’ и ‘p’ вещей = m+n+p C м . n+p C p =
(i) Если m = n = p, т. е. Вещи «3m» разбиты на три равные группы, тогда количество комбинаций равно 9.0003
е. Вещи «3m» разбиты на три равные группы, тогда количество комбинаций равно 9.0003
(ii) Buf, если «3m» вещей должны быть разделены между тремя людьми, то количество делений равно
Если mn отдельных предметов нужно разделить на m групп. Тогда число комбинаций равно , когда порядок групп не важен
и , когда важен порядок групп
Количество прямоугольников и квадратов
Количество прямоугольников любого размера в квадрате размера n × n и количество квадратов любого размера.
Количество прямоугольников любого размера в прямоугольнике размером n × p (n ,
Пример 16. Сколько клеток можно составить на шахматной доске?
Решение: Шахматная доска состоит из 9 равноотстоящих горизонтальных и вертикальных линий. Чтобы составить квадрат 1 × 1, мы должны выбрать из них две последовательные горизонтальную и вертикальную линии. Это можно сделать 8 × 8 = 8² способов.
Квадрат 2 × 2 требует трех последовательных горизонтальных и вертикальных линий, и мы можем сделать это 7 × 7 = 7² способов. Продолжая в том же духе, общее количество квадратов равно 9.0003
Продолжая в том же духе, общее количество квадратов равно 9.0003
= 204.
Что нужно запомнить
0! = 1
Факториалы дробей и отрицательных целых чисел не определены.
;
n C x = n C y ⇒ x + y = n
0 n 36 = n C r+1 = n+ 1 C rn C r = . н-1 С р-1
n C r = (n – r + 1) n C r-1
n C 1 5 0 9 = п-1 = п
Решенные примеры
1. Докажите, что
Решение:
= =
2. Докажите, что
Решение: 6
=
3. Есть 6 вопросов с несколькими вариантами ответов на экзамене. Сколько возможных последовательностей ответов, если в первых трех вопросах по 4 варианта, а в следующих трех по 5 вариантов?
Решение: На каждый из первых трех вопросов можно ответить 4 способами, а на каждый из следующих трех вопросов можно ответить 5 различными способами.
Отсюда искомое количество различных последовательностей ответов
= 4 × 4 × 4 × 5 × 5 × 5 = 8000.
4. Пять человек вошли в кабину лифта на первом этаже восьмиэтажного дома. дом. Предположим, что каждый из них может самостоятельно выйти из салона на любом этаже, начиная с первого. Каким общим числом способов каждый из пяти человек может покинуть каюту на любом из 7 этажей?
Решение: Любой из 5 человек может покинуть каюту 7 способами независимо от других.
Следовательно, необходимое количество способов = 7 × 7 × 7 × 7 × 7 = 7⁵.
5. Сколькими способами пять мальчиков и пять девочек могут образовать круг так, чтобы мальчики и девочки чередовались?
Решение: Поставив на стол одного мальчика, оставшихся можно разложить на 4! способы.
Будет 5 мест, по одному между двумя мальчиками
который могут заполнить 5 девушек из 5! способы.
Отсюда по принципу умножения искомое количество способов = 4! × 5! = 2880.
6. Сколькими способами можно рассадить 5 мальчиков и 5 девочек за круглым столом, при этом никакие две девочки не могут быть вместе?
Решение: Оставив одно место свободным между двумя мальчиками, можно сесть на 4! способы. Тогда на оставшихся 5 местах, 5 девушек сидят на 5! способы. Следовательно, искомое число = 4! × 5!
7. Сколько трехзначных чисел можно составить из цифр 1, 2, 3, 4, 5, если цифры могут повторяться?
Решение: Единичный разряд можно заполнить 5 способами, а так как повторы цифр разрешены, то и десятый разряд можно заполнить 5 способами.
Кроме того, сотое место можно заполнить также 5 способами.
Следовательно, искомое количество трехзначных чисел равно 5 × 5 × 5 = 125.
8. Сколькими способами можно расставить 8 человек по кругу?
Решение: Восемь человек можно расположить в круг
(8 – 1) ! = 7! = 5040.
ДАЛЕЕ: Перестановка Комбинация
1.2 Комбинации и перестановки
Сначала обратимся к , считая . Хотя это звучит просто, возможно, слишком просто учиться, это не так. Когда мы говорим о счете, это стенография для определения размера множества или, чаще, размеров многих наборы, все с чем-то общим, но разные размеры в зависимости от один или несколько параметров. Например: сколько исходов возможно когда бросают кубик? Две кости? $n$ кости? Как сказано, это двусмысленно: что мы подразумеваем под «результатом»? Предположим, мы бросаем две кости, скажем, красный кубик и зеленый кубик. Является ли «красный два, зеленый три» другим результат, чем «красное три, зеленое два»? Если да, мы подсчитываем количество возможных «физических» исходов, а именно 36. Если нет, то есть 21. Нас даже могут интересовать просто возможные итоги, т.е. в этом случае есть 11 исходов.
Даже довольно простая первая интерпретация опирается на некоторую степень
знание счета; мы сначала выясним два простых факта. В
с точки зрения размеров множества, предположим, что мы знаем, что множество $A$ имеет размер $m$ и множество
$B$ имеет размер $n$. Каков размер $A$ и $B$ вместе, то есть
размер $A\cup B$? Если мы знаем, что $A$ и $B$ не имеют элементов в
общий, то размер $A\cup B$ равен $m+n$; если у них есть элементы в
общее, нам нужно больше информации. Простая, но типичная проблема этого
тип: если мы бросим два кубика, сколько существует способов получить либо 7, либо
11? Так как есть 6 способов получить 7 и два способа получить 11,
ответ: $6+2=8$. Хотя этот принцип прост, его легко
забыть требование непересекаемости двух множеств и, следовательно, использовать
это когда обстоятельства иные. Этот принцип часто
называется 9п м_i$. Этот
может быть доказано простым рассуждением по индукции.
В
с точки зрения размеров множества, предположим, что мы знаем, что множество $A$ имеет размер $m$ и множество
$B$ имеет размер $n$. Каков размер $A$ и $B$ вместе, то есть
размер $A\cup B$? Если мы знаем, что $A$ и $B$ не имеют элементов в
общий, то размер $A\cup B$ равен $m+n$; если у них есть элементы в
общее, нам нужно больше информации. Простая, но типичная проблема этого
тип: если мы бросим два кубика, сколько существует способов получить либо 7, либо
11? Так как есть 6 способов получить 7 и два способа получить 11,
ответ: $6+2=8$. Хотя этот принцип прост, его легко
забыть требование непересекаемости двух множеств и, следовательно, использовать
это когда обстоятельства иные. Этот принцип часто
называется 9п м_i$. Этот
может быть доказано простым рассуждением по индукции.
Почему мы знаем, не перечисляя их всех, что существует 36 исходов?
когда бросают две игральные кости? Мы можем рассматривать результаты как два отдельных
результаты, то есть результат броска кубика номер один и
результат броска кубика номер два.
 Это часто называют
9п м_i$. Это тоже
можно доказать по индукции.
Это часто называют
9п м_i$. Это тоже
можно доказать по индукции.Пример 1.2.1 Сколько исходов возможно при броске трех игральных костей, если не может быть двух одинаковых? Первые две кости вместе имеют $6\cdot 5=30$ возможных исходов, сверху. Для каждого из этих 30 исходов, есть четыре возможных исхода для третьего кубика, поэтому общее количество исходов $30\cdot 4=6\cdot 5\cdot 4=120$. (Обратите внимание, что мы считаем кости различимыми, то есть броском 6, 4, 1 отличается от 4, 6, 1, потому что первое и второе кости различны в двух бросках, даже несмотря на то, что числа как набор одинаковы.) $\квадрат$
Пример 1.2.2. Предположим, что блоки с номерами от 1 до $n$ находятся в бочке; мы вытащите из них $k$, расположив их в линию, как мы. Сколько исходы возможны? То есть, сколько различных расположений $k$ блоки могли бы мы видеть?
По сути, это то же самое, что и в предыдущем примере: имеется $k$ «пятен».
заполняться блоками. Любой из блоков $n$ может появиться первым в
линия; то любой из оставшихся $n-1$ может появиться следующим, и, таким образом,
на. Таким образом, число исходов равно $n(n-1)(n-2)\cdots(n-k+1)$, согласно
принцип умножения. в
В предыдущем примере первое «пятно» было номером один, второе
точка была номером два, третья точка была номером три, и
$6\cdot5\cdot4=6(6-1)(6-2)$; обратите внимание, что $6-2=6-3+1$.
$\квадрат$
Таким образом, число исходов равно $n(n-1)(n-2)\cdots(n-k+1)$, согласно
принцип умножения. в
В предыдущем примере первое «пятно» было номером один, второе
точка была номером два, третья точка была номером три, и
$6\cdot5\cdot4=6(6-1)(6-2)$; обратите внимание, что $6-2=6-3+1$.
$\квадрат$
Это довольно общая проблема:
Определение 1.2.3 Количество перестановок $n$ вещи, взятые $k$ за раз, $$P(n,k)=n(n-1)(n-2)\cdots(n-k+1)={n!\over (n-k)!}.$$ $\квадрат$
Перестановка некоторых объектов представляет собой конкретное линейное упорядочение
объекты; Фактически $P(n,k)$ одновременно учитывает две вещи:
количество способов выбрать и упорядочить $k$ из $n$ объектов. Полезный
частный случай $k=n$, в котором мы просто считаем число
способов упорядочить все $n$ объектов. Это
$n(n-1)\cdots(n-n+1)=n!$. Обратите внимание, что вторая форма $P(n,k)$ из
определение дает
$${n!\over (n-n)!}={n!\over 0!}.$$
Это правильно, только если $0!=1$, поэтому мы принимаем стандартное соглашение
что это правда, то есть мы определите $0!$ как $1$.
Предположим, мы хотим подсчитать только количество способов выбрать $k$ предметов. из $n$, то есть порядок нам не важен. В Пример 1.2.1, мы подсчитали количество броски трех игральных костей с разными числами. Кости были различимы или в определенном порядке: первый кубик, второй и третий. Теперь мы хотим просто посчитать, сколько комбинаций чисел есть, причем 6, 4, 1 теперь считаются той же комбинацией, что и 4, 6, 1.
Пример 1.2.4
Предположим, нам нужно перечислить все 120 возможностей в
пример 1.2.1. Список будет содержать
множество исходов, которые мы теперь хотим считать одним исходом;
6, 4, 1 и 4, 6, 1 будут в списке, но не должны учитываться
в отдельности. Сколько раз один результат появится в списке?
Это задача на перестановку: есть $3!$ порядков, в которых 1, 4, 6
может появиться, и все 6 из них будут в списке. На самом деле каждый
исход появится в списке 6 раз, так как каждый исход может
появляются в заказах $3!$. Следовательно, список слишком велик в 6 раз;
правильный счет для новой задачи: $120/6=20$. $\квадрат$
$\квадрат$
Следуя тем же рассуждениям вообще, если у нас есть $n$ объектов, количество способов выбрать $k$ из них $P(n,k)/k!$, так как каждый набор из $k$ объектов будет посчитал $k!$ раз по $P(n,k)$.
Определение 1.2.5 Количество подмножеств размера $k$ множества размера $n$ (также называется $n$-множеством) $$C(n,k)={P(n,k)\более k!}={n!\over k!(n-k)!}={n\выбрать k}.$$ Обозначение $C(n,k)$ используется редко; вместо этого мы используем $n\выбрать k$, произносится как «$n$ выбирает $k$». $\квадрат$
Пример 1.2.6
Рассмотрим $n=0,1,2,3$. Несложно перечислить
подмножества малого $n$-множества; типичное $n$-множество
$\{a_1,a_2,\ldots,a_n\}$.
$0$-множество, а именно пустое множество, имеет
одно подмножество, пустой набор; $1$-множество имеет два подмножества, пустое множество
и $\{a_1\}$; $2$-подмножество имеет четыре подмножества, $\emptyset$, $\{a_1\}$,
$\{a_2\}$, $\{a_1,a_2\}$; а $3$-подмножество имеет восемь:
$\emptyset$, $\{a_1\}$, $\{a_2\}$, $\{a_3\}$, $\{a_1,a_2\}$,
$\{a_1,a_3\}$, $\{a_2,a_3\}$, $\{a_1,a_2,a_3\}$. Затем из этих списков легко вычислить $n\выбрать k$:
$$\displaylines{\cr
\матрица{
&\rlap{\lower 3pt\hbox{$\Rule{65pt}{0pt}{0.5pt}$}}\cr
&0\кр
п&1\кр
&2\кр
&3\кр
}\влево\верт
\матрица{
0&\нижний 3.5pt\hbox{}\rlap{\smash{\поднять 1.5em \hbox{$k$}}}1&2&3\cr
1\кр
1&1\кр
1&2&1\кр
1&3&3&1\кр
}\право.\cr}$$
$\квадрат$
Затем из этих списков легко вычислить $n\выбрать k$:
$$\displaylines{\cr
\матрица{
&\rlap{\lower 3pt\hbox{$\Rule{65pt}{0pt}{0.5pt}$}}\cr
&0\кр
п&1\кр
&2\кр
&3\кр
}\влево\верт
\матрица{
0&\нижний 3.5pt\hbox{}\rlap{\smash{\поднять 1.5em \hbox{$k$}}}1&2&3\cr
1\кр
1&1\кр
1&2&1\кр
1&3&3&1\кр
}\право.\cr}$$
$\квадрат$
Вы, наверное, узнаете эти цифры: это начало Треугольник Паскаля . Каждая запись в Треугольник Паскаля получается путем добавления двух элементов из предыдущего ряд: тот, что прямо сверху, и тот, что выше и левее. Этот предполагает, что ${n\выбрать k}={n-1\выбрать k-1}+{n-1\выбрать k}$, и действительно это правда. Чтобы сделать это аккуратно, мы принимаем соглашение о том, что ${n\choose k}=0$, когда $kn$.
Теорема 1.2.7 $\ds{n\выберите k}={n-1\выберите k-1}+{n-1\выберите k}$.
Доказательство. Типичным $n$-множеством является $A=\{a_1,\ldots,a_n\}$. Мы рассматриваем два типа
подмножества: содержащие $a_n$ и не содержащие. Если
$k$-подмножество $A$ не содержит $a_n$, то оно является $k$-подмножеством
$\{a_1,…,a_{n-1}\}$, и таких $n-1\выберите k$.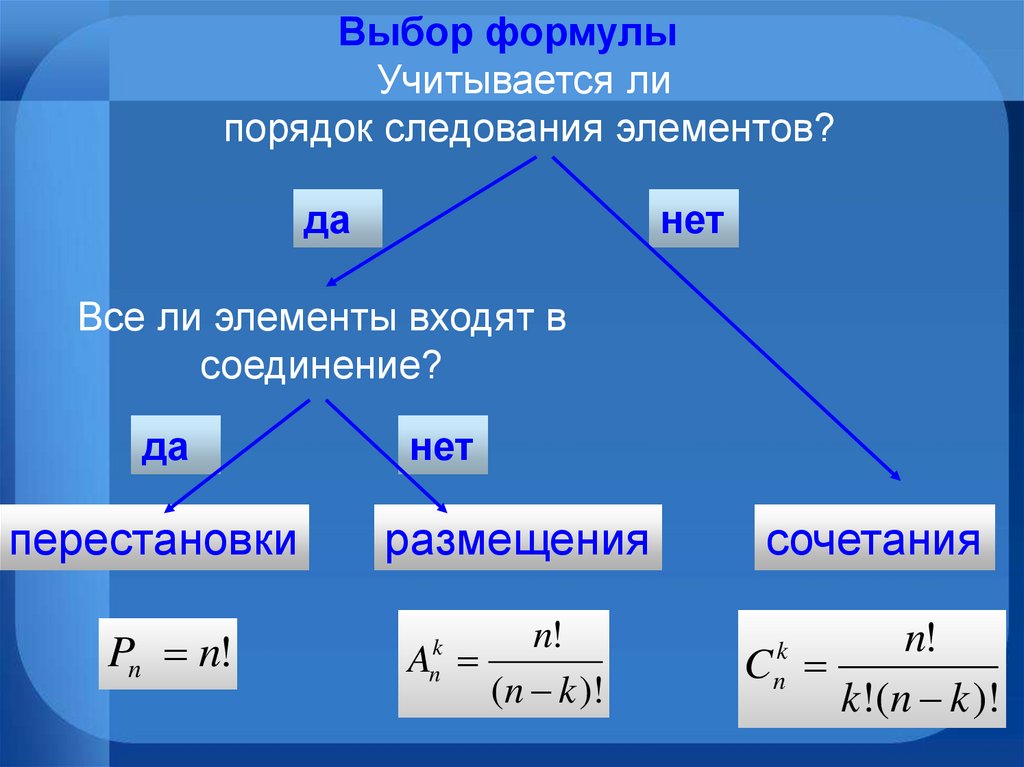 Если оно
содержит $a_n$, то он состоит из $a_n$ и $k-1$ элементов
$\{a_1,…,a_{n-1}\}$; так как их $n-1\выберите k-1$,
таких подмножеств $n-1\выберите k-1$. Таким образом, общее количество
$k$-подмножеств $A$ равно ${n-1\выбрать k-1}+{n-1\выбрать k}$.
Если оно
содержит $a_n$, то он состоит из $a_n$ и $k-1$ элементов
$\{a_1,…,a_{n-1}\}$; так как их $n-1\выберите k-1$,
таких подмножеств $n-1\выберите k-1$. Таким образом, общее количество
$k$-подмножеств $A$ равно ${n-1\выбрать k-1}+{n-1\выбрать k}$.
Обратите внимание, что когда $k=0$, ${n-1\выберите k-1}={n-1\выберите -1}=0$, и когда $k=n$, ${n-1\выбрать k}={n-1\выбрать n}=0$, так что ${n\выбрать 0}={n-1\выбрать 0}$ и ${n\выбрать n}={n-1\выбрать п-1}$. Эти значения являются граничными в треугольнике Паскаля. $\qed$
Многие проблемы со счетом основаны на рассуждениях, которые у нас есть. видимый. Вот несколько вариаций на тему.
Пример 1.2.8 Шесть человек должны сидеть за круглым столом; сколько сидячих мест аранжировки есть?
Не совсем ясно, что именно мы имеем в виду, чтобы считать здесь. если есть
«специальное место», например, может иметь значение, кто окажется на этом
сиденье. Если это не имеет значения, нас интересует только относительное положение
каждого человека. Тогда может или не может быть важно, является ли определенное лицо
находится слева или справа от другого. Так что этот вопрос можно
интерпретируется (по крайней мере) тремя способами. Давайте ответим на них все.
Тогда может или не может быть важно, является ли определенное лицо
находится слева или справа от другого. Так что этот вопрос можно
интерпретируется (по крайней мере) тремя способами. Давайте ответим на них все.
Во-первых, если имеют значение фактические стулья, на которых сидят люди, то это
точно так же, как выстраивание шести человек в ряд: 6 вариантов места
номер один, 5 для второго места и так далее, всего 6 долларов! Если
стулья не имеют значения, тогда $6!$ считают одно и то же расположение слишком большим
раз, по одному разу для каждого человека, который может быть на первом месте. Итак, общее количество в
в этом случае $6!/6=5!$. Другой подход к этому: поскольку фактическое
места не имеют значения, просто посадите одного из шести человек на стул. Тогда мы
нужно расставить оставшихся 5 человек в ряд, что можно сделать в
$5!$ способами. Наконец, предположим, что нас волнует только то, кто рядом с кем,
игнорируя право и лево. Тогда предыдущий ответ считает каждый
расположение дважды, один раз для порядка против часовой стрелки и один раз для
по часовой стрелке.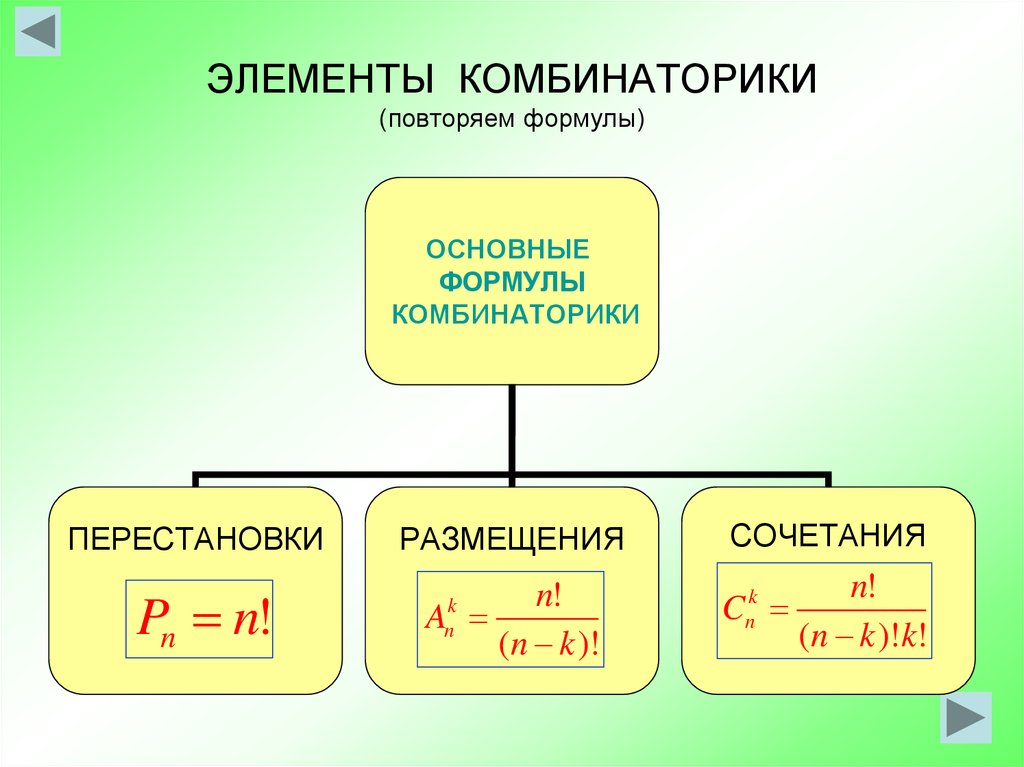 Итого $5!/2=P(5,3)$.
$\квадрат$
Итого $5!/2=P(5,3)$.
$\квадрат$
Мы дважды видели общий принцип в действии: если мы можем пересчитать желаемый набор таким образом, чтобы каждый элемент считался одинаковым количество раз, мы можем получить желаемое количество, просто разделив на общий фактор пересчета. Это по-прежнему будет полезной идеей. А вариация на эту тему состоит в том, чтобы пересчитать , а затем вычесть из сумма перерасчета.
Пример 1.2.9. Сколькими способами можно выстроить шесть человек так, чтобы конкретная пара людей не является соседней?
Обозначим людей $A$ и $B$.
Общее количество заказов составляет $6!$, но здесь учитываются заказы с
$A$ и $B$ рядом друг с другом. Сколько из них есть? Думать о
эти два человека как единое целое; сколько существует способов выстроить
Блок $AB$ с остальными четырьмя людьми? У нас есть 5 предметов, поэтому ответ
$5!$. Каждый из этих порядков соответствует двум различным порядкам в
которые $A$ и $B$ являются смежными, в зависимости от того, является ли $A$ или $B$
первый.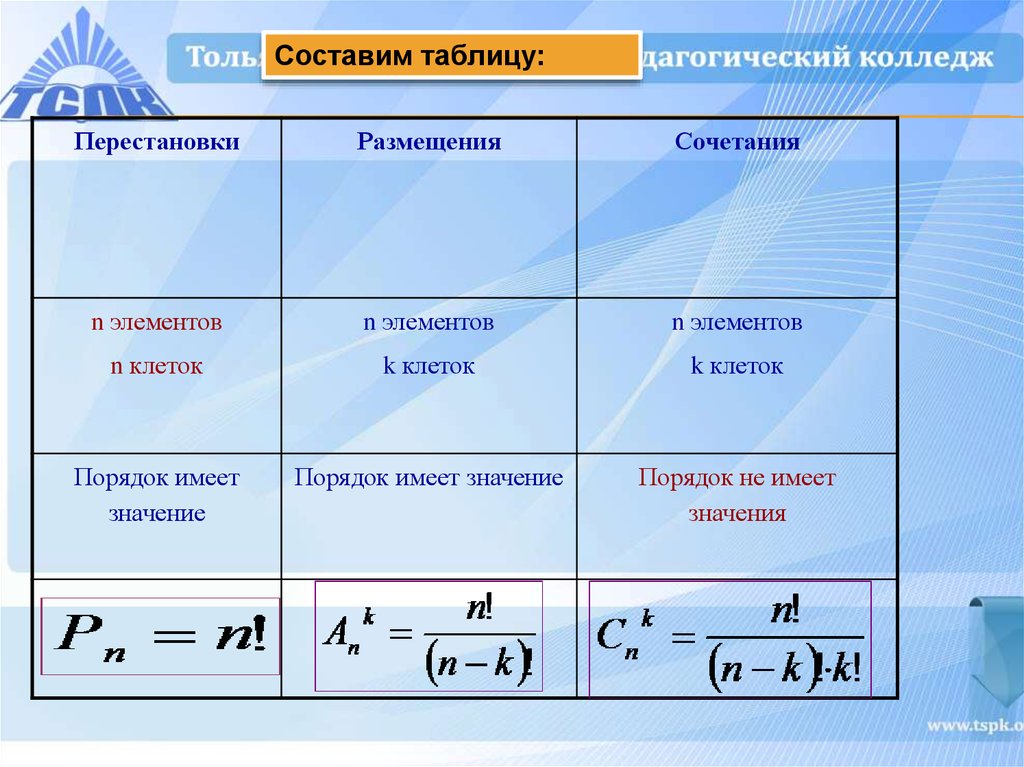 Таким образом, количество $6!$ слишком велико на $2\cdot5!$ и количество, которое мы
seek равен $6!-2\cdot 5!=4\cdot5!$.
$\квадрат$
9{e_n}$ есть, где
$p_i$ — различные простые числа?
Таким образом, количество $6!$ слишком велико на $2\cdot5!$ и количество, которое мы
seek равен $6!-2\cdot 5!=4\cdot5!$.
$\квадрат$
9{e_n}$ есть, где
$p_i$ — различные простые числа?
Пример 1.2.2 Покерная рука состоит из пяти карт из стандартных 52 карт. колода с четырьмя мастями и тринадцатью достоинствами в каждой масти; получатель чего-то карты в руке значения не имеют. Из скольких рук состоит 2 карты одного достоинства и 3 карты другого достоинства (фулл-хаус)? Сколько состоит из 5 карт одной масти (флеш)?
Пример 1.2.3 Шестеро мужчин и шесть женщин должны сидеть за столом, мужчины и женщины чередуются. Стулья не имеют значения, важно только, кто следующий кому, а правое и левое разные. Сколько сидячих мест аранжировки возможны?
Пример 1.2.4 Восемь человек должны сидеть за столом; стулья неважно, только кто рядом с кем, а справа и слева другой. Два человека, X и Y, не могут сидеть рядом друг с другом. Сколько посадочных мест возможно?
Пример 1. 2.5 В шахматах ладья атакует любую фигуру в той же строке или столбце.
как ладья, если между ними нет другой фигуры. Сколькими способами
можно ли разместить на шахматной доске восемь неразличимых ладей так, чтобы
двое не нападают друг на друга? Как насчет восьми неразличимых ладей на
доска $10\times 10$?
2.5 В шахматах ладья атакует любую фигуру в той же строке или столбце.
как ладья, если между ними нет другой фигуры. Сколькими способами
можно ли разместить на шахматной доске восемь неразличимых ладей так, чтобы
двое не нападают друг на друга? Как насчет восьми неразличимых ладей на
доска $10\times 10$?
Пример 1.2.6 Предположим, мы хотим поставить 8 неатакующих ладей на поле. шахматная доска. Сколькими способами мы можем это сделать, если 16 наиболее Квадраты «северо-запад» должны быть пустыми? А если только 4 самых Квадраты «северо-запад» должны быть пустыми?
Пример 1.2.7 «Правильная» последовательность скобок — это последовательность, в которой скобки
могут быть правильно сопоставлены, например $()(())$. Нетрудно заметить, что это
возможно именно тогда, когда число левых и правых скобок равно
то же самое, и каждый начальный сегмент последовательности имеет по крайней мере как
многие левые скобки как правые. Например, $())\ldots$ не может
возможно, будет расширена до юридической последовательности.