что это такое и как их найти
Существуют четыре основных арифметических действия: сложение, вычитание, умножение и деление. Они – основа математики, с их помощью производятся все остальные, более сложные вычисления. Сложение и вычитание – простейшие из них и взаимно противоположны. Но с терминами, используемыми при сложении, мы чаще сталкиваемся в жизни.
Говорим о «сложении усилий» при старании совместно получить нужный результат, о «слагаемых достигнутого успеха» и т.п. Названия же, связанные с вычитанием, остаются в пределах математики, редко появляясь в повседневной речи. Поэтому менее привычны слова «вычитаемое», «уменьшаемое», «разность». Правило нахождения каждого из данных компонентов возможно применить лишь при понимании значения этих названий.
Оглавление
- Значение терминов
- Что такое разность чисел в математике
- Что такое уменьшаемое и вычитаемое
- Правила нахождения неизвестного элемента
- Как найти уменьшаемое
- Как найти вычитаемое
Значение терминов
В отличие от многих научных терминов, имеющих греческое, латинское или арабское происхождение, в данном случае используются слова с русскими корнями.
Так что понять их значение несложно, а значит легко и запомнить, что каким термином обозначается.
Термины
Что такое разность чисел в математике
Если присмотреться к самому названию, становится заметно, что оно имеет отношение к словам «разный», «разница». Из этого можно заключить, что имеется в виду установленная разница между количествами.
Это интересно! Как раскрыть модуль действительного числа и что это такое
Данное понятие в математике означает:
- разницу между двумя числами;
- это показатель того, насколько одно количество больше или меньше другого;
- это результат, полученный при выполнении вычитания — такое определение предлагает школьная программа.
Обратите внимание! Если количества равны друг другу, то между ними нет разницы. Значит разность их равняется нулю.
Что такое уменьшаемое и вычитаемое
Как следует из названия, уменьшаемое – это то, что делают меньше.
А сделать количество меньшим можно, отняв от него часть. Таким образом, уменьшаемым называется число, от которого отнимают часть.
Вычитаемым, соответственно, называется то число, которое от него отнимают.
| Уменьшаемое | Вычитаемое | Разность | ||
| 18 | — | 11 | = | 7 |
| 14 | — | 5 | = | 9 |
| 26 | — | 22 | = | 4 |
Правила нахождения неизвестного элемента
Разобравшись в терминах, несложно установить, по какому правилу находится каждый из элементов вычитания.
Поскольку разность – результат данного арифметического действия, то ее и находят с помощью этого действия, никаких других правил тут не требуется.
Но они есть на случай, если неизвестен другой член математического выражения.
Это интересно! Уроки математики: умножение на ноль — главное правило
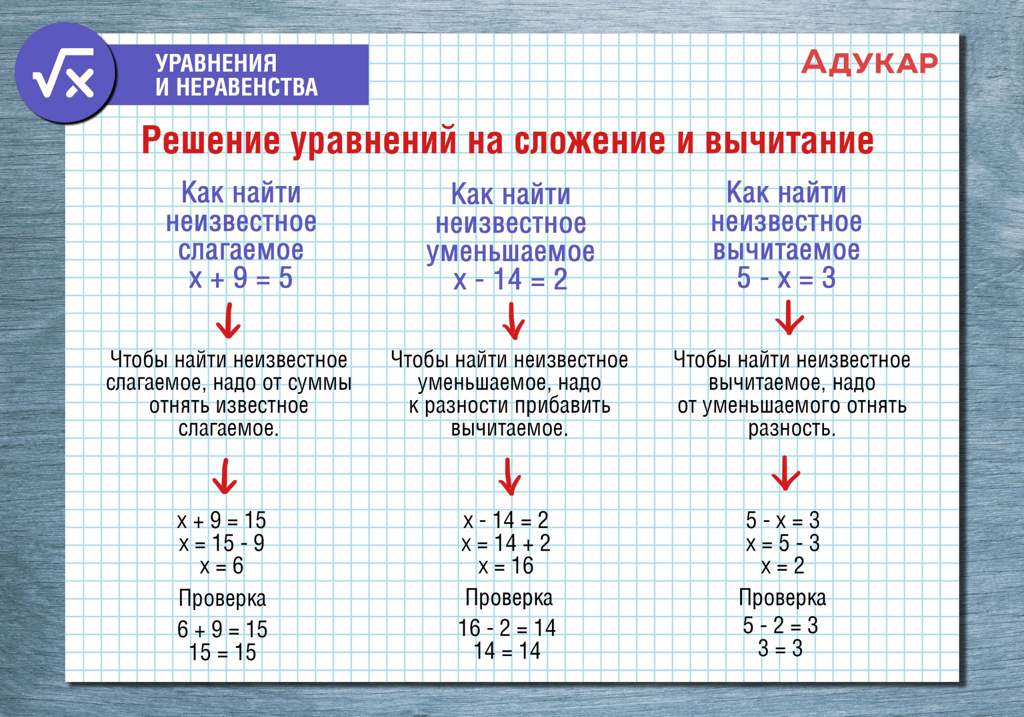
Как найти уменьшаемое
Данным термином, как было выяснено, называют количество, из которого вычли часть. Но если одну вычли, а другая осталась в итоге, следовательно, из этих двух частей число и состоит. Получается, что найти неизвестное уменьшаемое можно, сложив два известных элемента.
Итак, в данном случае, чтобы найти неизвестное, следует выполнить сложение вычитаемого и разности:
| ? | – | 11 | = | 7 |
Искомое находится путем сложения известных элементов:
| 7 | + | 11 | = | 18 |
Так же и во всех подобных случаях:
| ? | – | 5 | = | 9 |
| 9 | + | 5 | = | 14 |
| ? | – | 22 | = | 4 |
| 4 | + | 22 | = | 26 |
Как найти вычитаемое
Если целое состоит из двух частей (в данном случае количеств), то при вычитании одной из них в результате получится вторая.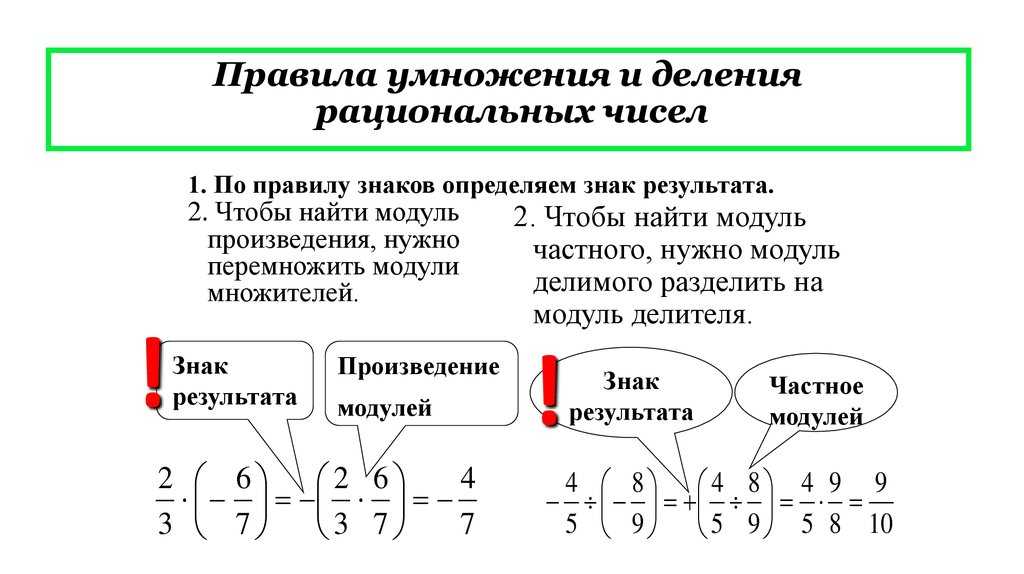
Таким образом, чтобы найти неизвестное вычитаемое, достаточно вместо него вычесть из целого разность.
| 18 | – | ? | = | 7 |
Из примера видно, что от 18 отняли некоторую величину, и осталось 7. Чтобы найти эту величину, надо от 18 отнять 7.
| 18 | – | 7 | = | 11 |
По тому же правилу решаются и другие подобные примеры.
| 14 | – | ? | = | 9 |
| 14 | – | 9 | = | 5 |
| 26 | – | ? | = | 4 |
| 26 | – | 4 | = | 22 |
Таким образом, зная точное значение названий, можно легко догадаться, по какому правилу следует искать каждый неизвестный элемент.
Это интересно! Как разложить на множители квадратный трехчлен: формула
Полезное видео: как найти неизвестное уменьшаемое.
Четыре основных арифметических действия – та база, на которой основываются все математические вычисления, от простых до самых сложных. Конечно, в наше время, когда люди стремятся перепоручить технике все вплоть до мыслительного процесса, привычнее и быстрее производить вычисления с помощью калькулятора. Но любое умение увеличивает независимость человека – от технических средств, от окружающих. Не обязательно делать математику своей специальностью, но обладать хотя бы минимальными знаниями и умениями – значит иметь дополнительную опору для собственной уверенности.
Вычитаемое уменьшаемое разность – правило: что это такое и как их найти
Существуют четыре основных арифметических действия: сложение, вычитание, умножение и деление.
Они – основа математики, с их помощью производятся все остальные, более сложные вычисления. Сложение и вычитание – простейшие из них и взаимно противоположны. Но с терминами, используемыми при сложении, мы чаще сталкиваемся в жизни.
Говорим о «сложении усилий» при старании совместно получить нужный результат, о «слагаемых достигнутого успеха» и т.п. Названия же, связанные с вычитанием, остаются в пределах математики, редко появляясь в повседневной речи. Поэтому менее привычны слова вычитаемое, уменьшаемое, разность. Правило нахождения каждого из данных компонентов возможно применить лишь при понимании значения этих названий.
Содержание
Значение терминов
В отличие от многих научных терминов, имеющих греческое, латинское или арабское происхождение, в данном случае используются слова с русскими корнями. Так что понять их значение несложно, а значит легко и запомнить, что каким термином обозначается.
Термины
Что такое разность чисел в математике
Если присмотреться к самому названию, становится заметно, что оно имеет отношение к словам «разный», «разница».
Из этого можно заключить, что имеется в виду установленная разница между количествами.
Это интересно! Как раскрыть модуль действительного числа и что это такое
Данное понятие в математике означает:
- разницу между двумя числами,
- это показатель того, насколько одно количество больше или меньше другого,
- это результат, полученный при выполнении вычитания такое определение предлагает школьная программа.
Обратите внимание! Если количества равны друг другу, то между ними нет разницы. Значит разность их равняется нулю.
Что такое уменьшаемое и вычитаемое
Как следует из названия, уменьшаемое – это то, что делают меньше. А сделать количество меньшим можно, отняв от него часть. Таким образом, уменьшаемым называется число, от которого отнимают часть.
Вычитаемым, соответственно, называется то число, которое от него отнимают.
| Уменьшаемое | Вычитаемое | Разность | ||
| 18 | 11 | = | 7 | |
| 14 | 5 | = | 9 | |
| 26 | 22 | = | 4 |
Полезное видео: уменьшаемое, вычитаемое, разность
youtube.com/embed/FXYHF-Tqwt8″ frameborder=»0″ allowfullscreen=»allowfullscreen»> Правила нахождения неизвестного элемента
Разобравшись в терминах, несложно установить, по какому правилу находится каждый из элементов вычитания.
Поскольку разность – результат данного арифметического действия, то ее и находят с помощью этого действия, никаких других правил тут не требуется. Но они есть на случай, если неизвестен другой член математического выражения.
Это интересно! Уроки математики: умножение на ноль главное правило
Как найти уменьшаемое
Данным термином, как было выяснено, называют количество, из которого вычли часть. Но если одну вычли, а другая осталась в итоге, следовательно, из этих двух частей число и состоит. Получается, что найти неизвестное уменьшаемое можно, сложив два известных элемента.
Итак, в данном случае, чтобы найти неизвестное, следует выполнить сложение вычитаемого и разности:
| ? | – | 11 | = | 7 |
Искомое находится путем сложения известных элементов:
| 7 | + | 11 | = | 18 |
Так же и во всех подобных случаях:
| ? | – | 5 | = | 9 |
| 9 | + | 5 | = | 14 |
| ? | – | 22 | = | 4 |
| 4 | + | 22 | = | 26 |
Как найти вычитаемое
Если целое состоит из двух частей (в данном случае количеств), то при вычитании одной из них в результате получится вторая.
Таким образом, чтобы найти неизвестное вычитаемое, достаточно вместо него вычесть из целого разность.
| 18 | – | ? | = | 7 |
Из примера видно, что от 18 отняли некоторую величину, и осталось 7. Чтобы найти эту величину, надо от 18 отнять 7.
| 18 | – | 7 | = | 11 |
По тому же правилу решаются и другие подобные примеры.
| 14 | – | ? | = | 9 |
| 14 | – | 9 | = | 5 |
| 26 | – | ? | = | 4 |
| 26 | – | 4 | = | 22 |
Таким образом, зная точное значение названий, можно легко догадаться, по какому правилу следует искать каждый неизвестный элемент.
Это интересно! Как разложить на множители квадратный трехчлен: формула
Полезное видео: как найти неизвестное уменьшаемое
Вывод
Четыре основных арифметических действия – та база, на которой основываются все математические вычисления, от простых до самых сложных. Конечно, в наше время, когда люди стремятся перепоручить технике все вплоть до мыслительного процесса, привычнее и быстрее производить вычисления с помощью калькулятора. Но любое умение увеличивает независимость человека – от технических средств, от окружающих. Не обязательно делать математику своей специальностью, но обладать хотя бы минимальными знаниями и умениями – значит иметь дополнительную опору для собственной уверенности.
В чем разница между делением и вычитанием?
отдел | вычитание | С арифметической точки зрения разница между делением и вычитанием заключается в том, что деление — это вычисление, включающее этот процесс, а вычитание — ( исчисляемое ) вычисление, включающее вычитание. Как существительные разница междуделением и вычитанием— это деление — это действие или процесс деления чего-либо, а вычитание — это ( неисчисляемое ) процесс вычитания одного числа из другого.
|
divisio ) ниже царства и выше класса, особенно используемый для растений]] или [[гриб, грибы, также (особенно для животных) называемый типом; таксон в этом ранге
также * разделение
* сложение, суммирование: (сложение) + (сложение) = (слагаемое) × (слагаемое) = (сумма, итого)
* вычитание: (уменьшаемое) ? (вычитаемое) = (разность)
* умножение: (множитель) × (множимое) = (множитель) × (множитель) = (произведение)
* деление: (делимое) ÷ (делитель) = (частное), остаток остается, если делитель не делит делимое
* знаменатель
* доля
* числитель
—- Повторное вычитание — Деление повторным вычитанием, примеры
Повторное вычитание — это процесс вычитания числа из большого числа до тех пор, пока конечный результат не будет равен нулю.
Этот процесс обычно наблюдается и используется при делении чисел, и это хороший способ ввести деление в младшие классы. Давайте узнаем больше о многократном вычитании, способах деления с помощью многократного вычитания и решим несколько примеров, чтобы лучше понять концепцию.
| 1. | Определение повторного вычитания |
| 2. | Методы многократного вычитания |
| 3. | Деление методом многократного вычитания |
| 4. | Часто задаваемые вопросы о повторном вычитании |
Определение повторного вычитания
Повторное вычитание определяется как процесс вычитания одного и того же числа из большого числа до тех пор, пока конечный результат или остаток не станет равным нулю или меньше вычитаемого числа. Этот процесс также называется делением. Другими словами, когда одно и то же число вычитается из другого числа до тех пор, пока остаток не станет равным нулю или пока он не станет меньше фактического числа, называется повторным вычитанием, и этот процесс также может быть выражен в форме деления.
Например, 25 — 5 = 20, 20 — 5 = 15, 15 — 5 = 10, 10 — 5 = 5, 5 — 5 = 0. Это означает, что число вычитается 5 раз и может быть записано в форме деления как 25. ÷ 5 = 5,
Деление Определение
Деление — это одна из основных арифметических операций в математике, при которой большее число разбивается на меньшие группы с одинаковым количеством элементов. Этот процесс также называется повторным вычитанием. Деление используется при умножении, длинном делении, коротком делении или многократном вычитании. Есть четыре части деления: делимое, делитель, частное и остаток.
Методы многократного вычитания
Повторное вычитание может быть полезным методом обучения младших школьников процессу простого деления. Есть два простых метода использования этого процесса, а именно:
1. Повторное вычитание можно рассматривать как процесс перехода назад от фактического числа, пока мы не получим требуемый ответ. И количество раз, когда одно и то же число вычитается, является остатком, когда оно используется в форме деления.
2. Повторное вычитание при делении также используется, когда остаток меньше фактического числа и не обязательно должен быть равен нулю. Например, 16 — 3 = 13, 13 — 3 = 10, 10 — 3 = 7, 7 — 3 = 4, 4 -3 = 1. Здесь остаток или конечный результат равен 1. Поскольку он меньше 3, мы можем остановить повторное вычитание.
Деление методом многократного вычитания
Повторное вычитание можно использовать для решения задач на деление так же, как многократное сложение используется для решения задач на умножение. При делении любых чисел учитываются четыре части деления: делимое, делитель, частное и остаток. Шаги, используемые при делении повторным вычитанием:
- Определите делимое и делитель.
Делимое — это число, которое делится на делитель, а делитель — это число, на которое делится делимое. - Начать вычитание делителя из делимого.
- После получения разности снова вычтите делитель из этого числа.
- Повторяйте процесс вычитания, пока не получите число, меньшее делителя, или ноль.
- Число завершений процесса вычитания называется частным.
- Число, оставшееся после вычитания, называется остатком.
Делимое — это число, которое делится на делитель, а делитель — это число, на которое делится делимое.Давайте посмотрим на пример, чтобы лучше понять это.
Пример: Разделите 120 ÷ 15 методом многократного вычитания.
Решение:
Дивиденд = 120
Делитель = 15
120 – 15 = 105
105 – 15 = 90
90 – 15 = 75
75 – 15 = 60
60 – 15 = 45
45 – 15 = 30
30 – 15 = 15
15 – 15 = 0
Здесь 120 вычитается 8 раз из 15 с остатком 0. Следовательно, 120 ÷ 15 = 8, 8 — это частное.
Связанные темы
Ниже перечислены некоторые темы, связанные с повторным вычитанием, взгляните!
- Умножение
- Сложение и вычитание
- Вычитание с перегруппировкой
- Двоичное вычитание
- Формула остатка делителя дивиденда
Часто задаваемые вопросы о повторном вычитании
Как называется повторное вычитание?
Повторное вычитание также называется делением. Это метод, который вычитает все число из группы.
Что такое повторное вычитание с примером?
Повторное вычитание — это процесс непрерывного вычитания числа из большого числа до тех пор, пока остаток не станет равным нулю или меньше фактического числа. Например, 20 — 4 = 16, 16 — 4 = 12, 12 — 4 = 8, 8 — 4 = 4, 4 — 4 = 0. Следовательно, 20 вычитается 5 раз, а остаток равен нулю.
Как сделать повторное вычитание?
Повторное вычитание выполняется путем непрерывного вычитания делителя из делимого до тех пор, пока остаток не станет равным нулю или меньше делимого.
Этот процесс также можно использовать при делении чисел, и количество вычитаний одного и того же числа является остатком, когда оно используется в форме деления. Например, 32 — 4 = 28, 28 — 4 = 24, 24 — 4 = 20, 20 — 4 = 16, 16 — 4 = 12, 12 — 4 = 8, 8 — 4 = 4, 4 — 4 = 0. Здесь 32 вычитается 8 раз из 4 с остатком 0. Следовательно, в форме деления это записывается как 32 ÷ 4 = 8.
Почему важно многократное вычитание?
Повторное вычитание важно при обучении младших школьников методу деления. Он действует как введение в деление, которое можно понять более простым и легким способом. Повторное вычитание используется для решения задач деления путем вычитания делителя из делимого до тех пор, пока остаток не станет меньше делителя.
Как найти квадратный корень повторным вычитанием?
Квадратный корень числа — это число, которое при умножении само на себя дает исходное число как произведение. Мы также можем сказать, что сумма первых n нечетных натуральных чисел равна n 2 .