Точки разрыва функции первого и второго рода
Функция f(x) называется непрерывной в точке х = а если:
1) она определена в этой точке;
2) существует предел функции в этой точке
3) значение предела равно значению функции в точке х = а, т.е.
Если одно из условий нарушается то функция называется разрывной в точке х = а, а сама точка х = а называется точкой разрыва. Все элементарные функции являются непрерывными на интервалах определенности.
Классификация точек разрыва
Точка х0 называется точкой разрыва первого рода функции у = f(x) если существуют конечные односторонние пределы справа
и слева
.
Если, кроме этого, выполняется хотя бы одно из условий
то функция в точке х = а имеет неустранимый разрыв первого рода.
Если пределы равны, однако функция не существует
то имеем устранимый разрыв первого рода.
Точка х0 называется точкой разрыва второго рода функции у= f(x) если граница справа или слева не существует или бесконечна.
Скачком функции в точке разрыва х = х0 называется разность ее односторонних границ
если они разные и не равны бесконечности.
При нахождении точек разрыва функции можно руководствоваться следующими правилами:
1) элементарная функция может иметь разрыв только в отдельных точках, но не может быть разрывной на определенном интервале.
2) элементарная функция может иметь разрыв в точке где она не определена при условии, что она будет определена хотя бы с одной стороны от этой точки.
3) Неэлементарные функция может иметь разрывы как в точках где она определена, так и в тех где она определена.
Например, если функция задана несколькими различными аналитическими выражениями (формулами) для различных интервалов, то на границе стыка может быть разрывной.
Рассмотрим несколько задач по данной теме.
Задача 1.
Найти точки разрыва функции
а)
Решение:
Функция определена во всех точках кроме тех где знаменатель обращается в нуль x = 1, x = 1. Область определения функции следующая
Найдем односторонние пределы в точках разрыва
При нахождении односторонних границ подобного вида достаточно убедиться в знаке функции и в том, что знаменатель стремится к нулю. В результате получим границу равную бесконечности или минус бесконечности.
Поскольку в точках x = 1, x = -1 функция имеет бесконечные односторонние пределы, то аргументы являются точками разрыва второго рода. График функции приведен на рисунке ниже
——————————————————-
б)
Решение:
Задача достаточно простая. В первую очередь находим нули знаменателя
Таким образом функция определена на всей действительной оси за исключением точек , которые являются точками разрыва. Вычислим односторонние пределы справа и слева
Пределы бесконечны поэтому, по определению, имеем точки разрыва второго рода.
Из графиков приведенных функций видим что для ряда из них отыскания точек разрыва сводится до нахождения вертикальных асимптот. Но бывают функции которые и без вертикальных асимптот имеют разрывы первого или второго рода.
——————————————————-
в)
Решение:
Заданная функция непрерывна на всей числовой оси кроме точки x = -3. Вычислим односторонние границы в этой точке
Они различаются по значениям, однако есть конечными. Итак точка x = -3 является неустранимой точкой разрыва І рода.
——————————————————-
Задача 2.
Най
Точки разрыва функции (определения, классификация, примеры)
Определения и классификация точек разрыва функции
Определение точки разрыва функции
Конечная точка x0 называется точкой разрыва функции f(x), если функция определена на некоторой проколотой окрестности точки x0, но не является непрерывной в этой точке.
То есть, в точке разрыва, функция либо не определена, либо определена, но хотя бы один односторонний предел в этой точке или не существует, или не равен значению f(x0) функции в точке x0. См. «Определение непрерывности функции в точке».
Определение точки разрыва 1-го рода
Точка называется точкой разрыва первого рода, если является точкой разрыва и существуют конечные односторонние пределы слева и справа :
.
Определение скачка функции
Скачком Δ функции в точке называется разность пределов справа и слева
.
Определение точки устранимого разрыва
Точка называется точкой устранимого разрыва, если существует предел
,
но функция в точке или не определена, или не равна предельному значению: .
Таким образом, точка устранимого разрыва – это точка разрыва первого рода, в которой скачек функции равен нулю.
Определение точки разрыва 2-го рода
Точка разрыва называется точкой разрыва второго рода, если она не является точкой разрыва 1-го рода. То есть если не существует, хотя бы одного одностороннего предела, или хотя бы один односторонний предел в точке равен бесконечности.
Исследование функций на непрерывность
При исследовании функций на непрерывность мы используем следующие факты.
- Элементарные функции и обратные к ним непрерывны на своей области определения. К ним относятся следующие функции:
, а также постоянная и обратные к ним функции. См. «Справочник по элементарным функциям». - Сумма, разность и произведение непрерывных, на некотором множестве функций, является непрерывной, функцией на этом множестве.
Частное двух непрерывных, на некотором множестве функций, является непрерывной, функцией на этом множестве, за исключением точек, в которых знаменатель дроби обращается в нуль. См. «Арифметические свойства непрерывных функций» - Сложная функция непрерывна в точке , если функция непрерывна в точке , а функция непрерывна в точке . См. «Предел и непрерывность сложной функции»
Примеры
Пример 1
Задана функция и два значения аргумента и . Требуется: 1) установить, является ли данная функция непрерывной или разрывной для каждого из данных значений аргумента; 2) в случае разрыва функции найти ее пределы в точке разрыва слева и справа, установить вид разрыва; 3) сделать схематический чертеж.
.
Решение
Заданная функция является сложной. Ее можно рассматривать как композицию двух функций:
, . Тогда
.
Рассмотрим функцию . Она составлена из функции и постоянных с помощью арифметических операций сложения и деления. Функция является элементарной – степенной функцией с показателем степени 1. Она определена и непрерывна для всех значений переменной . Поэтому функция определена и непрерывна для всех , кроме точек, в которых знаменатель дроби обращается в нуль. Приравниваем знаменатель к нулю и решаем уравнение:
.
Получаем единственный корень .
Итак, функция определена и непрерывна для всех , кроме точки .
Рассмотрим функцию . Это показательная функция с положительным основанием степени. Она определена и непрерывна для всех значений переменной .
Поэтому заданная функция определена и непрерывна для всех значений переменной , кроме точки .
Таким образом, в точке , заданная функция является непрерывной.

График функции y = 41/(x+2).
Рассмотрим точку . В этой точке функция не определена. Поэтому она не является непрерывной. Установим род разрыва. Для этого находим односторонние пределы.
Используя связь между бесконечно большими и бесконечно малыми функциями, для предела слева имеем:
при ,
,
,
.
Здесь мы использовали следующие общепринятые обозначения:
.
Также мы использовали свойство показательной функции с основанием :
.
Аналогично, для предела справа имеем:
при ,
,
,
.
Поскольку один из односторонних пределов равен бесконечности, то в точке разрыв второго рода.
Ответ
В точке функция непрерывна.
В точке разрыв второго рода,
.
Пример 2
Задана функция . Найти точки разрыва функции, если они существуют. Указать род разрыва и скачек функции, если есть. Сделать чертеж.
.
Решение

График заданной функции.
Функция является степенной функцией с целым показателем степени, равным 1. Такую функцию также называют линейной. Она определена и непрерывна для всех значений переменной .
В входят еще две функции: и . Они составлены из функции и постоянных с помощью арифметических операций сложения и умножения:
, .
Поэтому они также непрерывны для всех .
Поскольку функции, входящие в состав непрерывны для всех , то может иметь точки разрыва только в точках склейки ее составляющих. Это точки и . Исследуем на непрерывность в этих точках. Для этого найдем односторонние пределы.
Рассмотрим точку . Чтобы найти левый предел функции в этой точке, мы должны использовать значения этой функции в любой левой проколотой окрестности точки . Возьмем окрестность . На ней . Тогда предел слева:
.
Здесь мы использовали тот факт, что функция является непрерывной в точке (как и в любой другой точке). Поэтому ее левый (как и правый) предел равен значению функции в этой точке.
Найдем правый предел в точке . Для этого мы должны использовать значения функции в любой правой проколотой окрестности этой точки. Возьмем окрестность . На ней . Тогда предел справа:
.
Здесь мы также воспользовались непрерывностью функции .
Поскольку, в точке , предел слева не равен пределу справа, то в ней функция не является непрерывной – это точка разрыва. Поскольку односторонние пределы конечны, то это точка разрыва первого рода. Скачек функции:
.
Теперь рассмотрим точку . Тем же способом вычисляем односторонние пределы:
;
.
Поскольку функция определена в точке и левый предел равен правому, то функция непрерывна в этой точке.
Ответ
Функция имеет разрыв первого рода в точке . Скачек функции в ней: . В остальных точках функция непрерывна.
Пример 3
Определить точки разрыва функции и исследовать характер этих точек, если
.
Решение
Воспользуемся тем, что линейная функция определена и непрерывна для всех . Заданная функция составлена из линейной функции и постоянных с помощью арифметических операций сложения, вычитания, умножения и деления:
.
Поэтому она определена и непрерывна для всех , за исключением точек, в которых знаменатель дроби обращается в нуль.
Найдем эти точки. Приравниваем знаменатель к нулю и решаем квадратное уравнение:
;
;
; .
Тогда
.
Используем формулу:
.
С ее помощью, разложим числитель на множители:
.
Тогда заданная функция примет вид:
(П1) .
Она определена и непрерывна для всех , кроме точек и . Поэтому точки и являются точками разрыва функции.
Разделим числитель и знаменатель дроби в (П1) на :
(П2) .
Такую операцию мы можем проделать, если . Таким образом,
при .
То есть функции и отличаются только в одной точке: определена при , а в этой точке не определена.
Чтобы определить род точек разрыва, нам нужно найти односторонние пределы функции в точках и . Для их вычисления мы воспользуемся тем, что если значения функции изменить, или сделать неопределенными в конечном числе точек, то это не окажет ни какого влияние на величину или существование предела в произвольной точке (см. «Влияние значений функции в конечном числе точек на величину предела»). То есть пределы функции в любых точках равны пределам функции .
Рассмотрим точку . Знаменатель дроби в функции , при в нуль не обращается. Поэтому она определена и непрерывна при . Отсюда следует, что существует предел при и он равен значению функции в этой точке:
.
Поэтому точка является точкой устранимого разрыва первого рода.
Рассмотрим точку . Используя связь бесконечно малых и бесконечно больших функций, имеем:
;
.
Поскольку пределы бесконечные, то в этой точке разрыв второго рода.
Ответ
Функция имеет точку устранимого разрыва первого рода при , и точку разрыва второго рода при .
Использованная литература:
О.И. Бесов. Лекции по математическому анализу. Часть 1. Москва, 2004.
Автор: Олег Одинцов. Опубликовано:
Точки разрыва функции, с примерами
ОПРЕДЕЛЕНИЕ Если в точке функция не является непрерывной, то эта точка называется точкой разрыва функции.Классификация точек разрыва функции
Точка называется точкой устранимого разрыва функции , если в этой точке односторонние пределы конечны и равны между собой, но не равны значению функции в этой точке; или функция в точке не определена (рис. 1).
Рис. 1
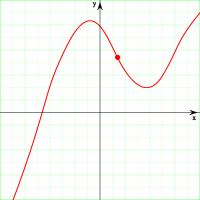
Точка называется точкой разрыва первого рода функции , если в этой точке односторонние пределы конечны и не равны между собой (рис. 2).
Рис. 2
Модуль разности значений односторонних пределов называется скачком функции.
Пример. На рисунке 2 скачок функции равен
Точка называется точкой разрыва второго рода функции , если в этой точке, по крайней мере, один из односторонних пределов равен бесконечности или не существует (рис. 3).
Рис. 3
Примеры решения задач
ПРИМЕР| Задание | Исследовать функцию на непрерывность и классифицировать точки разрыва.
|
| Решение | Функция является непрерывной как отношение двух непрерывных функций (многочленов), разрыв может быть лишь в точках, в которых знаменатель обращается в нуль, то есть
Итак, если разрыв есть, то он может быть лишь в точках . Исследуем функцию на непрерывность в этих точках. Для этого найдем односторонние пределы:
аналогично
Поскольку односторонние пределы бесконечны, то в точке функция имеет разрыв второго рода. Аналогично для второй точки :
то есть и точка – точка разрыва другого роду. |
| Ответ | Функция терпит разрыв второго рода в точках |
| Понравился сайт? Расскажи друзьям! | |||
Разрыв первого рода — это… Что такое Разрыв первого рода?
Непреры́вное отображе́ние или непрерывная функция — это такое отображение, у которого небольшие изменения аргумента приводят к небольшим изменениям значения отображения.
Это понятие определятся немного по-разному в различных разделах математики; наиболее общее определение используется в общей топологии.
Определения
Непрерывная числовая функция
Непрерывное отображение из Rm в Rn
Обобщая одномерный случай, функция 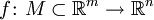 называется непрерывной в точке
называется непрерывной в точке  если
если 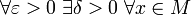
где
 — евклидова норма в
— евклидова норма в 
Непрерывное отображение метрических пространств
В предыдущем определении наличие операции вычитания, точнее линейной структуры, в евклидовых пространствах не играет принципиальной роли. Достаточно лишь иметь возможность измерять расстояния. Множества, на которых указан способ измерять расстояния, называются метрическими пространствами. Отображение 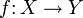 метрического пространства (X,ρX) в метрическое пространство (Y,ρY) называется непрерывным в точке a, если
метрического пространства (X,ρX) в метрическое пространство (Y,ρY) называется непрерывным в точке a, если 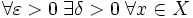
Непрерывное отображение топологических пространств
В предыдущих определениях важно не наличие точной меры расстояния, а лишь понятия близости. Непрерывное отображение переводит близкие точки в близкие. Множество, в котором указан некоторый набор подмножеств 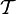 , позволяющий говорить о близких точках, называется топологическим пространством. Отображение
, позволяющий говорить о близких точках, называется топологическим пространством. Отображение 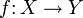 топологического пространства
топологического пространства 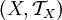 в топологическое пространство
в топологическое пространство 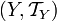 называется непрерывным, если прообраз любого открытого множества открыт:
называется непрерывным, если прообраз любого открытого множества открыт:
Связанные определения
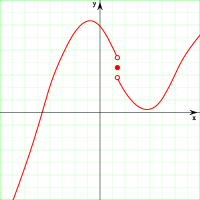
Если функция не является непрерывной в точке a, то говорят, что она в ней разры́вна и пишут 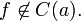 Согласно замечанию выше функция может быть разрывной только в предельной точке области определения, и справедливо одно из двух:
Согласно замечанию выше функция может быть разрывной только в предельной точке области определения, и справедливо одно из двух:
- Либо предел
 не существует;
не существует; - Либо он существует, но

Пусть существует 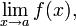 но
но 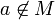 или
или 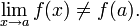 Тогда a называется то́чкой устрани́мого разры́ва. Положив
Тогда a называется то́чкой устрани́мого разры́ва. Положив  можно добиться непрерывности функции в этой точке. Такое изменение значения функции в точке, превращающее функцию в непрерывную в этой точке, называется доопределением по непрерывности.
можно добиться непрерывности функции в этой точке. Такое изменение значения функции в точке, превращающее функцию в непрерывную в этой точке, называется доопределением по непрерывности.
Пусть не сущестует двусторонний предел 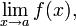 но существуют конечные (и различные) односторонние пределы
но существуют конечные (и различные) односторонние пределы 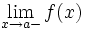 и
и 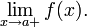 Тогда
Тогда 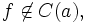 и a называется то́чкой разры́ва пе́рвого ро́да.
и a называется то́чкой разры́ва пе́рвого ро́да.
Если 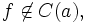 и a не является точкой устранимого разрыва или разрыва первого рода, то есть хотя бы один односторонний предел не существует или бесконечен, то она называется то́чкой разры́ва второ́го ро́да.
и a не является точкой устранимого разрыва или разрыва первого рода, то есть хотя бы один односторонний предел не существует или бесконечен, то она называется то́чкой разры́ва второ́го ро́да.
Свойства
- В предельной точке области определения непрерывность функции эквивалентна существованию предела, равного значению функции в точке:
Вещественнозначаные функции
- Функция сохраняет знак в окрестности точки непрерывности. Пусть
 Тогда существует окрестность U(a) такая, что
Тогда существует окрестность U(a) такая, что
Примеры
непрерывна в любой точке 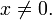 Точка x = 0 является точкой устранимого разрыва, ибо
Точка x = 0 является точкой устранимого разрыва, ибо
непрерывна в любом 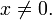
непрерывна в любом 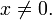
Вариации и бобщения
Односторнняя непрерывность
- Пусть дана функция
 и
и  Тогда говорят, что f непреры́вна спра́ва в точке a, если
Тогда говорят, что f непреры́вна спра́ва в точке a, если 
- Говорят, что f непреры́вна сле́ва в точке a, если

Замечания
- Функция непрерывна тогда и только тогда, когда она непрерывна одновременно справа и слева.
- Функция непрерывна справа в предельной точке области определения тогда и только тогда, когда существует правосторонний предел
- Функция непрерывна слева в предельной точке области определения тогда и только тогда, когда существует левосторонний предел
- Все базовые свойства непрерывных функций переносятся на односторонне непрерывные функции.
Примеры
непрерывна справа (но не слева) в точке x = 0. Во всех других точках она непрерывна.
См. также
Wikimedia Foundation. 2010.
определение понятия и подробное решение примера
Нахождение точек разрыва функции является одним из обязательных моментов исследования на непрерывность. Для кого-то это может прозвучать непонятно, а для остальных будет слишком банально.
Но и тем, и другим не стоит делать поспешные выводы: материал этой темы действительно предельно прост, но вместе с тем для успешного решения практических задач потребуется осмыслить и запомнить несколько технических приемов и нюансов.
Как минимум необходимо понимать, что за «зверь» кроется под понятием предела функции. И конечно же, нужно уметь их решать. Не менее полезным станет понимание геометрического смысла, дополненное графиком — большинство задач подобного характера требуют построения чертежа после решения.

Определение точки разрыва
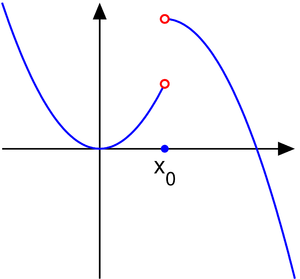
Как уже упоминалось, их поиск напрямую связан с темой непрерывности. Если говорить простым языком, то это не что иное, как координаты графика функции, в которых точки не соединяются между собой. Образуются «рваные области», которые и называют местом разрыва. Вообще, чтобы понять смысл, достаточно всего лишь взглянуть на рисунок:
Он более чем очевидно иллюстрирует определение понятия. Если функция прерывается в X0, то непрерывность в этом месте нарушена одним из двух возможных способов:
- первый род;
- второй род.
Задачи похожего типа, где необходимо находить точки разрыва, могут выступать не только, как один из этапов полного исследования на непрерывность, но и в качестве самостоятельных заданий. Чтобы определить их вид, потребуется отыскать предел для найденных значений. Поэтому, если вы еще не умеете их решать, самое время ненадолго отвлечься, чтобы изучить базовые основы.
К счастью, на практике это не так сложно — самый трудный этап заключается в приведении примера к одному из табличных. Остальные моменты легко запомнить. Не стоит забывать и о большом количестве сервисов, которые в несколько кликов выдадут значение предела любой сложности онлайн.
Классификация точек разрыва.
Точки разрыва первого и второго рода
Если функция не определена, но односторонние пределы имеют конечное значение, то ее относят к случаю первого рода. Который, в свою очередь, может иметь характеристику устранимого или конечного:
- Точки устранимого разрыва функции. Значения вычислений обоих пределов для них равны. Но также имеется возможность «исправить ситуацию»: нахождения между двумя координатами такой, левый и правый пределы которой будут одинаковы, а сама она — соединит «порванный» участок, сделав график непрерывным.
-
- Точки разрыва второго рода отличаются тем, что вычисляемые пределы не просто различны по значению, но результат хотя бы одного из них обязательно должен быть равен бесконечности или несуществующему числу.

Как найти точки разрыва функции
Если в условиях задачи не были даны координаты проверяемого отрезка, то процесс решения делится на несколько этапов. Для начала нужно найти область определенных значений, с которой в дальнейшем пойдет работа. После это вычисляются односторонние пределы функции. Полученные результаты необходимо будет сравнить, чтобы однозначно определить род и характеристику разрыва.
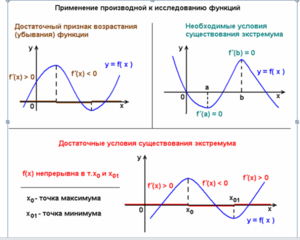
Рассмотрим более подробно каждый из этих моментов на примере нахождения нужных нам точек у конкретного примера f (y)=(y² — 25)/(y — 5):
- Областью определения называют множество значений, в котором существует функция. Здесь не нужны никакие сложные вычисления, достаточно взять лишь знаменатель. Если y=5, то он будет (5−5)=0 и, как всем известно, делить на него нельзя. Таким образом, получаем область допустимых y ∈ (-∞; 5) ∪ (5; +∞) и предполагаем, что наша y = 5 является точкой разрыва.
- Вычисление односторонних пределов. Это самая сложная для учеников часть, т. к. пределы не всегда бывают удобными для вычисления, да не все на них «собаку съели». Но в этом случае функцию можно значительно упростить еще до начала вычисления: f (y) = (y ²-25)/(y — 5) = ((y-5)(y+5)) /(y — 5) = y+5. Никогда не пренебрегайте такой возможностью, если она есть. Заметим, что новая функция непрерывна при любом численном значении, т. ч. по всем математическим правилам пределы будут равны: lim (y + 5) = 5 + 5 = 10.
- Проверяя совпадение результатов, мы выяснили, что левый и правый предел функции в точке y=5 одинаковые. Но вместе с тем функция f(y) не может быть определена в этой координате, иначе ее знаменатель обращается в ноль, что невозможно по условиям. Следовательно, она действительно является разрывом, а именно: устранимым и первого рода.
Видео
Из этого видео вы узнаете, как исследовать непрерывность функции.
Точки разрыва первого рода — Студопедия
Пусть дана функция 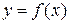 ,
, 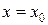 — точка разрыва 1 рода функции
— точка разрыва 1 рода функции 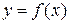 ,
,
если в точке 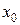 существуют конечные односторонние пределы функции справа и слева т.е.
существуют конечные односторонние пределы функции справа и слева т.е. 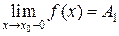 и
и 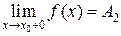 , при этом:
, при этом:
- если
 , то точка называется точкой устранимого разрыва 1 рода
, то точка называется точкой устранимого разрыва 1 рода - если
 , то точка называется точкой конечного разрыва (или неустранимого разрыва) 1 рода. Величину
, то точка называется точкой конечного разрыва (или неустранимого разрыва) 1 рода. Величину  называют скачком функции в точке разрыва первого рода.
называют скачком функции в точке разрыва первого рода.
Пример 1: Возьмём 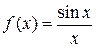 . Все точки области определения
. Все точки области определения 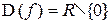 этой элементарной функции являются точками непрерывности. Поскольку
этой элементарной функции являются точками непрерывности. Поскольку 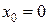 не входит в область определения функции
не входит в область определения функции 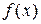 , то 0 — точка разрыва функции
, то 0 — точка разрыва функции 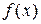 . Мы можем доопределить эту функцию при
. Мы можем доопределить эту функцию при 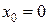 , положив
, положив 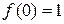 , тогда функция становится непрерывной в точке 0. Значит,
, тогда функция становится непрерывной в точке 0. Значит, 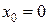 — точка разрыва первого рода для функции.
— точка разрыва первого рода для функции.
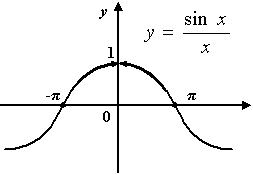
Рис. Устранимый разрыв функции 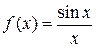
Пример 2: Рассмотрим функцию 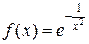 . Её область определения
. Её область определения 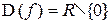 состоит из точек непрерывности, так как это элементарная функция. Точка
состоит из точек непрерывности, так как это элементарная функция. Точка 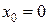 , в которой функция не определена, это точка разрыва функции. Поскольку
, в которой функция не определена, это точка разрыва функции. Поскольку 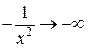 при
при 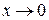 , то
, то 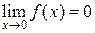 . Это означает, что при
. Это означает, что при 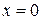 функция имеет устранимый разрыв и становится непрерывной на всей вещественной оси, если положить
функция имеет устранимый разрыв и становится непрерывной на всей вещественной оси, если положить 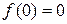 .
.
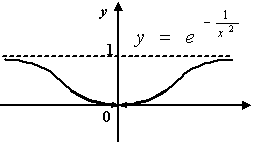
Рис. Устранимый разрыв функции 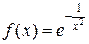
Пример 3: Рассмотрим функцию 
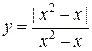 , для которой
, для которой 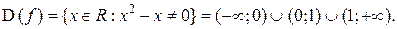 Функция имеет разрывы при
Функция имеет разрывы при 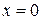 и при
и при 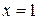 . Распишем модуль разности
. Распишем модуль разности 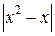 который может быть:
который может быть: 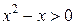 и
и 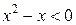 , решением первого неравенства
, решением первого неравенства 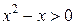 будут 2 интервала
будут 2 интервала 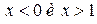 , решением второго
, решением второго 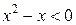 один интервал
один интервал 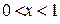 , таким образом
, таким образом 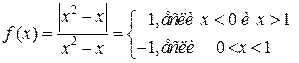
в точках 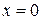 и
и 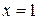 функция имеет неустранимые разрывы первого рода. В точке
функция имеет неустранимые разрывы первого рода. В точке 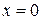 имеем:
имеем: 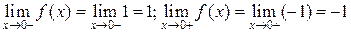 . Таким образом, предельные значения на краях разрыва существуют, но не совпадают; в точке
. Таким образом, предельные значения на краях разрыва существуют, но не совпадают; в точке 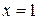 :
: 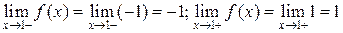 снова пределы слева и справа существуют, конечны, но не совпадают.
снова пределы слева и справа существуют, конечны, но не совпадают.
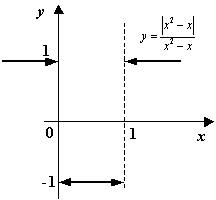
Рис. График функции 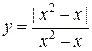 , имеющей точки
, имеющей точки 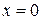 и
и 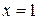 неустранимого разрыва 1 рода, в которых функция делает скачки, величиной
неустранимого разрыва 1 рода, в которых функция делает скачки, величиной 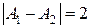
точка разрыва первого рода — ПриМат
Определение:
Точки в которых функция не является непрерывной называется точкой разрыва.
$latex=\lim_{x\rightarrow x_{0}}f(x)=f(x_{0})$
Классификация точек разрыва.
Определение:
Если существует конечный предел справа $latex=(f(a+0))$
$latex=\lim_{x\rightarrow a+0}f(x)(=f(a+0))$ и$latex=\lim_{x\rightarrow a-0}f(x)(=f(a-0))$,
причём $latex=f(a-0)=f(a+0)\neq f(a),$ то точка $latex=a$ называется точкой устранимого разрыва.(название устранимый, оправдывает себя), его можно устранить изменив значение функций в точке $latex=a$ .
Пример
1) $latex=f(x)=sgn^{2}x=\begin{cases}1, & \text{ } x\neq 0 \\ 0, & \text{ } x= 0 \end{cases}$
$latex=sgn {x}=\begin{cases}1, & \text{ } x> 0\\ 0, & \text{ } x=0 \\ -1, & \text{ } x< 0 \end{cases}$
$latex=\lim_{x\rightarrow +0}sgn^{2}x=1\neq 0$
точка 0-точка устранимого разрыва.
2) $latex=f(x)=\begin{cases}x\sin \frac{1}{x}, & \text{ } x\neq 0\\ 1, & \text{ } x=0 \end{cases}$
$latex=\lim_{x\rightarrow 0} f(x)=\lim_{x\rightarrow 0}\underbrace{x}_{0}\sin \frac{1}{x}=0\neq 1$
$latex=x=0$ точка устранимого разрыва.
Определение:
Если существуют конечные односторонние пределы
$latex=\exists f(a-0)< \infty$
$latex=\exists f(a+0)< \infty$ и $latex=f(a+0)\neq f(a-0)$, то точка $latex=a$ называется точкой разрыва первого рода.
Примеры
1) $latex=f(x)=sgnx=\begin{cases}1, & \text{ } x> 0\\ 0, & \text{ } x=0 \\ -1, & \text{ } x< 0 \end{cases}$
$latex=f(+0)=1< \infty$
$latex=f(-0)=-1< \infty$
2)$latex=f(x)=\begin{cases}x^{2}, & \text{ } x> 0 \\ 5, & \text{ } x=0 \\2x-2, & \text{ } x< 0 \end{cases}$
Определение:
Точка $latex=a$ называется точкой разрыва второго рода, если она не является точкой разрыва первого рода и точкой устранимого разрыва, то есть если хотя бы один из сторонних пределов либо не существует, либо бесконечен.
Пример
$latex=f(x)=\begin{cases}\frac{1}{x^{2}}, & \text{ } x\neq 0\\ 1, & \text{ } x=0 \end{cases}$
$latex=f(x)=\begin{cases}\frac{1}{x}, & \text{ } x> 0 \\ 1, & \text{ } x=0 \\ 2x, & \text{ } x< 0 \end{cases}$
$latex=\lim_{x\rightarrow 0}f(x)=\lim_{x\rightarrow 0}2x=0$
$latex=\lim_{x\rightarrow +0}f(x)=\lim_{x\rightarrow +0}\frac{1}{x}=\infty$
точка разрыва второго рода.
Рекомендации
Учебники :
- Кудрявцев Л.Д. «Математический анализ» Том 1, Глава 1, § 5, Тема 5.1 «Точки непрерывности и точки разрыва функции» стр.84-87;
- Фильтенгольц Г.М. «Курс дифференциального и интегрального исчисления» Том 1, Глава 2, § 4 «Непрерывность и разрывы функций» стр.146-167 ;
- Ильин В.А.,Позняк Э.Г. «Основы математического анализа» Часть1, Глава 4, § 8 «Классификация точек разрыва функции» стр.143-145.
Сборники задач:
- Демидович Б.П. «Сборник упражнений по амтематическому анализу» 13-еиздание, исправленное, Отдел 1, § 7 «Непрерывность функции» стр.77-87;
- Дороговцев А.Я. «Математический анализ» Глава 3, § 2 «Непрерывные функции» стр.50-58.
«Разрывность функции»
Лимит времени: 0
Информация
Тест расчитан на людей которые внимательно изучили разделы: «Точки разрыва монотонной функции» и «Классификация точек разрыва», и следовали всем рекомендациям
Вы уже проходили тест ранее. Вы не можете запустить его снова.
Тест загружается…
Вы должны войти или зарегистрироваться для того, чтобы начать тест.
Вы должны закончить следующие тесты, чтобы начать этот:
- С ответом
- С отметкой о просмотре
Задание 1 из 5
Количество баллов: 8Как классифицируются точки разрыва?
Правильно
Неправильно
Задание 2 из 5
Количество баллов: 6Доказательство теоремы о разрыве монотонной функции легко следует из …
Правильно
Неправильно
Задание 3 из 5
Количество баллов: 6Закончите выражение!
Правильно
Неправильно
Задание 4 из 5
Количество баллов: 6Соотнесите функции с их названиями!
- $$f(x)=\begin{cases}1, & \text{ } x\in \mathbb{Q}\\ 0, & \text{ } x\in \mathbb{R}\setminus \mathbb{Q} \end{cases}$$
- $$f(x)=\begin{cases}\frac{1}{q}, & \text{ } x=\frac{p}{q} ,p\in \mathbb{Z}, q\in \mathbb{N}\\ 0, & \text{ } x\in \mathbb{R}\setminus \mathbb{Q} \end{cases}$$
- $$f(x)=\begin{cases}\frac{\sin x}{x}, & \text{ } x\neq 0 \\ 0, & \text{ } x= 0 \end{cases}$$
- $$f(x)=\begin{cases}1, & \text{ } x\geq 0,x\in \mathbb{R}\\ 0, & \text{ } x
- $$f(x)=\begin{cases}-1, & \text{ } x 0 \end{cases}$$
Функция Дирихле
Функция Римана
Функция с устранимым разрывом
Ступенчатая функция
Функция знака
Правильно
Неправильно
Задание 5 из 5
Количество баллов: 6Если существуют конечные односторонние пределы и $latex=f(a+0)\neq f(a-0)$,то точка $latex=a$…
Правильно
Неправильно
Таблица лучших: «Разрывность функции»
| Место | Имя | Записано | Баллы | Результат |
|---|---|---|---|---|
| Таблица загружается | ||||
| Нет данных | ||||
(Основной материал был взят из курса Математического анализа ,1 курс,1 семестр (доц. Лысенко З.М.))
Поделиться ссылкой:
Как с уважением расстаться (для подростков)
Когда отношения заканчиваются
Вначале это интересно. Вам не терпится увидеть своего парня или подругу — и Приятно осознавать, что он или она чувствуют то же самое. Счастье и азарт новых отношений может пересилить все остальное
Однако ничто не остается новым навсегда. Все меняется, когда пары узнают друг друга лучше.Некоторые люди устанавливают комфортные, близкие отношения. Другие пары расходятся.
Есть много разных причин, по которым люди расстаются. Разрыв является одним. Вы можете обнаружить, что ваши интересы, идеи, ценности и чувства не так хорошо сочетаются, как вы думали. Изменить свое мнение или свои чувства про другого человека совсем другое. Возможно, вам просто не нравится быть вместе.Может быть, вы спорите или не хотите того же. Вы могли испытывать чувства к кто-то еще. Или, может быть, вы обнаружили, что вам просто неинтересны серьезные отношения прямо сейчас.
Большинство людей переживают разрыв (или несколько раз) в своей жизни. Если вы когда-либо проходили через это, вы знаете, что это может быть болезненно — даже если кажется, что это к лучшему.
Почему так сложно расстаться?
Если вы думаете о разрыве с кем-то, у вас могут быть смешанные чувства по поводу Это.В конце концов, вы собрались вместе по какой-то причине. Поэтому нормально задаться вопросом: «Будет ли поправиться? »« Могу ли я дать ему еще один шанс? »« Сожалею ли я об этом решении? » вверх — непростое решение. Возможно, вам потребуется время, чтобы подумать об этом.
Даже если вы уверены в своем решении, расставание означает неловкое или неловкое трудный разговор. Человек, с которым вы расстаетесь, может чувствовать себя обиженным, разочарованным, грустный, отвергнутый или убитый горем.Когда вы заканчиваете отношения, вы, вероятно, хотите делать это уважительно и чутко. Ты не хочешь другого человеку, чтобы его обидели — и ты тоже не хочешь расстраиваться.
Избежать этого? Или покончить с этим?
Некоторые люди избегают неприятной задачи завязать трудный разговор. Другие иметь отношение «просто-напросто». Но ни один из этих подходов не лучший один.Избегание просто продлевает ситуацию (и может в конечном итоге причинить вред другому человеку. Больше). А если броситься в трудный разговор, не обдумав, вы можете говорить то, о чем сожалеете.
Что-то среднее работает лучше всего: Подумайте, чтобы было ясно с самим собой о том, почему вы хотите расстаться. Тогда действуй.
Что можно и чего нельзя делать при расставании
Все ситуации разные.Не существует универсального подхода к взлому вверх. Но есть несколько общих правил, которые можно и нельзя делать, когда вы начните думать о том, чтобы поговорить о разрыве.
DO:
- Подумайте, чего вы хотите и зачем вам это нужно. Найдите время подумать ваши чувства и причины вашего решения. Будьте верны себе. Даже если ваше решение может обидеть другого человека, можно делать то, что ты. Просто нужно делать это осторожно.
- Подумайте, что вы скажете и как другой человек может отреагировать. Будет ли удивлен ваш парень или девушка? Печальный? Сумасшедший? Причинить боль? Или даже с облегчением? Думать о точка зрения и чувства другого человека могут помочь вам проявить чувствительность. Это также помогает Ты готовься. Вы думаете, что человек, с которым вы расстаетесь, может плакать? Терять самообладание? Как вы справитесь с такой реакцией?
- Имей добрые намерения. Сообщите другому человеку, что он важен тебе. Подумайте о качествах, которые вы хотите показать другому человеку — любят честность, доброту, чуткость, уважение и заботу.
- Будьте честны — но не жестоко. Расскажи другому человеку вещи что вас в первую очередь привлекло, и что вам в нем нравится. затем скажи, почему ты хочешь двигаться дальше. «Честность» не означает «суровый».»Не разбирай качества другого человека как способ объяснить, что не работает. Подумайте о способах быть добрый и нежный, но при этом честный.
- Скажите это лично. Вы многим поделились друг с другом. Уважение это (и показать свои хорошие качества), расстаясь лично. Если ты живешь далеко, попробуйте пообщаться в видеочате или хотя бы позвонить по телефону. Расставание через СМС или Facebook может показаться простым.Но подумайте, что бы вы почувствовали, если бы ваш парень или подруга сделали это с вами … и что ваши друзья скажут о характере этого человека!
- Если это поможет, доверьтесь тому, кому вы доверяете. Может помочь поговорите о своих чувствах с близким другом. Но убедитесь, что человек, которому вы доверяете in может держать это в секрете, пока вы не поговорите о разрыве BF или GF. Убедитесь, что ваш BF / GF сначала услышит это от вас, а не от кого-то другого.Это одна из причин, по которой родители, старшие сестры или братья и другие взрослые могут быть приятно поговорить. Они не собираются болтать или случайно выскользнуть.
НЕЛЬЗЯ:
- Не избегайте другого человека или разговора, который вам необходим. Вытягивание вещей усложняет задачу в долгосрочной перспективе — для вас и ваши BF или GF.К тому же, когда люди откладывают дела, информация все равно может просочиться. Вы никогда не хочу, чтобы человек, с которым вы расстаетесь, услышал это от кого-то раньше слышу это от вас.
- Не бросайтесь в трудный разговор, не обдумав его. Вы можете говорить то, о чем сожалеете.
- Не проявляйте неуважения. Расскажите о бывшем (или о будущем бывшем) с уважение.Будьте осторожны, чтобы не сплетничать и не ругать его или ее. Подумайте, как бы вы себя чувствовали. Вы бы хотели, чтобы ваш бывший говорил о вас только положительные вещи, когда вы больше не вместе. Кроме того, никогда не угадаешь — твой бывший может превратиться в друга, а ты можешь даже разжечь романтика когда-нибудь.
Эти правила поведения подходят не только для разрыва отношений. Если кто-то вас спросит но вам это не очень интересно, вы можете следовать тем же правилам, чтобы разрешить этого человека осторожно.
Что и как сказать
Вы приняли решение расстаться. Теперь вам нужно найти хорошее время, чтобы поговорить — и способ вести уважительный, справедливый, ясный и понятный разговор. Добрый. Расставание — это больше, чем просто планирование того, что сказать. Вы также хотите рассмотреть как вы это скажете.
Вот несколько примеров того, что вы могли бы сказать.Используйте эти идеи и измените их на под вашу ситуацию и стиль:
- Скажите своему другу или подруге, что хотите поговорить о чем-то важном.
- Начните с упоминания того, что вам нравится или что вы цените в другом человеке.
Например: «Мы давно близки, а вы важны ко мне «.
Или:» Ты мне очень нравишься, и я рад, что мы узнали каждого Другой.» - Скажите, что не работает (ваша причина разрыва отношений).
Например: «Но я не готова сейчас иметь серьезного парня».
Или: «Но вы изменили мне, и я не могу с этим согласиться».
Или: «Но мы больше спорим, чем развлекаемся «.
Или:» Но это просто не так теперь чувствую себя хорошо ».
Или:« Но есть еще кто-то ». - Допустим, вы хотите расстаться.
Например: «Итак, я хочу чтобы расстаться ».
Или:« Итак, я хочу, чтобы мы были друзьями, но не уходили ».
Или:« Итак, я хочу оставаться дружелюбным, но не хочу быть вашим другом больше. « - Извините, если это больно.
Например: «Я не хочу причинить тебе боль «.
Или:» Мне очень жаль, если это не то, что вы хотели вещи быть.«
Или:« Извините, если вам больно ».
Или: «Я знаю, что это трудно слышать». - Скажите что-нибудь доброе или позитивное.
Например: «Я знаю все будет хорошо ».
Или:« Я знаю, что мы всегда будем заботиться друг о друге ».
Или:« Я всегда буду помнить те хорошие времена, которые у нас были ».
Или:« Я буду всегда рад, что я узнал тебя.»
Или:» Я знаю, что есть другая девушка / парень кто будет счастлив встретиться с вами ». - Слушайте, что хочет сказать другой человек. Будьте терпеливы и не удивляйтесь, если другой человек расстроится или недоволен тем, что вы сказали.
- Дайте человеку пространство. Рассмотрите возможность последующего дружеского сообщение или беседа, которые дают понять бывшему, что вам небезразлично его состояние.
Отношения помогают нам учиться
Независимо от того, длятся ли они долго или недолго, отношения могут иметь особое значение. и ценность. Каждые отношения могут научить нас чему-то о себе, о другом человеке, и что мы хотим и нуждаемся в будущем партнере. Для нас это шанс научиться заботиться о другом человеке и о том, чтобы о нем заботились.
Расставание — тоже возможность чему-то научиться.Это не легко. Но это шанс изо всех сил уважайте чувства другого человека. Прекращение отношений — как как бы сложно — развивает наши навыки, когда дело доходит до честности и доброты во время сложные разговоры.
.Оператор Break в C ++ с примером
Оператор break используется в следующих двух сценариях:
a) Используйте оператор break для немедленного выхода из цикла. Всякий раз, когда внутри цикла встречается оператор break, управление сразу выходит из цикла, завершая его. Он используется вместе с оператором if всякий раз, когда используется внутри цикла (см. Пример ниже), так что он возникает только для определенного условия.
b) Используется в структуре управления корпусом переключателя после блоков корпуса.Как правило, за всеми случаями в switch case следует оператор break, чтобы избежать выполнения последующих случаев (см. Пример ниже). Всякий раз, когда он встречается в блоке корпуса переключателя, управление выходит из корпуса корпуса переключателя.
Синтаксис оператора break
перерыв;Блок-схема оператора прерывания
Пример — использование оператора break в цикле while
В приведенном ниже примере у нас есть цикл while, работающий от 10 до 200, но поскольку у нас есть оператор break, который встречается, когда значение переменной счетчика цикла достигает 12, цикл завершается, и управление переходит к следующему оператору в программе после тело цикла.
#includeиспользуя пространство имен std; int main () { int num = 10; while (num <= 200) { cout << "Значение числа:" << число << endl; if (num == 12) { перерыв; } число ++; } cout << "Эй, я не в курсе"; возврат 0; }
Выход:
Значение числа: 10 Значение числа: 11 Значение числа: 12 Эй, я не в курсе
Пример: оператор break в цикле
#includeиспользуя пространство имен std; int main () { int var; for (var = 200; var> = 10; var -) { cout << "var:" << var << endl; if (var == 197) { перерыв; } } cout << "Эй, я не в курсе"; возврат 0; }
Выход:
вар: 200 var: 199 var: 198 var: 197 Эй, я не в курсе
Пример: оператор break в Switch Case
#includeиспользуя пространство имен std; int main () { int num = 2; switch (num) { case 1: cout << "Case 1" << endl; перерыв; case 2: cout << "Case 2" << endl; перерыв; case 3: cout << "Case 3" << endl; перерыв; по умолчанию: cout << "По умолчанию" << endl; } cout << "Эй, я выхожу из корпуса выключателя"; возврат 0; }
Выход:
Корпус 2 Эй, я вышел из корпуса переключателя
В этом примере у нас есть оператор break после каждого блока Case, потому что, если у нас его нет, будет выполняться и следующий блок case.Результат этой же программы без перерыва будет:
Корпус 2 Случай 3 По умолчанию Эй, я вышел из корпуса переключателя.
R break и next (с синтаксисом и примерами)
Из этой статьи вы узнаете об операторах break и next в программировании на R. Вы узнаете их синтаксис и принцип работы с помощью примеров.
В программировании на языке R обычную последовательность цикла можно изменить с помощью оператора break или next .
оператор разрыва
Оператор break используется внутри цикла (repeat, for, while) для остановки итераций и передачи управления за пределы цикла.
В ситуации вложенного цикла, когда есть цикл внутри другого цикла, этот оператор выходит из самого внутреннего цикла, который оценивается.
Синтаксис оператора break:
if (test_expression) {
перерыв
}
Примечание: оператор break также может использоваться внутри else ветви if ... else оператора.
Блок-схема отчета о перерыве

Пример 1: оператор break
х <- 1: 5
for (val in x) {
if (val == 3) {
перерыв
}
печать (val)
}
Выход
[1] 1 [1] 2
В этом примере мы перебираем вектор x , который имеет порядковые номера от 1 до 5.
Внутри цикла for мы использовали условие if для прерывания, если текущее значение равно 3.
Как видно из выходных данных, цикл завершается, когда встречается оператор break .
следующая выписка
Следующий оператор полезен, когда мы хотим пропустить текущую итерацию цикла, не прерывая его. При обнаружении следующего анализатор R пропускает дальнейшую оценку и начинает следующую итерацию цикла.
Синтаксис следующего оператора:
if (test_condition) {
следующий
}
Примечание: следующий оператор также может использоваться внутри else ветки if...else выписка.
Блок-схема следующей выписки

Пример 2: Следующий оператор
х <- 1: 5
for (val in x) {
if (val == 3) {
следующий
}
печать (val)
}
Выход
[1] 1 [1] 2 [1] 4 [1] 5
В приведенном выше примере мы используем оператор next внутри условия, чтобы проверить, равно ли значение 3.
Если значение равно 3, текущая оценка останавливается (значение не печатается), но цикл продолжается со следующей итерации.
Выходные данные отражают эту ситуацию.
.Разрыв строки - определение и примеры
Определение разрыва строки
Что такое разрыв строки? Вот краткое и простое определение:
Разрыв строки - это завершение одной строки стихов и начало новой строки.
Некоторые дополнительные ключевые детали о переносах строк:
- Разрывы строк разделяют стихотворения на строки, и длина строк определяет внешний вид стихотворения на странице: длинные и тонкие, короткие и широкие или форма, полностью самостоятельная .
- Расположение разрыва строки часто определяется количеством слогов в строке, но столь же часто оно свободно выбирается поэтом.
- Разрывы строк служат важной функцией при установке ритма стихотворения, поскольку они вставляют паузу между последним словом одной строки и первым словом следующей строки. По этой причине разрывы строк обычно происходят там, где также встречаются естественные паузы в языке, например, после знаков препинания, в конце мысли или между отдельными изображениями.
Глубина разрывов строк
Даже больше, чем содержание стихотворения, часто именно разрывы строк делают текст узнаваемым для людей как стихи , то есть узнаваемыми как отличные от прозы, что не так. Не используйте разрывы строк таким же образом. Из-за этого строчку можно было считать фундаментальной единицей поэзии, а строчка - это маркер этих единиц. В следующих разделах рассматриваются основные характеристики и условные обозначения, которые определяют способ использования разрывов строк в поэзии.
Длина строки
Вплоть до недавнего времени, начиная с 19 века, единственным приемлемым способом разорвать строку был размер стихотворения. По этой причине полезно иметь четкое представление о том, что такое измеритель, чтобы понять, как он повлиял на использование разрывов строк. Мы предоставляем более подробную информацию о счетчике на отдельной странице, но предлагаем краткое руководство здесь.
- Метр: Образец ударных и безударных слогов, создающий ритм поэтических строк.Единицы измерения называются футами. Ноги подвержены разным нагрузкам. Например, ямб - это ступня с безударным слогом, за которым следует ударный слог (de- fine ), а хорея - противоположное: ударный слог, за которым следует безударный слог ( Po -et). Поэтические метры определяются как типа и числом футов, которые они содержат. Например, пентаметр ямба - тип измерителя, обычно используемый в поэзии, который содержит пять ямбов в строке (отсюда префикс «пента», что означает пять).
В формальном стихе (поэзия со строгим размером и схемой рифм), а также в пустом стихе (не рифмованная поэзия со строгим размером) метр стихотворения определяет длину каждой строки, требуя, чтобы каждая строка содержала определенное количество символов. слоги. Итак, стихотворение, написанное ямбическим пентаметром (пять ямбов на строку), будет иметь разрыв строки через каждые десять слогов, как в следующем примере:
Могу ли я сравнить тебя с летним днем?
Ты милее и умереннее.
В произвольном стихе (стихотворении без определенного размера или схемы рифм) длина строки определяется желанием поэта создать определенный ритм или сделать больший акцент на определенных словах, вставив вокруг них больше места. В произвольном стихе, в отличие от формального или пустого стиха, длина строки может значительно варьироваться на протяжении всего стихотворения, как в следующем примере:
Много способов танцевать Жизель, но сегодня, когда вы
смотрите, вы думаете, что она и есть искусство, существо, которое запоминает
каждый ее жест и ощущает его отношение ко времени
всего мгновением ранее, когда она сделала что-торядом с ним...
Использование заглавных букв
До 19 века первое слово каждой строки стихов, как правило, было написано с заглавной буквы, независимо от того, было ли оно началом нового предложения. Сегодня нет стандарта использования заглавных букв в начале строк; некоторые поэты делают это, а некоторые нет, хотя обычно это рассматривается как несколько формальная деталь, оставшаяся от ушедшей эпохи поэзии. Вот, например, первые строки раннего стихотворения Джона Эшбери, в котором в начале каждой новой строки используется заглавная буква, хотя позже в своей жизни Эшбери, как и многие другие современные поэты, перестал соблюдать это соглашение в своих стихах.
Сидеть между морем и зданиями
Ему нравилось рисовать портрет моря.
Но точно так же, как дети представляют молитву.
Это просто тишина, он ожидал, что его объект
Поднимется по песку, и, схватив кисть,
Нанесет на холст собственный портрет.
Пунктуация
Хотя разрывы строк сами по себе, как правило, создают паузу в ритме стихотворения - и поэты обычно используют знаки препинания в конце строк - разрывы строк не обязательно должны иметь совпадать с использованием знаков препинания.Строки, которые с по заканчиваются знаками препинания, называются линиями с остановкой в конце, а строки, которые с по не заканчиваются знаками препинания, называются строками с перекрытием. Например, в этих строках из «Ромео и Джульетта» первая, вторая и пятая строки остановлены, в то время как третья и четвертая замкнуты:
Когда он умрет,
Возьмите его и вырежьте маленькие звезды,
И он сделает лицо небес таким прекрасным
Чтоб весь мир полюбил ночь
И не поклонялся яркому солнцу.
Разрывы строк и синтаксис
Синтаксис - это термин, который относится к структуре и порядку слов в предложении. Вообще говоря, поэты помещают в свои стихи разрывы строк, чтобы они не нарушали существенным образом синтаксис предложения, а вместо этого создавали паузы, имитирующие естественные паузы речи. Однако это не всегда так; некоторые поэты используют разрывы строк, чтобы намеренно создать необычную каденцию или фразировку в своих стихах. Использование разрывов строк этими двумя разными способами дает совершенно разный эффект.Например, возьмем следующие два примера, в которых используются одни и те же слова, но в разных местах используются разрывы строк:
В нескольких минутах ходьбы от моей комнаты в Будапеште
под дворцовым кварталом
и заброшенной больницей в скале
была знаменитая баня под названием Рудас.
vs.
В нескольких минутах ходьбы от моей комнаты
в Будапеште, ниже дворцового квартала
и заброшенной больницы
в скале, находится
знаменитая баня под названием Рудас.
В первом приведенном выше примере разрывы строк используются таким образом, чтобы они следовали синтаксису предложения гораздо естественнее, чем во втором примере, который весьма неприятен. Но некоторые поэты хотят добиться этого резкого эффекта и используют разрывы строк, чтобы целенаправленно изменить способ, которым кто-то будет естественно читать данное предложение. Э.Е.Каммингс - поэт, который даже зашел в этом направлении настолько, что разрывал строки посреди слов. Вот отрывок из одного из стихотворений Камминга, в котором разрывы строк используются в агрессивном противопоставлении естественному синтаксису:
dim
i
nu
tive this park is e
mpty (everyb
body's elsewher
e except me 6 e
Разрывы строк vs.Разрывы строф
В то время как большая часть этой статьи посвящена разрывам строк, которые отделяют одну строку стихов от другой, разрывы строк тесно связаны с разрывами строф (также называемыми «двойными разрывами строк»), которые разделяют группировки строк на строфы. . Например, в первых двух строфах «Зеленых дорог» Эдварда Томаса есть два разрыва строки и один разрыв строфы:
Зеленые дороги, которые заканчиваются в лесу
В июне этого года усыпаны белыми гусиными перьями
сзади кто-то пошел в лес
Чтобы показать свой след.Но он больше не вернулся.
Разрыв строфы, как показано выше, обычно отличается от разрыва строки через увеличенный пробел между двумя строками. Однако иногда, особенно когда стихи взяты внутри фрагмента прозы, разрывы строк и строфы могут быть обозначены косой чертой (/) и двойной косой чертой (//) соответственно. В этой нотации первые две строфы «Зеленых дорог» будут выглядеть так:
Зеленые дороги, которые заканчиваются в лесу / В июне этого года усыпаны белыми гусиными перьями // Как следы, оставленные кем-то, кто пошел в лес / Чтобы показать его след.Но он больше не вернулся.
Поэзия без разрывов строк
Некоторые поэты пишут в форме абзацев, а не используют разрыв строки. Эти типы стихов называются стихотворениями в прозе, потому что они имеют вид прозы. Вот пример стихотворения в прозе современной поэтессы Луизы Глюк:
Давным-давно, еще до того, как я был измученным художником, страдающим тоской, но неспособным сформировать прочную привязанность, задолго до этого я был славным правителем, объединяющим всех. о разделенной стране - так мне рассказала гадалка, исследовавшая мою ладонь.Она сказала, что великие дела впереди или, возможно, позади вас; в этом трудно быть уверенным. И все же, добавила она, в чем разница? Прямо сейчас вы ребенок, держась за руки с гадалкой. Все остальное - гипотеза и мечта.
Как определить, что является стихотворением, а что нет, без разрывов строк? Ответ в том, что это во многом зависит от контекста. Это стихотворение в прозе было написано известным поэтом и опубликовано в книге, окруженной другими стихами. Но даже если бы это было не так, любой самодостаточный отрывок прозы, подобный этому - с началом и концом, - мог бы считаться стихотворением в прозе, если человек, написавший его, определил его таким образом.
Нетрадиционные разрывы строк
Хотя все показанные до сих пор разрывы строк представляют собой явные переходы от одной строки к другой, некоторые разрывы строк более неоднозначны или выглядят иначе, чем те, которые обсуждались выше.
Отступ
Строки стихов обычно выравниваются по левой стороне страницы, но поэты иногда делают отступы (отодвигая их от левого поля), чтобы усложнить традиционные разрывы строк. Отступ не означает, что линия не разорвана должным образом.Скорее, отступ, как и сам разрыв строки, дополнительно сообщает фразировку или ритм стихотворения. Например, строка, имеющая больший отступ, чем другие на странице, может быть прочитана как имеющая перед ней немного более длинную паузу или отсроченное начало, как если бы поэт переводил дыхание. В следующем примере из стихотворения Джори Грэхэм использование отступов непоследовательно и иногда даже попадает в середину строки, создавая прерывистый ритм в стихотворении. Однако, несмотря на неравномерность отступов, каждая новая строка в этом стихотворении имеет свой собственный разрыв строки.
Тогда цикады снова как растопка, которую не возьмут.
Застрявшая спичка какой-то утопии, которую мы уже не помним,
условия -
правила. Что его собирались упразднить, что восстановили
? Позади них гудок в гавани,
хриплые объявления о неторопливом прибытии,
паучьи девственные визги чаек, косой звук, скользкий
совершенно беззольный проступок
и затем подводные пастбища неиссякаемые
фосфорные почерки пены их собственных волнений теперь стирают
, борьба глубины с текущими коридорами глубины...
Пропущенные строки
«Пропущенная строка» - это термин для отдельной строки стихов, которая разделена на две отдельные строки с использованием определенного стиля отступа, так что первая строка выровнена по левой стороне страницы, но вторая строка имеет отступ, так что он начинается сразу под той точкой на странице, где закончилась первая строка. Следующий пример - отрывок из стихотворения Чарльза Райта, который часто использовал пропущенные строки:
Я стою внутри слова здесь
, поскольку это слово стоит в предложении:
Без тени, наполовину непринужденно.Религия была в руинах более тысячи лет.
Почему небо не должно быть в клочья,
потерянные ноты в забытых песнях?
Пропущенные линии могут использоваться по разным причинам. Они могут добавлять пространство в середине строки, которое одновременно больше и меньше места, добавляемого типичным разрывом строки, а также визуально добавляют размер стихотворению.
Повторяющиеся строки
Если поэт пишет стихотворную строку, которая оказывается слишком длинной, чтобы уместиться на странице без перерыва, когда книга отправляется в печать, эта строка обычно разбивается на две строки, где вторая Строка имеет отступ, чтобы указать, что она должна быть продолжением предыдущей строки.Следующий пример представляет собой отрывок из стихотворения К. К. Уильямса, который прославился использованием повторяющихся строк.
Девушка, которая в 1971 году, когда я жил одна, мучительно одинокая, лишенная, депрессивная,
небрежно упомянула мне в разговоре с друзьями, что, хотя сначала
она нашла меня -Я могу Не помню этот термин, какой-то устаревший разговорный язык, обозначающий странные, неприемлемые, необычные вещи -
, она решила, что я в конце концов прав.… двенадцать лет спустя она возвращается ко мне из «
нигде» ...
Эти повторяющиеся строки - хотя они кажутся новыми, с отступом - на самом деле , а не следуют за разрывами строк. Отступ в данном случае означает, что строка с отступом является частью предыдущей строки и не должна рассматриваться сама по себе.
Примеры разрывов строк
Пример разрывов строк в шекспировской книге Macbeth
Как и почти все произведения Шекспира, Macbeth был написан ямбическим пентаметром.Это означает, что перенос строки происходит (более или менее) через каждые десять слогов.
Было бы время для такого слова.
Завтра, и завтра, и завтра,
Подкрадывается в этом мелком шаге изо дня в день
До последнего слога записанного времени
И все наши вчерашние дни освещали дураков
Путь к пыльной смерти. Выходи, короткая свеча!
Жизнь - всего лишь ходячая тень, бедный игрок
Которая расхаживает и тревожит свой час на сцене
И затем больше не слышно: это сказка
Рассказанная идиотом, полная звука и ярости,
Ничего не значащая.
Пример разрывов строк в «Зеленых яйцах и ветчине» доктора Сьюза
В строках этой книги доктора Сьюза используется тетраметр ямба, так что каждая строка содержит восемь слогов.
Не люблю их в доме.
Не люблю их с мышкой.
Мне они здесь и там не нравятся.
Я их нигде не люблю.
Не люблю зеленые яйца и ветчину.
Я не люблю их, Сэм-я-Ам.
Пример разрывов строк в произведении Роберта Крили «Конец»
Это короткое стихотворение состоит из трех двустиший, в которых разрывы строк используются как традиционными, так и нетрадиционными способами.Показанный здесь отрывок представляет собой первые три строки стихотворения. Первый разрыв строки интуитивно соответствует синтаксису предложения, действуя как пауза там, где в противном случае могла бы быть запятая. Однако второй разрыв строки происходит в точке, которая явно расходится с тем местом, где синтаксис диктует паузу. Результатом этого объединения является то, что слова «Серый» странно висят в конце строки без какого-либо разрешения их значения.
Когда я знаю, что люди думают обо мне
, я погружаюсь в свое одиночество.Купленная ранее серая шляпаболеет.
Пример разрыва строки в произведении Чарльза Олсона «Я, Максим Глостерский, тебе»
Олсон был поэтом-новатором, который использовал разрывы строк нетрадиционным способом. В этом отрывке из его стихотворения «Я, Максим Глостерский, к Тебе» использование заглавных букв в начале строк и предложений непоследовательно, отступы используются идиосинкразически, а разрывы строк не всегда встречаются там, где синтаксис сделайте паузу естественной.
то, что вы ищете
, может лежать за поворотом
гнезда (второй, убитый раз, птица! Птица!
А там! (Сильный) толчок, мачта! Полет
(птицы
) o kylix, o
Антоний Падуанский
низко низко, o благословикрыши, старые, пологие, крутые
, на столбах коньков которых сидят чайки, с которых они уходят,И отщепные стойки
моего города!
Почему писатели используют разрывы строк?
Писатели используют разрывы строк, потому что это нормально rt того, что делает стихотворение стихотворением.Добавляя больше пробелов в текст, поэты могут в большей степени контролировать скорость и ритм чтения их стихов, тем самым отличая их как от повседневного языка, так и от прозы. Так что во многом вопрос «почему писатели используют перенос строки» не отличается от вопроса о том, почему люди вообще пишут стихи.
Но остается вопрос, как поэты используют разрывы строк для достижения различных эффектов, и ответ на этот вопрос иногда может иметь столько же ответов, сколько существует поэтов, пишущих сегодня.Однако чаще всего авторы используют разрывы строк, чтобы определить скорость и ритм стихотворения. Например, поэт может использовать более короткие строки и больше разрывов строк, чтобы замедлить читателя, и попросить их уделять особое внимание каждому отдельному слову, которое используется. С другой стороны, поэт может использовать длинные строки, если стиль стихотворения более разговорный или если предложения содержат сложные идеи с большим количеством предложений, поскольку более длинные строки легче и быстрее понять. В конечном счете, разрывы строк можно использовать любым способом, которым поэт хочет изменить способ представления текста стихотворения читателю.


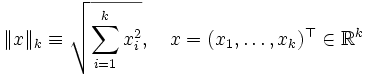 — евклидова норма в
— евклидова норма в 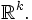
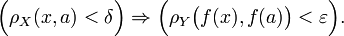

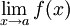 не существует;
не существует;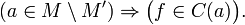
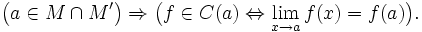
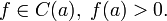 Тогда существует окрестность U(a) такая, что
Тогда существует окрестность U(a) такая, что
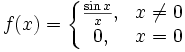
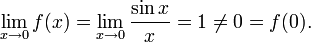
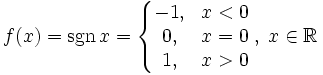
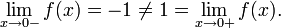
 и
и  Тогда говорят, что f непреры́вна спра́ва в точке a, если
Тогда говорят, что f непреры́вна спра́ва в точке a, если 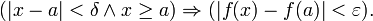
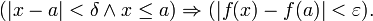
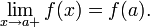
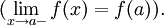
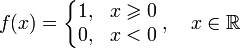
 , то точка называется точкой устранимого разрыва 1 рода
, то точка называется точкой устранимого разрыва 1 рода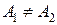 , то точка называется точкой конечного разрыва (или неустранимого разрыва) 1 рода. Величину
, то точка называется точкой конечного разрыва (или неустранимого разрыва) 1 рода. Величину  называют скачком функции в точке разрыва первого рода.
называют скачком функции в точке разрыва первого рода.