«Математика, Л.Г. Петерсон 1 класс», часть 3, урок №17 «Решение уравнений и составных задач» | Методическая разработка по математике (1 класс) по теме:
Муниципальное автономное общеобразовательное учреждение гимназия №69 им. С Есенина г. Липецка
ИТОГОВАЯ АТТЕСТАЦИОННАЯ РАБОТА
ТЕМА РАБОТЫ «Решение уравнений и составных задач»
Вид работы (конспект урока) по курсу повышения квалификации
«Реализация деятельностного подхода к обучению в соответствии с требованиями ФГОС НОО»
Выполнила
Калугина Елена Васильевна
учитель начальных классов
МАОУ гимназия №69
Форма обучения: дистанционная
Научный руководитель:
к.п.н., доцент НГПУ
Омельченко Е.А.
ПЛАН-КОНСПЕКТ УРОКА
Предмет — математика (по учебнику «Математика, 1 класс», часть 3, урок №17) (Школа 2000…).
Класс 1
Тип урока: урок общеметодологической направленности.
Цели:
1.Предметные:
1) формировать у учащихся способности фиксировать собственные затруднения в деятельности, выявлять их причины, строить и реализовать проект выхода из затруднения;
2) тренировать умения решать уравнения на сложение и вычитание, составные задачи на нахождение целого;
3) актуализировать мыслительные операции: сравнение, анализ, аналогию.
2.Метапредметные: формирование универсальных учебных действий.
Регулятивные: умение выполнять пробное учебное действие, фиксировать своё затруднение, анализировать ситуацию, определять цель деятельности, устранять причины затруднения.
Личностные: осознание математических составляющих окружающего мира.
Познавательные: формирование мыслительного умения переводить устную речь в письменную знаково-символическую, построение рассуждений.
Коммуникативные: умение работать в паре; умение использовать в устной речи математических терминов, изучаемых в данной теме; умение аргументировать свой ответ.
Раздаточный материал:
1) Алгоритм решения уравнений
1. Прочитать уравнение.
2. Найти части и целое (если нужно, составить схему).
3. Применить правило нахождения части и целого.
4. Выполнить действия и найти х.
5. Сделать проверку (устно или письменно).
х + а = б а – х = б х – а = б
х = б – а х = а – б х = а + б
Алгоритм решения задачи:
1.
Нахожу неизвестную часть.
2. Нахожу целое.
2) Самостоятельная работа № 1.
1) 4 + х = 6 7 – х = 3 х – 4 = 5
х= х = х =
2) В одной стопке 5 книг, а в другой – на 1 книгу меньше. Сколько книг в двух стопках?
3)* 3 + 1 = 8 — □
□ + 7 = 9 – 0
3) Образец самопроверки самостоятельной работы №1
1) х = 2 х = 4 х = 9
2) Ответ: в двух стопках 9 книг.
3) 4; 2
4) Самостоятельная работа № 2.
1) 7 + х = 9 8 – х = 5 х – 2 = 8
х= х = х =
2) У Риты было 4 яблока, а у Саши на 1 яблоко меньше. Сколько яблок у детей?
3)* 8 — 5 = 1 + □
□ — 3 = 5 – 3
5) Образец самопроверки самостоятельной работы №1
1) х = 2 х = 3 х = 10
2) Ответ: у детей 7 яблок.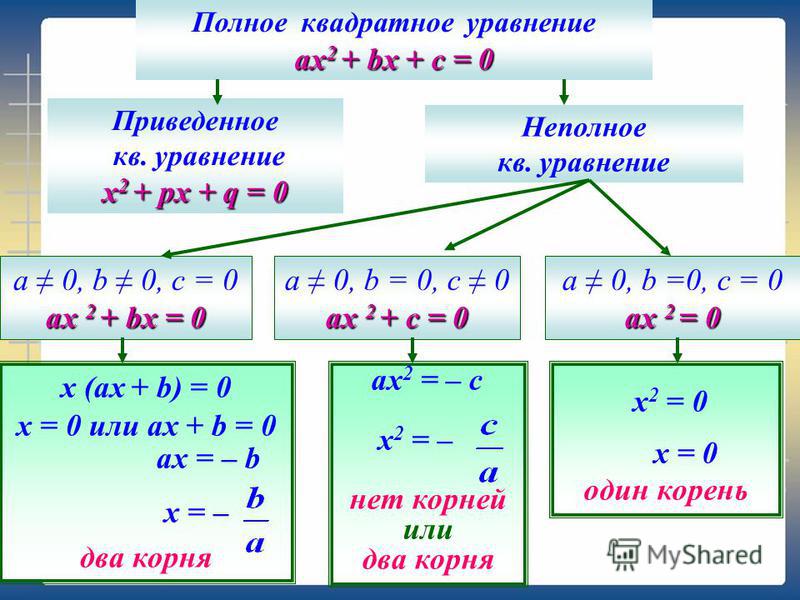
3) 2; 5
Ход урока:
1. Мотивация к коррекционной деятельности.
Цель:
1) создать условия для возникновения внутренней потребности включения в деятельность посредством обращения к опыту прошлого урока;
2) актуализировать требования к ученику со стороны коррекционной деятельности;
3) установить тематические рамки урока: решение уравнений на сложение и вычитание, решение составной задачи.
На доске открыта пословица:
Делу время – потехе час!
- Прочитайте пословицу. Как вы ее понимаете?
- Как эта пословица связана с работой на уроке? (На уроке необходимо учиться – либо самим добывать новые знания или повторять уже изученное.)
- Верно. Этот урок я предлагаю посвятить повторению ваших знаний. Над какими темами вы работали? (Мы изучали уравнения, решали составные задачи.)
- Что показала работа на прошлых уроках? (У нас еще возникали трудности при решении этих заданий.)
- А если ошибки не возникали, зачем этим ребятам повторять? (Еще раз проверить себя, убедиться в этом.
) - Как же вы будете работать? (Сначала повторим все необходимое, затем выполним самостоятельную работу, посмотрим, есть ли затруднения. Если они есть, будем над ними работать.)
- Я желаю вам удачи на уроке!
)2. Актуализация и фиксация затруднений в индивидуальной деятельности.
Цель:
1) организовать повторение алгоритмов решения уравнений на сложение и вычитание, решения составной задачи на нахождение целого;
2) активизировать мыслительные операции: сравнение, анализ, аналогию;
3) организовать мотивирование и выполнение учащимися самостоятельной работы № 1 на применение способов действий, запланированных для рефлексивного анализа;
4) организовать самопроверку учащимися своих работ по готовому образцу с фиксацией полученных результатов (без исправления ошибок).
1) Решение уравнений на сложение и вычитание.
Учитель открывает на доске задание №1
х + 3 = 6 9 – х = 4 х – 1 = 6
- Сформулируйте первое задание. (Решить уравнение.)
- Что вам поможет в решении уравнений? (Эталоны, открытые на прошлых уроках.)
(Решить уравнение.)Учитель фиксирует на доске эталон решения уравнений с неизвестным слагаемым, эталон решения уравнения с неизвестным вычитаемым, эталон решения равнений с неизвестным уменьшаемым.
- Решите данные уравнения с проверкой.
Один ученик решает первое уравнение у доски с проговариванием. Остальные учащиеся работают или на планшетках или в рабочих тетрадях. Работа над оставшимися уравнениями проводится аналогично.
- Сколько эталонов вы использовали? (Три.)
- Удобно ли это? Подумайте, есть ли общее в использовании этих эталонов? (Есть. Порядок работы одинаковый, отличие в том, что используем правила нахождения целого или части.)
- Объединим эти эталоны.
С помощью подводящего диалога учитель с учащимися конструирует общий эталон решения уравнений на сложение и вычитание.
- Вернитесь к ответам. Выпишите ответы и расположите их в порядке возрастания.
Учащиеся работают самостоятельно на планшетках. Проверка проводится фронтально: 3,5,7.
- Найдите закономерность. Продолжите ряд.
2) Решение составной задачи на нахождение целого.
Учитель открывает на доске задание: «Катя сделала 6 закладок, а Даша – на 4 закладки меньше. Сколько закладок сделали Катя и Даша?»
- Что вам поможет решить эту задачу? (Эталон.)
Учитель фиксирует на доске эталон решения задачи на нахождение целого.
- С чего вы начинаете решать задачи? (С ее анализа и заполнения схемы.)
Учитель заранее выносит схему к данной задаче на доску, учащиеся работаю с аналогичными схемами.
Один учащийся работает у доски с комментированием. Он заполняет схему и выстраивает ход решения задачи: « Известно, что Катя сделала 6 закладок, а Даша – на 4 закладки меньше. Нужно узнать, сколько закладок сделали дети. Чтобы ответить на вопрос задачи, нужно сложить закладки Кати и Даши.
Этого сделать не можем, так как не знаем, сколько закладок сделала Даша. Поэтому первым действием узнаем, сколько закладок у Даши, а вторым ответим на вопрос задачи».
- Что вы повторили? (Алгоритмы решения уравнений и решения составной задачи.)
- Что предстоит дальше? (Выполнить самостоятельную работу.)
3) Самостоятельная работа № 1.
Раздать листы с текстом самостоятельной работы № 1.Время выполнения ≈ 5–6 минут. Учитель нумерует эталоны на доске.
- Проверьте свои работы по образцу.
Раздать образец для самопроверки к с. р. № 1 или открыть его на доске.
- Как вы зафиксируете правильность выполнения каждого задания? (Поставим «+» рядом с верно выполненным заданием, «?» – если ответ не совпал.)
- Что вы выяснили для себя, проверив работы по образцу? (Где есть трудности, а где всё получилось.)
- Поднимите руку, кто допустил ошибки в задании № 1, №2, №3.
Учитель фиксирует на доске количество человек, допустивших ошибки в каждом из заданий (кроме № 3*).
- У кого всё верно?
- У кого ест затруднения?
- Что вы будете делать? (Проверять решение по эталону.)
- Для чего? (Чтобы проверить правильность наших рассуждений или определить место и причину возникшего затруднения.)
3. Локализация индивидуальных затруднений.
Цель:
1) организовать учащихся, не допустивших ошибок, на выполнение пошаговой проверки своих работ по эталону для самопроверки и на выполнение дополнительного задания;
2) организовать учащихся, допустивших ошибки, на проведение анализа своих работ с целью определения места затруднения и выявления и фиксации причины затруднений.
Раздать эталоны для самопроверки.
- Какие ошибки можно допустить при выполнении № 1? (Можно неверно выделить целое и части, применить правило нахождения целого, допустить вычислительные ошибки)
- У кого ошибки в № 1, поставьте рядом со знаком вопроса номер соответствующего эталона или коротко запишите суть ошибки, если нужно эталона на доске нет.
- Какие ошибки можно допустить при выполнении № 2? (Можно неверно построить сторону квадрата, построить перекошенную фигуру)
- У кого ошибки в № 2, поставьте рядом со знаком вопроса номер соответствующего эталона.
- Какие же правила были вами нарушены? (…)
— Что же является причиной ваших ошибок? (Нарушение правил.)
4. Коррекция выявленных затруднений.
Цель:
1) создать условия для формулирования учащимися индивидуальных целей будущих коррекционных действий;
2) организовать выбор учащимися способа и средств коррекции;
3) уточнить алгоритм исправления ошибок;
4) организовать самостоятельное (или с помощью эталона для самопроверки) исправление учащимися своих ошибок выбранным методом на основе применения выбранных средств;
5) придумать или выбрать из предложенных учителем задания на способы действий, в которых были допущены ошибки, и решить эти задания.
- Сформулируйте цель те, у кого нет затруднений? (Мы будем выполнять дополнительные задания. )
)Номера дополнительных заданий записаны на доске (№ 5, 6, стр. 33).
- Что делать тем, у кого возникли трудности при выполнении самостоятельной работы? (Подумать, почему эти трудности возникли.)
- Как же всем остальным ответить на возникшие вопросы? Что поможет? (Алгоритм исправления ошибок.)
- Какова дальнейшая цель вашей работы? (По алгоритму исправления ошибок найти, где конкретно и почему возникло затруднение, а потом исправить ошибки.)
- Перед выполнением работы над ошибками проговорите, какие правила вам нужно ещё раз осмыслить, понять? (…)
- Как вы будете это делать? (Будем пошагово применять правила, посмотрим, как выполнены аналогичные задания …)
- Начинайте работу над ошибками по алгоритму исправления ошибок.
Дети работают самостоятельно по алгоритму исправления ошибок. Учитель оказывает индивидуальную помощь.
Результатом работы на данном этапе должно быть выполнение работы над ошибками.
5. Обобщение затруднений во внешней речи.
Цель:
организовать обсуждение типовых затруднений с проговариванием во внешней речи формулировок соответствующих способов действий.
- Посмотрите на результаты самостоятельной работы. На какие правила возникло наибольшее количество ошибок? (…)
- Проговорите ещё раз для всех эти правила. (…)
- Что дальше делать тем, у кого при выполнении самостоятельной работы № 1 были трудности? (Выполнить ещё одну самостоятельную работу.)
6. Самостоятельная работа с самопроверкой по эталону.
Цель:
1) организовать выполнение учащимися, допустившими ошибки, тех заданий из самостоятельной работы № 2, аналогичной первой, в которых были допущены ошибки;
2) организовать самопроверку учащимися своих работ по эталону для самопроверки с фиксацией результатов;
3) создать условия для фиксации учащимися преодоления возникших ранее затруднений.
Учащиеся выполняют задания из самостоятельной работы № 2, которые вызвали у них затруднения, и самостоятельно сопоставляют полученное решение с эталоном для самопроверки.
В это время дети, не допустившие ошибок, проверяют дополнительное задание по подробному образцу на слайде.
- Какие задания вы будете выполнять? (Подобные тем, в которых были допущены ошибки.)
- Как будете проверять вашу работу? (По эталону, результат отметим «+» или «?».)
После самостоятельной работы организуется самопроверка по эталону.
- У кого ошибки в самостоятельной работе № 2?
- В чем их причина?
- Вы молодцы, что нашли ошибки и поняли их причину. Но какой вывод вы должны сделать? (Мы не справились с затруднением, нужно еще тренироваться.)
- Где вы можете это сделать? (При выполнении домашнего задания.)
- Кто не допустил ошибки в самостоятельной работе № 2?
- Сделайте вывод. (Нам удалось справиться с затруднением.)
7. Включение в систему знаний и повторение.
Цель:
повторить решение на целое части, актуализировать понятие «обратная задача».
– В конце урока я предлагаю потренировать в решении других видов задач: № 7 (3,4), стр.
33.
Учитель открывает схемы к задачам на доске.
- Сравните схемы. (Схемы одинаковые, задачи на целое, состоящее из трех частей.)
- Составьте задачи по каждой схеме.
Проверки проводится фронтально. Несколько учащихся произносят свои тексты.
Работу по решению задач можно организовать по группам.
- Я предлагаю решить эти задачи в группах. Вспомните основные правила работы в группах. (В группе есть ответственный, он распределяет обязанности и отвечает за результат. Каждый имеет право высказаться, остальные должны внимательно его выслушать.)
- Задача № 3
- 3 + 4 + 2 = 9 (л)
- Ответ: всего 9л
- Задача № 4
- 9 – 3 – 4 = 2 (л)
- Ответ: в 3 сосуде 2 л
- Посмотрите на решение этих задач. Какой вывод вы можете сделать. (Это обратные задачи.)
- Какие задачи называются обратными? (Это задачи, в которых неизвестное и одно из условий меняются местами.)
8. Рефлексия деятельности на уроке.
Цель:
1) зафиксировать правильные способы действий в заданиях, где были допущены ошибки;
2) уточнить алгоритм исправления ошибок;
3) зафиксировать степень соответствия поставленной цели и результатов деятельности;
4) оценить собственную деятельность на уроке;
5) согласовать домашнее задание.
- Чему был посвящён сегодняшний урок? (Повторению и работе над ошибками.)
- Какой инструмент помогает вам правильно работать над ошибками? (Алгоритм исправления ошибок.)
- Какие цели вы ставили перед собой на уроке? (Выяснить, есть ли трудности. Понять причину ошибок и устранить её…)
- Какие результаты вы получили? (…)
- В каких темах были затруднения? (В решении уравнений и составных задачах.)
- Удалось ли их преодолеть? Как?
- Оцените свою работу по лестнице «успеха».
- Сделайте вывод о том, зачем нужно домашнее задание? (Для того чтобы потренироваться в том, что ещё не очень хорошо получается,…)
- Я рада, что вы понимаете важность качественного выполнения домашнего задания.
Домашнее задание с.33 №7 (1,2).
Задачи к разделу Окислительно-восстановительные реакции
В данном разделе собраны задачи по теме Окислительно-восстановительные реакции. Приведены примеры задач на составление уравнений реакций, нахождение окислительно-восстановительного потенциал, и константы равновесия ОВР и другие.
Задача 1. Какие соединения и простые вещества могут проявлять только окислительные свойства? Выберите такие вещества из предложенного перечня: NH3, CO, SO2, K2MnO4, Сl2, HNO2. Составьте уравнение электронного баланса, расставьте коэффициенты в уравнении реакции:
HNO3 + H2S = H2SO4 + NO + H2O.
Показать решение »
Решение.
Простые вещества, атомы которых не могут отдать электрон, а могут только присоединить его в реакциях являются только окислителями.
Из простых веществ только окислителем может быть фтор F2, атомы которого имеют наивысшую электроотрицательность. В сложных соединениях – если атом, входящий в состав этого соединения (и меняющий степень окисления) находится в своей наивысшей степени окисления, то данное соединение будет обладать только окислительными свойствами.
Из предложенного списка соединений, нет веществ, которые обладали бы только окислительными свойствами, т.к. все они находятся в промежуточной степени окисления.
Наиболее сильный окислитель из них – Cl2, но в реакциях с более электроотрицательными атомами будет проявлять восстановительные свойства.
N-3H3, C+2O, S+4O2, K2Mn+6O4, Сl02, HN+3O2
HNO3 + H2S = H2SO4 + NO + H2O.
Составим электронные уравнения:
N+5 +3e— = N+2 | 8 окислитель
S-2 — 8e— = S+6 | 3 восстановитель
Сложим два уравнения
8N+5 +3S-2— = 8N+2 + 3S+6
Подставим коэффициенты в молекулярное уравнение:
8HNO3 +3H2S = 3H2SO4 + 8NO + 4H2O.
Задача 2. Почему азотистая кислота может проявлять как окислительные, так и восстановительные свойства? Составьте уравнения реакций HNO2: а) с бромной водой; б) с HI; в) с KMnO4. Какую функцию выполняет азотистая кислота в этих реакциях?
Показать решение »
Решение.
HN+3O2 — Степень окисления азота в азотистой кислоте равна +3 (промежуточная степень окисления). Азот в этой степени окисления может как принимать, так и отдавать электроны, т.е. может являться как окислителем, так восстановителем.
а) HNO2 + Br2 + H2O = 2HBr + HNO3
N+3 – 2 e = N+5 | 1 восстановитель
Br20 + 2 e = 2Br— | 1 окислитель
N+3 + Br2 = N+5 + 2Br—
б) HNO2 + 2HI = I2 + 2NO + 2H2O
N+3 + e = N+2 | 1 окислитель
2I— — 2 e = I2 | 1 восстановитель
N+3 + 2I— = N+2 + I2
в) 5HNO2 + 2KMnO4 + 3H2SO4 = 2MnSO4 + 5HNO3 + K2SO4 + 3H2O
N+3 – 2 e = N+5 | 5 восстановитель
Mn+7 + 5 e = Mn+2 | 2 окислитель
5N+3 + 2Mn+7 = 5N+5 + 2Mn+2
Задача 3.
Определите степени окисления всех компонентов, входящих в состав следующих соединений: HСl, Cl2, HClO2 , HClO3 , Cl2O7 . Какие из веществ являются только окислителями, только восстановителями, и окислителями и восстановителями? Расставьте коэффициенты в уравнении реакции:
КСlO3 → КС1 + КСlO4.
Укажите окислитель и восстановитель.
Показать решение »
Решение.
Хлор может проявлять степени окисления от -1 до +7.
Соединения, содержащие хлор в его высшей степени окисления, могут быть только окислителями, т.е. могут только принимать электроны.
Соединения, содержащие хлор в его низшей степени окисления, могут быть только восстановителями, т.е. могут только отдавать электроны.
Соединения, содержащие хлор в его промежуточной степени окисления, могут быть как восстановителями, так и окислителями, т.
е. могут отдавать, так и принимать электроны.
H+1Сl-1, Cl02, H+1Cl+3O2-2 , H+1Cl+5O3-2 , Cl2+7O7-2
Таким образом, в данном ряду
Только окислитель — Cl2O7
Только восстановитель – HСl
Могут быть как окислителем, так и восстановителем — Cl2, HClO2 , HClO3
КСlO3 → КС1 + КСlO4.
Составим электронные уравнения
Cl+5 +6e— = Cl— | 2 | 1 окислитель
Cl+5 -2e— = Cl+7 | 6 | 3 восстановитель
Расставим коэффициенты
4Cl+5 = Cl— + 3Cl+7
4КСlO3 → КС1 + 3КСlO4.
Задача 4. Какие из приведенных реакций являются внутримолекулярными? Расставьте коэффициенты в уравнениях реакций. Укажите восстановитель, окислитель.
а) KNO3 = KNO2 + O2;
б) Mq+ N2 = Mq3N2;
в) KClO3 = KCl + O2.
Показать решение »
Решение.
В реакциях внутримолекулярного окисления-восстановления перемещение электронов происходит внутри одного соединения, т.е. и окислитель и восстановитель входят в состав одного и того же сложного вещества (молекулы)
а) 2KNO3 = 2KNO2 + O2 — внутримолекулярная ОВР
N+5 +2e— = N+3 | 2 окислитель
2O-2 -4e— = O20 | 1 восстановитель
2N+5 + 2O-2 = 2N+3 + O20
б) 3Mq + N2 = Mq3N2 — межмолекулярная ОВР
N2 +6e— = 2N-3 | 2 | 1 окислитель
Mg0 -2e— = Mg+2 | 6 | 3 восстановитель
N2 + 3Mg0 = 2N-3 + 3Mg+2
в) 2KClO3 = 2KCl + 3O2 — внутримолекулярная ОВР
Cl+5 +6e— = Cl— | 4 | 2 окислитель
2O-2 -4e— = O20 | 6 | 3 восстановитель
2Cl+5+ 6O-2 = 2Cl— + 3O20
Задача 5.
Какие ОВР относятся к реакциям диспропорционирования? Расставьте коэффициенты в реакциях:
а) Cl2 + KOH = KCl + KClO3 + H2O;
б) KClO3 = KCl + KClO4 .
Показать решение »
Решение.
В реакциях диспропорционирования окислителем и восстановителем являются атомы одного и того же элемента в одинаковой степени окисления (обязательно промежуточной). В результате образуются новые соединения, в которых атомы этого элемента обладают различной степенью окисления.
а) 3Cl2 + 6KOH = 5KCl + KClO3 + 3H2O;
Cl20 +2e— = 2Cl— | 10| 5 окислитель
Cl20 -10e— = 2Cl+5 | 2 | 1 восстановитель
5Cl20 + Cl20 = 10Cl— + 2Cl+5
3Cl20 = 5Cl— + Cl+5
б) 4KClO3 = KCl + 3KClO4
Cl+5 +6e— = Cl— | 2 | 1 окислитель
Cl+5 -2e— = Cl+7 | 6 | 3 восстановитель
4Cl+5 = Cl— + 3Cl+7
Задача 6.
Составьте электронные уравнения и подберите коэффициенты ионно-электронным методом в реакции
KMnO4 + KNO2 + H2SO4 = K2SO4 + MnSO4 + KNO3 + H2O
Показать решение »
Решение.
Составим полуреакции:
MnO4— + 8H+ +5e— = Mn2+ + 4H2O | 2 окислитель
NO2— + H2O — 2e— = NO3— + 2H+ | 5 восстановитель
Сложим две полуреакции, умножив каждую на соответствующий коэффициент:
2MnO4— + 16H+ + 5NO2—+ 5H2O = 2Mn2+ + 8H2O + 5NO3— + 10H+
После сокращения идентичных членов, получаем ионное уравнение:
2MnO4— + 6H+ + 5NO2— = 2Mn2+ + 3H2O + 5NO3—
Подставим коэффициенты в молекулярное уравнение и уравняем его правую и левую части:
2KMnO4 + 5KNO2 + 3H2SO4 = K2SO4 + 2MnSO4 + 5KNO3 + 3H2O
Задача 7.
Определите методом электронного баланса коэффициенты в уравнениях окислительно-восстановительных реакций:
Zn + HNO3 = Zn(NO3)2 + NH4NO3 + H2O
Zn + H2SO4(конц) = ZnSO4 + SO2 + H2O
Показать решение »
Решение.
4Zn + 10HNO3 = 4Zn(NO3)2 + NH4NO3 + 3H2O
Составим электронные уравнения
Zn0 – 2 e = Zn2+ | 8 | 4 | восстановитель
N+5 + 8 e = N3- | 2 | 1 | окислитель
4Zn0 + N+5 = 4Zn2+ + N3-
Zn + 2H2SO4(конц) = ZnSO4 + SO2 + 2H2O
Составим электронные уравнения
Zn0 – 2 e = Zn2+ | 2 | 1 восстановитель
S+6 + 2 e = S+4 | 2 | 1 окислитель
Zn0 + S+6 = Zn2+ + S+4
Задача 8.
Можно ли в качестве окислителя в кислой среде использовать K2Cr2O7 в следующих процессах при стандартных условиях:
а) 2F— -2e— = F2, E0 = 2,85 В
б) 2Сl— -2e— = Cl2, E0 = 1,36 В
в) 2Br— -2e— = Br2, E0 = 1,06 В
г) 2I— -2e— = I2, E0 = 0,54 В
Стандартный окислительно-восстановительный потенциал системы
Cr2O72- + 14H+ + 6e— = 2Cr3+ + 7H2O равен E0 =1,33 В
Показать решение »
Решение.
Для определения возможности протекания ОВР в прямом направлении необходимо найти ЭДС гальванического элемента:
ЭДС = Е0ок — Е0восст
Если найденная величина ЭДС > 0, то данная реакция возможна.
Итак, определим, можно ли K2Cr2O7 использовать в качестве окислителя в следующих гальванических элементах:
F2|F— || Cr2O72-|Cr3+ E = 1,33 – 2,85 = -1,52 В
Cl2|Cl— || Cr2O72-|Cr3+ E = 1,33 – 1,36 = -0,03 В
Br2|Br— || Cr2O72-|Cr3+ E = 1,33 – 1,06 = +0,27 В
I2|I— || Cr2O72-|Cr3+ E = 1,33 – 0,54 = +0,79 В
Таким образом, в качестве окислителя дихромат калия можно использовать только для процессов:
2Br— -2e— = Br2 и 2I— -2e— = I
Задача 9. Вычислите окислительно-восстановительный потенциал для системы
MnO4— + 8H+ +5e— = Mn2+ + 4H2O
Если С(MnO4—)=10-5 М, С(Mn2+)=10-2 М, С(H+)=0,2 М.
Показать решение »
Решение.
Окислительно-восстановительный потенциал рассчитывают по уравнению Нернста:
E = E° + (0,059/n)lg(Cок/Cвос)
В приведенной системе в окисленной форме находятся MnO4— и H+, а в восстановленной форме — Mn2+, поэтому:
E = 1,51 + (0,059/5)lg(10-5*0,2/10-2) = 1,46 В
Задача 10. Рассчитайте для стандартных условий константу равновесия окислительно-восстановительной реакции:
2KMnO4 + 5HBr + 3H2SO4 = 2MnSO4 + 5HBrO + K2SO4 + 3H2O
Показать решение »
Решение.
Константа равновесия K окислительно-восстановительной реакции связана с окислительно-восстановительными потенциалами соотношением:
lgK = (E10 -E20 )n/0,059
Определим, какие ионы в данной реакции являются окислителем и восстановителем:
MnO4— + 8H+ +5e— = Mn2+ + 4H2O | 2 окислитель
Br— + H2O — 2e— = HBrO + H+ | 5 восстановитель
Общее число электронов, принимающих участие в ОВР n = 10
E10 (окислителя) = 1,51 В
E20 (восстановителя) = 1,33 В
Подставим данные в соотношение для К:
lgK = (1,51 — 1,33 )10/0,059
lgK = 30,51
K = 3,22*1030
Примеры ОВР с ответами приведены также в разделе тест Окислительно-восстановительные реакции
Категории ОБЩАЯ ХИМИЯ, Окислительно-восстановительные реакцииРешение уравнений· Темы на GitHub · GitHub
Здесь 160 общедоступных репозиториев соответствует этой теме.
..арабская погода / Афина
Звезда 68dbforge / SharpMath
Звезда 49кг / уравнение реакции
Звезда 31пронзительный / КубическоеУравнениеРешатель
Звезда 31Команда ИТМО-НСС / torch_DE_solver
Звезда 28ЮлияNLSolvers / NLSolversBase.jl
XCH-CEB / xch-проект
Звезда 23Эдуард Барг / Решатель нелинейных уравнений
Звезда 21еко0990 / MathSolver
Звезда 15млксд / GPUE
Звезда 14mssm199996 / решатель символических уравнений
Звезда 10Златанвасович / ChemEquations.
jl Звезда
9Нельсён / webgl-лаплас-решатель
Звезда 8себоспк / числовой_анализ_2s
Звезда 6АзизАлкасем / ФормулаЛаб
Звезда 6omarshawky15 / ArabicMathSolver-AndroidApp
Звезда 5ХогардДеЛаугер / lolcode-уравнение-решатель
Звезда 54рленрей / уравнение_решатель
Звезда 5Базовый Макс / QuadraticEquationCalculator
тачидок / scicellxx
Звезда 5Улучшить эту страницу
Добавьте описание, изображение и ссылки на
решатель уравнений
страницу темы, чтобы разработчикам было легче узнать о ней.
Курировать эту тему
Добавьте эту тему в свой репозиторий
Чтобы связать ваш репозиторий с решатель уравнений тему, перейдите на целевую страницу репозитория и выберите «управление темами».
Учить больше
Решатель диффузионно-волновых уравнений
Страница загрузки Решатель диффузионно-волновых уравнений.Обзор алгоритма дискретизации и решения DWE описан в разделе . Вывод начинается с дискретизации уравнения неразрывности и уравнения импульса. Затем дискретная форма ССВ получается из уравнений неразрывности и импульса. В заключение описывается алгоритм решения.
Уравнение неразрывности
Уравнение неразрывности дискретизируется для решателя DWE следующим образом:
| (1) 9n = Q_i |
где \Delta t — временной шаг, а скорости интерполированы по времени с использованием обобщенного метода Кранка-Николсона (который используется для взвешивания вклада скоростей в временных шагах и ).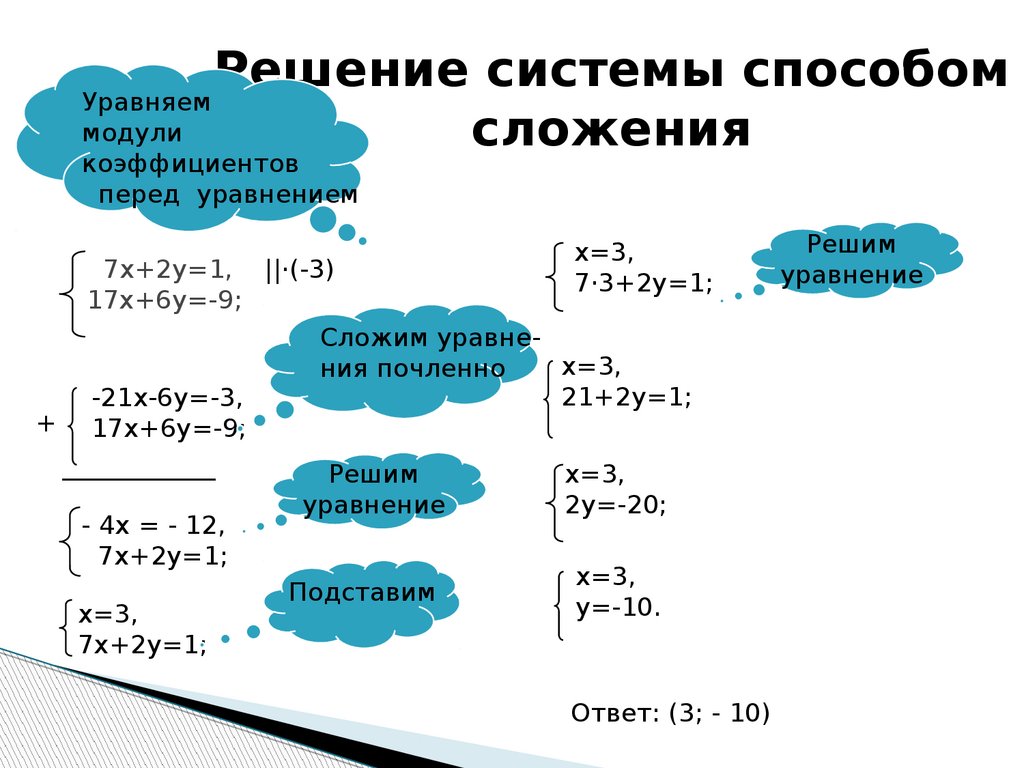
Поскольку уравнение импульса инвариантно относительно вращения, предполагается, что s_{i,k} является знаком внешнего направления на грани
Система уравнений для всех ячеек записывается в более компактной векторной форме как
| (5) | \boldsymbol{\Omega} (\boldsymbol{Z}) + \boldsymbol{\Psi} \boldsymbol{Z} = \textbf{b} |
Где \boldsymbol{\Omega} – вектор всех объемов ячеек, \boldsymbol{Z} – вектор высот поверхности воды во всех ячейках в момент времени n+1 , \boldsymbol{\Psi} – коэффициент матрица системы, а \textbf{b} – правый вектор.
где m обозначает индекс итерации (не путать с временным шагом).
При отсутствии потоков коэффициенты a_{i,j}=0 и Q=0, поэтому высота поверхности воды идентична предыдущему шагу. В частности, сухие ячейки остаются сухими до тех пор, пока в них не потечет вода. Уравнение (4) подразумевает, что коэффициенты a_{i,j} уравнения 2-170 будут зависеть от значения высоты поверхности воды. Чтобы сохранить согласованность с обобщенным методом Крэнка Николсона, члены a_{i,j} должны оцениваться в момент времени n+ \theta, создавая круговую зависимость от решения системы уравнений. Эта ситуация типична для нелинейных систем и исправляется путем итерации. Это представлено в шагах 5–8 ниже. 92} < \frac{1}{2 - 4 \theta}
При \theta = 1 полученная схема является неявной. Это соответствует использованию обратных разностей во времени и позиционированию пространственных производных на шаге 
Когда \ тета = 1/2, это схема Кранка-Николсона, полученная из центральных разностей во времени и позиционирующих пространственные производные при n + 1/2.
Линеаризованная схема имеет второй порядок пространственной точности. Точность времени зависит от выбора \theta; например, для \theta =1 это первый порядок точности, а для \theta =1/2 — второй порядок. 9{1/2} . Пограничные забойные течения входят во внутренние ячейки в качестве исходного члена в правой части системы уравнений.
Полный алгоритм решения приведен здесь: 9{n+1} можно рассчитать, используя дискретную версию уравнения импульса.
