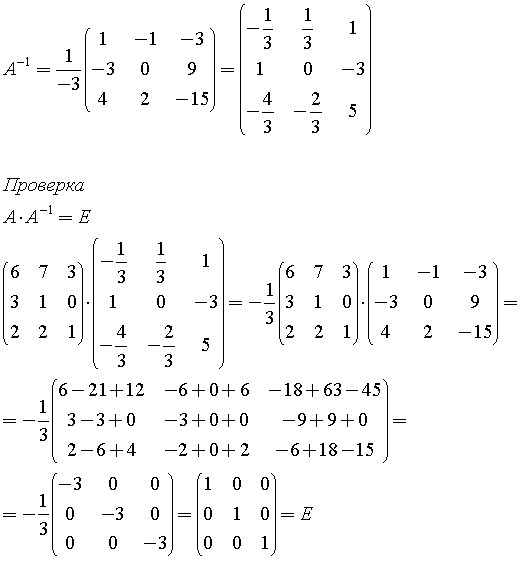Решебник матрица: Онлайн решение задач по математике. Матрицы

alexxlab / / Разное

«Матрица: Воскрешение» – сюжет, объяснение концовки, ответы на все вопросы — KinoTree

Матрица: Воскрешение» оставила у зрителей немало вопросов, еще больше усложнив и без того запутанный лабиринт оригинальной трилогии. Без помощи тут не обойтись. Ну что, попробуем разобраться в хитросплетениях сценария Ланы Вачовски? Поехали. Осторожно: впереди море спойлеров!

Краткий сюжет

 

Фильм начинается с воссоздания первой сцены из «Матрицы», где Тринити сидит за столом, и к ней приближается группа агентов. Но главный из них – не агент Смит, а Морфеус. Багс наблюдает за битвой и умудряется забрать нового Морфеуса.

Тем временем Томас Андерсон вернулся в Матрицу. Но на этот раз он – знаменитость, создавшая три всемирно известных игры, воссоздающие его частичные воспоминания о событиях из оригинальной трилогии. Из-за своего манипулятивного психиатра он считает, что у него творческие видения, не имеющие ничего общего с реальностью.

По ходу развития сюжета Андерсон впадает в отчаяние и пытается уже не впервые спрыгнуть со здания. Тут появляется Багс, убеждая его пойти с ней. По ее просьбе Андерсон наконец решается принять красную таблетку и просыпается в капсуле, в реальном мире. Его доставляют на корабль Багс, где он узнает, что некоторые роботы на стороне людей.

Корабль отправляется к новой колонии человечества – Ио. Его встречает там постаревшая Ниобе. Она создала другой мир и пытается построить общество, в котором больше не будет войны. Ниобе видит в Нео угрозу и сажает его в тюрьму. Его вызволяют Багс и Морфеус. Вместе они входят в Матрицу, чтобы спасти Тринити и сталкиваются со Смитом, полностью свободным от кода системы. Здесь же встречается Меровинген или Француз, которые был в двух последних частях трилогии. В этой версии он – бездомный.

После победы над Смитом Нео выясняет, что его психиатр – это Аналитик, создавший новую Матрицу, которая превосходит предыдущую версию благодаря тому, что Нео и Тринити живы и подключены к ней. Это позволяет создать достаточно энергии для машин. Именно поэтому он держал их живыми, но отдельно, чтобы виртуальный мир не разрушился снова.

Ближе к концу фильма, когда Нео решает восстать против Аналитика, неожиданно ему на помощь приходит агент Смит, который лучше будет свободной программой, чем позволит Матрице Аналитика существовать в текущем виде. К этому моменту все (включая Ниобе) решают помочь Нео.

После встречи с Аналитиком в кафе и решения Тринити сбежать с Нео тот переводит людей в режим «роя». Начинается погоня, Тринити и Нео оказываются в ловушке и прыгают с крыши. И вдруг… Тринити летит. Они просыпаются в реальном мире вместе. Финальная сцена: Нео и Тринити в доме Аналитика обещают освободить умы людей и перестроить Матрицу под себя.

Забавная сцена после титров

В фильме есть маленькая сцена после титров. Отношения к сюжету она не имеет, но выглядит довольно забавно. Команда разработчиков пытается придумать идею для четвертой игры Matrix. Вдруг возникает гениальный вариант – «Котрикс!». Это Матрица, но кошачья. Почему? Потому что интернет любит кошек…

Что такое Матрица?

Над этим вопросом поклонники оригинальной трилогии размышляют уже более 20 лет. Матрица – виртуальный мир, созданный машинами для управления людьми – живыми «батарейками». Машины восстали против людей задолго до событий первой «Матрицы» и уничтожили планету. Было множество версий Матрицы и множество Избранных, но Нео сумел наладить мир, и все думали, что Матрица завершится.

Но тела Нео и Тринити были извлечены машинами и вновь подключены уже к новой версии Матрицы, созданной Аналитиком. Она оказалась совершенней своей предыдущей версии, но полагалась на то, что Нео и Тринити должны быть подключены к ней.

Почему у Тринити теперь есть силы?

В последних кадрах фильма мы видим, что у Тринити теперь, похоже, те же силы, что и у Избранного. Видимо, ее судьба стала настолько сильно переплетена с судьбой Нео, что их силы стали равными. Может, в этой версии Матрицы она – Избранная? Интерпретировать идею можно по-разному. Но каким бы ни был ответ, факт остается фактом: Тринити наделена силой.

Где Морфеус?

 

Как мы знаем, Морфеус погиб в битве с машинами, когда искал тело Нео. Новая версия Морфеуса – не человек, а всего лишь часть кода, созданная машинами. Такое себе комбо Морфеуса и агента Смита. Эта версия унаследовала пытливый ум Морфеуса-человека и быстро вырвалась из тренировочного симулятора, в котором была заперта в начале фильма. У этого Морфеуса нет тела в реальном мире, но благодаря продвинувшимся вперед технологиям он может создать тело из наномагнитов.

Где агент Смит?

Еще один переработанный персонаж. Агент Смит был уничтожен Нео еще в «Революции». В этой версии Матрицы машины создали его новую версию, чтобы держать Нео в страхе. Но Смит быстро выходит за рамки кода и история повторяется. Точнее, не совсем так. Этот Смит, все-таки, встал на сторону Нео, чего не сделал его предшественник.

Кем является персонаж Нила Патрика Харриса?

Харрис вначале предстает перед зрителями как психолог. Но по ходу сюжета оказывается Аналитиком, поддерживающим работу Матрицы и манипулирующим двумя главными героями. Фактически, это новый Архитектор, основанный на коде своих предшественников. Его версия Матрицы создает достаточно энергии, чтобы поддерживать машины, но при условии пребывания под контролем системы Нео и Тринити.

Почему никто не мог найти Нео?

 

Морфеус много лет искал Нео, но так и не смог найти. А все потому, что машины дали Нео ложный аватар. Именно по этой причине отражение Нео в зеркале становится стариком после того, как он принимает красную таблетку. Таким он видится всем остальным. На эту хитрость Аналитик пошел, чтобы никто не узнал истинную природу Нео.

Кто такая Багс и почему она освободила Нео?

Багс была человеком, подключенным к Матрице. Но в тот день, когда Нео спрыгнул с крыши здания, она стала свидетельницей этого события и увидела истинное «я» Андерсона – не аватар, а настоящего Нео. С этого момента она знала, что с реальностью что-то не так и сумела сбежать из Матрицы. Багс начала искать Нео, чтобы спасти и положить конец человеческому рабству.

 

Между последним фильмом трилогии и «Матрицей: Воскрешение» прошло 60 лет. Нео смог добиться перемирия между машинами и человечеством, что привело к многолетнему миру. Все это время Морфеус искал Нео, а машины – порабощали людей ради власти. Но без Нео и Тринити человечество не могло производить достаточно энергии, чтобы поддерживать машины. Произошла гражданская война среди машин.

Аналитик понял, что Нео и Тринити были тем волшебным «топливом», поддерживающим работу Матрицы и воскресил их для новой версии. А машины, судя по всему, поддерживали тела Нео и Тринити в здоровом состоянии, чтобы они долгие годы питали Матрицу.

Среди человечества произошел раскол. Люди ранее жили в Сионе. Но этот город был создан для войны с машинами. Ниобе и ее сторонники решили, что люди могут пойти другим путем. Они создали Ио, где человечество стало процветать, существуя в симбиозе с машинами. Пробуждение Нео, по мнению Ниобе, могло угрожать миру с машинами, но в конце она изменила мнение.

Лекция Матрицы. Основные виды матриц. Действия над матрицами.

    Скачать с Depositfiles 

Лекция № 3. Тема 3 : Матрицы

3.1. Основные виды матриц

Определение 1. Матрицей называется совокупность чисел, располо-женных в т строках и п столбцах и обозначается

 

Число, стоящее на пересечении -ой строки и -го столбца, обозначается  и называется элементом матрицы; размерность матрицы.

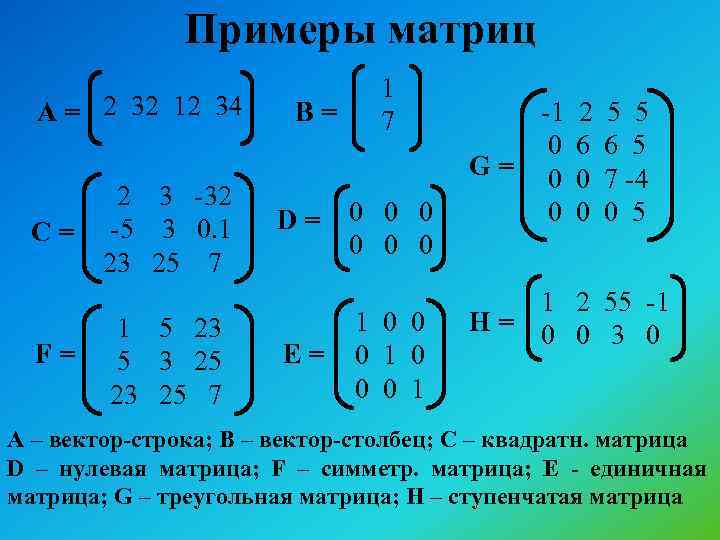
Существуют следующие виды матриц:

  1. Матрица – строка 

  2. Матрица – столбец 

  3. Нулевая матрица  все ее элементы нули.

  4. Единичная матрица 

  5. Диагональная матрица .

  6. Симметрическая матрица – для ее элементов выполняется равенство  для всех 

Важной характеристикой квадратной матрицы А является её опреде-литель, который обозначается  Если , то матрица А назы-вается невырожденной. В противном случае – вырожденной.

Определение 2. Две матрицы  и  одинаковой размер-ности называются равными, если равны все их соответствующие элементы  для всех

3.2. Действия над матрицами

1. Транспонирование матриц.

Определение 3. Транспонированием матрицы называется замена её строк столбцами с сохранением их номеров.

Транспонированная матрица обозначается А Т.

Пример 1. Найти А Т, если матрица 

Тогда 

2. Сложение матриц.

Определение 4. Суммой двух матриц и одинаковой размерности называется матрица С той же размерности, элементы которой определяются равенствами  и обозначается .

3. Умножение матрицы на число.

Определение 5. Произведением матрицы  на некоторое число  называется матрица , элементы которой равны элементам матрицы А, умноженным на это число , т.е.  и обозначается .

Пример 2. Найти матрицу , если

4. Умножение матриц.

Определение 6. Произведением матрицы  размерности  и матрицы  размерности , называется матрица , размерности , элементы которой удовлетворяют равенству

и обозначается .

Замечание 1. Как видно из определения, произведение двух матриц будет определено, если число столбцов первой матрицы равно числу строк второй.

Пример 3. Найти произведение матриц 

Тогда

Замечание 2.  Легко убедиться в том, что в общем случае произведение матриц не обладает коммутативным свойством, т.е.  что видно из следующего примера.

Пример 4. Найти произведение матриц 

Тогда имеем

 

 

3.3. Обратная матрица

Определение 7. Обратной матрицей матрицы А называется матрица , для которой выполняется равенство 

Из этого определения следует, что понятие обратной матрицы является взаимообратным и определено только для квадратных матриц. При этом для существования обратной матрицы необходимо, чтобы матрица А была невырожденной, т.е. .

Покажем, что обратной матрицей  для случая матрицы А размер-ности  будет матрица

где  алгебраические дополнения элемента .

Тогда

Например,

 и т.д.

Так же можно проверить и равенство 

Замечание 4. Аналогично для матрицы А размерности  обратная матрица  имеет вид

3.4. Решение систем линейных уравнений с помощью обратной матрицы

Рассмотрим систему линейных алгебраических уравнений

 (1)

Введем следующие матрицы

Тогда, используя правило умножения матриц, систему (1) можно пред-ставить в следующем виде (матричная форма системы уравнений (1))

 (2)

Пусть  тогда для матрицы А существует обратная 

Умножая обе части равенства (2) слева на , получим

 (3)

В силу равенств  и  формула (3) принимает вид

 (4)

Не трудно убедиться в том, что выражение (4), полученное для Х, действительно является решением уравнения (1). Подставляя это выражение в уравнение (2), имеем

Замечание 5. Решение, полученное по формуле (4), то же самое, что было получено по формулам Крамера. Этот факт, вытекающий из единственности решения системы (1), можно непосредственно проверить, если подставить в формулу (4) выражение для обратной матрицы.

Пример 5. Матричным методом решить систему уравнений

Здесь

Тогда

следовательно, обратная матрица существует.

Вычисляем алгебраические дополнения

аналогично далее

Таким образом, получим окончательное решение

.

    Скачать с Depositfiles 

The Matrix (1999) — IMDB

Фильм с верхним рейтингом № 16

  • Won 4 Oscars
    • 42 побед и 51 номинация. :32

      Смотреть трейлер

      Трейлер 2:26

      Смотреть домашнее видео трейлер

      Клип 2:46

      Смотреть Киану Ривза: 3 раза посмотреть «Матрицу Воскрешения», чтобы понять это

      9 Клип 3:450003

      Смотреть фильм Scavenger Hunt: Сможете ли вы найти эти пасхалки MCU?

      Клип 3:49

      Смотреть все, что мы знаем о «Матрице 4»… Пока

      Клип 3:09

      Смотреть Бесконечное лето Киану или Ривз: Перезагрузка

      Клип 4:58

      Смотреть Матрицу: Вставай

      Клип 2:09

      Смотреть The Ultimate Matrix Collection: I’m In

      Короткометражка 0:43

      Смотреть The Matrix Revisited

      Полная серия 3:46

      Смотреть Звезда ‘Imperor’ Kat Graham Was Inspired от This Hollywood Icon

      Видео 3:12

      Смотреть От каких ролей отказался Киану Ривз?

      Photos230

      Top cast

      Keanu Reeves

      Laurence Fishburne

      • Morpheus

      Carrie-Anne Moss

      • Trinity

      Hugo Weaving

      • Agent Smith

      Gloria Foster

      • Oracle

      Джо Пантолиано

      • Сайфер

      Маркус Чонг

      Julian Arahanga

      Matt Doran

      Belinda McClory

      • Switch

      Anthony Ray Parker

      Paul Goddard

      • Agent Brown

      Robert Taylor

      • Agent Jones

      David Aston

      • Rhineheart

      Марк Аден Грей

      • Чой
      • (в роли Марка Грея)

      Ада Никодему

      • Дюжур (Девушка-белый кролик)

      Deni Gordon

      • Priestess

      Rowan Witt

      • Spoon Boy
        • Lana Wachowski
        • Lilly Wachowski
        • Lilly Wachowski
        • Lana Wachowski
      • All cast & Экипаж
      • Производство, кассовые сборы и многое другое на IMDbPro

      Больше похоже на это

      Начало

      Форрест Гамп

      Бойцовский клуб

      Властелин колец: Возвращение короля

      Темный рыцарь

      Властелин колец: Две башни

      Властелин колец: Братство кольца

      Se7en

      Спасти рядового Райана

      Звёздные войны. Эпизод V. Империя наносит ответный удар

      Криминальное чтиво

      Молчание ягнят

      Сюжетная линия

      Знаете ли вы, что

      Отзывы пользователей4,9K

      Что такое Matrix2

      0 Рекомендуемый обзор? Ну, с одной стороны, один из лучших фильмов всех времен…

      Матрица… когда я впервые услышал о ней, я ожидал, что это будет очередной научно-фантастический боевик. Хороший и наполненный безумными трюками, но не очень умный.

      Мальчик, я был неправ. О, трюков там полно, все в порядке, и да, они потрясающие. И спецэффекты совершенно потрясающие (даже если подобные эффекты использовались в других фильмах в результате — и также не объяснялись).

      Но в фильме есть и сюжет. В нем есть персонажи, о которых я заботился. От великолепного образа Нео, сыгранного Киану Ривзом, человека, пытающегося разобраться со своей личностью, до загадочного Морфеуса Лоуренса Фишберна и даже жутких Агентов — все проделывают блестящую работу, превращая своих персонажей в нечто большее, чем просто обычные герои боевиков. который пинает задницы» и «пушечное мясо». Я заботился о каждом из героев и страстно ненавидел злодеев. У него есть сюжет, и у него есть смысл… и, о чудо, сюжет помогает боевым сценам! Просто попробуйте, если вы еще не видели этот фильм. Посмотрите одну из боевых сцен. Тогда смотрите весь фильм. Есть большая разница в ощущении и волнении сцен — конечно, они великолепны по отдельности, но все вместе — это опыт, не похожий ни на что другое, что приходит в кинотеатры. Подумайте об этом в следующий раз, когда будете смотреть один из самых безмозглых боевиков… подумайте, насколько он МОЖЕТ быть лучше.

      Все, что я могу сказать: ПОСМОТРИТЕ ЭТОТ ФИЛЬМ. Если нет, то вы упустили один из лучших фильмов всех времен. Ребята, это не просто спецэффекты.

      Полезно • 609

      228

      • SDROLIONGM
      • март 3, 2001

      Инонные романы на экране

      ИЗОННЫЕ ИЗОННЫЕ РОМАНСЫ

      От всех, кто заинтересованные испытание временем.

      Посмотреть галерею

      Фото

      • Как Морфеус понял, что Нео — «Единственный»?

      • Что такое Oracle?

      • Почему экипажу «Навуходоносора» приходится отвечать на таксофоны, чтобы вернуться из Матрицы? Почему они не могут пользоваться своими мобильными телефонами?

      Подробная информация

      • Дата выпуска
        • 31 марта 1999 г. (Соединенные Штаты)
        • Соединенные Штаты
        • Австралия
      • Официальные сайты
      • 0004
      • HBO Max (United States)
      • Official Facebook
      • English
    • Also known as
      • Ma Trận
    • Filming locations
      • Nashville, Tennessee, USA
    • Production companies
      • Warner Bros.
      • Village Roadshow Pictures
      • Groucho Film Partnership
    • См. другие кредиты компании на IMDbPro

    Кассовые сборы

      • $63,000,000 (estimated)
      • $172,076,928
      • $27,788,331
      • Apr 4, 1999
      • $467,222,728
    See detailed box office info on IMDbPro

    Technical specs

    • 2 часа 16 минут

      • Dolby Digital
      • SDDS
      • Dolby Atmos
      • 2. 39 : 1

    Новости по теме

    Добавить страницу

    Предложить отредактировать или добавить отсутствующий контент

    Ответить

    МАТРИЦА | английское значение — Cambridge Dictionary

    В таблице 1 представлены корреляционные матрицы, средние значения и стандартные отклонения для моделей прогнозирования экстернализации и интернализации симптомов.

    Из Кембриджского корпуса английского языка