§12. Множества и логика | Диаграммы Эйлера-Венна (informatika_09_34_pol)
Планирование уроков на учебный год (по учебнику К.Ю. Полякова, Е.А. Еремина, базовый уровень)
Главная | Информатика и информационно-коммуникационные технологии | Планирование уроков и материалы к урокам | 9 классы | Планирование уроков на учебный год (по учебнику К.Ю. Полякова, Е.А. Еремина, базовый уровень) | §12. Множества и логика
Содержание урока
Множества
Диаграммы Эйлера-Венна
Количество элементов во множестве
Сложные запросы в поисковых системах
Выводы
Вопросы и задания
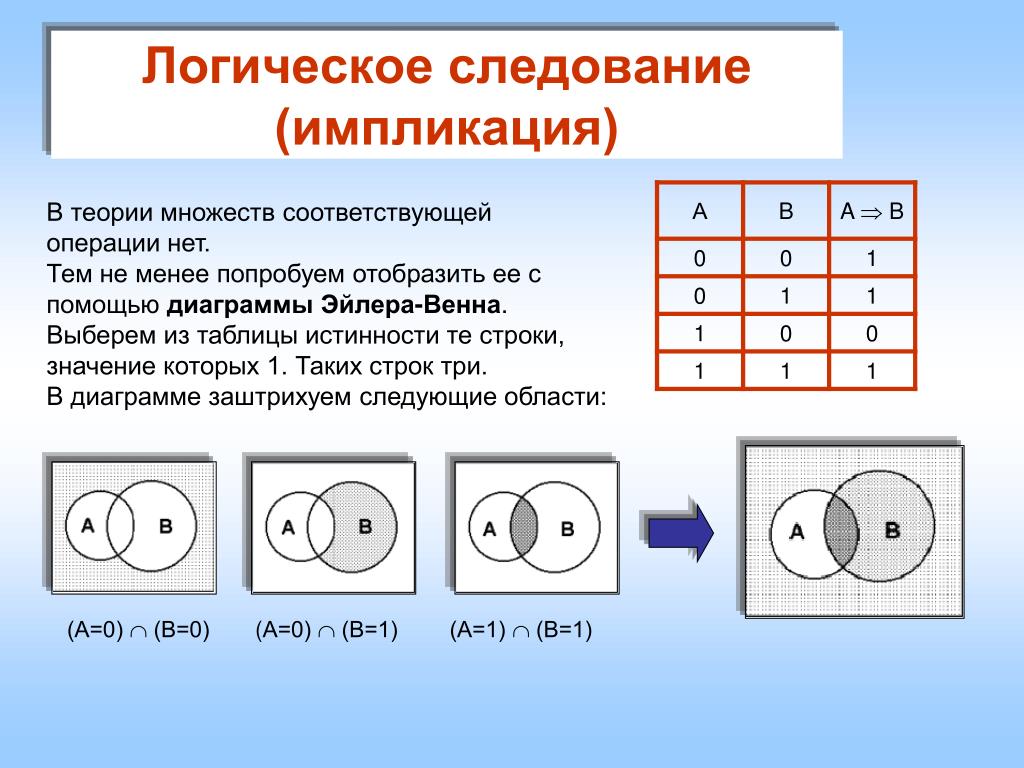
Множества удобно изображать графически, в виде диаграмм. Их называют диаграммами Эйлера—Венна в честь авторов этой идеи — математика Леонарда Эйлера и логика Джона Венна. На такой диаграмме каждому множеству соответствует какая-то область (круг, прямоугольник и др.) — рис. 2.34. Все элементы внутри этой области принадлежат множеству, все элементы вне области — не принадлежат.
На такой диаграмме каждому множеству соответствует какая-то область (круг, прямоугольник и др.) — рис. 2.34. Все элементы внутри этой области принадлежат множеству, все элементы вне области — не принадлежат.
Рис. 2.34
Вы уже знаете, что множество можно задать условием (логическим выражением), которое выполняется для всех элементов множества и не выполняется для всех элементов, не входящих в него. Дальше для сокращения записи мы будем вместо слов «множество, для которого выполняется условие А» писать просто «множество А». Тогда множество «НЕ А» на диаграмме — это все точки за границами круга (рис. 2.35).
Рис. 2.35
Такое множество называется дополнением множества А до универсального множества U, включающего все элементы некоторого класса. Например, если мы рассматриваем только целые числа и А — это множество чётных целых чисел, то А — множество нечётных целых чисел.
Можно считать, что дополнение А — это «разность» между универсальным множеством U и множеством А, т. е. все элементы из U, которые не входят в А.
Для каждого из следующих множеств выберите универсальное множество и запишите дополнение А:
а) А = {1, 3, 5, 7, 9};
б) А = {а, е, ё, и, о, у, ы, э, ю, я};
в) А = {17, 34, 51, 68, 85};
д) А = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, А, В, С};
е) А = отрезок [0; 1].
На диаграмме можно изображать несколько множеств, каждому из них соответствует своя область (круг). Круги на диаграмме могут пересекаться. Элементы, расположенные в общей части кругов А и В, — это пересечение множеств А и В. Для этих элементов выполняется как условие А, так и условие В, т. е. выполняется условие А и В (А • В) — рис. 2.36.
Рис. 2.36
Если круги не пересекаются (множества не содержат общих элементов), их пересечение — это пустое множество ∅.
Для пары множеств определите пересечение А • В:
а) А = {1, 3, 5, 7, 9}, В = {1, 5, 6, 9, 12};
б) А = {а, б, в, г, д, е, ё, ж}, В = {а, е, ё, и, о, у, ы, э, ю, я};
г) А = {00, 10}, В = {01, 11};
д) А = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, А, В, С}, В = {А, В, С, D, Е, F, G, Н};
е) А = [5; 15], В = [10; 20];
ж) А = [5; 15], В = [0; 20];
з) А = [5; 15], В = [10; 12];
и) А = [5; 15], В = [20; 30].
Элементы, входящие хотя бы в одно из множеств: в А или в В, образуют новое множество, которое называется объединением множеств А и В. Для всех элементов этого множества выполняется условие А или В (А + В) — рис. 2.37.
Рис. 2.37
Для пары множеств определите объединение А + В:
а) А = {1, 3, 5, 7, 9}, В = {1, 5, 6, 9, 12};
б) А = {а, б, в, г, д, е, ё, ж }, В = {а, е, ё, и, о, у, ы, э, ю, я};
в) А = {17, 34, 51, 68, 85}, В = {17, 34, 51, 68, 85};
г) А = {00, 10}, В = {01, 11};
д) А = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, А, В, С}, В = {А, В, С, D, Е, F, G, И};
ж) А = [5; 15], В = [0; 20];
з) А = [5; 15], В = [10; 12];
и) А = [5; 15], В = [20; 30].

Подобные диаграммы можно нарисовать для любого логического выражения, ведь каждое из них определяет некоторое множество. Например, возьмём выражение А + В. Оно равно 0 только при А = 1 и В = 0, поэтому на диаграмме незакрашенной останется только область, которая входит в круг А и не входит в круг В (рис. 2.38).
Рис. 2.38
В тетради постройте диаграммы для логических выражений:
а) А + B;
б) А • B + А • В;
в) А • B + А • B.
Диаграмма для трёх переменных содержит три круга, каждый из которых (в общем случае) пересекается с двумя другими (рис. 2.39).
Рис. 2.39
Для удобства на рис. 2.39 области пронумерованы. Запишем, для примера, логическое выражение для области 3. Эта область находится внутри кругов А и B (следовательно, выражения А и B истинны), но вне круга С, поэтому выражение С ложно. Получается условие А и B и (не С), или, в
других обозначениях, А • B • C.
Запишите в тетради логические выражения для остальных областей на рис. 2.39.
Для того чтобы найти выражение для объединения двух или нескольких областей, надо сложить (используя логическое сложение — операцию ИЛИ) выражения для всех составляющих. Например, выражение для объединения областей 3 и 4 на рис. 2.39 имеет вид:
3 + 4:А • В • C + А • В • C.
Вместе с тем точки в этих областях отличаются от других тем, что они входят в область Б и не входят в область С. Поэтому справедлива более простая формула:
3 + 4: B • C.
Это означает, что логические выражения в некоторых случаях можно упростить.
Следующая страница Количество элементов во множестве
Cкачать материалы урока
Диаграмма Венна — voxt
Диаграммы Венна относятся к схематическому представлению множеств с помощью кругов. Этот метод был представлен английским логиком Джоном Венном в 1880 году. Он также известен как диаграммы множеств или логические диаграммы и используется в таких дисциплинах, как математика, статистика и бизнес-исследования.
Он также известен как диаграммы множеств или логические диаграммы и используется в таких дисциплинах, как математика, статистика и бизнес-исследования.
Эта концепция отражает влияние теории множеств. Набор — это набор различных вещей или объектов или предметов; например, он может содержать числа, символы или фигуры. Теория множеств фокусируется на свойствах совокупности объектов. Он имеет дело с формулами теории множеств, отношениями, операциями и т. Д.
Оглавление
Программы для Windows, мобильные приложения, игры — ВСЁ БЕСПЛАТНО, в нашем закрытом телеграмм канале — Подписывайтесь:)
- Что такое Диаграмма Венна?
- Объяснение диаграммы Венна
- Формула с расчетом
- Символы диаграммы Венна
- Союз (У):
- Пересечение (∩):
- Дополнение: (Ас)
- Приложения
- Часто задаваемые вопросы (FAQ)
- Рекомендуемые статьи
Ключевые выводы
- Диаграммы Венна, основанные на теории множеств, относятся к схематическому представлению множеств с помощью кругов.
 Английский логик Джон Венн ввел его в 1880 году.
Английский логик Джон Венн ввел его в 1880 году. - Он имеет широкий спектр применения в академическом и деловом мире. Например, он широко используется в математике, статистике, информатике и дисциплинах управления бизнесом.
- Общие используемые символы: U (объединение), ⋂ (пересечение) и Ac (дополнение A).
- Основная формула для диаграммы, содержащей два набора:
n(AUB) = n(A) + n(B) – n (A ⋂ B)
Объяснение диаграммы Венна
Диаграмма Венна представляет различные наборы, рассматриваемые для изучения или сравнения, с помощью кружков. Круглая область представляет набор. Если между круговыми областями нет перекрытия, представленные множества не имеют ничего общего, а если круговая область перекрывается, между перекрывающимися множествами есть что-то общее. Кроме того, если набор является подмножеством другого набора, меньший круг будет виден внутри другого круга.
Метод может содержать любое количество кругов. Однако сложность схематического представления возрастает с увеличением количества кругов. Так, наиболее распространенным является использование двух или трех кругов. Каждый регион в представлении имеет свое значение, передавая определенную информацию. Как правило, перекрывающаяся или пересекающаяся область выделена графически, чтобы обозначить общность. Диаграмму Венна построить несложно; используя онлайн-шаблоны диаграмм Венна, Майкрософт офис инструменты или онлайн-конструктор диаграмм Венна.
Так, наиболее распространенным является использование двух или трех кругов. Каждый регион в представлении имеет свое значение, передавая определенную информацию. Как правило, перекрывающаяся или пересекающаяся область выделена графически, чтобы обозначить общность. Диаграмму Венна построить несложно; используя онлайн-шаблоны диаграмм Венна, Майкрософт офис инструменты или онлайн-конструктор диаграмм Венна.
Она очень похожа на диаграмму Эйлера, и определить разницу между ними непросто. Основное отличие состоит в том, что диаграммы Эйлера представляют только существующие отношения; не будет пустых перекрестков. Напротив, диаграмма Венна показывает все возможные логические отношения и представляет пересечения, даже если она пуста.
Формула с расчетомОсновная формула диаграммы Венна:
n(AUB) = n(A) + n(B) – n (A ⋂ B)
Здесь,
- n(AUB): все элементы множеств A и B
- n (A): количество элементов, присутствующих в наборе A.

- n(B): количество элементов, присутствующих в наборе B.
- n (A ⋂ B): количество элементов, общих как в A, так и в B.
Давайте рассмотрим следующий пример диаграммы ВеннаПример диаграммы ВеннаДиаграмма Венна — это один из видов диаграмм в Excel, который используется для анализа отношений, представленных между двумя или более группами через пересекающиеся части кругов. Чтобы лучше понять концепцию, читайте больше.
В отделе продаж и маркетинга компании работает 200 сотрудников, 140 сотрудников участвуют в продажах, а 120 сотрудников участвуют в маркетинговых мероприятиях. Сколько сотрудников принимают участие как в продажах, так и в маркетинге? Также найдите сотрудников, занимающихся только продажами.
Набор A: Сотрудники, участвующие в продажах
Набор B: Сотрудники, участвующие в маркетинговой деятельности
п(АУБ)= 200
п(А) = 140
п(В) = 120
n(A ⋂ B) — количество сотрудников, участвующих как в продажах, так и в маркетинге.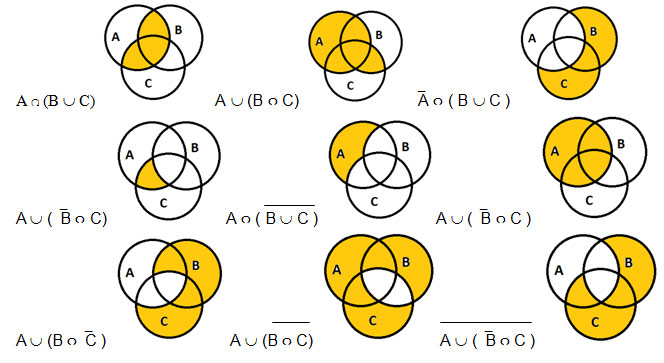 Следовательно, применение формулы дает следующее:
Следовательно, применение формулы дает следующее:
n(A ⋂ B) = n(A) + n(B) – n(AUB)
п(А ⋂ В) = 140 + 120 – 200
= 60
Сотрудники, занимающиеся только продажами = Сотрудники, занимающиеся продажами – Сотрудники, занимающиеся как продажами, так и маркетингом
= п (А) – п (А ⋂ В)
= 140 – 60
= 80
Следовательно, количество сотрудников, участвующих как в продажах, так и в маркетинге, составляет 60 человек, а количество сотрудников, занимающихся только продажами, составляет 80 человек.
Символы диаграммы ВеннаНаиболее часто используются следующие символы:
Союз (U):
Он представляет собой объединение всех множеств, представленных на диаграмме Венна. Так, например, если есть два набора, A и B, это будет (AUB).
Пересечение (∩):
Он представляет общие элементы всех присутствующих наборов. Так, например, если есть два множества A и B, это будет (A ⋂ B).
Так, например, если есть два множества A и B, это будет (A ⋂ B).
Дополнение: (Ас)
Он представляет то, чего нет в указанном наборе. Ac исключает элемент множества A. Уравнение Ac = U/A изображает дополнение A, где U — универсальное множество, A — подмножество U, а дополнение множества A — все элементы U, которые не являются в.
Приложения- Он используется в математике и других предметах, чтобы легко проиллюстрировать сложные проблемы или сценарии. Например, при правильном использовании диаграммы Венна избавляют экспертов от необходимости получать ответ, используя сложные шаги и формулы, особенно для ответов в цифрах и значениях. Это также упрощает представление факторов и сценариев, которые трудно объяснить словесно или математически.
- Он используется в бизнес-презентациях для отображения различных бизнес-концепций, визуализации идей и сравнения конкурентов.
 Например, это помогает обозначить сходства и различия между различными продуктами и прототипами.
Например, это помогает обозначить сходства и различия между различными продуктами и прототипами.
Часто задаваемые вопросы (FAQ)
Что такое диаграмма Венна?
Он обычно используется в математике, статистике, информатике, управлении бизнесом и т. д. для представления сложных сценариев или концепций. Метод, основанный на теории множеств, представляет конкретные множества с помощью окружностей. Перекрывающиеся кружки указывают на общность между обозначаемыми ими множествами. Отсутствие перекрытия или пересечения подразумевает отсутствие логической связи между множествами.
Что такое диаграмма Венна A ∩ B?
«∩» — это символ, используемый для обозначения операции пересечения. Например, если диаграмма состоит из двух кругов, представляющих два набора, A и B, то A ∩ B (пересечение A B) указывает на элементы, общие для обоих наборов, представленные перекрывающимся участком двух кругов. В то же время, если есть три множества, A, B и C, пересечение будет A ∩ B ∩ C.
В то же время, если есть три множества, A, B и C, пересечение будет A ∩ B ∩ C.
Всегда ли диаграмма Венна состоит из трех кругов?
Нет, теоретически он может содержать любое количество кругов. Однако по мере увеличения количества кругов возрастает и сложность. Следовательно, большинство представлений содержат два или три круга.
Рекомендуемые статьи
Это руководство к тому, что такое диаграмма Венна. Мы объясняем его пример, символы, формулу, приложения и то, как это сделать, используя такие параметры, как шаблоны. Вы можете узнать больше из следующих статей –
- Описательная статистика
- Статистика
- Рассеивание
Программы для Windows, мобильные приложения, игры — ВСЁ БЕСПЛАТНО, в нашем закрытом телеграмм канале — Подписывайтесь:)
Символы диаграммы Венна и набор обозначений
1. Установите обозначение
В качестве основы символов диаграммы Венна обозначение множества используется в математике для определения типа множества и его свойств.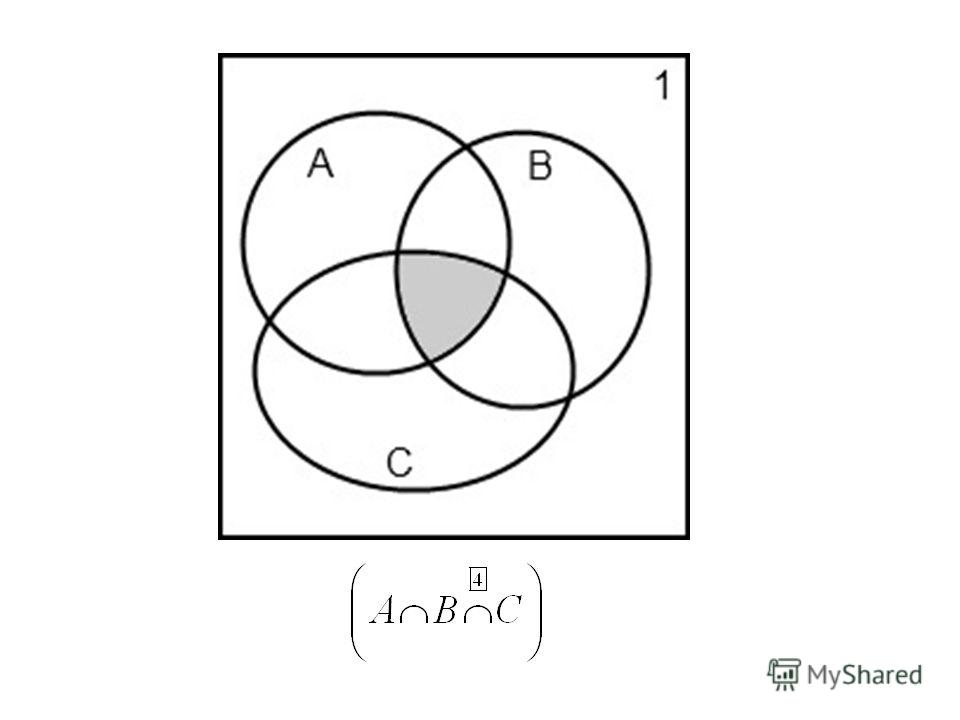 В обозначении набора используется система символов для:
В обозначении набора используется система символов для:
- Задайте свойства элементов в наборе.
- Покажите отношения между множествами.
- Показать операции между множествами.
Обозначение множества на диаграмме Венна имеет некоторые особые правила для описания множества. Он использует фигурные скобки или фигурные скобки { }, и члены набора, называемого элементами, помещаются в эти фигурные скобки, которые иногда называют фигурными скобками. Имена наборов обычно обозначаются заглавными английскими буквами.
Источник: EdrawMax Commnutiy — Символы диаграммы Венна
Ниже приведены некоторые примеры множеств в обозначениях множеств.
- Набор натуральных чисел: N = {1, 2, 3, 4, 5…}
- N = набор натуральных чисел больше или равный 1.
- N = {п | n ∈ ℕ, n ≥ 1}
- {} фигурные скобки — это символ набора, ограничивающий описание набора
- ∈ = элемент множества
- ∉ = «не является членом» или «не является элементом».

- | и: может использоваться, чтобы показать «где» или «такой, что»
- ⊂ : подмножество
- ⊄ : набор символов, показывающий, что это не подмножество
Например, если все элементы множества А также являются элементами множества В, то можно сказать, что А ⊂ В.
Если A = {1, 2, 3} и B = {1,2,3,4,5,6,7,8,9}
Тогда A ⊂ B, т. е. «A является подмножеством B».
2. Объяснение символов диаграммы Венна
В теории множеств над заданными множествами можно выполнять множество операций. Эти операции могут быть представлены с помощью символов диаграммы Венна . Диаграммы Венна являются эффективным инструментом для визуального описания операций теории множеств. Хотя существует около 30 символов диаграммы Венна, наиболее важные из них обсуждаются ниже.
- Союз Сета
- Пересечение множества
- Комплектация набора
- Разница в наборе
2.
 1 Объединение двух множеств: символ ∪
1 Объединение двух множеств: символ ∪На диаграмме Венна каждый круг представляет определенный набор или категорию. Символ ∪ в математике представляет собой объединение двух множеств или двух окружностей. В двухкруговой диаграмме Венна полная диаграмма иллюстрирует операцию A ∪ B. A ∪ B означает набор всех элементов A или B или обоих.
Например, набор A может представлять людей, которые любят суши, а набор B может изображать людей, которые хотят есть креветки. Таким образом, A ∪ B может представлять людей, которые любят суши, креветки или и то, и другое.
2.2 Пересечение двух множеств: ∩ символ
Пересечение двух множеств обозначается символом диаграммы Венна ∩. Набор пересечений имеет все элементы, общие для обоих наборов или категорий. На диаграмме Венна пересечение — это площадь, на которую накладываются обе окружности.
Итак, если A представляет людей, которые любят суши, а B — людей, которые хотят есть креветки. Итак, множество A ∩ B содержит всех людей, которые любят и суши, и креветки.
2.3 Комплектация набора: А
вЕсли вы хотите представить то, что не представлено в наборе, каждый член, не включенный в набор A, является дополнением набора A, A c . Он представляет элементы, которых нет в наборе A, и может быть представлен с помощью диаграммы Венна с кружком. Если буква U обозначает универсальный набор, то область, охватываемая универсальным набором, за исключением области, охватываемой набором A, представляет собой дополнение к A.
2.4 Отличие установленной диаграммы Венна
Различие множеств или относительное дополнение множества представлено символьной операцией A-B на диаграмме Венна. AB содержит все элементы A, которые не принадлежат B. На диаграмме Венна кружки показывают AB как область, покрытую множеством A, за исключением области, общей для множества B
2.5 Пустой набор
Пустое множество можно обозначить символом диаграммы Венна «Φ» и «φ» или {}. Пустое множество — это множество без элементов.
2.6 Универсальный набор
Универсальный набор — это набор, содержащий все релевантные элементы с точки зрения рассматриваемой проблемы. Универсальный символ набора — заглавная буква U. В универсальный набор входит все, что вас интересует или все, что имеет отношение к вашей проблеме.
3. Три или более множеств на диаграмме Венна
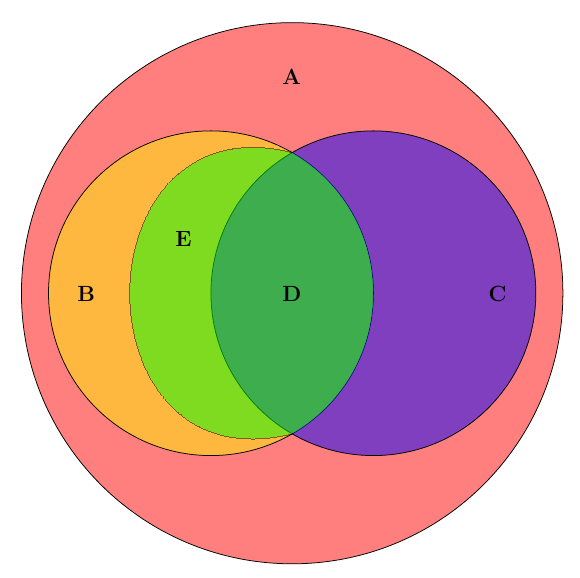
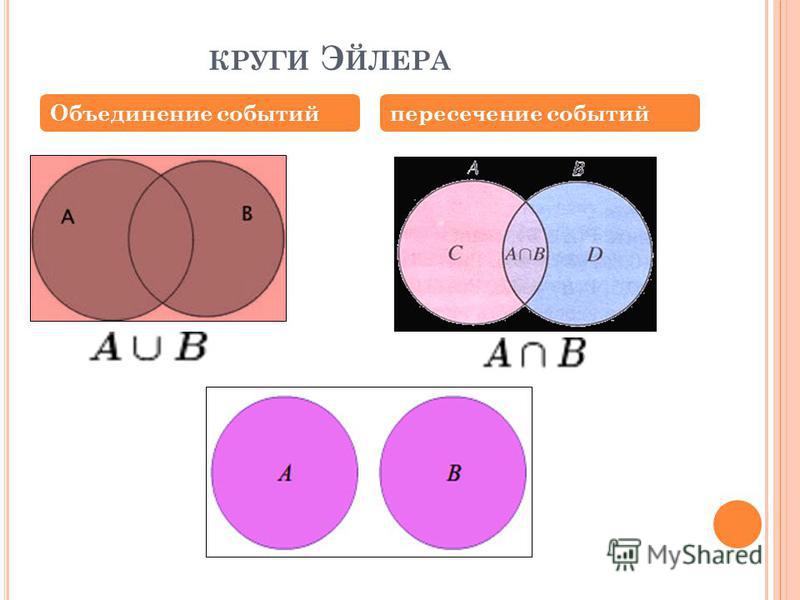
Диаграммы Венна с тремя наборами или диаграммы Венна с тремя кругами состоят из трех перекрывающихся кругов, чтобы показать взаимосвязь между элементами трех наборов. В диаграмме Венна с тремя множествами существует множество связей. Если A, B и C — три круга на диаграмме Венна, то мы можем наблюдать;
- Элементы, общие в A и B = только элементы в A и B плюс элементы в A, B и C.
- Элементы, общие для B и C = только элементы для B и C плюс элементы для A, B и C.
- Элементы, общие для A и C = только члены для A и C плюс элементы для A, B и C.
Поясним это на следующем примере.
| Животное | А | Б | С |
| Собака | Икс | ||
| Тигр | Икс | ||
| Жирафа | Икс | Икс | Икс |
| Муравей | Икс | ||
| Корова | Икс | Икс |
Область диаграммы Венна для шоу A U B {Собака, Жираф, Корова, Тигр}
Диаграмма Венна для шоу A U B U C {Собака, Жираф, Корова, Тигр, Муравей}
Диаграмма Венна для A ∩ C показывает {Жирафа}
Источник: EdrawMax Online
4. Советы по использованию символов диаграммы Венна
Диаграммы Венна очень полезны во многих областях. Математики используют их для решения сложных задач.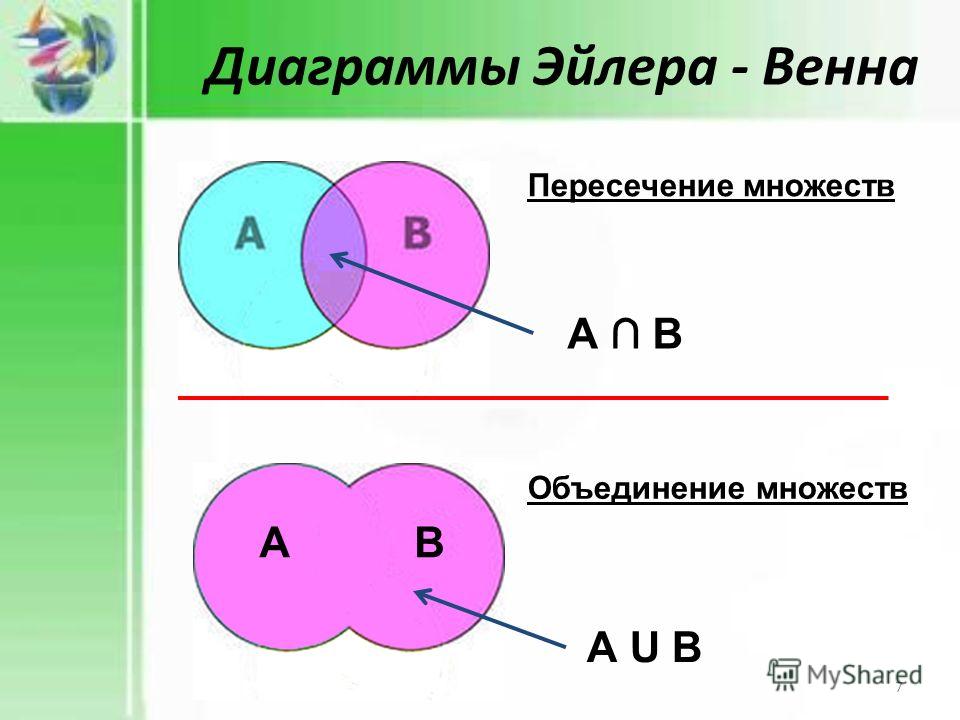 Эти диаграммы помогают в организации информации и представляют отношения для визуальной коммуникации.
Эти диаграммы помогают в организации информации и представляют отношения для визуальной коммуникации.
Вот несколько советов по использованию символов диаграммы Венна для ваших нужд.
- Важно, чтобы вы знали основную цель и ожидаемый результат диаграммы Венна. Он устанавливает прочную основу для эффективного и действенного использования вашей диаграммы. Поймите свою цель. Всегда полезно иметь готовое заявление о ваших основных намерениях, прежде чем приступать к фактическому рисованию.
- Далее аккуратно и правильно подберите свой образец. Это может показаться простым для тривиальных примеров, но для сложных систем определение образца требует надлежащего анализа и наблюдения. Вы должны уметь мыслить нестандартно и понимать разницу между наблюдениями, выбором, аргументами или решениями.
- После того, как ваша основа будет сделана, определите свой стиль диаграммы Венна. Вы можете обратиться к библиотеке шаблонов в EdrawMax, чтобы ознакомиться с различными примерами и методами построения диаграмм Венна.

- Быстро найдите символы диаграммы Венна в EdrawMax Online>Библиотека символов>Умные фигуры>Диаграмма Венна.
- EdrawMax Online имеет обширную библиотеку символов, но если вы не можете найти нужный символ диаграммы Венна, вы также можете импортировать символы в виде изображений, символов или данных из таких форматов файлов, как SVG, VSSX и т. д. Перейдите к опции библиотеки на боковой панели и щелкните значок импорта. Появится новое всплывающее окно, позволяющее импортировать файлы.
EdrawMax Online — это программное обеспечение для рисования премиум-класса с исчерпывающими символами, простой в использовании компоновкой и эксклюзивной коллекцией шаблонов. Вы можете легко использовать эту программу, используя следующие советы, чтобы сэкономить время и усилия.
Вы также можете узнать больше из этого видео. YouTube.
5. Вывод
Диаграммы Венна — это визуальное представление математических концепций теории множеств.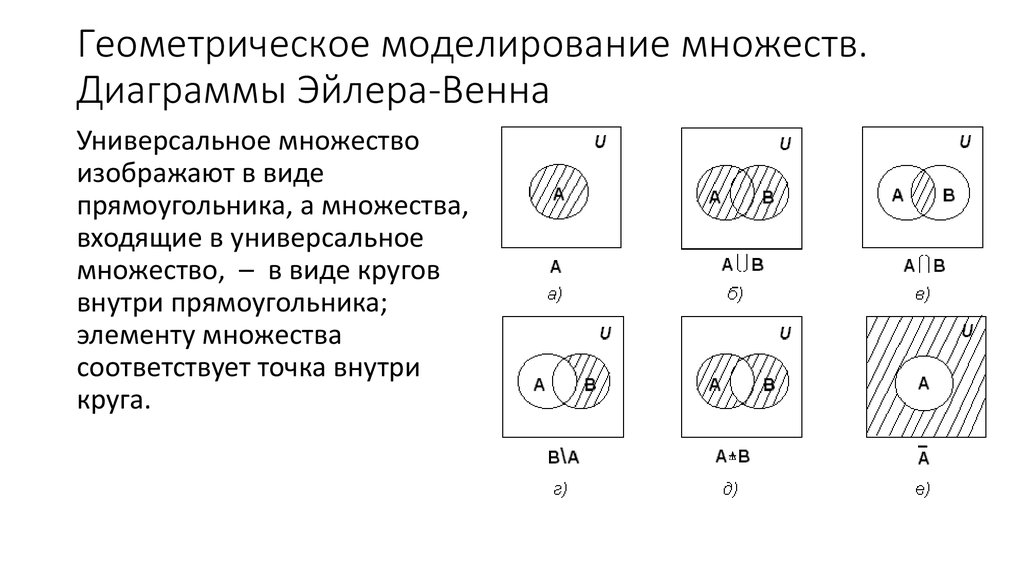 Они используют определенные символы диаграммы Венна , чтобы показать логические отношения между различными группами наборов. Эти диаграммы могут быть очень полезны в теории вероятностей, логике и статистике, математике и информатике, лингвистике, социологии и маркетинге.
EdrawMax Online — это мощное средство для создания диаграмм Венна с обширной библиотекой для символов UML, а также для других типов диаграмм, число которых превышает 280. Вы также можете использовать бесплатные и полностью настраиваемые профессиональные примеры диаграмм Венна, доступные в сообществе шаблонов. Многие общие сценарии уже доступны в сообществе шаблонов, так что вы можете быстро приступить к работе на прочной основе.
Они используют определенные символы диаграммы Венна , чтобы показать логические отношения между различными группами наборов. Эти диаграммы могут быть очень полезны в теории вероятностей, логике и статистике, математике и информатике, лингвистике, социологии и маркетинге.
EdrawMax Online — это мощное средство для создания диаграмм Венна с обширной библиотекой для символов UML, а также для других типов диаграмм, число которых превышает 280. Вы также можете использовать бесплатные и полностью настраиваемые профессиональные примеры диаграмм Венна, доступные в сообществе шаблонов. Многие общие сценарии уже доступны в сообществе шаблонов, так что вы можете быстро приступить к работе на прочной основе.
EdrawMax Онлайн
Создайте 280+ типов диаграмм онлайн
Доступ к диаграммам в любом месте и в любое время
Все на рабочем столе + Сообщество шаблонов
Управление командой и сотрудничество
Интеграция личного облака и Dropbox
ПОПРОБУЙТЕ ОНЛАЙН
EdrawMax Desktop
Создайте более 280 типов диаграмм
Поддержка Windows, Mac, Linux
Полный доступ к ресурсам и шаблонам
Локальное программное обеспечение для бизнеса
Безопасность данных корпоративного уровня
СКАЧАТЬ СКАЧАТЬ СКАЧАТЬ
СКАЧАТЬ
Как найти объединение диаграммы Венна
Все математические ресурсы ACT
14 Диагностические тесты 767 практических тестов Вопрос дня Карточки Учитесь по концепции
Справка по математике ACT » Анализ данных » Диаграммы Венна » Союз » Как найти объединение диаграммы Венна
Учитывая приведенную ниже диаграмму Венна, что из следующего не принадлежит ?
Возможные ответы:
Правильный ответ:
Объяснение:
Символ обозначает объединение двух наборов. Таким образом означает набор всех чисел, которые входят либо в A, либо в B. Если посмотреть на наш выбор, единственное число, которое не входит ни в A, ни в B, ни в то и другое, это 23.
Таким образом означает набор всех чисел, которые входят либо в A, либо в B. Если посмотреть на наш выбор, единственное число, которое не входит ни в A, ни в B, ни в то и другое, это 23.
Сообщить об ошибке
Шестьдесят старшеклассников были опрошены, чтобы узнать, изучают ли они историю и математику. В общей сложности 29 студентов заявили, что изучают математику, а 50 студентов заявили, что изучают историю. Каково минимальное количество студентов, которые изучают и историю, и математику?
Возможные ответы:
Правильный ответ:
Пояснение:
Мы можем нарисовать диаграмму Венна, чтобы увидеть эти две группы студентов.
Нам нужно найти пересечение между этими двумя множествами. Чтобы найти это, сложите общее количество студентов, изучающих историю, и общее количество студентов, изучающих математику.
Обратите внимание, что таким образом у нас больше учеников, чем общее число опрошенных. Это потому, что студенты, изучающие историю И исчисление, были учтены дважды. Вычтите общее количество опрошенных студентов, чтобы узнать, сколько студентов было подсчитано дважды.
Сообщить об ошибке
Группа старшеклассников изучает биологию, математический анализ и испанский язык, как показано выше. Какого ученика нет в наборе ?
Возможные ответы:
Энди
Стеф
Патрик
Молли
Боб
8Правильный ответ:
00004 Объяснение: Обозначение расшифровывается как «объединение», которое относится ко всему, что есть в любом наборе. относится к группе учащихся, изучающих математику или испанский язык (все на этой диаграмме, кроме тех, кто изучает только биологию). Судя по диаграмме, Патрик и Эшли — единственные учащиеся, не изучающие ни математический, ни испанский языки, поэтому правильный ответ — Патрик.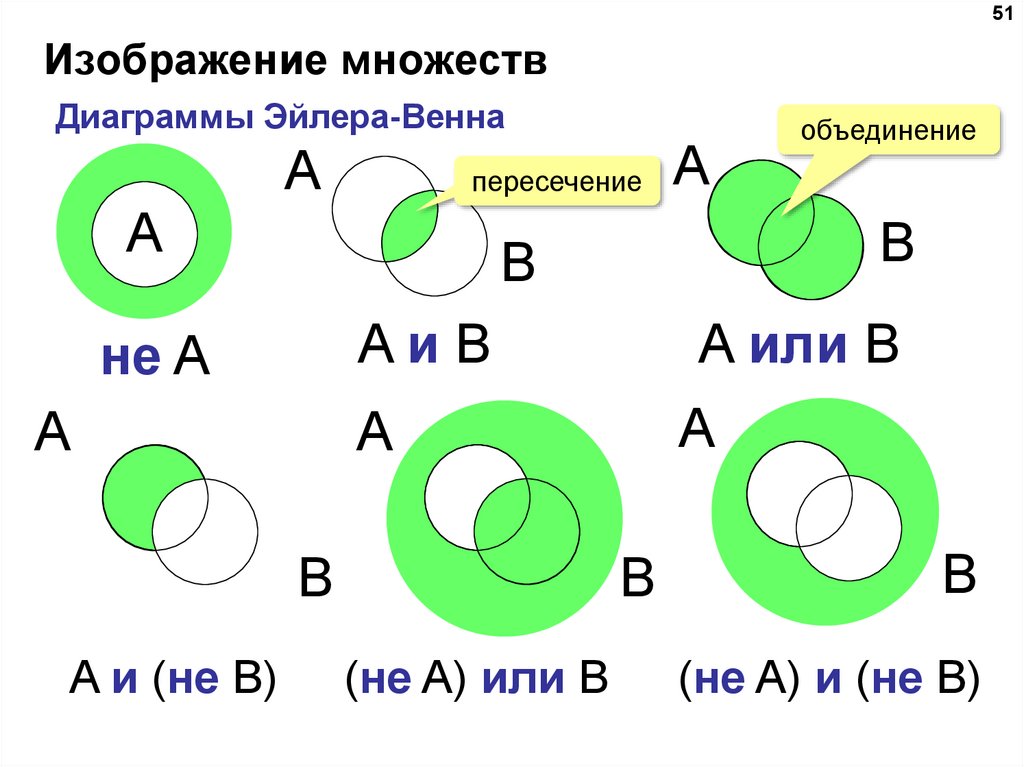
Сообщить об ошибке
Сорок учеников играют в футбол и/или баскетбол после школы. Двадцать четыре студента играют в футбол, а двадцать девять — в баскетбол. Сколько студентов играют и в футбол, и в баскетбол?
Возможные ответы:
Правильный ответ:
Пояснение:
Мы можем нарисовать диаграмму Венна для этих студентов.
Таким образом, на диаграмме Венна больше учеников, чем у нас.
Это связано с тем, что некоторые учащиеся занимаются обоими видами спорта и должны пересекаться на диаграмме Венна. Чтобы найти количество студентов в перекрытии, вычтите общее количество студентов из числа на диаграмме.
Представляет количество студентов, которые были подсчитаны дважды, или число в перекрытии.
С этим номером мы можем перерисовать правильную диаграмму Венна.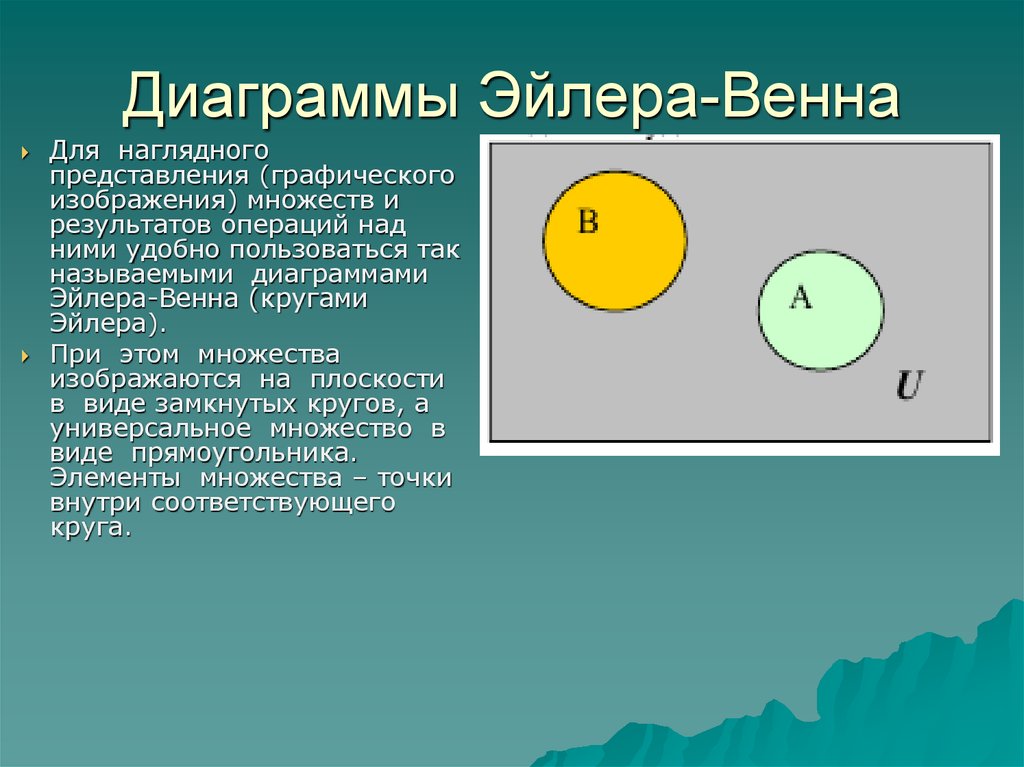
Сообщить об ошибке
Учитывая приведенную выше диаграмму Венна, какова сумма чисел в наборе ?
Возможные ответы:
Правильный ответ:
Объяснение:
Обозначение расшифровывается как «объединение C», которое относится ко всему, что находится либо в наборе, либо в наборе .
Если сложить числа вместе, мы получим:
Сообщить об ошибке кошки ни собаки. Сколько всего учеников в классе?
Возможные ответы:
Правильный ответ:
Пояснение:
Диаграмма Венна может помочь нам определить общее количество учеников в классе.
Во-первых, мы должны подсчитать количество учеников, у которых есть ТОЛЬКО кошки или ТОЛЬКО собаки. Во-первых, что касается кошек, у 15 учеников есть кошки, а у 5 учеников есть и кошки, и собаки.
Во-первых, что касается кошек, у 15 учеников есть кошки, а у 5 учеников есть и кошки, и собаки.
У десяти учеников есть только кошки.
Что касается собак, у 12 учащихся есть собаки, а у 5 учащихся есть и кошки, и собаки.
У семи учеников есть только собаки.
Используя эту информацию, мы можем заполнить диаграмму Венна.
На этой диаграмме показаны 10 учеников, у которых есть только кошки, 7 учеников, у которых только собаки, 5 учеников, у которых есть и то и другое, и 8 учеников, у которых нет ни одной кошки. Суммируя числа, мы получим общее количество студентов.
Сообщить об ошибке
На приведенной выше диаграмме Венна пусть набор и пусть, что такое набор Используйте обозначение набора для перечисления вашего ответа.
Возможные ответы:
Правильный ответ:
Объяснение:
означает пересечение множеств и на пересечении находятся только элементы, находящиеся в ОБОИХ множествах.

 Английский логик Джон Венн ввел его в 1880 году.
Английский логик Джон Венн ввел его в 1880 году.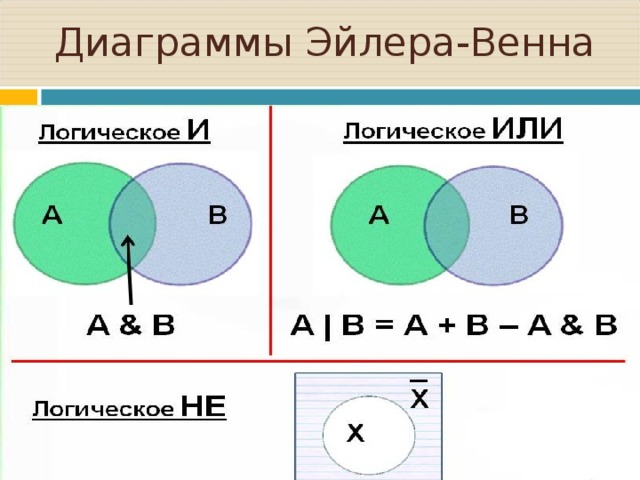
 Например, это помогает обозначить сходства и различия между различными продуктами и прототипами.
Например, это помогает обозначить сходства и различия между различными продуктами и прототипами.