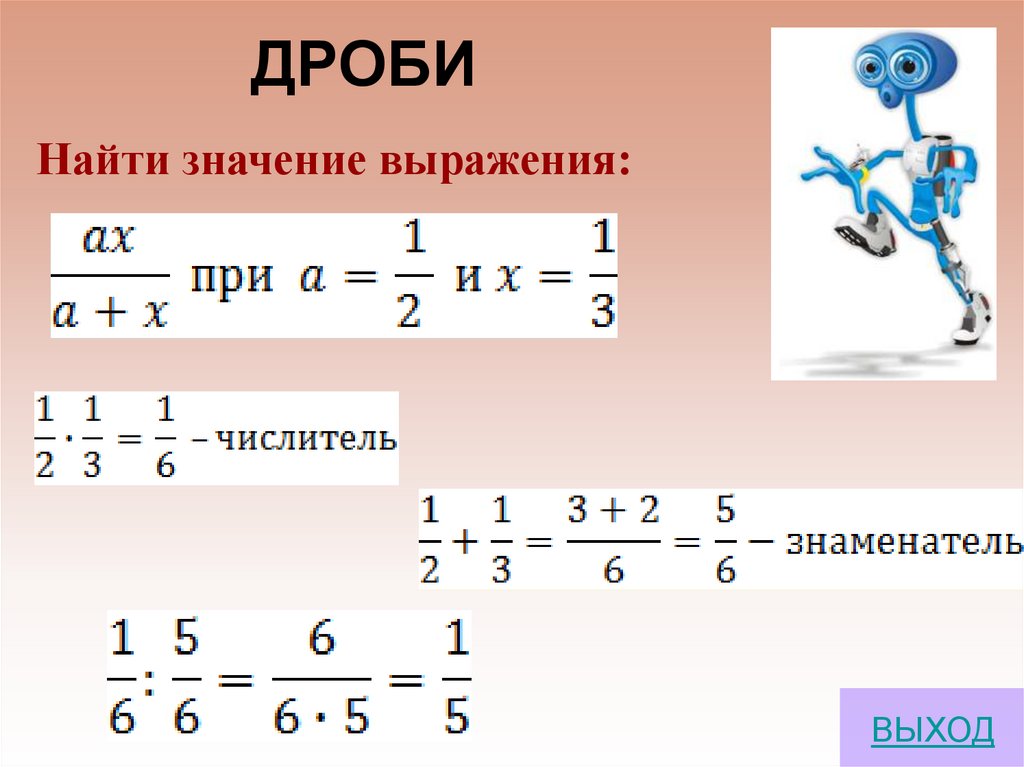
Решить пример по действиям. Уравнения онлайн
Удобный и простой онлайн калькулятор дробей с подробным решением может:
- Складывать, вычитать, умножать и делить дроби онлайн,
- Получать готовое решение дробей картинкой и удобно его переносить.
Результат решения дробей будет тут…
0
1
2
3
4
5
6
7
8
9
Знак дроби «/»
+
—
*
:
_cтереть
Очистить
У нашего онлайн калькулятора дробей быстрый ввод . Чтобы получить решение дробей, к примеру , просто напишите 1/2+2/7 в калькулятор и нажмите кнопку «Решать дроби «.
Калькулятор напишет вам подробное решение дробей и выдаст удобную для копирования картинку .
Знаки используемые для записи в калькуляторе
Набирать пример для решения вы можете как, с клавиатуры, так и используя кнопки.
Возможности онлайн калькулятора дробей
Калькулятор дробей может выполнить операции только с 2-мя простыми дробями.
Наш онлайн калькулятор решает дроби и приводит ответ к правильному виду — сокращает дробь и выделяет целую часть, если потребуется.
Если вам нужно решить отрицательные дроби, просто воспользуйтесь свойствами минуса.
При перемножении и делении отрицательных дробей минус на минус дает плюс. То есть произведение и делении отрицательных дробей, равно произведению и делению таких же положительных. Если одна дробь при перемножении или делении отрицательная, то просто уберите минус, а потом добавьте его к ответу.
При сложении отрицательных дробей, результат будет таким же как если бы вы складывали такие же положительные дроби. Если вы прибавляете одну отрицательную дробь, то это тоже самое, что вычесть такую же положительную.
При вычитании отрицательных дробей, результат будет таким же, как если бы поменяли их местами и сделали положительными.
Для решения смешанных дробей (дробей, в которых выделена целая часть) просто загоните целую часть в дробь. Для этого умножьте целую часть на знаменатель и прибавьте к числителю.
Если вам нужно решить онлайн 3 и более дроби, то решать их следует по очереди. Сначала посчитайте первые 2 дроби, потом с полученным ответом прорешайте следующую дробь и так далее. Выполняйте операции по очереди по 2 дроби, и в итоге вы получите верный ответ.
Математический-Калькулятор-Онлайн v.1.0
Калькулятор выполняет следующие операции: сложение, вычитание, умножение, деление, работа с десятичными, извлечение корня, возведение в степень, вычисление процентов и др. операции.
Решение:
Как работать с математическим калькулятором
| Клавиша | Обозначение | Пояснение |
|---|---|---|
| 5 | цифры 0-9 | Арабские цифры. Ввод натуральных целых чисел, нуля. Для получения отрицательного целого числа необходимо нажать клавишу +/- Ввод натуральных целых чисел, нуля. Для получения отрицательного целого числа необходимо нажать клавишу +/- |
| . | точка (запятая) | Разделитель для обозначения десятичной дроби. При отсутствии цифры перед точкой (запятой) калькулятор автоматически подставит ноль перед точкой. Например: .5 — будет записано 0.5 |
| + | знак плюс | Сложение чисел (целые, десятичные дроби) |
| — | знак минус | Вычитание чисел (целые, десятичные дроби) |
| ÷ | знак деления | Деление чисел (целые, десятичные дроби) |
| х | знак умножения | Умножение чисел (целые, десятичные дроби) |
| √ | корень | Извлечение корня из числа. При повторном нажатие на кнопку «корня» производится вычисление корня из результата. Например: корень из 16 = 4; корень из 4 = 2 |
| x 2 | возведение в квадрат | Возведение числа в квадрат. При повторном нажатие на кнопку «возведение в квадрат» производится возведение в квадрат результата Например: квадрат 2 = 4; квадрат 4 = 16 При повторном нажатие на кнопку «возведение в квадрат» производится возведение в квадрат результата Например: квадрат 2 = 4; квадрат 4 = 16 |
| 1 / x | дробь | Вывод в десятичные дроби. В числителе 1, в знаменателе вводимое число |
| % | процент | Получение процента от числа. Для работы необходимо ввести: число из которого будет высчитываться процент, знак (плюс, минус, делить, умножить), сколько процентов в численном виде, кнопка «%» |
| ( | открытая скобка | Открытая скобка для задания приоритета вычисления. Обязательно наличие закрытой скобки. Пример: (2+3)*2=10 |
| ) | закрытая скобка | Закрытая скобка для задания приоритета вычисления. Обязательно наличие открытой скобки |
| ± | плюс минус | Меняет знак на противоположный |
| = | равно | Выводит результат решения. Также над калькулятором в поле «Решение» выводится промежуточные вычисления и результат. Также над калькулятором в поле «Решение» выводится промежуточные вычисления и результат. |
| ← | удаление символа | Удаляет последний символ |
| С | сброс | Кнопка сброса. Полностью сбрасывает калькулятор в положение «0» |
Алгоритм работы онлайн-калькулятора на примерах
Сложение.
Сложение целых натуральных чисел { 5 + 7 = 12 }
Сложение целых натуральных и отрицательных чисел { 5 + (-2) = 3 }
Сложение десятичных дробных чисел { 0,3 + 5,2 = 5,5 }
Вычитание.
Вычитание целых натуральных чисел { 7 — 5 = 2 }
Вычитание целых натуральных и отрицательных чисел { 5 — (-2) = 7 }
Вычитание десятичных дробных чисел { 6,5 — 1,2 = 4,3 }
Умножение.
Произведение целых натуральных чисел { 3 * 7 = 21 }
Произведение целых натуральных и отрицательных чисел { 5 * (-3) = -15 }
Произведение десятичных дробных чисел { 0,5 * 0,6 = 0,3 }
Деление.

Деление целых натуральных чисел { 27 / 3 = 9 }
Деление целых натуральных и отрицательных чисел { 15 / (-3) = -5 }
Деление десятичных дробных чисел { 6,2 / 2 = 3,1 }
Извлечение корня из числа.
Извлечение корня из целого числа { корень(9) = 3 }
Извлечение корня из десятичных дробей { корень(2,5) = 1,58 }
Извлечение корня из суммы чисел { корень(56 + 25) = 9 }
Извлечение корня из разницы чисел { корень (32 – 7) = 5 }
Возведение числа в квадрат.
Возведение в квадрат целого числа { (3) 2 = 9 }
Возведение в квадрат десятичных дробей { (2,2) 2 = 4,84 }
Перевод в десятичные дроби.
Вычисление процентов от числа
Увеличить на 15% число 230 { 230 + 230 * 0,15 = 264,5 }
Уменьшить на 35% число 510 { 510 – 510 * 0,35 =331,5 }
18% от числа 140 это { 140 * 0,18 = 25,2 }
| + | сложение | ||||||||||||||||||||||||||
| — | вычитание | ||||||||||||||||||||||||||
| * | умножение | ||||||||||||||||||||||||||
| / | деление | ||||||||||||||||||||||||||
| ^ | возведение в степень | ||||||||||||||||||||||||||
| solve | решение уравнений, неравенств,
систем уравнений и неравенств | ||||||||||||||||||||||||||
| expand | раскрытие скобок | ||||||||||||||||||||||||||
| factor | разложение на множители | ||||||||||||||||||||||||||
| sum | вычисление суммы членов последовательности | ||||||||||||||||||||||||||
| derivative | дифференцирование (производная) | ||||||||||||||||||||||||||
| integrate | интеграл | ||||||||||||||||||||||||||
| lim | предел | ||||||||||||||||||||||||||
| inf | бесконечность | ||||||||||||||||||||||||||
| plot | построить график функции | ||||||||||||||||||||||||||
| log (a , b ) | логарифм по основанию a числа b | ||||||||||||||||||||||||||
| sin, cos, tg, ctg | синус, косинус, тангенс, котангенс | ||||||||||||||||||||||||||
| sqrt | корень квадратный | ||||||||||||||||||||||||||
| pi | число «пи» (3,1415926535. 2), {x, 0.5, 2} 2), {x, 0.5, 2}Дополнительные разъяснения по работе с решателем Построение графиков функции онлайн бесплатно или для решения математики. Быстро найти решение математического уравнения в режиме онлайн . Сайт www.сайт позволяет решить уравнение почти любого заданного алгебраического , тригонометрического или трансцендентного уравнения онлайн . При изучении практически любого раздела математики на разных этапах приходится решать уравнения онлайн . Чтобы получить ответ сразу, а главное точный ответ, необходим ресурс, позволяющий это сделать. Благодаря сайту www.сайт решение уравнений онлайн займет несколько минут. Основное преимущество www.сайт при решении математических уравнений онлайн — это скорость и точность выдаваемого ответа. Сайт способен решать любые алгебраические уравнения онлайн , тригонометрические уравнения онлайн , трансцендентные уравнения онлайн , а также уравнения с неизвестными параметрами в режиме онлайн . И вычислении значений выражений действия выполняются в определенной очередности, иными словами, нужно соблюдать порядок выполнения действий . В этой статье мы разберемся, какие действия следует выполнять сначала, а какие следом за ними. Навигация по странице. Сначала умножение и деление, затем сложение и вычитаниеВ школе дается следующее правило, определяющее порядок выполнения действий в выражениях без скобок :
Озвученное правило воспринимается достаточно естественно. Выполнение действий по порядку слева направо объясняется тем, что у нас принято вести записи слева направо. А то, что умножение и деление выполняется перед сложением и вычитанием объясняется смыслом, который в себе несут эти действия. Рассмотрим несколько примеров применения этого правила. Для примеров будем брать простейшие числовые выражения, чтобы не отвлекаться на вычисления, а сосредоточиться именно на порядке выполнения действий. Пример. Выполните действия 7−3+6 . Решение. Исходное выражение не содержит скобок, а также оно не содержит умножения и деления. Поэтому нам следует выполнить все действия по порядку слева направо, то есть, сначала мы от 7 отнимаем 3 , получаем 4 , после чего к полученной разности 4 прибавляем 6 , получаем 10 . Кратко решение можно записать так: 7−3+6=4+6=10 . Ответ: 7−3+6=10 . Пример. Укажите порядок выполнения действий в выражении 6:2·8:3 . Решение. Чтобы ответить на вопрос задачи, обратимся к правилу, указывающему порядок выполнения действий в выражениях без скобок. В исходном выражении содержатся лишь действия умножения и деления, а согласно правилу, их нужно выполнять по порядку слева направо. Ответ: Сначала 6
делим на 2
, это частное умножаем на 8
, наконец, полученный результат делим на 3. Пример. Вычислите значение выражения 17−5·6:3−2+4:2 . Решение. Сначала определим, в каком порядке следует выполнять действия в исходном выражении. Оно содержит и умножение с делением, и сложение с вычитанием. Сначала слева направо нужно выполнить умножение и деление. Так 5 умножаем на 6 , получаем 30 , это число делим на 3 , получаем 10 . Теперь 4 делим на 2 , получаем 2 . Подставляем в исходное выражение вместо 5·6:3 найденное значение 10 , а вместо 4:2 — значение 2 , имеем 17−5·6:3−2+4:2=17−10−2+2 . В полученном выражении уже нет умножения и деления, поэтому остается по порядку слева направо выполнить оставшиеся действия: 17−10−2+2=7−2+2=5+2=7 . Ответ: 17−5·6:3−2+4:2=7 . На первых порах, чтобы не перепутать порядок выполнения действий при вычислении значения выражения, удобно над знаками действий расставить цифры, соответствующие порядку их выполнения. Для предыдущего примера это выглядело бы так: . Этого же порядка выполнения действий – сначала умножение и деление, затем сложение и вычитание — следует придерживаться и при работе с буквенными выражениями. Действия первой и второй ступениВ некоторых учебниках по математике встречается разделение арифметических действий на действия первой и второй ступени. Разберемся с этим. Определение. Действиями первой ступени называют сложение и вычитание, а умножение и деление называют действиями второй ступени . В этих терминах правило из предыдущего пункта, определяющее порядок выполнения действий, запишется так: если выражение не содержит скобок, то по порядку слева направо сначала выполняются действия второй ступени (умножение и деление), затем – действия первой ступени (сложение и вычитание). Порядок выполнения арифметических действий в выражениях со скобкамиВыражения часто содержат скобки, указывающие порядок выполнения действий . В этом случае правило, задающее порядок выполнения действий в выражениях со скобками , формулируется так: сначала выполняются действия в скобках, при этом также по порядку слева направо выполняется умножение и деление, затем – сложение и вычитание. Итак, выражения в скобках рассматриваются как составные части исходного выражения, и в них сохраняется уже известный нам порядок выполнения действий. Рассмотрим решения примеров для большей ясности. Пример. Выполните указанные действия 5+(7−2·3)·(6−4):2 . Решение. Выражение содержит скобки, поэтому сначала выполним действия в выражениях, заключенных в эти скобки. Начнем с выражения 7−2·3 . В нем нужно сначала выполнить умножение, и только потом вычитание, имеем 7−2·3=7−6=1 . Переходим ко второму выражению в скобках 6−4 . Здесь лишь одно действие – вычитание, выполняем его 6−4=2 . Подставляем полученные значения в исходное выражение: 5+(7−2·3)·(6−4):2=5+1·2:2 . В полученном выражении сначала выполняем слева направо умножение и деление, затем – вычитание, получаем 5+1·2:2=5+2:2=5+1=6 . На этом все действия выполнены, мы придерживались такого порядка их выполнения: 5+(7−2·3)·(6−4):2 . Запишем краткое решение: 5+(7−2·3)·(6−4):2=5+1·2:2=5+1=6
. Ответ: 5+(7−2·3)·(6−4):2=6 . Бывает, что выражение содержит скобки в скобках. Этого бояться не стоит, нужно лишь последовательно применять озвученное правило выполнения действий в выражениях со скобками. Покажем решение примера. Пример. Выполните действия в выражении 4+(3+1+4·(2+3)) . Решение. Это выражение со скобками, это означает, что выполнение действий нужно начинать с выражения в скобках, то есть, с 3+1+4·(2+3) . Это выражение также содержит скобки, поэтому нужно сначала выполнить действия в них. Сделаем это: 2+3=5 . Подставив найденное значение, получаем 3+1+4·5 . В этом выражении сначала выполняем умножение, затем – сложение, имеем 3+1+4·5=3+1+20=24 . Исходное значение, после подстановки этого значения, принимает вид 4+24 , и остается лишь закончить выполнение действий: 4+24=28 . Ответ: 4+(3+1+4·(2+3))=28 . Вообще, когда в выражении присутствуют скобки в скобках, то часто бывает удобно выполнение действий начинать с внутренних скобок и продвигаться к внешним. Например, пусть нам нужно выполнить действия в выражении (4+(4+(4−6:2))−1)−1 . Сначала выполняем действия во внутренних скобках, так как 4−6:2=4−3=1 , то после этого исходное выражение примет вид (4+(4+1)−1)−1 . Опять выполняем действие во внутренних скобках, так как 4+1=5 , то приходим к следующему выражению (4+5−1)−1 . Опять выполняем действия в скобках: 4+5−1=8 , при этом приходим к разности 8−1 , которая равна 7 . Действия с дробямиКалькулятор дробей онлайн. Сложение дробей, вычитание дробей, умножение и деление дробей. Обыкновенная дробь. Смешанная дробь. Упрощение дроби. Десятичная дробь. Содержание Сложение дробей с одинаковыми знаменателямиСложение дробей бывает двух видов:
Сначала изýчим сложение дробей с одинаковыми знаменателями. Тут всё просто. Чтобы сложить дроби с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить без изменения. Например, слóжим дроби и . Складываем числители, а знаменатель оставляем без изменения: Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на четыре части. Если к пиццы прибавить пиццы, то получится пиццы: Пример 2. Сложить дроби и . Опять же складываем числители, а знаменатель оставляем без изменения: В ответе получилась неправильная дробь . Если наступает конец задачи, то от неправильных дробей принято избавляться. Чтобы избавится от неправильной дроби, нужно выделить в ней целую часть. В нашем случае целая часть выделяется легко — два разделить на два будет один: Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на две части. Если к пиццы прибавить еще пиццы, то получится одна целая пицца: Пример 3. Сложить дроби и . Опять же складываем числители, а знаменатель оставляем без изменения: Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на три части. Пример 4. Найти значение выражения Этот пример решается точно также, как и предыдущие. Числители необходимо сложить, а знаменатель оставить без изменения: Попробуем изобразить наше решение с помощью рисунка. Если к пиццы прибавить пиццы и ещё прибавить пиццы, то получится 1 целая и ещё пиццы. Как видите в сложении дробей с одинаковыми знаменателями нет ничего сложного. Достаточно понимать следующие правила:
Источник: http://spacemath.xyz/deistviya_s_drobyami/ Калькулятор дробей
Инструкция использования калькулятора дробейДля решения вашей задачи выполните следующие действия:
Ввод данных в калькулятор дробейВ калькулятор дробей можно вводить: целые числа, десятичные дроби, обыкновенные дроби и смешанные числа.Целые числа. Для ввода целых чисел используйте цифровые клавиши калькулятора или цифровые клавиши вашего компьютера.1234567890 Десятичные дроби. Десятичные дроби вводятся также как и целые числа, в качестве десятичного разделителя рекомендуется использовать точку . Обыкновенные дроби: Для ввода обыкновенной дроби нажмите клавишу на клавиатуре калькулятора – после чего введите значения числителя и знаменателя дроби используя числовые клавиши. Смешанные числа: Используя числовые клавиши введите целую часть смешанной дроби, нажмите клавишу дроби на клавиатуре калькулятора – после чего введите значения числителя и знаменателя дроби используя числовые клавиши. N.B. Калькулятор поддерживает только целые степени! N.B. Буквенные выражения, операции извлечения корня калькулятор не поддерживает! Дополнительные возможности калькулятора дробей – старая версия
Ввод данных в калькулятор дробей – старая версияВ калькулятор дробей можно вводить: целые числа, десятичные дроби, обыкновенные дроби и смешанные числа.Для ввода отрицательных чисел знак минус вводится в поле для целой части: N.B. Буквенные выражения, операции извлечения корня и возведения в степень калькулятор не поддерживает! Дополнительные возможности калькулятора дробей – старая версияИнструкция использования калькулятора дробей – старая версияДля сложения, вычитания, умножения или деление двух дробей выполните следующие действия:
Правила. Сложение, вычитание, умножение и деление дробей.Умножение обыкновенных дробей
Деление обыкновенных дробейЧтобы разделить одну обыкновенную дробь на другую, надо умножить первую дробь на дробь, обратную второй. Смотрите также все правила и примеры: сложение дробей, вычитание дробей, умножение дробей, деление дробей. Источник: http://ru.onlinemschool.com/math/assistance/fraction/fraction_calc/ Доля целогоДоля — это каждая равная часть, из суммы которых состоит целый предмет. Для примера возьмем два мандарина. Когда мы их почистим, то получим в каждом мандарине разное количество долек или долей. В одном может быть 6, а в другом — целых 9. Размеры долей у каждого мандарина тоже разные. У каждой доли есть свое название: оно зависит от количества долей в конкретном предмете.
Понятие доли можно применить не только к предметам, но и величинам. Так, например, картина занимает четверть стены — при этом ее ширина треть метра. Чтобы быстрее запомнить соотношения частей и целого, можно использовать наглядную табличку: Источник: http://skysmart.ru/articles/mathematic/obyknovennye-drobi Сокращение дробейЧислитель и знаменатель дроби можно разделить или умножить на одно и то же число. Дробь, которую мы при этом получим, равна исходной дроби. Когда мы делим числитель и знаменатель на одно и то же число, чтобы дробь стала проще, мы занимаемся сокращением дробей. Сократим дробь 1015frac{10}{15}1510. Перед тем как приступать к действиям с дробями, их бывает полезно сократить. Также постарайтесь сокращать слишком страшные дроби, которые получаются во время промежуточных вычислений. Чтобы сократить дробь abfrac{a}{b}ba, нужно вычислить наибольший общий делитель НОД(a,b)text{НОД}(a,b)НОД(a,b) и поделить на него числитель и знаменатель дроби. Для того чтобы вычислить НОДtext{НОД}НОД двух чисел, используют алгоритм Евклида. Однако на практике гораздо проще постепенно делить (сокращать) числитель и знаменатель на общие делители, которые ищутся с помощью признаков делимости. Например, можно заметить, что в дроби 2466frac{24}{66}6624 числитель и знаменатель – четные числа. Поэтому на 222 эту дробь точно можно сократить: 2466=1233frac{24}{66}=frac{12}{33}6624=3312. Теперь можно увидеть, что оба числа делятся на 333. Сокращаем дальше: 1233=411frac{12}{33}=frac{4}{11}3312=114. Получили несократимую дробь. Дробь abfrac{a}{b}ba является несократимой, если НОД(a,b)=1text{НОД}(a,b)=1НОД(a,b)=1. Сократите 3045frac{30}{45}4530. В ответе запишите обыкновенную дробь (через / ). Сократите 8517frac{85}{17}1785. Источник: http://lampa.io/p/действия-с-дробями-000000000244b193351cbbe5556c10c8 Обоснование правилОпределение 2 Существуют следующие математические моменты, на которые следует опираться при вычислении:
С их помощью можно производить преобразования вида: ad±cd=a·d-1±c·d-1=a±c·d-1=a±cd;ab±cd=a·pb·p±c·rd·r=a·ps±c·es=a·p±c·rs;ab·cd=a·db·d·b·cb·d=a·d·a·d-1·b·c·b·d-1==a·d·b·c·b·d-1·b·d-1=a·d·b·cb·d·b·d-1==(a·c)·(b·d)-1=a·cb·d Источник: http://zaochnik. Как устроена десятичная дробьВ десятичной дроби знаменатель всегда равен 10, 100, 1000, 10000 и т.д. Выходит, что десятичная дробь — это то, что получается, если разделить числитель на знаменатель. Десятичную дробь записывают в строчку через запятую, чтобы отделить целую часть от дробной. Вот так:
Конечная десятичная дробь — это дробь, в которой количество цифр после запятой точно определено. Бесконечная десятичная дробь — это когда после запятой количество цифр бесконечно. Для удобства математики договорились округлять эти цифры до 1-3 после запятой. Источник: http://skysmart.ru/articles/mathematic/obyknovennye-drobi Обобщения[править | править код]
Источник: http://ru.wikipedia.org/wiki/Дробь_(математика) Действия с дробямиС дробями можно выполнять те же действия, что и с обычными числами: складывать, вычитать, умножать и делить. Источник: http://skysmart.ru/articles/mathematic/obyknovennye-drobi Представление целого числа в виде дробиЛюбое целое число можно представить в виде дроби. Например, число 5 можно представить как . От этого пятёрка своего значения не поменяет, поскольку выражение означает «число пять разделить на единицу», а это, как известно равно пятёрке: Источник: http://spacemath.xyz/deistviya_s_drobyami/ Сокращение дробейСокращение дроби — это деление числителя и знаменателя дроби на одно и то же натуральное число. Сократить дробь значит сделать ее короче и проще для восприятия. Например, дробь 1/3 выглядит намного проще и красивее, чем 27/81. Сокращение дроби выглядит так: зачеркивают числитель и знаменатель, а рядом записывают результаты деления числителя и знаменателя на одно и то же число. В этом примере делим обе части дроби на двойку. Можно никуда не спешить и сокращать дроби последовательно, в несколько действий. Источник: http://skysmart.ru/articles/mathematic/obyknovennye-drobi Умножение и деление дробейПроизведение двух дробей равно дроби, числитель которой равен произведению числителей, а знаменатель — произведению знаменателей: Не забываем про сокращение. Это может облегчить вычисления. Чтобы умножить два смешанных числа, надо:
Чтобы разделить дробь на дробь нужно выполнить следующую последовательность действий:
Другими словами это правило звучит так: чтобы разделить одну дробь на другую, надо первую умножить на обратную от второй. Числа, произведение которых равно 1, называют взаимно обратными. Как делить дроби с разными знаменателями? На самом деле одинаковые или разные знаменатели у дробей — неважно, потому что все дроби делятся по правилу, описанному выше. Для деления смешанных чисел необходимо:
Источник: http://skysmart.ru/articles/mathematic/obyknovennye-drobi Задания для самостоятельного решения:Задание 1. Найдите значение выражения: Решение: Задание 2. Найдите значение выражения: Решение: Задание 3. Найдите значение выражения: Решение: Задание 4. Найдите значение выражения: Решение: Задание 5. Решение: Задание 6. Найдите значение выражения: Решение: Задание 7. Найдите значение выражения: Решение: Задание 8. Найдите значение выражения: Решение: Задание 9. Найдите значение выражения: Решение: Задание 10. Найдите значение выражения: Решение: Задание 11. Найдите значение выражения: Решение: Задание 12. Найдите значение выражения: Решение: Задание 13. Найдите значение выражения: Решение: Задание 14. Найдите значение выражения: Решение: Понравился урок? Возникло желание поддержать проект? Источник: http://spacemath.xyz/deistviya_s_drobyami/ Рациональные выражения Пошаговое решение математических задачДобро пожаловать в Quickmath Solvers!
Новый Пример Справка Учебник Решите уравнение, неравенство или систему. Пример: 2x-1=y,2y+3=x Чтобы увидеть учебник, прокрутите вниз
Выражение, представляющее собой частное двух алгебраических выражений (со знаменателем, отличным от 0), называется дробным выражением. Наиболее распространенными дробными выражениями являются те, которые являются частными двух многочленов; они называются рациональными выражениями. Поскольку дробные выражения включают частные, важно отслеживать значения переменной, которые удовлетворяют требованию, чтобы ни один знаменатель не был равен 0. Например, x != -2 в рациональном выражении: , потому что замена x на -2 делает знаменатель равным 0. Аналогично, в
x!=-2 и x!= -4
Ограничения на переменную находятся путем определения значения, при которых знаменатель равен нулю. Во втором приведенном выше примере для нахождения значений x, при которых (x + 2)(x + 4) = 0, необходимо использовать свойство, согласно которому ab = 0 тогда и только тогда, когда a = 0 или b = 0, следующим образом. (х+2)(х+4)=0 x+2=0 или x+4=0 x=-2 или x=-4 Так же, как дробь 6/8 записывается в самом низком выражении как 3/4, рациональные выражения также могут быть написано в самых низких терминах. Это делается по основному принципу. Пример 1Запишите каждое выражение в наименьших терминах. Разложите числитель и знаменатель на множители, чтобы получить По фундаментальному принципу В исходном выражении p не может быть 0 или -4, потому что Таким образом, этот результат действителен только для значений p, отличных от 0 и -4. Отныне мы всегда будем допускать такие ограничения при редукции рациональных выражений. Теперь давайте посмотрим на то, как наш пошаговый решатель фракций решает эту проблему: Решение озадачивания. — k и k — 2 имеют противоположные знаки. По этой причине умножьте числитель и знаменатель на -1 следующим образом. Так как (k-2)*(-1)=-k+2 или 2- k, Давая Работа альтернативным способом привела бы к эквивалентному результату 3 Наш Калькулятор дробей может решить эту и многие подобные проблемы. Если вы хотите, чтобы возникла похожая задача, нажмите кнопку «Решить похожую»: Решить похожую задачуВведите свою собственную задачу ВниманиеВероятно, самая распространенная ошибка в алгебре — неправильное использование фундаментального принципа для записи дроби. Проще говоря, помните, фундаментальный принцип требует наличия пары общих множителей, одного в числителе и одного в знаменателе. Например, С другой стороны, нельзя еще больше упростить по фундаментальному принципу, потому что числитель нельзя разложить на множители. ← Previous Page Next Page → Rational expression online calculator
|

 Уравнения служат мощным математическим аппаратом решения практических задач. C помощью математических уравнений можно выразить факты и соотношения, которые могут показаться на первый взгляд запутанными и сложными. Неизвестные величины уравнений можно найти, сформулировав задачу на математическом языке в виде уравнений и решить полученную задачу в режиме онлайн на сайте www.сайт. Любое алгебраическое уравнение , тригонометрическое уравнение или уравнения содержащие трансцендентные функции Вы легко решите онлайн и получите точный ответ. Изучая естественные науки, неизбежно сталкиваешься с необходимостью решения уравнений . При этом ответ должен быть точным и получить его необходимо сразу в режиме онлайн . Поэтому для решения математических уравнений онлайн мы рекомендуем сайт www.сайт, который станет вашим незаменимым калькулятором для решения алгебраических уравнений онлайн , тригонометрических уравнений онлайн , а также трансцендентных уравнений онлайн или уравнений с неизвестными параметрами.
Уравнения служат мощным математическим аппаратом решения практических задач. C помощью математических уравнений можно выразить факты и соотношения, которые могут показаться на первый взгляд запутанными и сложными. Неизвестные величины уравнений можно найти, сформулировав задачу на математическом языке в виде уравнений и решить полученную задачу в режиме онлайн на сайте www.сайт. Любое алгебраическое уравнение , тригонометрическое уравнение или уравнения содержащие трансцендентные функции Вы легко решите онлайн и получите точный ответ. Изучая естественные науки, неизбежно сталкиваешься с необходимостью решения уравнений . При этом ответ должен быть точным и получить его необходимо сразу в режиме онлайн . Поэтому для решения математических уравнений онлайн мы рекомендуем сайт www.сайт, который станет вашим незаменимым калькулятором для решения алгебраических уравнений онлайн , тригонометрических уравнений онлайн , а также трансцендентных уравнений онлайн или уравнений с неизвестными параметрами. Для практических задач по нахождению корней различных математических уравнений ресурса www.. Решая уравнения онлайн самостоятельно, полезно проверить полученный ответ, используя онлайн решение уравнений на сайте www.сайт. Необходимо правильно записать уравнение и моментально получите онлайн решение , после чего останется только сравнить ответ с Вашим решением уравнения. Проверка ответа займет не более минуты, достаточно решить уравнение онлайн и сравнить ответы. Это поможет Вам избежать ошибок в решении и вовремя скорректировать ответ при решении уравнений онлайн будь то алгебраическое , тригонометрическое , трансцендентное или уравнение с неизвестными параметрами.
Для практических задач по нахождению корней различных математических уравнений ресурса www.. Решая уравнения онлайн самостоятельно, полезно проверить полученный ответ, используя онлайн решение уравнений на сайте www.сайт. Необходимо правильно записать уравнение и моментально получите онлайн решение , после чего останется только сравнить ответ с Вашим решением уравнения. Проверка ответа займет не более минуты, достаточно решить уравнение онлайн и сравнить ответы. Это поможет Вам избежать ошибок в решении и вовремя скорректировать ответ при решении уравнений онлайн будь то алгебраическое , тригонометрическое , трансцендентное или уравнение с неизвестными параметрами. Начнем с самых простых случаев, когда выражение содержит лишь числа или переменные, соединенные знаками плюс, минус, умножить и разделить. Дальше разъясним, какого порядка выполнения действий следует придерживаться в выражениях со скобками. Наконец, рассмотрим, в какой последовательности выполняются действия в выражениях, содержащих степени, корни и другие функции.
Начнем с самых простых случаев, когда выражение содержит лишь числа или переменные, соединенные знаками плюс, минус, умножить и разделить. Дальше разъясним, какого порядка выполнения действий следует придерживаться в выражениях со скобками. Наконец, рассмотрим, в какой последовательности выполняются действия в выражениях, содержащих степени, корни и другие функции.






 Если к пиццы прибавить ещё пиццы, то получится пиццы:
Если к пиццы прибавить ещё пиццы, то получится пиццы:
 3)
3)
 Если в мандарите шесть долей — каждая из них будет определяться, как одна шестая от целого.
Если в мандарите шесть долей — каждая из них будет определяться, как одна шестая от целого.
 com/spravochnik/matematika/vyrazhenija/dejstvija-s-drobjami/
com/spravochnik/matematika/vyrazhenija/dejstvija-s-drobjami/ А еще дроби можно сокращать и сравнивать между собой. Давайте попробуем.
А еще дроби можно сокращать и сравнивать между собой. Давайте попробуем.

 Найдите значение выражения:
Найдите значение выражения:


 Затем мой друг рассказал мне об этом программном обеспечении «Алгебратор». Сначала я немного колебался, так как у меня были опасения по поводу отсутствия человеческого взаимодействия, которое обычно бывает у репетитора. Но я попросил сына попробовать. И я был очень удивлен, обнаружив, что ему понравилось это программное обеспечение. Я не могу сказать почему, так как я не по математике и забыл школьную алгебру. Но я вижу, что моему сыну сейчас комфортно с этой темой.
Затем мой друг рассказал мне об этом программном обеспечении «Алгебратор». Сначала я немного колебался, так как у меня были опасения по поводу отсутствия человеческого взаимодействия, которое обычно бывает у репетитора. Но я попросил сына попробовать. И я был очень удивлен, обнаружив, что ему понравилось это программное обеспечение. Я не могу сказать почему, так как я не по математике и забыл школьную алгебру. Но я вижу, что моему сыну сейчас комфортно с этой темой.