калькулятор онлайн сокращенного умножения
Вы искали калькулятор онлайн сокращенного умножения? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и калькулятор сокращенного умножения, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «калькулятор онлайн сокращенного умножения».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как калькулятор онлайн сокращенного умножения,калькулятор сокращенного умножения,калькулятор сокращенного умножения онлайн,калькулятор формул сокращенного умножения,калькулятор формул сокращенного умножения онлайн,калькулятор формула сокращенного умножения,калькулятор формулы сокращенного умножения,калькулятор фсу,онлайн калькулятор сокращенного умножения,онлайн калькулятор формул сокращенного умножения,онлайн калькулятор фсу,онлайн решение формулы сокращенного умножения,онлайн формулы сокращенного умножения,сокращенного умножения онлайн калькулятор,сокращенное умножение онлайн,формул сокращенного умножения калькулятор,формула сокращенного умножения калькулятор,формула сокращенного умножения калькулятор онлайн,формула сокращенного умножения онлайн калькулятор,формулы сокращенного умножения калькулятор,формулы сокращенного умножения калькулятор онлайн,формулы сокращенного умножения онлайн,формулы сокращенного умножения онлайн калькулятор,фсу калькулятор,фсу онлайн калькулятор.
Где можно решить любую задачу по математике, а так же калькулятор онлайн сокращенного умножения Онлайн?
Решить задачу калькулятор онлайн сокращенного умножения вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.
App Store: Формулы сокращенного умножения
Описание
Для этого необходимо ввести только две переменные. Все расчеты хранятся в истории. Окончательное решение можно поделиться.[Содержание]
— переменные для a и b должны быть введены
— вычисление бинома с основной теоремой бинома
— функция истории, которая сохраняет ввод
— краткое и подробное решение
— поддерживается ввод дробей и десятичных дробей
— константы и / или переменные могут быть введены
— возможность удалить рекламу
[ Использование ]
— есть 2 поля для ввода значений с использованием модифицированной клавиатуры
— если вы ввели неверные значения или значения пропущены, текстовые поля подсвечиваются красным
— вы можете переключаться между решением, видом ввода и историей, проводя и / или касаясь кнопок
— если вы выберете запись в истории, она будет автоматически загружена для расчета
— вся история может быть удалена нажатием клавиши
000Z» aria-label=»14 ноября 2022 г.»>14 нояб. 2022 г.
Версия 1.18
— Hindi and Indonesian translation added
— minor fixes
Разработчик Flooki указал, что в соответствии с политикой конфиденциальности приложения данные могут обрабатываться так, как описано ниже. Подробные сведения доступны в политике конфиденциальности разработчика.
Данные, используемые для отслеживания информации
Следующие данные могут использоваться для отслеживания информации о пользователе в приложениях и на сайтах, принадлежащих другим компаниям:
- Геопозиция
- Идентификаторы
- Данные об использовании
- Диагностика
Связанные с пользователем данные
Может вестись сбор следующих данных, которые связаны с личностью пользователя:
- Геопозиция
- Идентификаторы
- Данные об использовании
- Диагностика
Не связанные с пользователем данные
Может вестись сбор следующих данных, которые не связаны с личностью пользователя:
Конфиденциальные данные могут использоваться по-разному в зависимости от вашего возраста, задействованных функций или других факторов.
Информация
- Провайдер
- Glindemann, Sennoun, Langer GbR
- Размер
- 31,4 МБ
- Категория
- Образование
- Возраст
- 4+
- Copyright
- © 2018 Glindemann, Sennoun, Langer GbR
- Цена
- Бесплатно
- Сайт разработчика
- Поддержка приложения
- Политика конфиденциальности
Другие приложения этого разработчика
Вам может понравиться
Умножение двух чисел, близких к 100, но менее
!
| Чтобы умножить два числа, близких к 100, но меньше их, используйте следующие шаги:
Пример: 98 х 97 =
98 × 97 = 9506. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Все права защищены. Copyright 2005-2022
Как умножить дроби? Определение, примеры, факты
Перекрестное умножение: введение
Мы обычно используем метод перекрестного умножения, чтобы найти неизвестные значения в любом алгебраическом уравнении.
Давайте посмотрим на эти повседневные математические вопросы. Если один батончик стоит $\$$2, сколько будут стоить 10 таких батончиков?
Перекрестное умножение, как следует из названия, относится к умножению чисел, стоящих на перекрестных позициях.
Скрещиваем дроби $\frac{1}{10}$ и $\frac{2}{?}$.
$? \times 1= $\$$10$ $\times 2$
$? =$ $\$$20
Итак, 10 батончиков будут стоить $\$$20.
Давайте узнаем больше об этом методе и его применении.
Что такое перекрестное умножение?
Для любого алгебраического уравнения вида $\frac{a}{b}=\frac{c}{d}$ , метод перекрестного умножения использует следующую формулу:
$a\times d = b\times c$
Чтобы скрестить дроби, мы умножаем числитель первой дроби на знаменатель второй дроби и числитель второй дроби. вторую дробь со знаменателем первой дроби.
Перекрестное умножение можно использовать для сравнения дробей, сложения или вычитания разных дробей, поиска неизвестного значения в выражении и сравнения отношений.
Как скрестить дроби?
Давайте разберемся, как скрестить дроби на примере.
Мы знаем, что $\frac{3}{4} = \frac{6}{8}$
Скрестите дроби $\frac{3}{4}$ и $\frac{6}{8}$ .
Умножьте числитель первой дроби на знаменатель второй дроби.
Умножьте числитель второй дроби на знаменатель первой дроби.
Получаем
$3\times8=24$
$6\times4=24$
Итак, перемножая дроби $\frac{a}{b} = \frac{c}{d}$ , мы получить $a\times d = b\times c$
Перекрестное умножение дробей для сравнения в отличие от дробей
Мы только что научились скрещивать умножающие дроби. Когда вы скрещиваете умножение дробей? В отличие от дробей можно сравнивать путем перекрестного умножения. Отличие от дробей — это дроби с разными знаменателями.
Пример :
Сравните $\frac{3}{7}$ и $\frac{5}{8}$ используя перекрестное умножение.
Чтобы сравнить две дроби с разными знаменателями, мы делаем их знаменатели одинаковыми.
Мы делаем это, заменяя знаменатели произведением обоих знаменателей.
Итак, знаменатель обеих дробей становится $7 \times 8 = 56$
Теперь мы скрестим и умножим дроби , чтобы найти числители.
- Сначала умножим числитель первой дроби на знаменатель второй дроби.
$3 \times 8 = 24$
Таким образом, первая дробь принимает вид: $\frac{24}{56}$
- Далее умножаем числитель второй дроби на знаменатель первой дроби.
$5 \times 7 = 35$
Таким образом, вторая дробь становится: $\frac{35}{56}$
Так как $\frac{24}{56} \lt \frac{35}{56} $ , можно сказать, что $\frac{3}{7} \lt \frac{5}{8}$.
Перекрестное умножение для сравнения отношений
Если два отношения равны, т. е. $\frac{a}{b} = \frac{c}{d}$, (где b и d не равны нулю), то произведение после перекрестного умножения также равно.
- $\frac{a}{b} \lt \frac{c}{d}$, если $a\times d \lt b\times c$.
Пример: $\frac{1}{2} \lt \frac{3}{4}$, начиная с $4 \lt 6$.
- $\frac{a}{b} \gt \frac{c}{d}$, если $a \times d \gt b \times c$.
Пример: $\frac{1}{10}\gt \frac{1}{100}$, начиная с $100\gt 10$.
Мы можем использовать перекрестное умножение , чтобы найти значение переменной в уравнении, содержащем отношения. Давайте лучше поймем это на примере.
Пример : Если 8 подсвечников стоят $\$$40. Сколько будут стоить 12 таких подсвечников?
Стоимость 8 подсвечников = $\$$40
Стоимость 1 подсвечника $= \frac{40}{8}$ …………(i)
Пусть стоимость 12 подсвечников Икс.
Следовательно, стоимость 1 подсвечника составит $\frac{x}{12}$. …………..(ii)
Приравнивая (i) и (ii), получаем
$\frac{40}{8} = \frac{x}{12}$
Перемножить, чтобы получить
$40 \times 12 = 8 \times x$
$\frac{480}{8}=$ x
x $=60$
Следовательно, стоимость 12 подсвечников $\$$60.
Перекрестное умножение с одной переменной
Метод перекрестного умножения в основном используется для нахождения неизвестной переменной в уравнении. Давайте посмотрим на пример.
$\frac{4}{9} = \frac{x}{45}$
Когда мы пересекаем умножение:
$4 \times 45 = 180$ и $9 \times x = 9x$
Теперь, $9 x = 180$
x$ = \frac{180}{9} = 20$
Следовательно, получаем $x = 20$
Решенные примеры
1. Сравните дроби 57 и 49 путем перекрестного умножения.
Решение: Перемножая крест-накрест, мы находим
$5 \times 9 = 45$ и $4 \times 7 = 28$
Так как $45\gt 28, 57$ больше, чем 49.
2. Джимми хочет найти значение x в данном уравнении. Вы можете помочь ему?
$\frac{12}{15} = \frac{x}{10}$
Решение:
$\frac{12}{15} = \frac{x}{10}$ (дано)
При перекрестном умножении:
$12 \times 10 = 15 \times x$
$\frac{120}{15} =$ x
$8 =$ x
Итак, значение x равно 8.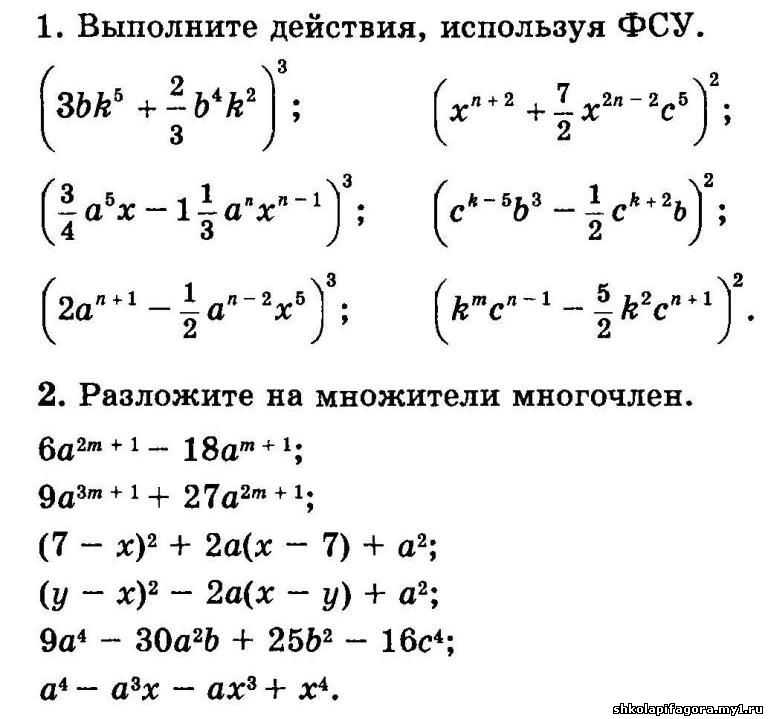
3. Что больше, $\frac{7} {12}$ или $\frac{6}{11}$ ?
Решение :
Когда мы скрещиваем умножаем, мы находим
$7 \times 11 = 77$ и $6 \times 12 = 72$
As, $77 \gt 72$
Следовательно, $\frac{7}{12} \gt \frac{6}{11}$ .
Практические задачи
1
Если дроби $\frac{4}{8}$ и $\frac{5}{x}$ равны, каково значение $x$?
40
5
15
10
Правильный ответ: 10
Поскольку данные дроби равны, мы можем перекрестно умножить и сказать, что $4x= 8 \times 5 = 40$
Таким образом, x $= $ 10
2
Если 4 кекса стоят $\$$12. Сколько будут стоить 10 таких кексов?
$\$30
$\$48
$\$40
$\$36
Правильный ответ: $\$30
Стоимость 4 кексов $\$$12.
Пусть стоимость 10 кексов равна x.
Если мы представим его в виде уравнения, мы получим:
$\frac{12}{4} = \frac{x}{10}$
При перекрестном умножении мы получим
$12 \times 10 = 4 \times x$
$\frac{120}{4} = x$
$30 = x$
Следовательно, стоимость 10 кексов составляет $\$$30.
3
Каково значение x, если $\frac{9}{11} = \frac{x}{33}$.
10
27
18
55
Правильный ответ: 27
$\frac{9}{11}= \frac{x}{33}$
При перекрестном умножении:
3 = $3 \times 11\times x$
$\frac{297}{11} = x$
$x = 27$
Итак, значение $x$ равно 27.
Часто задаваемые вопросы
Когда мы используем перекрестное умножение ?
Мы используем перекрестное умножение для следующего:
- Процесс перекрестного умножения используется для сравнения как дробей, так и отношений. Используя эти , , мы можем оценить, равны ли они, больше или меньше.
