Пример 1.1
Тонкая плёнка с показателем преломления n = 1,4 нанесена на стеклянную пластинку с показателем преломления nст = 1,6. Плёнка освещается параллельным пучком монохроматического света, длина волны которого 440 нм. Угол падения лучей 60о. Определить, при какой минимальной толщине плёнки в результате интерференции произойдёт максимальное усиление отражённого света.
Дано: Анализ и решение
отражённый свет,
max
n = 1,4
ncт = 1,6
nв = 1
λ = 440 нм = 4,4·10 –7м
——————————
Определить:
Выделим
из световой вол-ны, падающей на плёнку,
узкий пучок монохроматического света
– луч SA (рис.
1.4).
При попада-нии на плёнку в точке А часть волны отражается (луч S1),
а часть, преломившись, дважды проходит
плёнку толщиной d, отражаясь
при этом в точке В от стеклянной пластинки. Преломившись
в точке С, луч 2 выходит в воздух и идёт параллельно
лучу S1 (луч S2).
Лучи S1 и S2 когерентны.
Поэтому после их пересечения в главном
фокусе линзы, поставленной на их пути,
они интерферируют. Результат интерференции
зависит от оптической разности хода
лучей. Разность хода возникает за счёт
прохождения лучом 2 плёнки. Кроме того, нужно учесть условия
отражения лучей S1 в точке А
Поэтому попадают они на линзу в одинаковых
фазах и результат интерференции их
будет такой же, как если бы никакого
изменения фазы колебаний ни у 1-го,
ни у 2-го
луча не было.Как известно, оптическая разность хода лучей при интерференции на тонких плёнках
, (1)
где d – толщина плёнки; n – показатель преломления плёнки; i – угол падения световой волны на плёнку.
Условие максимального усиления света при интерференции состоит в том, что оптическая разность хода волн должна быть равна чётному числу длин полуволн, т. е.
(2)
где m = 0, 1, 2, … – порядок максимума; λ – длина волны падающего света.
Окончательно условие максимума интерференции в данном случае принимает вид
, (3)
откуда
(m = 1, 2,
3, …).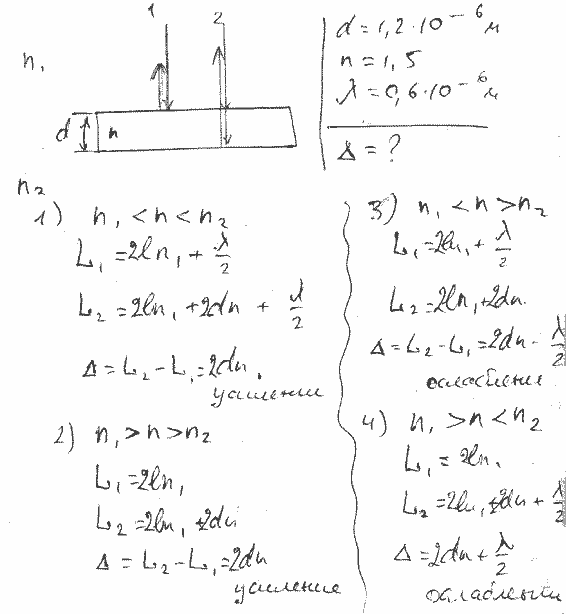
(4)
Как видно из (4), толщина d для данной плёнки может принимать различные значения в зависимости от m. Минимальная толщина плёнки будет при минимальном m, т. е. m = 1. Тогда (4) имеет вид
. (5)
Выполним расчёт для i = 60 o :.
Ответ: минимальная толщина плёнки dmin = 2 10 –7 м = 0,2 мкм.
Пример 1.2
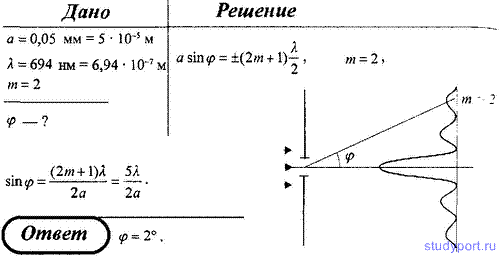
На стеклянный клин нормально к его грани падает монохроматический свет с длиной волны λ = 0,6 мкм. В возникшей при этом интерференционной картине на отрезке длиной l = 1 см наблюдается 10 полос. Определить преломляющий угол клина.
тёмные полосы –
min
N = 10
λ = 0,6 мкм = 6·10 -7м
l = 1см = 10 –2 м
——————————
Определить α
1.5). Эти пучки
когерентны и поэтому наблюдается
устойчивая картина интерференции. Так
как интерференционные полосы наблюдаются
при малых углах клина, то отражённые
пучки света 1 и 2 будут практически параллельны.Тёмные полосы видны на тех участках клина, для которых разность хода кратна нечётному числу длин полуволн:
Δ = (2m + 1) λ /2 (m = 0, 1, 2, …). (1)
Разность хода Δ двух волн складывается из разности оптических длин путей этих волн (2dn·cos r) и половины длины волны (λ/2). Величина λ/2 представляет собой добавочную разность хода, возникающую при отражении от оптически более плотной среды. Подставляя в формулу (1) значение разности хода Δ, получаем
2dm n cos r + λ/2 = (2m + 1) λ /2, (2)
где n – коэффициент преломления стекла (n
= 1,5); dm – толщина клина в том месте, где наблюдается
тёмная полоса, соответствующая номеру m; r – угол преломления.
Согласно условию, угол падения равен нулю, следовательно, и угол преломления r равен нулю, а cos r = 1. Раскрыв скобки в правой части равенства (2), после упрощения получим
2dm n = m λ . (3)
Пусть
произвольной тёмной полосе
sin α = (dm+10 – dm) / l (4)
Выразим из соотношения (3) dm и dm+10 и подставим их в формулу (4). Учитывая, что sin α α (из-за малости угла α), получим
α =
.
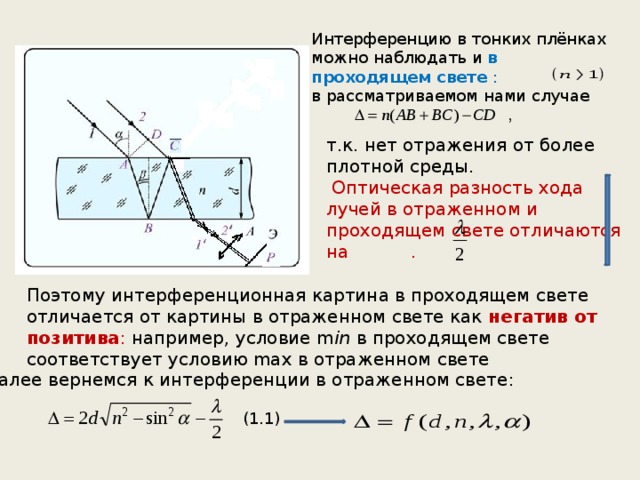
4.5. Интерференция света в тонких пленках
Радужная окраска мыльных пузырей или бензиновых пленок на воде возникает в результате интерференции солнечного света, отраженного двумя поверхностями пленки.
Пусть на плоскопараллельную прозрачную пленку с показателем преломления п и толщиной d под углом падает плоская монохроматическая волна с длиной (рис. 4.8).
Рис. 4.8. Интерференция света в тонкой пленке
Интерференционная картина в отраженном свете возникает из-за наложения двух волн, отраженных от верхней и нижней поверхностей пленки. Рассмотрим сложение волн, выходящих из точки С. Плоскую волну можно представить как пучок параллельных лучей. Один из лучей пучка (2) непосредственно попадает в точку С и отражается (2′)в ней наверх под углом, равным углу падения . Другой луч (1) попадает в точку С более сложным путем: сначала он преломляется в точке А и распространяется в пленке, затем отражается от нижней ее поверхности в точке 0 и, наконец, выходит, Преломившись, наружу (1′) в точке С под углом, равным углу падения .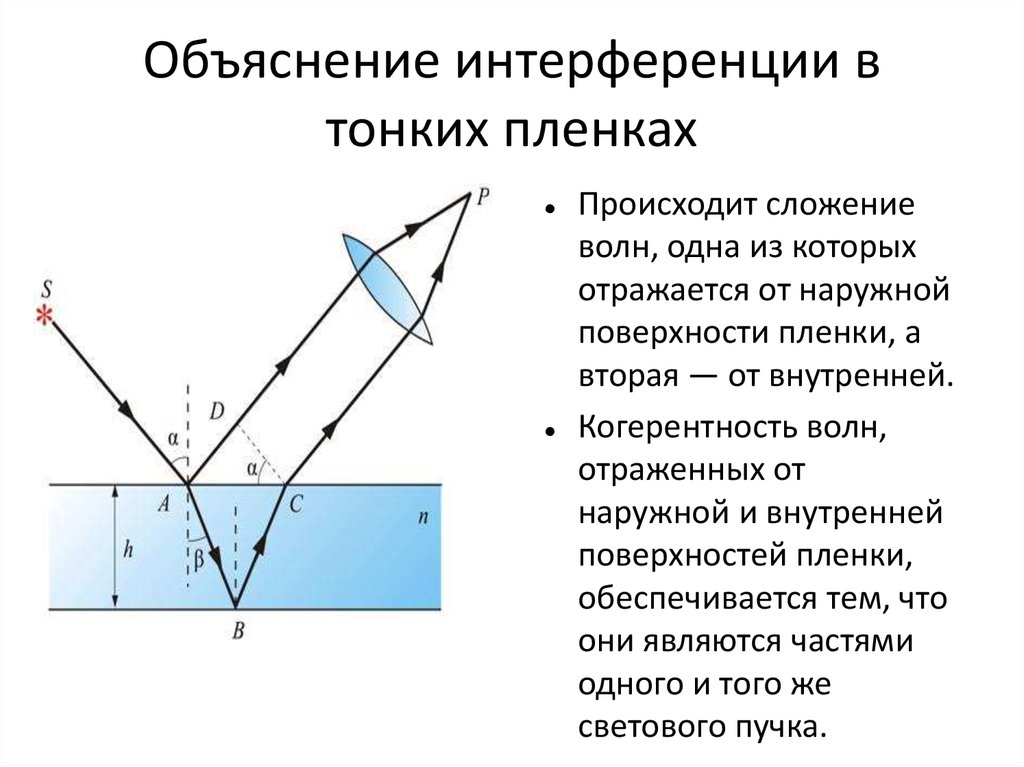
Оптическая разность хода, приобретаемая лучами 1 и 2 до того, как они сойдутся в точке С, равна
|
|
(4.23) |
Полагая показатель преломления воздуха и учитывая соотношения
и
а также
находим
|
|
(4. |
24)Используем закон преломления света
|
|
(4.25) |
откуда
|
|
|
(4.26) |
Таким образом,
|
|
(4. |
27)Кроме оптической разности хода , следует учесть изменение фазы волны при отражении. В точке С на границе раздела «воздух – пленка» происходит отражение от оптически более плотной среды, то есть среды с большим показателем преломления. При не слишком больших углах падения в этом случае фаза претерпевает изменение на . (Такой же скачок фазы происходит при отражении волны, бегущей вдоль струны, от ее закрепленного конца.) В точке 0 на границе раздела «пленка — воздух» свет отражается от оптически менее плотной среды, так что скачка фазы не происходит.
В итоге между лучами 1′ и 2′ возникает дополнительная разность фаз , соответствующая, как следует из формулы (4.12), оптической разности хода , которую можно учесть, если величину уменьшить или увеличить на половину длины волны в вакууме.
Следовательно, при выполнении соотношения
|
|
(4. |
28)получается максимум интерференции в отраженном свете, а в случае
|
|
(4.29) |
в отраженном свете наблюдается минимум.
Таким образом, при падении света на бензиновую пленку на воде в зависимости от угла зрения и толщины пленки наблюдается радужная окраска пленки, свидетельствующая об усилении световых волн с определенными длинами l. Интерференция в тонких пленках может наблюдаться не только в отраженном, но и в проходящем свете.
Как уже отмечалось, для возникновения наблюдаемой интерференционной картины оптическая разность хода интерферирующих волн не должна превышать длины когерентности , что накладывает ограничение на толщину пленки.
Пример. На мыльную пленку (п = 1.3), находящуюся в воздухе, падает по нормали пучок белого света. Определим, при какой наименьшей толщине d пленки отраженный свет с длиной волны мкм окажется максимально усиленным в результате интерференции.
Из условия интерференционного максимума (4.28) находим для толщины пленки выражение
(угол падения ). Минимальное значение d получается при :
3.4 Интерференция в тонких пленках — University Physics Volume 3
Цели обучения
К концу этого раздела вы сможете:
- Описать фазовые изменения, происходящие при отражении
- Опишите полосы, образованные отраженными лучами общего источника
- Объясните появление цветов в тонких пленках
Яркие цвета нефтяного пятна, плавающего на воде, или освещенного солнцем мыльного пузыря вызваны интерференцией. Самые яркие цвета — это те, которые конструктивно мешают.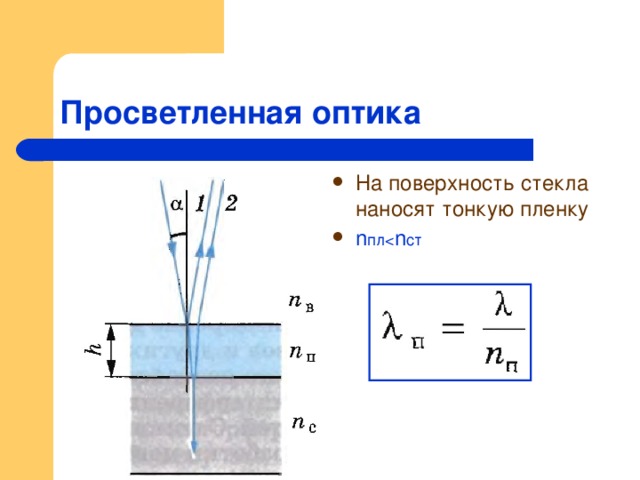
Эта интерференция возникает между светом, отраженным от разных поверхностей тонкой пленки; таким образом, эффект известен как тонкопленочная интерференция.
Как мы уже отмечали ранее, интерференционные эффекты наиболее заметны, когда свет взаимодействует с чем-то, размер которого подобен его длине волны. Тонкая пленка — это пленка, имеющая толщину t меньшую, чем в несколько раз длина волны света λλ. Поскольку цвет косвенно связан с λλ и поскольку вся интерференция каким-то образом зависит от отношения λλ к размеру рассматриваемого объекта, мы должны ожидать, что для пленок разной толщины будут разные цвета, как на рис. 3.11.
Рисунок 3.11 Эти мыльные пузыри проявляют яркие цвета при воздействии солнечного света. (кредит: Скотт Робинсон)
Что вызывает интерференцию тонкой пленки? На рис. 3.12 показано, как может интерферировать свет, отраженный от верхней и нижней поверхностей пленки. Падающий свет лишь частично отражается от верхней поверхности пленки (луч 1).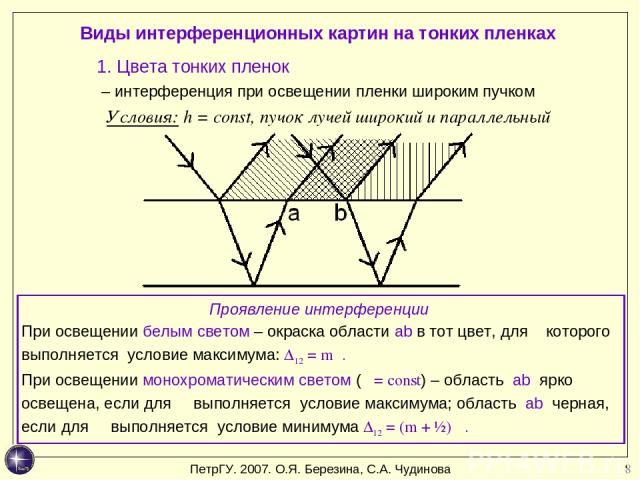
Остаток попадает на пленку и сам частично отражается от нижней поверхности. Часть света, отраженного от нижней поверхности, может выходить из верхней части пленки (луч 2) и мешать свету, отраженному сверху (луч 1). Луч, который входит в пленку, проходит большее расстояние, поэтому он может быть в фазе или не в фазе с лучом, отраженным сверху. Однако снова взгляните на кружки на рис. 3.11. Пузырьки самые темные там, где они самые тонкие. Более того, если вы внимательно понаблюдаете за мыльным пузырем, то заметите, что он темнеет в том месте, где лопается. Для очень тонких пленок разница в длинах хода лучей 1 и 2 на рис. 3.12 незначительна, так почему же они должны интерферировать деструктивно, а не конструктивно? Ответ заключается в том, что изменение фазы может произойти при отражении, как будет показано далее.
Рисунок
3.12
Свет, падающий на тонкую пленку, частично отражается (луч 1) и частично преломляется на верхней поверхности. Преломленный луч частично отражается от нижней поверхности и выходит как луч 2.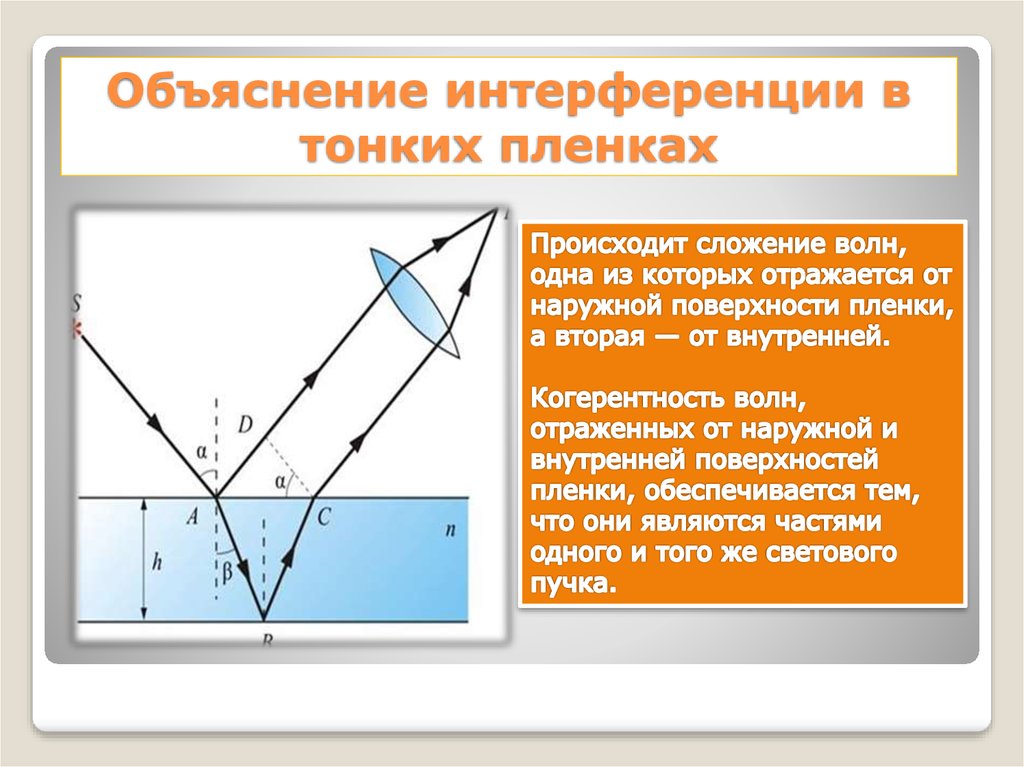
Эти лучи интерферируют способом, который зависит от толщины пленки и показателей преломления различных сред.
Изменения фазы из-за отражения
Ранее мы видели (Волны), что отражение механических волн может включать изменение фазы на 180°180°. Например, бегущая волна на струне инвертируется (т.е. изменяется фаза на 180°180°) при отражении от границы, к которой привязана более тяжелая струна. Однако, если вторая струна легче (точнее, имеет меньшую линейную плотность), инверсии не происходит. Световые волны производят тот же эффект, но решающим параметром для света является показатель преломления. Световые волны претерпевают изменение фазы на 180 ° 180 ° или ππ радиан при отражении от границы раздела, за которой находится среда с более высоким показателем преломления. При отражении от среды с меньшим показателем преломления фазового перехода не происходит (рис. 3.13). Из-за периодического характера волн это изменение фазы или инверсия эквивалентно ±λ/2±λ/2 по пройденному расстоянию или длине пути.
И длина пути, и показатели преломления являются важными факторами интерференции в тонких пленках.
Рисунок
3.13
Отражение на границе раздела для света, идущего из среды с показателем преломления n1n1 в среду с показателем преломления n2n2, n1 Если пленка на рис. 3.12 представляет собой мыльный пузырь (по сути, вода с воздухом с обеих сторон), то фазовый сдвиг λ/2λ/2 возникает для луча 1, но не для луча 2. Таким образом, когда пленка очень тонкая и разница в длине пути между двумя лучами незначительна, они точно не совпадают по фазе, и деструктивная интерференция возникает на всех длинах волн. Таким образом, мыльный пузырь здесь темный. Толщина пленки по отношению к длине волны света является другим решающим фактором в тонкопленочной интерференции. Луч 2 на рис. 3.12 проходит большее расстояние, чем луч 1. Если свет падает перпендикулярно поверхности, луч 2 проходит расстояние примерно 2 t дальше луча 1. В сложных камерах используется серия из нескольких объективов. Свет может отражаться от поверхностей этих различных линз и ухудшать четкость изображения. Чтобы ограничить эти отражения, линзы покрыты тонким слоем фторида магния, который вызывает деструктивную тонкопленочную интерференцию. Какой самой тонкой может быть эта пленка, если ее показатель преломления равен 1,38 и она предназначена для ограничения отражения света с длиной волны 500 нм, обычно самой интенсивной видимой длины волны? Предположим, что показатель преломления стекла равен 1,52. Обратитесь к рисунку 3.12 и используйте n1=1,00n1=1,00 для воздуха, n2=1,38n2=1,38 и n3=1,52n3=1,52. И луч 1, и луч 2 имеют сдвиг λ/2λ/2 при отражении. Таким образом, для получения деструктивной интерференции луч 2 должен пройти на половину длины волны дальше, чем луч 1. Для лучей, падающих перпендикулярно, разница в длине пути составляет 2 t . Чтобы получить деструктивную интерференцию здесь, 2t=λn222t=λn22 где λn2λn2 — длина волны в пленке, определяемая как λn2=λ/n2λn2=λ/n2. Таким образом, 2t=λ/n22.2t=λ/n22. Решение для t и ввод известных значений дает t=λ/n24=(500нм)/1,384=90,6нм.t=λ/n24=(500нм)/1,384=90,6нм. Пленки, такие как пленка в этом примере, наиболее эффективны в создании деструктивной интерференции, когда используется самый тонкий слой, поскольку интенсивность света в более широком диапазоне углов падения снижается. Тонкопленочная интерференция является наиболее конструктивной или наиболее разрушительной, когда разность длин пути для двух лучей составляет целую или полуцелую длину волны. То есть для лучей, падающих перпендикулярно, 2t=λn,2λn,3λn,…или2t=λn/2,3λn/2,5λn/2,….2t=λn,2λn,3λn,…или2t=λn/2,3λn/2,5λn/2,… . Чтобы узнать, является ли интерференция конструктивной или деструктивной, необходимо также определить, происходит ли изменение фазы при отражении. Таким образом, тонкопленочная интерференция зависит от толщины пленки, длины волны света и показателей преломления. Для белого света, падающего на пленку различной толщины, вы можете наблюдать радужные цвета конструктивной интерференции для различных длин волн при изменении толщины. а) При каких трех наименьших толщинах мыльного пузыря создается конструктивная интерференция красного света с длиной волны 650 нм? Показатель преломления мыла принимают равным показателю преломления воды. б) Какие три наименьшие толщины дают деструктивную интерференцию? Используйте рисунок 3.12, чтобы визуализировать пузырь, который действует как тонкая пленка между двумя слоями воздуха. Таким образом, n1=n3=1,00n1=n3=1,00 для воздуха и n2=1,333n2=1,333 для мыла (эквивалентно воде). Для луча 1, отраженного от верхней поверхности пузырька, имеется сдвиг λ/2λ/2, а для луча 2, отраженного от нижней поверхности, смещения нет. Тогда, чтобы получить конструктивную интерференцию, разность длин пути (2 t ) должно быть кратным половине длины волны — первые три равны λn/2,3λn/2λn/2,3λn/2 и 5λn/25λn/2. а. Конструктивное вмешательство имеет место, когда 2tc=λn2,3λn2,5λn2,….2tc=λn2,3λn2,5λn2,…. Таким образом, наименьшая конструктивная толщина tctc равна tc=λn4=λ/n4=(650нм)/1,3334=122нм.tc=λn4=λ/n4=(650нм)/1,3334=122нм. Следующая толщина, обеспечивающая конструктивную интерференцию, равна tc′=3λn/4tc′=3λn/4, так что tc′=366 нм.tc′=366 нм. Наконец, третья толщина, создающая конструктивную интерференцию, равна tc′=5λn/4tc′=5λn/4, так что tc′=610nm.tc′=610nm. б. Для деструктивной интерференции разность длин пути здесь является целым кратным длины волны. Первое имеет место при нулевой толщине, так как на верхней поверхности есть фазовый переход, т. е. td=0,td=0, очень тонкий (или пренебрежимо тонкий) случай, рассмотренный выше. 2td′=λn.2td′=λn. Замена известных значений дает td′=λ2=λ/n2=(650 нм)/1,3332=244 нм.td′=λ2=λ/n2=(650 нм)/1,3332=244 нм. Наконец, третья разрушающая толщина равна 2td″=2λn2td″=2λn, так что td″=λn=λn=650nm1.333=488nm.td″=λn=λn=650nm1.333=488nm. Если бы пузырь освещался чистым красным светом, мы бы увидели яркие и темные полосы с очень равномерным увеличением толщины. Сначала будет темная полоса толщиной 0, затем яркая полоса толщиной 122 нм, затем темная полоса 244 нм, яркая полоса 366 нм, темная полоса 488 нм и яркая полоса 610 нм. Если бы пузырек плавно менялся по толщине, как гладкий клин, то полосы располагались бы равномерно. Продолжая пример 3.4, каковы следующие две толщины мыльного пузыря, которые привели бы к (а) конструктивной интерференции и (б) деструктивной интерференции? Другой пример тонкопленочной интерференции можно увидеть при разделении предметных стекол микроскопа (см. Рисунок
3.14
(а) Полосы радужного цвета образуются в результате интерференции тонкой пленки в воздухе между двумя предметными стеклами. (б) Схема траекторий лучей в воздушном клине между слайдами. (c) Если воздушный клин освещается монохроматическим светом, получаются яркие и темные полосы, а не повторяющиеся цвета радуги. Важным применением тонкопленочной интерференции является производство оптических приборов. Линзу или зеркало можно сравнить с мастером, когда он шлифуется, что позволяет придать ему форму с точностью менее длины волны по всей его поверхности. На рис. 3.15 показано явление, называемое кольцами Ньютона, которое возникает, когда плоские поверхности двух линз помещаются вместе. (Круговые полосы называются кольцами Ньютона, потому что Исаак Ньютон подробно описал их и их использование. Ньютон их не открыл; открыл Роберт Гук, и Ньютон не верил, что они возникли из-за волнового характера света.) Каждое последующее кольцо данный цвет указывает на увеличение расстояния между линзой и бланком всего на половину длины волны, так что можно получить большую точность. Когда линза идеальна, колец не появляется. Рисунок
3.15
Интерференционные полосы «кольца Ньютона» образуются, когда две плосковыпуклые линзы помещают вместе, их плоские поверхности соприкасаются. Кольца создаются интерференцией света, отраженного от двух поверхностей в результате небольшого зазора между ними, что указывает на то, что эти поверхности не совсем плоские, а слегка выпуклые. Тонкопленочная интерференция имеет множество других применений как в природе, так и в производстве. Крылья некоторых мотыльков и бабочек имеют почти радужный цвет из-за интерференции тонкой пленки. Помимо пигментации, на цвет крыла большое влияние оказывает конструктивная интерференция определенных длин волн, отраженных от его пленочной поверхности. Некоторые производители автомобилей предлагают специальные покрасочные работы, в которых используется тонкопленочная интерференция для получения цветов, меняющихся под углом. Этот дорогостоящий вариант основан на изменении разности длины пути тонкой пленки в зависимости от угла. Защитные элементы на кредитных картах, банкнотах, водительских правах и подобных предметах, которые могут быть подделаны, используют тонкопленочные интерференционные материалы, дифракционные решетки или голограммы. Уже в 1998, Австралия лидировала с долларовыми купюрами, напечатанными на полимере с защитным элементом дифракционной решетки, что затрудняет подделку валюты. Глава 27 вопрос: 1PE2PE3PE4PE5PE6PE7PE8PE9PE10PE11PE12PE13PE14PE15PE16PE17PE18PE19PE20PE21PE22PE23PE24PE25PE26PE27PE28PE29PE30PE31PE32PE33PE34PE35PE36PE37PE38PE39PE40PE41PE43PE44PE45PE46PE47PE48PE49PE50PE51PE52PE53PE54PE55PE56PE57PE58PE59PE60PE61PE62PE63PE64PE65PE66PE67PE68PE70PE71PE72PE73PE74PE75PE76PE77PE78PE79PE80PE81PE82PE83PE84PE85PE86PE87PE88PE89PE90PE91PE92PE93PE94PE95PE96PE97PE98PE99PE100PE Расширенный поиск Вопрос На рис. 27.34 показаны два предметных стекла, освещенные светом чистой длины волны, падающим перпендикулярно. Вопрос Изображение Вопрос от OpenStax находится под лицензией
СС BY 4.0. Окончательный ответ $0,221 \textrm{ мм}$ Решение Видео Начать бесплатную неделю Trustpilot Рейтинг ПлохоНе так уж плохоСреднеХорошоОчень хорошо 1 голос с рейтингом 5 Стенограмма видео Это ответы по физике в колледже с Шоном Дычко.
Когда это расстояние является целым или полуцелым кратным длины волны в среде (λn=λ/n(λn=λ/n, где λλ — длина волны в вакууме, а n равно показатель преломления), происходит конструктивная или деструктивная интерференция, в зависимости также от того, имеет ли место изменение фазы того или иного луча. Пример
3.3
Расчет толщины неотражающего покрытия линзы
Стратегия
Раствор
Значение
Эти пленки называются неотражающими покрытиями; это лишь приблизительно правильное описание, поскольку другие длины волн компенсируются лишь частично. Неотражающие покрытия также используются в автомобильных стеклах и солнцезащитных очках. Объединение разности длин пути с изменением фазы
Пример
3.4
Мыльные пузыри
Стратегия
Чтобы получить деструктивную интерференцию, разность длин пути должна быть целым кратным длины волны — первые три равны 0, λnλn и 2λn2λn. Раствор
Первая ненулевая толщина, создающая деструктивную интерференцию, равна Значение
Проверьте свое понимание
3.2
рис. 3.14). Горки очень плоские, так что клин воздуха между ними очень равномерно увеличивается в толщине. Изменение фазы происходит на второй поверхности, но не на первой, поэтому в месте соприкосновения предметных стекол образуется темная полоса. Цвета радуги конструктивной интерференции повторяются, снова и снова переходя от фиолетового к красному по мере увеличения расстояния между слайдами. По мере увеличения слоя воздуха полосы становится труднее увидеть, потому что небольшие изменения угла падения больше влияют на различия в длине пути. Если использовать монохроматический свет вместо белого, то получаются яркие и темные полосы, а не повторяющиеся цвета радуги.
(кредит: Ульф Зайферт)
Другие страны, такие как Канада, Новая Зеландия и Тайвань, используют аналогичные технологии, в то время как валюта США включает интерференционный эффект тонкой пленки. OpenStax College Physics Solution, глава 27, задача 79 (задачи и упражнения)
Верхний слайд одним концом касается нижнего слайда, а другим концом опирается на волосок диаметром 0,100 мм, образуя воздушный клин. а) На каком расстоянии друг от друга находятся темные полосы, если предметные стекла имеют длину 7,50 см и 589-нм свет используется? (b) Есть ли разница в том, сделаны ли предметные стекла из коронки или бесцветного стекла? Объяснять. Зарегистрируйтесь, чтобы посмотреть видео с решением!
Скриншоты калькулятора
Два предметных стекла разделены на одном конце волоском диаметром 0,1 миллиметра. Итак, расстояние здесь равно 0,1 миллиметра. Тогда кусочки стекла соприкасаются на этом конце. Таким образом, между кусочками стекла образуется треугольный воздушный клин. Теперь здесь будет мешать падающий свет. Это будет один луч, который отразится от этой границы между стеклом и воздухом, а затем пойдет вверх. И тогда другой Луч отскочит от нижнего куска стекла, а затем вернется обратно. И этот рисунок не совсем точен, потому что он говорит о том, что свет падает перпендикулярно. Так что все эти лучи на самом деле перекрываются, но было бы слишком сложно нарисовать это и объяснить, откуда исходят разные лучи. Вот почему он показывает угол. Но имейте в виду, что он должен перекрываться, поэтому первый и второй лучи будут мешать. И в этом случае, поскольку мы ищем темные полосы, интерференция будет разрушительной. А потом в какой-то позиции чуть позже здесь на каком-то расстоянии delta x у вас будет следующая темная полоса, возникающая, когда снова возникнет деструктивная интерференция в результате этой увеличенной разницы в длине пути.
Итак, давайте вычислим выражения для фазовых сдвигов Лучей один и два, а затем посмотрим, как они меняются в зависимости от горизонтального положения. Теперь фазовый сдвиг Луча один равен нулю, потому что это отражение здесь происходит на границе раздела, где вы начинаете в среде с высоким показателем преломления и каком-то стекле, а затем переходите в среду с низким показателем преломления, которой является воздух. Так что фазового сдвига там нет. И затем для луча два, однако, есть отражение от этой границы между воздухом в стекле, и это действительно имеет фазовый сдвиг автоматически на половину длины волны при переходе от преломления с низким показателем преломления к преломлению с высоким показателем, а затем дополнительно есть фаза смещение из-за этой дополнительной длины пути, пройденного вторым лучом. Итак, мы вычисляем количество длин волн, которым соответствует длина пути, а затем умножаем на длину волны. И это хорошо работает, они на самом деле будут одинаковыми, потому что обычно у меня есть индекс n здесь, чтобы сказать, что вы знаете дополнительный путь, деленный на длину волны в этой среде.
Но в данном случае средой является воздух. Таким образом, они компенсируются, и у нас есть два, потому что луч проходит один раз вниз по этой толщине, а затем снова поднимается по толщине, он совершает путешествие туда и обратно, путешествуя по этой толщине, вдвое превышающей толщину этого воздушного зазора. И это соответствует Pi в два раза больше толщины воздушного зазора. Итак, теперь у нас есть фазовые сдвиги для каждого из двух лучей. Теперь общий фазовый сдвиг, когда вы складываете их вместе, должен быть некоторым целым числом плюс половина длины волны, чтобы иметь деструктивную интерференцию, и этот общий фазовый сдвиг будет равен 9.0185 Delta Phi 1 плюс Delta Phi 2 равно м плюс половина длины волны. И теперь мы можем заменить эти выражения для Delta Phi , которые мы нашли ранее в синем нуле четыре каждый один, а затем лямбда над двумя плюс 2t для второго луча, и мы собираемся решить это для t . Итак, я умножаю обе части на два здесь, а затем распределяю лямбда в скобки и получаю лямбда плюс 40 равно, я думаю, я просто умножил два в скобках.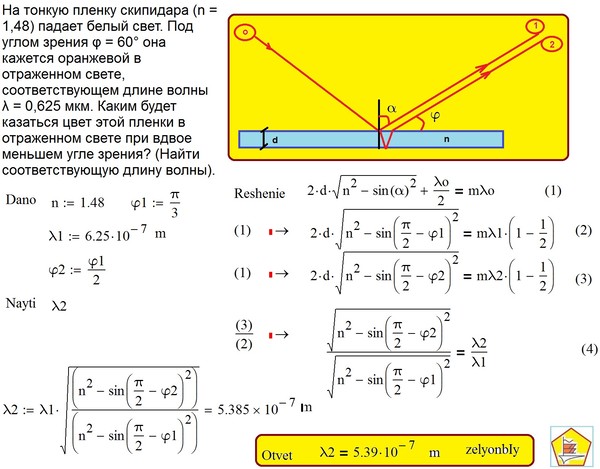
Так что 2 м плюс один раз лямбда , и вы получите 2 м лямбда плюс лямбда , а затем вычтите лямбда с обеих сторон, и вы получите 40 равно 2 м лямбда и затем 8 5 лямбда и 8 5 т . более двух. Итак, это выражение для толщины воздушного зазора, необходимого для возникновения деструктивной интерференции. И будет много таких толщин, вызывающих деструктивную интерференцию, потому что мы можем выбрать любое значение любое целое значение для м . Таким образом, мы собираемся иметь вот такое использование, когда кусочки стекла соприкасаются, и толщина некоторых t1 будет иметь разрушительные помехи. И это в горизонтальном положении x1 от этой точки, где они соприкасаются, а затем снова будет деструктивная интерференция, которая снова происходит в t2 . Таким образом, это будет соответствовать м, равно единице, а это соответствует м, равно двум этим двум толщинам. Мы подставим число один или два в это выражение для толщины, и это произойдет в позиции 9.
0185 х2 . И вопрос спрашивает нас, в чем разница между этими горизонтальными позициями. На каком расстоянии друг от друга расположены темные полосы по горизонтали. Что такое дельта x другими словами. Так что это подобные треугольники и потому, что углы все одинаковые. Я имею в виду, что они разделяют этот общий угол, а это угол 90 градусов. Это означает, что это два одинаковых угла, и поскольку они подобны, это означает, что отношение соответствующих сторон одинаково. Итак, когда вы берете х 2 разделить на t2 это будет то же самое, что x1 разделить на t1 . Так что давайте просто назовем это x поверх d . И d, это здесь, потому что мы знаем, каково соотношение для этого треугольника, и отношения, в которых все треугольники внутри здесь будут одинаковыми, потому что они все подобны. И я имею в виду подобное в математическом техническом смысле этого слова, означающее, что все время все углы в Треугольнике одинаковы и, следовательно, отношения соответствующих сторон одинаковы.
А мы знаем противоположное и соседнее для этого треугольника вот это высота 0,1 миллиметра и длина 7,5 сантиметра. Таким образом, мы можем сказать, что x2 равно t2 умножить на x на d и x1 на t1 умножить на x на d и мы заменим каждое из этих выражений на 10959 delta.18 delta. И это то, что я сделал здесь, и x на d можно вынести, и это будет t2 минус t1 умножить на x на d и 20185 Delta 9 на , затем заменив d на Delta и t1 используя здесь это выражение, заменив числа два и один на n . У нас есть два раза лямбда больше двух минус один раз лямбда больше двух раз x больше d и тогда это получается как лямбда больше двух, и тогда мы можем заменить числа. Итак, 589 нанометров — это длина волны, которую мы сказали, разделенная на два умноженных на семь с половиной сантиметров, записанная как умноженная на десять с точностью до минус двух метров, разделенная на 0,1 миллиметра, записанная как умноженная на десять с точностью до минус трех метров, дает нам столько нанометров, что составляет 0,221 мм.