Как вычислить двойной интеграл? Примеры решений
Прозвучал удар гонга, который открывает второй раунд в бою с двойными интегралами. Если вы недавно надели перчатки или вообще боксируете с грушей, то, пожалуйста, начните с первого раунда Двойные интегралы для чайников. Настоятельно рекомендую разобраться со всеми примерами вводного урока без халтуры, это очень важно. К тому же, добрый дядя Саша нарисовал много картинок, которые можно распечатать и наклеить у себя в туалете. Помните, что Коперник свои блестящие открытия в астрономии делал именно там.
Однако задорное получилось вступление…. Задумался вот… почему? Да потому что мне хорошо. А отчего хорошо, поясню в конце статьи.
Вспоминаем общую запись двойного интеграла:
В
первой статье Двойные
интегралы для чайников я
очень подробно рассмотрел понятие
двойного интеграла, алгоритм его решения,
важнейшие задачи на обход области
интегрирования. Также были прорешаны
простейшие двойные интегралы в примерах
на нахождение площади плоской фигуры.
Снова посмотрим на общую запись двойного интеграла и заметим, что в нём притаилась функция двух переменных . А когда речь заходит о функции двух переменных, то это часто попахивает сероводородом частными производными второго порядка. Поэтому для освоения примеров вам необходимо уметь более или менее уверенно их находить.
В большинстве практических задач требуется формально вычислить двойной интеграл, но, помимо этого, он обладает отличным геометрическим смыслом – с помощью двойного интеграла помимо площади можно вычислить еще и объём. Геометрический смысл двойного интеграла поясню ниже на конкретных примерах.
Начинаем набивать наш двойной интеграл разнообразной начинкой:
Пример 1
Вычислить двойной интеграл , Изменить порядок интегрирования и вычислить двойной интеграл вторым способом.
Решение: Изобразим область интегрирования на чертеже:
Напоминаю,
что выполнение чертежа – необходимый
начальный этап решения. Чертёж крайне важно выполнить правильно
и точно, поскольку ошибка в графике
незамедлительно запорет всё задание.
Чертёж крайне важно выполнить правильно
и точно, поскольку ошибка в графике
незамедлительно запорет всё задание.
Выберем следующий порядок обхода:
Вопросы порядка обхода области интегрирования, я комментировать практически не буду, пожалуйста, смотрите статью Двойные интегралы для чайников.
Таким образом:
Обратите внимание на следующее действие: в данном случае можно вынести «икс» из внутреннего интеграла во внешний интеграл. Почему? Во внутреннем интеграле интегрирование проводится по «игрек», следовательно, «икс» считается константой. А любую константу можно вынести за знак интеграла, что благополучно и сделано.
С интегралами настоятельно рекомендую разбираться по пунктам:
1) Используя формулу Ньютона-Лейбница, найдём внутренний интеграл:
2) Результат, полученный в первом пункте, подставим во внешний интеграл , при этом ни в коем случае не забываем про «икс», который там уже находится:
Готово.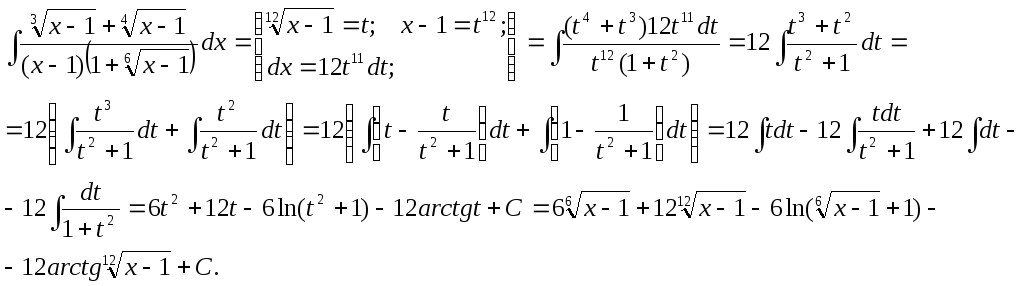
Замечательно, если у вас под рукой есть микрокалькулятор, на котором можно считать обыкновенные дроби, он значительно ускорит заключительные вычисления. В последующих примерах я не буду подробно расписывать приведение дробей к общему знаменателю, а просто запишу ответ.
Выполняем вторую часть задания: изменим порядок обхода области и вычислим двойной интеграл вторым способом.
Перейдём к обратным функциям:
Для наглядности еще раз приведу чертёж, он будет точно таким же, но с другими обозначениями графиков:
Второй способ обхода области:
Таким образом:
Вот здесь уже «икс» является «родным» для внутреннего интеграла, поэтому его нельзя вынести во внешний интеграл.
1) Используя формулу Ньютона-Лейбница, вычислим внутренний интеграл:
Вместо «икса» подставляются функции! Всегда проявляйте повышенное внимание при подстановке пределов интегрирования.
2) Результат, полученный в первом пункте, подставим во внешний интеграл и проведём окончательные вычисления:
Результаты
совпали, значит, задание выполнено
верно.
Если есть время, постарайтесь всегда проводить проверку, даже если этого не требуется в условии: вычислили интеграл одним способом – затем изменили порядок обхода области и вычислили вторым способом.
Ответ:
Пример 2
Вычислить двойной интеграл , Выполнить проверку: изменить порядок интегрирования и вычислить двойной интеграл вторым способом.
Это пример для самостоятельного решения. Обратите внимание, что в двойном интеграле изначально присутствует константа. А
Как видите, свойство линейности справедливо не только для «обычных», но и для кратных интегралов. Интеграл от интеграла недалеко падает.
Самое главное потом при вычислениях вынесенную константу не потерять. А забывают о ней часто.
Примерный
образец чистового оформления примера
в конце урока.
Задания на определенный интеграл. Интегралы – что это, как решать, примеры решений и объяснение для чайников. Правила вычисления интегралов для чайников
Данный калькулятор позволяет решить определенный интеграл онлайн. По сути, вычисление определенного интеграла — это нахождение числа, которое равно площади под графиком функции. Для решения необходимо задать границы интегрирования и интегрируемую функцию. После интегрирования система найдет первообразную для заданной функции, вычислит её значения в точках границах интегрирования, найдет их разность, что и будет являться решением определенного интеграла. Чтобы решить неопределенный интеграл вам необходимо воспользоваться похожим онлайн калькулятором, который находится на нашем сайте по ссылке — Решить неопределенный интеграл .
Мы позволяем вычислить определенный интеграл онлайн быстро и надежно. Вы получите всегда верное решение. Причем для табличных интегралов ответ будет представляться в классическом виде, то есть выражаться через известные константы, такие как число «пи», «экспонента» и т. д. Все вычисления полностью бесплатны и не требуют регистрации. Решая определенный интеграл у нас, вы избавите себя от трудоемких и сложных вычислений, либо решив интеграл самостоятельно — вы сможете проверить полученное вами решение.
д. Все вычисления полностью бесплатны и не требуют регистрации. Решая определенный интеграл у нас, вы избавите себя от трудоемких и сложных вычислений, либо решив интеграл самостоятельно — вы сможете проверить полученное вами решение.
Онлайн сервис на сайт позволяет находить решение определенного интеграла онлайн . Решение проводится автоматически на сервере и в течении нескольких секунд пользователю выдается результат. Все онлайн сервисы на сайте абсолютно бесплатны, а решение выдается в удобном и понятном виде. Также нашим преимуществом является, что мы предоставляем возможность пользователю ввести границы интегрирования, в том числе и пределы интегрирования: минус и плюс бесконечность. Таким образом, решить определенный интеграл становится просто, быстро и качественно. Важно, что сервер позволяет вычислять определенные интегралы онлайн сложных функций, решение которых на иных онлайн-сервисах часто является невозможным ввиду несовершенства их систем. Мы предоставляем очень простой и интуитивно понятный механизм для ввода функций и возможность выбора переменной интегрирования, для чего вам не приходится переводить заданную в одной переменной функцию в другую, исключая связанные с этим ошибки и опечатки.
Решая определенный интеграл у нас вы можете проверить своё собственное решение или избавиться от излишних трудоемких вычислений и довериться высокотехнологичной автоматизированной машине. Вычисляемая на сервисе точность удовлетворит практически любые инженерные нормы.
В каждой главе будут и задачи для самостоятельного решения, к которым можно посмотреть ответы.
Понятие определённого интеграла и формула Ньютона-Лейбница
Определённым интегралом от непрерывной функции f (x ) на конечном отрезке [a , b ] (где ) называется приращение какой-нибудь её первообразной на этом отрезке. (Вообще, понимание заметно облегчится, если повторить тему неопределённого интеграла) При этом употребляется запись
Как видно на графиках внизу (приращение первообразной функции обозначено ), определённый интеграл может быть как положительным, так и отрицательным числом (Вычисляется как разность между значением первообразной в верхнем пределе и её же значением в нижнем пределе, т. е. как F (b ) — F (a )).
Числа a и b называются соответственно нижним и верхним пределами интегрирования, а отрезок [a , b ] – отрезком интегрирования.
Таким образом, если F (x ) – какая-нибудь первообразная функция для f (x ), то, согласно определению,
(38)
Равенство (38) называется формулой Ньютона-Лейбница . Разность F (b ) – F (a ) кратко записывают так:
Поэтому формулу Ньютона-Лейбница будем записывать и так:
(39)
Докажем, что определённый интеграл не зависит от того, какая первообразная подынтегральной функции взята при его вычислении. Пусть
Тем самым установлено, что на отрезке [a , b ] приращения всех первообразных функции f (x ) совпадают.
Таким образом, для вычисления
определённого интеграла необходимо найти любую первообразную подынтегральной
функции, т. е. сначала следует найти неопределённый интеграл. Постоянная С из последующих вычислений исключается. Затем применяется формула Ньютона-Лейбница:
в первообразную функцию подставляется значение верхнего предела b , далее — значение
нижнего предела a и вычисляется разность F(b) — F(a) . Полученное число и будет
определённым интегралом.
.
е. сначала следует найти неопределённый интеграл. Постоянная С из последующих вычислений исключается. Затем применяется формула Ньютона-Лейбница:
в первообразную функцию подставляется значение верхнего предела b , далее — значение
нижнего предела a и вычисляется разность F(b) — F(a) . Полученное число и будет
определённым интегралом.
.
При a = b по определению принимается
Пример 1.
Решение. Сначала найдём неопределённый интеграл:
Применяя формулу Ньютона-Лейбница к первообразной
(при С = 0), получим
Однако при вычислении определённого интеграла лучше не находить отдельно первообразную, а сразу записывать интеграл в виде (39).
Пример 2. Вычислить определённый интеграл
Решение. Используя формулу
Найти определённый интеграл самостоятельно, а затем посмотреть решение
Свойства определённого интеграла
Теорема 2. Величина определённого интеграла не зависит от обозначения переменной интегрирования , т. е.
е.
(40)
Пусть F (x ) – первообразная для f (x ). Для f (t ) первообразной служит та же функция F (t ), в которой лишь иначе обозначена независимая переменная. Следовательно,
На основании формулы (39) последнее равенство означает равенство интегралов
Теорема 3. Постоянный множитель можно выносить за знак определённого интеграла , т.е.
(41)
Теорема 4. Определённый интеграл от алгебраической суммы конечного числа функций равен алгебраической сумме определённых интегралов от этих функций , т.е.
(42)
Теорема 5. Если отрезок интегрирования разбит на части, то определённый интеграл по всему отрезку равен сумме определённых интегралов по его частям , т.е. если
(43)
Теорема 6. При перестановке пределов интегрирования абсолютная величина определённого интеграла не меняется, а изменяется лишь его знак , т.е.
(44)
Теорема 7 (теорема о среднем). Определённый интеграл равен произведению длины отрезка интегрирования на значение подынтегральной функции в некоторой точке внутри его , т.е.
Определённый интеграл равен произведению длины отрезка интегрирования на значение подынтегральной функции в некоторой точке внутри его , т.е.
(45)
Теорема 8. Если верхний предел интегрирования больше нижнего и подынтегральная функция неотрицательна (положительна), то и определённый интеграл неотрицателен (положителен), т.е. если
Теорема 9. Если верхний предел интегрирования больше нижнего и функции и непрерывны, то неравенство
можно почленно интегрировать , т.е.
(46)
Свойства определённого интеграла позволяют упрощать непосредственное вычисление интегралов.
Пример 5. Вычислить определённый интеграл
Используя теоремы 4 и 3, а при нахождении первообразных – табличные интегралы (7) и (6), получим
Определённый интеграл с переменным верхним пределом
Пусть f (x ) – непрерывная на отрезке [a , b ] функция, а F (x ) – её первообразная. Рассмотрим определённый интеграл
Рассмотрим определённый интеграл
(47)
а через t обозначена переменная интегрирования, чтобы не путать её с верхней границей. При изменении х меняется и опредёленный интеграл (47), т.е. он является функцией верхнего предела интегрирования х , которую обозначим через Ф (х ), т.е.
(48)
Докажем, что функция Ф (х ) является первообразной для f (x ) = f (t ). Действительно, дифференцируя Ф (х ), получим
так как F (x ) – первообразная для f (x ), а F (a ) – постояная величина.
Функция Ф (х ) – одна из бесконечного множества первообразных для f (x ), а именно та, которая при x = a обращается в нуль. Это утверждение получается, если в равенстве (48) положить x = a и воспользоваться теоремой 1 предыдущего параграфа.
Вычисление определённых интегралов методом интегрирования по частям и методом замены переменной
где, по определению, F (x ) – первообразная для f (x ). Если в подынтегральном выражении произвести замену переменной
Если в подынтегральном выражении произвести замену переменной
то в соответствии с формулой (16) можно записать
В этом выражении
первообразная функция для
В самом деле, её производная, согласно правилу дифференцирования сложной функции , равна
Пусть α и β – значения переменной t , при которых функция
принимает соответственно значения a и b , т.е.
Но, согласно формуле Ньютона-Лейбница, разность F (b ) – F (a ) есть
Примеры вычисления неопределённых интегралов
Вычисление интеграла по таблице
Интегрирование подстановкой:
Примеры вычисления интегралов
Основная формула Ньютона – Лейбница
Вычисления подстановкой
Глава 4 Дифференциальные уравнения.
Дифференциальным уравнением называется уравнение, связывающее между собой независимую переменную х , искомую функции у и ее производные или дифференциалы.
Символически дифференцированное уравнение записывается так:
Дифференциальное уравнение называется обыкновенным , если искомая функция зависит от одного независимого переменного.
Порядком дифференциального уравнения называется порядок старшей производной (или дифференциала), входящей в данное уравнение.
Решением (или интегралом ) дифференциального уравнения называется такая функция, которая обращает это уравнение в тождество.
Общим решением (или общим интегралом ) дифференциального уравнения называется такое решение, в которое входит столько независимых произвольных постоянных, каков порядок уравнения. Так, общее решение дифференциального уравнения первого порядка содержит одну произвольную постоянную.
Частным решением дифференциального уравнения называется решение, полученное из общего при различных числовых значениях произвольных постоянных. Значения произвольных постоянных находятся при определенных начальных значениях аргумента и функции.
График частного решения дифференциального уравнения называется интегральной кривой.
Общему решению дифференциального уравнения соответствует совокупность (семейство) всех интегральных кривых.
Дифференциальным уравнением первого порядка называется уравнение, в которое входят производные (или дифференциалы) не выше первого порядка.
Дифференциальным уравнением с разделяющимися переменными называется уравнение вида
Для решения этого уравнения нужно сначала разделить переменные:
а затем проинтегрировать обе части полученного равенства:
1. Найти общее решение уравнения
o Разделив переменные имеем
Интегрируя обе части полученного уравнения:
Так как произвольная постоянная С может принимать любые числовые значения, то для удобства дальнейших преобразований вместо C мы написали (1/2) lnC. Потенцируя последнее равенство получим
Это и есть общее решение данного уравнения.
Литература
В. Г. Болтянский, Что такое дифференцирование, «Популярные лекции по математике»,
Выпуск 17, Гостехиздат 1955 г., 64 стр.
В. А. Гусев, А. Г. Мордкович «Математика»
Г. М. Фихтенгольц «Курс дифференциального и интегрального исчисления», том 1
В. М. Бородихин, Высшая математика, учеб. пособие, ISBN 5-7782-0422-1.
Никольский С. М. Глава 9. Определенный интеграл Римана // Курс математического анализа. — 1990. — Т. 1.
Ильин В. А., Позняк, Э. Г. Глава 6. Неопределенный интеграл // Основы математического анализа. — 1998. — Т. 1. — (Курс высшей математики и математической физики).
Демидович Б.П. Отдел 3. Неопределенный интеграл // Сборник задач и упражнений по математическому анализу. — 1990. — (Курс высшей математики и математической физики).
Валуцэ И.И., Дилигул Г.Д. Математика для техникумов на базе средней школы: Учеб.пособие-2-е изд.перераб. и доп. М.6Наука. 1989
Колягин Ю.М. Яковлев Г.Н. математика для техникумов. Алгебра и начала анализа 1 и 2 часть. Издательство «Наукка» М., 1981г.
Алгебра и начала анализа 1 и 2 часть. Издательство «Наукка» М., 1981г.
Щипачев В.С. Задачи по высшей математике: Учеб. Пособие для вузов. Высш. Шк. 1997г.
Богомолов Н.В практические занятия по математике: учеб. Пособие для техникумов. Высш. Шк 1997г.
Решение интегралов – задача легкая, но только для избранных. Эта статья для тех, кто хочет научиться понимать интегралы, но не знает о них ничего или почти ничего. Интеграл… Зачем он нужен? Как его вычислять? Что такое определенный и неопределенный интегралы?
Если единственное известное вам применение интеграла – доставать крючком в форме значка интеграла что-то полезное из труднодоступных мест, тогда добро пожаловать! Узнайте, как решать простейшие и другие интегралы и почему без этого никак нельзя обойтись в математике.
Изучаем понятие « интеграл»
Интегрирование было известно еще в Древнем Египте. Конечно, не в современном виде, но все же. С тех пор математики написали очень много книг по этой теме. Особенно отличились Ньютон и Лейбниц , но суть вещей не изменилась.
Особенно отличились Ньютон и Лейбниц , но суть вещей не изменилась.
Как понять интегралы с нуля? Никак! Для понимания этой темы все равно понадобятся базовые знания основ математического анализа. Сведения о , необходимые и для понимания интегралов, уже есть у нас в блоге.
Неопределенный интеграл
Пусть у нас есть какая-то функция f(x) .
Неопределенным интегралом функции f(x) называется такая функция F(x) , производная которой равна функции f(x) .
Другими словами интеграл – это производная наоборот или первообразная. Кстати, о том, как читайте в нашей статье.
Первообразная существует для всех непрерывных функций. Также к первообразной часто прибавляют знак константы, так как производные функций, различающихся на константу, совпадают. Процесс нахождения интеграла называется интегрированием.
Простой пример:
Чтобы постоянно не высчитывать первообразные элементарных функций, их удобно свести в таблицу и пользоваться уже готовыми значениями.
Полная таблица интегралов для студентов
Определенный интеграл
Имея дело с понятием интеграла, мы имеем дело с бесконечно малыми величинами. Интеграл поможет вычислить площадь фигуры, массу неоднородного тела, пройденный при неравномерном движении путь и многое другое. Следует помнить, что интеграл – это сумма бесконечно большого количества бесконечно малых слагаемых.
В качестве примера представим себе график какой-нибудь функции.
Как найти площадь фигуры, ограниченной графиком функции? С помощью интеграла! Разобьем криволинейную трапецию, ограниченную осями координат и графиком функции, на бесконечно малые отрезки. Таким образом фигура окажется разделена на тонкие столбики. Сумма площадей столбиков и будет составлять площадь трапеции. Но помните, что такое вычисление даст примерный результат. Однако чем меньше и уже будут отрезки, тем точнее будет вычисление. Если мы уменьшим их до такой степени, что длина будет стремиться к нулю, то сумма площадей отрезков будет стремиться к площади фигуры. Это и есть определенный интеграл, который записывается так:
Это и есть определенный интеграл, который записывается так:
Точки а и b называются пределами интегрирования.
« Интеграл»
Кстати! Для наших читателей сейчас действует скидка 10% на
Правила вычисления интегралов для чайников
Свойства неопределенного интеграла
Как решить неопределенный интеграл? Здесь мы рассмотрим свойства неопределенного интеграла, которые пригодятся при решении примеров.
- Производная от интеграла равна подынтегральной функции:
- Константу можно выносить из-под знака интеграла:
- Интеграл от суммы равен сумме интегралов. Верно также для разности:
Свойства определенного интеграла
- Линейность:
- Знак интеграла изменяется, если поменять местами пределы интегрирования:
- При любых точках a , b и с :
Мы уже выяснили, что определенный интеграл – это предел суммы. Но как получить конкретное значение при решении примера? Для этого существует формула Ньютона-Лейбница:
Но как получить конкретное значение при решении примера? Для этого существует формула Ньютона-Лейбница:
Примеры решения интегралов
Ниже рассмотрим неопределенный интеграл и примеры с решением. Предлагаем самостоятельно разобраться в тонкостях решения, а если что-то непонятно, задавайте вопросы в комментариях.
Для закрепления материала посмотрите видео о том, как решаются интегралы на практике. Не отчаиваетесь, если интеграл не дается сразу. Обратитесь в профессиональный сервис для студентов, и любой тройной или криволинейный интеграл по замкнутой поверхности станет вам по силам.
Как решать интегралы: Ускоренный курс AP® по математическому анализу
Интеграция может быть самой сложной концепцией в учебниках AP® по математическому анализу, но она также, возможно, и самая важная! При этом нет ничего постыдного в том, чтобы нервничать по поводу предстоящего экзамена AP®. Чтобы помочь подавить ваши страхи, я познакомлю вас с наиболее важными концепциями решения даже самых сложных интегралов. Прочитав этот обзор AP® Calculus, вы узнаете обо всех необходимых вам инструментах и, надеюсь, успокоите бабочек в вашем желудке.
Прочитав этот обзор AP® Calculus, вы узнаете обо всех необходимых вам инструментах и, надеюсь, успокоите бабочек в вашем желудке.
Интегралы можно разделить на две отдельные категории: определенные и неопределенные. Определенный интеграл имеет границы и дает числовой ответ, а неопределенный интеграл не имеет границ и дает алгебраический ответ. Неопределенные интегралы будут рассмотрены в первую очередь, так как метод их решения также используется как часть вычисления решений определенных интегралов.
Неопределенные интегралы могут быть решены двумя разными методами: методом антицепного правила и методом подстановки. Решение неопределенного интеграла — это то же самое, что нахождение первообразной или отмена производной и нахождение исходной функции. 92+с
Термин c представляет собой постоянное значение, которое является результатом интегрирования и никогда не следует забывать, особенно в вопросах с несколькими вариантами ответов экзамена AP® Calculus.
Пока все хорошо, правда? Становится хуже. Давайте теперь рассмотрим метод подстановки, также известный как u-подстановка. Что произойдет, если вам предложат функцию, которую нельзя интегрировать с правилом антицепочки? Это происходит, когда несколько функций умножаются таким образом, что их нельзя разложить, как, например, функция в примере 2 ниже. В этом случае мы должны сделать замену одной из величин, чтобы решить задачу. Именно здесь dx становится гораздо менее декоративным элементом на конце интеграла и гораздо более полезным. Поясним на примере: 99+с
Давайте теперь рассмотрим метод подстановки, также известный как u-подстановка. Что произойдет, если вам предложат функцию, которую нельзя интегрировать с правилом антицепочки? Это происходит, когда несколько функций умножаются таким образом, что их нельзя разложить, как, например, функция в примере 2 ниже. В этом случае мы должны сделать замену одной из величин, чтобы решить задачу. Именно здесь dx становится гораздо менее декоративным элементом на конце интеграла и гораздо более полезным. Поясним на примере: 99+с
Теперь мы ясно видим два основных метода решения неопределенных интегралов. Это было не так уж плохо, не так ли?
Давайте сделаем небольшую заметку, чтобы обсудить, как мы обращаемся с триггерными функциями в интегралах. Я уверен, что вы занимались триггерными функциями и их тождествами на предыдущих уроках математики. Это чрезвычайно важные функции, но их интегралы относительно просты. Единственный способ решить эти интегралы — запомнить решение. Они давно доказаны известными математиками, и в AP® Calculus нам не нужно беспокоиться о том, откуда они взялись. 92
92
Теперь, когда мы размялись в способах решения неопределенных интегралов, мы можем перейти к определенным интегралам. Это обсуждение будет включать некоторую теорию, но имейте в виду, что понимание некоторых теорий, лежащих в основе исчисления, поможет вашему пониманию.
Определенные интегралы, пожалуй, самое важное понятие в исчислении, потому что они часто дают действительные, точные числа. С инженерной точки зрения это идеальный вариант. Интегральное действие применяется ко многим реальным задачам, таким как нахождение профилей скорости движущихся жидкостей в трубах. Лучший способ разобраться с определенными интегралами — посмотреть на них с графической точки зрения. 9{{\mathbf b}}_{{\mathbf a}}{{\mathbf f}\left ({\mathbf x}\right){\mathbf dx}}
Этот интеграл представляет площадь под кривой на графике. Это сложная для понимания концепция. Область под кривой может представлять что угодно и обычно зависит от концепции, лежащей в основе проблемы. Для AP® Calculus концепция не имеет значения, и мы просто фокусируемся на математике; однако могут возникнуть концептуальные вопросы о том, что представляет собой интеграл и каков ответ? Правильно, площадь под кривой. Давайте посмотрим на пример, чтобы прояснить это! 92dx}
Это сложная для понимания концепция. Область под кривой может представлять что угодно и обычно зависит от концепции, лежащей в основе проблемы. Для AP® Calculus концепция не имеет значения, и мы просто фокусируемся на математике; однако могут возникнуть концептуальные вопросы о том, что представляет собой интеграл и каков ответ? Правильно, площадь под кривой. Давайте посмотрим на пример, чтобы прояснить это! 92dx}
Затем мы рисуем график этой функции и окрашиваем интересующий нас участок от -2 до 2.
Как видите, закрашена только область, которая буквально находится между функцией и осью X. Когда вы вычисляете определенный интеграл, вы получаете значение этой площади! Довольно аккуратно, правда? Так как же решить определенные интегралы на бумаге без графиков? Давай выясним!
При вычислении определенных интегралов в исчислении AP® мы используем основную теорему исчисления. Если это имя не докажет, насколько важна интеграция в исчислении, ничто не докажет. Основная теорема утверждает, что если функция f(x) непрерывна от x=a до x=b и F(x) является первообразной f(x), то 9{\dfrac{3}{2}}+с
Основная теорема утверждает, что если функция f(x) непрерывна от x=a до x=b и F(x) является первообразной f(x), то 9{\dfrac{3}{2}}+с
Следующая часть решения основана исключительно на Фундаментальной теореме. Постоянное значение, присутствующее во всех неопределенных интегральных решениях, представляет собой представление в неопределенности ответа. Когда нам не заданы границы или начальные условия, мы не можем найти постоянное значение. Однако когда мы решаем определенные интегралы, у нас есть границы, и реальное решение может быть получено без неопределенной константы. На самом деле в ответе вообще не будет алгебраических частей! Таким образом, чтобы включить основную теорему, мы опустим постоянный член и подставим его в уравнение теоремы:c_b{е\влево(х\вправо)dx}}}
Определенные интегралы также могут быть включены в другие теоремы. Например, теорему о среднем значении можно скорректировать для применения к интегралам. Вспомните из своих предыдущих знаний в области исчисления, что теорема о среднем значении обычно определяется как
f’\left(c\right)= \dfrac{f\left(b\right)-f(a)}{b-a}
Мы знаем, что теорема о среднем значении применима, когда f(x) является непрерывной и определенной функцией между x=a и b, тогда мы знаем, что существует по крайней мере одно значение c, такое что приведенное выше уравнение верно. x_a{f\left(t\right)dt } имеет производную в каждой точке x интервала, поэтому 9x_a {е \ влево (т \ вправо) d т} \ вправо) = е \ влево (х \ вправо)
x_a{f\left(t\right)dt } имеет производную в каждой точке x интервала, поэтому 9x_a {е \ влево (т \ вправо) d т} \ вправо) = е \ влево (х \ вправо)
Логично, правда? Я знаю, что эти теоремы — не самая захватывающая часть интегрирования, но они определенно так же важны, как умение решать интеграл на экзамене AP® по математическому анализу!
AP® Практика исчисления — один из лучших способов подготовиться к большому экзамену. Совет колледжей публикует бесплатные разделы ответов на старые экзамены в Интернете, и я призываю вас сдать как можно больше старых экзаменов! Во всех видах математики практика действительно помогает добиться совершенства. Здесь мы поработаем с примером вопроса с бесплатным ответом, чтобы вы начали. 92) для tge\quad 0.
1. В каком направлении (вверх или вниз) движется частица в момент времени t=1,5? Почему?
2. Найти ускорение частицы в момент времени t=1,5. Увеличивается ли скорость частицы? Почему или почему нет?
3. Учитывая, что y(t) — это положение частицы в момент времени t и что y\left(0\right)=3, найти y(2).
4. Найти полное расстояние, пройденное частицей от t=0 до t=2.
Во-первых, давайте сделаем шаг назад и рассмотрим структуру проблемы. Как и все задачи с бесплатными ответами AP® Calculus, этот пример состоит из нескольких частей, в которых требуется разное. Части (a) и (b) не требуют интегрирования, поэтому в этом упражнении мы пропустим эти проблемы.
Часть (c) запрашивает положение частиц в определенное время. Мы знаем, что скорость является производной от положения, и поэтому нам нужно будет проинтегрировать данное уравнение, чтобы найти профиль скорости. Используем ли мы определенный или неопределенный интеграл? Мы видим, что определенный интеграл дал бы нам полное смещение частицы. Мы этого не хотим. Мы также видим, что нам дано начальное условие для частицы; следовательно, мы можем использовать неопределенный интеграл и найти постоянное значение! 92\вправо)dt}=y\влево(2\вправо)-y(0)
Мы понимаем, что мы уже вычислили оба этих значения! Поэтому просто подставляем и решаем:
Смещение = у\влево(2\вправо)-у\влево(0\вправо) = 3,527 – 3 = 0,527
Эврика! Экзамен AP® Calculus часто заполнен такими небольшими сокращениями, потому что экзамен рассчитан на время. Обязательно следите за ними, чтобы вы могли закончить экзамен!
Обязательно следите за ними, чтобы вы могли закончить экзамен!
Как мы видели, интеграция не так уж и плоха. Теперь у вас есть все инструменты для успешной сдачи экзамена AP® Calculus! Имейте в виду, однако, что практика делает совершенным! Думаете, мы что-то упустили? Дайте нам знать! Заявки на интеграцию рассматриваются в других статьях!
Ищете практику AP® Calculus?Ознакомьтесь с другими нашими статьями об исчислении AP®.
Вы также можете найти тысячи практических вопросов на Albert.io. Albert.io позволяет вам настроить учебный процесс так, чтобы он ориентировался на практику, в которой вам больше всего нужна помощь. Мы дадим вам сложные практические вопросы, которые помогут вам достичь мастерства в исчислении AP®.
Начните тренироваться здесь .
Вы учитель или администратор, заинтересованный в повышении успеваемости учащихся AP® Calculus?
Узнайте больше о наших школьных лицензиях здесь .
Расчет 2 Справка
Студенты, нуждающиеся в помощи по исчислению 2, получат большую пользу от нашей интерактивной программы. Мы разбираем все ключевые элементы, чтобы вы могли получить адекватную помощь по исчислению 2. Имея под рукой обязательные концепции обучения и актуальные практические вопросы, вы быстро получите много помощи по Calculus 2. Получите помощь сегодня с нашей обширной коллекцией необходимой информации по исчислению 2.
Исчисление 2 продолжается математическим исследованием изменений, впервые представленным студентам во время Исчисления 1. Курс охватывает интеграцию, применение интегрирования и ряды, а также рассматривает и расширяет понятия, введенные в Исчислении 1, такие как пределы и производные. Это преимущественно курс математики на уровне колледжа, и большинство студентов, которые проходят этот курс, делают это либо на первом, либо на втором курсе. Поскольку «Исчисление 2» является продолжением «Исчисления 1», рекомендуется, чтобы учащиеся проходили два курса последовательно. Хотя Calculus 2 обычно не является обязательным курсом в колледже, он настоятельно рекомендуется студентам, изучающим математику или любую другую область, требующую продвинутых математических понятий, таких как инженерное дело, физика или экономика. Нужен ли вам репетитор по математическому анализу в Атланте, репетитор по математическому анализу в Хьюстоне или в Сан-Франциско, работа один на один с экспертом может быть именно тем, что вам нужно для учебы.
Хотя Calculus 2 обычно не является обязательным курсом в колледже, он настоятельно рекомендуется студентам, изучающим математику или любую другую область, требующую продвинутых математических понятий, таких как инженерное дело, физика или экономика. Нужен ли вам репетитор по математическому анализу в Атланте, репетитор по математическому анализу в Хьюстоне или в Сан-Франциско, работа один на один с экспертом может быть именно тем, что вам нужно для учебы.
Бесплатный инструмент обучения «Learn by Concept» от The Varsity Tutors предлагает учебные материалы для студентов, которым нужна помощь в изучении Calculus 2 или которые просто хотят повторить этот предмет. Инструмент обучения построен как интерактивная учебная программа с рядом разделов и тем, подробно описывающих исчисление 2. Нажав на любую тему, вы перейдете к серии примеров вопросов с несколькими вариантами ответов. Затем вы можете просмотреть образец вопроса и возможные ответы, решить проблему и выбрать ответ, который вы считаете правильным. Правильный ответ указан под вариантами ответов, что позволяет вам проверить правильность своего ответа. Varsity Tutors предлагает ресурсы, такие как бесплатные практические тесты по исчислению II, которые помогут вам в самостоятельном обучении, или вы можете подумать о репетиторах по исчислению II.
Правильный ответ указан под вариантами ответов, что позволяет вам проверить правильность своего ответа. Varsity Tutors предлагает ресурсы, такие как бесплатные практические тесты по исчислению II, которые помогут вам в самостоятельном обучении, или вы можете подумать о репетиторах по исчислению II.
Было бы полезно просто задавать вопросы и ответы, но инструмент «Узнай по концепции» делает больше. Подробное пошаговое описание того, как прийти к правильному ответу, прилагается к каждому примерному вопросу, что помогает упростить задачу. Эти описания показывают каждое уравнение, концепцию и теорию, которые применимы к проблеме, будь то получение производной функции или просто переписывание уравнения. Если вы дали неправильный ответ, вы можете выяснить, где вы ошиблись, и что вам нужно сделать, чтобы в будущем задать правильный вопрос. Если вы дали правильный ответ с первой попытки, вы можете проверить свою работу, чтобы убедиться, что понимаете, почему ваш ответ был правильным.
Независимо от того, начали ли вы изучение Calculus 2 или готовитесь к выпускному экзамену, вы можете использовать инструмент «Учись на основе концепции» в качестве учебного пособия. Инструмент охватывает широкие единицы деривативов; интегралы; лимиты; параметрический, полярный и векторный; и серии в исчислении. Это также входит в особенности в каждой категории. Вы можете пройти весь блок сразу или сосредоточиться на одной теме или подтеме. Благодаря тысячам примеров вопросов по Calculus 2 в базе данных средств обучения охвачены все возможные темы. В дополнение к справочному разделу по исчислению II и репетиторству по исчислению II вы также можете рассмотреть некоторые из наших карточек с исчислением II.
Инструмент охватывает широкие единицы деривативов; интегралы; лимиты; параметрический, полярный и векторный; и серии в исчислении. Это также входит в особенности в каждой категории. Вы можете пройти весь блок сразу или сосредоточиться на одной теме или подтеме. Благодаря тысячам примеров вопросов по Calculus 2 в базе данных средств обучения охвачены все возможные темы. В дополнение к справочному разделу по исчислению II и репетиторству по исчислению II вы также можете рассмотреть некоторые из наших карточек с исчислением II.
Инструмент «Обучение по концепции» лучше всего использовать вместе с другими инструментами обучения. Прохождение бесплатного полного практического теста поможет вам определить, какие темы Calculus 2 вы уже знаете и на чем следует сосредоточить свое внимание. Пройдя один из сотен бесплатных тематических практических тестов по исчислению 2, вы также можете использовать карточки по тем же темам. Практические тесты и карточки можно сортировать по категориям или настраивать в соответствии с вашими потребностями.
