Решение комбинаторных задач: Математическое Бюро. Страница 404

Решение нестандартных задач. Комбинаторика.

Дата: 17.02.2015

Автор: Коновалова Валентина Михайловна

Предмет: Математика.

Класс: 2.

Тема: «Решение нестандартных задач. Комбинаторика».

Цель: организовать деятельность по формированию новых способов решения задач комбинаторного содержания.

Задачи:

Образовательные: формировать умение решать комбинаторные задачи разными способами: «дерево возможностей», перебор вариантов, граф, таблица.

Развивающие: развивать умение сравнивать, анализировать, обобщать и делать выводы; развивать внимание, наблюдательность, воображение; развивать математически грамотную речь.

Воспитательные: воспитывать самостоятельность, усидчивость, трудолюбие, целеустремленность; воспитывать уважение к мнению других.

Оборудование:

— телевизор,

— аннотация к мультфильму «Алёша Попович и Тугарин Змей»,

— карточка с заданиями,

— бланк решения.

Ход занятия:

1 ведущий:

— Сегодня мы совершим путешествие в раздел математики «Комбинаторика» вместе с героями известного мультфильма. Чтобы узнать, как зовут главного героя этого мультфильма, нужно выполнить следующее задание.

Задание 1. Из цифр 1, 2, 3, 4, 5, 6 составьте нечётные двузначные числа, так чтобы цифры в записи числа не повторялись. Расположи их в порядке убывания. Решите задачу с помощью «дерева возможностей».

— Прочитайте задание. Что требуется сделать? (Составить двузначные числа из цифр 1, 2, 3, 4, 5, 6.)

— Какими должны быть составленные нами числа? (Нечетными.)

— Какие двузначные числа называются нечетными? (Нечетными называют числа, которые оканчиваются на нечетную цифру)

— Какие у нас нечетные цифры? (1, 3 и 5). Мы их поставим в разряде единиц.

— Какие цифры будут стоять на месте десятков? (2, 4, 6)

— Запишите эти числа с помощью «дерева возможностей»

(21, 23, 25, 41, 43, 45, 61, 63, 65)

 

— Что в задании требуется сделать с полученными числами? (Расположить их в порядке убывания)

— Какое число будет первым в ряду: наибольшее или наименьшее? (65)

— Выложите полученный ряд чисел: 65, 63, 61, 45, 43, 41, 25, 23, 21 (пригласить родителя или ученика)

— Перевернув карточки, получаем слово…? ( АЛЕША ПОВИ ). Какие буквы надо добавить, чтобы получилось имя? (П, О, Ч)

2 ведущий:

— Вспомним сюжет мультфильма: http://afisha.mail.ru/cinema/movies/496133_alesha_popovich_i_tugarin_zmej/#trailer

— Назовите главных героев этого мультфильма. (Алёша Попович, Тихон, Тугарин Змей, Любава, бабуля Любавы, конь богатырский Юлий и ослик Моисей)

— В поисках золота герои приходят к обрыву, Им необходимо перебраться на другую сторону.

Задание 2. В какой последовательности герои могут перебраться на другой берег, если бабуля возьмет на руки Любаву и Моисея, а Тихон по бревну не пойдет, так как боится высоты? Сколько всего способов существует? Решите задачу с помощью таблицы.

— Кто из героев будет идти по бревну? (Алеша, Юлий и бабуля). Обозначим их буквами А, Ю, Б.

— Кто может пойти первым? (Либо Алеша, либо Юлий, либо бабуля.)

— Найдем сколько всего способов существует с помощью таблицы:

Первый	А	А	Ю	Ю	Б	Б
Второй	Б	Ю	А	Б	А	Ю
Третий	Ю	Б	Б	А	Ю	А

— Всего 6 способов.

Герои благополучно переправились на другой берег.

3 ведущий:

Задание 3. На пути героев встретился камень волшебный, показывающий три дороги: 1, 2, 3. Алеше пришлось пройти по всем дорогам. Сколько различных вариантов прохождения этих дорог существует? Решите задачу перебором.

— Какие цифры используем? (1, 2, 3)

— Проверьте решение. Возможны варианты: 123, 132, 213, 231, 312, 321 (6 вариантов)

4 ведущий:

— По сюжету Любаву захватил Тугарин змей. На время золото оставили на сохранность в Киеве. Освободил Алеша с друзьями Любаву, связали Тугарина и отправились в Киев за золотом ростовским.

Задание 4. На гору до Киева ведут 3 дороги, с горы – 1 дорога. Сколькими способами Тихон вместе с бабулей могут попасть в Киев? Решите с помощью графа.

— Решите самостоятельно.

— Проверим решение с помощью графа: на гору до Киева ведут 3 дороги, с горы – 1 дорога. Героям нужно и подняться на гору, и спуститься с горы. Это можно сделать 3 способами.

5 ведущий.

— Хитрый князь не хочет возвращать золото. Он придумал, что перепутались ключи от хранилища. Помогите героям найти нужный ключ.

Задание 5. В связке 7 ключей. Нужно открыть 5 замков. Какое максимальное количество попыток нужно сделать князю, чтобы узнать, какой ключ подходит к каждому замку? Решите задачу с помощью таблицы.

— Что значит максимальное количество? (самое большое)

— Сколько ключей было в связке? (В связке было 7 ключей)

— Сколько замков нужно открыть? (Нужно открыть 5 замков)

— Что требуется узнать в задаче? (Сколько попыток нужно сделать)

— Решим задачу самостоятельно.

— Проверим. Подбирая ключ к первому замку, сколько попыток сделаем? Почему? (Сделаем 7 попыток, так как в связке 7 ключей)

— Внесем число 7 в столбец № 1. Подобрав ключ, мы знаем, какой из семи ключей подходит к первому замку. Сколько ключей, не подобранных к «своему» замку осталось в связке? ( В связке осталось 6 не подобранных ключей)

— Сколько попыток нужно сделать, чтобы наверняка подобрать ключ ко второму замку? Почему? (Чтобы наверняка подобрать ключ ко второму замку, нужно сделать 6 попыток, так как один ключ мы уже подобрали, а 6 ключей осталось) Внесем цифру 6 в столбец № 2.

— Третий замок точно откроется после 5 попыток, четвертый после 4 попыток, пятый после трех попыток.

№ замка	1	2	3	4	5	итого
Количество попыток	7	6	5	4	3	25

— Посчитаем, максимальное количество попыток – 25.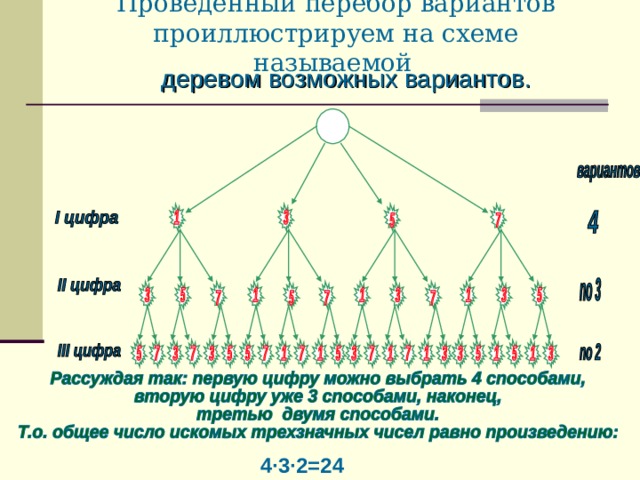 25 попыток нужно сделать, чтобы открыть все замки.

Учитель:

— Как всегда добро в сказке победило зло. Алеша вернул золото жителям Ростова.

Показ финала мультфильма (1:15:40-1:16:10)

А и сильные, могучие богатыри

На славной Руси!

Не скакать врагам по нашей земле!

Не топтать их коням землю Русскую!

Не затмить им солнце наше красное.

Век стоит Русь — не шатается!

И века простоит — не шелохнется!

— Из какого раздела математики мы выполняли задания? («Комбинаторика»)

— Какими способами мы решали комбинаторые задачи? (таблица, «дерево возможностей», граф, методом перебора)

— Какие чувства у вас вызывают такие задания?

След. новость

Пред. новость

Решение комбинаторных задач

Решение комбинаторных задач

Комбинаторные задачи

Комбинаторные задачи – это задачи, в которых требуется из элементов составить различные наборы, подсчитать количество всевозможных комбинаций элементов, составленных по определённому правилу.

Методы решения комбинаторных задач

1. Метод перебора вариантов

2. Дерево возможных вариантов

3. Табличный метод

4. Правило умножения

Метод перебора вариантов

Полный перебор вариантов без составления таблиц и схем

Пример:

Какие двузначные числа можно составить из цифр 1, 2, 3, 4, 5?

Решение:

Перебираем всевозможные варианты: 11, 12, 13, 14, 15, 21, 22, 23, 24, 25, 31, 32, 33, 34, 35, 41, 42, 43, 44, 45, 51, 52, 53, 54, 55.

Задача 1.

В финальном забеге на 100 м участвуют Смирнов, Петров и Орлов. Назовите возможные варианты распределения призовых мест.

Ответ:

Задача 1: Вариант1: 1) Смирнов, 2) Петров, 3) Орлов. Вариант2: 1) Смирнов, 2) Орлов, 3) Петров. Вариант3: 1) Орлов, 2) Смирнов, 3) Петров. Вариант4: 1) Орлов, 2) Петров, 3) Смирнов.

Вариант5: 1) Петров, 2) Орлов, 3) Смирнов. Вариант6: 1) Петров, 2) Смирнов, 3) Орлов .

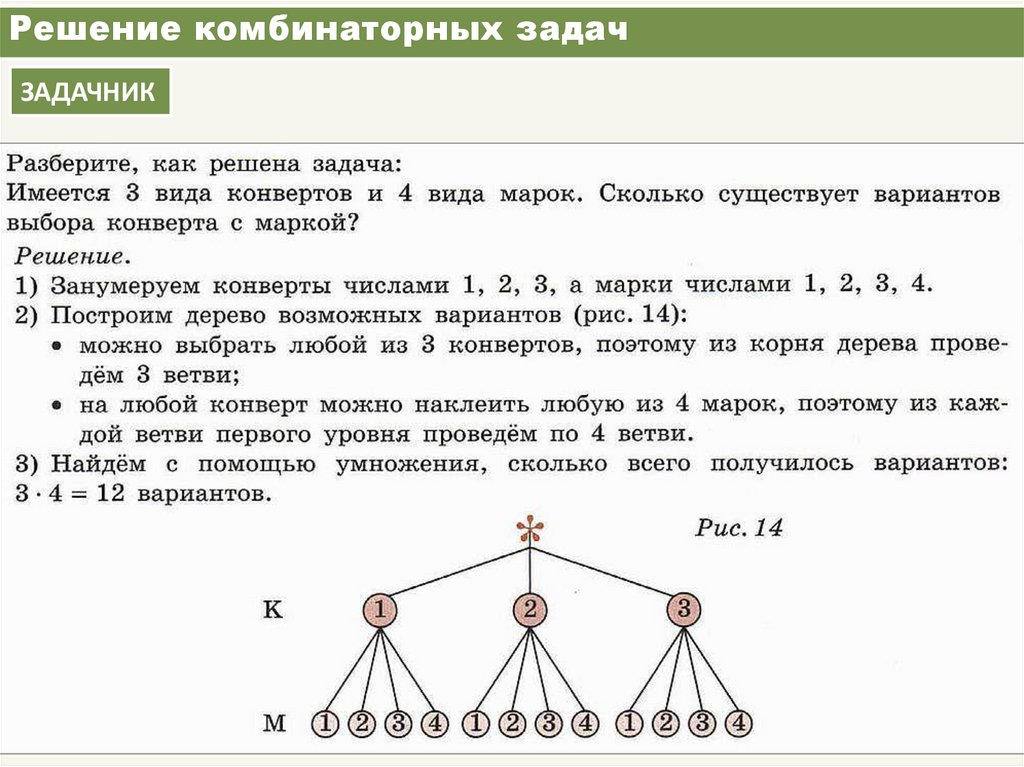
Дерево возможных вариантов

способ решения разнообразных задач, касающихся перебора вариантов происходящих событий.

Пример:

Какие трехзначные числа можно составить из цифр 0, 3, 8?

Решение:

Построим дерево возможных вариантов, учитывая, что 0 не может быть первой цифрой в числе.

???

3

8

8

3

0

3

8

0

8

0

3

3

3

0

8

3

0

8

0

8

3

0

8

3

0

8

Задача 2.

Сколько существует флагов составленных из трех горизонтальных полос одинаковой ширины и различных цветов: белого, синего, красного и зеленого? Есть ли среди них Государственный флаг Российской Федерации?

Ответ:

Задача 2: всего существует 24 флага, среди них есть Государственный флаг Российской Федерации.

Задача 3.

Запишите все возможные варианты расписания пяти уроков на день из предметов: математика, русский язык, история, английский язык, физкультура, причем математика должна быть вторым уроком.

Ответ:

Задача 3: обозначив М — математика, Р — русский язык, И — история, А — английский язык, Ф — физкультура и построив дерево возможных вариантов, получим всего 24 варианта .

Табличный метод

Решить комбинаторные задачи можно с помощью таблиц. Они, как и дерево возможных вариантов, наглядно представляют решение таких задач.

Задача 1. Сколько нечетных двузначных чисел можно составить из цифр 1, 3, 4, 6, 7, 8, 9?

Решение. Составим таблицу: слева первый столбец — первые цифры искомых чисел, вверху первая строка — вторые цифры.

Первая цифра может быть любая, а вторая только нечетная (1, 3, 7, 9)

 

1

1

3

3

11

7

31

13

4

17

41

33

6

9

61

37

43

19

7

47

39

8

63

71

67

81

9

49

73

77

83

69

91

87

79

93

89

97

99

Правило умножения

Применяется для нахождения числа всех возможных исходов независимого проведения двух испытаний А и В, перемножив число всех исходов испытания А и число всех исходов испытания В.

Пример:

Сколько трехзначных чисел можно составить из цифр: 1, 2, 5, 8 используя в записи числа каждую из них не более одного раза?

Решение:

Первую цифру выбираем четырьмя способами (1, 2, 5, 8), вторую цифру можно выбрать тремя способами, и на выбор третьей цифры остается два способа. Количество искомых трехзначных чисел равно произведению 4 · 3 · 2 = 24.

Задача 4.

Сколькими способами можно составить список из шести учеников 10 класса сдающих зачет по математике?

Решение: первого в списке ученика можно выбрать 6 способами,

второго – 5 способами,

третьего – 4 способами,

четвертого – 3 способами,

пятого – 2 способами,

шестого – 1 способом (оставшийся ученик).

Перемножив полученные результаты получим 6 · 5 · 4 · 3 · 2 · 1 = 720

Ответ: 720 способов. {20-k}.$$

---

Задача

Урна состоит из 30$ красных шаров и 70$ зеленых шаров. Какова вероятность получить ровно $k$ красные шары в выборке размером $20$, если выборка сделана без замены (повторение не допускается)?

• Раствор
  • Пусть $A$ — событие (множество) получения ровно $k$ красных шаров. Чтобы найти $P(A)=\frac{|A|}{|S|}$, мы нужно найти $|A|$ и $|S|$. Во-первых, обратите внимание, что $|S|={100 \выберите 20}$. Далее, чтобы найти $|A|$, нам нужно выяснить, сколькими способами мы можем выбрать $k$ красных шаров и $20-k$ зеленых шаров. Используя принцип умножения, имеем $$|A|= {30 \выберите k}{70 \выберите 20-k}.$$ Таким образом, у нас есть $$P(A)= \frac{{30 \выберите k}{70 \выберите 20-k}}{{100 \выберите 20}}.$$

---

Задача
. Предположим, что в комнате $k$ человек, и мы знаем, что:

• $k=5$ с вероятностью $\frac{1}{4}$;
• $k=10$ с вероятностью $\frac{1}{4}$;
• $k=15$ с вероятностью $\frac{1}{2}$.

1. Какова вероятность того, что по крайней мере двое из них родились в один и тот же месяц? Предположим, что все месяцы равновероятны.
2. Учитывая, что мы уже знаем, что по крайней мере два человека празднуют свой день рождения в том же месяце, какова вероятность того, что $k=10$? 9{10}})+ 2}$.
   

---

Задача

Сколько различных решений имеет следующее уравнение? $$x_1+x_2+x_3+x_4=100, \textrm{ такое, что }$$ $$x_1 \in \{1,2,3..\}, x_2 \in \{2,3,4,..\}, x_3,x_4 \in \{0,1,2,3,.. .\}.$$

• Решение
  • Мы уже знаем, что в общем случае число решений уравнения $$x_1+x_2+…+x_n=k, \textrm{ где } x_i \in \{0,1,2,3,…\}$$ равно $${n+k-1 \выбрать k}={n+k-1 \выбрать n-1}.$$ Нам нужно преобразовать ограничения в этой задаче, чтобы они соответствовали этой общей форме. Нам дано, что $x_1 \in \{1,2,3..\}$, поэтому, если мы определим $$y_1=x_1-1,$$ затем $y_1 \in \{0,1,2,3,. ..\}$. Аналогичным образом определите $y_2 =x_2-2$, поэтому $y_2 \in \{0,1,2,3,…\}$. Теперь вопрос становится эквивалентным нахождению числа решений уравнения $$y_1+1+y_2+2+x_3+x_4=100, \textrm{ где } y_1,y_2,x_3,x_4 \in \{0,1,2,3,…\},$$ или, что то же самое, количество решений уравнения $$y_1+y_2+x_3+x_4=97, \textrm{ где } y_1,y_2,x_3,x_4 \in \{0,1,2,3,…\}.$$ Как известно, это равно $${4+97-1 \выберите 3}={100 \выберите 3}.$$

---

Задача (Задача на сопоставление)

Вот известная задача: на вечеринку приходят $N$ гостей. Каждый человек носит шляпу. Мы собираем все шляпы, а затем случайным образом перераспределить шляпы, случайным образом раздав каждому человеку одну из $N$ шляп. Какова вероятность того, что хотя бы один человек получит свою шляпу?
Подсказка: Используйте принцип включения-исключения.

---

← предыдущая

следующая →

Печатная версия книги доступна на Amazon здесь.

Молекулярный расчет решений комбинаторных задач

Сохранить цитату в файл

Формат: Резюме (текст) PubMedPMIDAbstract (текст) CSV

Добавить в коллекции

• Создать новую коллекцию
• Добавить в существующую коллекцию

Назовите свою коллекцию:

Имя должно содержать менее 100 символов

Выберите коллекцию:

Невозможно загрузить вашу коллекцию из-за ошибки
Повторите попытку

Добавить в мою библиографию

• Моя библиография

Не удалось загрузить делегатов из-за ошибки
Повторите попытку

Ваш сохраненный поиск

Название сохраненного поиска:

Условия поиска:

Тестовые условия поиска

Эл. адрес: (изменить)

Который день? Первое воскресеньеПервый понедельникПервый вторникПервая средаПервый четвергПервая пятницаПервая субботаПервый деньПервый будний день

Который день? воскресеньепонедельниквторниксредачетвергпятницасуббота

Формат отчета: SummarySummary (text)AbstractAbstract (text)PubMed

Отправить максимум: 1 шт. 5 шт. 10 шт. 20 шт. 50 шт. 100 шт. 200 шт.

Отправить, даже если нет новых результатов

Необязательный текст в электронном письме:

Создайте файл для внешнего программного обеспечения для управления цитированием

Полнотекстовые ссылки

Атыпон

Полнотекстовые ссылки

. 1994 11 ноября; 266 (5187): 1021-4.

doi: 10.1126/science.7973651.

Л М Адлеман ¹

принадлежность

• ¹ Факультет компьютерных наук, Университет Южной Калифорнии, Лос-Анджелес.

• PMID: 7973651
• DOI: 10.1126/наука.7973651

Л. М. Адлеман. Наука. 1994 .

. 1994 11 ноября; 266 (5187): 1021-4.

doi: 10. 1126/science.7973651.

Автор

Л М Адлеман ¹

принадлежность

• ¹ Факультет компьютерных наук, Университет Южной Калифорнии, Лос-Анджелес.

• PMID: 7973651
• DOI: 10.1126/наука.7973651

Абстрактный

Инструменты молекулярной биологии были использованы для решения примера задачи о направленном гамильтоновом пути. Небольшой граф был закодирован в молекулах ДНК, а «операции» вычисления были выполнены со стандартными протоколами и ферментами. Этот эксперимент демонстрирует возможность проведения расчетов на молекулярном уровне.

Похожие статьи

• ДНК, вычисляющая проблему пути Гамильтона.

  Ли К.М., Ким С.В., Ким С.М., Сон У. Ли К.М. и др. Мол клетки. 1999 31 октября; 9 (5): 464-9. Мол клетки. 1999. PMID: 10597033

• Задача китайского почтальона, основанная на вычислениях ДНК.

  Инь З., Чжан Ф., Сюй Дж. Инь З. и др. J Chem Inf Comput Sci. 2002 март-апрель;42(2):222-4. doi: 10.1021/ci010046r. J Chem Inf Comput Sci. 2002. PMID: 11911690

• На пути к вычислениям с ДНК.

  Гиффорд, Д.К. Гиффорд ДК. Наука. 1994 11 ноября; 266 (5187): 993-4. doi: 10.1126/science. 7973681. Наука. 1994. PMID: 7973681 Аннотация недоступна.

• Сложности вычисления ДНК.

  Кокс Дж. К., Коэн Д. С., Эллингтон, АД. Кокс Дж. К. и соавт. Тенденции биотехнологии. 1999 апр; 17(4):151-4. doi: 10.1016/s0167-7799(99)01312-8. Тенденции биотехнологии. 1999. PMID: 10203773 Обзор.

• ДНК-вычисления.

  Гиббонс А., Амос М., Ходжсон Д. Гиббонс А. и др. Курр Опин Биотехнолог. 1997 февраля; 8(1):103-6. doi: 10.1016/s0958-1669(97)80164-4. Курр Опин Биотехнолог. 1997. PMID:

47 Обзор.

Посмотреть все похожие статьи

Цитируется

• Распределенное кодирование и декодирование информации с использованием самоорганизующихся пространственных шаблонов.

  Лу Дж., Цой Р., Луо Н., Ха И, Ван С., Квак М., Байг Ю., Моисеев Н., Тянь С., Чжан А., Гонг Н.З., Ю Л. Лу Дж. и др. Выкройки (Н Д). 2022 сен 23;3(10):100590. doi: 10.1016/j.patter.2022.100590. Электронная коллекция 2022 14 октября. Выкройки (Н Д). 2022. PMID: 36277815 Бесплатная статья ЧВК.

• Молекулярный храповик для чтения ленты.

  Рен Ю., Жамань Р., Тетлоу Д.Дж., Ли Д.А. Рен Ю и др. Природа. 19 октября 2022 г. doi: 10.1038/s41586-022-05305-9. Онлайн перед печатью. Природа. 2022. PMID: 36261530

• Кинетика гибридизации неравновесных смесей коротких олигонуклеотидов РНК.

  Тодиско М., Шостак Ю.В. Тодиско М. и др. Нуклеиновые Кислоты Res. 2022 23 сентября; 50 (17): 9647-9662. doi: 10.1093/nar/gkac784. Нуклеиновые Кислоты Res. 2022. PMID: 36099434 Бесплатная статья ЧВК.

• Параллельный ДНК-алгоритм для решения задачи коммивояжера по квоте на основе биокомпьютерной модели.

  Ван З., Ву С., Ву Т. Ван Цзи и др. Компьютер Intel Neurosci. 2022 31 августа; 2022:1450756. дои: 10.1155/2022/1450756. Электронная коллекция 2022. Компьютер Intel Neurosci. 2022. PMID: 36093485 Бесплатная статья ЧВК.

• Распознавание паттернов экспрессии микроРНК в жидкостях организма с использованием декодирования нанопор при субфемтомолярных концентрациях.

  Такеучи Н., Хиратани М., Кавано Р. Такеучи Н. и др. JACS Au. 2022 26 июня; 2 (8): 1829-1838. doi: 10.1021/jacsau.2c00117. Электронная коллекция 2022 22 августа.

  No related posts.