Решение квадратного уравнения без дискриминанта: Как найти корни квадратного уравнения без с. Квадратные уравнения

§ Неполные квадратные уравнения

Как решать квадратные уравнения Дискриминант Неполные квадратные уравнения

В уроке «Как решать квадратные уравнения» мы разобрали решение обычных квадратных уравнений, но есть уравнения, в которых не всегда очевидно, как найти коэффициенты «a», «b» и «c» для формулы поиска корней.

Например, рассмотрим такое квадратное уравнение.

4x² − 64 = 0

Давайте сравним это уравнение с общим видом квадратного уравнения
«ax² + bx + c = 0» и определим, чему в нем равны «a», «b» и «c».

4x² − 64 = 0

• a = 4
• b = ?
• c= −64

Возникает вопрос: «Чему здесь равен коэффициент «b»?» Ответ прост: «b = 0». На самом деле по-другому уравнение можно записать так:

4x² − 64 = 0
4x² + 0 · x − 64 = 0

Теперь очевидно, чему равны коэффициенты «a», «b» и «c» в этом уравнении .

4x² − 64 = 0
4x² + 0 · x − 64 = 0

• a = 4
• b = 0
• c = −64

Зная чему равны коэффициенты, можно применить формулу нахождения
корней «x_1;2 =

−b ± √b2 − 4ac

2a

».

4x² − 64 = 0

x_1;2 =

−0 ± √02 − 4 · 4 · (−64)

2 · 4

x_1;2 =

−0 ± √0 + 1024

8

x_1;2 =

± √1024

8

x1 =	x2 =
x1 = 4	x2 = −4

Ответ: x₁ = 4; x₂ = −4

Запомните!

Квадратные уравнения, в которых коэффициенты «b» и/или «c» равны нулю, называют неполными.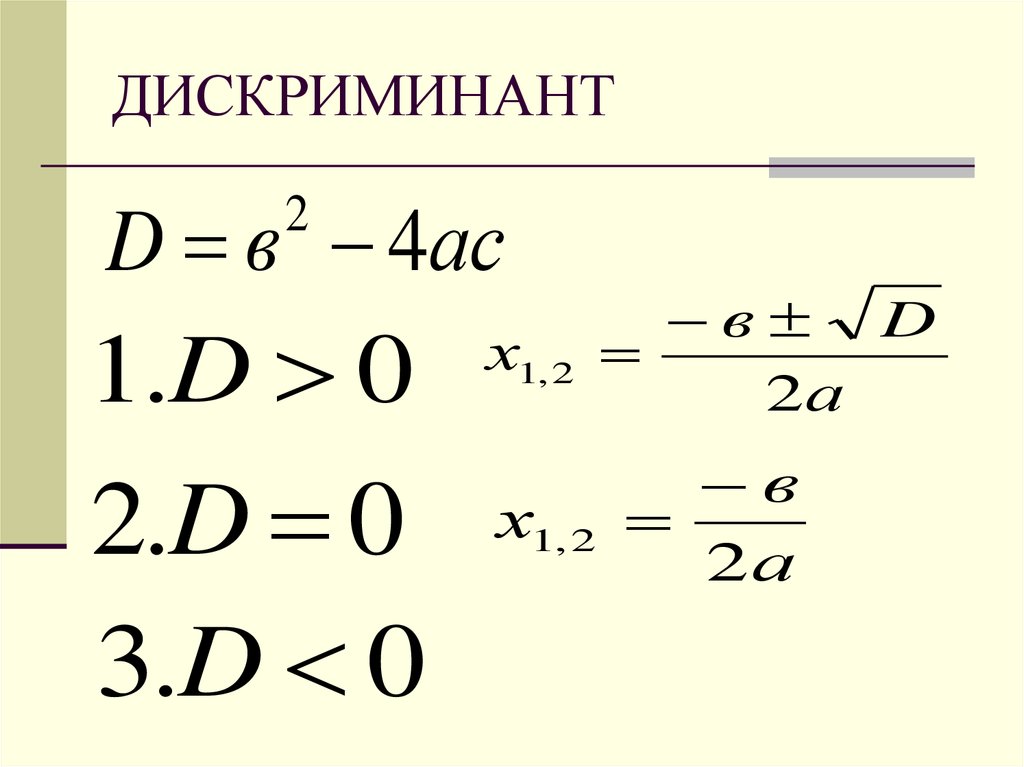

Примеры неполных квадратных уравнений

Рассмотрим другие примеры неполных квадратных уравнений. Выпишем их коэффициенты «a», «b» и «c» и найдем корни.

---

3x² = 0

Найдем коэффициенты:

• a = 3
• b = 0
• с = 0

Подставим коэффициенты в формулу для корней:

x_1;2 =

−0 ± √02 − 4 · 3 · 0

2 · 3

x_1;2 =

0 ± √0

6

x_1;2 =
x = 0

Ответ: x = 0

---

5x² = 125
5x² − 125 = 0

Найдем коэффициенты:

• a = 5
• b = 0
• с = −125

Подставим коэффициенты в формулу для корней:

x_1;2 =

−0 ± √02 − 4 · 5 · 125

2 · 5

x_1;2 =

0 ± √2500

10

x_1;2 =

0 ± 50

10

x1 =	x2 = −50 10
x1 = 5	x2 = −5

Ответ: x₁ = 5; x₂ = −5

---

9x² − x = 0

Найдем коэффициенты:

• a = 9
• b = −1
• с = 0

Подставим коэффициенты в формулу для корней:

x_1;2 =

−(−1) ± √(−1)2 − 4 · 9 · 0

2 · 9

x_1;2 =

1 ± √1 − 0

18

x_1;2 =

1 ± 1

18

x1 = 1 + 1 18	x2 = 1 − 1 18
x1 =	x2 =
x1 =	x2 = 0

Ответ: x₁ =

; x₂ = 0

Другие способы решения неполных квадратных уравнений

Любое неполное квадратное уравнение можно решить, не используя формулу для корней квадратного уравнения.

Корни в неполном квадратном уравнении можно найти, применяя формулы сокращенного умножения и правило деления уравнения на число.

Решим другим методом уравнения, которые мы решали по формуле выше.

---

3x² = 0

Вспомним, что только умножение на «0» даст в результате ноль. Поэтому становится понятно, что в этом уравнении только один корень «x = 0».

Ответ: x = 0

---

5x² = 125

Разделим левую и правую часть уравнению по правилу деления на «5».

5x² = 125         | (:5)
5x² (:5) = 125 (:5)
x² = 25

Перенесем все в левую часть.

x² − 25 = 0

Используем формулу разность квадратов.

(x − 5)(x + 5) = 0

Произведение многочленов в скобках будет равно нулю в том случае, когда любая из скобок окажется равна нулю. Приравняем каждую скобку к нулю и найдем корни уравнения.

(x − 5) = 0	(x + 5) = 0
x = 5	x = − 5

Ответ: x₁ = 5; x₂ = −5

---

9x² − x = 0

Вынесем общий множитель за скобки в левой части.

9x² − x = 0
x(9x − 1) = 0

Произведение будет равно нулю в том случае, когда один из множителей равен нулю.

x = 0	(9x − 1) = 0
	9x = 1         | (:9)
	9x (:9) = 1 (:9)
	x =

Ответ: x₁ = 0 ; x₂ =

Важно!

Если у вас не получается решить уравнение с помощью формул сокращенного умножения, используйте формулу для поиска корней квадратного уравнения.

С помощью этой формулы всегда можно решить любое квадратное уравнение!

Как решать квадратные уравнения Дискриминант Неполные квадратные уравнения

Что такое квадратное уравнение. — ответ на Uchi.ru

Ответ или решение2

П

Что такое квадратное уравнение

Уравнение вида ax² + bx + c = 0 называется квадратным.

Если коэффициент при х² равен 1 (a = 1), то уравнение называется приведенным квадратным уравнением.

Решение квадратного уравнения

Квадратное уравнение решается при помощи дискриминанта.

Дискриминант вычисляется по формуле:

D = b² — 4ac.

Далее вычисляются корни уравнения, при этом если:

• D > 0, то уравнение имеет два корня, которые вычисляются по формулам: х₁ = (-b + √D) / 2a и х₂ = (-b — √D) / 2a;
• D = 0, то уравнение имеет один корень, значение которого вычисляется по формуле: х = -b / 2a;
• D < 0, то уравнение не имеет решений.

 

Приведенное квадратное уравнение можно решить по теореме Виета, которая гласит, что сумма корней приведенного квадратного уравнения равна значению коэффициента b, взятому с противоположным знаком, а произведение корней равно значению коэффициента c:

х₁ + х₂ = -b,

х₁ * х₂ = c.

Примеры решения квадратных уравнений

1) Решим квадратное уравнение х² — 8х — 20 = 0 с помощью дискриминанта.

D = (-8)² — 4 * 1 * (-20) = 64 + 80 = 144.

Так как D > 0, то уравнение имеет два корня.

х₁ = (-(-8) + √144) / 2,

х₁ = (8 + 12) / 2,

х₁ = 20 / 2,

х₁ = 10;

х₂ = (-(-8) — √144) / 2,

х

2 = (8 — 12) / 2,

х₂ = -4 / 2,

х₂ = -2.

Ответ: х₁ = 10, х₂ = -2 — корни уравнения.

 

Решим это же уравнение с помощью теоремы Виета:

х₁ + х₂ = 8,

х₁ * х₂ = -20. 2 +- sqrt D) : 2 * a, где D — дискриминант, от него зависит, сколько корней будет иметь уравнение. При его положительном значении корней будет два, если D = 0, — один, а если D<0 то уравнение не имеет корней. Sqrt — квадратный корень. Часто квадратное уравнение имеет два корня, каждый из которых находится либо прибавлением, либо вычитанием дискриминанта (+-).

Знаешь ответ?

Как написать хороший ответ?Как написать хороший ответ?

Будьте внимательны!

• Копировать с других сайтов запрещено. Стикеры и подарки за такие ответы не начисляются. Используй свои знания. 🙂
• Публикуются только развернутые объяснения. Ответ не может быть меньше 50 символов!

0 /10000

linear алгебра — Решение квадратного уравнения без использования формулы?

спросил 5 лет, 8 месяцев назад

Изменено 2 года, 2 месяца назад

Просмотрено 8к раз

$\begingroup$

Я работал над некоторыми квадратными уравнениями и задался вопросом, могу ли я попытаться решить уравнение, не используя формулу.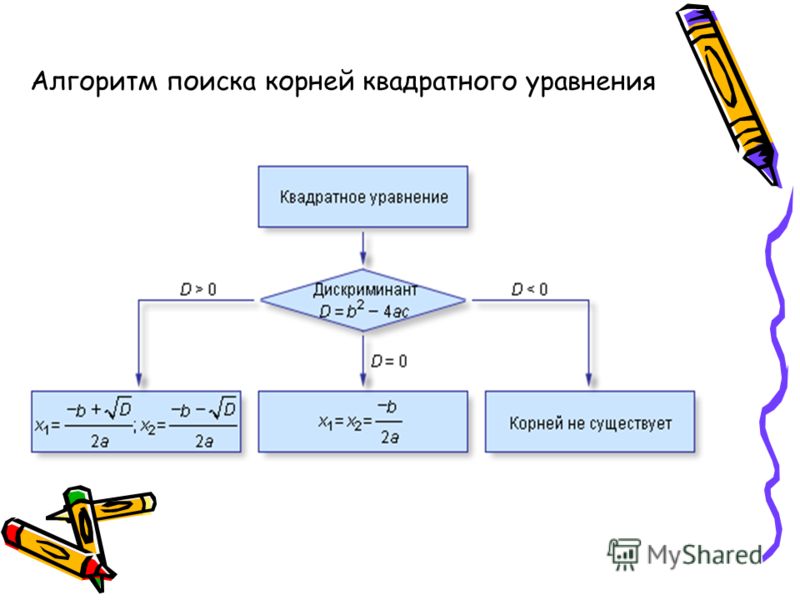 2 был > 1, и преобразовал его в вершинную форму для дальнейшего решения. 92=\frac{1}{3}+\frac{4}{9}$$ правая часть задается как $$\frac{1}{3}+\frac{4}{9}=\frac{ 7}{9}$$ таким образом, мы имеем $$|x+\frac{2}{3}|=\frac{\sqrt{7}}{3}$$ отсюда получаем $$x=-\frac{2}{3}+\frac{\sqrt{7}}{3}$$ $$x=-\frac{2}{3}-\frac{\sqrt{7}}{3}$$

$\endgroup$

$\begingroup$

1. Вы пропустили один корень при извлечении квадратного корня из обеих сторон. Однако вы восстановили его в следующей строке.
2. Вы можете проверить свои корни на вольфрамальфе. Как заявил Лорено Хир в комментарии к вопросу, в вашем выводе есть ошибка, которая привела к неправильным корням. 9{2}+bx+c=0$$ Итак, у вас есть $$x_{1}+x_{2}=-b,\quad x_{1}x_{2}=c,$$ где $x_{1,2}$ — ваши корни. Итак, вы можете выбрать целые делители $c$ и проверить, является ли один из них корнем $P(x) = 0$. В школьной практике довольно часто после 1-2 итераций удается найти корень. Более того, вам не нужно ничего путать с извлечением квадратного корня, поэтому вероятность ошибки меньше. Как только один корень $r_1$ найден, другой $r_2 = -b — r_1$. Но, конечно, это работает только для квадратных уравнений с целыми корнями. В противном случае вам лучше рассмотреть дискриминантную формулу.

$\endgroup$

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

.

Все признаки указывают на дискриминант

Вы когда-нибудь владели одним из этих Magic 8 Balls? Они выглядят как до смешного большие шары для бильярда, но в них встроено плоское окошко, так что вы можете видеть, что находится внутри 20-гранного кубика, плавающего в отвратительной непрозрачной синей слизи. Предположительно бильярдный шар обладает прогностической силой; все, что вам нужно сделать, это задать ему вопрос, встряхнуть его, и медленно, мистически, как покрытая нефтью печать, выходящая из разлива нефти, кубик поднимется к маленькому окошку и покажет ответ на ваш вопрос.

Квадратное уравнение содержит своего рода Magic Ball 8. Выражение b ² — 4 ac из-под знака радикала называется дискриминантом , и оно фактически может определить для вас, сколько решений имеет данное квадратное уравнение, если вы не хотите на самом деле вычислять их. Учитывая, что для решения неразложимого квадратного уравнения требуется много работы (квадратная формула изобилует тоннами арифметических действий, а для завершения метода квадрата требуется целый ряд шагов), часто бывает полезно заглянуть в мистику за ее пределами, чтобы понять. конечно уравнение даже имеет любых решений для действительных чисел, прежде чем вы потратите какое-то время, пытаясь их найти.

Talk The Talk

Дискриминантный — это выражение B ² — 4 AC , которое определено для любого квадратичного уравнения AX ² + BX + C ² + BX + 44444444444444444444444 2 + BX + 444444444. 2 + . Основываясь на знаке выражения, вы можете определить, сколько действительных чисел имеет решение квадратного уравнения.

Вот как работает дискриминант. Учитывая квадратное уравнение x ² + bx + c = 0, подставьте коэффициенты в выражение b ² — 4 ac , чтобы посмотреть, какие результаты вы получите:

9013 9013 квадратичный будет иметь два уникальных решения.

Если вы получите 0, квадратное число будет иметь ровно одно решение, двойной корень.

Если вы получите отрицательное число, у квадратного уравнения не будет действительных решений, а только два мнимых. (Другими словами, решения будут содержать i , о которых вы узнали из книги «Борьба с радикалами».)

Дискриминант — это не магия. Это просто показывает, насколько важен этот радикал в квадратной формуле. Например, если его подкоренная часть равна 0, вы получите

за одно решение. Если, однако, b ² — 4 ac отрицательно, то у вас будет отрицательное значение внутри знака квадратного корня в квадратной формуле, что означает только мнимые решения.

Пример 4 : Не вычисляя их, определите, сколько действительных решений уравнения 3 х ² — 2 х = -1 есть.

Решение : Установите квадратное уравнение равным 0, добавив 1 к обеим частям.

• 3 x ² — 2 x + 1 = 0

No related posts.