Квадратные уравнения с параметром.
Презентация на тему:
«Уравнения второй степени с параметром»
Выполнили ученицы 9 В класса:
Возиянова Светлана
Галиева Анастасия
Цели:
- Определение количества корней квадратного уравнения в зависимости от параметра;
- Решение уравнений с параметром.
Квадратное уравнение
Уравнение вида ах²+bx+с=0, где а, b, с Є R, а ≠ 0 называется квадратным уравнением. D=b²-4ac – дискриминант квадратного уравнения.
Если D0, то уравнение имеет два различных корня:
Если D=0, то уравнение имеет один корень.
Алгоритм решения квадратных уравнений с параметром
1)Если в квадратном уравнении главный коэффициент содержит параметр, то обязательно нужно выяснить, при каких значениях параметра главный коэффициент равен нулю. В этом случае квадратное уравнение превращается в линейное, которое имеет один корень.
2) Если в квадратном уравнении главный коэффициент не содержит параметра, то количество корней зависит только от значения дискриминанта.
Примеры:
Пример 1. При каком значение параметра b уравнение 2х²-bx+18=0 имеет единственный корень?
Решение: Данное уравнение является квадратным. Оно имеет единственный корень, если его дискриминант равен нулю. Имеем:
D=b²-4*2*18 = b²-144;
b²-144=0;
b= -12 или b= 12.
Ответ: b= -12, или b=12
Пример 2. При каком значение параметра b уравнение (b+6)x²-(b-2)x+1=0 имеет единственный корень?
Решение: Считать такое уравнение квадратным является ошибкой. Это уравнение степени не выше второй.
При b= -6 получаем линейное уравнение 8x+1=0, имеющее один корень.
При b ≠ -6 данное уравнение является квадратным; оно имеет единственный корень, если его дискриминант равен нулю:
D=(b-2)²-4(b+6) = b²-4b+4-4b-24 = b²-8b-20
Имеем: b²-8b-20=0, отсюда b= -2 или b=10.
Ответ: b= -2, или b=10, или b= -6
Пример 3. При каких значениях параметра а уравнение a(a+3)х²+(2a+6)x-3a-9=0 имеет больше одного корня?
Решение: При а=0 получаем линейное уравнение 6х-9=0, имеющее единственный корень.
При а=-3 получаем линейное уравнение 0х=0, имеющее бесконечно много корней.
Если а≠0 и а≠ -3, то, разделив обе части уравнения на а+3, получим квадратное уравнение ах²+2х-3=0. Дискриминант этого уравнения равен 4(1+3а). Для выполнения условия задачи он должен быть положительным, т.е. 4(1+3а)0. Отсюда а-1/3. Однако промежуток (-1/3;+∞) содержит значение а=0, при котором исходное уравнение имеет единственный корень, что не удовлетворяет условию задачи.
Ответ: а= -3, или -1/30
Пример 4.
Решить уравнение (a²-b²)х²-2ax+1=0.
Решение: Рассмотрим три случая:
1) a=b=0. Уравнение 0x+1=0 решений не имеет.
2) a²=b²≠0. Уравнение -2ax+1=0 имеет один корень x=1/2a.
3) a²-b²≠0. Корни уравнения: x1= 1/a-b, x2= 1/a+b.
При b=0 D=b²=0, поэтому уравнение имеет один корень x=1/a (a ≠0).
Ответ: x=1/2a при a²=b²≠0; x=1/a при a ≠0, b=0; ∅ при a=0, b=0; x1= 1/a-b, x2= 1/a+b при a ² ≠ b ², b ≠0
Пример 5. Решить уравнение (4a/x²-a²)+ (x-a/x(x+a))=(1/x(x-a))
Решение: При x≠0, x≠a, x≠-a уравнение приведём к равносильному 4ax+x²-2ax+a²-x-a=0.
(x+a)²-(x+a)=0
(x+a)(x+a-1)=0
Так как x≠-a, то уравнение имеет одно решение x=1-a. Условия x≠0, x≠a влекут за собой требования a≠1, a≠1/2. Уравнение 1-a=-a решений не имеет.
Ответ: x=1-a при a≠1/2; a≠1; ∅ при a=1/2, a=1
Пример 6. При каких значениях a уравнение aх²-x+3=0 имеет единственное решение?
Решение: Ошибочно считать данное уравнение квадратным.
На самом деле это уравнение степени не выше второй. Исходя из этого соображения, рассмотрим следующие случаи:
1)a=0. При этом уравнение принимает вид -x+3=0, откуда x=3, т.е. решение единственно.
2) a≠0, тогда aх²-x+3=0 – квадратное уравнение, дискриминант D=1-12a. Для того, чтобы уравнение имело единственное решение, нужно, чтобы D=0, откуда a=1/12.
Ответ: a=0 или a=1/12
Пример 7. Один из корней квадратного уравнения х²+2ах+2-3а=0 равен 1. Найдите значение параметра а и второй корень уравнения.
Решение: х1=1 подставим его в уравнение и получим верное равенство: 1²+2а*1+2-3а=0 или 3-а=0, откуда а=3. Подставим это значение параметра а в данное уравнение: х²+2*3*х²+2-3*3=0 или х²+6х-7=0.
Решим это квадратное уравнение: х1=1 и х2= -7.
Получили а=3 и х2= -7
Ответ: а=3; х2= -7
Пример 8. При каких значениях параметра а сумма квадратов корней уравнения x²+ax+a=0 равна 3?
Решение: Пусть x1 и x2 – корни данного уравнения.
По условию x1² + x2²=3, т.е. (x1+x2)²-2x1x2 = 3. Применяя теорему Виета, можно записать (-a)²-2a=3; a²-2a-3=0. Отсюда a=-1 или a=3.
Казалось бы, решение завершено. Однако теорема Виета «работает» лишь для тех квадратных уравнений, у которых есть корни. А данное квадратное уравнение имеет корни не при всех значениях параметра a. Существование корней определяется условием D ≥0. Для данного уравнения D=a ²-4a. Следовательно, найденные значения a= -1 и a=3 должны удовлетворять неравенству a²-4a≥0. Легко установить, что подходит только a= -1.
Ответ: а= -1
Пример 9. При каких значениях параметра а уравнение (a+6)х²+2ax+1=0 имеет единственное решение?
Решение: По условию задачи уравнение необязательно является квадратным, поэтому рассмотрим два случая:
1) а+6=0; а=-6
Если а = -6, то -12х+1=0, х = 1/12.
2) Если а ≠ -6, то квадратное уравнение имеет единственное решение, если D =0 D=4a²-4(a+6)=4(a²-a-6) a²-a-6=0 a1=3, a2=-2.
Ответ: при a ∈ {-6, -2, 3}
Пример 10. Найти наименьшее целое a, при котором уравнение x²+(2a+3)x+a²-a+5=0 имеет два различных корня.
Решение: Уравнение имеет два различных корня, если D0. Из неравенства (2a+3)²-4(a²-a+5)0 следует, что 16a-110, откуда a11/16. Наименьшее целое значение a ∈ (11/16; +∞) равно 1.
Ответ: a=1.
Источники:
- 1) Алгебра. Углублённый уровень. 8 класс (Мерзляк А. Г., Поляков В. М.)
- 2) Локоть В.В. Задачи с параметрами. Линейные и квадратные уравнения, неравенства, системы
Квадратные уравнения с параметрами
Тема занятия «КВАДРАТНЫЕ УРАВНЕНИЯ С ПАРАМЕТРАМИ»
Цели занятия:
Образовательная: углубить ранее полученные знания об уравнениях с параметрами, закрепить навыки решения уравнений;
Воспитательная: воспитывать навыки учебного труда, умение работать в группах;
Развивающая:
развивать логическое мышление, формировать потребность к приобретению знаний.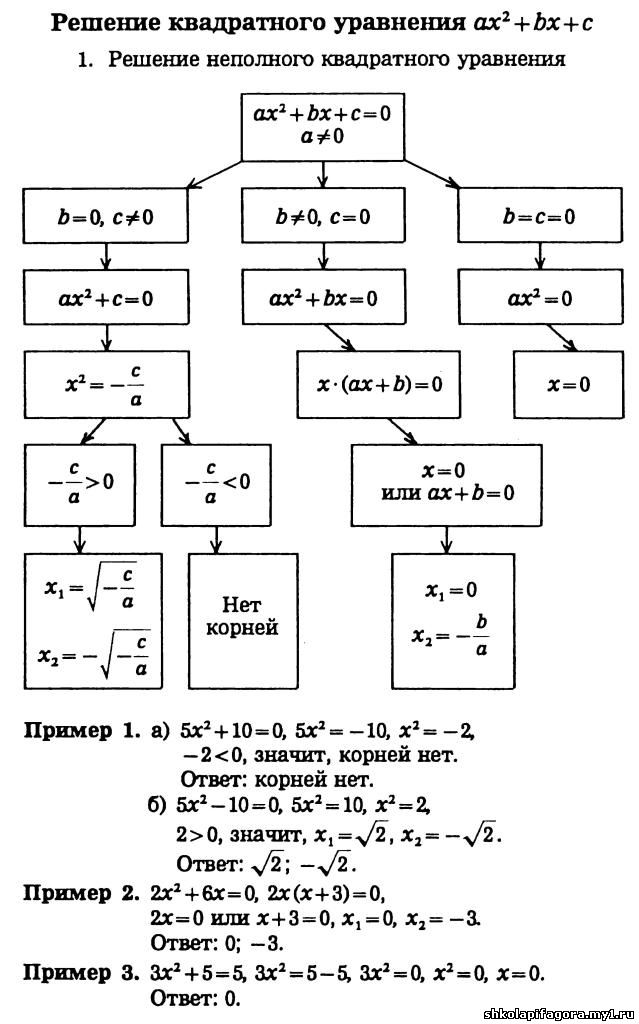
Опрос:
Вспомним условия расположения корней уравнения,при условии , что оба корня положительные, отрицательные, разных знаков.
Рассмотрим примеры решения квадратных уравнений с параметрами.
ПРИМЕР 1.
Решить уравнение
Решение:
1.Если , то мы имеем линейное уравнение:
2.Если найдём дискриминант D квадратного уравнения :
а)Если , то
б)Если т.е. то
в)Если то действительных корней нет .
Ответ: если
если
если
решений нет, если
ПРИМЕР 2.
Решить уравнение
Решение:
Уравнение равносильно системе:
Решим уравнение
1.
Если т.е. имеем :
Условие выполнено, т.к.
Выясним, при каких значениях Для этого решим уравнения :
и
Понятно, что при всех отрицательных значениях параметра равенство в первом уравнении невозможно, при возведя в квадрат обе части равенства , мы получим что невозможно.
Второе из рассматриваемых уравнений невозможно при положительных значениях ,а при имеем , как и в первом случае , неверное равенство
Таким образом , если
2.Если то
Т.е. в данном случае уравнение не имеет решений.
3.Если то дискриминант квадратного уравнения отрицательный и, таким образом, нет действительных корней.
Ответ: если
решений нет, если
ПРИМЕР 3.
Определить количество корней уравнения в зависимости от :
Решение:
Обозначим Тогда исходное уравнение имеет вид
или .
Количество корней зависит от знака D1 .
D1=
1.Если то данное уравнение не имеет корней.
2.При уравнение имеет единственный корень: Итак,
Это уравнение не имеет корней.
3.Если то корни уравнения
Итак ,необходимо выяснить , сколько корней имеет совокупность уравнений:
В первом уравнении дискриминант отсюда следует, что оно не имеет решений при любых значениях параметра
Во втором уравнении
1)Если т.е. то данное уравнение имеет один корень.
2)Если т.е.
Уравнение не имеет действительных корней.
3)Если т.е. уравнение имеет два корня .
Ответ: Два корня , если
один корень, если
действительных корней нет, если
ПРИМЕР 4.
При каких значениях параметра уравнение
имеет единственное решение?
Решение:
Данное уравнение равносильно системе :
Найдём дискриминант квадратного уравнения :
Если , уравнение имеет один корень что удовлетворяет условию
При получим:
Уравнение имеет одно
решение , если т.
е. при
Ответ: Уравнение имеет один корень, если
ПРИМЕР 5.
При каких значениях параметра уравнение имеет
два разных действительных корня?
Решение:
Данное биквадратное уравнение сводится к совокупности уравнений:
Уравнение имеет два разных корня, если
Ответ: уравнение имеет два разных корня , если
ПРИМЕР 6.
При каких значениях параметра уравнение
имеет единственное решение ?
Решение:
Данное уравнение равносильно системе :
система будет иметь одно решение ,если
т.е. при
Ответ: уравнение имеет единственное решение при
ПРИМЕР 7.
Сколько решений имеет уравнение в зависимости от значения параметра ?
Решение:
Данное уравнение равносильно системе :
При или уравнение
имеет два решения, в других случаях – три.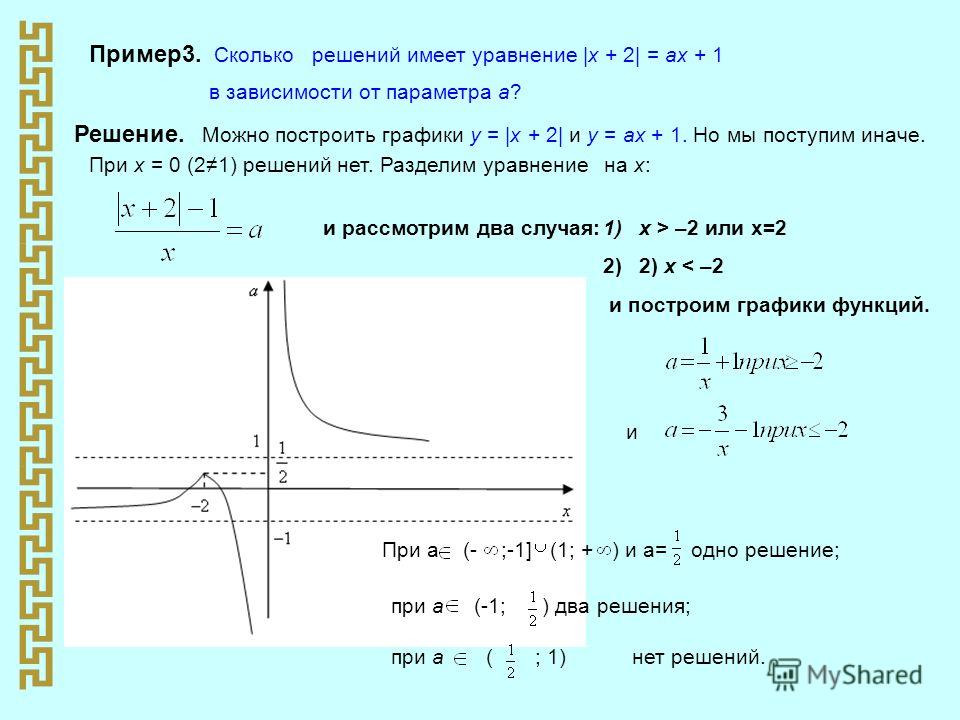
Ответ: два решения , если
три решения, если
ПРИМЕР 8.
При каких значениях параметра уравнение
имеет единственное решение ?
Решение:
Данное уравнение равносильно системе :
Решив квадратное уравнение , имеем :
Система имеет единственное решение, если т.е. или, когда
Ответ: уравнение имеет единственное решение, если
ПРИМЕР 9.
При каких значениях параметра уравнение
имеет единственное решение?
Решение:
1.Если то мы получим линейное уравнение
При
При решений нет .
2.При дискриминант D должен равняться нулю, т.е.
Случай уже рассмотрен .
Ответ:уравнение имеет единственное решение при
ПРИМЕР 10.
При каких значениях параметра сумма корней уравнения
равна 2?
Решение:
Чтобы уравнение имело корни ,
По теореме Виета,
Таким образом, имеем систему:
Ответ: при
ПРИМЕР 11.
При каких значениях параметра уравнение
имеет два разных положительных корня ?
Решение:
Для того, чтобы квадратное уравнение имело два разных действительных корня, необходимо, чтобы дискриминант
По теореме Виета:
Таким образом, имеем систему неравенств :
Ответ: уравнение имеет два разных положительных корня,
если .
ПРИМЕР 12.
При каких значениях параметра один корень уравнения
меньше, чем -2 , три других- больше -1 ?
Решение:
В условии задачи идёт речь о четырёх корнях , т.е. Пусть тогда
данное уравнение примет вид
.
Чтобы данное уравнение имело четыре действительных корня , которые удовлетворяют условию задачи , необходимо, чтобы корни уравнения относительно t удовлетворяли условиям:
Итак имеем систему неравенств :
где
Ответ: при
ПРИМЕР 13.
При каких значениях параметра уравнение имеет
единственный корень ? Найти его.
Решение:
а) тогда
б) тогда
Ответ: при
ПРИМЕР 14.
Определить количество целых значений параметра из промежутка ,
при которых квадратное уравнение имеет два разных корня.
Решение:
Для того , чтобы квадратное уравнение имело два разных корня, необходимо, чтобы
Ответ: 4.
ПРИМЕР 15.
При каком наименьшем целом значении уравнение
имеет четыре решения ?
Решение :
Построим в одной системе координат графики функций и
Видим, что при эти графики имеют четыре точки пересечения.
Ответ:
ПРИМЕР 16.
Найдите
количество целых значений , при которых сумма
корней уравнения принадлежит промежутку .
Решение:
Сумма корней уравнения равна
Итак ,
Целые числа, которые удовлетворяют условию 11, 12,13, 14,15.
Ответ: пять.
ПРИМЕР 17.
Найдите количество целых значений , при которых произведение корней уравнения принадлежит промежутку .
Решение:
Произведение корней уравнения равно
Итак,
Целые числа , которые удовлетворяют условию это 23, 24, 25.
Ответ:три.
ПРИМЕР 18.
При каком наименьшем натуральном значении параметра корни уравнения являются рациональными числами?
Решение:
Для того ,чтобы корни уравнения были рациональными числами, необходимо, чтобы выражение было полным квадратом ,т.е.
будет полным квадратом при наименьшем натуральном значении
Ответ: при
ПРИМЕР 19.
При каком значении параметра квадратное уравнение
имеет корни, равные по абсолютной величине и противоположные по значению ?
Решение:
разделим на
Ответ: при
ПРИМЕР 20.
При каком наибольшем целом значении параметра корни уравнения
находятся по разные стороны промежутка ?
Решение:
Запишем левую часть уравнения как функцию
Нарисуем график этой функции ( схематично).
Мы видим, что корни уравнения находятся по разные стороны промежутка
, если выполняются условия:
Ответ:
ПРИМЕР 21.
При каком значении параметра сумма квадратов корней уравнения
равна 12?
Решение:
По теореме Виета: По условию: тогда
Т.е.
Ответ:
ПРИМЕР 22.
При каком значении параметра произведение корней уравнения
будет наибольшим?
Решение:
По теореме Виета произведение корней этого уравнения равняется :
Сумма двух положительных чисел принимает наименьшее значение, если одно из слагаемых равно нулю. Итак ,
Ответ:
ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ.
1.Решить уравнение:
1)
2)
3)
Ответы:
1) если
корней нет, если если если
2) если
при корней нет при
3) если корней нет, если
2.При каких значениях параметра уравнение
имеет единственное решение ?
Ответ: ни при каких.
3.При каких значениях параметра уравнение
имеет два разных действительных корня?
Ответ: при
4.При каких значениях параметра уравнение
имеет единственное решение ?
Ответ: при
5.
Сколько решений
имеет уравнение в зависимости от параметра ?
Ответ: два корня, если
три корня, если
6.При каких значениях параметра уравнение
имеет единственное решение?
Ответ: при
7.При каком значении параметра произведение корней уравнения
равно 8?
Ответ: при
8.При каких значениях параметра уравнение имеет
два разных отрицательных корня ?
Ответ: при
9.При каких значениях параметра уравнение имеет
два разных действительных отрицательных корня?
Ответ: при
10.При каких значениях параметра уравнение имеет корни разных знаков ?
Ответ: при
11.При каких значениях параметра уравнение имеет
корни такие, что и ?
Ответ: при
12.Найти все значения , при которых один из корней уравнения
меньше чем 1, а второй – больше 1.
Ответ:
13.Найти все значения , при которых корни уравнения
больше, чем 1.
Ответ:
Урок «Решение квадратных уравнений с параметром»
Министерство образования и науки Самарской области
Государственное автономное образовательное учреждение дополнительного профессионального образования (повышения квалификации) специалистов
САМАРСКИЙ ОБЛАСТНОЙ ИНСТИТУТ ПОВЫШЕНИЯ КВАЛИФИКАЦИИ
И ПЕРЕПОДГОТОВКИ РАБОТНИКОВ ОБРАЗОВАНИЯ
Итоговая работа
На курсах повышения квалификации
«Методические особенности обучения решению задач с параметром в условиях перехода к новым образовательным стандартам».
По ИОЧ ВБ 13.03.2017г-17.03.2017г
по теме:
« Квадратные уравнения с параметрами»
Выполнила:
Тихонова Надежда Викторовна,
Преподаватель математики
БГПОУ Сызранский «политехнический колледж»
Сызрань 2017 г.
. КВАДРАТНЫЕ УРАВНЕНИЯ С ПАРАМЕТРАМИ
Уравнение вида ax2+bx+c=0, где a, b, c – числа, причем а≠0 называется
квадратным уравнением.
а – первый коэффициент, b – второй коэффициент, с – свободный член.
Например:
а) 2х2– 3х + 0,7 = 0
б) -0,9 х2+ 8 – 2 1/6х=0
Найти a, b, c?
Решим уравнение ax2+bx+c=0
а) если а=0, то уравнение имеет вид bx+c=0. Тогда x=-c|b
б) если а≠0, то уравнение имеет:
1) 2 различных корня х1≠х2, если Д>0,
2) 2 равных корня х1=х2, если Д=0
3) не имеет корней, если Д<0.
Рассмотрим примеры.
Пример №1. При каких значениях уравнение имеет 2 корня?
2х2+6х+b=0
Уравнение квадратное.
Найдем Д=36-4*2*b=36-8b. По условию задачи уравнение имеет 2 корня,
значит Д>0.
Решим неравенство 36-8b>0
-8b>-36
b<4,5.
Ответ: при b<4,5.
Пример № 2. При каких значениях имеет один корень?
3х2-6х+2v=0
Уравнение квадратное.
Д=36-4*3*2v=36-24v.
Так как уравнение имеет один корень, то Д=0.
36-24v=0
24v=36
V=1,5.
Пример № 3. При каких t уравнение не имеет корней?
2×2-15x+t=0
Уравнение квадратное. Д=225-4*2t=225-8 t По условию Д<0, то
225-8t<0
-8t<-225
t>281/8.
Ответ: при t>281/8/
Пример № 4.
При каких значениях m равно один из корней уравнения равен нулю. х2 – 2х + 2m – 3 = 0
Решение: Если х = 0, то имеем:
02 – 2 .0 + 2m – 3 = 0
2m = 3
m = 1,5
Проверим, не равняется ли второй корень уравнения нулю.
х = 0
х = 2
х2 – 2х = 0
Ответ: m = 1,5
При решении квадратного уравнения с параметрами контрольными будут те значения параметра, при которых коэффициент при х2 обращается в 0. Дело в том, что если этот коэффициент равен нулю, то уравнение превращается в линейное и решается по соответствующему алгоритму; если же этот коэффициент отличен от нуля, то имеем квадратное уравнение, которое решается по иному алгоритму.
Дальнейшее решение зависит от дискриминанта.
Пример №.5
Решить уравнение х2 – (2р + 1)х + (р2 + р – 2) = 0
Решение: Здесь коэффициент перед х2 отличен от нуля, значит данное уравнение при любых значениях параметра является квадратным. Найдем дискриминант:
D = (2р + 1)2 – 4∙1(р2 + р – 2) = (4р2 + 4р + 1) – (4р2 + 4р – 8) = 4р2 + 4р + 1 – – 4р2 – 4р + 8 = 9
D > 0, значит квадратное уравнение имеет два решения
х1 = р + 2
х2 = р – 1
Ответ: при любых значениях р х1 = р + 2; х2 = р – 1
Пример № 6.
Решить уравнение рх2 +( 1 – р)х – 1 = 0
Решение: Мы не можем утверждать, что данное уравнение является квадратным. Рассмотрим контрольные (точки) значения р = 0, имеем два случая.
Если р=0, то получается уравнение вида 0∙х2 + х – 1 = 0, которое является линейным и имеет корень х = 1
Если р ≠0, то уравнение является квадратным, можно применять формулы корней квадратного уравнения.
D = (1 – р)2 – 4∙.
р .(-1) = 1 – 2р + р2 + 4р = (1+ р)2
х1 = 1
х2 = –
Ответ: при р = 0 х = 1; при р ≠0 х1 = 1 х2 = –
Пример № 7
Решить уравнение: (а – 1)х 2 + 2(2а + 1)х + (4а + 3) = 0
Решение: здесь контрольными будут те значения параметра, при которых коэффициент при х2 обращается в 0.
Если а – 1 = 0, а = 1, уравнение имеет вид 0∙ х2 + 6х + 7 = 0 и является линейным. Корнем этого уравнения является х =
Если а–1 ≠ 0, а ≠ 0, уравнение является квадратным. Найдем его дискриминант.
D = (2∙(2а + 1))2 – 4(а – 1)(4а + 3) = 4(4а2 + 4а + 1) – 4(4а2 – а – 3) = 4(5а + 4)
Дальнейшие рассуждения зависят от значения дискриминанта.
Если D < 0, то квадратное уравнение не имеет корней; если D = 0, то уравнение имеет один корень, если D > 0, то уравнение имеет два корня.
Дискриминант обращается в нуль при а = – (можно сказать, что это – второе контрольное значение параметра; при переходе через него происходит качественное изменение уравнения – меняется число корней уравнения).
Если а < – , то D < 0 и следовательно, квадратное уравнение не имеет корней.
Если а > – , то если D > 0 и, значит квадратное уравнение имеет два корня:
х1 =
х2 =
Если а = – , то D = 0, то уравнение имеет единственное решение
х =
Ответ: при а = 1, х = – ;
при а = –, х = ;
при а < –, корней нет;
при а > –, х1 =
х2 =
Иногда задания сформулированы так, что искать корни нет необходимости.
Пример №8
При каких значениях m ровно один из корней х2+(m+3)х +|m| – 3 = 0
уравнения равен нулю.
Решение. Если нуль является корнем уравнения, квадратный трехчлен х2+(m+3)х +|m| – 3 при х = 0 обращается в нуль. 02+(m+3) .0 +|m| – 3 = 0
|m| – 3 = 0 m1 = 3 m2 = –3
Найдем второй корень при найденных значениях m.
Если m=3, то уравнение принимает вид х2+6х = 0; х1 = 0 х2 = –6
Если m= –3, то уравнение принимает вид х2 = 0, которое имеет два кратных корня, равных нулю.
Ответ: при m = 3
Пример №9
Сколько корней имеет уравнение 3х (х – 1) 2 = kх в зависимости от значения параметра k ?
Решение: 3х (х – 1) 2 = kх
3х (х – 1) 2 – kх = 0
х (3(х – 1) 2 – k) = 0
Один корень есть всегда – х0 = 0
Исследуем 3х 2 – 6х + 3 – k = 0
D = 32 – 3(3 – k) = 3k
а) Если k = 0, существует один корень х = 1;
б) Если k > 0, существуют два корня х1 = х2 = , но необходимо исследовать случай, когда один из корней равен 0.
Это так, если k = 3;
в) Если k < 0, корней нет.
Ответ: уравнение 3х (х – 1) 2 = kх имеет при
1) k > 0
k ≠ 3 три корня;
2) k = 0 два корня
3) k = 3 два корня
4) k < 0 один корень.
2-(4m+2)x+m-1=0$$ имеет два действительных корня $x_1$ и $x_2$, которые удовлетворяют условию: $x_1 Я обнаружил, что $$m\in\left(-\frac{1}{2}; -\frac{1}{3}\right).$$ Верно? $\endgroup$ 2 $\begingroup$ Эту главную задачу можно решить, не зная точных значений корней.
Формулы для корней затем упрощаются до: корнеплоды. Это означает, что $aP(2)>0$, т. е. $(2m+1)(m-1)>0$.
2+bx+c=0$, что
$$x_1 < x_2 < s \qquad \text{ для некоторого фиксированного } s \in \mathbb{R}$$ 92+bx+c$.
Общие решения всех неравенств из первого и второго условий дадут вам требуемый результат.
$\endgroup$
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
Решения квадратных уравнений | Superprof
В этой статье мы обсудим методы, которые используются для нахождения решений квадратных уравнений и свойства решений квадратных уравнений. Общая форма квадратного уравнения такова. Решения квадратных уравнений известны как корни или нули уравнения.
Мы можем решать квадратные уравнения, используя три метода, такие как разложение на множители, квадратная формула и завершение квадрата. Давайте обсудим каждый из методов один за другим с примерами.
Разложение на множители
Чтобы решить квадратное уравнение на множители, выполните следующие действия:
- Возьмите все члены квадратного уравнения с одной стороны и поставьте ноль с другой стороны уравнения
- Разложите средний член таким образом что его произведение равно ac, а сумма или разность равна среднему члену.
- На следующем шаге разложите уравнение и установите каждый фактор равным нулю.
- После установки каждого фактора равным нулю вы получите два новых уравнения. Вам нужно решить каждое из уравнений, чтобы получить значения переменной.
- На последнем шаге этого процесса вы можете подставить значение переменной в исходное уравнение, чтобы проверить, верен ли ваш ответ. Это не обязательный шаг.
Теперь мы увидим, как решать квадратные уравнения с помощью факторизации на следующих примерах.
Лучшие репетиторы по математике
Поехали
Пример 1
Решите факторингом.
Решение
Сначала мы внесем константу в левую часть уравнения и установим уравнение равным нулю следующим образом:
Теперь разложим на множители уравнение следующим образом:
Приравняв каждый множитель к нулю, мы получим два уравнения:
и
и
5 уравнения равны -2 и -6. Теперь мы подставим их в исходное уравнение, чтобы увидеть, верен наш ответ или нет.
в
в
Таким образом, доказано, что -2 и -6 являются решениями исходного уравнения.
Пример 2
Решите факторингом.
Решение
Сначала мы перенесем все члены в левую часть уравнения и приравняем уравнение к нулю следующим образом:
Теперь мы разложим уравнение на множители следующим образом:
Приравняв каждый множитель к нулю, мы получим два уравнения:
и
и
Следовательно, корни или нули уравнения равны -2 и -6. Теперь мы подставим их в исходное уравнение, чтобы увидеть, верен наш ответ или нет.
at
at
Поскольку подстановкой значений в исходное уравнение являются решения —
Найдите лучшего репетитора по математике на Superprof.
Квадратная формула
Некоторые квадратные уравнения нельзя решить с помощью факторизации. Особенно это происходит, когда решения квадратного уравнения не являются рациональными числами. В этих случаях вы можете использовать квадратную формулу, чтобы найти решения квадратного уравнения.
Для квадратного уравнения мы используем следующую формулу, чтобы найти решение:
Помните, что часть формулы под знаком радикала известна как дискриминант и определяет три возможности. Вот эти три возможности:
- Вы можете получить два различных действительных корня уравнения, если дискриминант является положительным числом.
- Вы получите один действительный корень или решение, если дискриминант равен нулю.
- Вы не получите реального решения уравнения, если дискриминант будет отрицательным числом.
Теперь давайте решим некоторые квадратные уравнения с помощью квадратной формулы.
Пример 1
Найдите корни уравнения
Решение
Это уравнение не может быть решено с помощью факторизации, поэтому мы будем использовать следующую квадратичную формулу, чтобы найти корни уравнения:
Здесь a = 5 , b = -8 и c = 2.
Подставим значения a, b и c в формулу:
.
Мы можем записать ответы в десятичной форме, решив приведенное выше выражение следующим образом:
и
Пример 2
Найдите корни уравнения
Решение
следовательно, мы будем использовать следующую квадратичную формулу, чтобы найти корни уравнения:
Здесь, a = 7, b = — 16 и c = 2.
Мы подставим значения a, b и c в формула:
Упрощая приведенные выше выражения, мы получим следующие ответы:
Мы можем записать ответы в десятичной форме, решив приведенное выше выражение следующим образом:
и более 9000 Найти Изучайте математику онлайн здесь, на Superprof.
Завершение квадрата
Еще один метод решения квадратного уравнения — завершение метода квадрата. Этот метод подходит как для действительных, так и для мнимых корней уравнения. Выполните следующие шаги, чтобы решить квадратное уравнение с помощью этого метода:
- Преобразуйте уравнение в вид
- Помните, что при решении уравнения этим методом а должно быть равно 1. Если оно не равно 1, то уравнение следует умножить на
- Составьте правильный квадрат на левую часть уравнения, используя значение b. Вы можете сделать это, добавив к обеим сторонам.
- Извлеките квадратный корень из обеих частей уравнения и решите оставшееся уравнение.
Если оно не равно 1, то уравнение следует умножить наДавайте теперь решим следующие примеры, выполнив метод квадратов.
Пример 1
Решите уравнение, выполнив метод квадратов.
Решение
Сначала переместим константу в правую часть уравнения:
Теперь возьмем и сложим полученное число с обеих сторон уравнения.
Возьмите квадратный корень из обеих частей уравнения следующим образом:0005
и
Пример 2
Решите уравнение, выполнив метод квадратов.
Сначала мы переместим константу в правую часть уравнения:
Поскольку для использования этого метода a должно быть равно 1, мы разделим все уравнение на 2.
Новое уравнение будет :
Теперь мы возьмем и сложим полученное число с обеих сторон уравнения.
Возьмите квадратный корень из обеих частей уравнения следующим образом:
или
В десятичной форме мы можем записать корни как:
Здесь мы обсудим некоторые свойства решений квадратных уравнений:
- Сумма решений квадратного уравнения равна
- Произведение решений квадратного уравнения равно
- Если известны корни уравнения, то его можно записать в виде , где и
Проверить наличие репетитора по математике можно здесь.
Анализ квадратичных функций | Колледж Алгебра
Результаты обучения
- Используйте квадратичную формулу и разложение на множители, чтобы найти действительные и комплексные корни ([латекс]х[/латекс]-перехваты) квадратичных функций.
- Используйте алгебру, чтобы найти [latex]y[/latex]-отрезки квадратичной функции.
- Решите задачи на корни и точки пересечения квадратичной функции.
- Используйте дискриминант для определения характера (действительного или комплексного) и количества решений квадратных уравнений.
- Определить минимальное или максимальное значение квадратичной функции.
- Решение задач на минимальное или максимальное значение квадратичной функции.
В этом разделе мы продолжим изучение квадратичных функций, в том числе решим задачи, связанные с площадью и движением снаряда. Работа с квадратичными функциями может быть менее сложной, чем работа с полиномиальными функциями более высокой степени, поэтому они предоставляют хорошую возможность для детального изучения поведения функции.
Точки пересечения квадратичных функций
Как и в предыдущих прикладных задачах, нам также нужно найти точки пересечения квадратных уравнений для построения параболы. Напомним, что мы находим [latex]y[/latex]-перехват квадратного числа, вычисляя функцию на входе, равном нулю, и мы находим [latex]x[/latex]-перехват в местах, где выход равен нулю.
Обратите внимание, что количество перехватов [latex]x[/latex] может варьироваться в зависимости от расположения графика.
Количество [latex]x[/latex]-пересечений параболы
Математики также определяют [latex]x[/latex]-отрезки как корни квадратичной функции.
Как сделать: по заданной квадратичной функции [латекс]f\влево(х\вправо)[/латекс] найдите точки пересечения
Y – и X .- Вычислить [latex]f\left(0\right)[/latex], чтобы найти [latex]y[/latex]-перехват.
- Решите квадратное уравнение [latex]f\left(x\right)=0[/latex], чтобы найти точки пересечения [latex]x[/latex].
Пример: Нахождение 9{2}+5x — 2[/латекс].
Показать решение
В приведенном выше примере квадратное уравнение было легко решено с помощью разложения на множители. Однако есть много квадратичных уравнений, которые нельзя разложить на множители. Мы можем решить эти квадратичные уравнения, предварительно переписав их в стандартной форме.
2+2x+3[/латекс] 9{2}-4ac<0[/latex], то число под радикалом будет отрицательным. Поскольку вы не можете найти квадратный корень из отрицательного числа, используя действительные числа, реальных решений нет. Однако вы можете использовать мнимые числа. Тогда у вас будет два сложных решения: одно путем добавления мнимого квадратного корня, а другое путем его вычитания.
Попробуйте
Приложения с квадратичными функциями
Существует множество реальных сценариев, в которых требуется найти максимальное или минимальное значение квадратичной функции, например, приложения, связанные с площадью и доходом.
Пример: нахождение максимального значения квадратичной функции
Фермер хочет выделить прямоугольное пространство для нового сада в своем огороженном заднем дворе. Она купила 80 футов проволочного ограждения, чтобы огородить три стороны, и она будет использовать часть забора заднего двора в качестве четвертой стороны.
- Найдите формулу площади ограждения, если стороны ограждения, перпендикулярные существующему ограждению, имеют длину [латекс]L[/латекс].
- Каких размеров она должна сделать свой сад, чтобы увеличить огороженную площадь?
Показать решение
Задача, которую мы решили выше, называется задачей оптимизации с ограничениями. Мы можем оптимизировать желаемый результат с учетом ограничения, которым в данном случае было ограниченное количество материалов для ограждения. Попробуйте сами в следующей задаче.
Попробуй
Как: Учитывая приложение, связанное с доходом, используйте квадратное уравнение, чтобы найти максимум.
- Напишите квадратное уравнение для дохода.
- Найдите вершину квадратного уравнения.
- Определите [latex]y[/latex]-значение вершины.
Пример: Определение максимального дохода
Цена за единицу товара влияет на его спрос и предложение. То есть, если цена за единицу растет, спрос на товар обычно снижается. Например, местная газета в настоящее время имеет 84 000 подписчиков при ежеквартальной оплате в размере 30 долларов.
Исследование рынка показало, что если владельцы поднимут цену до 32 долларов, они потеряют 5000 подписчиков. Предполагая, что подписка линейно связана с ценой, какую цену должна взимать газета за ежеквартальную подписку, чтобы максимизировать свой доход? 92-4ac[/latex]
Ключевые понятия
- Нули, или точки пересечения [latex]x[/latex], представляют собой точки, в которых парабола пересекает ось [latex]x[/latex]. Точка пересечения [latex]y[/latex] — это точка, в которой парабола пересекает ось [latex]y[/latex] — .
- Вершина может быть найдена из уравнения, представляющего квадратичную функцию.
- Минимальное или максимальное значение квадратичной функции определяется [latex]y[/latex]-значением вершины.
- Миниум или максимальное значение квадратичной функции можно использовать для определения диапазона функции и для решения многих видов реальных задач, включая задачи, связанные с площадью и доходом.
- Некоторые квадратные уравнения необходимо решать с помощью квадратной формулы.
