Как решать пределы с синусами и косинусами — Справочник
Задания с косинусами и синусами в егэ
Чтобы решать пределы с синусами и косинусами необходимо уметь выполнять элементарные преобразования под первый замечательный предел, а также знать основные тригонометрические формулы. Так же применимо правило Лопиталя для вычисления с помощью производной. Рассмотрим примеры решений.
Воспользуемся формулой первого замечательного предела $$ \lim_ \frac = 1 $$ Подстраиваем дробь под знаком предела путем элементарных преобразований. Одновременно умножаем и делим на 7 числитель со знаменателем: $$ \lim_ \frac = $$
Выносим множители из числителя и знаменателя за знак предела $$ = \frac \lim_ \frac = $$ Переворачиваем подпредельную дробь под вид общей формулы первого замечательного предела $$ = \frac \lim_ \frac = \frac \cdot 1 = \frac $$
Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!
Это поможет своевременно получить зачёт у преподавателя!
Используем тригонометрическую формулу разности косинусов: $$ \cos \alpha — \cos \beta = -2 \sin \frac \sin \frac $$
Выполняем преобразование разности косинусов в произведение синусов $$ \cos 3x — \cos x = -2 \sin \frac \sin \frac = -2 \sin x \sin 2x $$ Записываем предел с новым числителем $$ \lim_ \frac = $$
Разбиваем предел на два, чтобы воспользоваться первым замечательным пределом: $$ = -2\lim_ \frac \cdot \lim_ \frac = $$ Первый предел равен единице, поэтому остаётся разобраться со вторым. Подгоним его под формулу замечательного предела путем домножения числителя и знаменателя на число равное аргументу синуса $$ = -2 \lim_ \frac = -4 \lim_ \frac = -4 $$
В данном случае целесообразно прибегнуть к таблице эквивалентных элементарных функций, а именно $$ 1- \cos x = \frac $$
Подставляем в предел и получаем $$ \lim_ \frac = \lim_ \frac $$ Осталось выполнить сокращение числителя на знаменатель, чтобы записать ответ $$ \lim_ \frac = \frac $$
Подгоним его под формулу замечательного предела путем домножения числителя и знаменателя на число равное аргументу синуса -2 lim_ frac -4 lim_ frac -4.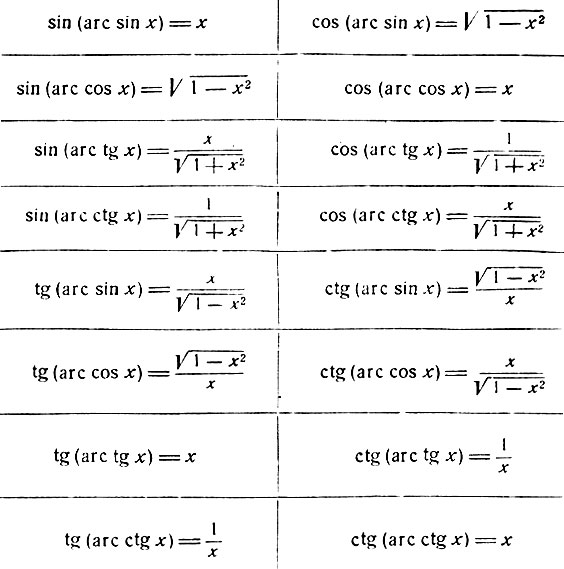
Xn—24-6kcaa2awqnc8dd. xn--p1ai
15.09.2020 7:29:36
2020-09-15 07:29:36
Источники:
Https://xn--24-6kcaa2awqnc8dd. xn--p1ai/predely-s-sinusami-i-kosinusami. html
ЕГЭ–2022, физика: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword { color: red; }
Задания с косинусами и синусами в егэ
Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!
—>
Задание 16 № 1838
При переходе луча света из одной среды в другую угол падения равен а угол преломления Каков относительный показатель преломления второй среды относительно первой? (Ответ округлить до сотых.)
Согласно закону преломления Снеллиуса, относительный показатель преломления второй среды относительно первой связан с синусами углов падения и преломления связаны с соотношением
—>
Задание 16 № 1838
За пи сы вай тесь на бес плат ное за ня тие.
Phys-ege. sdamgia. ru
05.08.2019 2:32:32
2019-08-05 02:32:32
Источники:
Https://phys-ege. sdamgia. ru/problem? id=1838
Замечательные отношения в прямоугольном треугольнике | Подготовка к ЕГЭ по математике » /> » /> .keyword { color: red; }
Задания с косинусами и синусами в егэ
Гипотенузой называется та сторона треугольника, что лежит против угла в 90 градусов, две оставшиеся стороны называются катетами прямоугольного треугольника.
Подробнее про прямоугольный треугольник здесь.
Синусом угла в прямоугольном треугольнике называется отношение противолежащего катета к гипотенузе.
Косинусом угла в прямоугольном треугольнике называется отношение прилежащего катета к гипотенузе.
Тангенсом угла в прямоугольном треугольнике называется отношение противолежащего катета к прилежащему.
Котангенсом угла
в прямоугольном треугольнике называется отношение прилежащего катета к противолежащему.
Бывает (и на ЕГЭ, ГИА), что приходится иметь дело с косинусами, синусами и тангенсами внешних углов треугольника. Формулы приведения позволяют увидеть, что есть еще и вот такая связь между смежными углами (помимо того, что их сумма равна 180):
Смотрите подборку задач на применение указанных соотношений в статье «Прямоугольный треугольник. Вычисление длин и углов» часть I, часть II.
Гипотенузой называется та сторона треугольника, что лежит против угла в 90 градусов, две оставшиеся стороны называются катетами прямоугольного треугольника.
Котангенсом угла в прямоугольном треугольнике называется отношение прилежащего катета к противолежащему.
Egemaximum. ru
19.09.2019 14:55:29
2019-09-19 14:55:29
Источники:
Https://egemaximum. ru/sinus-kosinus-tangens-v-pryamougolnom-treugolnike/
Чему эквивалентен sin x 2
Подставляем точку $x=0$ в предел и получаем неопределенность.
Замечаем под пределом две функции, для которых можно использовать формулы эквивалентных бесконечно малых функций. 2 = 0 $$
2 = 0 $$
Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!
В пределе получаем неопределенность ноль делить на ноль $[\frac]$. Замечаем, что числитель похож на формулу из таблицы эквивалентности пределов. Подставим в него точку $x=0$.
$$ 1- \cos (4 \cdot 0) = 1-\cos 0 = 1 — 1 = 0 $$
Получили, что числитель равен нулю при $x=0$, а это значит допустима замена на бесконечно малую функцию.
Возвращаемся к пределу, подставляя в него полученное выражение для числителя.
Подставив $x=1$ получаем неопределенность $[ \frac ] $. Замечаем, что в числителе присутствует синус, который есть в таблице эквивалентностей. По необходимому условию аргумент синуса должен стремиться к нулю, чтобы применить формулу эквивалентности. Проверим это подставив $x=1$ в него.
$$ \sin (1-1) = \sin 0 = 0 $$
Проверка показала, что формулу можно применить, так как аргумент равен нулю. 2 = (a-b)(a+b)$ для знаменателя упрощаем его.
2 = (a-b)(a+b)$ для знаменателя упрощаем его.
Как решать пределы с синусами и косинусами?
Чтобы решать пределы с синусами и косинусами необходимо уметь выполнять элементарные преобразования под первый замечательный предел, а также знать основные тригонометрические формулы. Так же применимо правило Лопиталя для вычисления с помощью производной. Рассмотрим примеры решений.
Воспользуемся формулой первого замечательного предела $$ \lim_ \frac = 1 $$ Подстраиваем дробь под знаком предела путем элементарных преобразований. Одновременно умножаем и делим на 7 числитель со знаменателем: $$ \lim_ \frac = $$
Выносим множители из числителя и знаменателя за знак предела $$ = \frac \lim_ \frac = $$ Переворачиваем подпредельную дробь под вид общей формулы первого замечательного предела $$ = \frac \lim_ \frac = \frac \cdot 1 = \frac $$
Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!
Это поможет своевременно получить зачёт у преподавателя!
Используем тригонометрическую формулу разности косинусов: $$ \cos \alpha — \cos \beta = -2 \sin \frac \sin \frac $$
Выполняем преобразование разности косинусов в произведение синусов $$ \cos 3x — \cos x = -2 \sin \frac \sin \frac = -2 \sin x \sin 2x $$ Записываем предел с новым числителем $$ \lim_ \frac = $$
Разбиваем предел на два, чтобы воспользоваться первым замечательным пределом: $$ = -2\lim_ \frac \cdot \lim_ \frac = $$ Первый предел равен единице, поэтому остаётся разобраться со вторым. Подгоним его под формулу замечательного предела путем домножения числителя и знаменателя на число равное аргументу синуса $$ = -2 \lim_ \frac = -4 \lim_ \frac = -4 $$
В данном случае целесообразно прибегнуть к таблице эквивалентных элементарных функций, а именно $$ 1- \cos x = \frac $$
Подставляем в предел и получаем $$ \lim_ \frac = \lim_ \frac $$ Осталось выполнить сокращение числителя на знаменатель, чтобы записать ответ $$ \lim_ \frac = \frac $$
Эквивалентность синуса
Для вычисления предела правой части воспользуемся непрерывностью логарифма и вторым замечательным пределом:
\[a = e \Rightarrow e^x — 1 \underset x\]
сделаем замену \(z = \log_a(1+x)\) и выразим \(x\) через \(z\) : \(x = a^z — 1\) . z — 1 \sim z\ln a\) при \(z \to 0\) . В этой формуле осталось лишь сменить обозначение переменного на
z — 1 \sim z\ln a\) при \(z \to 0\) . В этой формуле осталось лишь сменить обозначение переменного на
Бесконечно малые функции \(\alpha(x)\) и \(\beta(x)\) называются эквивалентными или равносильными бесконечно малыми одного порядка при \(x \to a\) , если:
Обозначают:
\(\alpha(x) \sim \beta(x)\) при \(x \to a\) или просто \(\alpha(x) \underset \beta(x)\)
Читайте также:
- Почему в planet zoo смотрители не кормят животных
- Titan quest токсей убийца как убивать
- Dead cells почему все открыто
- Где найти вампиров в ведьмаке 3
- Как сделать розу в колбе в майнкрафте
Ряд Фурье по ортогональной системе функций
№1 Ортогональные функции.
Две вещественные функции и на интервале называются ортогональными, если
Для
комплексных функций вводится комплексное
сопряжение одной
из функций под интегралом, для векторных
— скалярное
произведение функций
под интегралом, а также интегрирование
по отрезку заменяется на интегрирование
по области соответствующей размерности.
Полезным обобщением понятия ортогональности является ортогональность с определённым весом. Ортогональны с весом функции и , если
где — скалярное произведение векторов и — значений векторнозначных функций и в точке , — точка области , а — элемент её объёма (меры). Эта формула записана наиболее общим способом по сравнению со всеми выше. В случае вещественных скалярных , скалярное произведение следует заменить на обычное; в случае комплексных скалярных , : .
Определение. Функции j(х) и y(х), определенные на отрезке [a, b], называются ортогональными на этом отрезке, если
Определение. Последовательность функций j1(x), j2(x), …, jn(x), непрерывных на отрезке [a, b], называется ортогональной системой функций на этом отрезке, если все функции попарно ортогональны.
Отметим,
что ортогональность функций не
подразумевает перпендикулярности
графиков этих функций.
Определение. Система функций называется ортогональной и нормированной (ортонормированной), если
Определение. Рядом Фурье по ортогональной системе функций j1(x), j2(x), …,jn(x) называется ряд вида:
коэффициенты которого определяются по формуле:
,
где f(x) = — сумма равномерно сходящегося на отрезке [a, b] ряда по ортогональной системе функций. f(x) – любая функция, непрерывная или имеющая конечное число точек разрыва первого рода на отрезке [a, b].
[an error occurred while processing this directive]
В случае ортонормированной системы функций коэффициенты определяются:
№ 3 разложение в ряды фурье по системе косинусов и синусов
Разложение
в ряд Фурье по косинусам.
Ряд Фурье четной периодической функции f(x) с периодом 2π содержит только члены с косинусами (т.е. не содержит членов с синусами) и может включать постоянный член. Следовательно,
где коэффициенты ряда Фурье,
Разложение в ряд Фурье по синусам.
Ряд Фурье нечетной периодической функции f(x) с периодом 2π содержит только члены с синусами (т.е. не содержит членов с косинусами).
Следовательно,
где коэффициенты ряда Фурье,
№ 5 Предел ФКП. Непрерывность
ФКП. Производная ФКП. Условия
Каши-Римана. Предел
ФКП. Определение. Пусть
функция w = f(z)
определена в проколотой окрестности
точки z0 = x0 + iy0.
Комплексное число w0 = u0 + iv0 называется
пределом функции при z → z0,
если для любой ε-окрестности U(w0,
ε) (ε>0) точки w0 найдётся
такая проколотая δ-окрестность
точки z0,
что для всех
значения f(z)
принадлежат U(w0,
ε). Другими словами, если z0 —
собственная точка плоскости, то для
любого ε > 0 должно существовать такое
δ > 0, что из неравенства 0 < |z − z0|
< δ следует неравенство | f(z)
− w0|
< ε (аналогично расписывается определение
для несобственной точки z0 =
∞). Таким образом, на языке ε — δ определение
предела ФКП полностью совпадает с
определением предела функции одной
действительной переменной; обозначается
предел, как обычно:
.
Неравенство
| f(z)
− w0|
< ε означает, что |(u(x, y)
+ iv(x, y))
− (u0 + iv0)|
< ε, или |(u(x, y)
— u0)
+ i(v(x, y)
− v0)|
< ε.
Другими словами, если z0 —
собственная точка плоскости, то для
любого ε > 0 должно существовать такое
δ > 0, что из неравенства 0 < |z − z0|
< δ следует неравенство | f(z)
− w0|
< ε (аналогично расписывается определение
для несобственной точки z0 =
∞). Таким образом, на языке ε — δ определение
предела ФКП полностью совпадает с
определением предела функции одной
действительной переменной; обозначается
предел, как обычно:
.
Неравенство
| f(z)
− w0|
< ε означает, что |(u(x, y)
+ iv(x, y))
− (u0 + iv0)|
< ε, или |(u(x, y)
— u0)
+ i(v(x, y)
− v0)|
< ε. Для модуля комплексных чисел
справедливы все основные свойства
абсолютной величины, в частности
|z1 + z2|
≤ |z1|
+ |z2|,
поэтому |(u(x, y)
— u0)
+ i(v(x, y)
− v0)|
< ε
Отсюда
легко получить, что
.
Таким образом, существование предела
функции комплексной переменной
равносильно существованию пределов
двух действительных функций u(x, y)
и v(x, y)
двух действительных переменных. Поэтому
в комплексный анализ автоматически
переносятся все теоремы о пределах
функции в точке (предел суммы функций
и т.д.). Так же можно доказать, что если w0 =
|w0|·(cos
arg w0 + i sin
arg w0)
≠ 0, то
(для
существования нулевого предела
достаточно, чтобы
).
Для модуля комплексных чисел
справедливы все основные свойства
абсолютной величины, в частности
|z1 + z2|
≤ |z1|
+ |z2|,
поэтому |(u(x, y)
— u0)
+ i(v(x, y)
− v0)|
< ε
Отсюда
легко получить, что
.
Таким образом, существование предела
функции комплексной переменной
равносильно существованию пределов
двух действительных функций u(x, y)
и v(x, y)
двух действительных переменных. Поэтому
в комплексный анализ автоматически
переносятся все теоремы о пределах
функции в точке (предел суммы функций
и т.д.). Так же можно доказать, что если w0 =
|w0|·(cos
arg w0 + i sin
arg w0)
≠ 0, то
(для
существования нулевого предела
достаточно, чтобы
). .
.
Непрерывность ФКП. Пусть функция w = f (z) определена в окрестности точки z0 = x0 + iy0. Функция называется непрерывной в точке z0, если: 1. существует ; 2. Как и в случае предела, можно показать, что w = f(z) будет непрерывной в точке z0 = x0 + iy0 тогда и только тогда, когда функции u(x, y) и v(x, y) непрерывны в точке (x0, y0), поэтому на ФКП переносятся все основные теоремы о непрерывности функций.
Определение производной. Аналитичность ФКП. Пусть w = f(z) определена, однозначна и принимает собственные значения в окрестности точки z = x
 Производной функции w = f(z)
в точке z называется
предел
.
Функция, имеющая конечную производную
в точке z,
называется дифференцируемой в этой
точке.
В
этом определении важно, что стремление
Δz →
0 может проходить по любому пути. Как мы
увидим дальше, вследствие этого
обстоятельства существование
производной f’(z)
не сводится к существованию частных
производных функций u(x, y)
и v(x, y),
а требует некоторых дополнительных
условий. Сейчас мы дадим определение
основного в теории ФКП понятия
—аналитичности
функции в
точке и в области. Определение.
Однозначная функция называется аналитической
(регулярной, голоморфной) в
точке z,
если она дифференцируема в некоторой
окрестности этой точки.
Однозначная
функция называется аналитической в
области D, если
она аналитична в каждой точке этой
области.
Производной функции w = f(z)
в точке z называется
предел
.
Функция, имеющая конечную производную
в точке z,
называется дифференцируемой в этой
точке.
В
этом определении важно, что стремление
Δz →
0 может проходить по любому пути. Как мы
увидим дальше, вследствие этого
обстоятельства существование
производной f’(z)
не сводится к существованию частных
производных функций u(x, y)
и v(x, y),
а требует некоторых дополнительных
условий. Сейчас мы дадим определение
основного в теории ФКП понятия
—аналитичности
функции в
точке и в области. Определение.
Однозначная функция называется аналитической
(регулярной, голоморфной) в
точке z,
если она дифференцируема в некоторой
окрестности этой точки.
Однозначная
функция называется аналитической в
области D, если
она аналитична в каждой точке этой
области. Примеры. 1. f(z)
= z 2. В
этом случае f (z +
Δz)
= (z +
Δz)2 = z 2 +
2 z·Δz +
(Δz) 2;
. Таким
образом , эта функция дифференцируема
в любой точке, и её производная равна
2z. 2. f(z)
= | z |2 = x2 + y2. Докажем,
что эта функция не имеет производной
ни в какой точке
Примеры. 1. f(z)
= z 2. В
этом случае f (z +
Δz)
= (z +
Δz)2 = z 2 +
2 z·Δz +
(Δz) 2;
. Таким
образом , эта функция дифференцируема
в любой точке, и её производная равна
2z. 2. f(z)
= | z |2 = x2 + y2. Докажем,
что эта функция не имеет производной
ни в какой точке  В первом случае , во
втором . Эти
пределы равны, только если 2х =
−2iy ⇒ х = y =
0. Таким образом, функция f(z)
= | z |2 = x2 + y2 может
быть дифференцируема в единственной
точке z =
0, во всех остальных точках пределы
различны
в зависимости от способа стремления
Δz →
0, т.е.
не
существует.
В первом случае , во
втором . Эти
пределы равны, только если 2х =
−2iy ⇒ х = y =
0. Таким образом, функция f(z)
= | z |2 = x2 + y2 может
быть дифференцируема в единственной
точке z =
0, во всех остальных точках пределы
различны
в зависимости от способа стремления
Δz →
0, т.е.
не
существует. Условия
Коши-Римана (Даламбера-Эйлера).Сейчас
мы сформулируем и докажем важнейшую в
теории ФКП теорему о необходимых и
достаточных условиях дифференцируемости
(а, следовательно, аналитичности)
функции.
Для
того, чтобы функция w = f(z)
= u(x, y)
+ i v(x, y)
была дифференцируема в точке z = x + iy,
необходимо и достаточно, чтобы
функции u(x, y)
= Re f(z) и v(x, y)
= Im f(z)
были дифференцируемы в точке (х,у), и
чтобы в этой точке выполнялись
соотношения
. Доказательство. Необходимость. Здесь
мы применим идею, которой воспользовались,
когда доказывали, что функция f(z)
= | z |2 = x2 + y2 не
имеет производных в точках z ≠
0: подойдём к точке z двумя
путями — по направлениям Δz =
Δх (Δy =
0) и Δz = iΔy (Δx =
0).
В
первом случае: Δw =
(u(x +
Δx, y)
+ iv(x +
Δx, y))
− (u(x, y)
+ iv(x, y))
=
=
(u(x +
Δx, y)
− u(x, y))
+ i(v(x +
Δx, y)
− v(x, y))
= Δxu + iΔxv;
.
Доказательство. Необходимость. Здесь
мы применим идею, которой воспользовались,
когда доказывали, что функция f(z)
= | z |2 = x2 + y2 не
имеет производных в точках z ≠
0: подойдём к точке z двумя
путями — по направлениям Δz =
Δх (Δy =
0) и Δz = iΔy (Δx =
0).
В
первом случае: Δw =
(u(x +
Δx, y)
+ iv(x +
Δx, y))
− (u(x, y)
+ iv(x, y))
=
=
(u(x +
Δx, y)
− u(x, y))
+ i(v(x +
Δx, y)
− v(x, y))
= Δxu + iΔxv;
. Во
втором случае: (напомню, что
)
Δw =
(u(x, y +
Δy)
+ iv(x, y +
Δy))
− (u(x, y)
+ iv(x, y))
=
=
(u(x, y +
Δy)
− u(x, y))
+ i(v(x, y +
Δy)
− v(x, y))
= Δyu + iΔyv;
.
Пределы должны быть равны,
поэтому
. Достаточность. По
предположению теоремы, функции u(x, y), v(x, y)
дифференцируемы в точке (х,у),
поэтому
где
α(Δx,
Δy),
β(Δx,
Δy)
— бесконечно малые более высокого порядка
по сравнению с
,
т.
Во
втором случае: (напомню, что
)
Δw =
(u(x, y +
Δy)
+ iv(x, y +
Δy))
− (u(x, y)
+ iv(x, y))
=
=
(u(x, y +
Δy)
− u(x, y))
+ i(v(x, y +
Δy)
− v(x, y))
= Δyu + iΔyv;
.
Пределы должны быть равны,
поэтому
. Достаточность. По
предположению теоремы, функции u(x, y), v(x, y)
дифференцируемы в точке (х,у),
поэтому
где
α(Δx,
Δy),
β(Δx,
Δy)
— бесконечно малые более высокого порядка
по сравнению с
,
т. е.
,
.
Найдём
.
.
Последнее
слагаемое — бесконечно малая высшего
порядка по сравнению с Δz =
Δx + iΔy:
;
далее, в предыдущих слагаемых, пользуясь
формулами Коши-Римана, оставим только
частные производные по х,
т.е. заменим
на
,
на
;
тогда
.
Отсюда следует, что существует
,
т.е. функция дифференцируема в точке
(х,у).
Производная
дифференцируемой функции может находиться
по любой из формул
,
эти равенства следуют из условий
Коши-Римана. При вычислении производных
можно пользоваться всеми правилами
действительного анализа:
(в
точках, где g(z)
≠ 0.
е.
,
.
Найдём
.
.
Последнее
слагаемое — бесконечно малая высшего
порядка по сравнению с Δz =
Δx + iΔy:
;
далее, в предыдущих слагаемых, пользуясь
формулами Коши-Римана, оставим только
частные производные по х,
т.е. заменим
на
,
на
;
тогда
.
Отсюда следует, что существует
,
т.е. функция дифференцируема в точке
(х,у).
Производная
дифференцируемой функции может находиться
по любой из формул
,
эти равенства следуют из условий
Коши-Римана. При вычислении производных
можно пользоваться всеми правилами
действительного анализа:
(в
точках, где g(z)
≠ 0.
№ 7. Вычеты и их приложения. Основная теорема теории вычетов.
основная теорема о вычетах: если функция является аналитической всюду в замкнутой области , за исключением конечного числа изолированных особых точек , лежащих внутри , то
Пример:
Вычислить интеграл
.
Решение: Точка является особой для подынтегральной функции, причем, согласно классификации, это полюс третьего порядка. Тогда
и соответственно .
| 1 | Найти производную — d/dx | бревно натуральное х | |
| 2 | Оценить интеграл | интеграл натурального логарифма x относительно x | |
| 3 | Найти производную — d/dx | 92)||
| 21 | Оценить интеграл | интеграл от 0 до 1 кубического корня из 1+7x относительно x | |
| 22 | Найти производную — d/dx | грех(2x) | |
| 23 | Найти производную — d/dx | 9(3x) по отношению к x||
| 41 | Оценить интеграл | интеграл от cos(2x) относительно x | |
| 42 | Найти производную — d/dx | 1/(корень квадратный из х) | |
| 43 | Оценка интеграла 9бесконечность | ||
| 45 | Найти производную — d/dx | х/2 | |
| 46 | Найти производную — d/dx | -cos(x) | |
| 47 | Найти производную — d/dx | грех(3x) | 92+1|
| 68 | Оценить интеграл | интеграл от sin(x) по x | |
| 69 | Найти производную — d/dx | угловой синус(х) | |
| 70 | Оценить предел | ограничение, когда x приближается к 0 из (sin(x))/x 92 по отношению к х | |
| 85 | Найти производную — d/dx | лог х | |
| 86 | Найти производную — d/dx | арктан(х) | |
| 87 | Найти производную — d/dx | бревно натуральное 5х92 |
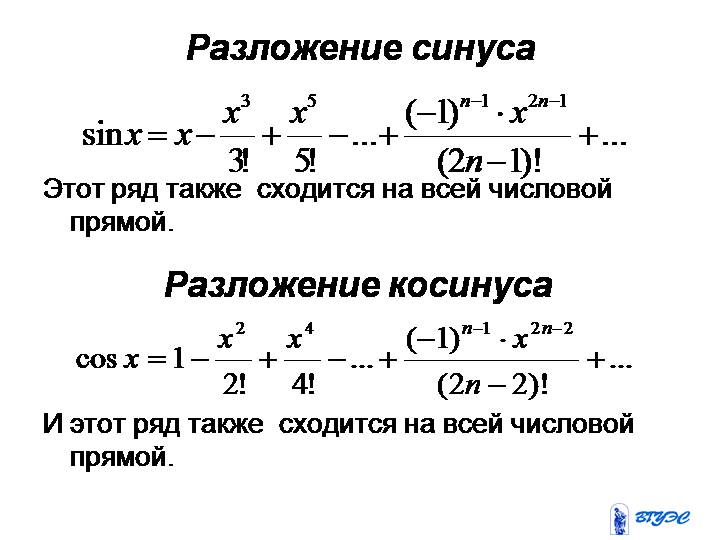
Производные тригонометрических функций
Производные тригонометрических функций В этом разделе я буду обсуждать пределы и производные триггера. функции. Сначала я рассмотрю важное правило ограничения, потому что я
использовать его в вычислении производной от .
функции. Сначала я рассмотрю важное правило ограничения, потому что я
использовать его в вычислении производной от .
Если вы рисуете и , вы видите, что графики становятся почти неразличимы рядом:
То есть как, . Этот аппроксимация часто используется в приложениях — например. анализ движение простого маятника при малых перемещениях. я буду использовать его, чтобы вывести формулы дифференцирования триг-функций.
С точки зрения пределов это приближение говорит
(Обратите внимание, что подстановка дает .) Для вывода требуется теорема о сжатии и немного геометрии. То, что я дам, на самом деле не является доказательством с первого раза. принципы; вы можете думать об этом как о аргументе, который делает результат правдоподобный.
Я нарисовал сектор, образующий угол внутри круга радиуса 1. (Я использую вместо x, так как чаще используется
для центрального угла.) Внутренний прямоугольный треугольник имеет высоту , а внешний прямоугольный треугольник имеет высоту . Длина дуги радиуса 1 и угла как раз .
Длина дуги радиуса 1 и угла как раз .
(Я нарисовал картинку так, как будто она неотрицательна. А аналогичный аргумент может быть приведен, если .)
Четко,
Разделить на:
Как , — просто подключите. По теореме сжатия,
Принимая взаимность, я получаю
Пример. Вычислить .
Подключение дает. я должен сделать еще немного работы.
\ деф \ квадрат {\ vbox {\ hrule \ hbox {\ vrule height1.5ex\hskip1.5ex\vrule}\hrule}}
Формула предела имеет вид
В этом примере . Для того, чтобы применить формула, мне нужна в нижней части дроби а также внутри синуса: они должны «совпадать». я не могу сделать много о внутренней части синуса, но я могу легко сделать внизу, используя алгебру:
Позволять . В качестве , . Так
Я часто опускаю замену, например . Как только я увижу, что у меня есть что-то вроде where , я знаю, что оно имеет предел 1.
Как только я увижу, что у меня есть что-то вроде where , я знаю, что оно имеет предел 1.
Пример. Вычислить .
Подключение дает.
Идея здесь состоит в том, чтобы создать термины вида , к которым я могу применить свой предел правило. Сначала я опишу шаги, которые я предприму, затем вычисление.
(a) Я преобразую тангенс в синус и косинус. Это потому что мое основное правило включает синус, и я также знаю, что как (поэтому косинус выражает не являются большой проблемой).
(b) Я разделю все члены сверху и снизу на x. Это при подготовке к вынесению условий формы.
(c) Я воспользуюсь приемом, который использовал ранее, чтобы исправить числа так, чтобы синус термины все имеют вид , где вещь внутри синуса и вещь на нижнее совпадение.
Вот вычисление:
Как , условия и оба
перейти к 1 по формуле предела синуса. С другой стороны, члены и оба стремятся к 1, так как и непрерывно.
Пример. (а) Вычислить .
(б) Вычислить.
(a) Подключение дает . Лимит может и не быть.
Идея состоит в том, чтобы использовать триггерную идентичность для преобразования косинусов в синусы, чтобы я мог использовать свой Формула предела синусов. Это как перемножить верх и низ дроби на сопряженную, чтобы упростить подкоренное выражение.
(b) Если вы нарисуете график рядом с графиком калькулятор или компьютер, вы, вероятно, получите необычные результаты. Вот картинка:
Проблема в том, что когда x близок к 0, оба и очень близки к 0 — производя перелив и недолив.
На самом деле предел прост: пусть . Когда , так
Для последнего шага я использовал результат предыдущей задачи.
Пример. Вычислить .
Если вы установите , вы получите . Вздох.
Я посмотрю, что я могу сказать по графику:
Похоже, что предел определен, и картинка наводит на мысль. что это около 3,5.
что это около 3,5.
Сначала я разобью тангенсы на синусы и косинусы:
Далее я заставлю форму появиться. Поскольку у меня есть и , мне нужно сделать и чтобы они соответствовали:
Теперь возьмем предел каждой части:
Предел произведения есть произведение пределов:
Производные триггерных функций.
Я начну с леммы, которая мне понадобится для вывода формул производных.
Лемма. .
Доказательство.
Предложение.
(а) .
(б) .
(с) .
(г) .
(е) .
(е) .
Доказательство. Чтобы доказать (а), я буду использовать предел синусов формула
Мне также понадобится формула сложения углов для синуса:
Позволять . затем
Первый член обращается в 0 по предыдущей лемме. Следовательно,
Следовательно,
То есть,
Чтобы вывести формулу косинуса, я буду использовать формулу сложения углов для косинуса:
Позволять . затем
Я не буду делать доказательства для оставшихся триггерных функций. Идея в том, написать
Затем вы можете использовать производные формулы для синуса и косинуса вместе с частным правилом или цепным правилом для вычисления производных.
В качестве примера я выведу формулу для косеканса:
Пример. Вычислите следующие производные.
(а) .
(б) .
(с) .
(г) .
(е) .
(а)
(б)
(с)
(г)
(е)
Пример. При каких значениях х есть касательная по горизонтали?
Так где . В диапазоне
, это происходит в . Итак, для , где n — любое целое число.
В диапазоне
, это происходит в . Итак, для , где n — любое целое число.
Контактная информация
Домашняя страница Брюса Икенаги
Copyright 2018 Брюс Икенага
Math Tutor — Функции — Теория
Math Tutor — Функции — Теория — Элементарные функцииЗдесь мы предполагаем, что вы знакомы с углами и как они измерено, в частности, с радиан . Если вы не уверены, вы можете посмотри на это примечание.
Существует несколько способов определения тригонометрических функций. Мы кратко вспомните два из них, основанные на геометрических представлениях. Тогда мы посмотрим на характеристики тригонометрических функций, вспомните некоторые триггер тождества, попробуйте сделать некоторые смысл их инверсий и заключаем с краткое примечание относительно секанса и косеканса.
Геометрические определения
Единица измерения. Пусть α — любой угол.
Рассмотрим единичный круг на плоскости и луч, идущий
от начала под углом α . Пусть ( x , y ) координаты пересечения луча и
единичный круг.
Затем мы определяем
Пусть ( x , y ) координаты пересечения луча и
единичный круг.
Затем мы определяем
Конечно, некоторые определения не имеют смысла, если 91 184 x 91 185 = 0, соответственно. г = 0,
Ясно, что тогда мы имеем
Функции sec( α ) (секанс) и csc( α ) (косеканс) был очень популярен в старые времена, когда людям еще приходилось вычислять вещи сами по себе, так как они упростили вычисления с помощью триггера функции. Сегодня они в основном забыты, и мы включаем их сюда для ради полноты. Мы вернемся к ним в конце этого раздела.
Обратите внимание, что при таком определении все эти функции 2π-периодический, при ближайшем рассмотрении тангенс и котангенс равны π-периодический.
Прямоугольный треугольник. Пусть α — угол от интервал (0,π/2). Рассмотрим произвольный прямоугольный треугольник с другой угол равен α . Тогда у нас есть следующие определения:
Эти функции связаны теми же формулами, что и выше. Как мы продлеваем
эти определения под любым углом α ? Сначала мы определяем
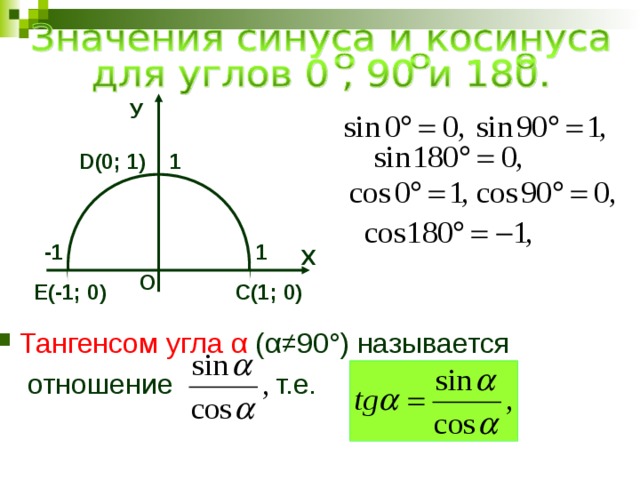
sin(0)=0,cos(0)=1,sin(π/2)=1,cos(π/2)=0,
Как мы продлеваем
эти определения под любым углом α ? Сначала мы определяем
sin(0)=0,cos(0)=1,sin(π/2)=1,cos(π/2)=0,
Для α от [π/2,π] мы определяем грех( α ) = sin(π − α ) а также cos( α ) = -cos(π — α ).
Для α от [п, 2п] мы определяем sin( α ) = -sin( α — π) а также cos( α ) = -cos(2π — α ).
Таким образом, мы получаем синус и косинус на [0,2π], то расширяем их для всех углов, повторяя этот основной период. Остальные функции могут быть все определяется с помощью синуса и косинуса и приведенных выше формул.
В заключение мы напомним значения синуса и косинуса для популярные ракурсы:
Eсть простой способ запомнить их, используя левая рука.
Еще одно практическое замечание, вместо того, чтобы писать
[sin( x )] n мы обычно пишем
sin n ( x ), аналогично для других триггерных функций.
Свойства тригонометрических функций
Синус. Домен:
D (sin) = &реал;.
График:
Функция непрерывна в своей области определения, 2π-периодический, ограниченный, и симметричным, а именно нечетным, так как имеем sin(- x ) = -sin( x ). У нас также есть
sin( x + π) = −sin( x ), sin( x + π/2) = cos( x ), sin( x — π/2) = −cos( x ).
Из периодичности имеем
sin( x + 2 k π) = sin( x ), грех( x + (2 k + 1)π) = −sin( x ).
Нулевыми точками синуса являются точки вида k π, где k — любое целое число; это также точки перегиба. Локальные экстремумы находятся в точках π/2 + k π.
Что касается пределов на концах области, пределов синуса на бесконечности и
отрицательной бесконечности не существует.
Производная:
[sin(x)]′ = cos(x).
Косинус. Домен:
D (cos) = &реал;.
График:
Функция непрерывна в своей области определения, 2π-периодическая, ограниченная, и симметричным, а именно четным, так как имеем cos(− x ) = cos( x ). У нас также есть
cos( x + π) = −cos( x ), cos( x + π/2) = −sin( x ), cos( x — π/2) = sin( x ).
Из периодичности имеем
cos( x + 2 k π) = cos( x ), cos( x + (2 k + 1)π) = −cos( x ).
Нулевые точки косинуса — это точки вида π/2 + 91 184 k 91 185 π, где k — любое целое число; это тоже точки перегиб. Локальные экстремумы находятся в точках к π.
Что касается пределов на концах области, пределов косинуса на бесконечности
и отрицательной бесконечности не существует.
Производная:
[cos( x )]′ = −sin( x ).
Тангенс. Домен:
График:
Функция непрерывна в своей области определения, π-периодическая, неограниченная, и симметричным, а именно нечетным, так как имеем загар (− x ) = −загар ( x ). У нас также есть
загар( x + π) = загар( x ), тангенс (π — 91 184 x 91 185 ) = — тангенс ( х ).
Нулевыми точками касательной являются точки вида к π, где к любое целое число; это также точки перегиба. нет местных экстремумы.
Что касается пределов на концах области, пределов касательной в бесконечности и отрицательная бесконечность не имеют смысла, так как домен не включает никаких окрестности бесконечности или отрицательной бесконечности. Пределы на конечных точках домена не существует, но у нас там односторонние лимиты:
Производная:
[tan( x )]’ = 1/cos 2 ( x ).
Котангенс. Домен:
График:
Функция непрерывна в своей области определения, π-периодическая, неограниченная, и симметричным, а именно нечетным, так как имеем детская кроватка(- x ) = -кроватка( x ). У нас также есть
детская кроватка( x + π) = детская кроватка( x ), раскладушка (π − х ) = — раскладушка ( х ).
Нулевыми точками котангенса являются точки вида π/2 + 91 184 k 91 185 π, где 91 184 k 91 185 — любое целое число; это также точки перегиба. Локальных экстремумов нет.
Что касается пределов на концах области, пределов котангенса на бесконечности и отрицательная бесконечность не имеют смысла, так как домен не включает никаких окрестности бесконечности или отрицательной бесконечности. Пределы на конечных точках домена не существует, но у нас там односторонние лимиты:
Производная:
[кроватка( x )]’ = -1/sin 2 ( x ).
Триггерные идентификаторы
Сначала некоторые популярные тождества для синуса и косинуса.
Следующие тождества менее популярны, но иногда они очень полезны.
Синус и косинус также можно получить (или даже определить) с помощью экспонент и комплексные числа.
Наконец, иногда этот трюк тоже полезен.
У нас очевидная проблема, когда C 2 = 0. Тогда мы можем взять φ = π/2 если C 2 > 0 а также φ = -π/2 если C 2 < 0,
Теперь некоторые популярные тождества для тангенса и котангенса.
Поскольку синус и косинус могут быть выражены с помощью комплексных экспонент, то одно и то же верно для тангенса и котангенса.
Наконец, мы покажем некоторые формулы, связывающие синус/косинус и тангенс.
Обратные тригонометрические функции
Когда мы смотрим на графики выше, мы сразу видим, что ни один из четырех основные триггерные функции 1-1, поэтому у них нет инверсий. С другой стороны, с практической точки зрения было бы чрезвычайно полезно нечто обратное, и действительно, люди приписывали углы сторонам треугольников задолго до математики придумали понятие обратного. Для этого правильно, мы используем обычный трюк, мы ограничим триггерные функции до интервалы, на которых они уже 1-1. Выберем интервалы так, чтобы они как можно больше (чтобы они покрывали весь диапазон), а также чтобы они давали «разумные» углы, т.е. около 0. Действительно, больше Практично узнать, что угол в треугольнике равен 30 градусам, а затем узнать что это 750 градусов (на самом деле мы должны использовать радианы, но градусы легче представить и напечатать в Интернете, поэтому здесь я сделал исключение).
Обратные тригонометрические функции. Они определяются следующим образом. Сначала мы ограничиваем четыре тригонометрические функции интервалами, как указано.
Сначала мы ограничиваем четыре тригонометрические функции интервалами, как указано.
Затем рассмотрим обратные к этим ограничениям. Они называются дуга синус (обозначается arcsin), арккосинус (обозначается arccos), arc тангенс (обозначается arctan) и арккотангенс (обозначается arccot). Графики этих функций здесь:
Перечислим теперь основные свойства этих обратных триггерных функций. Они есть все непрерывны, монотонны и ограничены.
Примечание: Многие авторы (и большинство производителей калькуляторов) на самом деле используют
другое обозначение, а именно sin -1 ( x ), cos -1 ( x ) и т. д. Это обозначение чрезвычайно вводит в заблуждение и
многие студенты действительно видят, по общему признанию, сильное сходство между
sin −1 ( x ) и, скажем,
грех 2 ( x ) для квадрата
синуса; логически они затем ожидают, что
грех -1 ( x ) есть
на самом деле 1/sin( x ). Конечно, обратному синусу и
1/sin( x )
это совсем разные функции. Хотя есть достаточно хороший
обоснование этого обозначения (см. наше изложение
обратные функции в теории —
Реальные функции), очень жаль из-за этих недоразумений.
Поскольку существует вполне приемлемая альтернатива, которая также широко известна,
а именно эти дуги, мы всегда будем использовать их здесь.
Конечно, обратному синусу и
1/sin( x )
это совсем разные функции. Хотя есть достаточно хороший
обоснование этого обозначения (см. наше изложение
обратные функции в теории —
Реальные функции), очень жаль из-за этих недоразумений.
Поскольку существует вполне приемлемая альтернатива, которая также широко известна,
а именно эти дуги, мы всегда будем использовать их здесь.
Примечание: Вернемся к исходному вопросу: нам дано число y , и мы хотим найти число х , удовлетворяющее, скажем, sin( x ) = y . Если это x из региона в которое мы только что ограничили синусом, то у нас есть решение 91 184 x 91 185 = arcsin( 91 184 y 91 185 ). Но что, если по какой-то причине нам нужно х из другой части реальной линии? Или взято из другую точку зрения, если мы ограничим синус другим разумным интервала, какова будет формула обратной функции к такому ограниченный синус? (И, конечно, косинус и т. д.) Следующие формулы верны:
Пусть sin( x ) = y .

Если 2 k π − π/2 ≤ x ≤ 2 k π + π/2 для некоторого целого числа k , тогдаx = arcsin( y ) + 2 k π.
Если (2 k + 1)π − π/2 ≤ x ≤ (2 k + 1)π + π/2 для некоторого целого числа k , тогда
x = (2 k + 1)π − arcsin( y ).
Пусть cos( x ) = y .
Если 2 k π ≤ x ≤ 2 k π + π для некоторого целого числа k , тогдаx = arccos( y ) + 2 k π.
Если (2 k + 1)π ≤ x ≤ (2 k + 1)π + π для некоторого целого числа k , тогда
x = (2 k + 2)π − arccos( y ).
Пусть tan( x ) = y .
Если k π − π/2 < x < k π + π/2 для некоторого целого числа k , тогдаx = arctan( y ) + k π.



