применив свойство значения логарифма с одинаковым основанием и подлогарифмическим числом, получим:
$=2 \cdot 1-\lg e=2-\lg e$.
Ответ: $\lg \frac{100}{e}=2-\lg e$.
Сообщество экспертов Автор24
Автор этой статьи Дата последнего обновления статьи: 20.07.2022
Подготовка школьников к ЕГЭ (Справочник по математике — Алгебра
| Справочник по математике | Алгебра | Логарифмы |
| Определение логарифма, основное логарифмическое тождество |
| Свойства логарифмов |
| Использование свойств логарифмов при решениии логарифмических уравнений и неравенств |
| Десятичные логарифмы и натуральные логарифмы |
Определение логарифма, основное логарифмическое тождество
Рассмотрим два произвольных действительных числа a и b, удовлетворяющих условиям
| (1) |
Определение.
Логарифмом числа b по основанию a называют такую степень, в которую надо возвести число a, чтобы получить число b.
Другими словами, логарифм числа b по основанию a – это такое число x, которое является решением уравнения
| a x= b . | (2) |
Доказательство того, что решение уравнения (2) существует и единственно, выходит за рамки школьной программы.
Для логарифма числа b по основанию a используется обозначение:
loga b .
Таким образом, для всех действительных чисел a и b, удовлетворяющих условиям (1), справедливо равенство
которое часто называют основным логарифмическим тождеством.
Замечание. Обратим особое внимание на то, что при решении уравнения (2) мы ищем показатель степени, а при решении уравнения
x a = b.
мы ищем основание степени, которое вычисляется по формуле
и в случае, когда a – натуральное число, является корнем натуральной степени из числа b.
Пример 1. Решить уравнение
x3 = 81 .
Решение. Воспользовавшись понятием кубического корня и свойствами степеней, получаем
Ответ: .
Пример 2. Решить уравнение
3x= 81 .
Решение. Воспользовавшись тем, что число 81 является четвертой степенью числа 3 , получаем:
Ответ: 4 .
Задача. Доказать, что число
log2 3
иррационально.
Решение. Предположим противное, т.е. предположим, что указанное число рационально. Тогда существует несократимая дробь
,
числитель и знаменатель которой являются натуральными числами и такая, что справедливо равенство:
Из определения логарифма отсюда вытекает равенство:
следствием которого является равенство:
2m= 3n .
Но последнее равенство невозможно, поскольку его левая часть четное число, а правая – нечетное. Полученное противоречие доказывает требуемое в задаче утверждение.
Свойства логарифмов
Перечисленные ниже свойства логарифмов вытекают из основного логарифмического тождества:
(основное свойство логарифмов), | |
(основное свойство логарифмов), | |
(формула перехода к новому основанию логарифмов), | |
(основное свойство логарифмов), |
(основное свойство логарифмов), |
(формула перехода к новому основанию логарифмов), |
Использование свойств логарифмов при решении логарифмических уравнений и неравенств
Для того, чтобы не ошибаться при решении логарифмических уравнений и неравенств, свойства логарифмов, перечисленные в предыдущем разделе, следует применять внимательно и аккуратно.
Например, если при решении уравнения или неравенства требуется преобразовать выражение
loga ( f (x)2 ) ,
то вместо формулы
следует применять формулу
поскольку в противном случае можно потерять корни.
По той же причине при преобразовании выражений
loga ( f (x) g (x)) и
следует использовать формулы:
и
Замечание. Желающим усовершенствовать свои знания и умения при решении уравнений и неравенств с логарифмами мы рекомендуем ознакомиться с нашими учебными пособиями «Решение логарифмических уравнений» и «Решение логарифмических неравенств».
Десятичные логарифмы и натуральные логарифмы
В математике, физике и во многих других областях естествознания и технологий важное место занимают десятичные логарифмы и натуральные логарифмы.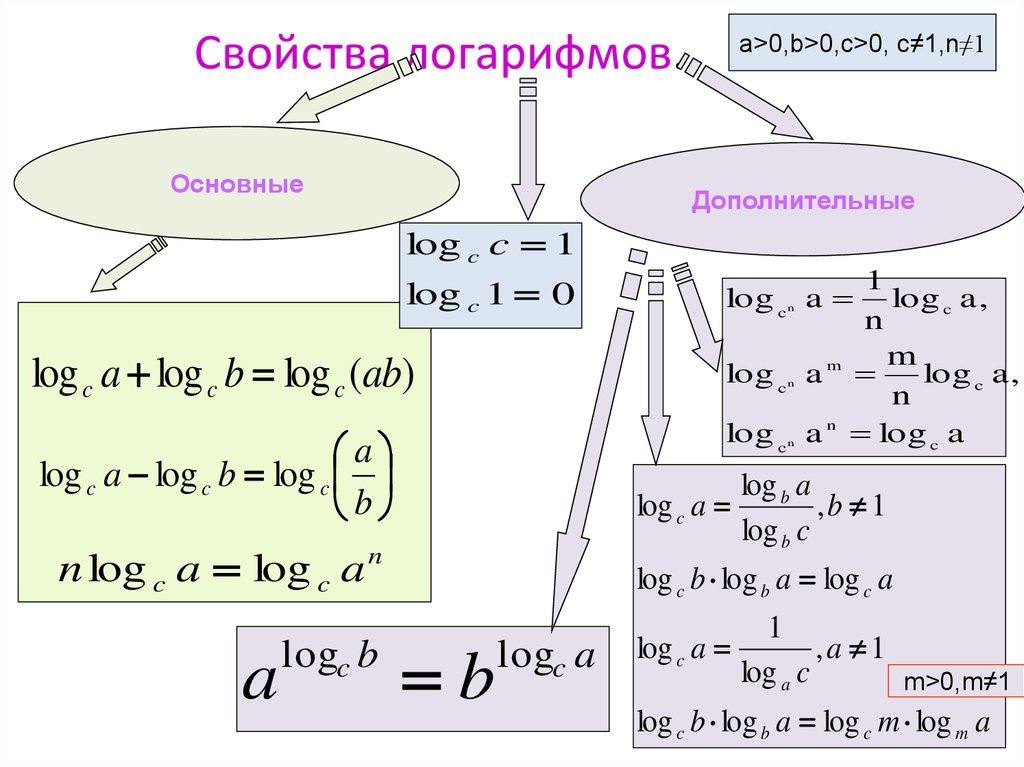
Десятичные логарифмы – это логарифмы с основанием 10, а основанием натуральных логарифмов является иррациональное и трансцендентное число e, которое определяется по формуле
доказательство которой выходит за рамки школьной программы.
Для десятичных и натуральных логарифмов используются соответственно обозначения:
lg b и ln b,
причем
lg e = 0,43429…,
ln 10 = 2,30259…
Графики логарифмических функций представлены в разделе «Графики степенных, показательных и логарифмических функций» нашего справочника.
На сайте можно также ознакомиться с нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
Десятичный логарифм | это… Что такое Десятичный логарифм?
Десятичный логарифм — логарифм по основанию 10.
Другими словами, десятичный логарифм числа есть решение уравнения
Десятичный логарифм числа существует, если Принято (спецификация ISO 31-11) обозначать его . Примеры:
В зарубежной литературе, а также на клавиатуре калькуляторов встречаются и другие обозначения десятичного логарифма: , причём следует иметь в виду, что первые 2 варианта могут относиться и к натуральному логарифму.
Содержание
|
Алгебраические свойства
В нижеследующей таблице предполагается, что все значения положительны[1]:
| Формула | Пример | |
|---|---|---|
| Произведение | ||
| Частное от деления | ||
| Степень | ||
| Корень |
Существует очевидное обобщение приведенных формул на случай, когда допускаются отрицательные переменные, например:
Формула для логарифма произведения без труда обобщается на произвольное количество сомножителей:
Вышеописанные свойства объясняют, почему применение логарифмов (до изобретения калькуляторов) существенно облегчало вычисления.
- Найти в таблицах логарифмы чисел .
- Сложить эти логарифмы, получая (согласно первому свойству) логарифм произведения .
- По логарифму произведения найти в таблицах само произведение.
Деление, которое без помощи логарифмов намного более трудоёмко, чем умножение, выполнялось по тому же алгоритму, лишь с заменой сложения логарифмов на вычитание. Аналогично производились возведение в степень и извлечение корня.
Связь десятичного и натурального логарифмов[2]:
Знак логарифма зависит от логарифмируемого числа: если оно больше 1, логарифм положителен, если оно между 0 и 1, то отрицателен. Пример:
Чтобы унифицировать действия с положительными и отрицательными логарифмами, у последних целая часть (
Мантисса логарифма, выбираемая из таблиц, при таком подходе всегда положительна.
Функция десятичного логарифма
Если рассматривать логарифмируемое число как переменную, мы получим функцию десятичного логарифма: . Она определена при всех . Область значений: . График этой кривой часто называется логарифмикой[3].
Функция монотонно возрастает, непрерывна и дифференцируема всюду, где она определена. Производная для неё даётся формулой:
Ось ординат является левой вертикальной асимптотой, поскольку:
Применение
Логарифмы по основанию 10 до изобретения в 1970-е годы компактных электронных калькуляторов широко применялись для вычислений. Как и любые другие логарифмы, они позволяли многократно упростить и облегчить трудоёмкие расчёты, заменяя умножение на сложение, а деление на вычитание; аналогично упрощались возведение в степень и извлечение корня. Но десятичные логарифмы обладали преимуществом перед логарифмами с иным основанием: целую часть логарифма числа ( характеристику логарифма) легко определить.
- Если то на 1 меньше числа цифр в целой части числа . Например, сразу очевидно, что lg 345 находится в промежутке (2, 3).
- Если то ближайшее к целое (в меньшую сторону) равно общему числу нулей в перед первой ненулевой цифрой, взятому со знаком минус. Например, lg 0,0014 находится в интервале (-3, -2).
Кроме того, при переносе десятичной запятой в числе на разрядов значение десятичного логарифма этого числа изменяется на Например:
Отсюда следует, что достаточно составить таблицу мантисс (дробных частей) десятичных логарифмов для чисел в диапазоне от 1 до 10. Такие таблицы, начиная с XVII века, выпускались большим тиражом и служили незаменимым расчётным инструментом учёных и инженеров.
Поскольку применение логарифмов для расчётов с появлением вычислительной техники почти прекратилось, в наши дни десятичный логарифм в значительной степени вытеснен натуральным[4]. Он сохраняется в основном в тех математических моделях, где исторически укоренился — например, при построении логарифмических шкал.
| Число | логарифм | характеристика | мантисса | запись |
|---|---|---|---|---|
| n | lg(n) | C = floor(lg(n) ) | M = (lg(n) − характеристика) | |
| 5 000 000 | 6.698 970… | 6 | 0.698 970… | 6.698 970… |
| 50 | 1.698 970… | 1 | 0.698 970… | 1.698 970… |
| 5 | 0.698 970… | 0 | 0.698 970… | 0.698 970… |
| 0.5 | −0.301 029… | −1 | 0.698 970… | 1.698 970… |
| 0.000 005 | −5.301 029… | −6 | 0.698 970… | 6.698 970… |
Обратите внимание, что у всех приведенных в таблице чисел одна и та же мантисса.
Десятичная логарифмическая шкала на логарифмической линейке
История
Первые таблицы десятичных логарифмов опубликовал в 1617 году оксфордский профессор математики Генри Бригс для чисел от 1 до 1000, с восемью (позже — с четырнадцатью) знаками.
Поэтому за рубежом десятичные логарифмы часто называют
В России первые таблицы логарифмов были изданы в 1703 году при участии Л. Ф. Магницкого[6]. В СССР выпускались несколько сборников таблиц логарифмов[7]:
- Брадис В. М. Четырехзначные математические таблицы. М.: Дрофа, 2010, ISBN 978-5-358-07433-0. Таблицы Брадиса, издаваемые с 1921 года, использовались в учебных заведениях и в инженерных расчётах, не требующих большой точности. Они содержали мантиссы десятичных логарифмов чисел и тригонометрических функций, натуральные логарифмы и некоторые другие полезные расчётные инструменты.
- Вега Г. Таблицы семизначных логарифмов, 4-е издание, М.: Недра, 1971. Профессиональный сборник для точных вычислений.
Литература
- Теория логарифмов
- Выгодский М. Я. Справочник по элементарной математике. — изд. 25-е. — М.: Наука, 1978. — ISBN 5-17-009554-6
- Корн Г., Корн Т. Справочник по математике (для научных работников и инженеров). — М.: Наука, 1973. — 720 с.
- Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления. — изд. 6-е. — М.: Наука, 1966. — 680 с.
- История логарифмов
- Клейн Ф. Элементарная математика с точки зрения высшей. — М.: Наука, 1987. — Т. I. Арифметика. Алгебра. Анализ. — 432 с.
- Математика XVII столетия // История математики / Под редакцией А. П. Юшкевича, в трёх томах. — М.: Наука, 1970. — Т. II.
- Математика XVIII столетия // История математики / Под редакцией А. П. Юшкевича, в трёх томах. — М.: Наука, 1972. — Т. III.
- Успенский Я. В. Очерк истории логарифмов. — Петроград: Научное книгоиздательство, 1923. — 78 с.
Ссылки
- Десятичные (бригсовы) логарифмы. (англ.)
(англ.)Примечания
- ↑ Выгодский М. Я. Справочник по элементарной математике, 1978, с. 187.
- ↑ Выгодский М. Я. Справочник по элементарной математике, 1978, с. 189.
- ↑ Логарифмическая функция. // Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1982. — Т. 3.
- ↑ Клейн Ф. Элементарная математика с точки зрения высшей, 1987, с. 406.
- ↑ История математики, том II, 1970, с. 62.
- ↑ Гнеденко Б. В. Очерки по истории математики в России, издание 2-е.. — М.: КомКнига, 2005. — С. 66.. — 296 с. — ISBN 5-484-00123-4
- ↑ Логарифмические таблицы //Большая советская энциклопедия.
Пример: решение логарифмов в уме
Решите [латекс]у={\матрм{лог}}_{4}\влево(64\вправо)[/латекс] без использования калькулятора.
Показать решение
Попробуйте
Решите [латекс]y={\mathrm{log}}_{121}\left(11\right)[/latex] без использования калькулятора.
Показать решение
Пример: вычисление логарифма обратной калькулятор.
Показать решение
Попробуйте
Оцените [латекс]y={\mathrm{log}}_{2}\left(\frac{1}{32}\right)[/latex] без использования калькулятора.
Показать решение
Использование натуральных логарифмов
Наиболее часто используемым основанием для логарифмов является e . База e логарифмы важны в вычислениях и некоторых научных приложениях; они называются натуральных логарифмов . Основание e логарифм, [латекс]{\mathrm{log}}_{e}\left(x\right)[/latex], имеет собственное обозначение, [латекс]\mathrm{ln}\left(x \справа)[/латекс].
Большинство значений [латекс]\mathrm{ln}\left(x\right)[/latex] можно найти только с помощью калькулятора.
{y}=x[/latex] 9{\ mathrm {ln} \ left (x \ right)} = x [/latex] для [латекс] x> 0 [/ латекс].
Как: Имея натуральный логарифм вида [латекс]у=\mathrm{ln}\left(x\right)[/latex], оцените его с помощью калькулятора+
- Нажмите [LN] .
- Введите значение, данное для x , а затем [)] .
- Нажмите
Пример: вычисление натурального логарифма с помощью калькулятора
Вычислите [latex]y=\mathrm{ln}\left(500\right)[/latex] с точностью до четырех знаков после запятой с помощью калькулятора.
Показать решение
Попробуйте
Оценить [латекс]\mathrm{ln}\left(-500\right)[/latex].
Показать решение
Поддержите!
У вас есть идеи по улучшению этого контента? Мы будем признательны за ваш вклад.
Улучшить эту страницуПодробнее
Значимые цифры
Значимые цифры Ненулевые целые числа всегда считаются значащими цифрами. | 511 | 3 ст.ф. |
| Начальные нули это нули, которые предшествуют всем ненулевым цифрам. Они не считаются значительными цифрами. | 0,0025 | 2 ст.ф. |
| Закрепленные нули нули между ненулевыми цифрами. Эти всегда считают значащими цифрами. | 1008 1,008 | 4 п/ф 4 ст.ф. |
| Нули в конце нули в правом конце числа. В целом предполагается, что они значимы только в том случае, если число содержит десятичную точку или они указаны как значимые в вопросе. | 100 1,00 100. 102. | 1 ст.ф. 3 ст.ф. 3 ст.ф. 3 ст.ф. |
| Точные цифры не получаются с помощью измерительных приборов, а определяются путем подсчета или определения (как коэффициенты пересчета) и не влияют на количество значащих цифр в результате расчета. | 10 испытаний 8 молекул 1 г = 100 кг 1 дюйм = 2,54 см | бесконечная н.ф. |
Умножение или деление. Количество значащих цифр в результате совпадает с числом в наименее точном измерении, используемом в расчете. | 99.11.11=89.198919892…=89,2 | 3 ст.ф. |
| Сложение или вычитание. Результат имеет то же количество десятичных знаков, что и наименее точное измерение, использованное в расчете. | 99,1+1,1543=100,2543=100,3 | 1 десятичный |
| Логарифм. При логарифмировании числа оставляйте справа от запятой столько значащих цифр, сколько значащих цифр в исходном числе. Например, log 4,000 (4 ст.ф.) = 0,6021 (4 ст.ф. справа от запятой). | pH раствора с H+=3,44M: pH=-logH+=-log3,44=3,463 | 3,44 имеет три sf, поэтому 3,463 сообщается с точностью до трех знаков после запятой. |
| Антилогарифмы; рН. И наоборот, при логарифмировании числа результат должен иметь такое же количество значащих цифр, как и количество значащих знаков после запятой в основном значении. Например, антилогарифм 0,0334 (3 ст.ф. справа от запятой) = 1,08 (3 ст.ф.). | Н+ в растворе с рН 2,55: Н+=10-2,55=2,8×10-3 | 2,55 имеет два десятичных знака, поэтому 2,8 сообщается с двумя значащими цифрами. |
Округление ответов. Используйте только первую цифру справа от последней значащей цифры. Если эта цифра равна 5 или больше, округлите последнюю значащую цифру в большую сторону (от нуля). | Округление до двух значащих цифр: 6,597=6,6 6,547=6,5 6,019=6,0 |
| Важно отложить округление до завершения всех вычислений. По крайней мере, одна дополнительная цифра помимо значащих цифр должна использоваться во всех вычислениях, чтобы избежать ошибки округления. Округляйте только окончательный ответ до правильного количества значащих цифр. |
| Как рассчитать вопрос, требующий, чтобы все цифры (или как минимум одна дополнительная цифра) учитывались при расчете: |
Образец бензола C6H6 имеет массу 4,25 грамма. 4,25 г × 1 моль 78,11 г × 6,022 × 1023 молекул моль = 5,441045 × 10-2 моль × 6,022 × 1023 молекул моль =3,276597×1022=3,28×1022 молекулы |
| В этом примере показано, как переносить значащие цифры в расширенные вычисления, где может потребоваться сообщить округленные промежуточные значения. (Вы должны переносить полные значения между шагами, но если ваш калькулятор не позволяет переносить, перенесите хотя бы одну дополнительную цифру.) |
Образец бензола, C6H6 имеет массу 4,25 грамма. Молярная масса =78,11 г/моль. (а) Сколько молей C6H6 есть в образце? 4,25 г × 1 моль78,11 г = 5,441045 × 10-2 моль = 5,44 × 10-2 моль (b) Сколько молекул C6H6 есть в образце? N=6,022×1023 5,441045×10-2моль×6,022×1023молекулмоль=3,276597×1022=3,28×1022молекул (c) Каково общее число атомов в образце? Каждая молекула C6H6 содержит 6 атомов C + 6 атомов H = всего 12 атомов. 3,276597 × 1022 молекул × 12 атомов 1 молекула = 3,931917 × 1023 = 3,93 × 1023 атомов 3 ст. |
Молярная масса = 78,11 г/моль. Сколько молекул C6H6 в образце? N=6,022×1023
12.6: Решение экспоненциальных и логарифмических уравнений
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 50019
- OpenStax
- OpenStax
Цели обучения
К концу этого раздела вы сможете:
- Решать логарифмические уравнения, используя свойства логарифмов
- Решение показательных уравнений с использованием логарифмов 9{2}−5x+6=0\).
Если вы пропустили эту проблему, просмотрите пример 6. 45. - Решите: \(x(x+6)=2x+5\).
Если вы пропустили эту проблему, просмотрите пример 6.47. - Ответ
\(х=6\)
- Ответ
\(х=4\)
- Ответ
\(х=4\)
- Ответ
\(х=8\)
- Ответить
\(х=3\)
- Ответить
\(x=\frac{\log 98}{\log 8} \приблизительно 2,205\)
- Ответить
\(x=\frac{\ln 5}{2} \приблизительно 0,805\)
- Ответить
\(г \ок 9,3 \%\)
- Ответить
\(г \около 11,9 \%\)
9{k t}\)- Ответить
Будет \(62 500\) бактерий.
- Ответить
Будет \(5 870 061\) бактерий.
- Ответить
Остается \(6,43\) мг.
- Ответить
Остается \(31,5\) мг.
- Решение логарифмических уравнений
- Решение логарифмических уравнений
- Нахождение скорости или времени в словесной задаче на экспоненциальный рост или затухание
- Нахождение скорости или времени в словесной задаче на экспоненциальный рост или затухание
- Свойство взаимно однозначного логарифмического уравнения: Для \(M>0, N>0, a>0\) и \(a≠1\) любое действительное число:
Если \(\log _{a} M=\log _{a} N,\), то \(M=N\)
- Сложные проценты: 9{г т}\).
45.Решение логарифмических уравнений с использованием свойств логарифмов
В разделе, посвященном логарифмическим функциям, мы решили некоторые уравнения, переписав уравнение в экспоненциальной форме. Теперь, когда у нас есть свойства логарифмов, у нас есть дополнительные методы, которые мы можем использовать для решения логарифмических уравнений.
Если наше уравнение имеет два логарифма, мы можем использовать свойство, которое говорит, что если \(\log _{a} M=\log _{a} N\), то верно, что \(M=N\). Это однозначное свойство логарифмических уравнений .
Определение \(\PageIndex{1}\)
Однозначное свойство логарифмических уравнений
Для \(M>0,N>0,a>0\) и \(a≠1\) любое действительное число:
Если \(\log _{a} M=\log _{a} N,\), то \(M=N\).
Чтобы использовать это свойство, мы должны быть уверены, что обе части уравнения записаны с одним и тем же основанием.
9{2} & \stackrel{?}{=}\log _{5} 81 \\ \log _{5} 81 & =\log _{5} 81\end{aligned}\)
Упражнение \(\ PageIndex{1}\)
Решите: \(2 \log _{3} x=\log _{3} 36\)
Упражнение \(\PageIndex{2}\)
Решить: \(3 \log x=\log 64\)
Еще одна стратегия, используемая для решения логарифмических уравнений, состоит в том, чтобы сжать суммы или разности в единый логарифм. 9{2}-8 х-9\)
Коэффициент.
\(0=(x-9)(x+1)\)
Использовать свойство нулевого произведения
\(x-9=0, \quad x+1=0\)
Решить каждое уравнение.
\(x=9, \quad \cancel{x=-1}\)
Проверить. \(x=-1\)
\(\begin{aligned} \log _{3} x+\log _{3}(x-8)&=2 \\ \log _{3}(-1) +\log _{3}(-1-8) &\stackrel{?}{=}2\end{aligned}\)
Мы не можем взять журнал отрицательного числа.
Чек. \(x=9\)
\(\begin{align} \log _{3} x+\log _{3}(x-8) &=2 \\ \log _{3} 9+\log _{3}(9-8) & \stackrel{?}{=} 2 \\ 2+0 &\stackrel{?}{=}2 \\ 2 &=2 \end{aligned}\)
Упражнение \(\PageIndex{3}\)
Решить: \(\log _{2} x+\log _{2}(x-2)=3\)
Упражнение \(\PageIndex{4}\)
Решить: \(\log _{2} x+\log _{2}(x-6)=4\)
Когда с обеих сторон есть логарифмы, мы сжимаем каждую сторону в один логарифм. Не забудьте использовать свойство Power по мере необходимости. 9{2}+4 x-5=0\)
Коэффициент.
\((x+5)(x-1)=0\)
Использовать свойство нулевого произведения.
\(x+5=0, \quad x-1=0\)
Решите каждое уравнение.
\(\cancel{x=-5}, \quad x=1\)
Проверить.
Мы оставляем вам чек.
Упражнение \(\PageIndex{5}\)
Решите: \(\log (x+2)-\log (4 x+3)=-\log x\).
Упражнение \(\PageIndex{6}\) 9{х}=98\). Найдите точный ответ и аппроксимируйте его до трех знаков после запятой.
Когда мы логарифмируем обе части, мы получаем один и тот же результат независимо от того, используем ли мы десятичный или натуральный логарифм (попробуйте использовать натуральный логарифм в последнем примере. Вы получили тот же результат?) Когда экспонента имеет основание \ (e\), мы используем натуральный логарифм.
9{2x}=25\). Найдите точный ответ и аппроксимируйте его до трех знаков после запятой.Использование экспоненциальных моделей в приложениях
В предыдущих разделах мы смогли решить некоторые приложения, которые моделировались с помощью экспоненциальных уравнений.
{r t } \end{выровнено}\) 9{17 r}\)
Используйте свойство Power.
\(\ln 5=17 r \ln e\)
Упростить.
\(\ln 5=17 r\)
Разделите каждую сторону на \(17\).
\(\frac{\ln 5}{17}=r\)
Приблизительный ответ.
\(r \примерно 0,095\)
Преобразование в проценты.
\(r \примерно 9,5\%\)
Им нужно, чтобы скорость роста была примерно \(9,5\)%.
Упражнение \(\PageIndex{11}\)
Гектор инвестирует $\(10 000\) в возрасте \(21\). Он надеется, что инвестиции будут стоить $\(150 000\), когда ему исполнится \(50\). Если проценты начисляются непрерывно, какой примерно темп роста ему потребуется для достижения своей цели?
Упражнение \(\PageIndex{12}\)
Рэйчел инвестирует $\(15 000\) в возрасте \(25\). Она надеется, что инвестиции будут стоить $\(90 000\), когда ей исполнится \(40\). Если проценты начисляются непрерывно, какой примерно темп роста ей потребуется для достижения цели?
Теперь мы можем решать приложения, которые дают нам достаточно информации для определения скорости роста.
Затем мы можем использовать эту скорость роста для прогнозирования других ситуаций.
Пример \(\PageIndex{7}\)
Исследователи зафиксировали рост определенной популяции бактерий с \(100\) до \(300\) за \(3\) часов. При такой скорости роста сколько бактерий будет через \(24\) часов с начала эксперимента?
Решение :
Эта проблема требует двух основных шагов. Сначала мы должны найти неизвестную скорость \(k\). Затем мы используем это значение \(k\), чтобы найти неизвестное количество бактерий. 9{3 k}\)
Используйте свойство Power.
\(\ln 3=3 k \ln e\)
Упростить.
\(\ln 3=3 k\)
Разделите каждую сторону на \(3\).
\(\frac{\ln 3}{3}=k\)
Приблизительный ответ.
\(k \приблизительно 0,366\)
Мы используем эту скорость роста, чтобы предсказать количество бактерий, которое будет через \(24\) часа.
\(\begin{align} A &=? \\ A_{0} &=100 \\ k &=\frac{\ln 3}{3} \\ t &=24 \text {часы} \\ A &=A_{0} e^{k t} \end{aligned}\) 9{\frac{\ln 3}{3} \cdot 24}\)
Вычислить.
\(A \примерно 656 100\)
При такой скорости роста можно ожидать \(656 100\) бактерий.
Упражнение \(\PageIndex{13}\)
Исследователи зафиксировали рост определенной популяции бактерий с \(100\) до \(500\) за \(6\) часов. При такой скорости роста сколько бактерий будет через \(24\) часов с начала эксперимента?
Упражнение \(\PageIndex{14}\)
Исследователи зафиксировали, что популяция определенных бактерий уменьшилась с \(700 000\) до \(400 000\) через \(5\) часов после введения лекарства. При такой скорости разложения сколько бактерий останется \(24\) часов с начала эксперимента?
Радиоактивные вещества распадаются или разлагаются по формуле экспоненциального распада. Время, за которое вещество распадается до половины своего первоначального количества, называется 9-м.
0077 период полураспада вещества.
Как и в предыдущем примере, мы можем использовать данную информацию для определения константы распада, а затем использовать эту константу для ответа на другие вопросы.
Пример \(\PageIndex{8}\)
Период полураспада радия-226 составляет \(1590\) лет. Сколько от \(100\) мг образца останется через \(500\) лет?
Решение :
Эта проблема требует двух основных шагов. Сначала мы должны найти постоянную затухания \(k\). Если мы начнем с \(100\)-мг, в период полураспада останется \(50\)-мг. Мы будем использовать эту информацию, чтобы найти \(k\). Затем мы используем это значение \(k\), чтобы найти объем выборки, который останется через \(500\) лет. 9{\frac{1 \mathrm{n} 0,5}{1500} \cdot 500}\)
Вычислить.
\(A \приблизительно 80,4 \mathrm{мг}\)
Через \(500\) лет останется приблизительно \(80,4\) мг.
Упражнение \(\PageIndex{15}\)
Период полураспада магния-27 составляет \(9,45\) минут.
Сколько \(10\) мг образца останется через \(6\) минут?
Упражнение \(\PageIndex{16}\)
Период полураспада радиоактивного йода составляет \(60\) дней. Сколько \(50\) мг образца останется через \(40\) дней?
Доступ к этим онлайн-ресурсам для получения дополнительных инструкций и практики решения экспоненциальных и логарифмических уравнений.
