Решение логической задачи: методы, примеры, идеи как научить детей решать задачи и головоломки

Содержание

Page not found — Сайт skobelevserg!

Главная
Информатика
Практикумы
Подготовка к ОГЭ
Рабочие программы
Используемая литература
Об авторах

Unfortunately the page you’re looking doesn’t exist (anymore) or there was an error in the link you followed or typed. This way to the home page.

Главная
Информатика
- 5 класс (ФГОС)
- - Информация вокруг нас
  - Компьютер — универсальная машина для работы с информацией
  - Ввод информации в память компьютера
  - Управление компьютером
  - Хранение информации
  - Передача информации
  - Кодирование информации
  - Текстовая информация
  - Представление информации в виде таблиц
  - Наглядные формы представления информации
  - Компьютерная графика
  - Обработка информации
- 6 класс (ФГОС)
- - Объекты окружающего мира
  - Компьютерные объекты
  - Отношения объектов и их множеств
  - Разновидности объектов и их классификация
  - Системы объектов
  - Персональный компьютер как система
  - Как мы познаем окружающий мир
  - Понятие как форма мышления
  - Информационное моделирование
  - Знаковые информационные модели
  - Табличные информационные объекты
  - Графики и диаграммы
  - Схемы
  - Что такое алгоритм
  - Исполнители вокруг нас
  - Формы записи алгоритмов
  - Типы алгоритмов
  - Управление исполнителем Чертежник
  - Компьютерный практикум
- 7 класс (ФГОС)
- - Информация и информационные процессы
  - Компьютер универсальное устройство для работы с информацией
  - Обработка графической информации
  - Обработка текстовой информации
  - Технология мультимедиа
- 8 класс (ФГОС)
- - Математические основы информатики
  - Основы алгоритмизации
  - Начала программирования
- 9 класс (ФГОС)
- - Моделирование и формализация
  - Алгоритмизация и программирование
  - Обработка числовой информации в электронных таблицах
  - Коммуникационные технологии
- 10 класс (ФГОС)
- - Информация и информационные процессы
  - Компьютер и его программное обеспечение
  - Представление информации в компьютере
  - Элементы теории множеств и алгебры логики
  - Современные технологии создания и обработки информационных объектов
- 11 класс (ФГОС)
- - Обработка информации в электронных таблицах
  - Алгоритмы и элементы программирования
  - Информационное моделирование
  - Сетевые информационные технологии
  - Основы социальной информатики
Практикумы
- Google формы
- Основы работы в Microsoft PowerPoint
- Создание анимации в презентациях
- Основы работы в Microsoft Word
- Основы работы в Microsoft Excel
- Создание простейшей базы данных
- Практикум по MS Excel
Подготовка к ОГЭ
Рабочие программы
Используемая литература
Об авторах
- Блоги
- Сайты

Способы решения логических задач.

Метод рассуждений

Значит остается другой случай: истинно Б_Х. Этот случай приводит к цепочке умозаключений:
Б_Х истинно, следовательно Б_М ложно, следовательно В_Т истинно, следовательно А_Т ложно, следовательно Г_Ч истинно, следовательно В_Б ложно, следовательно А_М истинно.

Ответ: Откровеннее был китайский министр, осторожнее — российский, скрытнее — министр США.

Пример 4. Разбитое стекло

Три школьника, Миша (М), Коля (К) и Сергей (С), остававшиеся в классе на перемене, были вызваны к директору по поводу разбитого в это время окна в кабинете. На вопрос директора о том, кто это сделал, мальчики ответили следующее:

Миша: «Я не бил окно, и Коля тоже…»

Коля: «Миша не разбивал окно, это Сергей разбил футбольным мячом!»

Сергей: «Я не делал этого, стекло разбил Миша».

Стало известно, что один из ребят сказал чистую правду, второй в одной части заявления соврал, а другое его высказывание истинно, а третий оба факта исказил.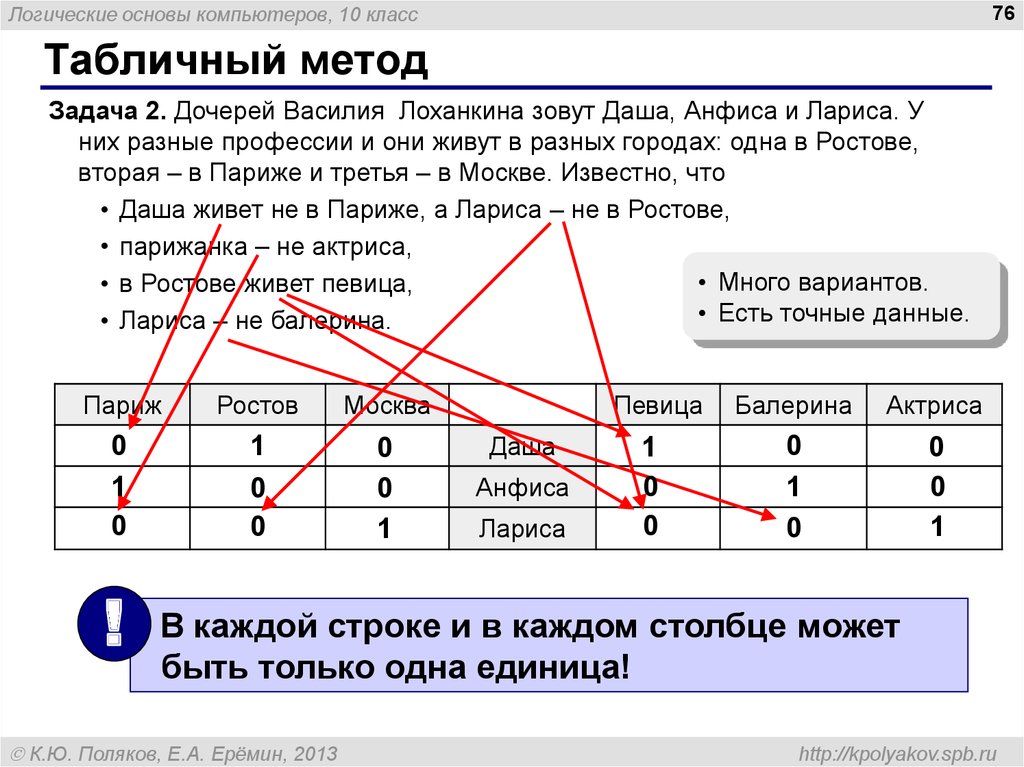 Зная это, директор смог докопаться до истины.

Кто разбил стекло в классе?

Решение. Начнем рассуждение с того, что Миша не может быть неправ в обоих своих высказываниях, потому что в этом случае получится, что стекло разбили одновременно и Миша, и Коля.

Значит, Миша говорит правду или полуправду.

1. Если Миша говорит правду, то стекло однозначно разбил Сергей.

Тогда остается два варианта — лжет либо Коля, либо Сергей.

2. Допустим, лжет Коля. Тогда из его высказываний следует, что стекло разбил Миша. Несоответствие у Коли с Мишей.

3. Допустим, лжет Сергей. Тогда из его высказываний следует, что стекло разбил он, а Миша не бил. Пока все логично. Допустим, Коля лжет в своем первом утверждении, но тогда стекло разбил Миша, а не Сергей. Что-то не сходится.

Допустим, Коля лжет в своем втором утверждении, но тогда стекло разбил сам Коля. Не годится…

Итак, ситуация несколько прояснилась — Миша не лжет, но и правды не говорит.

Значит, он прав только наполовину.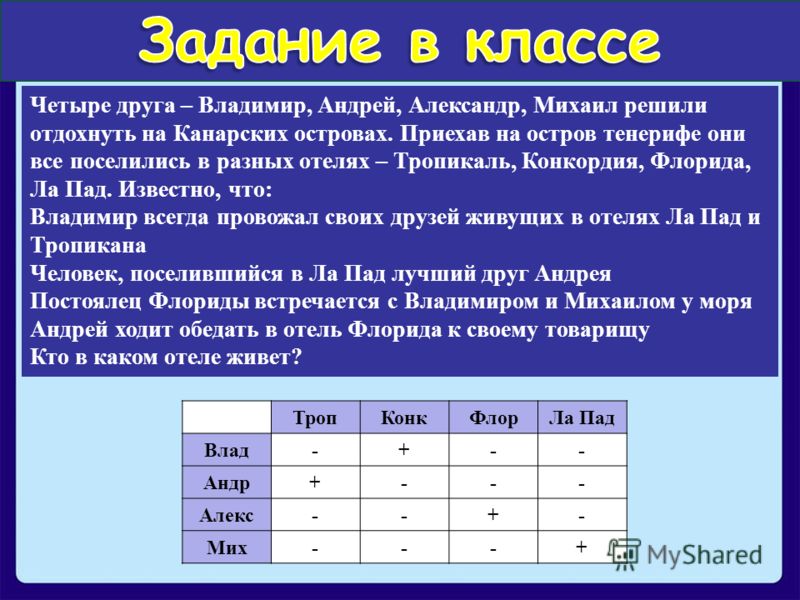

· Допустим, на первую. Тогда стекло разбил Коля.

Но из высказываний Коли, что бы он ни говорил — правду или ложь, никак не следует, что стекло разбил Коля. Этот вариант отпал.

·Остался последний вариант: Миша говорит правду только во втором своем высказывании.

Из этого следует, что стекло разбил собственно он.

И дальше все просто — Коля лжет, а Сергей говорит чистую правду.

Ответ: стекло разбил Михаил

Пример 5. Четыре подруги — Маша, Полина, Ольга и Наташа — участвовали в соревнованиях по бегу и заняли первые четыре места.

Установите, какое место заняла каждая девушка, если известно, что в каждом из приведенных ниже ответов, которые дали

девушки опоздавшему к финишу корреспонденту, верной является лишь половина.

Наташа: «Ольга была второй, а Полина — первой».

Маша: «Нет, Наташа. Ольга была первой, а второй была ты».

Ольга: «Да, что вы, девочки! Маша была третьей, а Полина прибежала четвертой».

Решение. Начнём рассуждение с предположения: 1. Пусть в ответе Наташи первое утверждение истинное, а второе — ложное, т. е. Ольга — вторая, Полина не первая.

2. Так как Ольга — вторая (по предположению), то в ответе Маши первое утверждение ложное, а второе истинное, т. е. Наташа — вторая. Но вторая — Ольга (по предположению).

Получили противоречие, значит, наше предположение неверно.

Тогда предположим, что

1. в ответе Наташи первое утверждение — ложное, а второе — истинное, т. е. Ольга не вторая, Полина — первая.

2. Так как Полина — первая (по предположению), то в ответе Маши первое утверждение — ложное, а второе — истинное, т. е. Ольга не первая, Наташа — вторая.

3. Так как Полина — первая (по предположению), то в ответе Ольги второе утверждение — ложное, а первое — истинное, т. е. Маша была третьей. Тогда сама Ольга была четвертой.

Решение логических задач

Роберт Лами, Prentice Hall 2002, 0-13-061882-9

(Перефразировано; примеры добавлены для пояснения)

a.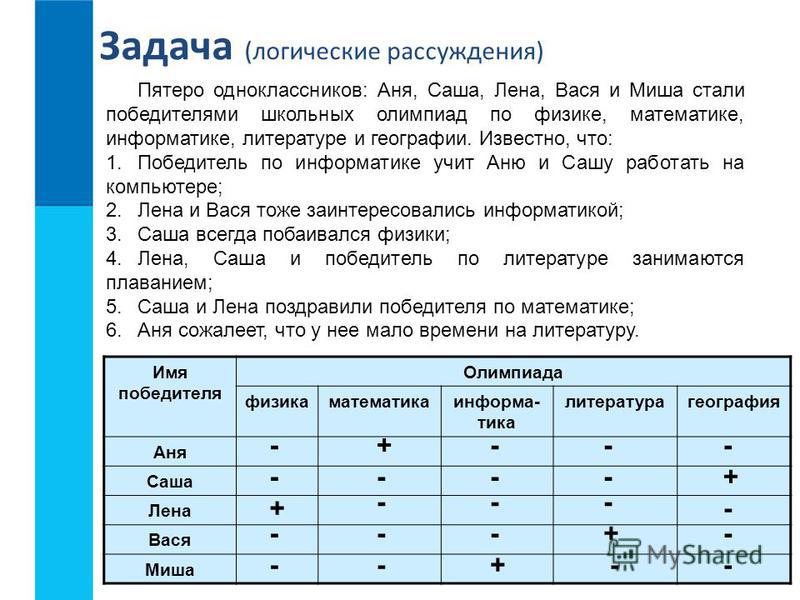 Быть ясно, с какой информацией вам предстоит работать.

б. Быть ясно о том, какую информацию вы пытаетесь обнаружить.

Пример: определить шт. за доллар , учитывая дату и время , стоимость за вес , возраст продавца , и штук на вес .

Обратите внимание на единицы измерения. Если единица измерения сохраняется с каждым числом, математическая операция быть выполненным будет очевидным без знания какой-либо формулы. Правильный операции приведут к отмене единиц. Неправильные действия приведут к единицы, которые соединяются и смешиваются.

Пример: получить расстояние из скорость и время , где скорость в километрах в час и время в часах. Скорость умножить на время дает расстояние (км/ч * ч км)

По возможности оформить картина.

Пример: направить вывод grep в more :

группа		\|		больше	дисплей
источник	стандартный вывод	труба	стандартный	пункт назначения	стандартный вывод

Вместо работы с начало проблемы спрашивать, какой первый шаг к концу, начать в конце и спросите, что нужно для выполнения последнего шага. Оттуда осмотр что необходимо для предпоследнего шага и работы к началу.

Пример: напишите команду, которая имеет некоторые параметры «тире», за которыми следует имя входного файла, за которым следует вывод имя файла, например:

команда 1 2 3 infile outfile

Outfile всегда равно argv[argc 1] и в файле есть всегда по адресу argv[argc 2] . Все между argv[1] и argv[argc 3] включительно (если там вообще ничего нет) должны быть все варианты тире.

При приближении к проблема ищите повторные операции. Сколько раз операция повторение обычно не имеет значения.

Пример: преобразовать десятичное целое число в двоичное для вывести (и учитывать также Правило 4):

BEGIN

ПОЛУЧИТЬ положительное целое число конвертировать

ПОКА номер не ноль

правый бит = остаток по модулю 2

ЕСЛИ правый бит равен нулю

УСТАНОВИТЬ следующий крайний правый символ = ‘0’

ELSE

УСТАНОВИТЬ следующий самый правый char = ‘1’

Номер = номер / 2

Конец, пока

Результат дисплея

Конец

, когда заинтересована. повторяющиеся операции, четко понимать, какие операции повторяются и принадлежат внутри циклической структуры и какие операции происходят только один раз и должны быть вне петли.

Пример: суммируйте целые числа от 1 до некоторого потолка:

Begin

для 1 до потолка

Получить потолок OOPS

Общая сумма oOp

Всего ПЕЧАТЬ

КОНЕЦ ДЛЯ

КОНЕЦ

Когда проблема слишком сложно решить, рассмотрите возможность ограничения задачи, чтобы найти частный случай решение.

Пример: рассчитать высоту здания по сбросив предмет с крыши и рассчитывая время его падения, пока не услышите, как он ударился о земля. Игнорировать изменения местной гравитации, сопротивление воздуха при падении, ветер силы и скорости звука при ударе.

При осмотре общего Проблема часто более информативна для работы с конкретным экземпляром. Ан пример с числовыми значениями всегда легче понять, чем общий случай.

Пример: вычислить факториал числа ( 1 x 2 x N ). Протестируйте свое решение (сначала PDL) с несколькими числами, такими как 3, 5, 10 и 20. Проверьте граничные случаи насколько малы и насколько велики п быть?

При точном решении слишком сложно вычислить, приблизительный ответ произвольной точности может часто можно найти, добавляя термины, которые еще больше приближают частичное решение к верное решение.

Пример: рассчитать p (пи) до определенного числа цифры с максимально возможной точностью. Решение состоит в том, чтобы найти, что формула ниже (среди прочего) становится все ближе и ближе к значению p как больше члены добавляются к сумме:

p = 4 * ( 1 1/3 + 1/5 1/7 + )

См. также Правило 5, так как петля будет работать довольно хорошо здесь (и проверьте также Правило 15).

а. Сделайте разумное начальное предположение.

б. Проверьте правильность предположения.

в. Неоднократно уточняйте предположение, пока не будет достигнута желаемая точность. достигнуто.

Пример: вычислить квадратный корень числа, сделав догадка, возведение в квадрат догадки и измерение ее ошибки, затем корректировка догадки и повторять до тех пор, пока результат не будет «достаточно близок» к правильному ценить.

Этот метод был впервые описан мне в 1961 году как «способ, которым компьютеры вычисляют квадратные корни» программиста на древний (ныне) компьютер IBM 650 в Оттавском университете.

По мере того, как проблем становится больше сложной становится все более важным разделить логику на более мелкие единицы, решающие отдельные части задачи. Эти единицы соответствуют функции программирования.

Пример: ни один сегмент кода не должен превышать один или, возможно, 2 экрана. Выберите самодостаточные фрагменты, которые возвращают один или несколько получается из небольшого количества аргументов, так что каждая часть (функция) может быть проверено самостоятельно и полностью понято с относительной легкостью.

Когда ничего не помогает, попробуйте систематически рассматривая все возможные решения.

Пример: многие алгоритмы сортировки полагаются на сравнение каждого и каждые пары элементов, чтобы переставить их в желаемый порядок.

Если выписка предполагается истинным, а затем приводит к выводу, противоречащему какому-либо известному факту, исходное предположение должно быть ложным. Если утверждение считается ложным и приводит к выводу, противоречащему какому-то известному факту, исходному предположению должно быть правдой. Все сценарии реального мира должны быть непротиворечивыми.

Пример: приложение для расчета площади пола жилого дома в тысячи квадратных метров, вероятно, завышенные расчеты, но если это офисная башня и всего сотни квадратных метров, то, скорее всего, это будет заниженный расчет.

Когда вероятности или шансы должны быть рассчитаны, грубая сила обычно может быть применена путем моделирования сценарий и подсчет того, сколько раз происходит интересующее событие.

Пример: если подбросить монету миллиард раз (1 000 000 000) сколько раз выпадает решка? А для цикла и случайного числа Генератор хорошо справляется с этим.

Ищите приближения которые упрощают задачу, но не влияют заметно на точность решение.

Пример: значение p что-то близкое, но большее, чем 3,141592653589793239462643, но 3,14159265 вероятно, достаточно близко для большинства целей большую часть времени.

При обобщении решение, охватывающее больший диапазон, большую сложность, более широкие условия, или большей полезности, сосредоточьтесь на различиях между условиями, когда решение работает и новые условия.

Пример: рабочий раствор не обязательно переписан, чтобы добавить еще одну функцию. На самом деле, очень практично написать решение в несколько шагов, начиная с очень ограниченной реализации и добавление дополнительных функций (и сложности) на хорошо спланированных этапах, тестирование (и делать резервные копии!) на каждом этапе.

Проблема может быть решена рекурсивно если :

а. Заключительный шаг или базовое условие известны.

б. Первый шаг задачи приводит точно к такому же проблема, но на один шаг ближе к решению.

Пример: рекурсия (вызов функции через и так далее) — это хорошо известный метод вычисления факториалов или других математические значения, для обхода бинарных деревьев и для многих других программ. проблемы.

Это правило было оставлено до последнего, потому что без других правил нет отправной точки, ничего записать, нечего пробовать.

Что следует попробовать при столкновении с новой проблемой?

Перепишите проблему.

Перечислите доступную информацию.

Нарисуй картинку.

Придумайте конкретный пример.

Ограничьте проблему.

Ищите повторяющиеся операции.

Изучите единицы.

Попробуйте решить задачу в обратном порядке.

Попробуйте угадать ответ.

Попробуйте перебором проложить путь к ответу.

Попробуйте симуляцию.

Создайте объект [или структуру].

Попробуйте рекурсию.

Но сделайте что-нибудь !

Логического решения проблем никогда не бывает достаточно

Каждый день мы сталкиваемся с проблемами, требующими решения, как личными, так и организационными. Чем сложнее проблема, тем больше мы должны быть уверены, что у нас есть надежный способ анализа того, что не так, чтобы мы могли найти и эффективно реализовать подходящее решение. Это может показаться очевидным, но сколько лиц, принимающих решения, на самом деле проходят через структурированный мыслительный процесс для принятия решений? Сколько решений являются просто результатом встреч, разговоров, мнений, предубеждений и компромиссов?

Сложное человеческое взаимодействие: потребности и желания

Любой, кто думает, что логики достаточно для решения проблем, не понимает человеческого познания. (И любой, кто думает, что мыслительный процесс означает логику, должен больше заниматься искусством. ) Человеческое взаимодействие всегда сложно, потому что мы состоим из очень многих элементов. Мы до сих пор не до конца понимаем взаимодействие синапсов, гормонов, разума, тела и духа. Однако фундаментальный вклад в разработку процесса принятия решений внес доктор Эли Голдратт. Он смог увидеть, что любую ситуацию, когда необходимо принять решение, можно представить как две конфликтующие позиции. Эти позиции существуют только потому, что они защищают две фундаментальные потребности человека: с одной стороны, потребность в контроле (сдерживание), с другой, потребность в видении (рост). Когда мы создаем решения, они должны полностью защищать эти две потребности, чтобы быть полными. Компромисс не нужен, когда мы можем поднять наше мышление и решать проблемы и принимать решения на более высоком уровне.

Контроль и зрение

Доктор Голдратт был физиком, но он также происходил из семьи ученых, изучавших Талмуд (и сам он очень хорошо в нем разбирался). Действительно, когда Доменико Лепоре, наш основатель, тоже физик, спросил Голдрата, что он может сделать, чтобы глубже понять Теорию ограничений, Голдратт ответил: «Изучайте Талмуд».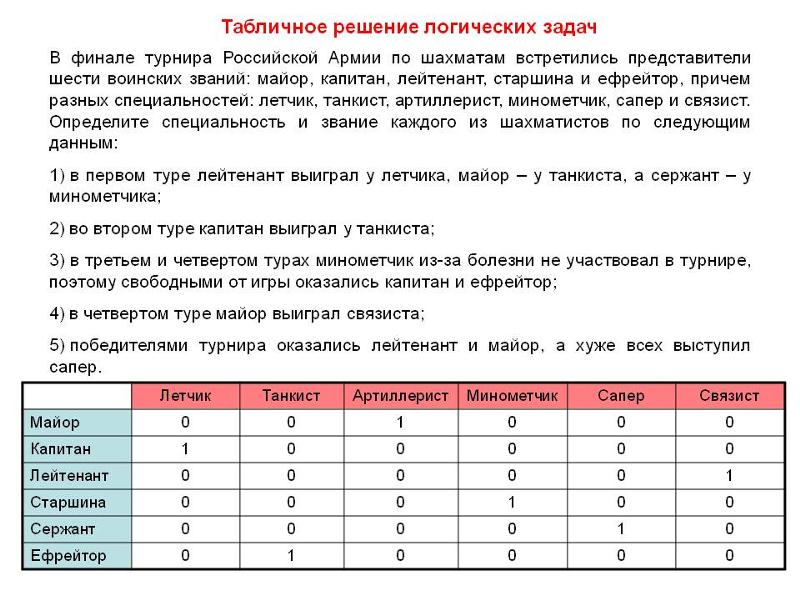 ученых в Нью-Йорке, чтобы принять вызов, поднятый Голдраттом. Мы бы сказали, что весьма вероятно, что, когда Голдрат вывел две потребности контроля и видения для своих Инструментов мыслительного процесса, он имел в виду концепции, которые на иврите означают «Гвура» (ограничение) и «Хесед» (любовь, сострадание). Эти два элемента всегда глубоко присутствуют в человеческом мышлении и взаимодействии и должны быть в равновесии. Когда мы осознаем это, мы можем сделать наши мыслительные процессы для принятия решений и разрешения конфликтов намного более эффективными и удовлетворительными.

Помимо решения логических задач – научиться мыслить

То, что Голдрат дал нам в своих инструментах процесса мышления, представляет собой чрезвычайно сложный и в то же время простой образец для системного мышления. Он позволяет нам всегда видеть общую картину, соединять точки и поднимать наши рассуждения на более высокий уровень, где не должно существовать компромиссов. Описывать эти инструменты как «логические инструменты», как это делают некоторые практики, значит упускать суть; он сводит инструменты Теории ограничений к технике без понимания лежащего в основе мышления непрерывного прорыва, роста и единства. Подчеркивая потребности в контроле и видении, Голдратт позволяет нам фильтровать нашу логику И эмоции с помощью точного шаблона, который приводит нас к надежным, подходящим для всего человека решениям. Он также предоставил нам инструменты для создания, мониторинга и планирования действий, необходимых для практического применения надежных решений.

Если невозможно эффективно применить стратегию для изменения реальности в желаемом направлении, нет смысла искать «решение». (Мы оставляем это консультантам, которые пишут отчеты.)

Подпишитесь на наш блог здесь и переключите свое мышление на более широкие, системные возможности для себя.

Об авторе

Анджела Монтгомери Ph.D. является партнером и соучредителем Intelligent Management и автором бизнес-роман+ веб-сайт Человеческое ограничение . В этом загружаемом романе используется повествование, чтобы посмотреть, как Деминг подход и Теория ограничений могут создать организацию будущего, основанную на сотрудничестве 4 903 8 и социальных инновациях.