Презентация на тему «Решение уравнений, содержащих модуль» по математике для 9 класса
Пояснительная записка
Урок алгебры и начал анализа по теме « Решение уравнений, содержащих модуль» проводится в четвёртой четверти при проведении уроков повторения для учащихся 11-класса.
Это урок обобщения и систематизации знаний с элементами исследования и организации проектной деятельности.
В течение урока используется режим смены динамических поз (работа сидя — стоя).
Урок рассчитан на класс, в котором есть дети с математическими способностями. На уроке проводится совместная работа в группах над проектом. Это является прекрасной возможностью дать шанс каждому школьнику проявить свою творческую индивидуальность. Учащиеся с разным уровнем подготовки могут участвовать в работе над проектом.
Одни учащиеся решают более простые задания, другие более сложные.
Урок – проект ценен тем, что учащиеся учатся самостоятельно добывать знания, учатся анализировать, обобщать, сопоставлять факты, делать выводы и заключения.
�
Тема: « Решение уравнений, содержащих модуль».
Урок алгебры и начал анализа в 10 классе.
Мартышова Людмила Иосифовна
учитель математики МОУ — СОШ №6 г. Маркса.
Вид урока: урок – проект.
Тип урока: обобщение и систематизация знаний с элементами исследования и организации проектной деятельности.
Технологии: проблемно- исследовательского обучения, проектного обучения, здоровьесберегающие по профилактике нарушений опорнодвигательной системы.
Цели урока:
Образовательные: обобщить и систематизировать знания учащихся о модуле и его свойствах; умения решать различные уравнения, содержащие модуль и уравнения, приводимые к уравнениям, содержащим модуль.
Развивающие: развивать творческую и мыслительную деятельность учащихся, навыки проектно-исследовательской деятельности, способствовать формированию навыков коллективной работы, развивать умение чётко и ясно излагать свои мысли.
Воспитательные: формирование интереса к предмету посредством вовлечения их в проектную деятельность, способствовать формированию навыков взаимодействия в малых группах.
Оборудование: компьютер, проектор, экран, кодоскоп, кодопозитивы, карточки – задания, инструкция о работе над проектом, информационные мини-проекты учащихся.
Ход урока.
Оргмомент.
Сообщение темы и цели урока. (В течение урока будет использоваться режим смены динамических поз).
Актуализация опорных знаний.
1.Повторение теоретического материала о модуле и его свойствах:
( Используются информационные мини — проекты учащихся).
— Дайте определение модуля.
— Объясните геометрический смысл модуля.
— Назовите свойства модуля.
— Чему равен
?
— Чему равен
�� EMBED Equation.3 ?
2.Устная работа (по кодопозитивам).
Постановка проблемы:
Учитель: 1). Можно ли свести решение данных уравнений к решению линейных уравнений? 2).Как бы вы сгруппировали данные уравнения по способам решения?
�
Ответы учащихся:
-Уравнения 1, 7, 10 можно решить на основании определения модуля.
-Уравнение 2 не имеет решений, так как модуль — величина неотрицательная.
В ходе рассуждений сделали выводы:
1).Если
То есть указали способ решения уравнений 3 и 8.
2).Если
то должно выполняться условие:
, так как модуль величина неотрицательная, тогда по определению модуля
�� EMBED Equation.
3
То есть указали способ решения уравнений 4 и 9.
Учитель: Как же можно решить уравнение 5,12?
Ответы учащихся:
-Воспользоваться определением модуля и рассмотреть 2 условия:
5). x -1
0 и x -1< 0; 12).
Учитель: Разве уравнение 11 имеет отношение к теме «Модуль»?
Ответы учащихся:
-По свойству модуля:
получим уравнение, содержащее модуль.
Учитель: А как же решить уравнение 6?
Ответы учащихся:
— Постепенно раскрывать модули.
— Методом интервалов.
Учитель: Каковы ваши предложения по применению метода интервалов?
Ответы учащихся:
1). Найдём значения х, при которых значения выражений, стоящих под знаком модуля равны нулю.
2). Эти значения х разбивают ОДЗ на промежутки.
3). На каждом из полученных промежутков можно записать уравнение без знаков модуля.
Получим совокупность систем.
IV. Минута отдыха.
Встаньте. Закройте глаза. Представьте, что вы на солнечной поляне.
Встали на цыпочки. Ваши руки тянутся к солнышку – яркому, тёплому.
Встали на ступни. Руки перед собой.
Увидели высокое апельсиновое дерево и потянулись сорвать апельсин.
Опустите руки вниз. Откройте глаза. Тихо сядьте.
Урок продолжается.
V. Актуализация деятельности учащихся.
(Работа в группах по 5-6 человек).
Ваша задача: решить предлагаемые уравнения, проанализировать способы их решения, провести классификацию уравнений, содержащих модуль по способам решения, составить таблицу « Решение уравнений, содержащих модуль». Провести защиту вашего проекта.
(Вначале более простые примеры выбирают те учащиеся, которым труднее даётся предмет; более сложные примеры выбирают те учащиеся, у которых есть математические способности.
После обмена примерами, более сильные учащиеся могут выступать в роли консультантов.)
Каждая группа получает инструкцию. Прежде, чем приступить к работе над проектом, внимательно ознакомьтесь с инструкцией.
VI. Работа над проектом.
Инструкция по работе над проектом.
1. Решить уравнения.
2. Проанализировать способы решения.
3. Провести классификацию данных уравнений:
а) сгруппировать примеры по способам решения;
б) определить, в чём заключается общий вид уравнений в каждой группе;
в) дать название каждой группе уравнений.
4. Создать проект таблицы: « Решение уравнений, содержащих модуль».
5. Подготовить защиту проекта.
VII. Защита проектов.
Оценочный лист. (5-бальная система)
Владеет докладчик терминологией, которую использует в своём проекте | |
Смог докладчик проекта доказать, что разработанная группой структура самая оптимальная для решения поставленной задачи | |
Выполнила ли группа все поставленные перед ней задачи | |
Творческие способности докладчика | |
Оформление проекта |
VIII.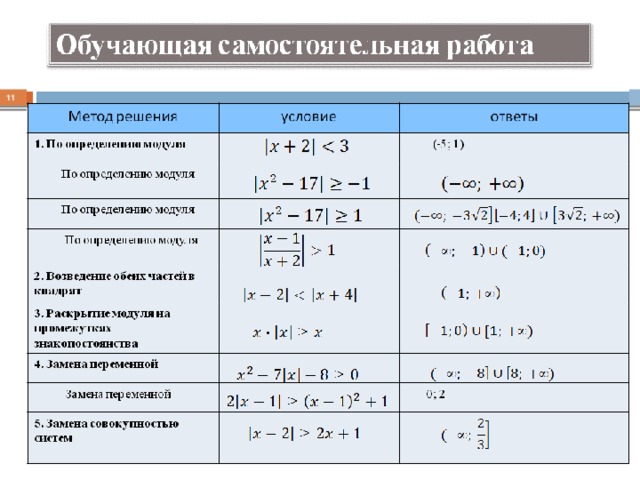
Домашнее задание. ( Слушают стоя).
Сформировать 2 группы учащихся (по 2-3 человека), которые представят результаты исследования в виде презентации и буклета к следующему уроку. Остальные учащиеся (работая в парах) подготовят проект в виде плаката, стендового доклада, сообщения (по их выбору).
IX. Итог урока.
Проводится анализ работы всего класса и индивидуальной работы в группах и выставление оценок. (Учитывается защита проекта, количество примеров, решённых каждым индивидуально).
�
Приложение 1.
Инструкция по работе над проектом.
1. Решить уравнения.
2. Проанализировать способы решения.
3. Провести классификацию данных уравнений:
а) сгруппировать примеры по способам решения;
б) определить, в чём заключается общий вид уравнений в каждой группе;
в) дать название каждой группе уравнений.
4. Создать проект таблицы: « Решение уравнений, содержащих модуль».
5. Подготовить защиту проекта.
Приложение 2.
Приложение 3.
Решение.
I группа. Простейшие уравнения вида ,b>0.
(Решаемые по определению модуля.)
1.
Ответ: -19;21.
II группа. Уравнения более общего вида .
(Решаемые по определению модуля, где рассматривается условие g(x)
)
III группа. Уравнения вида
IV группа. Уравнения, содержащие несколько модулей.
( Решаемые с помощью метода интервалов)
1.Найдём значения х, при которых значение выражений, стоящих под знаком модуля, равны 0:
х -1 = 0 при х = 1.
х – 2=0 при х = 2.
2. Эти значения разбивают ОДЗ на промежутки:
3.
Запишем на каждом из промежутков данное уравнение без знаков модуля.
Получим совокупность систем.
1.Найдём значения х, при которых значение выражений, стоящих под знаком модуля, равны 0:
х + 2=0 при х = -2.
2. Эти значения разбивают ОДЗ на промежутки:
�� EMBED Equation.3
3.Запишем на каждом из промежутков данное уравнение без знаков модуля.
Получим совокупность систем.
V группа. Уравнения, приводимые к уравнениям, содержащим модуль.
�� EMBED Equation.3
VI группа. Иррациональные уравнения, содержащие модуль.
В силу того, что
модуль
раскрывается двузначно.
Ответ: -4,5; -0,75; 0.
14.
.
Решение.
В силу того, что
модуль
раскрывается однозначно.
Ответ: 0.
VII группа. Замена модуля.
� EMBED Equation.3 ���
Конспект урока по теме: «Решение уравнений, содержащих переменную под знаком модуля» | План-конспект урока по алгебре (7 класс) на тему:
Конспект урока по теме: «Решение уравнений, содержащих переменную под знаком модуля»
ЦЕЛИ УРОКА:
- Закрепить умение решать уравнения, содержащие переменную под знаком модуля.
- Проверить, как учащиеся научились решать такие уравнения.
- Развить навыки самостоятельной работы учащихся и работы в группах.
- Повысить интерес учащихся к математике.
ПЛАН УРОКА:
- Проверка домашней работы.
- Сообщение целей урока, угадывание пропущенного слова в теме урока.
- Устные упражнения:
а) нахождение модуля числа;
б) решение вычислительных примеров, содержащих модуль;
в) решение несложных уравнений.
- Работа учащихся в парах.
- Решение сложных уравнений с модулем.
- Самостоятельная работа учащихся.
- . Итоги урока, домашнее задание.
I. Проверка домашней работы.
На дом были даны такие задания:
- Найдите значение выражения (№1209(1)):
( 0,7245 : 0,23 – 2,45 ) · 0,18 + 0,074
- Решите с помощью уравнения задачу(№1226,б):
“ В первом классе 42 ученика, во втором на 3 ученика меньше, чем в третьем. Сколько учеников в третьем классе, если всего в этих трех классах 125 учеников?”
- Решите уравнение(№1201):
а) | x | = 5,2; б) | а | = -3; в) | у | = 0.
- Дополнительное задание:
Составить уравнение для решения задачи:“ Пешеход прошел от автобусной остановки по прямой дороге 4 км. Укажите координаты точки, где будет находиться пешеход”.
Домашнее задание проверяется следующим образом:
№1 – ученики по очереди (глядя в свои тетради) называют действие и ответ к нему.
№2 – на одном из крыльев доски заранее написано:
При проверке этого номера учащиеся устно поясняют смысл выражений:
х ; х + 3 и х + х + 3 + 42, а решение полученного уравнения проверяют самостоятельно.
Классу задаются дополнительные вопросы:
1) что называется уравнением?
2) что называется корнем уравнения?
3) что значит- решить уравнение?
№ 3 проверяется следующим образом.
На доске написано такое решение уравнений
а) х = 5,2 | б) а = — 3 | в) у = 0 |
х = 5,2 | а = — 3 | у = 0 |
Ответ : х = 5,2. | Ответ : а = — 3. | Ответ : у = 0. |
Ответ: х = 5,2.
Ответ: а = — 3. Ответ: у = 0.
Учащиеся исправляют ошибки, допущенные при решении пунктов а) и б), повторив при этом определение модуля числа и каким может быть модуль числа.
При ответе на последний вопрос используется плакат:
(В 6 классе я использую именно такой вариант раскрытия модуля числа).
К № 4 на доске чертеж:
Решение: (разбирается устно ). В задаче не уточняется, в какую именно сторону двигался пешеход. Значит, он может находиться на расстоянии 4 км вправо или 4 км влево от остановки.
Ответ: уравнение: | х | = 4.
После проверки домашней работы учитель вытирает ту часть доски, где было записано домашнее задание.
II. Сообщение темы и целей урока.
На доске записаны слова.
Решение уравнений, содержащих…..
А дальше висит плакат рисунком к доске. Учитель предлагает узнать недостающее слово в теме урока, расшифровав ребус. Для этого плакат переворачивается рисунком к учащимся. .
Дети угадывают слово “ модуль ”, плакат убирается, учащиеся пишут в тетрадях, а учитель дописывает на доске тему “ Решение уравнений, содержащих переменную под знаком модуля ”.
Далее учитель сообщает цели урока и план работы.
III . Устные упражнения.
а) Вычислить: | 18 |,| -7,1 |, | |,| -0,3 |, | 19 |, | -19 |, (здесь обращается внимание на то, что числа 19 и –19 — противоположные, но их модули равны и повторяется формула | a | = | — а |).
б) Следующее задание – взобраться по ступенькам к открытке и угадать написанную на открытке загадку. При этом на первую ступеньку помещается ответ к примеру под № 1, на вторую ступеньку – ответ к примеру № 2 и т.д. Примеры записаны на обратном крыле доски, а ступеньки нарисованы на магнитной доске. Карточки с ответами крепятся к магнитной доске с помощью магнитов, их легко двигать. Карточек дано больше, чем примеров, чтобы учащиеся считали, а не “подгоняли” оставшиеся ответы. .
Если все примеры решены правильно, то перевернув карточки, учащиеся прочитают слово “молодцы”. .
На открытке дана загадка : “ Это есть у растения, может быть у уравнения ”.
Ответ : корень.
Значит в следующем задании мы будем искать корни уравнений.
в) Решить уравнения:
| х | = 7, | -х | = 7, | х | + 5 = 20, | х | = -5, | у | — 5 = 15,
| 2х – 6 | = 0, | х – 1 | = 0, 2 ·| у | = 4,6 .
Здесь используется плакат, на котором данные уравнения написаны в кроне деревьев, в бутонах цветов, а ответы спрятаны под травой в корнях. .
Как только учащиеся решили уравнение, учитель вынимает из прорези траву и детям видно, верно или нет решено уравнение. .
Здесь учитель должен обратить внимание на то, что один листик пожелтел и упал. Почему? Потому что уравнение | х | = — 5 не имеет корней.
IV. Работа в парах.
У каждого ученика на столе лежит карточка – консультант с решенными пятью примерами (эти примеры характеризуют обязательный минимум). Учащиеся первого варианта берут в руки карточки со вторым вариантом, диктуют задания учащимся, сидящим на втором варианте, следят за решением, тут же исправляют ошибки – это легко сделать, глядя в карточку – консультант (которую я больше люблю называть шпаргалкой) и выставляют оценки.
Затем происходит все наоборот.
Карточка – консультант для групповой работы
I вариант
1. | у | = 8
у = 8, у = -8.
Ответ: у = 8, у = -8.
2. | у | = 0
у = 0.
Ответ: у = 0.
3. | у | = -8
нет решений (т.к. модуль числа не может быть отрицательным).
Ответ: нет решений.
4. | х + 7| = 0
х + 7 = 0
х = 0 – 7
х = 0 + (-7)
х = -7
Ответ: х = -7
5. | х | — 6 = 10
(Вспомни правило, как найти неизвестное уменьшаемое)
| х | = 10 + 6
| х | = 16
х = 16, х = -16 . Ответ: х = 16, х = -16.
Карточка – консультант для групповой работы
II вариант
1. | х | = 5
х = 5, х = -5.
Ответ: х = 5, х = -5.
2. | х | = 0
х = 0.
Ответ: х = 0.
3. | у | = -6
нет решений (т.к. модуль числа не может быть отрицательным).
Ответ: нет решений.
4. | х + 4| = 0
х + 4 = 0
х = 0 – 4
х = 0 + (-4)
х = -4.
Ответ: х = -4
5.
15 — | х | = 12
( Вспомни правило, как найти неизвестное вычитаемое)
| х | = 15 — 12
| х | = 3
х = 3, х = -3, Ответ: х = 3, х = — 3.
V. Решение уравнений.
№ 1.(решает у доски ученик) 2 + | х + 3 | = 5 ( | х + 3 | — неизвестное слагаемое )
| х + 3 | = 5 – 2
| х + 3 | = 3
х + 3 = 3 или х + 3 = -3
х = 3 – 3 или х = -3 – 3
х = 0 или х = -6
Проверка : если х = 0, то 2 + | 0 + 3 | = 2 + 3 = 5, 5 = 5, верно
если х = -6, то 2 + | -6 + 3 | = 2 + | -3| = 2 + 3 =5, 5 = 5, верно
( можно сделать устно ).
Ответ : х = 0, х = -6.
№ 2.(решает у доски ученик) 7 — | 2х – 1 | = 4 ( | 2х – 1 | — неизвестное вычитаемое)
| 2х – 1 | = 7 – 4
| 2х – 1 | = 3
2х – 1 = 3 или 2х – 1 = -3
2х = 3 + 1 или 2х = -3 + 1
2х = 4 или 2х = -2
х = 4 : 2 или х = -2 : 2
х = 2 или х = -1
Ответ : х = 2, х = -1 .
№ 3. Решают самостоятельно, а один ученик решает на обратной стороне крыла доски, затем решение проверятся
15 — | х + 4 | = 3
| х + 4 | = 15 – 3
| х + 4 | = 12
х + 4 = 12 или х + 4 = -12
х = 12 – 4 или х = -12 – 4
х = 8 или х = -16.
Ответ: х = 8, х = -16.
Замечание : так как урок проводился до изучения п.42 “Решение уравнений”, где изучается правило о переносе слагаемых из одной части уравнения в другую, то мы данные уравнения решали выделением неизвестного слагаемого, множителя и т.д. А после изучения п.42 стали применять данное правило и при решении уравнений с модулем.
VI. Самостоятельная работа учащихся (на два варианта).
У каждого учащегося есть заранее напечатанный текст самостоятельной работы, учащиеся дописывают туда решение и ответы. За первые пять примеров ставится только “3”. Тому, кто решил все задания, дополнительно даются карточки с уравнениями :
К – 1 4·| х – 2 | — 6 = 10
К – 2 | х – 5 | — 7 = 3
К – 3 3·| х – 3 | — 5 = 4
К – 4 | 8 — х | = 12
К – 5 3·| х – 2 | — 4 = 11
К – 6 2 -| х + 3 | = 0
К – 7 21 😐 х – 5 | = 3
К – 8 | 2 + х | = 6
Самостоятельные работы собираются на проверку.
Самостоятельная работа 1 вариант | Самостоятельная работа 2 вариант |
Фамилия | Фамилия |
Решить уравнения: | Решить уравнения: |
1) | x | = 0,2 | 1) | y | = 2,5 |
Ответ: | Ответ: |
2) | x | = 0 | 2) | y | = 0 |
Ответ: . | Ответ: . |
3) | x | = — 26 | 3) | y | = — 32 |
Ответ: | Ответ:. |
4) | x – 3,5| = 0 | 4) | y — 0,7 | = 0 |
Ответ: . | Ответ: |
5) 12 : | x | = 6 | 5) 2 · | y | = 10 |
Ответ: | Ответ: |
6) | x + 6 | = 10 | 6) | y + 8 | = 15 |
Ответ: | Ответ: |
7) | 8- x | — 2 = 4 | 7) | 9 – y | — 3 = 4 |
Ответ: | Ответ: |
VII: Итоги урока, домашнее задание.
Выставляю оценки за урок. Первому варианту даю решить дома самостоятельную работу второго варианта и наоборот.
Решение уравнений— Решить переменную внутри модуля
Задавать вопрос
спросил
Изменено 2 года, 8 месяцев назад
Просмотрено 95 раз
$\begingroup$
Предположим, у меня есть модуль , в котором я использую Solve[] . Если я сделаю переменную решения локальной,
Я получаю это:
f[a_] := Module[{soln, x},
soln = Solve[2 x == a, {x}];
Возврат [солн]
];
ф[5]
(*{{x$117834 -> 5/2}}*)
Если вместо этого я оставлю переменную решения глобальной, я получу более чистый результат:
g[a_] := Module[{soln},
soln = Solve[2 x == a, {x}];
Возврат [солн]
];
г[5]
(*{{х -> 5/2}}*)
Но если глобально x имеет значение x=7, это не удается:
(*7 недопустимая переменная*)
Почему локальная переменная x в первом примере становится x$117834 ? Что это
лучший способ использовать такие переменные, как x в этом случае?
- решение уравнений
- обзор
$\endgroup$
2
$\begingroup$
(1) Метод, используемый модулем 9 0016 для имитации лексической области видимости включает в себя переименование так, как вы видите.
Обычно это невидимо, потому что обычно переменные, локальные для модуля , не возвращаются явно в результате.
(2) Если вашей переменной было присвоено значение, то даже если вам удастся пройти мимо переименования, результат все равно будет не таким, как вы могли ожидать.
Один из способов обойти переименование — использовать блок вместо модуля (блок эмулирует динамическую область видимости, временно «забывая» любые значения, прикрепленные к символу).
f[a_] := Блок[{soln, x},
soln = Solve[2 x == a, {x}];
раствор]
ф[5]
(* Выход[68]= {{x -> 5/2}} *)
Ну и хорошо. Теперь присвойте значение x .
х = 7;
ф[5]
(* Выход[70]= {{7 -> 5/2}} *)
В итоге сделать это с переменной, которой было присвоено значение, будет сложно. Никаких сюрпризов; так было бы на любом языке.
$\endgroup$
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
График- Как упаковать уравнение в частных производных первого порядка в модуль и проверить решение
спросил
Изменено 2 года, 7 месяцев назад 92 и граничное условие u(t,0)=0. Решите это УЧП аналитически, затем нарисуйте решение для следующего диапазона значений x и t: x от 0 до 3 и t от 0 до 3. Прокомментируйте характер решения.
Три вопроса:
(1) Как проверить решение с помощью сокращенной формы функции ReplaceAll? Цель состоит в том, чтобы вернуть True или False. (2) Как починить модуль? Или я должен использовать вложенные модули или какую-то другую конструкцию, возможно, блок? (3) Правильно ли я использую функцию If, потому что она не возвращает True или False.
92; bc = u[t, 0] == 0;
соль = и[t, х]/. DSolve[{pde, ic, bc}, u[t, x], {t, x}];
Если[ПолноеУпрощение[pde/. sol], Print["Подтверждено верно"],
Print["Подтверждено False"]];
Plot3D[{u[t, x] /. соль[[1]]}, {t, 0, 3}, {x, 0, 3}], Print[соль[[1]]]]
- построение графиков
- дифференциальные уравнения
$\endgroup$
6
$\begingroup$
Пара , и ; пришлось заменить, а Plot3D вернуть с Print . Более того, вы использовали
sol = u[t, x] /. DSolve[{pde, ic, bc}, u[t, x], {t, x}];
там, где вы действительно хотели получить решение Правило , поэтому я изменил строку на
sol = DSolve[{pde, ic, bc}, u[t, x], {t, x}];
Вот исправленный код
sol = Module[{pde, ic, bc, sol},
pde = D[u[t, x], t] + D[u[t, x], x] == 0;
ic = u[0, x] == Exp[-x] Sin[x]^2;
bc = u[t, 0] == 0;
sol = DSolve[{pde, ic, bc}, u[t, x], {t, x}];
Если[
Полное упрощение[pde/.