Исследование сходимости рядов. Разложение в степенной ряд по степеням функции f(x) и нахождение множества сходимости ряда
титульном листе должны быть указаны следующие данные: кафедра, дисциплина, вариант, специальность, курс, фамилия, имя, отчество, идентификатор.
Каждый обучаемый выбирает номер варианта в соответствии с тремя последними цифрами идентификатора. Если идентификатор (три последние цифры) больше количества вариантов заданий, то номер варианта рассчитывается делением идентификатора (три последние цифры) на количество вариантов и остаток от деления – это Ваш вариант. Если остаток от деления равен нулю, то Ваш вариант соответствует последнему номеру варианта лабораторной работы. (Пример. Идентификатор – m02e1g1-025. Количество вариантов – 14. Расчет: 25:14=1 с остатком 11. Ваш вариант – 11).
При наличии пакета Математика 4 на компьютере, полученный
окончательный численный результат решения заданий лабораторной работы должен
быть проверен при помощи пакета Математика 4.
Решение необходимо оформлять при помощи компьютерных редакторов и представлять в электронном виде для регистрации на учебном Web-сайте.Обязательное требование — имя отчетного файла должно содержать только латинские символы (пример:lab3vmat.doc).
Вариант 1
1. Исследовать сходимость рядов:
|
1. ; |
2. ; |
2. Разложить в степенной ряд по степеням функцию f(x) и найти множество сходимости ряда:
3. Разложить функции по степеням (x–a) и найти множество сходимости ряда:
4. Используя разложение в ряд подынтегральной функции, вычислить с точностью до 0,0001 интеграл :
5.
Найти решение задачи Коши:
6. Найти общее решение уравнения:
Вариант 2
1. Исследовать сходимость рядов:
|
1. ; |
2. ; |
2. Разложить в степенной ряд по степеням функцию f(x) и найти множество сходимости ряда:
3. Разложить функции по степеням (x–a) и найти множество сходимости ряда:
4. Используя разложение в ряд подынтегральной функции, вычислить с точностью до 0,0001 интеграл :
5. Найти решение задачи Коши:
6. Найти общее решение уравнения:
Вариант 3
1.
Исследовать сходимость рядов:|
1. ; |
|
2. Разложить в степенной ряд по степеням функцию f(x) и найти множество сходимости ряда:
3. Разложить функции по степеням (x–a) и найти множество сходимости ряда:
4. Используя разложение в ряд подынтегральной функции, вычислить с точностью до 0,0001 интеграл :
5. Найти решение задачи Коши:
6. Найти общее решение уравнения:
Вариант 4
1. Исследовать сходимость рядов:
|
1. ; |
2. |
;2. Разложить в степенной ряд по степеням функцию f(x) и найти множество сходимости ряда:
3. Разложить функции по степеням (x–a) и найти множество сходимости ряда:
4. Используя разложение в ряд подынтегральной функции, вычислить с точностью до 0,0001 интеграл :
5. Найти решение задачи Коши:
6. Найти общее решение уравнения:
Вариант 5
1. Исследовать сходимость рядов:
|
1. ; |
2. ; |
2. Разложить в степенной ряд по степеням функцию f(x) и найти множество сходимости ряда:
3.
4. Используя разложение в ряд подынтегральной функции, вычислить с точностью до 0,0001 интеграл :
5. Найти решение задачи Коши:
6. Найти общее решение уравнения:
Вариант 6
1. Исследовать сходимость рядов:
|
1. ; |
2. ; |
2. Разложить в степенной ряд по степеням функцию f(x) и найти множество сходимости ряда:
3. Разложить функции по степеням (x–a) и найти множество сходимости ряда:
4. Используя разложение в ряд подынтегральной функции, вычислить с точностью до 0,0001 интеграл :
5.
Найти решение задачи Коши:
6. Найти общее решение уравнения:
Вариант 7
1. Исследовать сходимость рядов:
|
1. ; |
2. ; |
2. Разложить в степенной ряд по степеням функцию f(x) и найти множество сходимости ряда:
3. Разложить функции по степеням (x–a) и найти множество сходимости ряда:
4. Используя разложение в ряд подынтегральной функции, вычислить с точностью до 0,0001 интеграл :
5. Найти решение задачи Коши:
6. Найти общее решение уравнения:
Вариант 8
1.
Исследовать сходимость рядов:|
1. ; |
2. ; |
2. Разложить в степенной ряд по степеням функцию f(x) и найти множество
Решение задач по математике | Исследовать сходимость рядов
1.2.9. Пользуясь известными признаками сходимости, исследовать сходимость следующих рядов:
Воспользуемся признаком Даламбера:
При решении использовали – второй замечательный предел.
Так как – то данный ряд сходится.
По радикальному признаку Коши:
Так как – то данный ряд расходится.
По интегральному признаку Коши:
Ряд расходится.
1.3.9. Исследовать на сходимость знакочередующийся ряд:
Воспользуемся достаточным признаком сходимости знакопеременных рядов. Для этого определим сходимость ряда составленного из модулей членов данного ряда:
Воспользуемся признаком Даламбера:
Так как , то ряд, составленный из модулей членов данный ряд, сходится.
Таким образом, исходный ряд является абсолютно сходящимся.
Воспользуемся достаточным признаком сходимости знакопеременных рядов. Для этого определим сходимость ряда составленного из модулей членов данного ряда:
По интегральному признаку Коши:
Ряд, составленный из модулей членов данный ряд, расходится.
Исследуем исходный ряд по признаку Лейбница:
1. последовательность абсолютных величин членов ряда монотонно убывает:
2. Общий член ряда стремится к нулю, при этом сумма S ряда удовлетворяет неравенствам :
;
с погрешность вычисления равной .
Таким образом,
Ряд является
1.4.9. Найти область сходимости степенного ряда:
По признаку Даламбера:
Область сходимости ряда: => =>
При имеем ряд:
По интегральному признаку Коши:
Ряд расходится.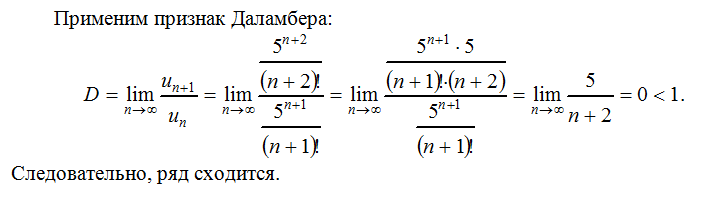
Тогда область сходимости ряда:
1.5.9. Разложить в ряд Маклорена функцию . Указать область сходимости полученного ряда:
Преобразуем функцию:
Разложим подынтегральную функцию в ряд Маклорена:
Тогда:
Область сходимости ряда: => =>
Тогда область сходимости ряда:
1.8.9. Используя разложение подынтегральной функции в степенной ряд, вычислить указанный определенный интеграл с точностью до 0,001.
Разложим подынтегральную функцию в ряд Маклорена:
Тогда:
Найдем значение интеграла:
1.9.9. Найти разложение в степенной ряд по степеням х решения дифференциального уравнения (записать три первых, отличных от нуля члена этого разложения).
,
Будем искать решение уравнения в виде:
Здесь:
Будем искать:
при x=0
при x=0
Подставляем найденные значения производных в исходный ряд, получаем:
Окончательно:
4.
1.9. Основные понятия и теоремы теории вероятностей:
Вероятность попадания в цель равна 0,003. Сколько нужно произвести выстрелов, чтобы с вероятностью, большей 0,94, можно было утверждать, что цель будет поражена?
По условию:
; ; ;
По формуле Бернулли:
Подставим исходные значения:
Найдем максимальное значение n, решая правую часть неравенства.
Чтобы найти максимум данной функции, найдем ее производную:
Найдем критические точки:
Тогда:
Тогда неравенство никогда не будет выполнено:
С вероятностью, большей 0,94, мы не можем утверждать, что цель будет поражена, если вероятность попадания в цель равна 0,003.
4.3.9. Схема повторных испытаний:
Из каждого десятка деталей 9 удовлетворяют стандарту. Найти вероятность того, что из 50 взятых со склада деталей число стандартных окажется между 42 и 48.
По интегральной теореме Лапласа: Вероятность того, что в n независимых испытаниях, в каждом из которых вероятность появления события равна (0 при этом , событие наступит не менее k1 раз и не более k2 раз, приближенно равна:
Здесь:
– функция Лапласа
;
Значения функции Лапласа находим по специальной таблице.
Найдем вероятность появления стандартной детали и вероятность появления нестандартной:
;
Подставим все известные значения:
Функция Лапласа (по таблице):
Искомая вероятность:
4.4.9. Случайные величины:
Дискретная случайная величина Х имеет только два возможных значения: и , причем . Вероятность того, что Х примет значения , равна 0,2. Найти закон распределения Х, зная математическое ожидание и среднее квадратичное отклонение .
Запишем закон распределения Х в общем виде:
X | ||
P(X) |
Впишем все известные значения:
X | ||
P(X) | 0,2 | 0,8 |
Найдем возможные значения Х:
Находим математическое ожидание:
Подставляем все известные значения:
Находим среднее квадратичное отклонение:
Находим дисперсию:
Подставляем все известные значения:
Составим систему уравнения для нахождения возможных значений Х:
Подставляем все известные значения:
=>=>=>
или
Тогда:
или
Принимая во внимание условие выбираем пару: и
Запишем закон распределения Х:
X | 1 | 3 |
P(X) | 0,2 | 0,8 |
4.
5.9. Случайные величины:
Случайная величина Х задана функцией распределения:
Выбрать коэффициенты a, b и c таким образом, чтобы данное распределение соответствовало случайной величине непрерывного типа, написать выражение для плотности р(х).
По условию задачи функция F(x) непрерывна. Выберем коэффициенты a, b и c таким образом, чтобы не было разрыва, для этого составим систему уравнений:
Тогда:
=> => => =>
Выберем: , тогда , .
Подставим найденные значения в функцию распределения:
Плотностью распределения (иначе – «плотность вероятности») непрерывной случайной величины – характеризует как бы плотность, с которой распределяются значения случайной величины в данной точке и является производной функции распределения.
Дифференциальные уравнения — Обзор: Power Series
Онлайн-заметки Пола
Главная
/
Дифференциальные уравнения
/
Серийные решения для DE
/ Обзор : Серия Power
Показать мобильное уведомление Показать все примечания Скрыть все примечания
Мобильное уведомление
Похоже, вы используете устройство с «узкой» шириной экрана ( т.
е. вы, вероятно, используете мобильный телефон). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
Раздел 6.1: Обзор: Power Series 9n}} \label{eq:eq1}\end{уравнение}\]
где \(x_{0}\) и \(a_{n}\) — числа. Отсюда видно, что степенной ряд является функцией \(х\). Обозначение функции не всегда включается, но иногда это так, что мы поместили его в определение выше.
Прежде чем приступить к нашему обзору, наверное, стоит вспомнить, что же такое сериалы на самом деле. Вспомните, что ряды на самом деле являются просто суммированием. Тогда один из способов записать наш степенной ряд:
. \[\begin{equation}\begin{align}f\left( x \right) &= \sum\limits_{n = 0}^\infty {{a_n}{{\left({x — {x_0}} \right)}^n}} \\ & = {a_0} + {a_1}\left( {x — {x_0}} \right) + {a_2}{\left( {x — {x_0}} \right) ^2} + {a_3}{\left( {x — {x_0}} \right)^3} + \cdots \end{aligned}\label{eq:eq2}\end{equation}\] 9п}} \]
Иногда нам нужно это сделать, поэтому убедитесь, что вы можете это сделать.
n}} \]
9п}} = {а_0}\]
Теперь мы знаем, что степенные ряды гарантированно существуют хотя бы для одного значения \(x\). Имеем следующий факт о сходимости степенного ряда.
Факт
Дан степенной ряд \(\eqref{eq:eq1}\), будет существовать число \(0 \le \rho \le \infty \), так что степенной ряд будет сходиться для \( \left| {x — {x_0}} \right| < \rho \) и расходятся при \(\left| {x - {x_0}} \right| > \rho \). Это число называется радиус схождения .
Определение радиуса сходимости для большинства степенных рядов обычно довольно просто, если мы используем критерий отношения.
Проверка соотношения
Учитывая вычисление степенного ряда,
\[L = \влево| {x — {x_0}} \right|\mathop {\lim }\limits_{n \to \infty} \left| {\ frac {{{a_{n + 1}}}}{{{a_n}}}} \right|\]
затем
\[\begin{align*}& L < 1 & \Rightarrow \hspace{0,25in} &{\mbox{ряд сходится}}\\ & L > 1 & \Rightarrow \hspace{0,25in} &{\mbox {ряд расходится}}\\ & L = 1 & \Rightarrow \hspace{0,25 дюйма} &{\mbox{ряд может сходиться или расходиться}}\end{выравнивание*}\] 9n}}}} \right|\\ & = \left| {x — 5} \right|\mathop {\lim }\limits_{n \to \infty} \left| {\ frac {{ — 3}} {{\ left ( {n + 1} \ right) \, 7}} \, \, \ frac {n} {1}} \ right | \\ & = \ frac { 3}{7}\влево| {x — 5} \right|\end{align*}\]
Теперь мы знаем, что ряд сойдется, если
\[\frac{3}{7}\left| {х — 5} \право| < 1\hspace{0,25 дюйма} \Rightarrow \hspace{0,25 дюйма}\left| {х - 5} \право| < \фракция{7}{3}\]
и ряд будет расходиться, если
\[\frac{3}{7}\left| {х — 5} \право| > 1\hspace{0,25 дюйма} \Rightarrow \hspace{0,25 дюйма}\left| {х — 5} \право| > \фракция{7}{3}\]
Другими словами, радиус сходимости этого ряда равен
\[\rho = \frac{7}{3}\]
Как показал этот последний пример, радиус сходимости находится практически сразу после использования критерия соотношения.
Итак, почему нас беспокоит сходимость степенных рядов? Что ж, для того, чтобы рядовое решение дифференциального уравнения существовало в конкретном \(x\), оно должно сходиться в этом \(x\). Если он не сходится при заданном \(x\), то решение ряда не будет существовать при этом \(x\). Итак, сходимость степенных рядов весьма важна.
Далее нам нужно сделать краткий обзор некоторых основ манипулирования сериями. Начнем со сложения и вычитания. 9{n + c}}} \end{align*}\]
Итак, все, что нам нужно сделать, это умножить член впереди в ряд и добавить показатели степени. Также обратите внимание, что для этого как коэффициент перед рядом, так и член внутри ряда должны быть в форме \(x-x_{0}\). Если они не совпадают, мы не можем этого сделать, в конце концов мы увидим, как поступать с терминами, которые не находятся в этой форме.
Далее нужно поговорить о дифференцировании степенного ряда. Глядя на \(\eqref{eq:eq2}\), должно быть довольно легко увидеть, как мы будем дифференцировать степенной ряд.
Поскольку ряд — это всего лишь гигантская сумма, все, что нам нужно сделать, — это дифференцировать отдельные члены. Производная степенного ряда будет равна 9{n — 1}}} \end{align*}\]
Итак, все, что нам нужно сделать, это просто дифференцировать термин внутри ряда, и все готово. Обратите также внимание на то, что на самом деле существует две формы производной. Поскольку \(n = 0\) член производной равен нулю, это не изменит значение ряда, и поэтому мы можем включать его или нет по мере необходимости. В нашей работе мы обычно хотим, чтобы производная начиналась с \(n = 1\), однако иногда будет возникать проблема, когда было бы удобнее начинать ее с \(n = 0\). 9{п + 2}}} \]
Показать решение
Сдвиг индекса — довольно простая манипуляция. Во-первых, заметим, что если мы определим \(i=n-3\), то при \(n = 3\) мы получим \(i=0\). Итак, что мы сделаем, так это перепишем ряд в терминах \(i\) вместо \(n\). Мы можем сделать это, заметив, что \(n=i+3\).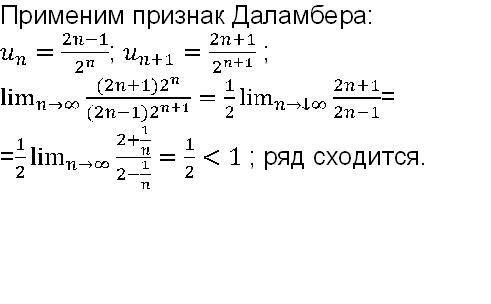
{n + 2}}} \]
9{n + 1}}} \) Показать решение
Во-первых, обратите внимание, что здесь две серии, а инструкции явно требуют только одну серию. Итак, нам нужно будет вычесть два ряда в какой-то момент времени. Подавляющее большинство нашей работы будет состоять в том, чтобы подготовить два ряда для вычитания. Это означает, что перед двумя рядами не может быть никаких коэффициентов (кроме одного, конечно…), они должны начинаться с одного и того же значения \(n\), и им потребуется один и тот же показатель степени в \ (х-х_{0}\). 9п}} \]
Наконец, чтобы вычесть два ряда, нам нужно, чтобы они начинались с одного и того же значения \(n\). В зависимости от ряда в задаче мы можем сделать это разными способами. В этом случае заметим, что, поскольку во второй серии есть n-1 , мы фактически можем начать вторую серию с \(n = 1\), не меняя ее значения. Также обратите внимание, что при этом мы получим, что оба ряда начинаются с \(n = 1\), и поэтому мы можем выполнить вычитание.
Тогда наш окончательный ответ: 9п}} \]
В этом случае мы не можем просто начать первую серию с \(n = 3\), потому что в этой серии нет \(n-3\), чтобы сделать член \(n = 3\) равным нулю . Таким образом, мы не сможем сделать эту часть, как в первой части этого примера.
В этой части нам нужно удалить \(n = 3\) из второго ряда, чтобы они оба начинались с \(n = 4\). Затем мы сможем сложить две серии вместе. Удаление члена \(n = 3\) из второго ряда дает 9п} = 0} \]
для всех \(x\), тогда
\[{a_n} = 0,\,\,\,n = 0,1,2, \ldots\]
Этот факт будет ключевым в нашей работе с дифференциальными уравнениями, так что не забывайте об этом.
Радиус сходимости решений рядов
Радиус сходимости решений рядов В последнем разделе мы рассмотрели один из самых простых примеров линейного однородного уравнения второго порядка с непостоянными коэффициентами: Уравнение Эйри
г »- т г = 0,
который используется в физике для моделирования преломления света.
Мы узнали, что
и
образуют фундаментальную систему решений дифференциального уравнения Эйри.
Возникают естественные вопросы, при каких значениях t эти ряды сходятся и при каких значениях t эти ряды решают дифференциальное уравнение.
Первый вопрос
можно ответить, найдя
радиус сходимости степенного ряда,
но оказывается, что есть элегантная теорема из-за Лазарь Фукс (1833-1919 гг.)02), что решает оба эти вопроса одновременно.
| Теорема Фукса. Рассмотрим дифференциальное уравнение y »+ p ( t ) y ‘+ q ( t ) y =0 с начальными условиями вида y (0)= y 0 и y ‘(0)= y ‘ 0 . Пусть r >0.
Если оба p ( t ) и q ( t ) имеют ряды Тейлора, сходящиеся на отрезке (- r , r ), то дифференциальное уравнение имеет единственное решение степенного ряда y ( t ), который также сходится на отрезке (- r , r ). Другими словами, радиус сходимости решения ряда не меньше минимума радиусов сходимости p ( t ) и q ( т ). |
В частности, если оба p ( t ) и q ( t ) являются полиномами, то y ( t ) решает дифференциальное уравнение для всех .
Поскольку в случае уравнения Эйри p ( t )=0 и q ( t )=- t являются полиномами, фундаментальный набор решений y 10262 ) и y 2 ( t ) сходятся и решают уравнение Эйри для всех .
Давайте посмотрим на некоторые другие примеры:
Уравнение Эрмита порядка n имеет вид
y »-2 ty ‘+2 ny =0,
где n обычно неотрицательное целое число. Как и в случае уравнения Эйри, оба p ( t )=-2 t и q ( t )=2 n являются полиномами, поэтому уравнение Эрмита имеет решения степенного ряда, которые сходятся и решают дифференциальное уравнение для всех .
Уравнение Лежандра порядка
имеет форму
где является действительным числом.
Будь осторожен! Мы должны переписать это уравнение, чтобы применить теорему Фукса. Разделим на 1- t 2 :
Теперь коэффициент перед y » равен 1, как и требовалось.
Каков радиус сходимости представлений степенного ряда
(Центр, как и во всех наших примерах, будет t = 0.) Нам действительно нужно исследовать этот вопрос только для функции
так как умножение на полином (-2 t , и , соответственно) не меняет радиус сходимости.
Геометрический ряд
сходится, когда -1 < x <1. Если мы подставим х = t 2 , мы получаем искомое представление степенного ряда:
который будет сходиться, когда -1< x = t 2 <1, т.
е. , когда -1< t <1. Таким образом, оба
будет сходиться на интервале (-1,1). Следовательно, по результату Фукса ряды решений уравнения Лежандра будут сходиться и решать уравнение на интервале (-1,1).
Уравнение Бесселя порядка
имеет форму
где является неотрицательным действительным числом.
Мы снова должны быть осторожны! Разделим на t 2 :
Теперь коэффициент перед y » равен 1, как того требует теорема Фукса.
Функция имеет особенность при t = 0, таким образом, p ( t ) не имеет ряда Тейлора с центром t = 0. Следовательно, результат Фукса не гарантирует даже существования степенных рядов решений уравнения Бесселя.
Как оказалось, уравнение Бесселя действительно не всегда имеет решения, которые можно записать в виде степенных рядов. Тем не менее, существует метод, аналогичный представленному здесь, для нахождения решения уравнения Бесселя.