Таблица косинусов синусов тангенсов углов: Таблица тригонометрических функций.

Таблица тангенсов

Математика 

21.10.202021.10.2021 Виктор Потехин

Таблица тангенсов.

 

Поделиться в:

 

Таблица тангенсов:

Таблица тангенсов – это таблица, содержащая значения тангенсов углов от 0° до 360°.

Тангенсом угла α называется отношение синуса этого угла к косинусу. Либо отношение противолежащего катета (дальнего/противоположного) прямоугольного треугольника к прилежащему (который находится рядом с углом α).

 

Таблица синусов. Таблица косинусов. Таблица тангенсов. Таблица котангенсов. 

 

Таблица тангенсов углов от 0 до 180 градусов:

tg(0°) = 0 tg(1°) = 0. 017455 tg(2°) = 0.034921 tg(3°) = 0.052408 tg(4°) = 0.069927 tg(5°) = 0.087489 tg(6°) = 0.105104 tg(7°) = 0.122785 tg(8°) = 0.140541 tg(9°) = 0.158384 tg(10°) = 0.176327 tg(11°) = 0.194380 tg(12°) = 0.212557 tg(13°) = 0.230868 tg(14°) = 0.249328 tg(15°) = 0.267949 tg(16°) = 0.286745 tg(17°) = 0.305731 tg(18°) = 0.324920 tg(19°) = 0.344328 tg(20°) = 0.363970 tg(21°) = 0.383864 tg(22°) = 0.404026 tg(23°) = 0.424475 tg(24°) = 0.445229 tg(25°) = 0.466308 tg(26°) = 0.487733 tg(27°) = 0.509525 tg(28°) = 0.531709 tg(29°) = 0.554309 tg(30°) = 0.577350	tg(61°) = 1.804048 tg(62°) = 1.880726 tg(63°) = 1.962611 tg(64°) = 2.050304 tg(65°) = 2.144507 tg(66°) = 2.246037 tg(67°) = 2.355852 tg(68°) = 2.475087 tg(69°) = 2.605089 tg(70°) = 2.747477 tg(71°) = 2.904211 tg(72°) = 3.077684 tg(73°) = 3.270853 tg(74°) = 3.487414 tg(75°) = 3. 732051 tg(76°) = 4.010781 tg(77°) = 4.331476 tg(78°) = 4.704630 tg(79°) = 5.144554 tg(80°) = 5.671282 tg(81°) = 6.313752 tg(82°) = 7.115370 tg(83°) = 8.144346 tg(84°) = 9.514364 tg(85°) = 11.430052 tg(86°) = 14.300666 tg(87°) = 19.081137 tg(88°) = 28.636253 tg(89°) = 57.289962 tg(90°) не определено	tg(121°) = -1.664279 tg(122°) = -1.600335 tg(123°) = -1.539865 tg(124°) = -1.482561 tg(125°) = -1.428148 tg(126°) = -1.376382 tg(127°) = -1.327045 tg(128°) = -1.279942 tg(129°) = -1.234897 tg(130°) = -1.191754 tg(131°) = -1.150368 tg(132°) = -1.110613 tg(133°) = -1.072369 tg(134°) = -1.035530 tg(135°) = -1 tg(136°) = -0.965689 tg(137°) = -0.932515 tg(138°) = -0.900404 tg(139°) = -0.869287 tg(140°) = -0.839100 tg(141°) = -0.809784 tg(142°) = -0.781286 tg(143°) = -0.753554 tg(144°) = -0.726543 tg(145°) = -0.700208 tg(146°) = -0. 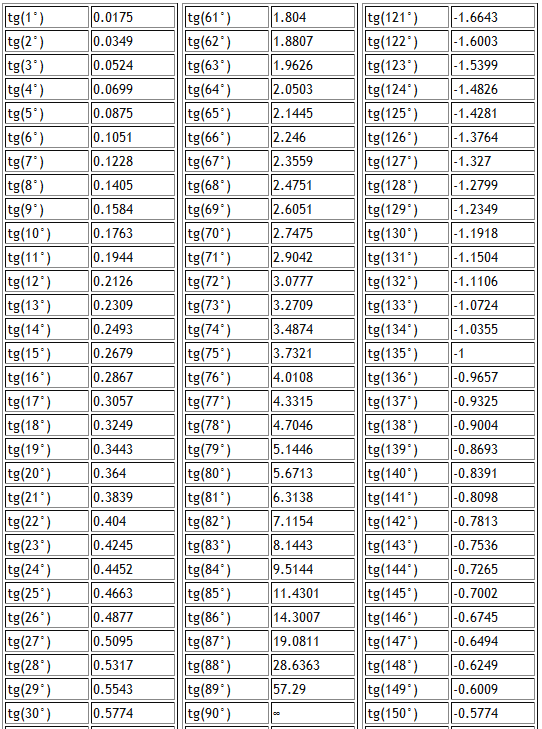674509 tg(147°) = -0.649408 tg(148°) = -0.624869 tg(149°) = -0.600861 tg(150°) = -0.577350
tg(31°) = 0.600861 tg(32°) = 0.624869 tg(33°) = 0.649408 tg(34°) = 0.674509 tg(35°) = 0.700208 tg(36°) = 0.726543 tg(37°) = 0.753554 tg(38°) = 0.781286 tg(39°) = 0.809784 tg(40°) = 0.839100 tg(41°) = 0.869287 tg(42°) = 0.900404 tg(43°) = 0.932515 tg(44°) = 0.965689 tg(45°) = 1 tg(46°) = 1.03553 tg(47°) = 1.072369 tg(48°) = 1.110613 tg(49°) = 1.150368 tg(50°) = 1.191754 tg(51°) = 1.234897 tg(52°) = 1.279942 tg(53°) = 1.327045 tg(54°) = 1.376382 tg(55°) = 1.428148 tg(56°) = 1.482561 tg(57°) = 1.539865 tg(58°) = 1.600335 tg(59°) = 1.664279 tg(60°) = 1.732051	tg(91°) = -57.289962 tg(92°) = -28.636253 tg(93°) = -19.081137 tg(94°) = -14.300666 tg(95°) = -11.430052 tg(96°) = -9.514364 tg(97°) = -8.144346 tg(98°) = -7.115370 tg(99°) = -6. 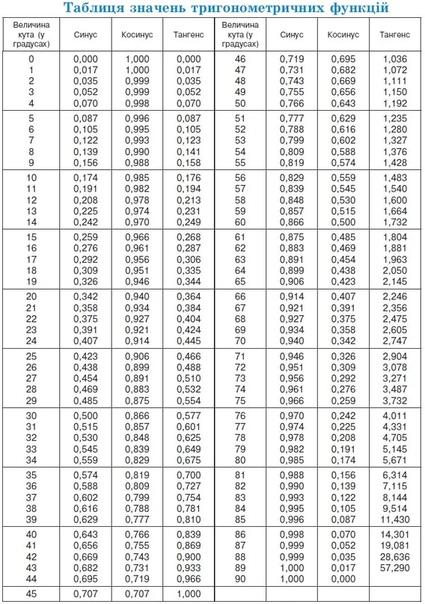313752 tg(100°) = -5.671282 tg(101°) = -5.144554 tg(102°) = -4.704630 tg(103°) = -4.331476 tg(104°) = -4.010781 tg(105°) = -3.732051 tg(106°) = -3.487414 tg(107°) = -3.270853 tg(108°) = -3.077684 tg(109°) = -2.904211 tg(110°) = -2.747477 tg(111°) = -2.605089 tg(112°) = -2.475087 tg(113°) = -2.355852 tg(114°) = -2.246037 tg(115°) = -2.144507 tg(116°) = -2.050304 tg(117°) = -1.962611 tg(118°) = -1.880726 tg(119°) = -1.804048 tg(120°) = -1.732051	tg(151°) = -0.554309 tg(152°) = -0.531709 tg(153°) = -0.509525 tg(154°) = -0.487733 tg(155°) = -0.466308 tg(156°) = -0.445229 tg(157°) = -0.424475 tg(158°) = -0.404026 tg(159°) = -0.383864 tg(160°) = -0.363970 tg(161°) = -0.344328 tg(162°) = -0.324920 tg(163°) = -0.305731 tg(164°) = -0.286745 tg(165°) = -0.267949 tg(166°) = -0.249328 tg(167°) = -0.230868 tg(168°) = -0.212557 tg(169°) = -0. 194380 tg(170°) = -0.176327 tg(171°) = -0.158384 tg(172°) = -0.140541 tg(173°) = -0.122785 tg(174°) = -0.105104 tg(175°) = -0.087489 tg(176°) = -0.069927 tg(177°) = -0.052408 tg(178°) = -0.034921 tg(179°) = -0.017455 tg(180°) = 0

 

Таблица синусов. Таблица косинусов. Таблица тангенсов. Таблица котангенсов. 

 

Таблица тангенсов углов от 181 до 360 градусов:

tg(181°) = 0.017455 tg(182°) = 0.034921 tg(183°) = 0.052408 tg(184°) = 0.069927 tg(185°) = 0.087489 tg(186°) = 0.105104 tg(187°) = 0.122785 tg(188°) = 0.140541 tg(189°) = 0.158384 tg(190°) = 0.176327 tg(191°) = 0.194380 tg(192°) = 0.212557 tg(193°) = 0.230868 tg(194°) = 0.249328 tg(195°) = 0.267949 tg(196°) = 0.286745 tg(197°) = 0.305731 tg(198°) = 0.324920 tg(199°) = 0.344328 tg(200°) = 0.363970 tg(201°) = 0.383864 tg(202°) = 0.404026 tg(203°) = 0. 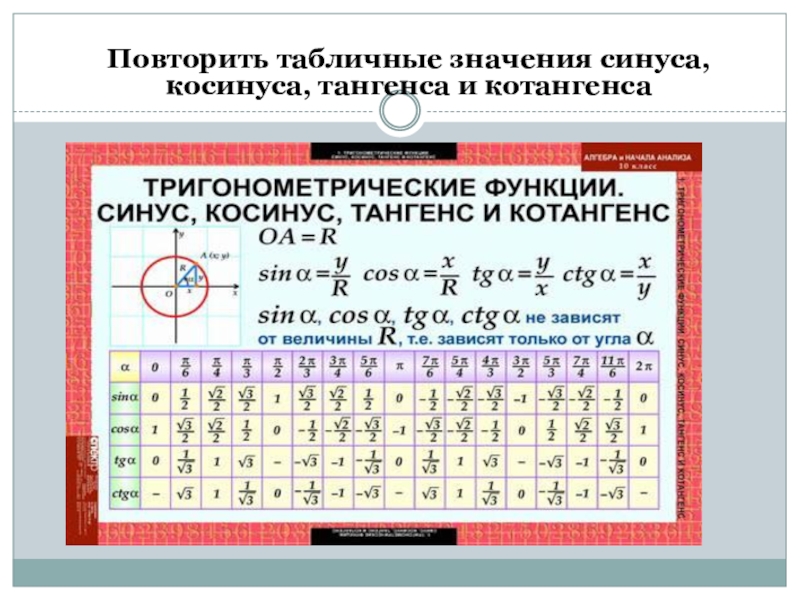424475 tg(204°) = 0.445229 tg(205°) = 0.466308 tg(206°) = 0.487733 tg(207°) = 0.509525 tg(208°) = 0.531709 tg(209°) = 0.554309 tg(210°) = 0.577350	tg(241°) = 1.804048 tg(242°) = 1.880726 tg(243°) = 1.962611 tg(244°) = 2.050304 tg(245°) = 2.144507 tg(246°) = 2.246037 tg(247°) = 2.355852 tg(248°) = 2.475087 tg(249°) = 2.605089 tg(250°) = 2.747477 tg(251°) = 2.904211 tg(252°) = 3.077684 tg(253°) = 3.270853 tg(254°) = 3.487414 tg(255°) = 3.732051 tg(256°) = 4.010781 tg(257°) = 4.331476 tg(258°) = 4.704630 tg(259°) = 5.144554 tg(260°) = 5.671282 tg(261°) = 6.313752 tg(262°) = 7.115370 tg(263°) = 8.144346 tg(264°) = 9.514364 tg(265°) = 11.430052 tg(266°) = 14.300666 tg(267°) = 19.081137 tg(268°) = 28.636253 tg(269°) = 57.289962 tg(270°) не определено	tg(301°) = -1.664279 tg(302°) = -1.600335 tg(303°) = -1.539865 tg(304°) = -1. 482561 tg(305°) = -1.428148 tg(306°) = -1.376382 tg(307°) = -1.327045 tg(308°) = -1.279942 tg(309°) = -1.234897 tg(310°) = -1.191754 tg(311°) = -1.150368 tg(312°) = -1.110613 tg(313°) = -1.072369 tg(314°) = -1.035530 tg(315°) = -1 tg(316°) = -0.965689 tg(317°) = -0.932515 tg(318°) = -0.900404 tg(319°) = -0.869287 tg(320°) = -0.839100 tg(321°) = -0.809784 tg(322°) = -0.781286 tg(323°) = -0.753554 tg(324°) = -0.726543 tg(325°) = -0.700208 tg(326°) = -0.674509 tg(327°) = -0.649408 tg(328°) = -0.624869 tg(329°) = -0.600861 tg(330°) = -0.577350
tg(211°) = 0.600861 tg(212°) = 0.624869 tg(213°) = 0.649408 tg(214°) = 0.674509 tg(215°) = 0.700208 tg(216°) = 0.726543 tg(217°) = 0.753554 tg(218°) = 0.781286 tg(219°) = 0.809784 tg(220°) = 0.839100 tg(221°) = 0.869287 tg(222°) = 0.900404 tg(223°) = 0.932515 tg(224°) = 0.965689 tg(225°) = 1 tg(226°) = 1. 03553 tg(227°) = 1.072369 tg(228°) = 1.110613 tg(229°) = 1.150368 tg(230°) = 1.191754 tg(231°) = 1.234897 tg(232°) = 1.279942 tg(233°) = 1.327045 tg(234°) = 1.376382 tg(235°) = 1.428148 tg(236°) = 1.482561 tg(237°) = 1.539865 tg(238°) = 1.600335 tg(239°) = 1.664279 tg(240°) = 1.732051	tg(91°) = -57.289962 tg(272°) = -28.636253 tg(273°) = -19.081137 tg(274°) = -14.300666 tg(275°) = -11.430052 tg(276°) = -9.514364 tg(277°) = -8.144346 tg(278°) = -7.115370 tg(279°) = -6.313752 tg(280°) = -5.671282 tg(281°) = -5.144554 tg(282°) = -4.704630 tg(283°) = -4.331476 tg(284°) = -4.010781 tg(285°) = -3.732051 tg(286°) = -3.487414 tg(287°) = -3.270853 tg(288°) = -3.077684 tg(289°) = -2.904211 tg(290°) = -2.747477 tg(291°) = -2.605089 tg(292°) = -2.475087 tg(293°) = -2.355852 tg(294°) = -2.246037 tg(295°) = -2.144507 tg(296°) = -2.050304 tg(297°) = -1. 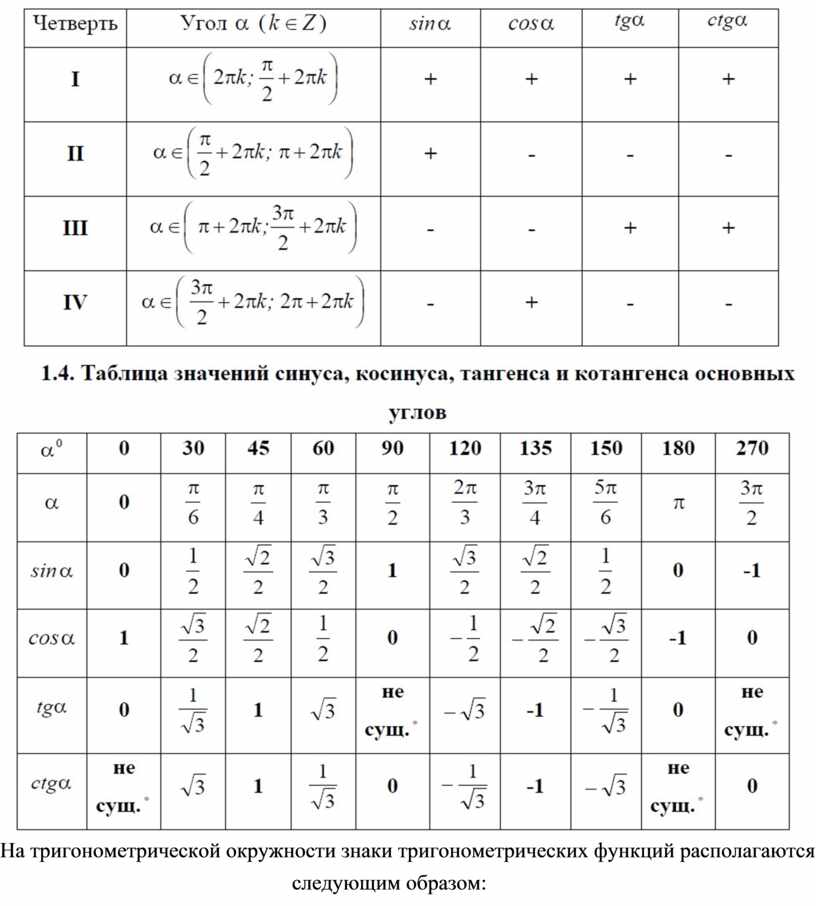962611 tg(298°) = -1.880726 tg(299°) = -1.804048 tg(300°) = -1.732051	tg(331°) = -0.554309 tg(332°) = -0.531709 tg(333°) = -0.509525 tg(334°) = -0.487733 tg(335°) = -0.466308 tg(336°) = -0.445229 tg(337°) = -0.424475 tg(338°) = -0.404026 tg(339°) = -0.383864 tg(340°) = -0.363970 tg(341°) = -0.344328 tg(342°) = -0.324920 tg(343°) = -0.305731 tg(344°) = -0.286745 tg(345°) = -0.267949 tg(346°) = -0.249328 tg(347°) = -0.230868 tg(348°) = -0.212557 tg(349°) = -0.194380 tg(350°) = -0.176327 tg(351°) = -0.158384 tg(352°) = -0.140541 tg(353°) = -0.122785 tg(354°) = -0.105104 tg(355°) = -0.087489 tg(356°) = -0.069927 tg(357°) = -0.052408 tg(358°) = -0.034921 tg(359°) = -0.017455 tg(360°) = 0

 

Таблица синусов. Таблица косинусов. Таблица тангенсов. Таблица котангенсов. 

 

Примечание: © Фото https://www.pexels.com, https://pixabay. com

 

Коэффициент востребованности 37

Тригонометрическая таблица

Автор Admin На чтение 5 мин Просмотров 48 Опубликовано 26.02.2010

Тригонометрическая таблица представляет собой таблицу значений тригонометрических функций. Эта

тригонометрическая таблица содержит углы в градусах и радианах, что очень удобно для перевода градусов в радианы и наоборот, радианов в градусы. Таблица значений тригонометрических функций составлена с корнями квадратными и дробями, что позволяет сокращать дроби при решении школьных примеров. В таблице представлены синус sin, косинус cos, тангенс tg, котангенс ctg, секанс sec, косеканс cosec.

Специально для самых умных умников сообщаю. Это правильная таблица. Где-то между роддомом и сегодня, вы учили свойства дробей. Так вот, с тех самых пор ничего не изменились. Что для школьных малявок, что для здоровых дядек и теток, свойства дробей одинаковы. Даже президент Путин не в состоянии ничего поменять. Одно из волшебных свойств дроби гласит: если числитель и знаменатель дроби умножить на одно и то же число, дробь не изменится. И ни какое стадо депутатов этот закон отменить не в состоянии. Математика — это не соседей или собственный народ грабить. Даже Боги могут только пользоваться законами математики, но не изменять их. Хотя, дуракам закон не писан.

Свойства дробей

Чтобы облегчить жизнь блондинкам, мы еще не раз будем разбирать эту тригонометрическую таблицу на строчки синусов, косинусов, тангенсов, котангенсов, секансов и косекансов, на столбики градусов и радиан, на отдельные квадратики значений тригонометрических функций.

В тригонометрической таблице представлены синус угла sin 0, 30, 45, 60, 90, 180, 270 и 360 градусов или 0, пи/6, пи/4, пи/3, пи/2, пи, 3пи/2, 2пи радиан. Значения синуса угла sin 0, 1/2, корень из 2 деленный на 2, корень из 3 деленный на 2, единица и минус единица. Строчка напротив буквочек sin називается еще таблица синусов.

Таблица значений тригонометрических функций содержит косинус угла cos 0, 30, 45, 60, 90, 180, 270, 360 градусов. Если перевести эти углы в радианы, мы получим 0 пи, пи на 6, пи на 4, пи на 3, пи на 2, пи, 3 пи на 2, 2 пи радиан. Таблица косинусов этих углов представляет собой строчку напротив букв cos, в которой записаны единица, корень из трех деленный на два, корень из двух деленный на два, одна вторая, ноль и минус единица.

Первых две строчки этой таблицы sin и cos — это таблица синусов и косинусов.

Таблица тангенсов спряталась ниже таблицы синусов и косинусов в строчке с двумя буковками tg. Как это ни странно, но здесь присутствуют те же тангенс угла tg 0, 30, 45, 60, 90, 180, 270, 360 градусов. И в радианы они переводятся точно так же 0 пи, пи / 6, пи / 4, пи / 3, пи / 2, пи, 3 пи / 2, 2 пи радиан. Значения тангенсов этих углов составляют ноль, единица деленная на корень из трех, единица, корень из трех и черточка, которую иногда заменяют знаком бесконечности. Это означает, что математики не могут определить значение тригонометрической функции тангенс для углов 90 и 270 градусов. Так что, блондинки, не отчаивайтесь, даже математики могут не всё!

Еще ниже находится таблица котангенсов. Повторим еще раз те углы, для которых в тригонометрической таблице записан котангенс ctg: 0, 30, 45, 60, 90, 180, 270, 360 градусов. И еще раз потренируемся переводить градусы в радианы: 0 пи, пи / 6, пи / 4, пи / 3, пи / 2, пи, 3 пи / 2, 2 пи радиан. Начинается котангенс угла ctg с неопределенности, обозначенной черточкой, дальше идут корень из трех, единица, единица деленная на корень из трех, ноль.

Две средние строчки тригонометрической таблицы складываются в таблицу тангенсов и котангенсов.

Две последние строчки тригонометрической таблицы занимают секанс, который обозначается sec, и косеканс, который обозначается cosec. Поскольку эти тригонометрические функции обратны косинусу и синусу соотвественно, то и значения этих функций обратны значениям косинуса и синуса. Обращаю ваше особое внимание на то, что математики в очередной раз попытались запутать блондинок, нарушив логику применения приставки КО. У них получилось, что секанс — это тригонометрическая функция, обратная КОсинусу, а КОсеканс — обратная синусу. Естественно, что для секанса и косеканса есть углы, значения функций для которых не определены.

В завершение немного ваших вопросов и моих ответов на них:

Таблица тригонометрических функций основных углов — в тригонометрической таблице приведены самые распространенные в учебниках и примерах углы.

Таблица косинуса синуса тангенса и котангенса бесплатно — все эти функции здесь собраны в одну кучку и смотреть на них можно совершенно бесплатно.

Тригонометрическая таблица sin cos tg ctg — а еще здесь есть sec и cosec, в градусах и радианах.

Тангенс пи на 4 — как же только не извращаются математики, чтобы замаскировать обыкновенную единичку.

Синус 180 градусов равен — а вот так математики могут замаскировать обыкновенный ноль. Прямо не математика, а женская сумочка какая-то — покуда что-нибудь найдешь…

sin нуля — ну вот, ещё один ноль они спрятали, правда не очень далеко, но коварно — в cos 0 за нулем прячется единица. Попробуй тут не запутаться.

Таблица синусов и косинусов в радианах — ну, здесь не самая большая таблица, но кое-какие радианы имеются. Нужно будет соорудить что-нибудь монументальное, в духе Зураба Церетели.

Таблица часто встречающихся значений синуса косинуса тангенса котангенса — здесь есть нужные вам значения. Если вы считаете, что другие значения встречаются чаще, сообщите мне об этом, я исправлю досадное недоразумение.

ctg 225 градусов — равен единице (1). В таблице для ботаников этого нет, приходится самим додумывать. Плохая тригонометрическая таблица, нужно другую нарисовать, специально для серии «Тригонометрия для блондинок».

Таблица синусов и косинусов в дробях — да, именно в виде дроби записаны значения шести тригонометрических функций для некоторых углов в таблице на рисунке.

Таблиця косинусів синусів тангенсів котангенсів — вау! в Украине тоже изучают тригонометрическую таблицу! А я считал, что там только выборами занимаются. Наверное, они по этим таблицам прогнозы выборов считают.

Школьная таблица тангенса — есть здесь и тангенс в виде дроби, специально для школьников.

Вычислить cosekans — здесь есть косекансы в таблице. Хотя, в сокращенном виде косеканс пишется как «cosec», а по-английски это пишется «cosecant».

Таблица тангенсов с использованием пи — за неимением лучшей, пока могу предложить только эту таблицу.

Используйте таблицы, чтобы найти острый угол, учитывая, что tan 9347…

Перейти к

• Тригонометрические таблицы. Упражнение 19.

• налог на товары и услуги
• Банковское дело
• Акции и дивиденды
• Квадратные уравнения с одной переменной
• Факторизация
• Соотношение и пропорция
• Матрицы
• Арифметика и геометрическая прогрессия
• Отражение
• Формула раздела
• Уравнение прямой линии
• Сходство
• Локус
• Круги
• Конструкции
• Измерение
• Тригонометрические тождества
• Тригонометрические таблицы
• Высоты и расстояния

Главная > ML Aggarwal Solutions Класс 10 Математика > Глава 19. Тригонометрические таблицы > Тригонометрические таблицы. Упражнение 19.> Вопрос 20

Вопрос 20 Тригонометрические таблицы Упражнение 19

Используйте таблицы для нахождения острого угла θ, учитывая, что: tan θ = 0,9347

Ответ:

таблицы натуральных синусов, натуральных косинусов , а натуральные тангенсы можно использовать для получения приблизительных значений синуса, косинуса и тангенса с точностью до четырех знаков после запятой для любых углов от 0 до 90 градусов.

В таблице натуральных тангенсов найдите значение (≤ .9347), что достаточно близко к 0,9347.

Мы находим значение 0,9325 в горизонтальной строке, начинающейся с 43 ^o , и в средней разнице мы видим 0,9347 – 0,9325 = 0,0022 в столбце 4’.

Получаем, что θ = 43 ^o + 4’ = 43 ^o 4’.

Связанные вопросы

Найдите значение следующего выражения: cos 62^o 27′

Найдите значение следующего выражения: sin 65^o 20′

Найдите значение следующего выражения: sin 35^o 22′

Найдите значение следующего выражения: sin 23^o 56′

Найдите значение следующего выражения: cos 3^o 11′

Используйте таблицы, чтобы найти острый угол θ, учитывая, что: sin θ = 0,2357

Фейсбук WhatsApp

Копировать ссылку

Было ли это полезно?

Упражнения

Тригонометрические таблицы Упражнение 19

Главы

GST

Банковское дело

Акции и дивиденды

Квадратные уравнения с одной переменной

Факторизация

Отношение и пропорция

Матрицы

Арифметика и геометрическая прогрессия

Отражение

Формула сечения

Уравнение прямой

Подобие

Геометрическое место

Окружности

Построения

Измерения

Тригонометрические тождества

Тригонометрические таблицы

Высоты и расстояния

Курсы

Быстрые ссылки

Условия и политика

Условия и политика

2022 © Quality Tutorials Pvt Ltd Все права защищены

Наконечник с памятью для синуса, косинуса и тангенса специальных углов (тригонометрия)

9015 4 НАКОНЕЧНИК ПАМЯТИ ТРИГОНОМЕТРИИ

простой способ запомнить синус, косинус и тангенс специальных углов тригонометрии.

Специальные триггерные углы: 0º, 30º, 45º, 60º и 90º. Что делает эти углы особенными? Треугольник 30º-60º-90º является половиной равностороннего треугольника, а треугольник 45º-45º-9Треугольник 0º составляет половину квадрата. В обоих случаях триггерные функции (синус, косинус и тангенс) могут быть выражены в виде простых отношений.

Вот способ быстрого вычисления синуса, косинуса и тангенса углов 0°, 30°, 45°, 60° и 90°.

ШАГ 1: Специальные углы.

Запишите специальные углы по порядку.

ШАГ 2: Целые числа.

Запишите целые числа от 0 до 4 по порядку.

ШАГ 3: Квадратные корни.

Квадратный корень каждого числа.

ШАГ 4: Найдите синус тета.

Разделите каждое число на 2.

Это синус 0°, 30°, 45°, 60° и 90°.

Это так просто. Вот резюме:

• Напишите числа от 0 до 4.
• Квадратный корень каждого числа.
• Разделите каждое число на 2.

ШАГ 5: Найдите косинус тета.

Просто запишите предыдущие числа в обратном порядке.

Почему это работает? Поскольку синус теты равен косинусу дополнения теты: sin( θ )=cos(90º– θ ). То, что противоположно тэте, соседствует с ее дополнением.

ШАГ 6: Найдите тангенс теты.

Разделите синус тета на косинус тета.

TRIG CHART

На этой диаграмме показаны все этапы вместе.

• Напишите специальные углы.
• Запишите целые числа от 0 до 4.
• Квадратный корень каждого числа.
• Разделите каждое число на 2. Это даст вам синус тета.
• Напишите числа в обратном порядке. Это дает вам косинус тета.
• Разделить две предыдущие строки (синус на косинус). Это дает вам касательную тета.

ПРИМЕЧАНИЕ

Существует два разных, но эквивалентных способа записи приведенной выше таблицы.

Это связано со следующими свойствами иррациональных чисел:

Так, например, существуют альтернативные способы выражения следующих значений триггера:

В диаграмме в этом блоге используется стандартная форма . В большинстве математических курсов используется стандартная форма, что означает, что в знаменателе нет иррациональных чисел (например, корня 2).

Иногда вы найдете триггерную таблицу в другой нестандартной форме. В этой форме вы видите 1 над корнем 2 вместо корня 2 над 2, и вы видите 1 над корнем 3 вместо корня 3 над 3.

Важно понимать, что обе формы верны. Однако стандартная форма ожидается в большинстве математических курсов.

КРИС МАКМУЛЛЕН, PH.D.

Copyright © 2015 Chris McMullen, автор серии учебных пособий по математике «Улучшите беглость математики»

• Практическое пособие по основам тригонометрии с ответами
• Изучите или повторите основные навыки тригонометрии
• Флэш-карты тригонометрии (для Kindle)
• Рабочая тетрадь по основам алгебры с ответами
• Системы уравнений: одновременные, замена, правило Крамера
• Другие тома охватывают дроби, деление в длинных числах, арифметику и т.

  No related posts.