Решение натурального логарифма – Натуральный логарифм ln — онлайн калькулятор, формула, график

Натуральный логарифм | Логарифмы

Число e — иррациональное число.

   

Определение

Натуральный логарифм — это логарифм по основанию e, то есть показатель степени, в который надо возвести основание e, чтобы получить число, стоящее под знаком логарифма.

Как и в случае десятичного логарифма, для натурального логарифма принята укороченная форма записи и чтения.

Вместо

   

пишут

   

Читают не «логарифм a по основанию e», а «натуральный логарифм a».

Как и для других логарифмов, натуральный логарифм единицы равен нулю:

   

Найдем натуральные логарифмы некоторых чисел:

   

   

   

   

   

   

   

   

   

   

   

   

Если под знаком натурального логарифма стоит корень, то переходим от корня к дробной степени и получаем:

   

В частности,

   

В общем случае, для любого k

   

Например,

   

www.logarifmy.ru

Логарифм — Sandbox

Материал из Sandbox.

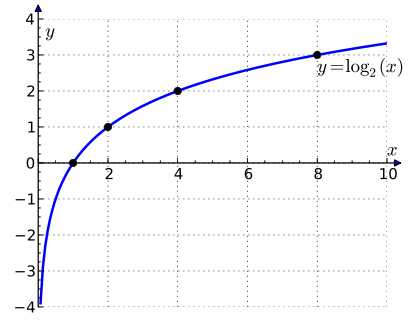
Логарифм числа по основанию определяется как показатель степени, в которую надо возвести основание , чтобы получить число . Обозначение: , произносится: логарифм по основанию .

Из определения следует, что нахождение равносильно решению уравнения . Например, потому что .

Вычисление логарифма называется логарифмированием. Числа чаще всего числа вещественные, но существует также теория комплексных логарифмов.

Логарифмы обладают уникальными свойствами, которые определили их широкое использование для существенного упрощения трудоёмких вычислений. При переходе «в мир логарифмов» умножение заменяется на значительно более простое сложение, деление — на вычитание, а возведение в степень и извлечение корня преобразуются соответственно в умножение и деление на показатель степени. Лаплас говорил, что изобретение логарифмов, «сократив труд астронома, удвоило его жизнь».

Определение логарифмов и таблицу их значений (для тригонометрических функций) впервые опубликовал в 1614 году шотландский математик Джон Непер. Логарифмические таблицы, расширенные и уточнённые другими математиками, повсеместно использовались для научных и инженерных расчётов более трёх веков, пока не появились электронные калькуляторы и компьютеры.

Со временем выяснилось, что логарифмическая функция незаменима и во многих других областях человеческой деятельности: решение дифференциальных уравнений, классификация значений величин (например, частота и интенсивность звука), аппроксимация различных зависимостей, теория информации, теория вероятностей и т. д. Эта функция относится к числу элементарных, она обратна по отношению к показательной функции. Чаще всего используются вещественные логарифмы с основанием (натуральный логарифм), (десятичный) и (двоичный).

Вещественный логарифм

Логарифм вещественного числа по определению есть решение уравнения . Случай интереса не представляет, поскольку тогда при это уравнение не имеет решения, а при любое число является решением; в обоих случаях логарифм не определён. Аналогично заключаем, что логарифм не существует при нулевом или отрицательном ; кроме того, значение показательной функции всегда положительно, поэтому следует исключить также случай отрицательного . Окончательно получаем:

Вещественный логарифм имеет смысл при

Как известно, показательная функция (при выполнении указанных условий для ) существует, монотонна и каждое значение принимает только один раз, причём диапазон её значений содержит все положительные вещественные числа. Отсюда следует, что значение вещественного логарифма положительного числа всегда существует и определено однозначно.

Наиболее широкое применение нашли следующие виды логарифмов.

Свойства

Основное логарифмическое тождество

Из определения логарифма следует основное логарифмическое тождество:

Следствие: из равенства двух вещественных логарифмов следует равенство логарифмируемых выражений. В самом деле, если , то , откуда, согласно основному тождеству: .

Логарифмы единицы и числа, равного основанию

Два равенства, очевидных из определения логарифма:

.

Логарифм произведения, частного от деления, степени и корня

Приведём сводку формул в предположении, что все значения положительны:

Существует очевидное обобщение приведённых формул на случай, когда допускаются отрицательные значения переменных, например:

Формула для логарифма произведения без труда обобщается на произвольное количество сомножителей:

Вышеописанные свойства объясняют, почему применение логарифмов (до изобретения калькуляторов) существенно облегчало вычисления. Например, умножение многозначных чисел с помощью логарифмических таблиц производилось по следующему алгоритму:

1. Найти в таблицах логарифмы чисел .
2. Сложить эти логарифмы, получая (согласно первому свойству) логарифм произведения .
3. По логарифму произведения найти в таблицах само произведение.

Деление, которое без помощи логарифмов намного более трудоёмко, чем умножение, выполнялось по тому же алгоритму, лишь с заменой сложения логарифмов на вычитание. Аналогично упрощались возведение в степень и извлечение корня.

Замена основания логарифма

Логарифм по основанию можно преобразовать в логарифм по другому основанию :

Следствие (при ) — перестановка основания и логарифмируемого выражения:

Другие тождества и свойства

Если выражения для основания логарифма и для логарифмируемого выражения содержат возведение в степень, для упрощения можно применить следующее тождество:

.

Это тождество сразу получается, если в логарифме слева заменить основание на по вышеприведенной формуле перехода. Следствия:

Ещё одно полезное тождество:

Для его доказательства заметим, что логарифмы левой и правой частей по основанию совпадают (равны ), а тогда, согласно следствию из основного логарифмического тождества, левая и правая части тождественно равны.

Логарифмическая функция

Основные характеристики

Логарифмическая функция обратна к показательной

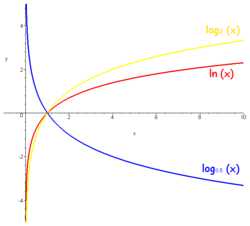Графики логарифмических функций

Натуральный логарифм равен площади под гиперболой

Если рассматривать логарифмируемое число как переменную, мы получим логарифмическую функцию . Она определена при . Область значений: . Эта кривая часто называется

логарифмикой. Из формулы замены основания логарифма видно, что графики логарифмических функций с разными основаниями, бо́льшими единицы, отличаются один от другого только масштабом по оси ; графики для оснований, меньших единицы, являются их зеркальным отражением относительно горизонтальной оси.

Из определения следует, что логарифмическая зависимость есть обратная функция для показательной функции , поэтому их графики симметричны относительно биссектрисы первого и третьего квадрантов (cм. рисунок). Как и показательная, логарифмическая функция относится к категории трансцендентных функций.

Функция является строго возрастающей при (см. далее графики) и строго убывающей при . График любой логарифмической функции проходит через точку $$(1;0). Функция непрерывна и неограниченно дифференцируема] всюду в своей области определения.

Ось ординат является левой вертикальной асимптотой, поскольку:

при ;

при .

Производная логарифмической функции равна:

С точки зрения алгебры, логарифмическая функция осуществляет (единственно возможный) изоморфизм мультипликативной группы положительных вещественных чисел и аддитивной группы всех вещественных чисел. Другими словами, логарифмическая функция есть единственное (определённое для всех положительных значений аргумента) непрерывное решение функционального уравнения:

Натуральный логарифм

Из приведённой выше общей формулы производной для натурального логарифма получаем особенно простой результат:

По этой причине в математических исследованиях преимущественно используют именно натуральные логарифмы. Они нередко появляются при решении дифференциальных уравнений, исследовании статистических зависимостей (например, распределения простых чисел) и т. п.

Проинтегрировав формулу для производной в интервале от до , мы получаем:

Другими словами, натуральный логарифм равен площади под гиперболой для указанного интервала x.

Неопределённый интеграл от натурального логарифма легко найти интегрированием по частям:

В математическом анализе и теории дифференциальных_уравнений большую роль играет понятие логарифмической производной функции :

Разложение в ряд и вычисление натурального логарифма

Разложим натуральный логарифм в ряд Тейлора вблизи единицы:

(Ряд 1)

Это ряд сходится при . В частности:

Формула ряда 1 непригодна для практического расчёта логарифмов из-за того, что ряд сходится очень медленно и только в узком интервале. Однако нетрудно получить из неё более удобную формулу:

(Ряд 2)

Этот ряд сходится быстрее, а кроме того, левая часть формулы теперь может выразить логарифм любого положительного числа. Данный алгоритм уже пригоден для реальных численных расчётов значений логарифмов, однако не является наилучшим с точки зрения трудоёмкости. Существуют более эффективные алгоритмы.

Десятичный логарифм

Логарифмы по основанию 10 (обозначение: ) до изобретения калькуляторов широко применялись для вычислений. Они обладали преимуществом перед логарифмами с иным основанием: целую часть логарифма числа легко определить.

Кроме того, при переносе десятичной запятой в числе на разрядов значение десятичного логарифма этого числа изменяется на . Например, . Отсюда следует, что достаточно составить таблицу десятичных логарифмов для чисел в диапазоне от до , причём привести в таблице только мантиссы (дробную часть) логарифмов.

Связь с натуральным логарифмом:

Поскольку применение логарифмов для расчётов с появлением вычислительной техники почти прекратилось, в наши дни десятичный логарифм в значительной степени вытеснен натуральным. Он сохраняется в основном в тех математических моделях, где исторически укоренился — например, при построении логарифмических шкал.

Предельные соотношения

Приведём несколько полезных пределов, содержащих логарифмы.

Другие свойства

cisserver.muctr.edu.ru

Натуральный логарифм Википедия

Функция натурального логарифма (синяя кривая) обратна к экспоненте (красная кривая) График функции натурального логарифма. Функция медленно приближается к положительной бесконечности при увеличении x и быстро приближается к отрицательной бесконечности, когда x стремится к 0

Натуральный логарифм — это логарифм по основанию e, где e{\displaystyle e} — иррациональная константа, равная приблизительно 2,72. Он обозначается как ln⁡x{\displaystyle \ln x}, loge⁡x{\displaystyle \log _{e}x} или иногда просто log⁡x{\displaystyle \log x}, если основание e{\displaystyle e} подразумевается^[1]. Обычно число x{\displaystyle x} под знаком логарифма вещественное, но можно расширить это понятие и на комплексные числа.

Из определения следует, что логарифмическая зависимость есть обратная функция для экспоненты y=ex{\displaystyle y=e^{x}}, поэтому их графики симметричны относительно биссектрисы первого и третьего квадрантов (см. рисунок справа). Как и экспонента, логарифмическая функция относится к категории трансцендентных функций.

Натуральные логарифмы полезны для решения алгебраических уравнений, в которых неизвестная присутствует в качестве показателя степени, они незаменимы в математическом анализе. Например, логарифмы используются для нахождения постоянной распада для известного периода полураспада или для нахождения времени распада в решении проблем радиоактивности. Они играют важную роль во многих областях математики и прикладных наук, применяются в сфере финансов для решения многих задач, включая нахождение сложных процентов.

ru-wiki.ru

Натуральный логарифм | Математика, которая мне нравится

Теорема. Пусть , — промежуток, функция непрерывна. Тогда у функции есть первообразная.

Рассмотрим функцию на промежутке . По предыдущей теореме, эта функция имеет первообразную. Все первообразные ее имеют вид . Выберем из всех этих первообразных такую, значение которой при равно . Такая первообразная найдется (почему?). Назовем ее натуральным логарифмом.

Обозначение: .

Свойства натурального логарифма

1. Область определения натурального логарифма .

2. .

3. Натуральный логарифм — дифференцируемая функция, и , .

4. Натуральный логарифм строго возрастает, так как .

5. .

Доказательство. Зафиксируем и докажем, что для любого это равенство выполняется.

   

   

Значит, — постоянная. Подставим вместо — :

   

Следовательно, .

6. Натуральный логарифм — функция, выпуклая вверх.

Доказательство. убывает.

7. .

8. Множество значений натурального логарифма есть вся числовая ось.

Доказательство. Так как функция непрерывна, то, по сформулированной ранее теореме, множество ее значений — промежуток.

Возьмем произвольное число . Нужно доказать, что : . Для этого достаточно доказать, что

   

   

hijos.ru