Исследование несобственного интеграла на сходимость. Контрольные онлайн
Решения типовых задач — Математический анализ
Исследование несобственного интеграла на сходимость
Задача1 Исследовать на сходимость несобственный интеграл . Решение Для решения вопроса о сходимости данного интеграла удобно воспользоваться предельным признаком сравнения: если и существует конечный предел то и ведут себя одинаково.
Известно, что, если , то
Для исследуемого интеграла .
При эквивалентна функции , интеграл от которой в пределах от 2 до расходится.
Так как и
расходится, то, следовательно, расходится и .
Задача2
Вычислить несобственные интегралы или доказать их расходимость.
1 – й интеграл является несобственным. Обойдем особую точку :
Таким образом.:
Интеграл сходится.
Задача3
,
т.е. интеграл расходится.
5- 7_Высшая математика_3
9
Рецензия
на контрольную работу № 5
по высшей математике
В
задаче 14 вычислять интеграл было
необязательно, достаточно было найти
порядок малости подынтегральной функции
при
.
В данном случае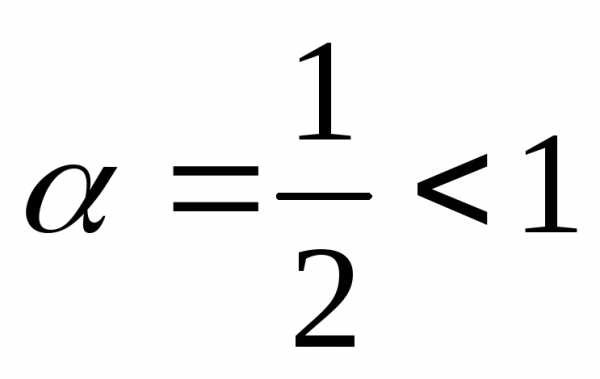 ,
следовательно, по предельному признаку
сходимости для интегралов первого рода
исходный интеграл расходится.
,
следовательно, по предельному признаку
сходимости для интегралов первого рода
исходный интеграл расходится.
В
задаче 15 также для решения достаточно
было найти порядок роста подынтегральной
функции при 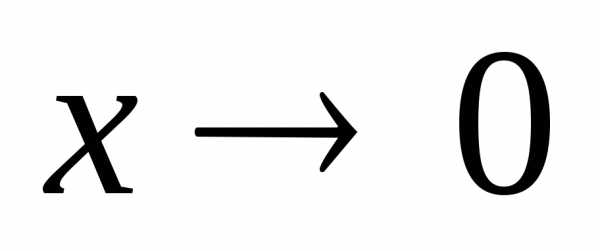 ,
здесь
,
здесь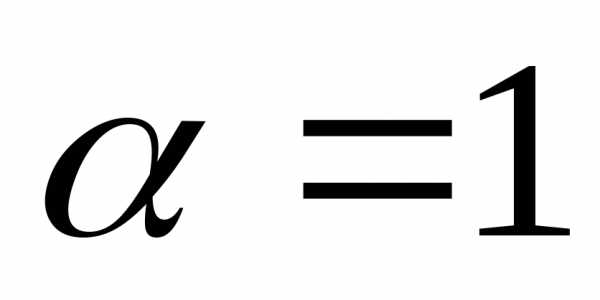
Работа зачтена Ельцов А.А.
Министерство образования
Российской Федерации
ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ (ТУСУР)
Кафедра компьютерные системы
в управлении и проектировании (СУ)
КОНТРОЛЬНАЯ РАБОТА № 5
по дисциплине « Высшая математика- 2 »
«Интегральное исчисление. Дифференциальные уравнения»
А.А. Ельцов
2004
Вариант 5.7
1. 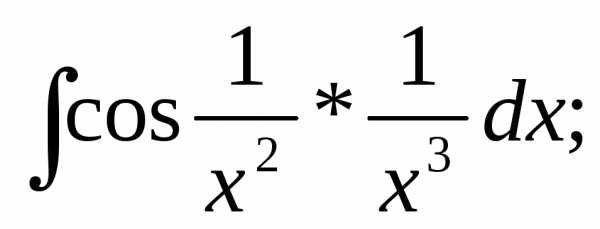 2.
2. 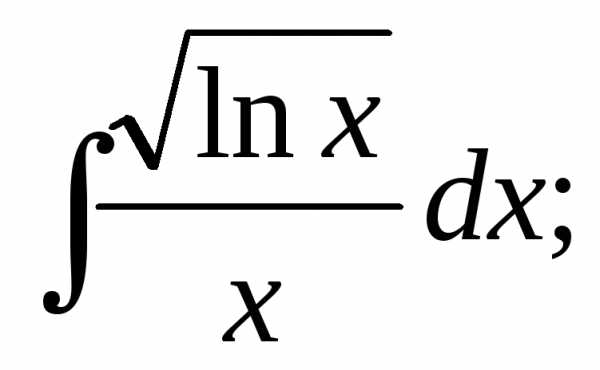 3.
3.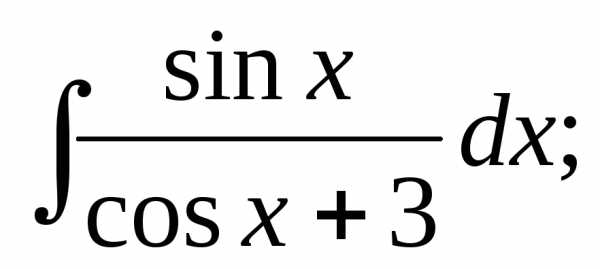
4.
5.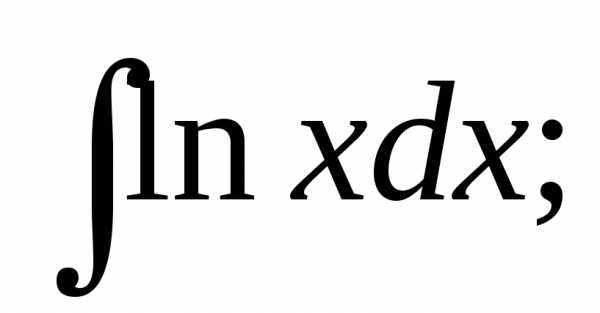 6.
6.
7. 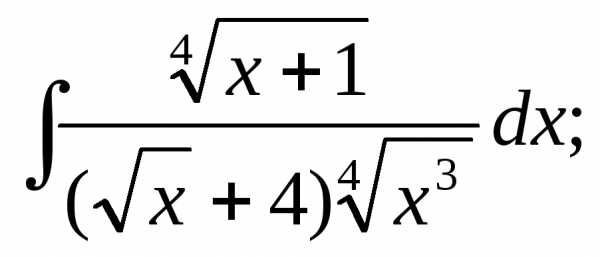
 8.
8.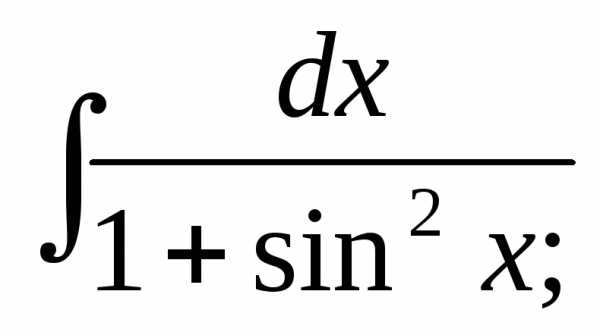 9.
9.
10. 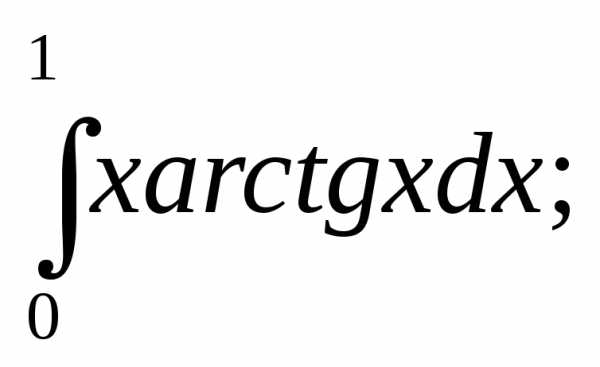
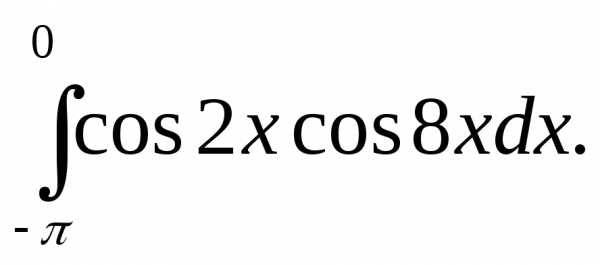
Вычислить несобственные интегралы или установить их расходимость
12. 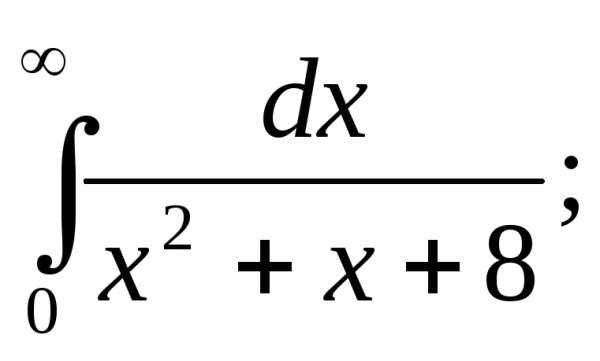 13.
13.
Выяснить сходимость несобственных интегралов
14. 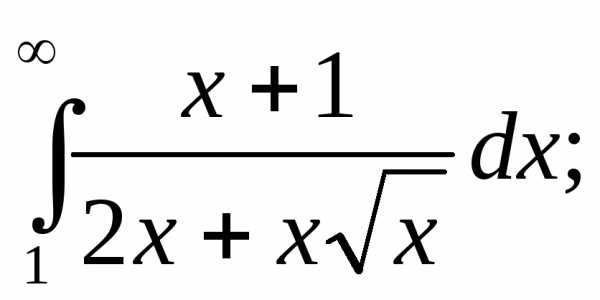 15.
15.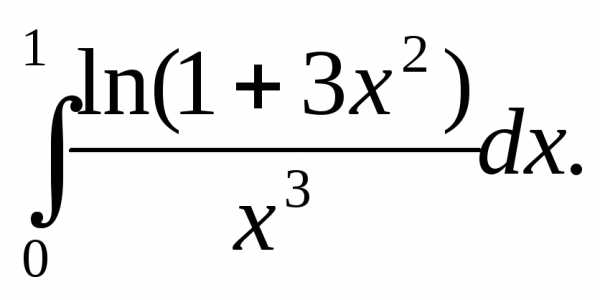
16. Найти площадь области, ограниченной линиями
х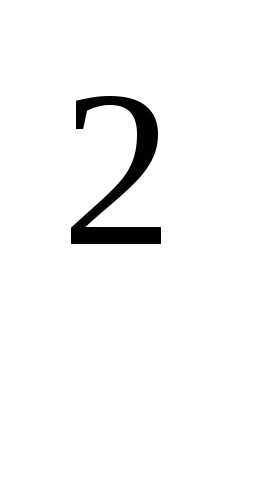 +
8у – 16 = 0, х
+
8у – 16 = 0, х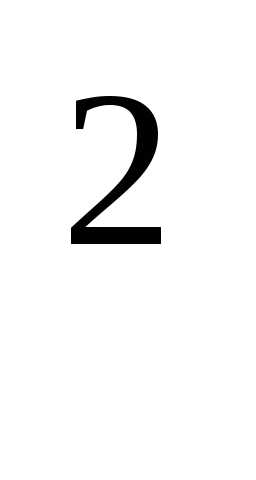
17. Найти длину дуги кривой
y
= ln cos x + 5? 0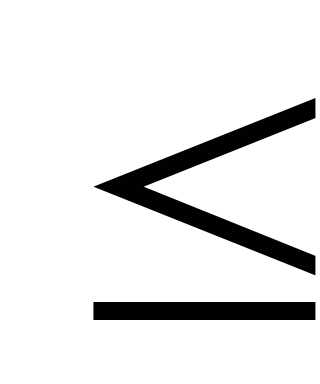 x
x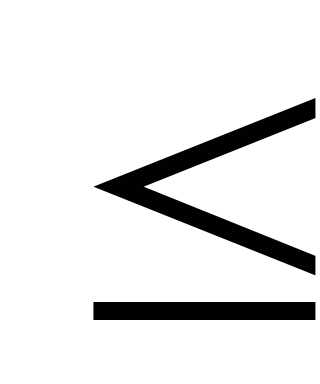
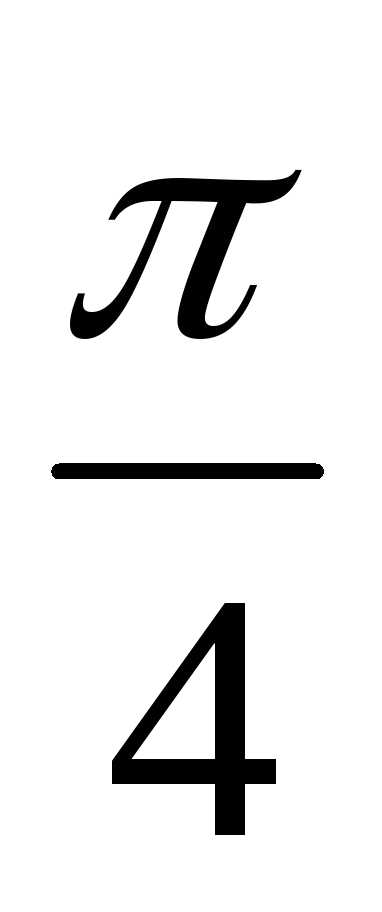 .
.
Содержание:7
Титульный лист.
Задание. Содержание.
Пример № 1, 2, 3, 4, 5, 6, 7,
Пример № 8, 9,
Пример № 10, 11,
Пример № 12, 13, 14, 15, 16,
Пример № 17.
Вариант 5.7
1. 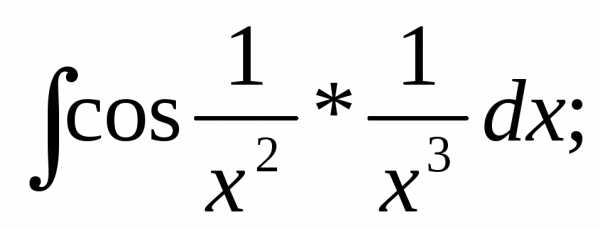
Решение:
Ответ: 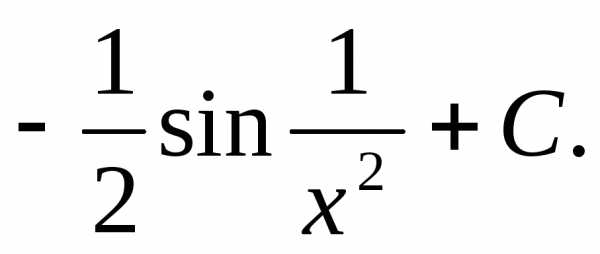
2. 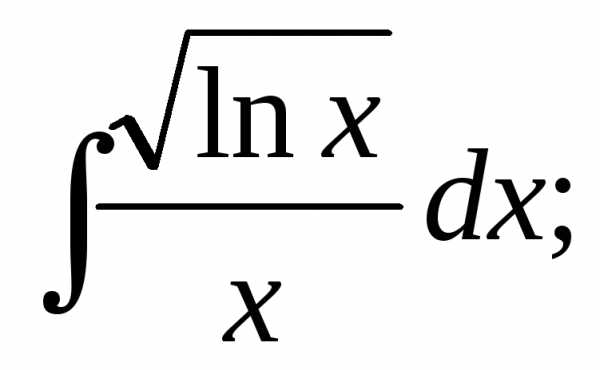
Решение:
Ответ:
3. 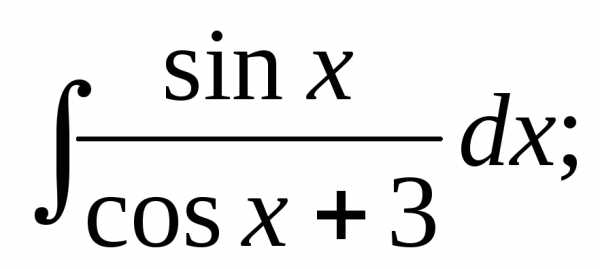
Решение: 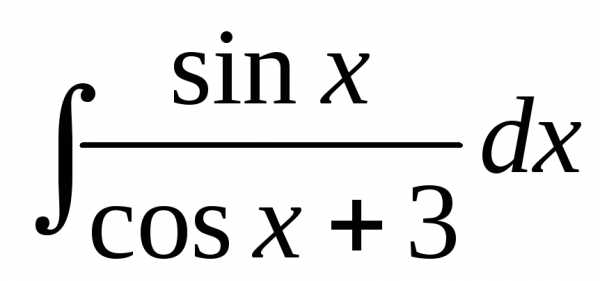 =
—
=
—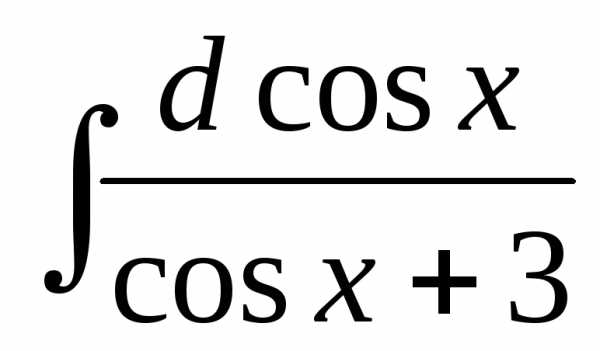 =-
=-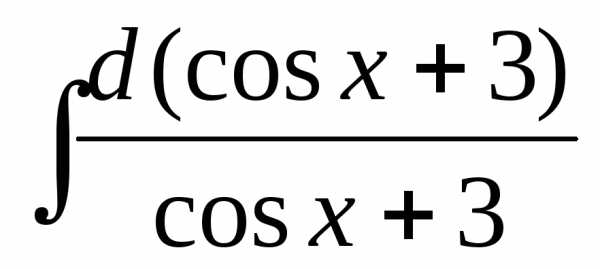 =
=
Ответ: .
4.
Решение:
Ответ: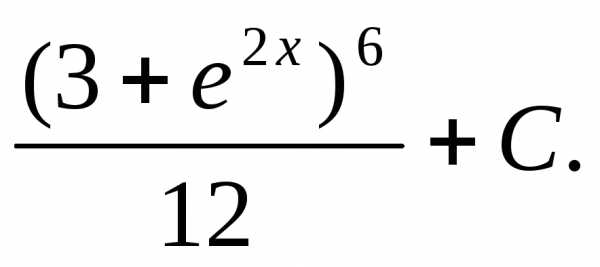
5. 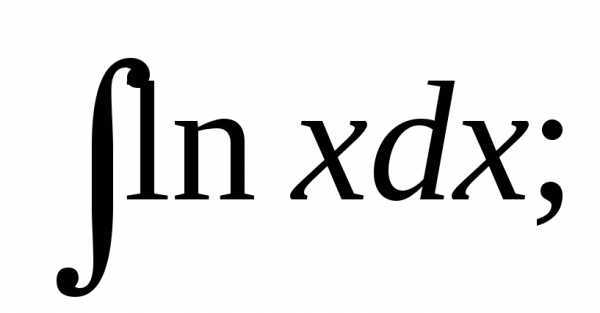
Решение: 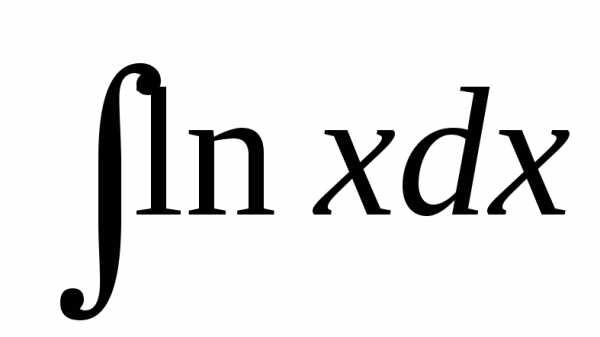 =x
ln
x
—
=x
ln
x
— 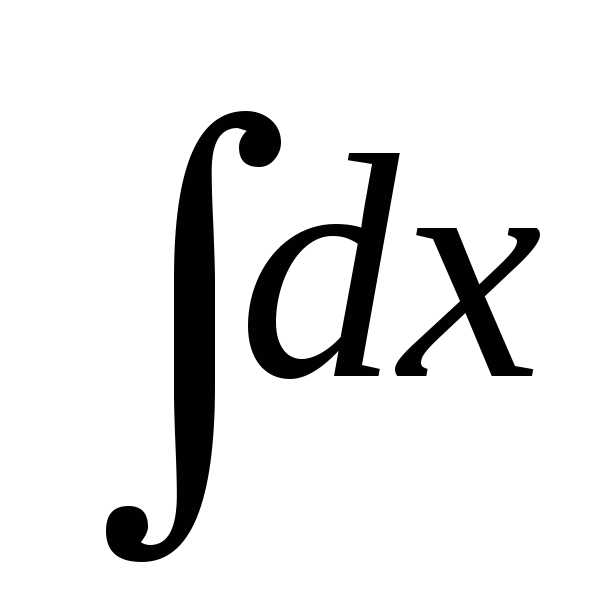 = x
ln
x
– x
+ C.
= x
ln
x
– x
+ C.
Ответ: x ln x – x + C.
6.
Решение:
Ответ: .
7. 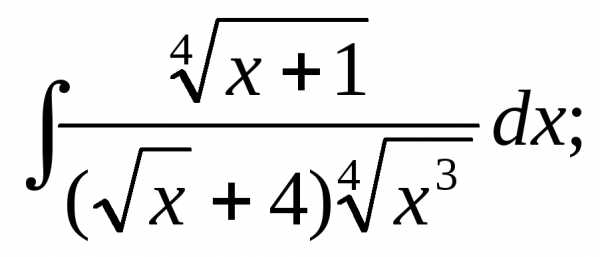

Ответ:
8. 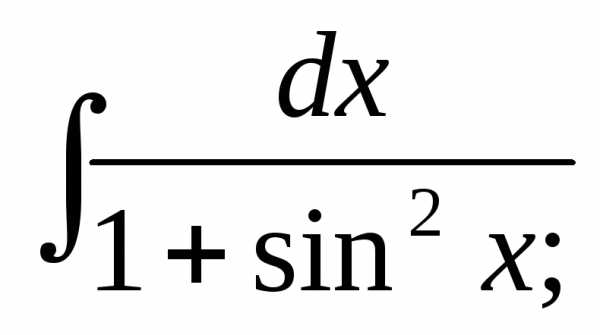
Решение:  воспользуемся универсальной
подстановкой
воспользуемся универсальной
подстановкой
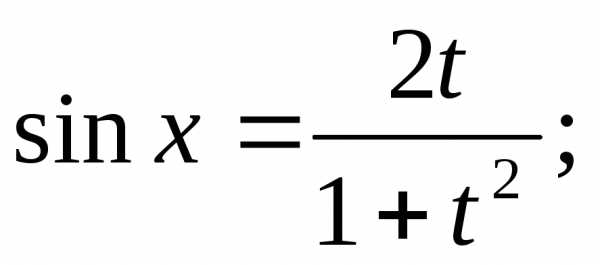
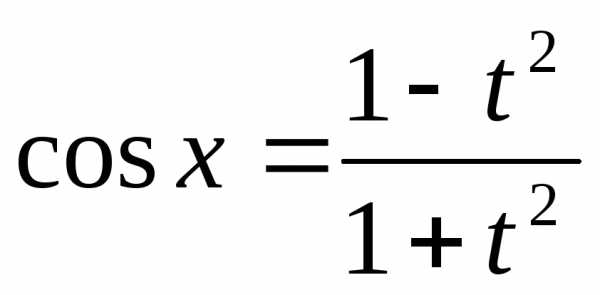 :
: 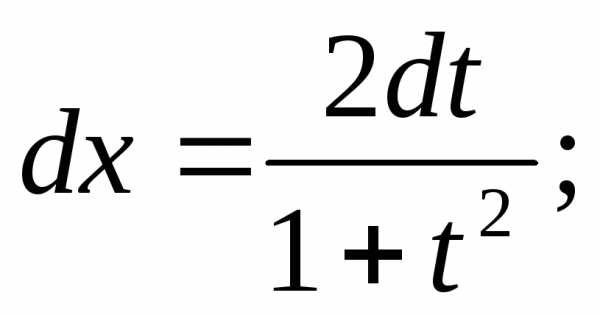 где
где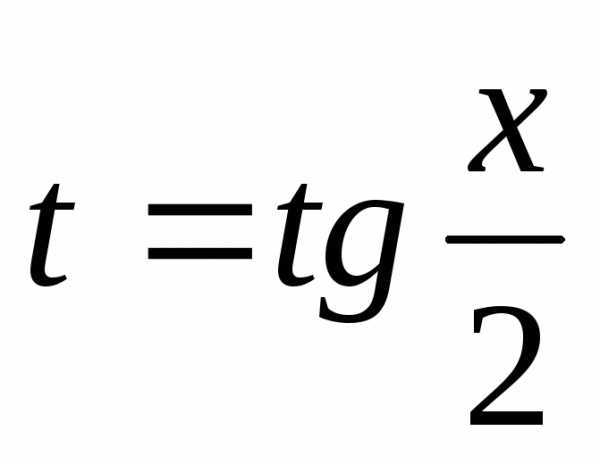
9.
Решение:
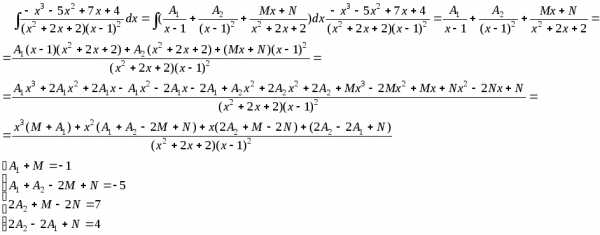

Вычислить определённые интегралы
Ответ: 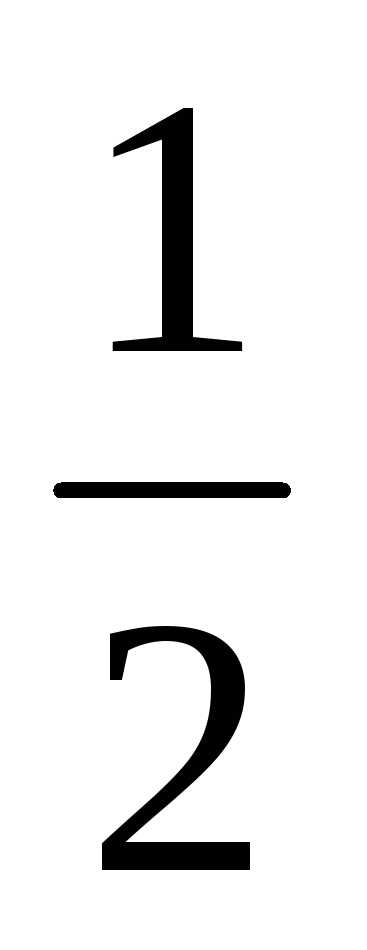 .
.
Ответ: 0
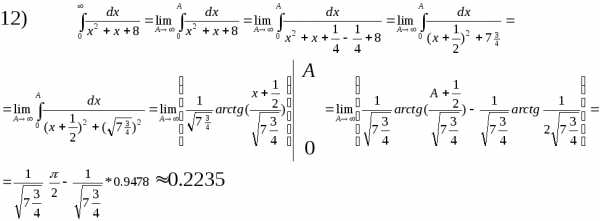
Ответ: 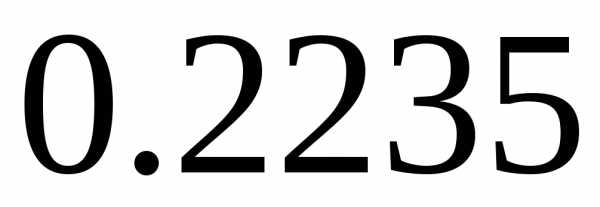 .
.
Выяснить сходимость несобственных интегралов
14. 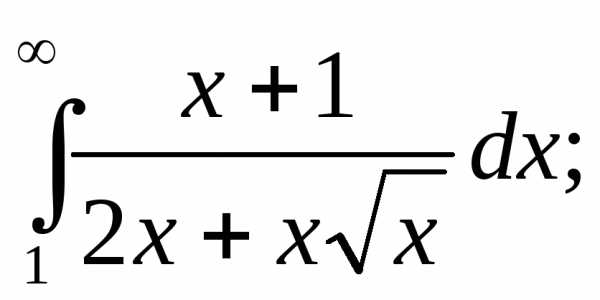
Решение:
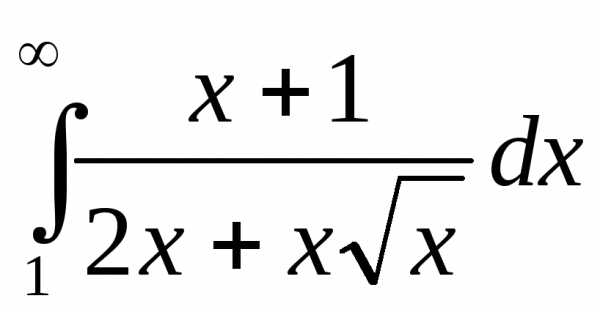
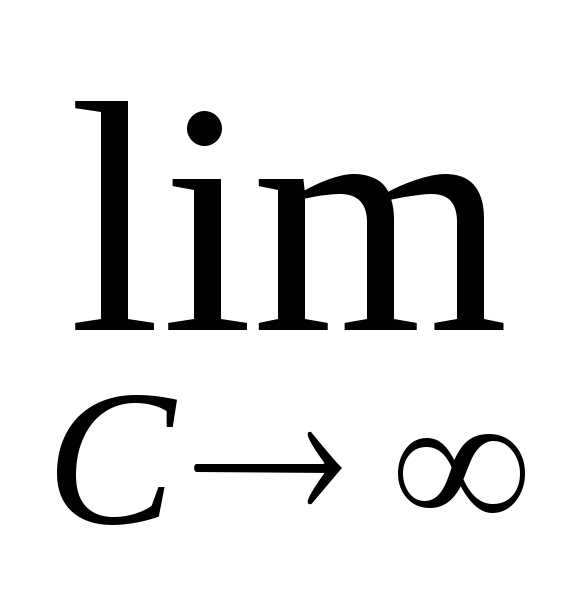
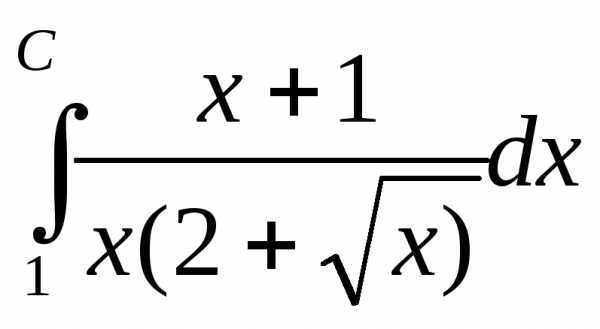 ==
==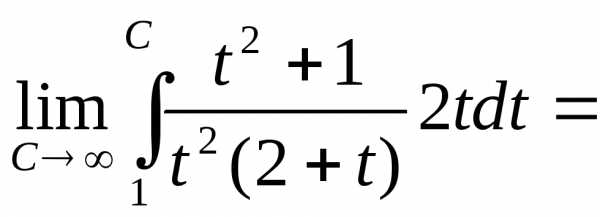 =
=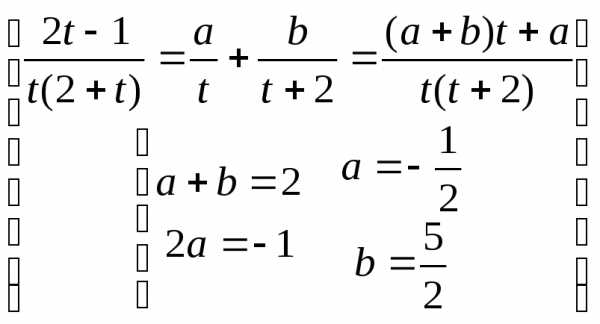 =
===
=
[Скорость
изменения функции 2(t+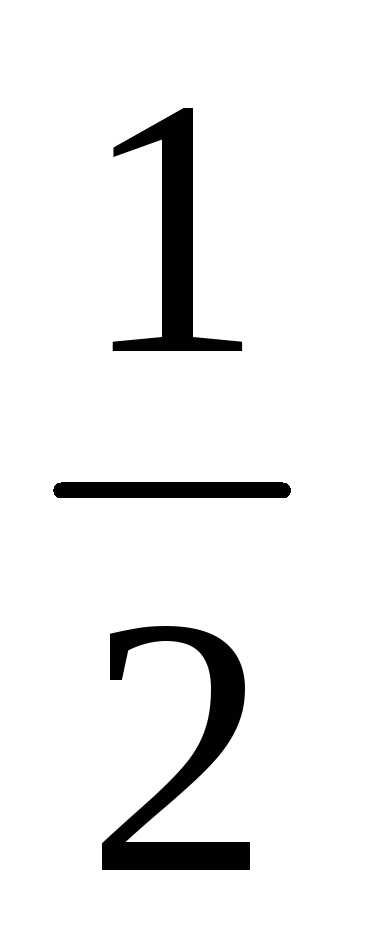 ln
t)
больше, чем скорость изменения функции
5 ln
(t+2).
ln
t)
больше, чем скорость изменения функции
5 ln
(t+2).
]
Поэтому интеграл расходится.
15. 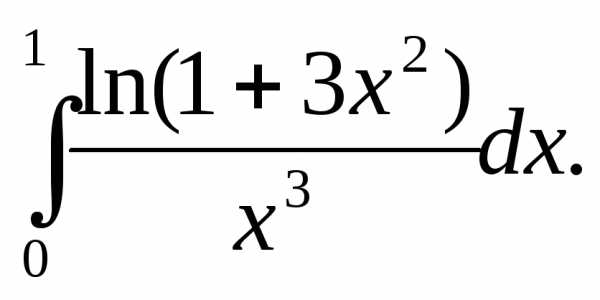
Решение:
Особая точка х=0
=
[при 
при 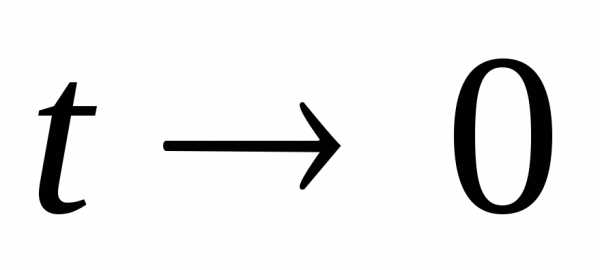 ,
поэтомуи]
,
поэтомуи]
Интеграл расходиться.
16) Найти площадь области, ограниченной линиями
х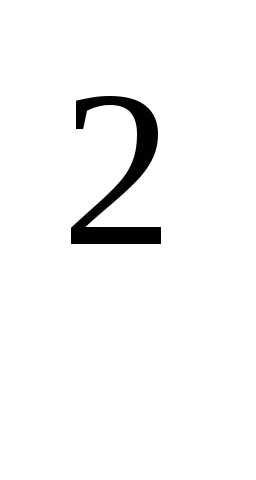 +
8у – 16 = 0, х
+
8у – 16 = 0, х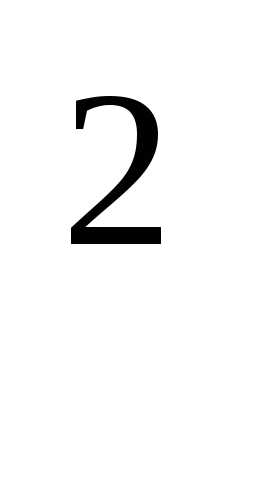 —
24у – 48 = 0.
—
24у – 48 = 0.
Решение:
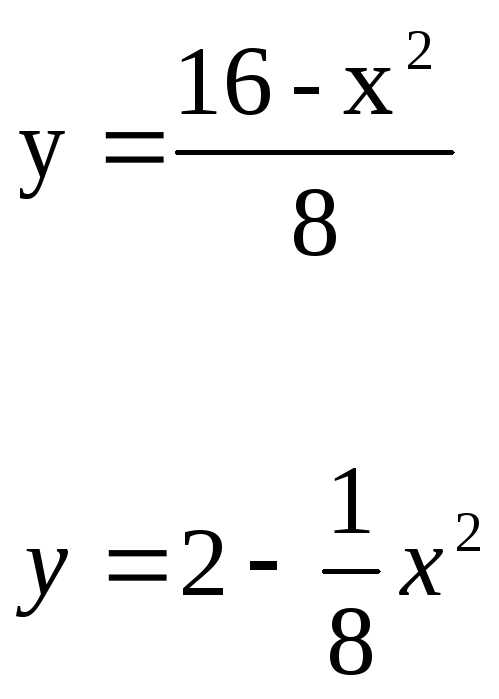
x0 4 2 -4
y 2 0 1.5 0
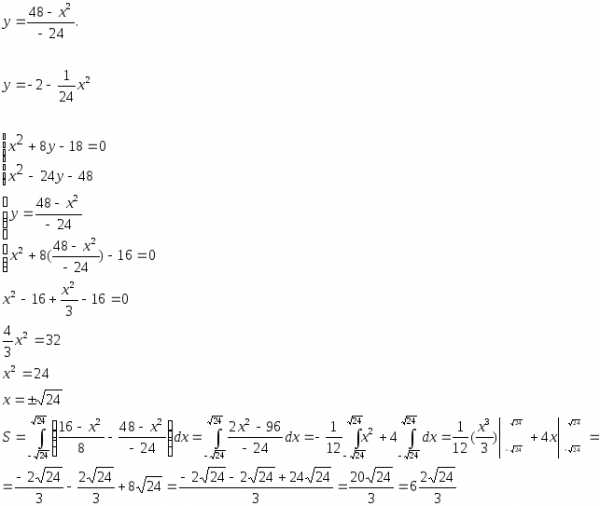
Ответ: 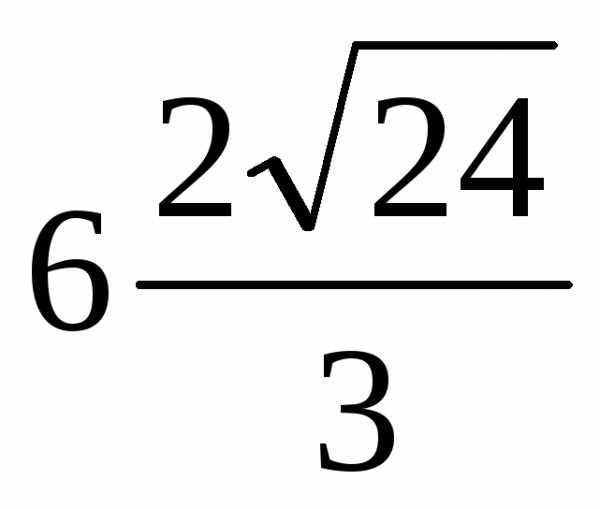 .
.

Ответ: 0,88.
studfiles.net
Определенный интеграл онлайн
Определенный интеграл онлайн для решения математики. Быстро решить задачу по нахождению определенного интеграла в режиме онлайн. Сайт www.matcabi.net позволяет найти определенный интеграл почти от любой математической функции онлайн. Правильно решить определенный интеграл функции, по заданному интервалу вычислить определенный интеграл от сложной функции — это быстро и легко с нашим сайтом, позволяющим находить определенный интеграл онлайн от математических функций. Найти определенный интеграл онлайн, при этом получить точный ответ. На сайте www.matcabi.net решение определенного интеграла онлайн осуществляется мгновенно. Достаточно ввести заданную функцию, указать пределы интегрирования, и ответ получите сразу в режиме онлайн. Ввести функцию, определить пределы интегрирования у определенного интеграла, получить мгновенный ответ и найти определенный интеграл онлайн от заданной функции. В математике понятие определенного интеграла широко применимо, поэтому задачи нахождения определенного интеграла онлайн встречаются часто. Не все математические сайты способны находить определенные интегралы функций в режиме онлайн быстро и качественно, особенно если требуется найти определенный интеграл от сложной функции или таких функций, которые не включены в общий курс высшей математики. Сайт www.matcabi.net поможет найти определенный интеграл онлайн и решить поставленную задачу. Используя онлайн решение определенного интеграла на сайте www.matcabi.net, вы получите точный ответ. Вы можете находить определенные интегралы от сложных математических функций в режиме онлайн, при этом пределы интегрирования могут варьироваться от минус бесконечности до плюс бесконечности. Для практических задач по нахождению определенного интеграла функции онлайн этого достаточно. Решая задачи по нахождению определенного интеграла онлайн, полезно проверить полученный ответ, используя онлайн решение определенных интегралов на сайте www.matcabi.net. Необходимо ввести заданную функцию, указать или выбрать пределы интегрирования, получить онлайн решение определенного интеграла и сравнить ответ с вашим решением. Проверка ответа займет не более минуты, достаточно решить определенный интеграл онлайн и сравнить ответы. Это поможет Вам избежать ошибки в решении и вовремя скорректировать ответ при взятии определенного интеграла онлайн от функции.
www.matcabi.net
