Теоремы о структуре общего решения однородной и неоднородной системы линейных уравнений.
С
труктура общего решения неоднородной линейной системы.
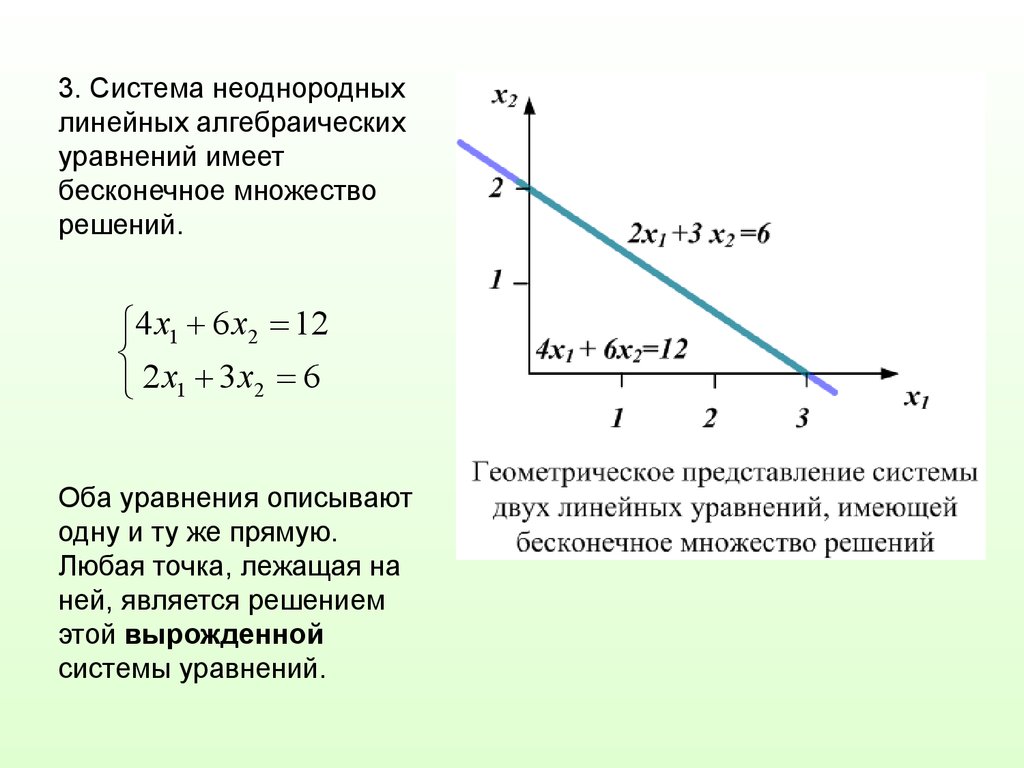
Рассмотрим неоднородную линейную систему (2.2):
.
Докажем следующие свойства ее решений:
Свойство 1. Сумма любого решения системы (2.2) и любого решения соответствующей однородной системы (4.2) является решением системы (2.2).
Доказательство.
Пусть с1, с2,…,сn – решение системы (2.2), а d1, d2,…,dn – решение системы (4.2) с теми же коэффициентами при неизвестных. Подставим в систему (2.2) xi=ci+di: .
После
перегруппировки слагаемых получим: .
Св. 2. Разность любых двух решений неоднородной системы (2.2) является решением соответствующей однородной системы (4.2).
Доказательство.: Пусть и — решения системы (2.2). Тогда
Утверждение доказано.
Следствие 3. Общее решение неоднородной системы (2.2) представляет собой сумму общего решения соответствующей однородной системы (4.2) и частного решения системы (2.2).
Тема 5. Квадратичные формы
Квадратичная форма, ее матрица, матричная запись квадратичной формы.
Однородный
многочлен второй степени относительно
переменных х1 и х2 : Ф(х1, х2)
= а11не
содержащий свободного члена и неизвестных
в первой степени называется квадратичной
формой переменных х1 и х 2.
Однородный многочлен второй степени относительно переменных х1, х2 и х3
не содержащий свободного члена и неизвестных в первой степени называется квадратичной формой переменных х1, х2 и х3.
Рассмотрим квадратичную форму двух переменных. Квадратичная форма имеет симметрическую матрицу А = . Определитель этой матрицы называется определителем квадратичной формы.
Пусть
на плоскости задан ортогональный базис .
Каждая точка плоскости имеет в этом
базисе координаты х1,
х2.
Если задана квадратичная форма Ф(х1, х
Тема 6. Алгебра векторов
Геометрический вектор, модуль вектора, коллинеарные и компланарные вектора.
Вектором называется направленный отрезок. К векторам относится также и нулевой вектор, начало и конец которого совпадают.
Длиной (модулем) вектора называется расстояние между началом и концом вектора.
Векторы называются коллинеарными, если они расположены на одной или параллельных прямых. Нулевой вектор коллинеарен любому вектору.
Векторы называются компланарными, если существует плоскость, которой они параллельны. Коллинеарные векторы всегда компланарны, но не все компланарные векторы коллинеарны.
Векторы называются равными, если они коллинеарны, одинаково направлены и имеют одинаковые модули.
Всякие
векторы можно привести к общему началу,
т.е. построить векторы, соответственно
равные данным и имеющие общее начало.
Из определения равенства векторов
следует, что любой вектор имеет бесконечно
много векторов, равных ему.
Свободные, скользящие и связанные вектора.
Свободные векторы – это векторы, начальная точка которых может быть выбрана произвольно.
Скользящие векторы – это равные между собой векторы, расположенные на одной прямой.
Связанные (присоединённые) векторы – это векторы, для которых важна точка приложения (пример: использующихся в физике).
Решение высшей математики онлайн
‹— Назад
Систему неоднородных уравнений запишем в матричном виде , где матрица имеет размеры .
Предложение 15.4 Пусть и — решения неоднородной системы . Тогда их разность является решением однородной системы с той же матрицей, то есть решением системы .
Доказательство. По условию и .
Тогда
Так как , то — решение однородной системы.
Предложение 15.5 Пусть — решение неоднородной системы , — любое решение однородной системы . Тогда — решение неоднородной системы.
Доказательство предоставляется читателю.
Определение 15.7 Пусть — некоторое решение неоднородной системы линейных уравнений , — общее решение однородной системы . Тогда выражение называется общим решением неоднородной системы.
Учитывая запись общего решения однородной системы через фундаментальную систему ее решений , получаем для общего решения неоднородной системы формулу
Из двух последних предложений следует, что любое решение неоднородной системы может быть получено из общего решения при некоторых числовых значениях коэффициентов .
Теорема 15.4 Система линейных уравнений может иметь либо бесконечно много решений, либо одно решение, либо не иметь решений.
Доказательство. Пусть система имеет решение . Если однородная система имеет только одно решение, то из формулы общего решения будет следовать, что — единственное решение неоднородной системы. Если однородная система имеет хотя бы одно ненулевое решение, то ее фундаментальная система решений будет состоять не менее, чем из одного решения. В формуле общего решения неоднородной системы будет произвольный коэффициент , и при различных его значениях мы будем получать различные решения неоднородной системы.
Математика, вышка, высшая математика, математика онлайн, вышка онлайн, онлайн математика, онлайн решение математики, ход решения, процес решения, решение, задачи, задачи по математике, математические задачи, решение математики онлайн, решение математики online, online решение математики, решение высшей математики, решение высшей математики онлайн, матрицы, решение матриц онлайн, векторная алгебра онлайн, решение векторов онлайн, система линейных уравнений, метод Крамера, метод Гаусса, метод обратной матрицы, уравнения, системы уравнений, производные, пределы, интегралы, функция, неопределенный интеграл, определенный интеграл, решение интегралов, вычисление интегралов, решение производных, интегралы онлайн, производные онлайн, пределы онлайн, предел функции, предел последовательности, высшие производные, производная неявной функции
Неоднородные линейные системы — дифференциальные уравнения
- Войти
- Биографии репетитора
- Подготовка к тесту
СРЕДНЯЯ ШКОЛА
- ACT Репетиторство
- SAT Репетиторство
- Репетиторство PSAT
- ASPIRE Репетиторство
- ШСАТ Репетиторство
- Репетиторство STAAR
ВЫСШАЯ ШКОЛА
- Репетиторство MCAT
- Репетиторство GRE
- Репетиторство по LSAT
- Репетиторство по GMAT
К-8
- Репетиторство AIMS
- Репетиторство по HSPT
- Репетиторство ISEE
- Репетиторство ISAT
- Репетиторство по SSAT
- Репетиторство STAAR
Поиск 50+ тестов
- Академическое обучение
репетиторство по математике
- Алгебра
- Исчисление
- Элементарная математика
- Геометрия
- Предварительный расчет
- Статистика
- Тригонометрия
репетиторство по естественным наукам
- Анатомия
- Биология
- Химия
- Физика
- Физиология
иностранные языки
- французский
- немецкий
- Латинский
- Китайский мандарин
- Испанский
начальное обучение
- Чтение
- Акустика
- Элементарная математика
прочие
- Бухгалтерия
- Информатика
- Экономика
- Английский
- Финансы
- История
- Письмо
- Лето
Поиск по 350+ темам
- О
- Обзор видео
- Процесс выбора наставника
- Онлайн-репетиторство
- Мобильное обучение
- Мгновенное обучение
- Как мы работаем
- Наша гарантия
- Влияние репетиторства
- Обзоры и отзывы
- Освещение в СМИ
- О преподавателях университета
Звоните прямо сейчас, чтобы записаться на обучение:
(888) 888-0446
Все ресурсы по дифференциальным уравнениям
1 Диагностический тест 29 практических тестов Вопрос дня Карточки Learn by Concept
Дифференциальные уравнения Помощь » Система линейных дифференциальных уравнений первого порядка » Неоднородные линейные системы
Решите следующую систему.
Возможные ответы:
Правильный ответ:
Сначала нам понадобится дополнительное решение и фундаментальная матрица для однородной системы. Таким образом, находим характеристическое уравнение заданной матрицы.
Используя , мы затем находим собственные векторы путем решения для собственного пространства.
У этого есть решения , или . Таким образом, подходящий собственный вектор — это просто .
Повторение для ,
У этого есть решения, и, следовательно, подходящий собственный вектор есть . Таким образом, наше дополнительное решение равно и наша фундаментальная матрица (хотя в данном случае не экспоненциальная матрица) равна . Изменение параметров говорит нам о том, что конкретное решение дается , поэтому сначала мы находим, используя обратное правило для матриц 2×2.
Таким образом, . При подключении имеем . Так .
Заканчиваем, у нас есть .
Прибавляя частное решение к однородному, получаем окончательное общее решение
Сообщить об ошибке
Уведомление об авторских правах
Просмотр дифференциальных уравнений для преподавателей
Роберт
Сертифицированный преподаватель
Политехнический институт Ренсселера, бакалавриат, электротехника. Бруклинский политехнический институт, магистр компьютерных наук.
Посмотреть Дифференциальные уравнения Репетиторы
Реза
Сертифицированный репетитор
Университет Шербрука, доктор философии, математики. Университет Манитобы, магистр наук, математика.
View Дифференциальные уравнения Репетиторы
Амелия
Сертифицированный репетитор
Колледж Остина, бакалавр искусств, прикладная математика. Университет Северной Каролины в Шарлотте, магистр наук, прикладные …
Все ресурсы по дифференциальным уравнениям
1 Диагностический тест 29 практических тестов Вопрос дня Карточки Learn by Concept
Решение неоднородного уравнения с использованием вариации параметров — Криста Кинг Математика
Вариация параметров для общего решения неоднородного дифференциального уравнения
Как и метод неопределенных коэффициентов, вариация параметров — это метод, который можно использовать для нахождения общего решения неоднородного дифференциального уравнения второго (или более высокого) порядка.
.
Привет! Я Криста.
Я создаю онлайн-курсы, чтобы помочь вам в учебе по математике. Читать больше.
Помните, что однородные дифференциальные уравнения имеют ???0??? в правой части, где неоднородные дифференциальные уравнения имеют ненулевую функцию в правой части.
Общее решение ???Y(x)??? неоднородному дифференциальному уравнению всегда будет суммой дополнительного решения ???y_c(x)??? и конкретное решение ???y_p(x)???.
???Y(x)=y_c(x)+y_p(x)???
Мы начнем с поиска дополнительного решения, предположив, что неоднородное уравнение на самом деле является однородным уравнением. Другими словами, мы просто заменяем ???g(x)??? с ???0??? а затем решить для значений ???x??? которые являются решениями однородного уравнения.
В зависимости от значений ???x??? которое мы найдем, мы сгенерируем дополнительное решение дифференциального уравнения.
Из дополнительного решения выберем фундаментальный набор решений ???\{y_1,y_2\}???.
В наборе решений будет все, кроме коэффициентов ???c_1??? и ???c_2???. Другими словами,
Это означает, что мы могли бы переписать дополнительные решения как
Как только у нас будет фундаментальный набор решений, мы включим его в простую систему линейных уравнений
???u_1’y_1+u_2’y_2=0???
???u_1’y_1’+u_2’y_2’=g(x)???
и затем решить систему для ???u_1′??? и ???u_2′???. Причина, которую мы хотим решить для ???u_1′??? и ???u_2′??? так что мы можем объединить их обоих, чтобы найти ???u_1??? и ???u_2???.
Если мы сможем найти ???u_1??? и ???u_2???, то можно сказать, что частное решение равно
???y_p(x)=u_1y_1+u_2y_2???
Поскольку общее решение является суммой дополнительного и частного решений,
???Y(x)=y_c(x)+y_p(x)???
мы просто добавляем частное решение к дополнительному решению, которое мы нашли ранее, чтобы получить общее решение.
{(n)}??? для дифференциальных уравнений более высокой степени) равным ???1???. Если это еще не ???1???, просто разделите его, чтобы получилось ???1???.
Как использовать изменение параметров для решения общего решения
Пройти курс
Хотите узнать больше о дифференциальных уравнениях? У меня есть пошаговый курс для этого. 🙂
Решение неоднородных дифференциальных уравнений методом вариации параметров
Пример
Варьирование параметров позволяет найти общее решение дифференциального уравнения. 9{-2x}}{2x}???
Большие наборы решений
Легко решить систему линейных уравнений
???u_1’y_1+u_2’y_2=0???
???u_1’y_1’+u_2’y_2’=g(x)???
потому что в наборе решений ???\{y_1,y_2\}??? было только два решения, и поэтому было только два неизвестных, ???u_1′??? и ???u_2′???.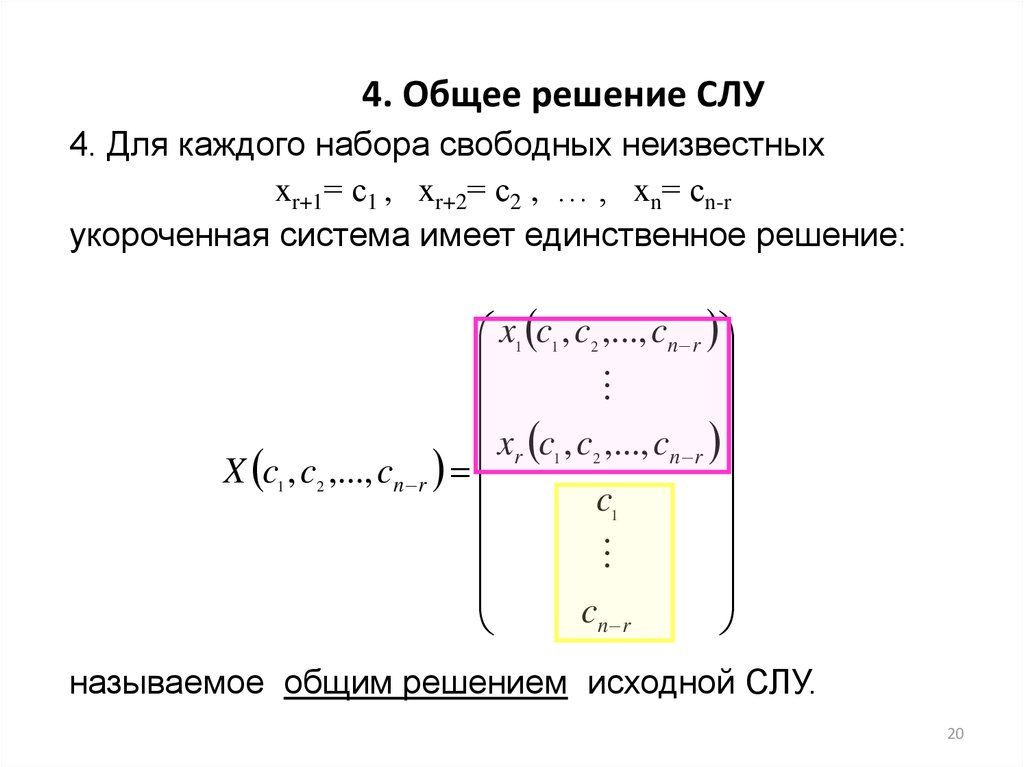
Но иногда набор решений будет больше, например ???\{y_1,y_2,y_3,y_4,…,y_n\}???. Например, если бы в наборе решений было четыре решения, нам пришлось бы решить эту систему:
???u_1’y_1+u_2’y_2=0???
???u_1’y_1’+u_2’y_2’=0???
???u_1’y_1»+u_2’y_2»=0???
???u_1’y_1»’+u_2’y_2»’=g(x)???
, потому что вам нужно столько же уравнений в системе, сколько решений в наборе решений. ???г(х)??? всегда является правой частью последнего уравнения системы; каждое из других уравнений имеет ???0??? как его правая сторона.
Если размер набора решений, а, следовательно, и размер системы линейных уравнений становится неуправляемым, для нахождения частного решения будет удобнее использовать правило Крамера.
Мы по-прежнему начнем с замены неоднородного уравнения на однородное, чтобы мы могли найти дополнительное решение и выделить фундаментальный набор решений.
Чтобы найти каждое неизвестное, ???u_1′???, ???u_2′???, ???u_3′??? и т. д., вместо решения системы линейных уравнений будем использовать набор матриц.
Предположим, что в нашем фундаментальном множестве есть четыре решения. Затем нам нужно найти определители этих матриц:
Тогда в этом примере
Следовательно,
Это означает, что конкретное решение
???y_p(x)=u_1y_1+u_2y_2+u_3y_3+u_4y_4???
, который действительно совпадает с
???y_p(x)=y_1\int\frac{g(x)W_1}{W}+y_2\int\frac{g(x)W_2}{W}+ y_3\int\frac{g(x)W_3}{W}+y_4\int\frac{g(x)W_4}{W}???
Помните, что вы можете изменить систему линейных уравнений и эти формулы для дополнительных и частных решений в зависимости от того, сколько решений у вас есть в фундаментальном наборе решений.
Давайте рассмотрим пример, в котором мы используем правило Крамера вместо решения системы линейных уравнений. Вы обычно используете правило Крамера с дифференциальными уравнениями более высокого порядка, потому что часто оказывается, что они имеют более двух решений в фундаментальном множестве.