Решение неравенств с модулем методом интервалов
Если неравенство содержит два и более модуля, его удобнее решать методом интервалов.
Процесс решения неравенств с модулем методом интервалов во многом похож на процесс решения уравнений с модулем методом интервалов.
Рассмотрим несколько примеров.
Пример 1. Решить неравенство |7 − x|+|2x + 3|< 16
Решение
Для начала находим такие x, при которых подмодульные выражения 7 − x и 2x + 3 обращаются в ноль. Для этого приравняем эти выражения к нулю и решим простейшие линейные уравнения:
Отметим числа 7 и на координатной прямой. Мéньшие числа отмечаем левее, бóльшие правее:
Получили три промежутка: , и Теперь необходимо решить исходное неравенство на каждом из этих промежутков. Надо иметь ввиду, что на каждом из этих промежутков модули исходного неравенства могут раскрываться по-разному.
Решим исходное неравенство на первом промежутке
Далее рассуждаем так:
Если , то при любом значении x на данном промежутке подмодульное выражение 7 − x станет неотрицательным, а значит модуль |7 − x| на промежутке будет раскрываться со знаком плюс.
Второй модуль |2x + 3| на промежутке будет раскрываться со знаком минус.
Тогда в результате раскрытия модулей на промежутке исходное неравенство примет вид:
Решим данное неравенство:
Итак, сейчас мы рассматриваем промежуток . И решив на этом промежутке исходное неравенство мы получили неравенство x > −4.
Теперь начинается самое интересное. Надо выяснить выполняется ли неравенство x > −4 на промежутке . Или задать такой вопрос: «при каких значениях промежутка выполняется неравенство x > −4»
Для наглядности нарисуем еще одну координатную прямую и изобразим на ней решения неравенства x > −4 и
На рисунке видно при каких значениях промежутка выполняется неравенство x > −4. Эти значения лежат в промежутке от −4 до
Значит первым нашим решением будет промежуток от −4 до
Решим теперь исходное неравенство на промежутке
Если , то при любом значении x на данном промежутке подмодульное выражение 7 − x станет неотрицательным, а значит модуль |7 − x| на промежутке будет раскрываться со знаком плюс.
Второй модуль |2x + 3| на промежутке тоже будет раскрываться со знаком плюс.
После раскрытия модулей на промежутке исходное неравенство примет вид:
Решим данное неравенство:
Cейчас мы рассматриваем промежуток . И решив на этом промежутке исходное неравенство мы получили неравенство x < 6. Теперь надо выяснить выполняется ли неравенство x < 6 при
Неравенство x < 6 выполняется не на всём промежутке , а лишь на промежутке до 6. Запишем наше второе решение:
Решим теперь исходное неравенство на последнем промежутке
Если , то при любом значении x на данном промежутке подмодульное выражение 7 − x станет отрицательным, а значит модуль |7 − x| на промежутке будет раскрываться со знаком минус. Второй модуль |2x + 3| на промежутке будет раскрываться со знаком плюс.
Тогда в результате раскрытия модулей на промежутке исходное неравенство примет вид:
Решим данное неравенство:
Cейчас мы рассматриваем промежуток .
И решив на этом промежутке исходное неравенство мы получили неравенство , Теперь надо выяснить выполняется ли неравенство при
Мы видим, что неравенство не выполняется ни при каких значениях промежутка . Это значит, что исходное неравенство на промежутке решений не имеет.
Действительно, возьмём любое число из промежутка , например, число 9 и подставим его в исходное неравенство. В результате получим неравенство которое не выполняется:
Теперь нужно собрать воедино ответы, которые мы получили на каждом промежутке. Чтобы сделать это, просто объединим промежутки и
Ответ: (−4 ; 6).
Пример 2. Решить неравенство: 3|x − 2|+|5x − 4| ≤ 10
Решение
Найдём x, при которых подмодульные выражения x − 2 и 5x − 4 обращаются в ноль. Для этого приравняем эти выражения к нулю и решим простейшие линейные уравнения:
Отметим числа 2 и на координатной прямой:
Решим исходное неравенство на промежутке .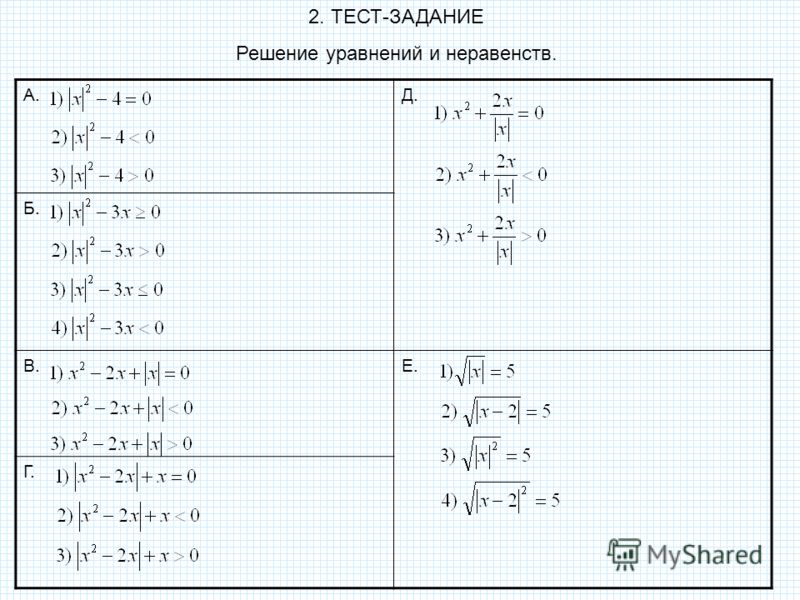
Оба модуля на данном промежутке раскрываются с минусом:
Полученное неравенство x ≥ 0 выполняется не на всем промежутке , а только на промежутке от 0 до
Решим теперь исходное неравенство на следующем промежутке . На данном промежутке модуль|x − 2| раскрываются с минусом, а модуль |5x − 4| с плюсом:
Полученное неравенство x ≤ 4 выполняется на всём промежутке . Значит на промежутке исходное неравенство имеет следующее решение:
Решим исходное неравенство на следующем промежутке x ≥ 2. Оба модуля на данном промежутке раскрываются с плюсом:
Полученное неравенство выполняется не на всем промежутке x ≥ 2, а только на промежутке от 2 до
Запишем окончательный ответ. Для этого объединим промежутки , и
Ответ: .
Задания для самостоятельного решения
Задание 1. Решить неравенство:
Решение:
Ответ: .
Показать решение
Задание 2. Решить неравенство:
Решение:
Ответ: решений нет.
Показать решение
Задание 3. Решить неравенство:
Решение:
Ответ: .
Показать решение
Задание 4. Решить неравенство:
Решение:
Ответ: .
Показать решение
Задание 5. Решить неравенство:
Решение:
Ответ: .
Показать решение
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
Урок по теме «Уравнение и неравенства с модулем». 10-й класс
Тип урока: урок совершенствования умений и навыков.
Цели урока:
Дидактическая: научить применять полученные знания при решении заданий повышенного уровня сложности, стимулировать учащихся к овладению рациональными приёмами и методами решения.
Развивающая: развивать логическое мышление, память познавательный интерес, вырабатывать умение анализировать и сравнивать.
Воспитательная: развивать аккуратность и трудолюбие, продолжить формирование навыков контроля и самоконтроля.
Ход урока
1. Организационный этап (1 минута).
2. Постановка цели (3 минуты).
Сегодня на уроке мы продолжим отрабатывать навыки решения уравнений и неравенств с модулем, используя как традиционные методы, так и нестандартные подходы.
3. Проверка домашнего задания (10 минут).
Если учащиеся не готовы показать все способы, то решение показывается на экране интерактивной доски. (Приложение 1)
Учитель вызывает по желанию 7-х человек к доске, параллельно проводит
фронтальную беседу по теоретическим вопросам.
(Приложение
2) Выставляет оценку за д/з.
На дом вам было предложено решить уравнения
|x – 6| = x2 – 5x + 9
|x2 + 4x + 3| = x + 3
|x – 6| = |x2 – 2x|
|x – 2| + |x – 1| = x – 8
и неравенства |x + 2| < 3 различными способами. Посмотрим ваше решение.
4. Выполнение упражнений (20 минут).
Многообразие приёмов решения задач с модулем подталкивает нас к выбору более рационального из них при решении конкретных уравнений или неравенств.
№ 1 (устно).
Учитель направляет на выбор рационального метода решения.
Учащиеся предлагают методы решения, один учащийся устно объясняет решение уравнения №1.
Решить уравнение |x2 – 6x – 7| = 7 + 6x – x2.
Решение (на основе аналитического определения модуля).
№2 Решить уравнение .
Учитель совместно с учащимися выбирает метод решения уравнения.
Следит за грамотным решением предложенного уравнения и одновременно проверяет индивидуальные решения уравнений у учащихся работающих на боковой доске по карточке, выставляет оценки за работу.
2 человека работают на боковой доске индивидуально
(Приложение 3), остальные записывают в тетрадь решение уравнения №2.Решение (применение геометрической интерпретации модуля).
На геометрическом языке: требуется найти точки с координатами х такие, что сумма расстояний от этих точек до точек с координатами -1 и 1 равна 2. Очевидно, что эти точки располагаются на отрезке [–1;1]
Ответ: [–1;1].
№3 Решите неравенство
Учитель направляет на выбор рационального метода решения.
Один ученик решает неравенство № 3. Остальные участвуют в выборе
рационального метода решения неравенства.
Записывают решение в тетрадь.
Решение (функционально графический метод).
Обе части неравенства определены на R. Левая часть неравенства принимает значения из отрезка [–1;1], а значения правой части составляют луч [1;∞]. Следовательно, исходное неравенство может иметь решение только, если выполняется система
Ответ: 0
№ 4 Найти все значения параметра b при которых уравнение ||x + 1| – 2| – 3 = b имеет ровно три различных корня.
Один ученик решает задание № 4 у доски. Три ученика работают по карточкам (Приложение 4), остальные записывают в тетрадь решение задания № 4.
Учитель следит за верностью рассуждений учащихся и одновременно проверяет решение заданий по карточкам, выставляет оценки за работу.
Решение (графический способ).
Рассмотрим функцию у = ||x + 1| – 2| – 3 и построим её график
используя преобразования, содержащие модуль, а также параллельный перенос.
Графиком функции у = b является прямая параллельная оси х.
Очевидно, что исходное уравнение имеет ровно три различных корня при b=-1.
Ответ: b = -1.
№ 5 Решить неравенство
Один ученик решает у доски, остальные записывают решение неравенства №5 в тетради.
Учитель обсуждает совместно с учащимися метод решения неравенства, следит за грамотностью рассуждений учащихся и верной записью решения неравенства. Выставляет оценку за работу.
Решение (метод интервалов).
Решим уравнение f(x)=0. Получим:
5. Домашнее задание (3 минуты).
(Заранее приготовлен слайд на интерактивной доске.)
1) Решить неравенство ||2x – 1| – 3| > 3.
2) Найти все значения параметра b при которых
уравнение |x – 3| + |x + 1| = b
имеет ровно два различных корня.
3) Решить уравнение cosx = |cosx|(x + 1.5)2.
(Приложение №5)
Учитель поясняет домашнее задание, обращая внимание учащихся на то, что аналогичные задания были разобраны на уроке.
Первое неравенство можно решить методом интервалов, второе уравнение – графически, а третье-с помощью аналитического определения модуля, рассматривая три случая (подмодульное выражение больше нуля, равно нулю и меньше нуля ) отдельно.
6. Подведение итогов урока (3 минуты).
Решение уравнений и неравенств с модулем требует от учащихся глубоких теоретических знаний, умений применять их на практике, требует внимания трудолюбия, сообразительности. Наверное, поэтому такие задания и включены в материалы ЕГЭ.
Сегодня на уроке все очень хорошо поработали, 15 человек получили оценки. Молодцы ребята!
Исследовательская работа на тему «Решение неравенств с модулем»
РАССМОТРЕНО Педагогическим советом МОУ «Зашижемская СОШ» Протокол № 1 от
« 14 » августа 2015г. | СОГЛАСОВАНО Заместитель директора по УВР _______ /Сидоркина Р.Л./ « 14 » августа 2015 г. | УТВЕРЖДАЮ Директор школы: ________ А.П.Конаков Приказ №63 от « 01» сентября 2015 г. |
Решение уравнений и неравенств с модулем
Исследовательская работа
Программу составила:
учитель математики высшей
категории МОУ «Зашижемская СОШ»
Сидоркина
Р.
Л.
с.Зашижемье, 2014 г.
Оглавление
1. Введение…………………………………………………………………3
2. Простейшие уравнения и неравенства с модулем……………………5
3. Графическое решение уравнений и неравенств с модулем………….8
4. Иные способы решения уравнений и неравенств с модулем…………10
5. Заключение ……………………………………………………………..16
6. Список литературы………………………………………………………18
Понятие абсолютной величины (модуля) является одной из важнейших характеристик числа как в области действительных, так и в области комплексных чисел.
Это
понятие широко применяется не только в различных разделах школьного курса
математики, но и в курсах высшей математики, физики и технических наук,
изучаемых в вузах.
Например, в теории приближенных вычислений используются
понятия абсолютной и относительной погрешностей приближенного числа. В механике
и геометрии изучаются понятия вектора и его длины (модуля вектора). В
математическом анализе понятие абсолютной величины числа содержится в
определениях таких основных понятий, как предел, ограниченная функция и др.
Задачи, связанные с абсолютными величинами, часто встречаются на математических
олимпиадах, вступительных экзаменах в вузы и на ЕГЭ. И
поэтому для нас стало важно изучить некоторые аспекты этой темы.
Главной целью в нашей работе является изучение различных методов решения уравнений и неравенств с модулями.
Данная цель должна быть достигнута при решении следующих задач:
· Изучить определение и некоторые свойства модуля.
· Освоить решение простейших уравнений и неравенств с модулем через равносильные переходы
·
Рассмотреть различные методы решения
уравнений и неравенств с модулем.
Объектом исследования являются некоторые типы уравнений и неравенств с модулем.
Предмет исследования – различные методы решения уравнений и неравенств с модулем, а именно: графический способ, метод геометрической интерпретации, использование тождества , применение теоремы о знаках, метод перехода к следствию, метод интервалов, метод домножения на положительный множитель ,метод раскрытия модулей.
В ходе исследования применялись такие методы, как изучение литературы по данному вопросу и практический метод.
В ходе работы мы исследовал такие источники, как:
1. «Большая математическая энциклопедия» для школьников и студентов;
2. Математика. ЕГЭ – 2011-2012. Типовые экзаменационные варианты. / Под редакцией А.Л. Семенова, И.В. Ященко.
3. М.Я. Выгодский. Справочник по элементарной математике
4. «Новейший справочник школьника»;
5. Энциклопедия «Я познаю мир» Математика;
6.
http://ru.wikipedia.
org/wiki/Заглавная_страница;
К простейшим уравнениям мы будем относить уравнения, решаемые одним из нижеприведенных равносильных переходов:
Примеры решения простейших уравнений.
Пример 1 Решим уравнение .
Решение.
Ответ. .
Пример 2 Решим уравнение .
Решение.
Ответ. .
Пример 3 Решим уравнение .
Решение.
Ответ. .
Ряд уравнений решается с использованием следующей теоремы.
Теорема.4 Сумма модулей равна алгебраической сумме подмодульнх величин тогда и только тогда, когда каждая величина имеет тот знак, с которым она входит в алгебраическую сумму.
Пример 5 Решить уравнение
Решение. Так как , то мы имеем равенство вида , где ,
.
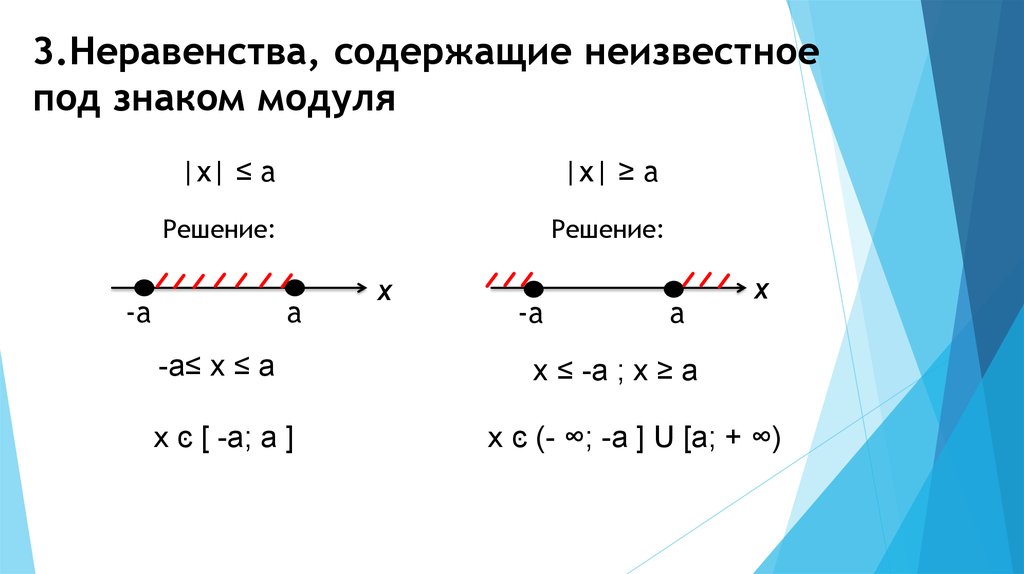Поэтому исходное уравнение равносильно
системе:
Ответ. .
Примеры решения простейших неравенств.
Пример 6 Решим неравенство .
Решение.
.
Ответ. .
Пример 7 Решим неравенство .
Решение.
Ответ. .
Как ни странно, но достаточно, чтобы избавиться от знака модуля в любых неравенствах.
Пример 8 Решить неравенство
Решение.
Ответ. .
3. Графическое решение уравнений и неравенств с модулем
Решение уравнений, содержащих знак абсолютной величины часто гораздо удобнее решать не аналитически, а графически (особенно уравнения содержащие параметры).
Пример 9 (С5, ЕГЭ — 2010)
C5.
Для каждого значения a укажите
число решений уравнения
Решение. Построим график функции . Для этого выделим полный квадрат :
Число точек пересечения графика функции у = с горизонтальными прямыми у = а равно числу решений уравнения.
Ответ: если < 0, то решений нет; если а= 0, то два решения, если 0 < а < 4, то четыре решения; если а=4, то три решения; если а > 4, то два решения.
Метод раскрытия модулей рассмотрим на примере:
Пример 10 Решить уравнение
Решение. Это уравнение содержит более одного модуля.
Метод решения уравнений, содержащих переменные под знаком двух и более модулей, состоит в следующем.
1. Найти значения переменной, при которых каждый из модулей обращается в нуль: , ; , ; , .
2.
Отметить эти точки на числовой прямой.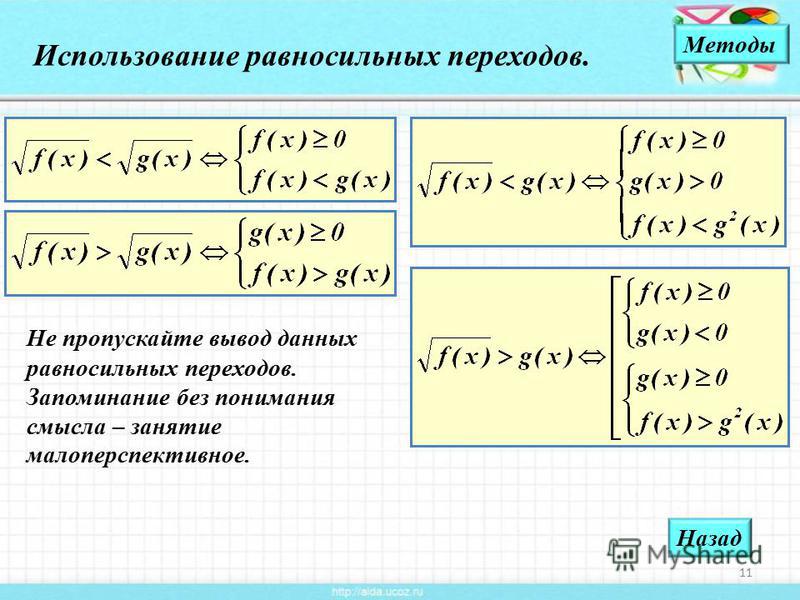
3. Рассматриваем уравнение на каждом из промежутков и устанавливаем знак выражений, которые находятся под модулями.
1) При или . Чтобы определить знак каждого из выражений под модулем на этом промежутке, достаточно взять любое значение из этого промежутка и подставить в выражение. Если полученное значение отрицательно, значит, при всех из этого промежутка выражение будет отрицательным; если полученное числовое значение положительно, значит, при всех значениях из этого промежутка выражение будет положительным.
Возьмем значение из промежутка и подставим его значение в выражение , получаем , значит на этом промежутке отрицательно, а следовательно «выйдет» из под модуля со знаком «минус», получим: .
При этом значении , выражение получит значение , значит, оно на промежутке также принимает отрицательные значения и «выйдет» из модуля со знаком «минус», получим: .
Выражение получит значение и «выйдет» из под модуля со знаком «минус»: .
Уравнение
на этом промежутке получится таким: , решая его,
находим: .
Выясняем, входит ли это значение в промежуток . Оказывается входит, значит является корнем уравнения.
2) При . Выбираем любое значение из этого промежутка. Пусть . Определяем знак каждого из выражений под модулем при этом значении . Оказывается, что выражение положительно, а два других отрицательны.
Уравнение на этом промежутке примет вид: . Решая его, находим . Это значение не входит в промежуток , а значит, не является корнем уравнения.
3) При . Выбираем произвольное значение из этого промежутка, скажем, и подставляем в каждое из выражений. Находим, что выражения и положительны, а — отрицательно. Получим следующее уравнение: .
После преобразования, получим: , а значит, уравнение не имеет корней на этом промежутке.
4) При . Нетрудно установить, что все выражения на этом промежутке положительны, а значит получим уравнение: , , которое входит в промежуток и является корнем уравнения.
Ответ. , .
Пример 11 Чему равна сумма корней уравнения (корень, если он один) уравнения
Решение.
Рассмотрим выражение
и преобразуем его к виду
Очевидно, что числитель дроби при любых значениях переменной является положительным числом. Значит дробное выражение положительно, если (т.к. ). Преобразуем полученное выражение, при условии . Получим уравнение, равносильное исходному:
Ответ. .
Пример 12 Решить уравнение
Решение. Поскольку левая часть уравнения неотрицательна, при всех допустимых значениях переменной, на множестве корней уравнения правая его часть тоже должна быть неотрицательной, отсюда условие , на этом промежутке знаменатели обеих дробей равны, и остается решить уравнение . Решая его и учитывая ограничение , получаем
Ответ. .
Геометрический смысл выражения — длина отрезка координатной оси, соединяющего точки с абсциссами и . Перевод алгебраической задачи на геометрический язык часто позволяет избежать громоздких выкладок.
Пример 13 Решим уравнение .
Решение. Будем рассуждать следующим образом: исходя из геометрической интерпретации модуля, левая часть уравнения представляет собой сумму расстояний от некоторой точки с абсциссой до двух фиксированных точек с абсциссами 1 и 2. Тогда все точки с абсциссами из отрезка обладают требуемым свойством, а точки, расположенные вне этого отрезка, — нет.
Ответ. .
Пример 14 Решить неравенство .
Решение. Изобразим на координатной прямой точки, сумма расстояний от которых до точек и в точности равна . Это все точки отрезка . Для всех чисел вне данного отрезка сумма расстояний будет больше двух.
Ответ. .
· Решение уравнений с использованием тождества
Пример (С3, ЕГЭ — 2010)15 Решить уравнение
Решение. Дважды применяя тождество , получим уравнение
решением которого является интервал .
Ответ.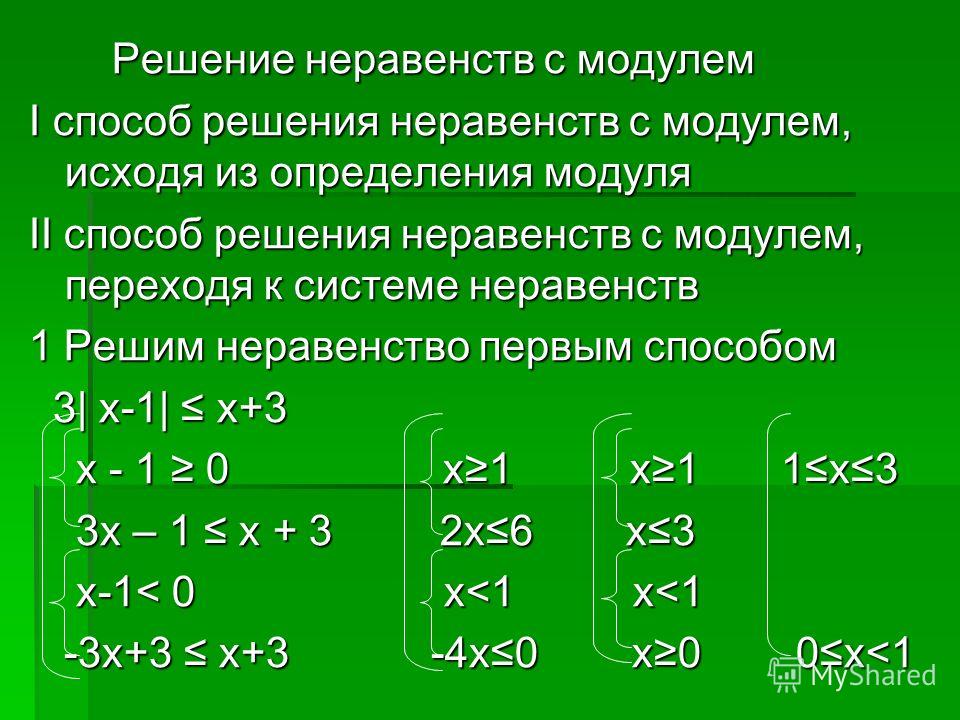
.
Пример (С3, ЕГЭ — 2011)16 17 Решить уравнение
Решение. .
Ответ. .
Сформулируем теорему, удобную при решении неравенств, относительно произведений или частных разности модулей:
Теорема 18 Знак разности модулей двух выражений совпадает со знаком разности квадратов этих выражений.
Пример 19 Решить неравенство
Решение. Воспользуемся теоремой:
Используя формулу разности квадратов, разложим числитель и знаменатель на множители и решим полученное рациональное неравенство.
Ответ.
Все
уравнения с модулями могут быть решены следующим образом: рассмотрим весь набор
уравнений, который может получится при раскрытии модулей, но не будем
выписывать соответствующие промежутки. Решая каждое из полученных уравнений,
получим следствия исходного уравнения. Остается только проверить не приобрели
ли мы посторонних корней прямой их подстановкой в исходное уравнение.
Пример 20 Решим уравнение
Решение. Последовательно переходя к следствиям, получаем:
Нетрудно убедиться, что найденные числа не являются корнями исходного уравнения.
Ответ. нет решения.
Применение метода интервалов основано на следующей теореме.
Теорема 21 Функция, непрерывная на промежутке и необращающаяся на нем в нуль, сохраняет на этом промежутке свой знак.
Это означает, что нули функции и границы промежутков ее непрерывности разделяют область определения функции на участки, где она сохраняет постоянный знак. Применение метода поясним на примере.
Пример 22 Решим неравенство
Пусть
. Областью определения данной функции есть
. Решая уравнение получим, что функция не обращается в нуль ни при каком
значении переменной. Это означает, что на всей области определения функция
является знакопостоянной.
Вычисляя, например, ,
получаем, что функция принимает только положительные значения.
Ответ. .
Метод интервалов позволяет решать более сложные уравнения и неравенства с модулями, но в этом случае он имеет несколько иное назначение. Суть состоит в слудующем. Находим корни всех подмодульных выражений и разбиваем числовую ось на промежутки знакопостоянства этих выражений. Это позволяет, последовательно перебирая эти промежутки, одновременно избавляться от всех модулей и решать обычное уравнение или неравенство (проверяя при этом, что найденный ответ входит в данный промежуток).
Пример 23 Решить неравенство
Решение. «Ловушка» заключается в том, что в задаче имеется несколько модулей, раскрывать которые — значит получить, громоздкое решение. Умножим дробь на некоторое выражение, принимающее лишь положительные значения и такое, чтобы упростить исходное неравенство:
Ответ. .
Заключение.
Подводя итог нашей работы, можно сказать следующее.
Целью работы было изучение различных методов решения уравнений и неравенств с модулями.
Рассмотрены некоторые разновидности простейших уравнений и неравенств с модулем, решаемых с помощью равносильных переходов,а также теоремы о сумме модулей; графический способ решения уравнений. Нужно сказать, что в школьном курсе математики именно эти методы решения наиболее часто используются. Графический метод особо актуален при решении задач C5 из контрольно-измерительных материалов ЕГЭ.
Далее
мы изучили на нескольких примерах иные способы решения уравнений и неравенств с
модулями, а именно: метод раскрытия модулей; решение уравнений, содержащих
модули неотрицательных выражений; решение уравнений с использованием
геометрической интерпретации; с использованием тождества ; применение теоремы о знаках; решение
уравнений переходом к следствию, домножением на положительный множитель,а
также решение неравенств методом интервалов.
Таким образом, в ходе исследования мы пришли к следующим выводам.
Наиболее универсальными и применимыми к наибольшему количеству задач мы считаем метод раскрытия модулей, графический метод и метод интервалов. Это убеждение возникло в результате решения большого числа задач из контрольно-измерительных материалов ЕГЭ, предметных чемпионатов, олимпиадных задач, а также изучение литературы по данному вопросу. Также очень важным мы считаем знание и применение тождества , так как оно используется не только при решении уравнений и неравенств, но и для преобразования многих выражений с радикалами. Остальные методы решения, которые мы рассмотрели, безусловно, представляют большой интерес в плане расширения математического кругозора и общего математического развития. Поэтому мы планируем использовать их для подготовки к государственной итоговой аттестации в форме ЕГЭ и подготовке к обучению в высшем учебном заведении.
Список
используемой литературы.
1. «Большая математическая энциклопедия» для школьников и студентов;
2. Математика. ЕГЭ – 2011, 2012. Типовые экзаменационные варианты. / Под редакцией А.Л. Семенова, И.В. Ященко.
3. М.Я. Выгодский. Справочник по элементарной математике
4. «Новейший справочник школьника»;
5. Энциклопедия «Я познаю мир. Математика»;
6. http://ru.wikipedia.org/wiki/Заглавная_страница;
6.3 – Уравнения и неравенства с абсолютными значениями
Цели обучения
- (6.3.1) – Решение уравнений, содержащих абсолютные значения
- Уравнения с одним абсолютным значением
- Уравнения с двумя абсолютными значениями
- Распознать, когда линейное уравнение, содержащее абсолютное значение, не имеет решения
- (6.3.2) – Решение неравенств, содержащих абсолютные значения
Далее мы научимся решать уравнение абсолютного значения . Чтобы решить такое уравнение, как [латекс]|2x — 6|=8[/латекс], мы замечаем, что абсолютное значение будет равно 8, если количество внутри столбцов абсолютного значения равно [латекс]8[/латекс] или [латекс]-8[/латекс].
Это приводит к двум различным уравнениям, которые мы можем решить независимо.
[латекс]\begin{array}{lll}2x — 6=8\hfill & \text{ или }\hfill & 2x — 6=-8\hfill \\ 2x=14\hfill & \hfill & 2x= -2\hfill \\ x=7\hfill & \hfill & x=-1\hfill \end{массив}[/latex]
Полезно знать, как решать задачи, связанные с функциями абсолютного значения. Например, нам может понадобиться идентифицировать числа или точки на линии, которые находятся на заданном расстоянии от заданной контрольной точки.
Уравнения с одним абсолютным значением
A Общее примечание: Уравнения с абсолютными значениями
Абсолютное значение x записывается как [латекс]|х|[/латекс]. Он имеет следующие свойства:
[латекс]\begin{array}{l}\text{If } x\ge 0,\text{ then }|x|=x.\hfill \\ \text{If }x <0,\text{ затем }|x|=-x.\hfill \end{массив}[/latex]
Для вещественных чисел [латекс]А[/латекс] и [латекс]В[/латекс] уравнение вида [латекс]|А|=В[/латекс], где [латекс]В\ge 0[ /латекс], будут иметь решения, когда [латекс]А=В[/латекс] или [латекс]А=-В[/латекс].
Если [латекс]В<0[/латекс], уравнение [латекс]|А|=В[/латекс] не имеет решения.
Уравнение абсолютного значения в форме [латекс]|ax+b|=c[/латекс] имеет следующие свойства:
[латекс]\begin{array}{l}\text{If }c< 0,|ax+b|=c\text{ не имеет решения}.\hfill \\ \text{Если }c=0,|ax+b|=c\text{ имеет одно решение}.\hfill \\ \ text{Если }c>0,|ax+b|=c\text{ имеет два решения}.\hfill \end{array}[/latex]
Как: Решите уравнение с абсолютной величиной.
- Изолируйте выражение абсолютного значения с одной стороны от знака равенства.
- Если [latex]c>0[/latex], напишите и решите два уравнения: [latex]ax+b=c[/latex] и [latex]ax+b=-c[/latex].
В следующем видео мы покажем примеры решения простого уравнения модуля.
Пример: Решение уравнений абсолютного значения
Решите следующие уравнения абсолютного значения:
- [латекс]|6x+4|=8[/латекс]
- [латекс]|3x+4|=-9[/латекс]
- [латекс]|3x — 5|-4=6[/латекс]
- [латекс]|-5x+10|=0[/латекс]
Раствор
В двух следующих видеороликах мы показываем примеры того, как решить уравнение абсолютного значения, которое требует, чтобы вы сначала изолировали абсолютное значение с помощью математических операций.
Попробуйте
Решите уравнение абсолютного значения: [латекс]|1 — 4x|+8=13[/латекс].
Решение
Уравнения с двумя абсолютными значениями
Некоторые из наших уравнений с абсолютными значениями могут иметь вид [латекс]|u|=|v|[/латекс] где [латекс]u[/латекс] и [латекс]v[/ латекс] – это алгебраические выражения. Например, [латекс]|x-3|=|2x+1|[/латекс].
Как бы мы их решили? Если два алгебраических выражения равны по модулю, то они либо равны друг другу, либо отрицательны друг другу. Свойство уравнений с абсолютными значениями гласит, что для любого алгебраического выражения [latex]u[/latex] и положительного действительного числа [latex]a[/latex], если [latex]|u|=a[/latex] , тогда [латекс]u=a[/латекс] или [латекс]u=-а[/латекс].
Это приводит нас к следующему свойству для уравнений с двумя абсолютными значениями:
Уравнения с двумя абсолютными значениямиДля любых алгебраических выражений [latex]u[/latex] и [latex]v[/latex], если [латекс]|u|=|v|[/латекс], то:
[латекс]u=v[/латекс] или [латекс]u=-v[/латекс].
Когда мы берем противоположное количество, мы должны быть осторожны со знаками и добавлять круглые скобки там, где это необходимо.
ПРИМЕР
Решите: [латекс]|5x-1|=|2x+3|[/латекс].
Показать ответ
Попробуйте
Уравнения с абсолютными значениями без решений
При решении уравнений с абсолютными значениями важно помнить об особых случаях. Абсолютное значение определяется как расстояние от 0 на числовой прямой, поэтому оно должно быть положительным числом. Когда выражение абсолютного значения равно отрицательному числу, мы говорим, что уравнение не имеет решения, или DNE.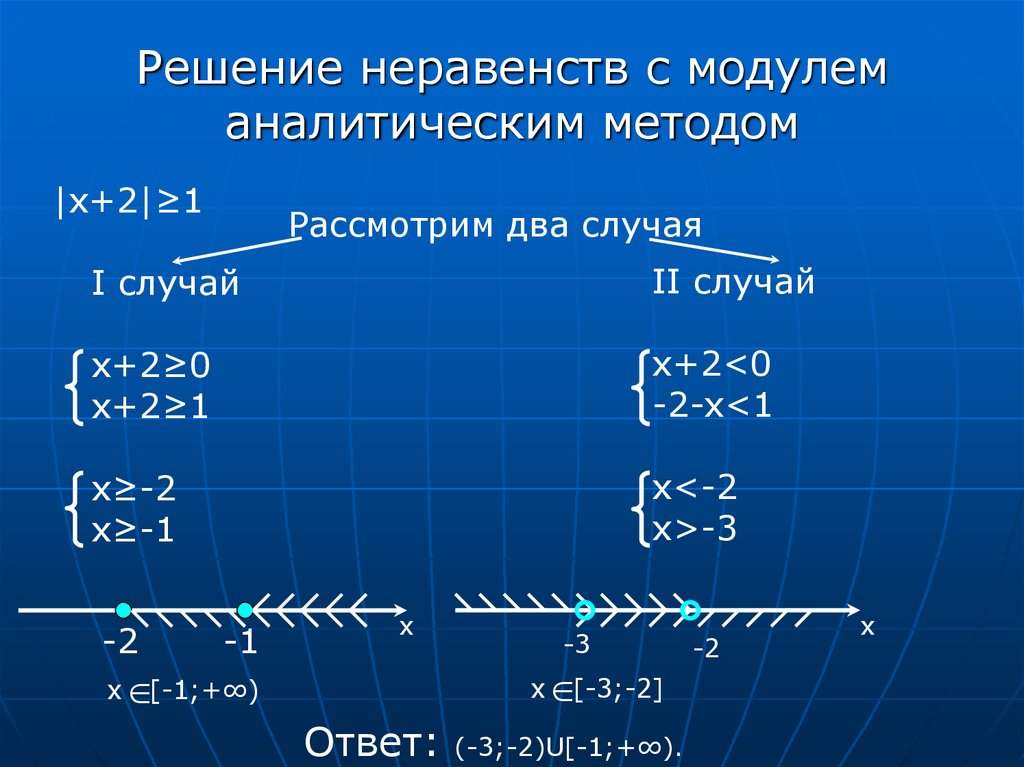
Обратите внимание, как это происходит в следующих двух примерах.
В этом последнем видео мы показываем больше примеров уравнений абсолютного значения, которые не имеют решений.
Давайте применим то, что вы знаете о решении уравнений, содержащих абсолютные значения, и то, что вы знаете о неравенствах, для решения неравенств, содержащих абсолютные значения. Начнем с простого неравенства.
[латекс]\левый|х\правый|\leq 4[/латекс]
Это неравенство читается как «абсолютное значение [латекс]х[/латекс] меньше или равно 4». Если вас попросят решить для [латекс]х[/латекс], вы хотите узнать, какие значения [латекс]х[/латекс] находятся на расстоянии 4 или менее единиц от 0 на числовой прямой. Вы могли бы начать с размышлений о числовой прямой и о том, какие значения [latex]x[/latex] удовлетворяют этому уравнению.
4 и [латекс]−4[/латекс] находятся на расстоянии четырех единиц от 0, поэтому они являются решениями. 3 и [латекс]-3[/латекс] также являются решениями, потому что каждое из этих значений меньше, чем на 4 единицы от 0. Так же как 1 и [латекс]-1[/латекс], 0,5 и [латекс]-0,5[ /latex] и т. д. Существует бесконечное количество значений для [latex]x[/latex], удовлетворяющих этому неравенству.
График этого неравенства будет иметь две замкнутые окружности, 4 и [латекс]−4[/латекс]. Расстояние между этими двумя значениями на числовой прямой окрашено в синий цвет, поскольку все эти значения удовлетворяют неравенству.
Решение можно записать так:
Неравенство: [латекс]-4\leq x\leq4[/латекс]
Интервал: [латекс]\влево[-4,4\вправо][/латекс]
Ситуация немного отличается, когда знак неравенства стоит «больше» или «больше или равно». Рассмотрим простое неравенство [латекс]\влево|х\вправо|>3[/латекс]. Опять же, вы можете подумать о числовой прямой и о том, какие значения [latex]x[/latex] отличаются от нуля более чем на 3 единицы.
На этот раз 3 и [латекс]−3[/латекс] не включены в решение, поэтому оба этих значения отмечены незакрашенными кружками. 2 и [латекс]-2[/латекс] не будут решениями, потому что они не более чем в 3 единицах от 0. Но 5 и [латекс]-5[/латекс] будут работать, как и все значения, расширяющие слева от [латекс]−3[/латекс] и справа от 3. График будет выглядеть так, как показано ниже.
Решение этого неравенства можно записать следующим образом:
Неравенство : [латекс]x<−3[/латекс] или [латекс]x>3[/латекс].
Интервал: [latex]\left(-\infty, -3\right)\cup\left(3,\infty\right)[/latex]
В следующем видео вы увидите примеры решения и выразить решение абсолютных неравенств с использованием И и ИЛИ.
Написание решений абсолютных неравенств
Для любого положительного значения [latex]a[/latex] и [latex]x[/latex] , одна переменная или любое алгебраическое выражение:
| Неравенство абсолютного значения | Эквивалентное неравенство | Обозначение интервала |
| [латекс]\влево|{х}\вправо|\ле{а}[/латекс] | [латекс]{-a}\le{x}\le{a}[/латекс] | [латекс]\влево[-а, а\вправо][/латекс] |
| [латекс]\левый| х \право|\lt{a}[/латекс] | [латекс]{ -a}\lt{x}\lt{ a}[/латекс] | [латекс]\влево(-а, а\вправо)[/латекс] |
| [латекс]\левый| х \право|\ge{ а}[/латекс] | [латекс]{x}\le\text{−a}[/latex] или [латекс]{x}\ge{ a}[/latex] | [латекс]\влево(-\infty,-a\право]\чашка\влево[a,\infty\вправо)[/латекс] |
| [латекс]\левый| х \right|\gt\text{a}[/latex] | [латекс]\displaystyle{x}\lt\text{−a}[/latex] или [латекс]{x}\gt{a}[/latex] | [латекс]\влево(-\infty,-a\вправо)\чашка\влево(a,\infty\вправо)[/латекс] |
Рассмотрим еще несколько примеров неравенств, содержащих абсолютные значения.
Определите случаи неравенств, содержащих абсолютные значения, которые не имеют решений
Как и в случае с уравнениями, могут быть случаи, когда неравенство не имеет решения.
Резюме
Абсолютные неравенства можно решить, переписав их с помощью составных неравенств. Первым шагом к решению абсолютных неравенств является выделение абсолютного значения. Следующий шаг — решить, работаете ли вы с неравенством ИЛИ или с неравенством И. Если неравенство больше числа, мы будем использовать ИЛИ. Если неравенство меньше числа, мы используем И. Помните, что если мы получим абсолютное значение больше или меньше отрицательного числа, решения не будет.
PDF НЕРАВЕНСТВА И АБСОЛЮТНЫЕ УРАВНЕНИЯ Обзор устройства Введение в решение неравенств
*Решение неравенств аналогично решению уравнений, используйте противоположные операции, чтобы изолировать переменную.
Решение неравенств: две операции (01:25) Для < и > незакрашенный кружок используется для обозначения того, что номер решения не включен в решение . Для и закрашенный кружок используется для обозначения того, что номер решения равен , включенному в решение.Составные неравенства
Чтобы решить составное неравенство, объединенное с « и », найдите значения переменной, которые удовлетворяют неравенствам и .
Чтобы решить составное неравенство, соединенное с « или », найдите значения переменной, которые удовлетворяют хотя бы одному неравенству.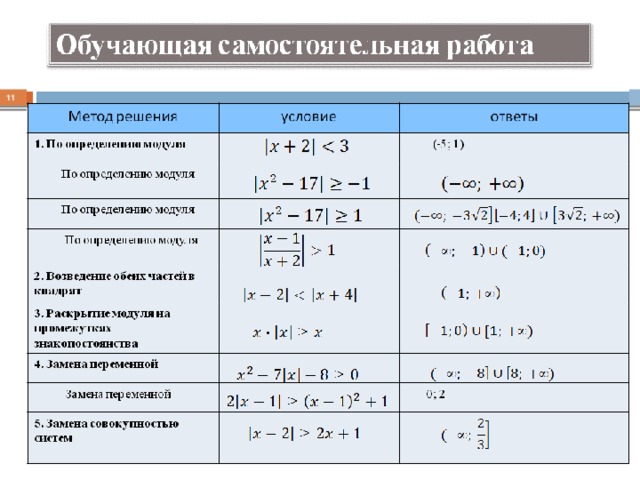 
Решение сложных неравенств (02:25) Стоп! Перейдите к вопросам № 1–13 по этому разделу, затем вернитесь, чтобы перейти к следующему разделу. Решение уравнений и неравенств с абсолютными значениями
Почему уравнения абсолютного значения имеют два решения? В простом уравнении абсолютного значения, таком как | х | = 5, давайте посмотрим, какие два значения x делают выражение верным? Поскольку | 5 | = 5, тогда х = 5. Следовательно, решение | х | = 5 равно х = 5 или х = –5. Давайте еще больше расширим понимание уравнения абсолютного значения. Давайте подумаем над следующим вопросом: В уравнении абсолютного значения |3 x + 4| = 19, какими двумя значениями может быть 3 x + 4 и почему? Абсолютное значение |19| = 19, поэтому 3 x + 4 может равняться 19. «Нажмите здесь», чтобы проверить ответ. Значение 3 x + 4 в |3 x + 4| = 19 может быть –19, потому что почему? Абсолютное значение |19| = 19, поэтому 3 x + 4 может равняться 19. «Нажмите здесь», чтобы проверить ответ. Какие два уравнения можно написать, чтобы найти значения x , которые решают |3 x + 4| = 19? 3 x + 4 = 19 ИЛИ 3 x + 4 = 19 «Нажмите здесь», чтобы проверить ответ. 1.) Перепишите уравнение без обозначения абсолютного значения.
Для решения абсолютных неравенств:
Стоп! Перейдите к вопросам 14–33, чтобы завершить этот модуль. Уравнения и неравенства с абсолютными значениями: Уравнения с абсолютными значениями очень полезны при решении задач, связанных со значениями, которые не могут быть отрицательными, например расстоянием. Например, представьте, что вы идете навестить своего друга Тони, который живет на улице 4 9.0563-й этаж многоквартирного дома, всего 10 этажей. Когда вы приходите, вы не можете вспомнить, на каком этаже живет Тони, поэтому вы пробираетесь внутрь, звоните ему с лестницы и спрашиваете, на каком он этаже. Он говорит, что находится на 4-м -м -м этаже, а вы говорите, вы в 2 этажах от него. Означает ли это, что вы находитесь на 2 -м -м этаже или на 6-м -м -м этаже? Это может быть и то, и другое, потому что оба варианта находятся на 2 этажах от квартиры Тони. Что касается абсолютных неравенств, они очень удобны при расчете погрешностей или допусков, которые можно применять, например, к измерениям веса, длины и температуры в производственном процессе. В этой статье мы определим, что такое уравнения и неравенства с абсолютной величиной, и их правила, а также покажем вам, как их решать на практических примерах. Абсолютное значение числа x — число той же величины, но положительное. Абсолютные значения обычно представляются как |x|. Но что стоит за этим? Это происходит потому, что абсолютное значение представляет собой расстояние от нуля до числа x на числовой прямой . Расстояние от нуля до 2 равно 2, и расстояние от нуля до -2 также равно 2, поэтому |2|=2 и |-2|=2. Пример абсолютного значения, представленного на числовой прямой, Марилу Гарсиа Де Тейлор — StudySmarter Originals Вот почему |x| представляет значение числа x без учета его знака. Если у вас есть выражение внутри абсолютного значения, вычислите значение внутри, а затем найдите положительную версию результата. Вычислить |x-3|+1, еслиx=-2 |x-3|+1=|-2-3|+1=|-5|+1=5+1=6 Обозначение абсолютного значенияАбсолютное значение для любого действительного числа x обозначается следующим образом: |x|=xifx≥0-xifx<0 Из приведенных выше выражений мы можем сказать, что если число внутри абсолютного значения уже положительное, вы оставляете его таким, но если число отрицательное, то результатом будет положительная версия этого числа (как если бы вы были умножение отрицательного числа на -1). Свойства абсолютных значенийСвойства абсолютных значений: |4|=4,|-5|=5 |x|=|-x|=x |4|=|-4 |=4 |a×b|=|a|×|b| |2(-3)|=|2|×|-3||-6|=2×36=6 ab=|a||b| -93=|-9||3||-3|=933=3 |a±b|≠|a|±|b| Сумма: |1+(-2)|≠|1|+|-2||-1|≠1+21≠3 Вычитание: |1-(-2) |≠|1|-|-2||3|≠1-23≠-1 Решение уравнений с абсолютными значениями Уравнения с абсолютными значениями — это уравнения, включающие в себя выражения для абсолютных значений. Для любых действительных чисел a и b, где b ≥ 0: If|a|=ba=bifa≥0-a=bifa<0 Как видно из приведенного выше выражения, когда решают уравнения , абсолютные значения включают дополнительный шаг . Имея в виду, что значение внутри абсолютного значения может быть положительным или отрицательным, вам необходимо решить уравнение, учитывая оба случая, поэтому вы получите два решения . шагов для решения уравнений абсолютного значения следующим образом:
Для уравнения |x-5|=4 можно получить 2 возможных решения следующим образом: 1. x-5=4x=4+5x=9 2. Решение 2 (-a=b): -(x-5)=4-x+5=4-x=4-5-x=-1x=1 3. Проверить решения: a) Проверить решение 1 (x= 9) |x-5|=4|9-5|=4|4|=4 4=4 ✔ b) Проверить решение 2 (x=1) |x-5|=4 |1-5|=4|-4|=4 4=4 ✔ 4. Набор решений: Было доказано, что оба решения делают исходное уравнение верным. Следовательно, мы можем сказать, что набор решений равен 1,9 5. График на числовой прямой: Если мы представим решение на числовой прямой, мы увидим, что они оба отстоят на 4 единицы от 5. Решения уравнения с абсолютной величиной на числовой прямой, Марилу Гарсия Де Тейлор — StudySmarter Originals Уравнение например, x=-1 никогда не будет истинным, потому что абсолютное значение числа x всегда будет положительным числом. решение абсолютных неравенствабсолютных неравенств — это неравенства, которые включают выражения абсолютных значений. Вы можете решить абсолютные неравенства, переписав их как составные неравенства. Составные неравенства — это два неравенства, соединенные словами и или или . Для всех действительных чисел a и b, где b ≥ 0: 1.Ifa Символы > (больше) и < (меньше) исключают конкретное значение как часть решение. Символы ≥ (больше или равно) и ≤ (меньше или равно) включают конкретное значение как часть решения, а не исключают его. Решение неравенства может быть представлено на числовой прямой с помощью пустого кружка для обозначения того, что значение x не является частью решения , а замкнутый круг , если значение x является частью решения . Пример 1: Решите 2x-3≥5 Это второй случай: Ifa>b,thena>bora<-b Следовательно, мы можем сказать следующее: 2x-3≥5эквивалентно2x-3 ≥5or2x-3≤-5 Теперь нам нужно найти оба решения: 1. Решение 1: 2x-3≥52x≥5+32x≥8x≥82x≥4 8 2. 8 2.Решение 2:2x-3≤-52x≤-5+32x≤-2x≤-22x≤-1 3. Набор решений: Набор решений: x|x≥4orx≤-1 4. График на числовой прямой: Набор решений абсолютного неравенства на числовой прямой — Пример 1, Марилу Гарсия Де Тейлор — StudySmarter Originals Пример 2: Решить 2x-1<7 Это первый случай: Ifa Следовательно, 2x-1<7эквивалентно-7<2x-1<7 В этом случае мы можем записать неравенство в виде составного неравенства и соединить их вместе словами и , а затем решить каждое по отдельности. 1. |
Составное неравенство — это пара неравенств, соединенных числом 9.0031 и или или . В этом модуле свойства неравенств будут использоваться для решения линейных неравенств и составных неравенств с одной переменной. Модуль завершается изучением уравнений и неравенств с абсолютной величиной.
Независимо от того, идете ли вы вверх или вниз, расстояние одинаково.
Решение 1 (a=b): 
Следовательно, этот тип уравнения не имеет возможного решения. В этом случае мы можем сказать, что набор решений равен пустой набор , который можно обозначить как { } или ∅.
