Умножить число на число в степени: Свойства степеней, действия со степенями

3. Умножение и деление натуральных чисел

---

---

п1. Умножение натуральных чисел и его свойства

Умножить число m на натуральное число n  — значит найти сумму n слагаемых, каждое из которых равно m.

Выражение m·n и значение этого выражения называют произведением чисел m и n. Числа m и n называют множителями.

Свойства умножения: 

1. Переместительное свойство умножения: Произведение двух чисел не изменяется при перестановке множителей: a · b = b · а
2. Сочетательное свойство умножения: Чтобы умножить число на произведение двух чисел, можно сначала умножить его на первый множитель, а потом полученное произведение умножить на второй множитель: a · (b · с) = (а · b) · c.
3. Свойство умножения на единицу: Сумма n слагаемых, каждое из которых равно 1, равна n: 1 · n = n.
4. Свойство умножения на ноль: Сумма n слагаемых, каждое из которых равно нулю, равна нулю: 0 · n = 0.

Знак умножения можно опускать: 8 · х = 8х, или а · b = ab, или a · (b + с) = a(b + с)

п2. Деление

Действие, по которому по произведению и одному из множителей находят другой множитель, называют делением. 

Число, которое делят, называют делимым; число, на которое делят, называют делителем, результат деления называют частным.

Частное показывает, во сколько раз делимое больше, чем делитель.

На нуль делить нельзя!

Свойства деления: 

1. При делении любого числа на 1 получается это же число: а : 1 = а.
2. При делении числа на это же число, получается единица: а : а = 1.
3. При делении нуля на число получается нуль: 0 : а = 0.

Чтобы найти неизвестный множитель, надо произведение разделит на другой множитель.

5х = 45 х  = 45 : 5 х = 9 Чтобы найти неизвестное делимое, надо частное умножить на делитель.  х : 15 = 3 х = 3 · 15 х = 45

Чтобы найти неизвестный делитель, надо делимое разделить на частное.

48 : х = 4 х = 48 : 4

х = 12

п3. Деление с остатком

Остаток всегда меньше делителя.

Здесь число 23 – делимое, 4 – делитель, 5 – неполное частное и 3 – остаток.

Если остаток равен нулю, то говорят, что делимое делится на делитель без остатка или, иначе, нацело.

Чтобы найти делимое a при делении с остатком, надо умножить неполное частное  с на делитель b и к полученному произведению прибавить остаток d.  а = с · b + d

п4. Упрощение выражений

Свойства умножения:

1. Распределительное свойство    умножения относительно      сложения: Чтобы умножить сумму на число, можно умножить на это число каждое слагаемое и сложить получившиеся произведения: (а + b)с = ас + bc.
2. Распределительное свойство умножения относительно вычитания: Чтобы умножить разность на число , можно умножить на это число уменьшаемое и вычитаемое и из первого произведения вычесть второе: (а — b)с = ас — bc.

3а + 7а = (3 + 7)а = 10а

Решить уравнение: 

3у + 7у + 25 = 85

(3 + 7)у + 25 = 85

10у + 25 = 85

10у  = 85 – 25

10у = 60

у = 60 : 10

у = 6

п5. Порядок выполнения действий

Сложение и вычитание чисел называют действиями первой ступени, а умножение и деление чисел – действиями второй ступени.

Правила порядка выполнения действий:

1. Если в выражении нет скобок и оно содержит действия только одной ступени, то их выполняют по порядку слева направо.
2. Если выражение содержит действия первой и второй ступени и в нем нет скобок, то сначала выполняют действия второй ступени, потом – действия первой ступени.
3. Если в выражении есть скобки, то сначала выполняют действия в скобках (учитывая при этом правила 1 и 2).

Каждое выражение задает программу своего вычисления. Она состоит из команд.

 

п6. Квадрат и куб

Произведение, в котором все множители равны друг другу, записывают короче: 

а · а · а · а · а · а = а⁶

Читают: а в шестой степени. Число а называют основанием степени, число 6 – показателем степени, а выражение  а⁶ — называют степенью.

Произведение n и n называют квадратом числа n и обозначают n² (эн в квадрате):  n² = n · n

Таблица квадратов:

n	1	2	3	4	5	6	7	8	9	10
n2	1	4	9	16	25	36	49	64	81	100

 

n	11	12	13	14	15	16	17	18	19	20
n2	121	144	169	196	225	256	289	324	361	400
Произведение n · n · n называют кубом числа n и обозначают n3 (эн в кубе):  n3 = n · n · n Таблица кубов:
n	1	2	3	4	5	6	7	8	9	10
n3	1	8	27	64	125	216	343	512	729	1000

 

Первая степень числа равна самому числу.

Если в числовое выражение входят степени чисел, то их значения вычисляют до выполнения остальных действий.

Таблица степеней по алгебре. Степень числа: определения, обозначение, примеры.

Содержание

1. Свойства степени с натуральным показателем.
2. Степень с натуральным показателем, квадрат числа, куб числа
3. Таблица степеней от 1 до 10
4. Возведение числа в нулевую степень
5. Первая степень числа
6. Отрицательный показатель степени
7. Возведение в степень
8. Последовательность выполнения расчетов при работе с выражениями содержащими степень.
9. Теория множеств
10. Как возвести число в натуральную степень?
11. Как возвести число в целую отрицательную степень?
12. Теория
13. Как возвести число в степень.
14. Парадокс нуля
15. Как пользоваться таблицей степеней числа два?
16. Как пользоваться калькулятором степеней
17. Возведение в степень отрицательного числа
18. Степень с целым показателем
19. Порядок действий в примерах со степенями
20. Вывод

Свойства степени с натуральным показателем.

Чтобы умножить степени с одинаковыми основаниями мы основания не меняем, а показатели степеней складываем:

х^m · хⁿ = х^{m + n}

например: 7^1.7 · 7 ^{– 0.9} = 7^{1.7+( – 0.9)} = 7^{1.7 – 0.9} = 7^0.8

Чтобы разделить степени с одинаковыми основаниями основание не меняем, а показатели степеней вычитаем:

х^m / хⁿ = х^{m — n} , где, m > n,

например: 13^3.8 / 13 ^-0.2 = 13^{(3.8 -0.2)} = 13^3.6

При расчетах возведения степени в степень основание не меняем, а показатели степеней умножаем друг на друга.

(у^m )ⁿ = у ^{m · n}

например: (2³)² = 2 ^3·2 = 2⁶

Если необходимо рассчитать возведение в степень произведения, то в эту степень возводится каждый множитель

(х · у)ⁿ = хⁿ · у ^m ,

например:(2·3)³ = 2ⁿ · 3 ^m ,

При выполнении расчетов по возведению в степень дроби мы в данную степень возводим числитель и знаменатель дроби

(х / у)ⁿ = хⁿ / уⁿ

например: (2 / 5)³ = (2 / 5) · (2 / 5) · (2 / 5) = 2³ / 5³.

Степень с натуральным показателем, квадрат числа, куб числа

Для начала дадим определение степени числа с натуральным показателем. Забегая вперед, скажем, что определение степени числа a с натуральным показателем n дается для действительного числа a, которое будем называть основанием степени, и натурального числа n, которое будем называть показателем степени. Также отметим, что степень с натуральным показателем определяется через произведение, так что для понимания нижеизложенного материала нужно иметь представление об умножении чисел.

Определение.

Степень числа a с натуральным показателем n – это выражение вида aⁿ, значение которого равно произведению n множителей, каждый из которых равен a, то есть, .
В частности, степенью числа a с показателем 1 называется само число a, то есть, a¹=a.

Из данного определения понятно, что с помощью степени с натуральным показателем можно кратко записывать произведения нескольких одинаковых множителей. Например, 8·8·8·8 можно записать как степень 8⁴. Это аналогично тому, как с помощью произведения записывается сумма одинаковых слагаемых, к примеру, 8+8+8+8=8·4 (смотрите статью общее представление об умножении натуральных чисел).

Сразу стоит сказать о правилах чтения степеней. Универсальный способ чтения записи aⁿ таков: «a в степени n». В некоторых случаях также допустимы такие варианты: «a в n-ой степени» и «n-ая степень числа a». Для примера возьмем степень 8¹², это «восемь в степени двенадцать», или «восемь в двенадцатой степени», или «двенадцатая степень восьми».

Вторая степень числа, а также третья степень числа имеют свои названия. Вторую степень числа называют квадратом числа, например, 7² читается как «семь в квадрате» или «квадрат числа семь». Третья степень числа называется кубом числа, к примеру, 5³ можно прочитать как «пять в кубе» или сказать «куб числа 5».

Пришло время привести примеры степеней с натуральными показателями. Начнем со степени 5⁷, здесь 5 – основание степени, а 7 – показатель степени. Приведем еще пример: десятичная дробь 4,32 является основанием, а натуральное число 9 – показателем степени (4,32)⁹.

Обратите внимание, что в последнем примере основание степени 4,32 записано в скобках: чтобы избежать разночтений мы будем брать в скобки все основания степени, которые отличны от натуральных чисел. В качестве примера приведем следующие степени с натуральными показателями , их основания не являются натуральными числами, поэтому они записаны в скобках. Ну и для полной ясности в этом моменте покажем разницу, заключенную в записях вида (−2)³ и −2³. Выражение (−2)³ – это степень отрицательного числа −2 с натуральным показателем 3, а выражение −2³ (его можно записать как −(2³)) соответствует числу, противоположному значению степени 2³.

Заметим, что встречается обозначение степени числа a с показателем n вида a^n. (155). В дальнейшем мы преимущественно будем пользоваться обозначением степени вида aⁿ.

Данное выше определение позволяет находить значение степени с натуральным показателем. Для этого нужно вычислить произведение n одинаковых множителей, равных a. Эта тема заслуживает детального рассмотрения в отдельной статье – смотрите возведение в степень с натуральным показателем.

Одной из задач, обратной возведению в степень с натуральным показателем, является задача нахождения основания степени по известному значению степени и известному показателю. Эта задача приводит к понятию корня из числа.

Также стоит изучить свойства степени с натуральным показателем, которые вытекают из данного определения степени и свойств умножения.

Таблица степеней от 1 до 10

1 1 = 1 1 2 = 1 1 3 = 1 1 4 = 1 1 5 = 1 1 6 = 1 1 7 = 1 1 8 = 1 1 9 = 1 1 10 = 1	2 1 = 2 2 2 = 4 2 3 = 8 2 4 = 16 2 5 = 32 2 6 = 64 2 7 = 128 2 8 = 256 2 9 = 512 2 10 = 1024	3 1 = 3 3 2 = 9 3 3 = 27 3 4 = 81 3 5 = 243 3 6 = 729 3 7 = 2187 3 8 = 6561 3 9 = 19683 3 10 = 59049	4 1 = 4 4 2 = 16 4 3 = 64 4 4 = 256 4 5 = 1024 4 6 = 4096 4 7 = 16384 4 8 = 65536 4 9 = 262144 4 10 = 1048576	5 1 = 5 5 2 = 25 5 3 = 125 5 4 = 625 5 5 = 3125 5 6 = 15625 5 7 = 78125 5 8 = 390625 5 9 = 1953125 5 10 = 9765625
6 1 = 6 6 2 = 36 6 3 = 216 6 4 = 1296 6 5 = 7776 6 6 = 46656 6 7 = 279936 6 8 = 1679616 6 9 = 10077696 6 10 = 60466176	7 1 = 7 7 2 = 49 7 3 = 343 7 4 = 2401 7 5 = 16807 7 6 = 117649 7 7 = 823543 7 8 = 5764801 7 9 = 40353607 7 10 = 282475249	8 1 = 8 8 2 = 64 8 3 = 512 8 4 = 4096 8 5 = 32768 8 6 = 262144 8 7 = 2097152 8 8 = 16777216 8 9 = 134217728 8 10 = 1073741824	9 1 = 9 9 2 = 81 9 3 = 729 9 4 = 6561 9 5 = 59049 9 6 = 531441 9 7 = 4782969 9 8 = 43046721 9 9 = 387420489 9 10 = 3486784401	10 1 = 10 10 2 = 100 10 3 = 1000 10 4 = 10000 10 5 = 100000 10 6 = 1000000 10 7 = 10000000 10 8 = 100000000 10 9 = 1000000000 10 10 = 10000000000

Возведение числа в нулевую степень

Известно, что при x⁰ любое x равно 1 (x⁰ = 1). Чтобы доказать это, нужно выяснить, откуда собственно взялся этот ноль? Для этого вспомним формулы сложения и вычитания степеней. Итак: 7³ = 7²⁺¹ = 7² × 7¹ = 7 × 7 × 7, ⇒ 7³ = 7^9-6 = 7⁹ ÷ 7⁶, ⇒ 7⁰ = 7^3-3 = 7³ ÷ 7³ = 1 Доказательство получено. Однако есть исключение из этого правила.

Первая степень числа

Любое число в первой степени равно самому себе, так как показатель степени 1 указывает что число берётся сомножителем всего один раз, то есть оно ни на что не умножается,а просто остаётся без изменений.

Примеры:

7¹ = 7, 100¹ = 100, -25¹ = -25

Отрицательный показатель степени

Показатели степени могут быть не только положительными, но и отрицательными.

Например,

а

Возведение в степень

Возведение числа в степень – это вычисление произведения одинаковых множителей. Например, возвести число 2 в третью степень (2³) – это значит найти произведение 2 · 2 · 2 , то есть

2³ = 2 · 2 · 2 = 8.

Результат возведения в степень называется степенью (также как и само выражение, значение которого вычисляется). В выражении:

2³ = 8,

2 – это основание степени, ³ – показатель степени, 8 – степень.

Пример. Вычислите:

a) 11²>;

б) 2⁵>;

в) 10⁴.

Решение:

a) 11² = 11 · 11 = 121;

б) 2⁵ = 2 · 2 · 2 · 2 · 2 = 32;

в) 10⁴ = 10 · 10 · 10 · 10 = 10000.

Последовательность выполнения расчетов при работе с выражениями содержащими степень.

При выполнении расчетов выражений без скобок, но содержащих степени, в первую очередь производят возведение в степень, потом действия умножение и деление, и лишь потом операции сложения и вычитания.

Если необходимо вычислить выражение содержащие скобки, то сначала в указанном выше порядке делаем вычисления в скобках, а потом оставшиеся действия в том же порядке слева направо.

Очень широко в практических вычислениях для упрощения расчетов используют готовые таблицы степеней.

Теория множеств

Вроде на этом можно остановиться, но есть еще одно элегантное доказательство. Дело в том, что математика, это не только цифры и числовые оси. Есть комбинаторика, теория функций, множество других разделов, где нужно значение 0 в степени 0.

Итак, есть три блогера смежной тематики: Я, Артур Шарифов и Топа. И есть две обалденные темы для ролика, например, искусственный интеллект и космос! Каждый записывает 1 ролик на 1 тему, повторяться, конечно, можно. Вопрос: сколькими вариантами они могут это сделать? Ну то есть все на одну тему, или двое одну, третий другую?

К чему эта задача? В теории множеств есть теорема, согласно которой множество с количеством элементов M можно отобразить на множество с количеством элементов N вот столькими вариантами N в степени M.

Здесь как раз множество блогеров (3 элемента) отображается на множество тем (2 элемента). В итоге получается 8 вариантов.

Если что, вот они все перед вами:

Дело в том, что бывают и пустые множества! И есть только один вариант отображения пустого множества на пустое. А это значит, что 0 в степени 0 и есть единица! Это чисто символическое доказательство, не такое серьезное. Но все равно, логично что, ноль блогеров может записать ноль роликов только одним способом.

Как возвести число в натуральную степень?

Чтобы понять, как возводить различные числа в натуральные степени, рассмотрим несколько примеров:

Пример 1. Возвести число три в четвёртую степень. То есть необходимо вычислить 3⁴
Решение: как было сказано выше, 34 = 3·3·3·3 = 81.
Ответ: 34 = 81.

Пример 2. Возвести число пять в пятую степень. То есть необходимо вычислить 5⁵
Решение: аналогично, 55 = 5·5·5·5·5 = 3125.
Ответ: 55 = 3125.

Таким образом, чтобы возвести число в натуральную степень, достаточно всего лишь умножить его само на себя n раз.

Как возвести число в целую отрицательную степень?

Чтобы возвести отличное от нуля число в отрицательную степень, нужно вычислить значение этого числа в той же положительной степени и разделить единицу на полученный результат.

Пример 1. Возвести число два в минус четвёртую степень. То есть необходимо вычислить 2^-4

Решение: как было сказано выше, 2-4 =

=

1

2·2·2·2

= 0.0625.

Ответ: 2-4 = 0.0625.

Теория

Степень числа – это сокращенная запись операции многократного умножения числа самого на себя. Само число в данном случае называется – основанием степени, а количество операций умножения – показателем степени.

aⁿ = a×a … ×a

запись читается: «a» в степени «n».

«a» – основание степени

«n» – показатель степени

Пример:

46 = 4 × 4 × 4 × 4 × 4 × 4 = 4096

Данное выражение читается: 4 в степени 6 или шестая степень числа четыре или возвести число четыре в шестую степень.

Как возвести число в степень.

Давайте рассмотрим процесс возведения в степень на примере. Пусть нам необходимо возвести число 5 в 3-ю степень. На языке математики 5 — это основание, а 3 — показатель (или просто степень). И записать это можно кратко в таком виде:

Возведение в степень

А чтобы найти значение, нам будет необходимо число 5 умножить на себя 3 раза, т. е.

5³ = 5 x 5 x 5 = 125

Соответственно, если мы хотим найти значение числа 7 в 5 степени, мы должны число 7 умножить на себя 5 раз, т. е. 7 x 7 x 7 x 7 x 7. Другое дело когда требуется возвести число в отрицательную степень.

Парадокс нуля

Здесь все гораздо сложнее, но не настолько, чтобы не разобраться. Известно, что 0^x = 0.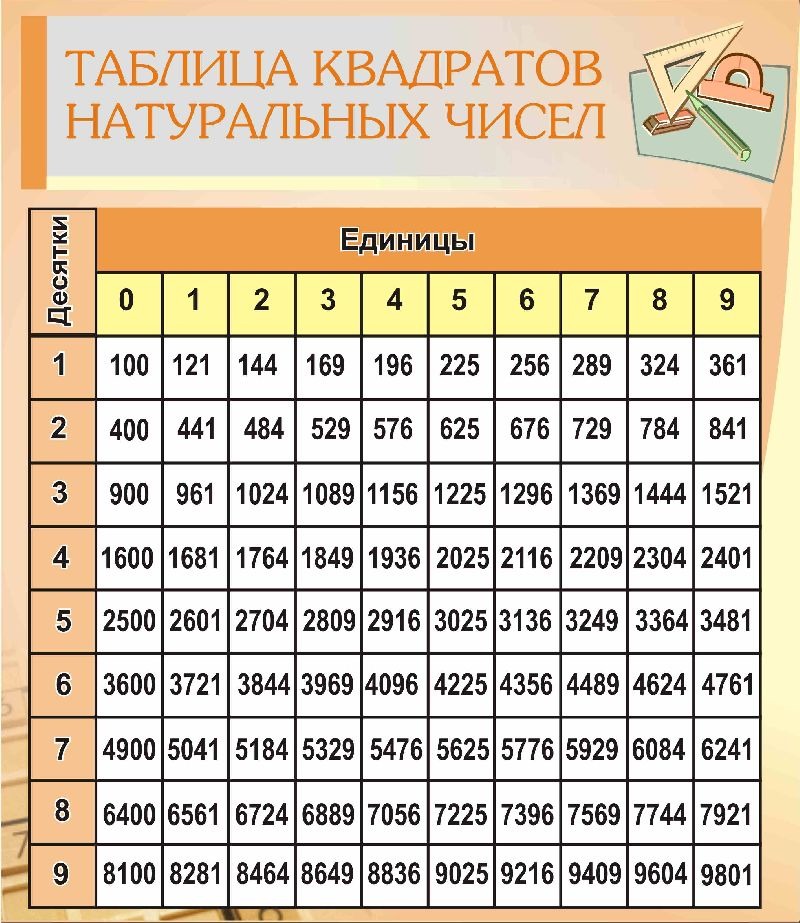 Например: 0⁴ = 0 × 0 × 0 × 0 = 0 Почему же мы часто встречаем выражение 0⁰ = 1? На самом деле это не совсем верно. Возьмем функцию y = ƒ (x) = x^x. Подберем значения по табл.1.

Таблица 1. Функция ƒ(x) = x^x

x	xx
1	1
0,9	0,909
0,8	0,836
0,7	0,779
0,6	0,736
0,5	0,707
0,4	0,693
0,3	0,697
0,2	0,725
0,1	0,794
0,01	0,955
0,001	0,993

Как видим, с определенного момента значение x^x растет вместе с уменьшением x. В этом нет ничего сверхъестественного, это всего лишь пример действия формулы

Изобразим это на графике

Рис.1 График y = ƒ(x) = x^x

Таким образом, делаем предположение, что это выражение является пределом. Выразить это можно так:

Проверим, вычислив это значение. Преобразуем основание выражения. Получаем:

x^x = (e^{ln x})^x = e^{x ln x}

В этом случае x → 0, а ln x → -∞ Получаем следующее выражение:

Пользуемся правилом Лопиталя:

Получаем:

Доказательство получено. Официальная позиция современной математики гласит, что выражение 0⁰– представляет собой неопределенность, то есть не имеет точного значения. Однако на практике, при расчетах, его значение подстраивается под конкретные требования. И чаще всего в этих случаях оно равно единице. Чтобы лучше разобраться с темой нулевой степени, советуем посмотреть видео ниже.

Как пользоваться таблицей степеней числа два?

Первый столбец – это степень двойки, который одновременно, обозначает число бит, которое представляет число.

Второй столбец – значение двойки в соответствующей степени (n).

Пример нахождения степени числа 2. Находим в первом столбце число 7. Смотрим по строке вправо и находим значение два в седьмой степени (2⁷) – это 128

Третий столбец – максимальное число, которое можно представить с помощью заданного числа бит (в первом столбце).

Пример определения максимального целого числа без знака. Если использовать данные из предыдущего примера, мы знаем, что 2⁷ = 128. Это верно, если мы хотим понять, какое количество чисел, можно представить с помощью семи бит. Но, поскольку первое число – это ноль, то максимальное число, которое можно представить с помощью семи бит 128 – 1 = 127 . Это и есть значение третьего столбца.

Степень двойки (n)	Значение степени двойки 2n	Максимальное число без знака, записанное с помощью n бит	Максимальное число со знаком, записанное с помощью n бит
0	1	–	–
1	2	1	–
2	4	3	1
3	8	7	3
4	16	15	7
5	32	31	15
6	64	63	31
7	128	127	63
8	256	255	127
9	512	511	255
10	1 024	1 023	511
11	2 048	2 047	1023
12	40 96	4 095	2047
13	8 192	8 191	4095
14	16 384	16 383	8191
15	32 768	32 767	16383
16	65 536	65 535	32767
17	131 072	131 071	65 535
18	262 144	262 143	131 071
19	524 288	524 287	262 143
20	1 048 576	1 048 575	524 287
21	2 097 152	2 097 151	1 048 575
22	4 194 304	4 194 303	2 097 151
23	8 388 608	8 388 607	4 194 303
24	16 777 216	16 777 215	8 388 607
25	33 554 432	33 554 431	16 777 215
26	67 108 864	67 108 863	33 554 431
27	134 217 728	134 217 727	67 108 863
28	268 435 456	268 435 455	134 217 727
29	536 870 912	536 870 911	268 435 455
30	1 073 741 824	1 073 741 823	536 870 911
31	2 147 483 648	2 147 483 647	1 073 741 823
32	4 294 967 296	4 294 967 295	2 147 483 647

Необходимо принять во внимание, что не все числа в компьютере представлены таким образом. Существуют и другие способы представления данных. Например, если мы хотим записывать не только положительные, но и отрицательные числа, то нам потребуется еще один бит для хранения значения “плюс/минус”. Таким образом, количество бит, предназначенных для хранения чисел у нас уменьшилось на один. Какое максимальное число может быть записано в виде целого числа со знаком можно посмотреть в четвертом столбце.

Для этого же самого примера ( 2⁷ ) семью битами можно записать максимум число +63, поскольку один бит занят знаком “плюс”. Но мы можем хранить и число “-63“, что было бы невозможно, если бы все биты были бы зарезервированы под хранение числа.

Как пользоваться калькулятором степеней

Калькулятор помогает возводить число в степень онлайн. Основанием степени могут быть любые целые числа и десятичные дроби. Показатель степени тоже может быть любой десятичной дробью, однако следует помнить о том, что для отрицательных чисел не определена операция возведения в нецелую степень.

При записи дробных чисел можно использовать как точку, так и запятую. В ответе большие числа записываются в так называемом «научном формате», то есть число выглядит как <число>e<количество нулей>. Например, , а , а

Возведение в степень отрицательного числа

Основание степени (число, которое возводят в степень) может быть любым числом — положительным, отрицательным или нулём.

Запомните!

При возведении в степень положительного числа получается положительное число.

При возведении нуля в натуральную степень получается ноль.

При возведении в степень отрицательного числа в результате может получиться как положительное число, так и отрицательное число. Это зависит от того чётным или нечётным числом был показатель степени.

Рассмотрим примеры возведения в степень отрицательных чисел.

Из рассмотренных примеров видно, что если отрицательное число возводится в нечётную степень, то получается отрицательное число. Так как произведение нечётного количество отрицательных сомножителей отрицательно.

Если же отрицательное число возводится в чётную степень, то получается положительное число. Так как произведение чётного количество отрицательных сомножителей положительно.

Запомните!

Отрицательное число, возведённое в чётную степень, есть число положительное.

Отрицательное число, возведённое в нечётную степень, — число отрицательное.

Квадрат любого числа есть положительное число или нуль, то есть:
a² ≥ 0 при любом a.

• 2 · (−3)² = 2 · (−3) · (−3) = 2 · 9 = 18
• −5 · (−2)³ = −5 · (−8) = 40

Степень с целым показателем

После того как мы определили степень числа a с натуральным показателем, возникает логичное стремление расширить понятие степени и перейти к степени числа, показателем которой будет любое целое число, в том числе и отрицательное и нуль. Это следует делать так, чтобы оставались справедливыми все свойства степени с натуральным показателем, так как натуральные числа являются частью целых чисел.

Степень числа a с целым положительным показателем есть не что иное как степень числа a с натуральным показателем: , где n – целое положительное число.

Теперь определим нулевую степень числа a. Будем исходить из свойства частного степеней с одинаковыми основаниями: для натуральных чисел m и n, m<n и отличного от нуля действительного числа a выполняется равенство a^m:aⁿ=a^m−n (условие a≠0 необходимо, так как в противном случае мы бы имели деление на нуль). При m=n записанное равенство нас приводит к следующему результату aⁿ:aⁿ=aⁿ⁻ⁿ=a⁰. Но с другой стороны aⁿ:aⁿ=1 как частное равных чисел aⁿ и aⁿ. Следовательно, приходится принять a⁰=1 для любого отличного от нуля действительного числа a.

А как же быть с нулем в нулевой степени? Подход, примененный в предыдущем абзаце, не подходит для этого случая. Можно вспомнить про свойство произведения степеней с одинаковыми основаниями a^m·aⁿ=a^m+n, в частности при n=0 имеем a^m·a⁰=a^m (из этого равенства тоже видно, что a⁰=1). Однако, при a=0 мы получим равенство 0^m·0⁰=0^m, которое можно переписать как 0=0, оно верно при любом натуральном m вне зависимости от того, чему равно значение выражения 0⁰. Иными словами, 0⁰ может быть равно любому числу. Чтобы избежать этой многозначности, не будем приписывать нулю в степени нуль никакого смысла (по этим же соображениям при изучении деления мы не стали придавать смысл выражению 0:0).

Несложно проверить, что принятое нами равенство a⁰=1 для отличных от нуля чисел a согласуется со свойством степени в степени (a^m)ⁿ=a^m·n. Действительно, при n=0 имеем (a^m)⁰=1 и a^m·0=a⁰=1, а при m=0 имеем (a⁰)ⁿ=1ⁿ=1 и a^0·n=a⁰=1.

Так мы пришли к определению степени с нулевым показателем. Степень числа a с нулевым показателем (a отличное от нуля действительное число) равна единице, то есть, a⁰=1 при a≠0.

Приведем примеры: 5⁰=1, (33,3)⁰=1, , а 0⁰ – не определено.

Нулевую степень числа a определили, осталось определить целую отрицательную степень числа a. В этом нам поможет все то же свойство произведения степеней с одинаковыми основаниями a^m·aⁿ=a^m+n. Примем m=−n, что требует условия a≠0, тогда a⁻ⁿ·aⁿ=a⁻ⁿ⁺ⁿ=a⁰=1, откуда заключаем, что aⁿ и a⁻ⁿ – взаимно обратные числа. Таким образом, логично определить число a в целой отрицательной степени −n как дробь . Несложно проверить, что при таком задании степени отличного от нуля числа a с целым отрицательным показателем остаются справедливыми все свойства степени с натуральным показателем (смотрите свойства степени с целым показателем), к чему мы и стремились.

Озвучим определение степени с целым отрицательным показателем. Степень числа a с целым отрицательным показателем −n (a отличное от нуля действительное число) – это есть дробь , то есть, при a≠0 и натуральном n.

Рассмотрим данное определение степени с целым отрицательным показателем на конкретных примерах: .

Подытожим информацию этого пункта.

Определение.

Степень числа a с целым показателем z определяется так:
 

Порядок действий в примерах со степенями

Вычисление значения называется действием возведения в степень. Это действие третьей ступени.

Запомните!

В выражениях со степенями, не содержащими скобки, сначала выполняют вовзведение в степень, затем умножение и деление, а в конце сложение и вычитание.

Если в выражении есть скобки, то сначала в указанном выше порядке выполняют действия в скобках, а потом оставшиеся действия в том же порядке слева направо.

Пример. Вычислить:

Вывод

Если мы находимся в рамках алгебры, простых арифметических вычислений, теории множеств, комбинаторики, находим суммы рядов, то без проблем можем считать это равным единице, и это во многих случаях будет даже упрощать наши вычисления.

Но в общем случае, особенно в рамках математического анализа, при вычислении пределов, говорят, что значение 0 в степени 0 – не определено. Его не существует, вот и все. И вообще, это только одна из многих неопределенностей, возникающих в матане, которая разрешается по-своему в каждом конкретном случае.

Так что чему равняется 0 в степени 0 зависит от контекста. Во многих случаях можно считать это единицей, но нужно помнить, что не во всех! И в разных языках программирования, разных калькуляторах тоже может быть по-разному. Где-то один, где-то не определено. В любом случае, практического применения у этого выражения нет, поэтому математики особо от него не страдают, хоть и иногда спорят, считать 0 в степени 0 равным единице, или нет. Но это не мешает быть ему таким интересным.

Источники

• https://www.calc.ru/Stepen-Chisla.html
• http://www.cleverstudents.ru/powers/powers.html
• https://calcsbox.com/post/tablica-stepenej.html
• https://nauka. club/matematika/chislo-v-nulevoj-stepeni.html
• https://naobumium.info/algebra/stepen1.php
• https://umath.ru/calc/vozvedenie-chisla-v-stepen-onlajn/
• https://izamorfix.ru/matematika/arifmetika/stepen_chisla.html
• https://zen.yandex.ru/media/id/5c1780145bee8800a916afc6/pochemu-0-v-stepeni-0-ravno-1-5dcbd8f61322b67386d1996f
• https://programforyou.ru/calculators/calculator-stepenej
• https://doza.pro/art/math/algebra/table-degrees
• https://calculat.ru/kalkulyator-stepenej
• https://profmeter.com.ua/communication/learning/course/course19/lesson747/
• http://math-prosto.ru/?page=pages%2Fstepeni%2Fstepeni1.php

Как возвести число в квадрат в Python

Чтобы возвести число в квадрат, нужно умножить это число само на себя. В Python есть несколько способов сделать это.

Во-первых, вы можете напрямую умножить число само на себя (число * число). Однако в данной статье мы покажем вам три способа сделать это без перемножения чисел напрямую. Ведь когда это возведение в квадрат, нужно написать число только два раза. Но что если потребуется возвести число в куб, в пятую степень, в десятую? Тогда непосредственно перемножать число на само себя N раз покажется не такой уж привлекательной идей.

Существует три способа возведения числа в указанную степень в Python:

• оператор возведения в степень **
• встроенная функция pow()
• функция math.pow() из математического модуля math

Как возвести число в квадрат при помощи оператора возведения в степень (**)

** называется оператором возведения в степень. Синтаксис данного оператора выглядит следующим образом:

number ** exponent

Здесь number — число, а exponent — степень, в которую нужно это число возвести. В целом это выражение оценивается как number * number... (количество number равно значению показателя степени).

С помощью этого оператора мы можем возвести число в любую степень, в том числе и в квадрат. К примеру, чтобы найти квадрат числа 5, вы можете написать следующий код:

square = 5 ** 2
print(square)
# 25

Оператор степени оценивает выражение как 5 * 5, в результате чего мы получаем 25.

Английский для программистов

Наш телеграм канал с тестами по английскому языку для программистов. Английский это часть карьеры программиста. Поэтому полезно заняться им уже сейчас

Подробнее

×

Конечно, этот оператор можно использовать не только для возведения чисел в квадрат. Вы можете возвести любое число в любую степень. Например, чтобы получить пять в седьмой степени (5⁷), нужно написать следующий код:

square = 5 ** 7
print(square)
# 78125

Как видите, это намного удобнее, чем писать number * number… N раз.

Как использовать функцию pow() в Python

Python также имеет встроенную функцию pow(), которая возводит число в указанную степень. Синтаксис данной функции выглядит следующим образом:

pow(base, exponent)

Приведенный выше код интерпретируется как baseexponent, то есть число base в степени exponent.

Функция pow() принимает два аргумента: число (известное как основание или base) и степень, в которую число должно быть возведено (показатель степени — exponent).

Например, чтобы найти квадрат числа 5, мы можем воспользоваться этой функцией следующим образом:

square = pow(5, 2)
    
print(square)
# 25

Не трудно догадаться, что эту функцию также можно использовать для возведения в куб, седьмую и любую другую степень. Просто будет меняться значение степени exponent.

Кроме того, функция pow() также может принимать и третий аргумент: modulo (модуль). Знак модуля — %. Этот аргумент оценивает остаток при делении одного числа на другое.

Например, 5 % 2 дает 1, потому что 5 разделить на 2 равно 2, а остаток — 1. То есть функция pow(), когда ей переданы три аргумента, делает следующее:

1. Возводит number (первый аргумент) в степень exponent (второй аргумент)
2. Находит остаток от деления результата на modulo (третий аргумент)

Применение функции pow() с тремя аргументами выглядит следующим образом:

mod = pow(5, 2, 3)
print(mod)
## 1
## 5 * 5 = 25
## 25 % 3 = 1

Согласно документации Python по pow(), этот подход работает более эффективно, чем pow(5,2) % 3.

Как возвести число в квадрат (и любую другую степень) при помощи функции math.pow()

math.pow() берется из математического модуля Python — math. Эта функция похожа на встроенную функцию pow() в использовании и синтаксисе, за исключением двух отличий:

• она принимает только два аргумента: основание base и показатель степени exponent
• она всегда возвращает число с плавающей запятой, даже если результат является целым числом

К примеру, math.pow(5, 2) вернет нам 25.0.

Встроенная функция pow() возвращает число с плавающей запятой только тогда, когда число является дробным. При этом, если результат является целым числом, она вернет целое число. А вот math.pow() в любом случае возвращает число с плавающей запятой.

Заключение

Итак, мы обсудили, как возвести число в квадрат в Python. Мы разобрали три основных способа: оператор возведения в степень **, встроенную функцию pow() и функцию math. pow() из модуля math. Теперь вы точно знаете, как возводить числа в степень в Python! 

Надеемся данная статья была вам полезна! Успехов в написании кода!

Перевод статьи «How to Square a Number in Python – Squaring Function».

Умножение и деление на 10 — Полный курс арифметики

Навыки в A R I T H M E T I C Таблица Содержание | Главная | Введение Урок 4 Значение процента Метрическая система Благодаря нашей системе позиционной нумерации умножать или разделить на степень 10. Он никогда не требует письменных методов, которые мы используем с другими числа (Урок 9). И уж точно не требует калькулятора. Для оставшаяся часть этого курса, умножение и деление на степени 10 будет базовый навык. В этом уроке мы ответим на следующие вопросы: Как умножить целое число на степень из 10? Как умножить десятичное число на степень 10? Как разделить десятичную дробь на мощность 10? Как разделить целое число на мощность 10? Раздел 2: Значение процента Что означает «процент» имеется в виду? Как можно берем 1% от числа? Как можно берем 10% от числа? Как мы меняем процент на число? Как мы меняем число на процент? Раздел 3 Когда число записывается в «научная нотация»? Что такое метрика система? Как мы конвертируем единицы в метрическая система?

1.    Как умножить целое число на степень 10? 36 × 10     Добавьте столько нулей, сколько указано в степени.

Примеры. 36 × 10  =  360     Добавить один 0.   36 × 100  =  3600     Добавьте два нуля.   36 × 1000  =  36 000     Добавьте три нуля. Это пример арифметического мастерства, заключающегося в том, чтобы решить задачу как можно быстрее и проще. Традиционное умножение в конечном итоге даст правильный ответ (мы надеемся). Но это неумело и не использует преимущества позиционной нумерации. Студент должен немедленно отказаться от этого письменного метода.

2.    Как умножить десятичное число на степень 10?   7,32 × 10     Переместить запятую вправо на столько знаков так как в степени 0. Если цифр недостаточно, добавьте 0 с.

примеров. 7 . 32 × 10 = 73 . 2 Переместить десятичную точку на одну позицию вправо. 7 . 32 × 100 = 732 Переместите точку на две цифры вправо:  732 . Однако, поскольку все цифры падают слева от десятичной точки, ответ — целое число, 732, которое мы пишем без десятичной точки точка. 7 . 32 × 1000 = 7 320  Переместите точку на три цифры вправо. Сделать это, мы должны добавить 0, Опять же, ответ — целое число. Проблема. Если 5 фунт сахара стоит 2,79 доллара, сколько будет стоить 50 фунтов? Ответить . Поскольку 50 фунтов — это десять раз по 5 фунтов, они будут стоить десять раз больше. Переместите запятую на одно место вправо: $27,90. Поскольку деньги состоят из двух десятичных цифр, мы добавили 0. (Урок 3, вопрос 8)

3.    Как разделить десятичную дробь на степень 10?   63,4 ÷ 10   «63,4 разделить на 10».     Переместить запятую влево на столько мест, сколько в степени есть 0. Если цифр недостаточно, добавьте на 0 с.

Примеры. 63,4 ÷ 10 = 6,34 Переместите точку на одну позицию влево.   63,4 ÷ 100 = .634   Переместите точку на две цифры влево.   63,4 ÷ 1000 = .0634    Переместить точку на три цифры влево. Кому сделайте это, добавьте 0, Эти примеры показывают, что всякий раз, когда мы умножаем или делим в степени 10, цифры не меняются  Мы просто перемещаем десятичную точку или добавить 0. Наконец, мы должны увидеть, как разделить целое число на степени 10. Теперь в Уроке 2 мы видели, что когда целое число оканчивается на 0, мы просто снимите 0. (Урок 2, Вопрос 10) 265 000 ÷ 100 = 2 650 Но если целое число не заканчивается на 0, как 265, тогда нет нулей, которые можно было бы отрезать. Мы увидим, что мы должны поставить десятичную точку отдельные цифры справа.

4.    Как разделить целое число на степень 10?   265 ÷ 10     Начиная справа от целого числа, разделять как много десятичных цифр, как в степени 0. Если не хватает цифр, добавить 0-е.

Примеры. 265 ÷ 10  = 26 . 5 Начиная справа от 265, отделите одной десятичной цифрой .   265 ÷ 100  = 2 . 65 Разделить два десятичных разряда .   265 ÷ 1000 = . 265 Разделите на три десятичных цифры. Когда мы делим целое число на степень 10, ответ будет иметь столько десятичных цифр, сколько нулей. 8 ÷ 100 = . 08 Два нуля. Две десятичные цифры. Снова, как и в Уроке 2, рассмотрим этот массив: По мере того, как мы продвигаемся вверх по списку — когда мы сдвигаем цифры на одну позицию вправо — число равно , деленное на 10, потому что каждая позиция справа стоит в 10 раз меньше. (Двигаясь от 26 . 58 к 2 . 658 , мы переходим от 2 десятков на 2 единиц .)  Однако кажется, что десятичная точка сместилась на один разряд влево или, с целым числом 26580, 0 был удален. По мере продвижения вниз по списку — когда мы сдвигаем цифры влево через десятичная точка — каждое число было умножено на 10. Итак, мы можем легко умножать или делить на 10 благодаря нашей системе позиционной нумерации. Каждое место принадлежит следующей степени числа 10. В этот момент, пожалуйста, «переверните» страницу и сделайте что-нибудь Проблемы. или Перейдите к Разделу 2: Значение процентов Введение | Главная | Содержание Copyright © 2021 Лоуренс Спектор Вопросы или комментарии? Электронная почта: [email protected]

Освежите свою математику: Пауэрс

Освежите свою математику: Силы

Возведение в степень

Мы уже рассматривали возведение в степень 2. Например, 5 ² = 5 × 5 = 25. Мы называем это 5 в степени 2 или 5 в квадрате. Мы называем его 5 в квадрате, потому что это площадь квадрата, длина стороны которого равна 5 единицам.

Мы можем возвыситься до других сил. Например, 5 ³ = 5 × 5 × 5 = 125. Мы называем это 5 в степени 3 или 5 в кубе. Мы называем его 5-кубическим, потому что это объем куба, длина стороны которого равна 5 единицам.

Точно так же 5 ⁴ = 5 × 5 × 5 × 5 = 625. Мы называем это 5 в степени 4 или 5 в четвертой степени. У него нет геометрического названия.

Когда мы возводим число в степень, мы умножаем его копии в степени. Когда у нас мощность = 1, мы получаем само число: 5 ¹ = 5. У нас есть одна копия умноженного числа.

Упражнение: возведение в степень

Что мы получим, если возведем 2 в степени 1, 2, 3, 4, 5 и 6?

Проверьте ответ на подъем на силовое упражнение.

Умножение и деление со степенями

Если мы умножаем два числа, возведенные в степени, вместе, мы складываем степени. Например, 3 ² = 3 × 3 = 9, 3 ¹ = 3. Если мы умножим 3 ^{на 2} × 3 ^{на 1} , то получим 3 × 3 × 3 = 27. Мы также можем сложить степени: 3 ² × 3 ¹ = 3 ²⁺¹ = 3 ³ = 27. Мы складываем общее количество троек, которые мы будем умножать.

Точно так же 4 ² × 4 ³ = 4 ²⁺³ = 4 ⁵ = 1024. Сравните 4 ² = 16, 4 ³ = 64, 16 × 64 = 1024.

Это должно быть то же число, которое мы возводим в каждую степень. Мы не можем умножить 4 ² × 3 ³ таким образом.

Если мы разделим два числа, возведённые в степень, мы вычтем степени. Например, 3 ² / 3 ¹ = 9/3 = 3. Если мы разделим 3 ² / 3 ¹ , мы получим (3 × 3) / 3 = 3. Мы также можем вычесть вторую степень из первой: 3 ² / 3 ¹ = 3 ^2–1 = 3 ¹ = 3.

Упражнение: умножение и деление со степенями

Что получится, если 6 ³ умножить на 6 ² ?

Что получится, если 6 ³ разделить на 6 ² ?

Проверьте ответ на упражнение на умножение и деление со степенями.

Отрицательные и нулевые степени

Что означало бы возведение в нулевую степень? Любое число, возведенное в нулевую степень, равно единице. Например, 5 ⁰ = 1, 2 ⁰ = 1 и 345 ⁰ = 1.

Мы можем увидеть это, если разделим число само на себя. Ясно, что 5 / 5 = 1. Мы можем записать 5 как 5 ¹ . Если мы разделим 5 на 5, мы получим 1 = 5 / 5 = 5 ¹ / 5 ¹ = 5 ^1–1 = 5 ⁰ . Следовательно, 5 в нулевой степени = 1. Точно так же любое число в нулевой степени = 1.

Теперь мы не можем объяснить возведение в нулевую степень как умножение чисел вместе, это не имеет смысла. Это типичное поведение математиков. Первоначальное определение возведения в степень применялось только к степеням, которые были целыми положительными числами. Узнаем, каким должно быть возведение в нулевую степень согласовываться с этим первоначальным определением.

Мы делаем то же самое для отрицательных степеней.

1
5 ^–1   =   –––
5

Легко понять, почему это должно быть так. Делим 1 на 5. Мы можем написать 1 = 5 ⁰ и 5 = 5 ¹ . затем

1
––   =   5 ⁰ ÷ 5 ¹   = 5 ^0–1   =   5 ^–1
5

Точно так же 5 ^{– 2} = 1/5 ² = 1/25 = 0,04 и т. д.

Упражнение: отрицательные и нулевые степени

Что мы получим, если возведем 2 в степени 0, –1, –2 и –3?

Чему равно 3 ⁴ , умноженное на 3 ^{– 4} ?

Чему равно 4 ² , умноженное на 4 ^{– 3} ?

Проверьте ответ на упражнение с отрицательными и нулевыми степенями.

Дробные полномочия

Что будет означать возведение в степень 1/2? Возведение в степень 1/2 означает, что мы нашли квадратный корень, число, умноженное само на себя, дает исходное число. Это еще один пример расширения вещей математиками.

Мы можем понять, почему это так, если мы умножим 3 ^½ на 3 ^½ . Получаем 3 ^½ × 3 ^½ = 3 ^½+½ = 3 ¹ = 3. Итак 3 ^½ должно быть квадратным корнем из 3.

Таким же образом, возведение в степень 1/3 дает кубический корень, где умножение трех из них вместе дает исходное число, возведение в степень 1/4 дает корень четвертой степени, где умножение четырех из них вместе дает исходное число, и так далее.

Можем возвести в любую степень. Возведение в степень 2/3 даст, например, кубический корень из квадрата числа. Возведение в степень –½ будет обратной величиной квадратного корня.

Упражнение: дробные степени

Чему равно число 9, возведенное в степень ½?

Чему равно число 8, возведенное в степень -1/3?

Проверьте ответ на упражнение с дробными степенями.

---

Вернуться к главному меню «Освежить математику».

Мартину Бланду, получившему степень магистра наук. индекс.

На домашнюю страницу Мартина Блэнда.

Эта страница поддерживается Мартином Бландом.
Последнее обновление: 26 ноября 2007 г.

Назад к началу.

Умножение и деление на степени 10 — Криста Кинг Математика

Эффект умножения и деления на некоторую степень числа 10

Мы хотим освоиться со степенями ???10???, так как мы будем использовать их все время для научной записи. Когда мы говорим о степени ???10???, мы имеем в виду результат возведения ???10??? в некоторой степени: 94??? равно ???4???, а в ???10 000??? есть четыре ???0???.

Главное, что нужно помнить, это то, что когда мы умножаем число на степень ???10???, все, что мы делаем, это подсчитываем ???0??? в степени ??? 10???, а затем переместите запятую на столько же знаков вправо в другом числе, и это даст нам произведение.

Как при десятичной степени перемещается десятичная точка

Пройти курс

Хотите узнать больше о Pre-Algebra? У меня есть пошаговый курс для этого. 🙂

Учить больше

Умножение на степень 10

Пример

Найдите произведение.

???67\times1,000???

Поскольку мы умножаем на степень ???10???, нам нужно посчитать ???0??? в степени ???10???. В ???1,000??? есть три ???0???, поэтому нам нужно переместить десятичную точку в ???67??? три места вправо. С ???67??? не имеет десятичной точки (поэтому кажется, что нет способа переместить десятичную точку вправо), мы должны сначала поставить десятичную точку справа от ???7??? (что дает ???67???.), а затем (чтобы мы могли переместить десятичную точку на три знака вправо) мы ставим три ???0??? справа от десятичная точка.

На этом этапе процесса у нас есть ???67. 000???, поэтому, если мы переместим запятую на три знака вправо, мы получим

???67,000???

Мы можем делить на степени ???10??? так же легко. Когда мы умножаем на степень ???10???, мы перемещаем десятичную точку вправо, но когда мы делим на степень ???10??? (что эквивалентно умножению на число, которое мы получили бы, если бы возвели ???10??? в соответствующую отрицательную степень), мы перемещаем десятичную точку влево. 9{-3}=0,001???

и т. д.

Обратите внимание, что степень (показатель степени) числа 10 совпадает с количеством нулей в степени 10.

Пример

Выполните деление.

???4.3\дел100???

В ???100??? два нуля, и так как мы делим, нам нужно переместить запятую на два знака влево. С ???4.3??? имеет только одну цифру слева от запятой (поэтому кажется, что нет возможности переместить запятую на два знака влево), мы должны сначала поставить ???0??? слева от ???4??? (чтобы дать нам в общей сложности две цифры слева от десятичной точки).