01Математика — 8 класс. Алгебра — Элементарные неравенства с модулем
Skip to main content- Классы
- 8 класс. Алгебра
- 04. Системы линейных неравенств, элементарные неравенства с модулем
- Теория: 10 Элементарные неравенства с модулем
- 1Пример
- 2Пример
- 3Пример
- 4Пример
Задание
Решение
Запишем неравенство \(\displaystyle |x|>7\) в виде совокупности двух систем.
По определению
Определение
Модуль
Для переменной \(\displaystyle x\) функция модуль \(\displaystyle x{ \small ,}\) обозначаемая \(\displaystyle |x|{ \small ,}\) определена как
\(\displaystyle |x|=\left\{\begin{aligned}x, & \text{ если } x\ge 0{ \small ,}\\-x,& \text{ если } x< 0{\small .}\end{aligned}\right.\)
получаем два случая:
- \(\displaystyle x\ge 0{ \small ,}\) тогда \(\displaystyle |x|=x{ \small ,}\)
- \(\displaystyle x<0{ \small ,}\) тогда \(\displaystyle |x|=-x{\small .
 }\)
}\)
Поэтому,
- если \(\displaystyle x\ge 0{ \small ,}\) то \(\displaystyle x >7{\small .}\) То есть
\(\displaystyle \left\{\begin{aligned} x&\ge 0{ \small ,}\\ x &>7{\small .} \end{aligned} \right.\)
- если \(\displaystyle x< 0{ \small ,}\) то \(\displaystyle -x >7{\small .}\) То есть
\(\displaystyle \left\{ \begin{aligned} x&< 0{ \small ,}\\ -x &>7{\small .} \end{aligned} \right.\)
Значит, неравенство \(\displaystyle |x| >7\) эквивалентно совокупности двух систем:
| \(\displaystyle \left\{ \begin{aligned} x&\ge 0{ \small ,}\\ x &>7 \end{aligned} \right.\) | или | \(\displaystyle \left\{ \begin{aligned} x&<0 { \small ,}\\ -x &>7{\small .} \end{aligned} \right.\) |
Решим эти две системы.
\(\displaystyle \left\{ \begin{aligned} x&\ge 0{ \small ,}\\ x &>7 \end{aligned} \right. Неравенство \(\displaystyle x\ge 0\) соответствует множеству точек на прямой: Неравенство \(\displaystyle x>7\) соответствует множеству точек на прямой: Таким образом, переменная \(\displaystyle x\) одновременно больше либо равна \(\displaystyle 0\) и больше \(\displaystyle 7{\small :}\) Получившееся пересечение и будет решением исходной системы неравенств. Значит, решение – \(\displaystyle x\in (7;+\infty){\small .} \)
| или | \(\displaystyle \left\{ \begin{aligned} x&<0 { \small ,}\\ -x &>7{\small .} \end{aligned} \right.\) Умножим обе части второго неравенства на \(\displaystyle -1{\small : } \) \(\displaystyle \left\{ \begin{aligned} x&<0 \\ -x &>7 \,| \cdot (\color{blue}{ -1}) \end{aligned} \right.\) \(\displaystyle \left\{ \begin{aligned} x&<0 { \small ,}\\ x &<-7{\small .} \end{aligned} \right. Неравенство \(\displaystyle x< 0\) соответствует множеству точек на прямой: Неравенство \(\displaystyle x<-7\) соответствует множеству точек на прямой: Таким образом, переменная \(\displaystyle x\) одновременно меньше \(\displaystyle 0\) и меньше \(\displaystyle -7{\small :}\) Получившееся пересечение и будет решением исходной системы неравенств. Значит, решение – \(\displaystyle x\in (-\infty;-7){\small .} \) |
Таким образом, получили:
\(\displaystyle x\in (7;+\infty)\qquad\) или \(\displaystyle \qquad x\in (-\infty;-7) \)
Ответ: \(\displaystyle x\in (-\infty;-7)\cup (7;+\infty){\small .} \)
Вход
Войти через
Регистрация
Муниципальное бюджетное нетиповое общеобразовательное учреждение «Лицей № 4» НОУ «Прорыв» Решение уравнений и неравенств с модулем Исследовательская работа Выполнил: Холодных Сергей Александрович,11 класс, Научный руководитель : Атапина Елена Никаноровна, учитель математики Ленинск-Кузнецкий, 2012
Понятие абсолютной величины (модуля) является одной из важнейших характеристик числа как в области действительных, так и в области комплексных чисел. Это понятие широко применяется не только в различных разделах школьного курса математики, но и в курсах высшей математики, физики и технических наук, изучаемых в вузах. Например, в теории приближенных вычислений используются понятия абсолютной и относительной погрешностей приближенного числа. В механике и геометрии изучаются понятия вектора и его длины (модуля вектора). В математическом анализе понятие абсолютной величины числа содержится в определениях таких основных понятий, как предел, ограниченная функция и др. Задачи, связанные с абсолютными величинами, часто встречаются на математических олимпиадах, вступительных экзаменах в вузы и на ЕГЭ. Главной целью в нашей работе является изучение различных методов решения уравнений и неравенств с модулями. Данная цель должна быть достигнута при решении следующих задач:
Объектом исследования являются некоторые типы уравнений и неравенств с модулем. Предмет исследования – различные методы решения уравнений и неравенств с модулем, а именно: графический способ, метод геометрической интерпретации, использование тождества , применение теоремы о знаках, метод перехода к следствию, метод интервалов, метод домножения на положительный множитель ,метод раскрытия модулей. В ходе исследования применялись такие методы, как изучение литературы по данному вопросу и практический метод. В ходе работы мы исследовал такие источники, как: 1. «Большая математическая энциклопедия» для школьников и студентов;
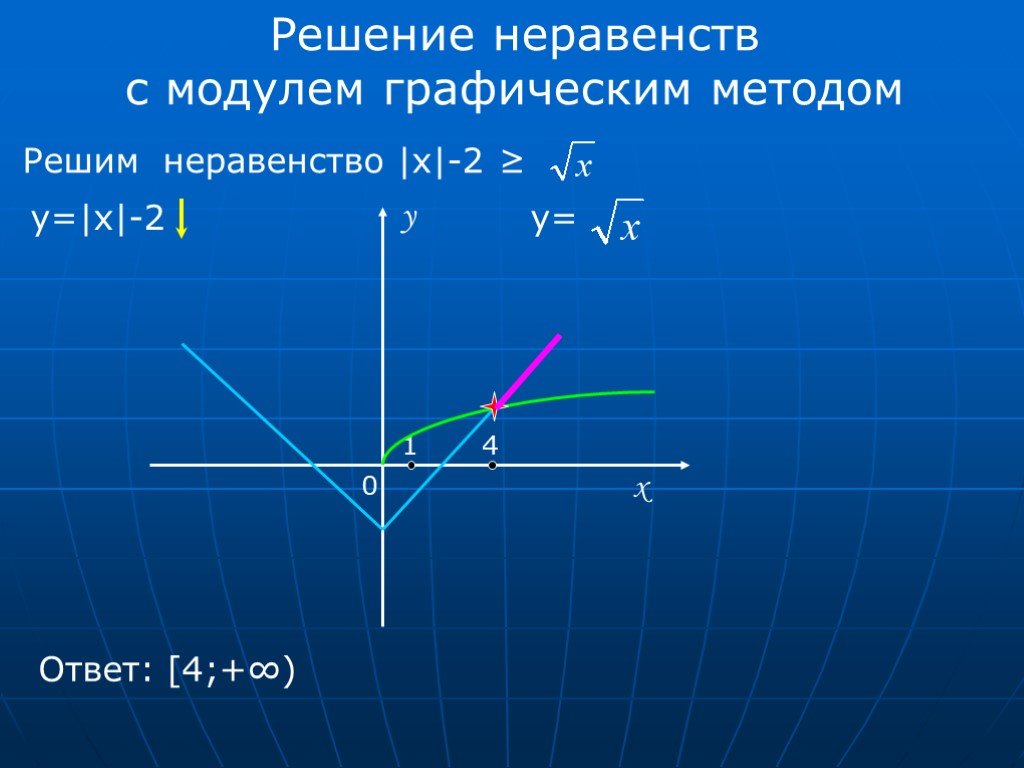
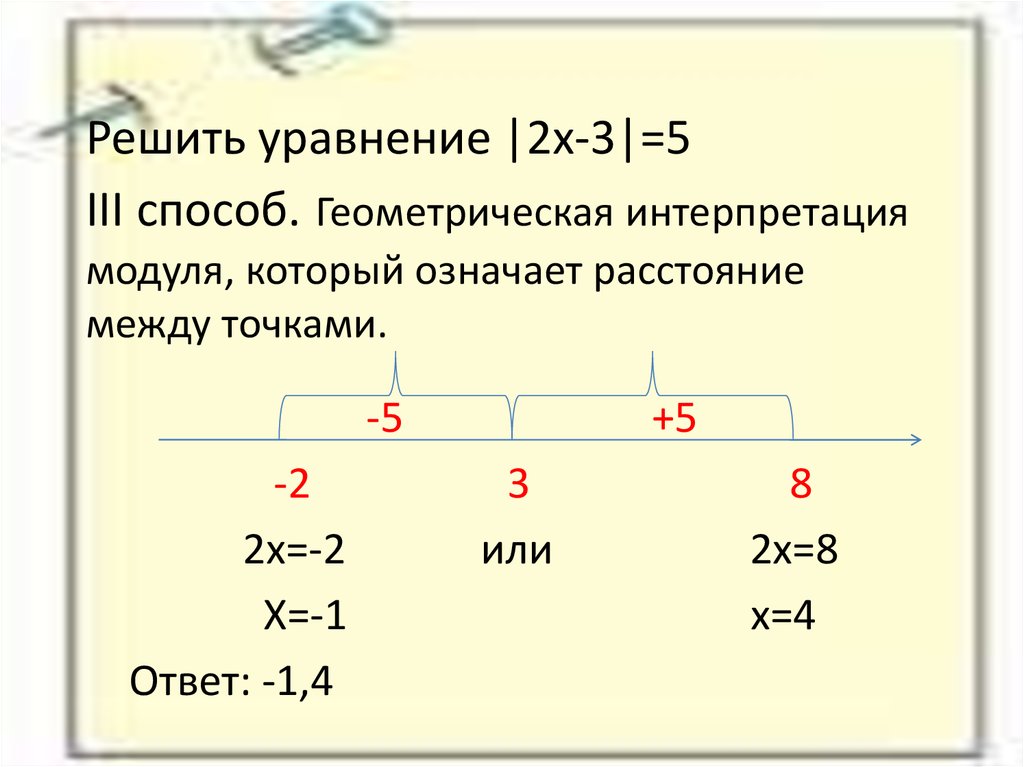
К простейшим уравнениям мы будем относить уравнения, решаемые одним из нижеприведенных равносильных переходов: Примеры решения простейших уравнений. Пример 1 Решим уравнение . Решение. Ответ. . Пример 2 Решим уравнение . Решение. Ответ. Пример 3 Решим уравнение . Решение. Ответ. . Ряд уравнений решается с использованием следующей теоремы. Теорема.4 Сумма модулей равна алгебраической сумме подмодульнх величин тогда и только тогда, когда каждая величина имеет тот знак, с которым она входит в алгебраическую сумму. Пример 5 Решение. Так как , то мы имеем равенство вида , где , . Поэтому исходное уравнение равносильно системе: Ответ. . Примеры решения простейших неравенств. Пример 6 Решим неравенство . Решение. . Ответ. . Решение. Ответ. . Как ни странно, но достаточно, чтобы избавиться от знака модуля в любых неравенствах. Пример 8 Решить неравенство Решение. Ответ. . 3. Графическое решение уравнений и неравенств с модулем Решение уравнений, содержащих знак абсолютной величины часто гораздо удобнее решать не аналитически, а графически (особенно уравнения содержащие параметры). Пример 9 (С5, ЕГЭ — 2010)C5. Для каждого значения a укажите число решений уравнения Решение. Построим график функции . Для этого выделим полный квадрат : Число точек пересечения графика функции у = с горизонтальными прямыми у = а равно числу решений уравнения. Ответ: если 0 4, то два решения. Иные способы решения уравнений и неравенств с модулемМетод раскрытия модулей рассмотрим на примере: Пример 10 Решить уравнение Решение. Это уравнение содержит более одного модуля. Метод решения уравнений, содержащих переменные под знаком двух и более модулей, состоит в следующем. 1. Найти значения переменной, при которых каждый из модулей обращается в нуль: , ; , ; , . 2. Отметить эти точки на числовой прямой. 3. Рассматриваем уравнение на каждом из промежутков и устанавливаем знак выражений, которые находятся под модулями. 1) При или . Чтобы определить знак каждого из выражений под модулем на этом промежутке, достаточно взять любое значение из этого промежутка и подставить в выражение. Если полученное значение отрицательно, значит, при всех из этого промежутка выражение будет отрицательным; если полученное числовое значение положительно, значит, при всех значениях из этого промежутка выражение будет положительным. Возьмем значение из промежутка и подставим его значение в выражение , получаем , значит на этом промежутке отрицательно, а следовательно «выйдет» из под модуля со знаком «минус», получим: . При этом значении , выражение получит значение , значит, оно на промежутке также принимает отрицательные значения и «выйдет» из модуля со знаком «минус», получим: . Выражение получит значение и «выйдет» из под модуля со знаком «минус»: . Уравнение на этом промежутке получится таким: , решая его, находим: . Выясняем, входит ли это значение в промежуток . Оказывается входит, значит является корнем уравнения. 2) При . Выбираем любое значение из этого промежутка. Пусть . Определяем знак каждого из выражений под модулем при этом значении . Оказывается, что выражение положительно, а два других отрицательны. Уравнение на этом промежутке примет вид: . Решая его, находим . Это значение не входит в промежуток , а значит, не является корнем уравнения. 3) При . Выбираем произвольное значение из этого промежутка, скажем, и подставляем в каждое из выражений. Находим, что выражения и положительны, а — отрицательно. Получим следующее уравнение: . После преобразования, получим: , а значит, уравнение не имеет корней на этом промежутке. 4) При . Нетрудно установить, что все выражения на этом промежутке положительны, а значит получим уравнение: , , которое входит в промежуток и является корнем уравнения. Ответ. , . Пример 11 Чему равна сумма корней уравнения (корень, если он один) уравнения Решение. Рассмотрим выражение и преобразуем его к виду Очевидно, что числитель дроби при любых значениях переменной является положительным числом. Значит дробное выражение положительно, если (т.к. ). Преобразуем полученное выражение, при условии . Получим уравнение, равносильное исходному: Ответ. . Пример 12 Решить уравнение Решение. Поскольку левая часть уравнения неотрицательна, при всех допустимых значениях переменной, на множестве корней уравнения правая его часть тоже должна быть неотрицательной, отсюда условие , на этом промежутке знаменатели обеих дробей равны, и остается решить уравнение . Решая его и учитывая ограничение , получаем Ответ. . Геометрический смысл выражения — длина отрезка координатной оси, соединяющего точки с абсциссами и .  Перевод алгебраической задачи на геометрический язык часто позволяет избежать громоздких выкладок. Перевод алгебраической задачи на геометрический язык часто позволяет избежать громоздких выкладок.Пример 13 Решим уравнение . Решение. Будем рассуждать следующим образом: исходя из геометрической интерпретации модуля, левая часть уравнения представляет собой сумму расстояний от некоторой точки с абсциссой до двух фиксированных точек с абсциссами 1 и 2. Тогда все точки с абсциссами из отрезка обладают требуемым свойством, а точки, расположенные вне этого отрезка, — нет. Ответ. . Пример 14 Решить неравенство . Решение. Изобразим на координатной прямой точки, сумма расстояний от которых до точек и в точности равна . Это все точки отрезка . Для всех чисел вне данного отрезка сумма расстояний будет больше двух. Ответ. .
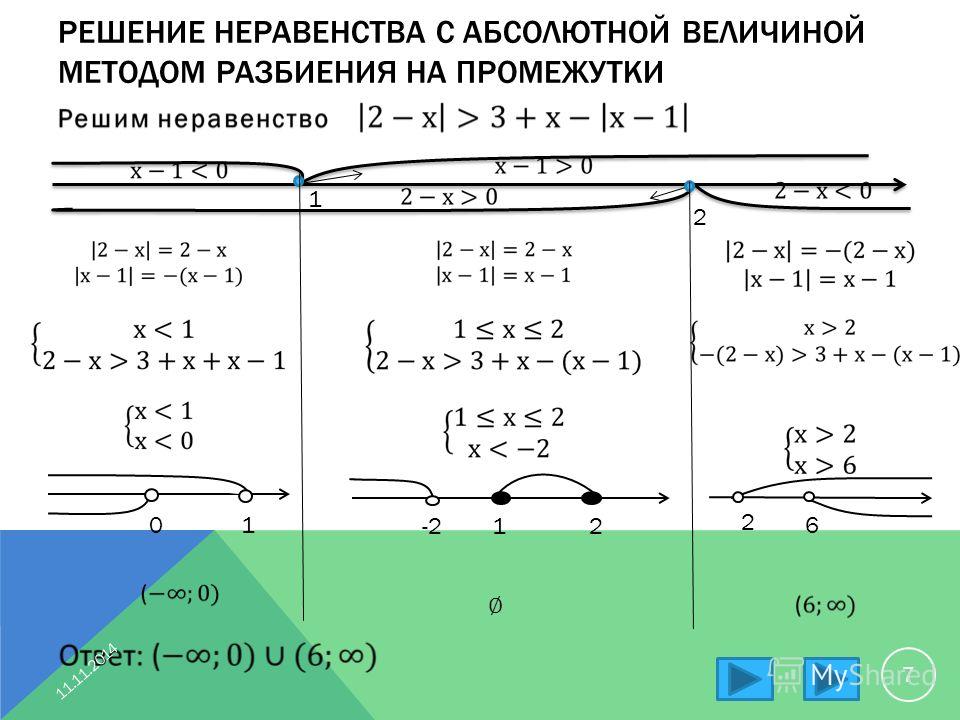
Пример (С3, ЕГЭ — 2010)15 Решить уравнение Решение. решением которого является интервал . Ответ. . Пример (С3, ЕГЭ — 2011)16 17 Решить уравнение Решение. . Ответ. . Сформулируем теорему, удобную при решении неравенств, относительно произведений или частных разности модулей: Теорема 18 Знак разности модулей двух выражений совпадает со знаком разности квадратов этих выражений. Пример 19 Решить неравенство
Используя формулу разности квадратов, разложим числитель и знаменатель на множители и решим полученное рациональное неравенство. Ответ. Все уравнения с модулями могут быть решены следующим образом: рассмотрим весь набор уравнений, который может получится при раскрытии модулей, но не будем выписывать соответствующие промежутки. Решая каждое из полученных уравнений, получим следствия исходного уравнения.  Остается только проверить не приобрели ли мы посторонних корней прямой их подстановкой в исходное уравнение. Остается только проверить не приобрели ли мы посторонних корней прямой их подстановкой в исходное уравнение.Пример 20 Решим уравнение Решение. Последовательно переходя к следствиям, получаем: Нетрудно убедиться, что найденные числа не являются корнями исходного уравнения. Ответ. нет решения. Применение метода интервалов основано на следующей теореме. Теорема 21 Функция, непрерывная на промежутке и необращающаяся на нем в нуль, сохраняет на этом промежутке свой знак. Это означает, что нули функции и границы промежутков ее непрерывности разделяют область определения функции на участки, где она сохраняет постоянный знак. Применение метода поясним на примере. Пример 22 Решим неравенство Пусть . Областью определения данной функции есть . Решая уравнение получим, что функция не обращается в нуль ни при каком значении переменной. Это означает, что на всей области определения функция является знакопостоянной. Ответ. . Метод интервалов позволяет решать более сложные уравнения и неравенства с модулями, но в этом случае он имеет несколько иное назначение. Суть состоит в слудующем. Находим корни всех подмодульных выражений и разбиваем числовую ось на промежутки знакопостоянства этих выражений. Это позволяет, последовательно перебирая эти промежутки, одновременно избавляться от всех модулей и решать обычное уравнение или неравенство (проверяя при этом, что найденный ответ входит в данный промежуток). Пример 23 Решить неравенство Решение. «Ловушка» заключается в том, что в задаче имеется несколько модулей, раскрывать которые — значит получить, громоздкое решение. Умножим дробь на некоторое выражение, принимающее лишь положительные значения и такое, чтобы упростить исходное неравенство: Ответ. . Заключение. Подводя итог нашей работы, можно сказать следующее. Целью работы было изучение различных методов решения уравнений и неравенств с модулями. Мы рассмотрели некоторые разновидности простейших уравнений и неравенств с модулем, решаемых с помощью равносильных переходов,а также теоремы о сумме модулей; графический способ решения уравнений. Нужно сказать, что в школьном курсе математики именно эти методы решения наиболее часто используются. Графический метод особо актуален при решении задач C5 из контрольно-измерительных материалов ЕГЭ. Далее мы изучили на нескольких примерах иные способы решения уравнений и неравенств с модулями, а именно: метод раскрытия модулей; решение уравнений, содержащих модули неотрицательных выражений; решение уравнений с использованием геометрической интерпретации; с использованием тождества ; применение теоремы о знаках; решение уравнений переходом к следствию, домножением на положительный множитель,а также решение неравенств методом интервалов. Таким образом, в ходе исследования мы пришли к следующим выводам. Наиболее универсальными и применимыми к наибольшему количеству задач мы считаем метод раскрытия модулей, графический метод и метод интервалов. Это убеждение возникло в результате решения большого числа задач из контрольно-измерительных материалов ЕГЭ, предметных чемпионатов, олимпиадных задач, а также изучение литературы по данному вопросу. Также очень важным мы считаем знание и применение тождества , так как оно используется не только при решении уравнений и неравенств, но и для преобразования многих выражений с радикалами. Остальные методы решения, которые мы рассмотрели, безусловно, представляют большой интерес в плане расширения математического кругозора и общего математического развития. Поэтому мы планируем использовать их для подготовки к государственной итоговой аттестации в форме ЕГЭ и подготовке к обучению в высшем учебном заведении. Список используемой литературы.
|
Модуль 1.6 – Линейные неравенства – Математика для бизнеса
В этом разделе вы:
- Использовать запись интервала.
- Использовать свойства неравенств.
- Алгебраически решать неравенства с одной переменной.
В большинстве ведущих университетов нелегко получить почетную должность. Предположим, что студенты должны были нести нагрузку по курсу не менее 12 кредитных часов и поддерживать средний балл 3,5 или выше. Как можно математически выразить эти требования к спискам почета? В этом разделе мы рассмотрим различные способы выражения различных наборов чисел, неравенств и неравенств с абсолютными значениями.
Указание решения такого неравенства, как $x \geq 4$, может быть достигнуто несколькими способами.
Мы можем использовать числовую линию, как показано на Рисунок 1 . Синий луч начинается с $x = 4$ и, как показано стрелкой, продолжается до бесконечности, что показывает, что набор решений включает все действительные числа, большие или равные 4.
Рисунок 1Мы можем использовать нотацию построителя множеств: $\{\, x \,|\, x \geq 4 \,\}$, что переводится как «все действительные числа $x$, такие что $x$ больше или равно 4». Обратите внимание, что фигурные скобки используются для обозначения набора.
Третий метод — это интервальная нотация , в которой наборы решений обозначаются скобками или квадратными скобками. Решения $x \geq 4$ представлены в виде $[4, \infty)$. Это, пожалуй, самый полезный метод, так как он применяется к понятиям, изучаемым позже в этом курсе, и к другим математическим курсам более высокого уровня.
Основная концепция, которую следует помнить, заключается в том, что круглые скобки представляют решения, большие или меньшие, чем число, а скобки представляют решения, которые больше или равны или меньше или равны числу. Используйте круглые скобки для обозначения бесконечности или отрицательной бесконечности, поскольку положительная и отрицательная бесконечность не являются числами в обычном смысле этого слова и, следовательно, не могут быть «приравнены». Несколько примеров интервал , или набор чисел, в которые попадает решение, $[-2, 6)$, или все числа от -2 до 6, включая -2, но не включая 6; $(-1, 0)$, все действительные числа между, но не включая -1 и 0; и $(-\infty, 1]$, все действительные числа меньше 1 включительно. Таблица 1 описывает возможные варианты.
| Набор указан | Обозначение Set-Builder | Обозначение интервала |
| Все действительные числа от $a$ до $b$, кроме $a$ или $b$ | $\{\, x \,|\, a| $(а,б)$ | |
| Все действительные числа больше $a$, но не включая $a$ | $\{\, х \,|\, х>а \,\}$ | $(а,\infty)$ |
| Все действительные числа меньше $b$, но не включая $b$ | $\{\, x \,|\, x | $(-\infty,b)$ |
| Все действительные числа больше $a$, включая $a$ | $\{\, x \,|\, x \geq a \,\}$ | $[а,\infty)$ |
| Все действительные числа меньше $b$, включая $b$ | $\{\, x \,|\, x \leq b \,\}$ | $(-\infty,b]$ |
| Все действительные числа от $a$ до $b$, включая $a$ | $\{\, x \,|\, a \leq x < b \,\}$ | $[а,б)$ |
| Все действительные числа от $a$ до $b$, включая $b$ | $\{\, x \,|\, a < x \leq b \,\}$ | $(а,б]$ |
| Все действительные числа от $a$ до $b$, включая $a$ и $b$ | $\{\, x \,|\, a \leq x \leq b \,\}$ | $[а,б]$ |
| Все действительные числа меньше $a$ или больше $b$ | $\{\, x \,|\, x < a \text{ или } x > b \,\}$ | $(-\infty,a) \cup (b,\infty)$ |
| Все действительные числа | $\{\, x \,|\, x \in \textbb{R} \,\}$ | $(-\infty,\infty)$ |
Используйте запись интервала для обозначения всех действительных чисел, больших или равных -2.
Решение Используйте квадратную скобку слева от -2 и круглые скобки после бесконечности: $[-2, \infty)$. Скобка указывает, что -2 включено в набор со всеми действительными числами от -2 до бесконечности.
Используйте интервальную нотацию для обозначения всех действительных чисел от -3 до 5 включительно.
Запишите интервал, выражающий все действительные числа, меньшие или равные -1 или большие или равные 1.
Решение Для этого примера нужно написать два интервала. Первый интервал должен указывать все действительные числа, меньшие или равные 1. Таким образом, этот интервал начинается с $-\infty$ и заканчивается на -1, что записывается как $(-\infty, -1]$.
Второй интервал должен отображать все действительные числа, большие или равные 1, что записывается как $[1, \infty)$. Однако мы хотим объединить эти два набора. Мы достигаем этого, вставляя символ объединения $\cup$ между двумя интервалами.
\[
(-\infty, -1] \cup [1, \infty)
\]
Выразите все действительные числа, меньшие -2 или большие или равные 3, в интервальной записи.
Когда мы работаем с неравенствами, мы обычно можем обращаться с ними так же, как и с равенствами, но не совсем так. Мы можем использовать свойство сложения и свойство умножения, чтобы решить их. Единственное исключение — когда мы умножаем или делим на отрицательное число; при этом символ неравенства переворачивается.
свойства неравенств
\begin{align*}
&\textbf{Свойство сложения} & \text{Если $a
\end{align*}
Эти свойства также применимы к $a \leq b$, $a > b$ и $a \geq b$.
Проиллюстрируйте свойство сложения неравенств, решив каждое из следующих действий:
- $x-15<4$
- $6\geq x-1$
- $x+7>9$
Решение Свойство сложения для неравенств гласит, что если неравенство существует, добавление или вычитание одного и того же числа с обеих сторон не меняет неравенства.
- $\quad$
\begin{align*}
x – 15 &< 4 \\
x – 15 + 15 &< 4 + 15 & \text{Прибавьте 15 к обеим сторонам.} \\
x & < 19
\end{выравнивание*} - $\quad$
\begin{align*}
6 &\geq x – 1 \\
6 + 1 &\geq x – 1 + 1 & \text{Добавьте 1 к обеим сторонам.} \\
7 &\geq x
\ конец{выравнивание*} - $\quad$
\begin{align*}
x + 7 &> 9 \\
x + 7 – 7 &> 9 – 7 & \text{Вычтите 7 с обеих сторон.} \\
x &> 2
\end{выравнивание*}
Решите: $3x – 2 < 1$.
Проиллюстрируйте свойство умножения неравенств, решив каждое из следующих действий:
- $3x < 6$
- $-2x – 1\geq 5$
- $5 – x > 10$
Решение
- $\quad$
\begin{align*}
3x &< 6 \\
\dfrac{1}{3}(3x) &< (6)\dfrac{1}{3 } & \text{Умножить на $\dfrac{1}{3}$.} \\
x &< 2
\end{align*} - $\quad$
\begin{align*}
-2x – 1 &\geq 5 \\
-2x &\geq 6 \\
\left(-\dfrac{1}{2}\right)(- 2x) &\geq (6)\left(-\dfrac{1}{2}\right) & \text{Умножить на $-\dfrac{1}{2}$. } \\
} \\
x &\leq -3 & \text{Обратное неравенство.} \\
\end{align*} - $\quad$
\begin{align*}
5 – x &> 10 \\
-x &> 5 \\
(-1)(-x) &> (5)(-1) & \text {Умножить на -1.} \\
x &< -5 & \text{Обратное неравенство.}
\end{align*}
Решите: $4x + 7 \geq 2x – 3$.
Как показали примеры, мы можем производить одни и те же операции с обеих сторон неравенства, как и с уравнениями; мы объединяем подобные термины и выполняем операции. Чтобы решить, мы изолируем переменную.
Решите неравенство: $13 – 7x \geq 10x – 4$.
Решение Решение этого неравенства аналогично решению уравнения до последнего шага.
\begin{align*}
13 – 7x &\geq 10x – 4 \\
13 – 17x &\geq -4 & \text{Переместите переменные члены в одну сторону неравенства.} \\
-17x &\geq -17 & \text{Изолировать переменный член.} \\
x &\leq 1 & \text{Деление обеих частей на -17 меняет неравенство на противоположное. }
}
\end{align*}
Набор решений задается интервалом $(-\infty, 1]$ или всеми вещественными числами, меньшими 1 включительно.
Решите неравенство и запишите ответ, используя интервальную запись: $-x + 4 < \frac{1}{2}x + 1$.
Решите следующее неравенство и запишите ответ в интервальной записи: $-\frac{3}{4}x \geq -\frac{5}{8} + \frac{2}{3}x$.
Решение Мы начинаем решать так же, как и при решении уравнения.
\begin{align*}
-\frac{3}{4}x &\geq -\frac{5}{8} + \frac{2}{3}x \\
-\frac{3 {4}x – \frac{2}{3}x &\geq -\frac{5}{8} & \text{Поместите переменные термины на одну сторону.} \\
-\frac{9}{ 12}x – \frac{8}{12}x &\geq -\frac{5}{8} & \text{Запишите дроби с общим знаменателем.} \\
-\frac{17}{12}x &\geq -\frac{5}{8} \\
x &\leq -\frac{5}{8} \left( -\frac{12}{17} \right) & \text{Обратить неравенство.}\
x &\leq \frac{15}{34}
\end{align*}
Множество решений представляет собой интервал $\left( -\infty, \frac{15}{34} \right]$
Решите неравенство и запишите ответ в интервальной записи: $-\frac{5}{6}x \leq \frac{3}{4} + \frac{8}{3}x$.
Графические решения систем линейных неравенств
Результаты обучения
- Графические системы линейных неравенств
График системы двух неравенств
Помните из модуля по построению графиков, что график одного линейного неравенства разбивает координатную плоскость на две области. На одной стороне лежат все решения неравенства. С другой стороны решений нет. Рассмотрим график неравенства [latex]y<2x+5[/latex].
Пунктирная линия: [латекс]у=2х+5[/латекс]. Каждая упорядоченная пара в заштрихованной области под линией является решением [латекс]y<2x+5[/латекс], так как все точки под линией сделают неравенство верным. Если вы сомневаетесь в этом, попробуйте заменить x и y координаты точек A и B в неравенстве; вы увидите, что они работают. Итак, заштрихованная область показывает все решения этого неравенства.
Линия границы делит координатную плоскость пополам. В этом случае она показана пунктирной линией, так как точки на прямой не удовлетворяют неравенству.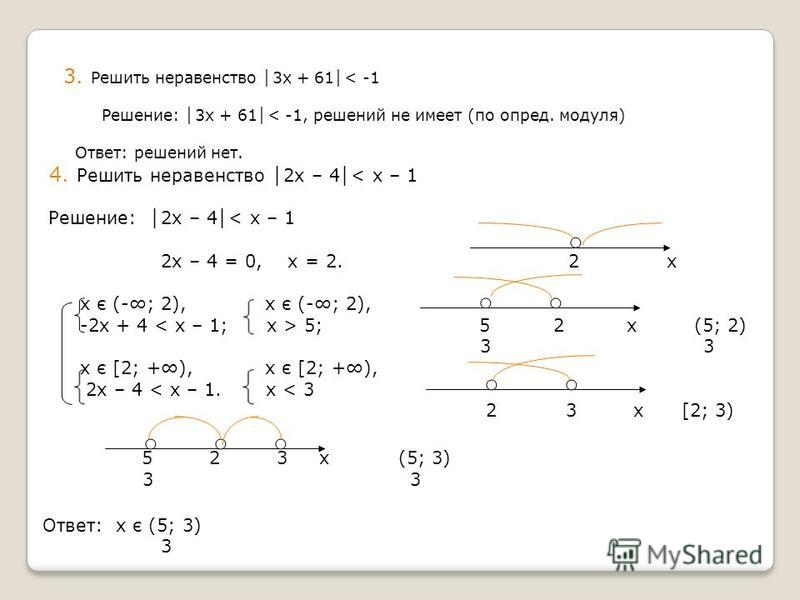 Если бы неравенство было [латекс]y\leq2x+5[/латекс], то граница была бы сплошной.
Если бы неравенство было [латекс]y\leq2x+5[/латекс], то граница была бы сплошной.
Теперь нарисуйте другое неравенство: [latex]y>−x[/latex]. Вы можете проверить пару точек, чтобы определить, какую сторону линии границы следует заштриховать. Проверка точек M и N дает верные утверждения. Итак, заштриховываем область над линией. Линия пунктирная, так как точки на прямой не соответствуют действительности.
Чтобы создать систему неравенств, вам нужно построить график двух или более неравенств. Давайте использовать [latex]y<2x+5[/latex] и [latex]y>−x[/latex], так как мы уже построили график каждого из них.
Фиолетовая область показывает, где перекрываются решения двух неравенств. Эта область является решением системы неравенств. Любая точка в этой фиолетовой области будет верна как для [латекс]у>-х[/латекс], так и для [латекс]у<2x+5[/латекс].
Как показано выше, найти решения системы неравенств можно путем построения графика каждого неравенства и определения области, которую они разделяют. Общие шаги описаны ниже:
Общие шаги описаны ниже:
- Изобразите каждое неравенство в виде линии и определите, будет ли она сплошной или пунктирной
- Определите, какая сторона каждой граничной линии представляет решения неравенства, проверив точку на каждой стороне
- Закрасьте область, представляющую решения для обоих неравенств
Продолжим практиковаться в графическом построении области решения систем линейных неравенств. Мы также построим графики решений системы, включающей сложное неравенство.
Пример
Закрасьте область графика, которая представляет решения для обоих неравенств. [латекс]x+y\geq1[/латекс] и [латекс]у–х\geq5[/латекс].
Показать решение
В следующих видеороликах показано больше примеров построения графика множества решений системы линейных неравенств.
youtube.com/embed/cclh3h2NurM?feature=oembed&rel=0″ frameborder=»0″ allow=»accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture» allowfullscreen=»»>Система в нашем следующем примере включает составное неравенство. Мы увидим, что сложное неравенство можно рассматривать как две линии, когда вы рисуете их на графике.
Пример
Найдите решение системы [латекс] 3x + 2y < 12 [/латекс] и [латекс] -1 ≤ у ≤ 5 [/латекс].
Показать решение
В следующем видеоролике мы покажем, как решить другую систему неравенств, содержащую сложное неравенство.
Попробуйте
Системы без решений
В следующем примере мы покажем решение системы двух неравенств, граничные линии которых параллельны друг другу. Когда графики системы двух линейных уравнений параллельны друг другу, мы обнаружили, что система не имеет решения. Аналогичный результат мы получим для следующей системы линейных неравенств.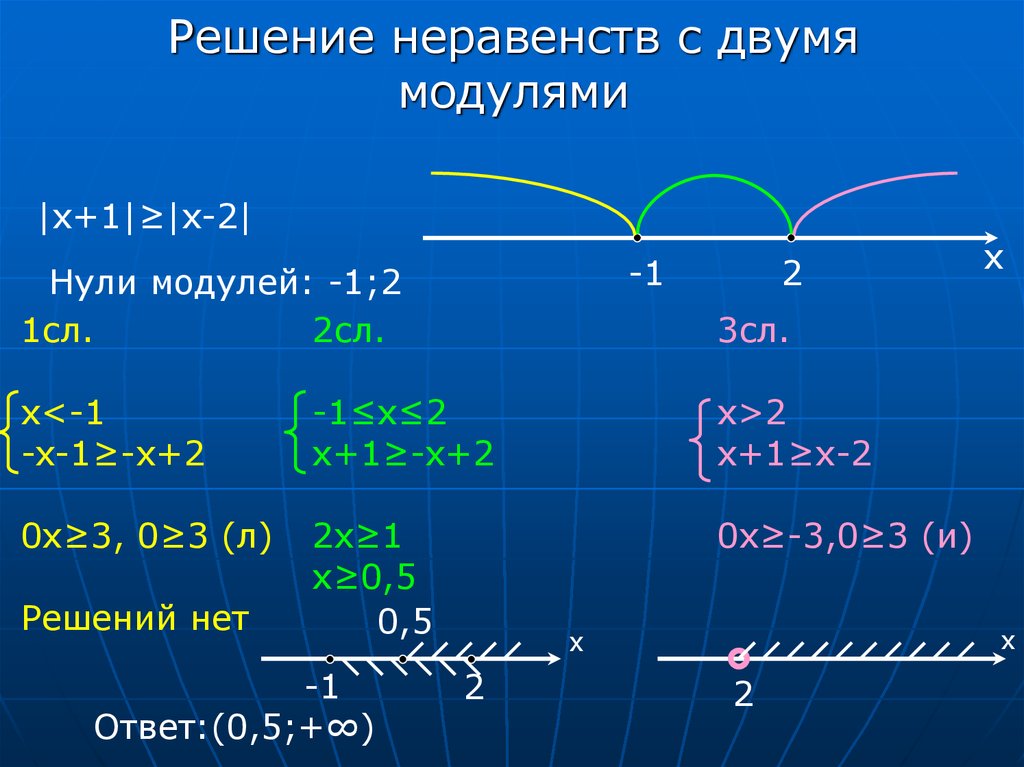

 }\)
}\) \)
\) \)
\)


 .
.


 Дважды применяя тождество , получим уравнение
Дважды применяя тождество , получим уравнение Вычисляя, например, , получаем, что функция принимает только положительные значения.
Вычисляя, например, , получаем, что функция принимает только положительные значения.

 ЕГЭ – 2011, 2012. Типовые экзаменационные варианты. / Под редакцией А.Л. Семенова, И.В. Ященко.
ЕГЭ – 2011, 2012. Типовые экзаменационные варианты. / Под редакцией А.Л. Семенова, И.В. Ященко.  } \\
} \\