Решение онлайн метод интервалов: Решение неравенств с модулем онлайн · Как пользоваться Контрольная Работа РУ

Содержание

Метод интервалов ℹ️ определение, способы и алгоритмы решения

Общие сведения

Под неравенством в математике понимаются функции, связанные между собой знаками больше, меньше, больше — равно, меньше — равно. Оптимальным методом их решения является нахождение способом интервалов. Его возможно применять к рациональным уравнениям, то есть к тем, в состав которых входят числа и переменная x с указанием различных алгебраических действий над ними, например, умножение, деление, возведение в степень с натуральным показателем.

Решить неравенство, значит, найти множество, при котором будет выполняться заданное условие. Между вычислением неравенств и уравнений много общего, главное отличие лишь в том, что для первых ответ представляет собой область решений, а для вторых — конкретные числовые значения. Многие методы нахождения ответа являются громоздкими, например, приведение уравнения к совокупности системы, построение графиков функций. Для небольших выражений их ещё можно применять, но когда в задании стоит шесть, семь множителей или больше, то решить его такими методами самостоятельно очень сложно, а сама операция займёт много времени.

Поэтому был разработан простой алгоритм, позволяющий вычислять сложные неравенства вида (x) > 0 и f (x) < 0. Знакомят с ним в восьмом классе средней школы. Он довольно легко запоминается учащимися. Алгоритм решения состоит из пяти шагов:

Имеющееся уравнение нужно приравнять к нулю, получив вместо неравенства равенство. Найти его корни.
Нарисовать координатную ось, на которой отметить точки, соответствующие решению полученного равенства. В итоге должны получиться различные области.
Определить кратность возможных решений. Для этого нужно исследовать корни. Если они чётные, то над равенством изображается петля.
На каждом выделенном интервале определить знак функции. Для этого нужно взять произвольное число, попадающее в область исследуемого интервала, и подставить его в заданное неравенство.
Подписать полученные знаки, соответствующие областям на координатной оси. Проанализировать соответствие интервалов удовлетворению условию задания.

Следует отметить, что кратным называют корень, при котором существует чётное число одинаковых решений. При нестрогом неравенстве в интервал включаются и корни уравнения (обозначают их на графике кружком).

Нужно запомнить, что при переходе через решение равенства знак будет меняться на противоположный. Также нужно знать, что показательная функция f (x) = ax + b является линейной и при a, не равном нулю, называется многочленом первой степени.

Суть метода

Справедливо считается, что решение неравенств методом интервалов — это довольно быстрый и эффективный инструмент. Это своего рода волшебная кнопка, которую можно нажать и найти необходимый ответ.

При этом не имеет значения, насколько сложный многочлен записан в уравнении.

Пусть имеется неравенство простого вида: aх² + bx + c > 0. Конечно же, это несложное уравнение, которое проще всего решать методом выражения неизвестной. Но для понимания принципа вычисления с помощью интервалов нужно начинать именно с простых примеров.

Для применения способа необходимо выражение приравнять к нулю, то есть переписать его как aх² + bx + c = 0. Так как это квадратное уравнение, то у него может быть два действительных корня: x1 один и x2. Равенство примет вид: a * (x — x1) * (x — x2).

Затем можно нарисовать числовую прямую с изображением на ней предполагаемых корней. В итоге получится линия, разбитая на три интервала. Теперь задача состоит в том, чтобы оценить знак каждой полученной области. Для этого нужно взять любое число в первом интервале от минус бесконечности до x1 (границы не включаются) и подставить в исходное неравенство. Следует решить его и определить знак.

Пусть это будет число k. Заменив им неизвестную в заданном выражении, получится следующее: ak² + bk + c. Получив числовой ответ, его нужно просто сравнить с нулём, понятие модуль тут не используется. При этом существует всего два возможных варианта:

k > 0 — это говорит о том, что на первом интервале все числа будут давать положительный ответ;
k < 0 — значит, в ограниченной области все возможные результаты решения имеют знак минус.

Пусть для рассматриваемого примера первый знак будет плюс, тогда очевидно, что на втором интервале будет знак минус, а в третьей области ответ снова будет иметь положительное значение.

Так как по условию неравенство должно быть больше нуля, то в ответ пойдут только области, которые определены со знаком плюс. Это можно записать как x Є (- ∞, x1) U (x2, +∞). Скобки строгие из-за того, что решается неравенство с конкретным указанием, поэтому x1 и x2 в возможное решение не включены.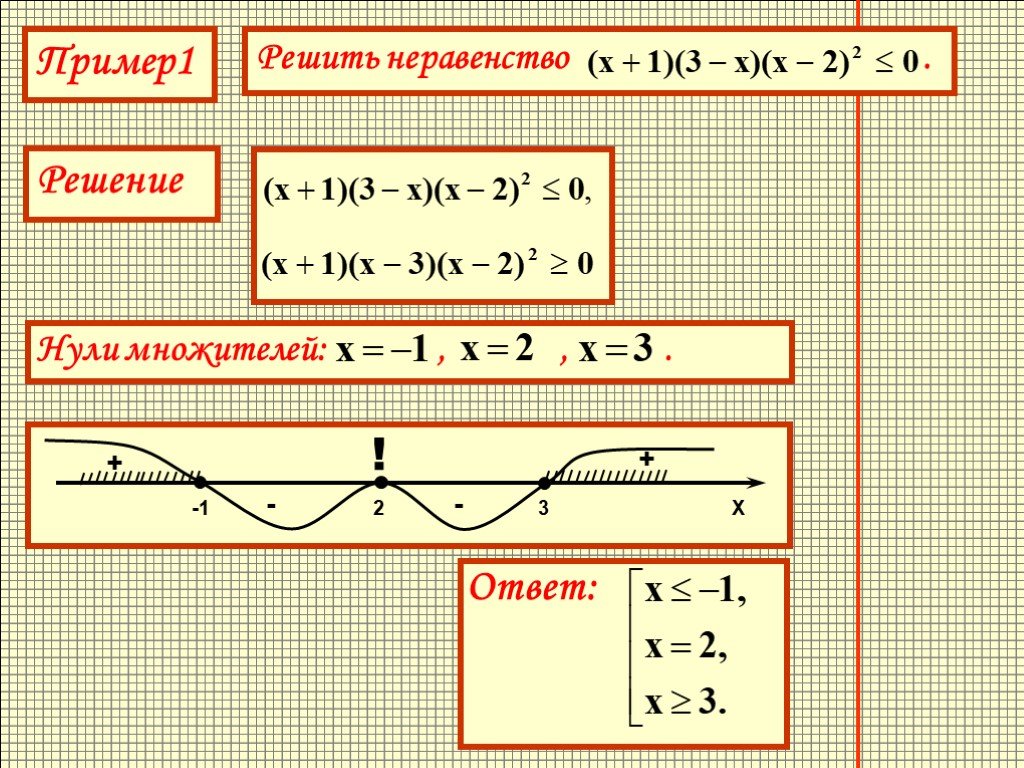

Простой пример

Ученикам на уроках для закрепления теории предлагается решить несколько типовых заданий, касающихся вычисления неравенств методом интервалов. В своём большинстве они несложные и позволяют на практике воспользоваться полученными знаниями. Ниже представлен один из таких примеров.

Пусть имеется неравенство (2x + 3) / (x — 4) > 0. На первый взгляд кажется, что нужно избавиться от знаменателя, умножив левую и правую часть на x — 4. Но это делать нельзя, потому что при разных значениях неизвестной уравнение может иметь как знак плюс, так и минус, а иногда и быть равным нулю. Поэтому правильным решением будет перенести свободный член с правой стороны в левую, а затем упростить выражение через приведение к общему знаменателю. После этого получится неравенство больше нуля.

Сделать это можно следующим способом: ((2x + 3) / (x — 4)) — 3 > 0. Отсюда: (2 x + 3 — 3 x + 12) / (x — 4) > 0. Найдя подобные и выполнив преобразование, исходное неравенство примет вид: (-x + 15) / (x-4) > 0.

Согласно алгоритму, используемому для решения методом интервалов, полученное выражение нужно приравнять к нулю и решить: (-x + 15) / (x- 4) = 0. Дробное отношение равняется нулю лишь в том случае, если делимое будет равно ему, а делитель в него не обращается. Поэтому уравнение можно представить в виде следующей системы:

{-x — 15 = 0.

{x — 4 ≠ 0.

Выразив икс из каждого условия, можно получить: x = 15; x ≠ 4. Это и есть решение уравнения. Далее полученные значения следует перенести на числовую прямую, обозначив промежутки. Отмеченные точки закрашивать не нужно, так как равенство строгое. Получится три интервала на каждом, из которых необходимо определить знак. Осуществлять подстановку можно как в исходное неравенство, так и в приравненное к нулю.

Из первого интервала можно взять ноль. Подставив его вместо икса, получится деление положительного числа на отрицательное (знак минус). Из второго интервала от четырёх до пятнадцати можно взять число десять. После подстановки получится знак плюс. Аналогично и с третьим интервалом, например, можно взять число 100. В итоге получится знак минус. Тут нужно отметить, что выполнять определение знака нужно на каждом интервале, так как использовать правило знакопостоянства не всегда возможно.

По условию решением уравнения будут числовые значения больше нуля. Этому удовлетворяет интервал от четырёх до пятнадцати. Таким образом, решением неравенства будет: x Є (4; 15). Неравенство решено.

Решение сложного задания

Решение сложных неравенств способом интервалов занимает гораздо меньше времени, чем альтернативными методами. Например, нужно вычислить выражение (x³ — 6x² + 11 — 6) / (x⁴ + 9x

2 — 10) ≥ 0.

К этому неравенству нужно применить рассматриваемый метод, поэтому вместо исходного выражения нужно решать уравнение (x³ — 6x² + 11 — 6) / (x⁴ + 9x² — 10) = 0.

Дробь может быть равной нулю лишь в том случае, когда числитель будет равняться нулю, а знаменатель нет. Отсюда следует, что нужно найти корни делителя и делимого. После выполнения ряда преобразований результат должен получиться следующий: (x — 1) * (x — 2) * (x — 3) / (x — 1) * (x + 1) * (x² + 10) = 0.

Анализируя найденное выражение, можно заметить, что в числителе и знаменателе есть одинаковая скобка, поэтому кажется, что на x — 1 можно сократить. Но делать это ни в коем случае нельзя, так как изначально решается неравенство.

Итак, если в равенстве делимое равняется нулю, то это значит, что одна из скобок числителя должна быть нулевой (произведение на ноль даёт ноль). Таким образом, икс может равняться одному, двум или трём.

Это и есть совокупность условий для числителя.

Знаменатель дроби не должен равняться нулю, иначе возникнет неопределённость. Возможным корнем в этом случае будет x, отличный от -1 и 1. Следует отметить, что третья скобка в делителе в ноль обратиться не может, поэтому она не учитывается. Для удобства полученные корни можно переписать в таблицу:

Переменная	Знак, возможное значение
x1	= 1
x2	= 2
x3	= 3
x4	≠ -1
x5	≠ 1

Из таблицы полученные значения необходимо перенести на числовую прямую. Так как равенство нестрогое, на оси точки будут как закрашенные (их ещё называют выколотыми), так и белые. Первые — это те, что получились за счёт знаменателя, а вторые — числителя. Затем нужно в каждом из них определить знак. В результате получится:

(- ∞, -1) — белая точка -;
(-1, 1) — белая точка +;
(1, 2) — белая точка +;
(2, 3) — закрашенная точка -;
(3, + ∞) — закрашенная точка +.

Таким образом, по условию задания ответ будет иметь следующий вид: X Є (-1; 1) U (1; 2] U [3; + ∞). Квадратные скобки в записи обозначают, что корни уравнения также включаются во множество решения.

Применение онлайн-калькулятора

Алгоритм решения методом интервалов является довольно простым. Чтобы его освоить, нужно самостоятельно решить несколько примеров. Но на практике может случиться так, что исходное выражение будет изначально довольно сложным. Это не значит, что его нельзя решить, применив способ нахождения интервалов, просто понадобится проявить повышенное внимание и затратить определённое время.

При этом ошибки, скорее всего, могут возникнуть не при применении последовательности, а в результате арифметических действий. В таких случаях хорошим подспорьем будет использование так называемых математических онлайн-калькуляторов. Это обыкновенные сайты, на страницах которых расположен скрипт, выполняющий автоматическое вычисление примеров по заданному алгоритму.

Воспользоваться услугами сервисов, предлагающих вычисление неравенств способом интервалов, сможет каждый желающий. При этом доступ к решателю предоставляется не только бесплатно, но и без регистрации. Необходимо просто ввести в специальную форму условие примера и нажать интерактивную кнопку, запускающую автоматическое вычисление. Из множества онлайн-калькуляторов, расположенных в российском сегменте интернета, можно выделить следующие:

Kontrolnaya-rabota.
Math-solution.
Mathforyou.
Math34.
Matcabi.

Все эти сайты имеют интуитивно понятный интерфейс на русском языке. Кроме получения услуги математического онлайн-решателя на их страницах можно найти всю необходимую теорию, помогающую понять, как происходит нахождение ответа, а также изучить различные типы примеров с подробным комментарием к решению.

Такого рода сервисы — отличные помощники учащимся, студентам и инженерам. Что интересно, кроме непосредственного нахождения ответа эти сайты предоставляют возможность посмотреть подробное решение. То есть ими может пользоваться даже неподготовленный пользователь, ничего не понимающий в методе. Просматривая пошаговое решение примеров, со временем он поймёт суть способа и научится самостоятельно выполнять вычисления.

Метод интервалов 9 класс онлайн-подготовка на Ростелеком Лицей

Определение рационального неравенства

Определение. Рациональные неравенства с одной переменной – это неравенства вида где – рациональное выражение, т.е. выражение, составленное из чисел, степеней с помощью арифметических операций.

Знакомство с методом интервалов на примере

Эффективным методом решения рациональных неравенств является метод интервалов. Изложим его на примере.

1. Решить неравенство:

До сих пор мы рассматривали линейные и квадратные неравенства, в данном случае имеем произведение трех скобок.

Рассмотрим функцию

Изучим свойства этой функции, из которых вытекает решение неравенства.

1. Область определения: .

2. Корни или нули функции: Эти числа являются корнями каждого множителя.

3. Интервалы знакопостоянства. Нанесем все точки, в которых функция может изменять знак, на ось ox (Рис. 1).

4. Определим знак функции на каждом интервале. Рассмотрим два способа.

I. Метод пробной точки — будем находить значения функции в удобной точке каждого интервала.

Рассмотрим точку из интервала

В точке (5) функция положительна, значит и в остальных точках этого интервала функция положительна. По знаку функции в одной точке мы заключаем, что и в остальных точках этого интервала функция имеет тот же знак.

Рассмотрим точку из интервала

Аналогично действуя, можно найти знак функции на каждом интервале.

Иногда интервалы бывают настолько малы, что найти пробную точку в каждом из них затруднительно. Тогда можно использовать табличный способ

II. Табличный способ.

Выпишем все значения, которые может принимать x.Также выпишем все множители и определим знак каждого множителя. Знак функции y определяем, уже зная знаки всех сомножителей.

x				2	(2;4)	4
	—	—	—	—	—	0	+
	—	—	—	0	+	+	+
	—	0	+	+	+	+	+
	—	0	+	0	—	0	+

Таким образом, мы определили знаки функции на каждом интервале.

5. Проверим граничные точки и выпишем ответ.

Ответ:

Мы изложили метод интервалов для конкретной функции.

Мы рассматриваем функцию и изучаем ее свойства – область определения, интервалы знакопостоянства, знаки функции на каждом интервале.

Аналогично решается неравенство

Запишем ответ в виде неравенства:

Граничные точки включаем, т.к. неравенство нестрогое.

Построение эскиза графика функции

Рассмотрим одну из сопутствующих задач: Построим эскиз графика рассмотренной функции (Рис. 2).

Мы знаем, что кривая будет проходить через все нули функции. Далее нам существенно помогут интервалы знакопостоянства. Например, мы знаем, что в окрестности точки -2 функция меняет свой знак с минуса на плюс, значит, в этом промежутке график проходит снизу вверх, функция возрастает. В окрестности точки 2 знак функции меняется с плюса на минус, значит, график идет вниз, функция убывает. В окрестности точки 4 функция также возрастает, и стремится к т. к. если Аналогично слева от точки -2

Метод интервалов позволяет решать не только неравенства, но и сопутствующие задачи.

При решении неравенств возможны типовые ошибки. Укажем на одну из них, решив неравенство.

Решение примера с возможной типовой ошибкой

Рассмотрим функцию

1. Область определения функции:

2. Корни функции:

3. Определим интервалы знакопостоянства.

4. Определим знак функции на каждом интервале (Рис. 3).

Проверим по методу пробной точки. На интервале функция положительна.

На интервале возьмем точку (0). функция также положительна.

При переходе через точку (-4) функция меняет знак.

5. Выберем по рисунку множество решений.

Ответ:

Ответ неверный!

Мы не учли изолированное решение. Знак нестрогий, поэтому нам подходят точки, в которых функция обращается в ноль. Таким образом,

Ответ:

Это была типовая ошибка.

Чтобы избежать ее, можно отдельно рассматривать те значения, в которых функция равна нулю, а затем те, где функция меньше нуля.

Построим эскиз графика функции (Рис. 4).

В окрестности точки -4 функция меняет знак с минуса на плюс, значит, график идет вверх, функция возрастает. В окрестности точки 2 знак функции не меняется, значит, график только касается точки 2, не пересекая ось ox. Справа от точки 2 график резко уходит вверх, функция стремится к Левее точки -4 функция стремится к

Заключение

Мы рассмотрели решение рациональных неравенств методом интервалов, который является мощным методом решения неравенств. Для его освоения предлагается перечень задач, а мы продолжим решение рациональных неравенств на следующем уроке.

Список рекомендованной литературы

1. Мордкович А.Г. и др. Алгебра 9 кл.: Учеб. Для общеобразоват. Учреждений.- 4-е изд. – М.: Мнемозина, 2002.-192 с.: ил.

2. Мордкович А.Г. и др. Алгебра 9 кл.: Задачник для учащихся общеобразовательных учреждений / А. Г. Мордкович, Т. Н. Мишустина и др. — 4-е изд. — М.: Мнемозина, 2002.-143 с.: ил.

3. Макарычев Ю. Н. Алгебра. 9 класс : учеб. для учащихся общеобразоват. учреждений / Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, И. Е. Феоктистов. — 7-е изд., испр. и доп. — М.: Мнемозина, 2008.

4. Алимов Ш.А., Колягин Ю.М., Сидоров Ю.В. Алгебра. 9 класс. 16-е изд. — М., 2011. — 287 с.

5. Мордкович А. Г. Алгебра. 9 класс. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений / А. Г. Мордкович, П. В. Семенов. — 12-е изд., стер. — М.: 2010. — 224 с.: ил.

6. Алгебра. 9 класс. В 2 ч. Ч. 2. Задачник для учащихся общеобразовательных учреждений / А. Г. Мордкович, Л. А. Александрова, Т. Н. Мишустина и др.; Под ред. А. Г. Мордковича. — 12-е изд., испр. — М.: 2010.-223 с.: ил.

Рекомендованное домашнее задание

1. Мордкович А.Г. и др. Алгебра 9 кл.: Задачник для учащихся общеобразовательных учреждений / А. Г. Мордкович, Т. Н. Мишустина и др. — 4-е изд. — М. : Мнемозина, 2002.-143 с. : ил.№№ 25; 26; 27; 34.

Рекомендованные ссылки на интернет-ресурсы

1. Портал Естественных Наук (Источник).

2. Портал Естественных Наук (Источник).

3. Электронный учебно-методический комплекс для подготовки 10-11 классов к вступительным экзаменам по информатике, математике, русскому языку (Источник).

4. Виртуальный репетитор (Источник).

5. Центр образования «Технология обучения» (Источник).

6. Раздел College.ru по математике (Источник).

Калькулятор записи интервалов

+ онлайн-решатель с бесплатными шагами

Калькулятор записи интервалов выражает неравенство на основе выбранной топологии и определяет расстояние между любыми двумя значениями.

Числовая строка для ввода интервала отображается калькулятором записи интервала . Наш онлайн-калькулятор интервальной записи делает расчеты быстрее и отображает числовую строку за доли секунды.

Что такое калькулятор интервальных обозначений?

Калькулятор записи интервалов — это онлайн-инструмент, который помогает отображать заданный интервал на числовой прямой, показывает неравенство по выбранной топологии и определяет расстояние между двумя заданными целыми числами.

Это метод записи подмножеств действительной числовой строки в соответствии с математическим определением. Пример обозначения интервала включает интервалы, выраженные в соответствии с заданными условиями.

Например, если у нас есть множество $x |2 \leq x \leq 1$, оно будет выражено как [2,1] по определению.

Формула для обозначения интервала (построителя множества):

n1 представляет первое число
n2 представляет второе число

Чтобы вычислить обозначение и найти значения интервала, используйте онлайн-решатель интервальных обозначений .

Когда число выражается как [a,x], это означает, что и «a», и «x» являются частью набора. С другой стороны, (a,x) означает отсутствие «a» и «x» в наборе.

Полузакрытый символ «[b,y)» означает, что b включено, а y нет. Подобно (b,y], что указывает на то, что b исключено, а y включено в коллекцию, (b,y] будет распознано как полуоткрытое.

Как использовать калькулятор интервальных обозначений используйте Калькулятор интервальных обозначений , следуя приведенным подробным инструкциям, и калькулятор обязательно даст вам желаемые результаты.Поэтому вы можете следовать данным инструкциям, чтобы получить значение переменной для данного уравнения.
Шаг 1
Заполните предоставленные поля ввода интервалом (закрытым или открытым интервалом).
Шаг 2
Нажмите кнопку «ОТПРАВИТЬ» , чтобы получить обозначение интервала, а также отобразится полное пошаговое решение для параметрического уравнения в декартово уравнение .
Наконец, в новом окне будет отображена числовая строка за указанный период.
Как работает калькулятор интервальных обозначений?
I Калькулятор записи интервалов работает, выражая подмножество действительных чисел, используя запись интервала, через целые числа, которые их ограничивают. Неравенства могут быть представлены с использованием этого обозначения.
Обозначения для различных типов интервалов
Чтобы представить интервальные обозначения для различных типов интервалов, мы можем придерживаться набора правил и символов. Давайте рассмотрим различные символы, которые можно использовать для представления определенного типа интервала.
Символы, используемые для обозначения интервала
Мы используем следующие обозначения для различных интервалов:
[ ]: Когда обе конечные точки являются частью набора, используется эта квадратная скобка.
( ): если обе конечные точки не включены в набор, используется эта круглая скобка.
( ]: когда правая конечная точка включена в набор, а левая конечная точка исключена, используется полуоткрытая скобка.
[ ]: когда левая конечная точка набора включена, а правая конечная — открытая скобка также используется.
Что такое интервал?
Группа действительных чисел, которые лежат между любыми двумя заданными действительными числами, называется Интервалом и представляется с использованием записи интервалов. Интервалы могут использоваться для изображения неравенств. Интервалы можно разделить на четыре категории.
Если x и y являются двумя конечными точками, а x y, интервалы можно разделить на следующие категории:
Открытый интервал

В этом типе интервала два конца не включены в этот интервал. Неравенство записывается как x < z < y, если z — число, лежащее между x и y. Круглые скобки используются для обозначения числа 9.0003 открытый интервал , т.е. (x, y).

Закрытый интервал

Этот тип интервала включает обе конечные точки. В виде $x \leq z \leq y$ неравенство можно выразить. Закрытые интервалы выражаются квадратными скобками, например [x, y].

Полузакрытый правый интервал

В этот тип интервала включается только левая конечная точка; правая конечная точка исключена. Неравенство x z y. Левая часть интервала заключена в квадратную скобку, а правая часть заключена в круглую скобку, как в [x, y).

Полузакрытый левый интервал

Левая конечная точка исключается, и в этот интервал включается только правая конечная точка. В соответствии с этим x < z ≤ y будет неравенством. В левой части используется круглая скобка, а в правой — квадратная, т. е. (x, y].

Длина интервала между конечными точками x и y может быть рассчитана следующим образом:

Длина = y – x

Преобразование неравенства в интервальную запись

Чтобы преобразовать неравенство в интервальную нотацию , выполните шаги, показанные ниже.

Нарисуйте набор решений интервала на числовой прямой.
Числа должны быть записаны в интервальной записи с меньшим номером в левой числовой строке.
Используйте знак $-\infty$, если множество неограниченно слева, и $\infty$, если оно неограниченно справа.

Давайте рассмотрим несколько примеров неравенства и преобразуем их в интервальную запись.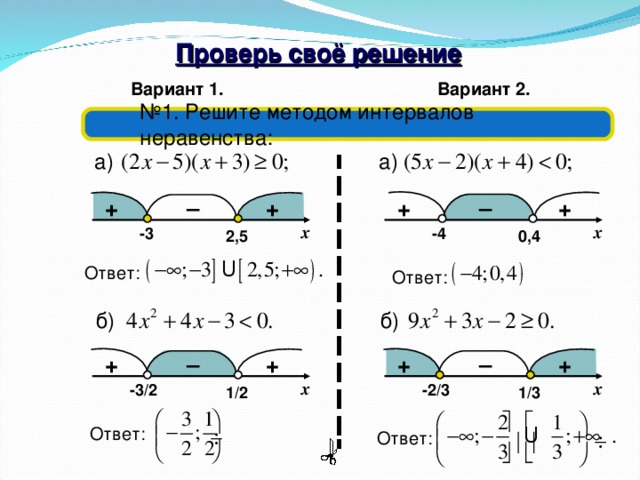

Неравенство $x \leq 3$ имеет интервальную запись $(-\infty, 3]$
Неравенство $x < 5$ имеет интервальную запись $(-\infty, 5)$
Неравенство $x \geq 2$ имеет интервальное обозначение $(2, \infty]$

Представление неравенств на числовой прямой

Математическое утверждение , известное как неравенство, сравнивает два выражения, используя понятия больше и меньше. В этих утверждениях используются уникальные символы Неравенство следует читать слева направо, как текст на странице.

Большие наборы решений описываются неравенствами в алгебре. Мы создали некоторые методы для краткого представления очень больших списков чисел, поскольку иногда существует бесконечное количество чисел, которые удовлетворяют неравенству.

Вероятно, вы уже знаете о фундаментальном неравенстве в первом случае. Например:

Список чисел меньше 9 отображается выражением $x \leq 9$.
Символ $-5 \leq t$ обозначает все числа, большие или равные -5.

Имейте в виду, что поиск больше или меньше зависит от того, находится ли переменная слева или справа от знака неравенства.

Важные примечания по интервальным обозначениям

Набор неравенств выражается с использованием интервальных обозначений.
Открытый интервал, закрытый интервал и полуоткрытый интервал — это три различных варианта обозначения интервала .
В ограниченном интервале отсутствует знак бесконечность .
Неограниченный интервал — это диапазон, включающий символ бесконечности.

Решенные примеры

Давайте рассмотрим несколько примеров, чтобы лучше понять работу калькулятора интервальных обозначений .

Пример 1

Проверить решение \[ x -10 \leq -12\]

Решение

Подставить конечную точку -2 в соответствующее уравнение следующим образом:

x -10 $\leq$ — 12

x -10 = -12

Проверим следующее равенство:

-2 -10 = -12

Подберем такое значение, как -12, меньше, чем,

900
-5 -10 $\leq$ -12
-15 $\ leq$ -12
Проверяется как:
-5 -10 $\leq$ -12 92 – 1\]
Решение
Знаменатель равен 0 – это единственное, о чем нам нужно беспокоиться. Мы понимаем, что в результате х в квадрате минус один не может равняться нулю. Из-за этого х в квадрате не может равняться единице.
Тогда x не может быть больше или меньше единицы, если мы возьмем квадратный корень из обеих сторон. Следовательно, мы сможем двигаться от бесконечности к бесконечности, когда укажем нашу область в интервальной нотации. Мы даже дойдем до противоположного.
\[ (- \infty, – 1) \cup (-1, 1) \cup (1, \infty) \]
В итоге это наш домен.
Пример 3:
Каково обозначение интервала для данной функции f(x)=2 по корню из 3x+5?
Решение
В этом уравнении нет отрицательного корня, но есть квадратный корень. Мы знаем, что 3x +5 никогда не может равняться нулю. Он должен быть больше нуля или равен ему. Это должно вдохновлять.
Кроме того, поскольку он находится в знаменателе, он не может быть равен нулю или быть отрицательным из-за радикала в выражении. Следовательно, когда мы решаем это для «x», мы видим, что «3x» должно быть больше, чем -5.
Кроме того, мы обнаруживаем, что «x» должно быть больше, чем $-\frac{5}{3}$, разделив обе части на «3». Это означает, что вы должны начать с -0,33 и двигаться до бесконечности, чтобы описать домен с использованием интервальной записи.
За скобками всегда следует бесконечность. Единственная проблема заключается в том, хотим ли мы включить отрицательные пять третей, чего мы не делаем.
\[(-\frac{5}{3}, \infty)\]
Итак, здесь тоже есть скобки, и вот наш домен.
Список математических калькуляторов
Дифференциальные уравнения. Интервалы достоверности
Онлайн-заметки Пола
Главная / Дифференциальные уравнения / DE первого порядка / Интервалы действия
Показать мобильное уведомление Показать все примечания Скрыть все примечания
Мобильное уведомление
Похоже, вы используете устройство с «узкой» шириной экрана ( т. е. вы, вероятно, используете мобильный телефон). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
Раздел 2-6: Интервалы действия
Мы назвали этот раздел «Интервалы достоверности», поскольку они будут использоваться во всех примерах. Тем не менее, в этом разделе есть намного больше. Мы увидим пару теорем, которые подскажут нам, когда мы сможем решить дифференциальное уравнение. Мы также увидим некоторые различия между линейными и нелинейными дифференциальными уравнениями.
Сначала рассмотрим теорему о линейных дифференциальных уравнениях первого порядка. Это очень важная теорема, хотя мы не собираемся использовать ее в ее самом важном аспекте.
Теорема 1
Рассмотрим следующую IVP.
\[y’ + p\left( t \right)y = g\left( t \right)\hspace{0.25in}y\left({{t_0}} \right) = {y_0}\]
Если $p(t)$ и $g(t)$ являются непрерывными функциями на открытом интервале $\alpha < t < \beta $ и интервал содержит $t_{o}$ , то на этом интервале существует единственное решение IVP.
Так что же говорит нам эта теорема? Во-первых, он говорит нам, что для достаточно хороших линейных дифференциальных уравнений первого порядка решения гарантированно существуют и, что более важно, решение будет уникальным. Возможно, мы не сможем найти решение, но знаем, что оно существует и будет только одно из них. Это очень важный аспект этой теоремы. Знать, что дифференциальное уравнение имеет единственное решение, иногда важнее, чем иметь само решение!
Далее, если интервал в теореме — это максимально возможный интервал, на котором $p(t)$ и $g(t)$ непрерывны, то этот интервал является интервалом применимости решения. Это означает, что для линейных дифференциальных уравнений первого порядка нам не нужно будет фактически решать дифференциальное уравнение, чтобы найти интервал достоверности. Заметьте также, что интервал действия будет лишь частично зависеть от начального условия. Интервал должен содержать $t_{o}$, но значение $y_{o}$ не влияет на интервал действия. 92} — 9}}\]
Далее нам нужно определить, где две функции не являются непрерывными. Это позволит найти все возможные интервалы справедливости дифференциального уравнения. Таким образом, $p(t)$ будет разрывным в $t = \pm \,3$, так как эти точки дадут деление на ноль. Точно так же $g(t)$ также будет разрывным в $t = \pm \,3$, а также в $t = 5$, поскольку в этой точке мы будем иметь натуральный логарифм нуля. Обратите внимание, что в этом случае нам не придется беспокоиться о натуральном логарифме отрицательных чисел из-за абсолютных значений.
Теперь, имея на руках эти точки, мы можем разбить прямую с действительными числами на четыре интервала, где и $p(t)$, и $g(t)$ будут непрерывными. Эти четыре интервала равны
. \[ — \ infty < t < - 3 \ hspace {0,25 дюйма} - 3 < t < 3 \ hspace {0,25 дюйма} 3 < t < 5 \ hspace {0,25 дюйма} 5 < t < \ infty \]
Конечные точки каждого интервала — это точки, в которых хотя бы одна из двух функций является разрывной. Это гарантирует, что обе функции непрерывны всюду на каждом интервале.
Наконец, давайте определим фактический интервал достоверности для проблемы начального значения. Фактический интервал действия — это интервал, который будет содержать $t_{o} = 4$. Итак, интервал действия для задачи с начальным значением равен.
\[3 < т < 5\]
В этом последнем примере мы должны быть осторожны, чтобы не сделать поспешный вывод о том, что остальные три интервала не могут быть интервалами достоверности. Изменяя начальное условие, в частности значение $t_{o}$, мы можем сделать любой из четырех интервалов интервалом достоверности.
Первая теорема требовала линейного дифференциального уравнения. Аналогичная теорема имеет место для нелинейных дифференциальных уравнений первого порядка. Эта теорема не так полезна для нахождения интервалов достоверности, как первая теорема, поэтому мы не будем много с ней делать.
Вот теорема.
Теорема 2
Рассмотрим следующую ИВП.
\[y’ = f\left( {t,y} \right)\hspace{0.25in}y\left({{t_0}} \right) = {y_0}\]
Если $f(t,y)$ и $\frac{{\partial f}}{{\partial y}}$ являются непрерывными функциями в некотором прямоугольнике $\alpha < t < \beta \ ), \(\gamma < y < \delta $, содержащий точку ($t_{o}\, y_{o})$, то существует единственное решение ЗВП в некотором интервале $t_{o} – h < t < t_{o} + h$, содержащееся в $\alpha < t < \beta $.
Вот и все. В отличие от первой теоремы, эту нельзя использовать для нахождения интервала достоверности. Итак, мы будем знать, что единственное решение существует, если выполняются условия теоремы, но на самом деле решение нам понадобится, чтобы определить интервал его применимости. Также обратите внимание, что для нелинейных дифференциальных уравнений оказывается, что значение $y_{0}$ может влиять на интервал достоверности. 9{\ гидроразрыва {2} {3}}}}} \]
Итак, функция непрерывна на любом интервале, но производная не непрерывна на $y = 0$ и, следовательно, не будет непрерывной на любом интервале, содержащем $y = 0$. Чтобы использовать теорему, оба должны быть непрерывными на интервале, содержащем $y_{o} = 0$, и это проблема для нас, поскольку у нас есть $y_{o} = 0$.
Теперь давайте решим задачу. Это дифференциальное уравнение разделимо и решается довольно просто. 9{\ гидроразрыва {3} {2}}} \ конец {выравнивание *} \]
Итак, у нас есть два возможных решения, каждое из которых удовлетворяет дифференциальному уравнению и начальному условию. Существует также третье решение IVP. $y(t) = 0$ также является решением дифференциального уравнения и удовлетворяет начальному условию.
В этом последнем примере у нас была очень простая IVP, и она нарушала только одно из условий теоремы, но имела три разных решения. Все примеры, с которыми мы работали в предыдущих разделах, удовлетворяли условиям этой теоремы и имели единственное единственное решение IVP. Этот пример — полезное напоминание о том, что в области дифференциальных уравнений не всегда бывает хорошо. Об этом легко забыть, так как большинство задач, которые решаются в классе дифференциальных уравнений, хороши и ведут себя хорошо и предсказуемо. 92}\hspace{0,25 дюйма}y\влево( 0 \вправо) = {y_0}\]
Показать решение
Прежде чем приступить к решению этой задачи, отметим, что дифференциальное уравнение нелинейно и удовлетворяет обоим условиям теоремы 2, поэтому для каждого возможного значения $y_{o}$ будет единственное решение IVP. ).
Также обратите внимание, что задача требует какой-либо зависимости интервала достоверности от значения $y_{o}$. Это сразу иллюстрирует разницу между линейными и нелинейными дифференциальными уравнениями. Интервалы справедливости для линейных дифференциальных уравнений не зависят от значения $y_{o}$. { — 2}}dy}} & = \int{{dt}}\\ — \frac{1}{y} & = t + c\end {выровнять*}\]
Применение начального условия дает
\[c = — \frac{1}{{{y_0}}}\]
Решение есть.
\[\begin{align*} — \frac{1}{y} & = t — \frac{1}{{{y_0}}}\\ y\left( t \right) & = \frac{1} {\frac{1}{{{y_0}}} — t}}\\ y\left( t \right) & = \frac{{{y_0}}}{{1 — {y_0}t}}\ конец {выравнивание *} \]
Теперь, когда у нас есть решение задачи о начальных значениях, мы можем приступить к поиску интервалов достоверности. Из решения мы видим, что единственная проблема, которая у нас будет, это деление на ноль на 9.0005
\[t = \frac{1}{{{y_0}}}\]
Это приводит к двум возможным интервалам действия.
\[\begin{align*} — \infty < & t < \frac{1}{{{y_0}}}\\ \frac{1}{{{y_0}}} < & t < \infty \end{ выровнять*}\]
Фактическим интервалом действия будет интервал, содержащий $t_{o} = 0$. Однако это зависит от значения $y_{o}$. Если $y_{o} < 0 $, то $\frac{1}{{{y_0}}} < 0$ и, следовательно, второй интервал будет содержать $t_{o} = 0$. Аналогично, если $y_{o} > 0$, то $\frac{1}{{{y_0}}} > 0$, и в этом случае первый интервал будет содержать $t_{o} = 0\ ).
Это приводит к следующим возможным интервалам достоверности, в зависимости от значения \(y_{o}$.
\[\begin{align*}& {\mbox{If }}{y_0} > 0 & \hspace{0,25in} & — \infty < t < \frac{1}{{{y_0}}}{\mbox { - интервал достоверности}}{\mbox{.}}\\ & {\mbox{If }}{y_0} = 0 & \hspace{0,25in} & - \infty < t < \infty {\mbox{ - интервал достоверности}}{\mbox{.}}\\ & {\mbox{If }}{y_0} < 0 & \hspace{0,25in} & \frac{1}{{{y_0}}} < t < \infty \,{\mbox{ — интервал действия}}{\mbox{.}}\end{align*}\]
Кстати, обратите внимание, что решение в его окончательной форме также будет работать, если $y_{o} = 0$.
Итак, что этот пример показал нам о разнице между линейными и нелинейными дифференциальными уравнениями?
Во-первых, как указано в решении примера, интервалы применимости нелинейных дифференциальных уравнений могут зависеть от значения $y_{o}$, тогда как интервалы применимости линейных дифференциальных уравнений не зависят.
No related posts.