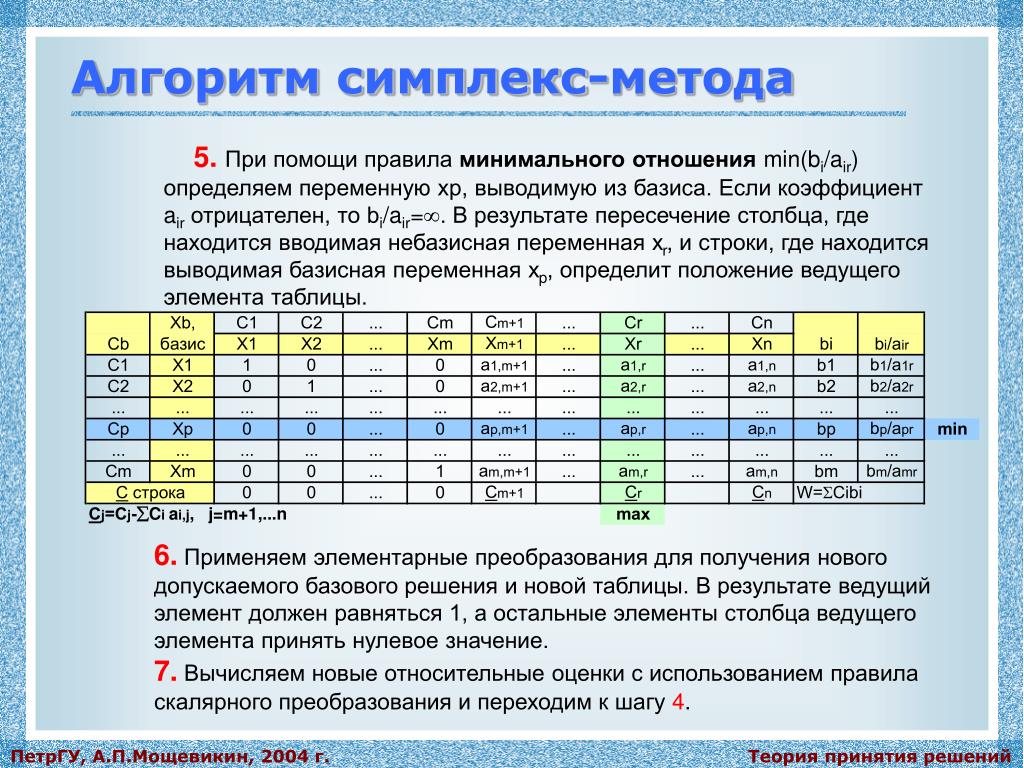
Метод искусственного базиса
Идея использования искусственных переменных предполагает включение неотрицательных переменных в левую часть каждого из уравнений, в которых не содержится очевидных начальных базисных переменных (когда неравенство имеет знак ≥ или задано в виде равенства). Эти дополнительно вводимые переменные выполняют ту же роль, что и остаточные переменные. Но так как искусственные переменные не имеют отношения к поставленной задаче (отсюда их название — искусственные), то их введение допустимо только в том случае, если симплекс метод будет обеспечивать получение оптимального решения, в котором все искусственные переменные будут равны 0, то есть эти переменные следует использовать только для стартовой точки, причем итерационный метод оптимизации должен «вынуждать» эти переменные принимать нулевые значения в конечном оптимальном решении, обеспечивая допустимость оптимума.Разработаны два метода получения стартовой точки:
- М — метод или метод больших штрафов.
- Двухэтапный метод.
Инструкция. Выберите количество переменных и количество строк (количество ограничений). Полученное решение сохраняется в файле Word и Excel.
Количество переменных
2345678910
Количество строк (количество ограничений)
2345678910
При этом ограничения типа xi ≥ 0 не учитывайте. Если в задании для некоторых xi отсутствуют ограничения, то ЗЛП необходимо привести к КЗЛП, или воспользоваться этим сервисом.
Пример. Решить задачу ЛП, найдя начальный опорный план методом искусственного базиса.
Определим максимальное значение целевой функции F(X) = 3x3 — 2x4 — x5 при следующих условиях:
2x1 + x2 + x3 + x4 + 3x5=5
3x1 + 2x3 — x4 + 6x5=7
x 1 — x3 + 2x4 + x5=2
Решим прямую задачу линейного программирования двухфазным симплекс-методом.
Введем искусственные переменные x.
2x1 + 1x2 + 1x3 + 1x4 + 3x5 + 1x6+ 0x7 + 0x8 = 5
3x1 + 0x2 + 2x3-1x4 + 6x5 + 0x6+ 1x7 + 0x8 = 7
1x1 + 0x2-1x3 + 2x4 + 1x5 + 0x6+ 0x7 + 1x8 = 2
Для постановки задачи на максимум целевую функцию запишем так:
F(X) = — Mx6 — Mx7 — Mx8 => max
Полученный базис называется искусственным, а метод решения называется методом искусственного базиса.
Из уравнений выражаем искусственные переменные:
x6 = 5-2x1-x2-x3-x4-3x5
x7 = 7-3x1-2x3+x4-6x5
x8 = 2-x1+x3-2x4-x5
которые подставим в целевую функцию:
F(X) = — M(5-2x1-x2-x3-x4-3x5) — M(7-3x1-2x3+x4-6x5) — M(2-x1+x3 -2x4-x5)=> max
или
F(X) = (6M)x1+(1M)x2+(2M)x3+(2M)x4+(10M)x5+(-14M)=> max
Введем новую переменную x0 = 6x1 + x2 + 2x3 + 2x4+ 10x5.
Выразим базисные переменные <6, 7, 8> через небазисные.
x0 = -14+6x1+x2+2x3+2x4+10x5
x6 = 5-2x1-x2-x3-x4-3x5
x7 = 7-3x1-2x3+x4-6x5
x8 = 2-x1+x3-2x4-x5
Переходим к основному алгоритму симплекс-метода.
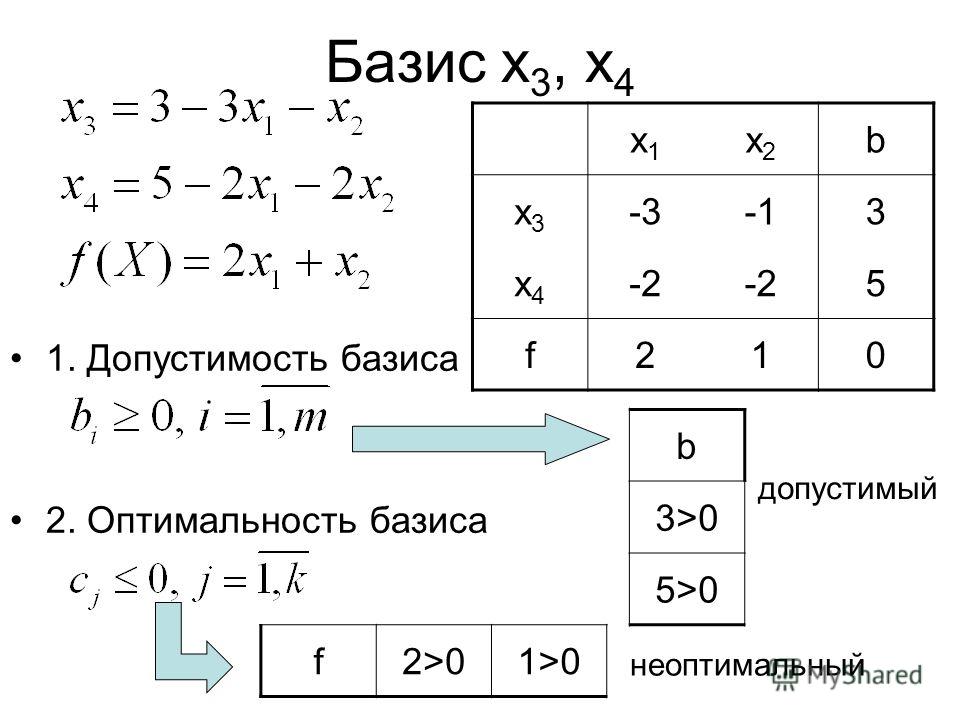
Поскольку задача решается на максимум, то переменную для включения в текущий план выбирают по максимальному положительному числу в уравнении для x
max(6,1,2,2,10,0,0,0) = 10
x0 = -14+6x1+x2+2x3+2x4+10x5
x6 = 5-2x1-x2-x3-x4-3x5
x7 = 7-3x1-2x3+x4-6x5
x8 = 2-x1+x3-2x4-x5
В качестве новой переменной выбираем x5.
Вычислим значения D5 по всем уравнениям для этой переменной.
и из них выберем наименьшее:
min (5 : 3 , 7 : 6 , 2 : 1 ) = 11/6
Вместо переменной x7 в план войдет переменная x5.
Выразим переменную x5 через x7
x5 = 11/6-1/2x1-1/3x 3+1/6x4-1/6x7
и подставим во все выражения.
x0 = -14+6x1+x2+2x3+2x4+10(11/6-1/2x1-1/3x3+1/6x4-1/6x7)
x6 = 5-2x1-x2-x3-x4-3(11/6-1/2x1-1/3x3+1/6x4-1/6x7)
x8 = 2-x1+x3-2x4-(11/6-1/2x1-1/3x3+1/6
После приведения всех подобных, получаем новую систему, эквивалентную прежней:
x0 = -21/3+x1+x2-11/3x3+32/3x4-12/3x7
x6 = 11/2-1/2x1-x2-11/2x4+1/2x7
x5 = 11/6-1/2x1-1/3x3+1/6x4-1/6x7
x8 = 5/6-1/2x1+11/3x3-21/6x4+1/6x7
Полагая небазисные переменные x = (6, 5, 8) равными нулю, получим новый допустимый вектор и значение целевой функции:
x = (-1, -1, 11/3, -32/3, 0, 0, 12/3,0), x0 = -21/3
max(1,1,-11/3,32/3,0,0,-12/3,0)= 32/3
x0 = -21/3+x1+x2-11/3x3+32/3x4-12/3x7
x6 = 11/2-1/2x1-x2-11/2x4+1/2x7
x5 = 11/6-1/2x1-1/3x3+1/6x4-1/6x7
x8 = 5/6-1/2x
В качестве новой переменной выбираем x4.
Вычислим значения D4 по всем уравнениям для этой переменной.
и из них выберем наименьшее:
min (11/2 : 11/2 , — , 5/6 : 21/6) = 5/13
Вместо переменной x8 в план войдет переменная x4.
Выразим переменную x4 через x8
x4 = 5/13-3/13x1+8/13x3+1/13x7-6/13x8
и подставим во все выражения.
x0=-21/3+x1+x2-11/3x3+32/3(5/13-3/13x1+8/13x3+1/13x7-6/13x8)-12/3x7
x6=11/2-1/2x1-x2-11/2(5/13-3/13x1+8/13x3+1/13x7-6/13x8)+1/2x7
x5=11/6-1/2x1-1/3x3+1/6(5/13-3/13x1+8/13x3+
После приведения всех подобных, получаем новую систему, эквивалентную прежней:
x0 = -12/13+2/13x1+x2+12/13x3-15/13x7-19/13x8
x6 = 12/13-2/13x1-x2-12/13x3+5/13x7+9/13x8
x5 = 13/13-7/13x1-3/13x3-2/13x7-1/13x8
x4 = 5/13-3/13x1+8/13x3+1/13x7-6/13x8
Полагая небазисные переменные x = (6, 5, 4) равными нулю, получим новый допустимый вектор и значение целевой функции:
x = (-2/13, -1, -12/13, 0, 0, 0, 15/13, 19/13),x0 = -12/13
max(2/13,1,12/13,0,0,0,-15/13,-19/13)= 1
x0 = -12/13+2/13x1+x2+12/13x3-15/13x7-19/13x8
x6 = 12/13-2/13x1-x2-12/13x3+5/13x7+9/13x8
x5 = 13/13-7/13x1-3/13x3-2/13x7-1/13x8
x4 = 5/13-3/13x1+8/13x3+1/13x7-6/13x8
В качестве новой переменной выбираем x2.
Вычислим значения D2 по всем уравнениям для этой переменной.
и из них выберем наименьшее:
min (12/13 : 1 , — , — ) = 12/13
Вместо переменной x6 в план войдет переменная x2.
Выразим переменную x2 через x6
x2 = 12/13-2/13x1-12/13x3-x6+5/13x7+9/13x8
и подставим во все выражения.
x0=-12/13+2/13x1+(12/13-2/13x1-12/13x3-x6+5/13x7+9/13x8)+12/13x3-15/13x7-19/13x8
x5 = 13/13-7/13x1-3/13x3-2/13x7-1/13x8
x4 = 5/13-3/13x1+8/13x3+1/13x7-6/13x8
После приведения всех подобных, получаем новую систему, эквивалентную прежней:
x0 = 0-x6-x7-x8
x2 = 12/13-2/13x1-12/13x3-x6+5/13x7+9/13x8
x5 = 13/13-7/13x1-3/13x3-2/13x7-1/13x8
x4 = 5/13-3/13x1+8/13x3+1/13x7-6/13x8
Полагая небазисные переменные x = (2, 5, 4) равными нулю, получим новый допустимый вектор и значение целевой функции:
x = (0, 0, 0, 0, 0, 1, 1, 1), x0 = 0
Выражение для x0 не содержит положительных элементов.
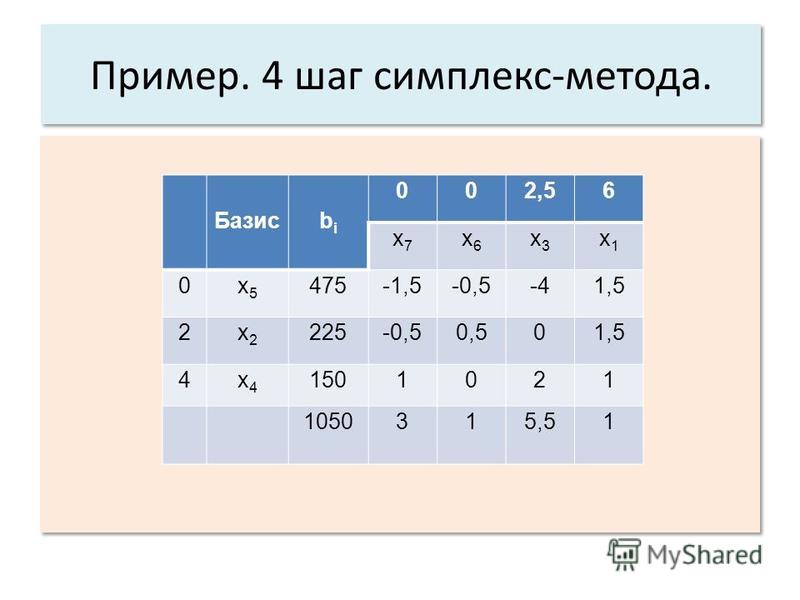Найден оптимальный план.
x0 = 0-x6-x7-x8
x2 = 12/13-2/13x1-12/13x3-x6+5/13x7+9/13x8
x5 = 13/13-7/13x1-3/13x3-2/13x7-1/13x8
x4 = 5/13-3/13x1+8/13x3+1/13x7-6/13x8
На этом первый этап (первая фаза) симплекс-метода завершен. Переходим ко второму этапу. Удаляем переменные с искусственными переменными.
x2 = 12/13-2/13x1-12/13x3
x5 = 13/13-7/13x1-3/13x3
x4 = 5/13-3/13x1+8/13x3
Выразим базисные переменные:
x5 = 13/13-7/13x1-3/13x3
x4 = 5/13-3/13x1+8/13x3
которые подставим в целевую функцию:
F(X) = + 3x3-2(5/13-3/13x1+8/13x3)-(13/13-7/13x1-3/13x3)
или
F(X) = -2+x1+2x3
Получаем новую систему переменных.
x0 = -2+x1+2x3
x2 = 12/13-2/13x1-12/13x3
x5 = 13/13-7/13x1-3/13x3
x4 = 5/13-3/13x1+8/13x3
max(1,0,2,0,0) = 2
x0 = -2+x1+2x3
x2 = 12/13-2/13x1-12/13x3
x5 = 13/13-7/13x1-3/13x3
x4 = 5/13-3/13x1+8/13x3
В качестве новой переменной выбираем x3.
Вычислим значения D3 по всем уравнениям для этой переменной.
и из них выберем наименьшее:
min (12/13 : 12/13 , 13/13 : 3/13, — ) = 1
Вместо переменной x2 в план войдет переменная x3.
Выразим переменную x3 через x2
x3 = 1-1/6x1-11/12x2
и подставим во все выражения.
x0 = -2+x1+2(1-1/6x1-11/12x2)
x5 = 13/13-7/13x1-3/13(1-1/6x1-11/12x2)
x4 = 5/13-3/13x1+8/13(1-1/6x1-11/12x2)
После приведения всех подобных, получаем новую систему, эквивалентную прежней:
x0 = 0+2/3x1-21/6x2
x3 = 1-1/6x1-11/12x2
x5 = 1-1/2x1+1/4x2
x4 = 1-1/3x1-2/3x2
Полагая небазисные переменные x = (3, 5, 4) равными нулю, получим новый допустимый вектор и значение целевой функции:
x = (-2/3, 21/6, 0, 0, 0), x0 = 0
max(2/3,-21/6,0,0,0) = 2/3
x0 = 0+2/3x1-21/6x2
x3 = 1-1/6x1-11/12x2
x5 = 1-1/2x1+1/4x2
x4 = 1-1/3x1-2/3x2
В качестве новой переменной выбираем x1.
Вычислим значения D1 по всем уравнениям для этой переменной.
и из них выберем наименьшее:
min (1 : 1/6 , 1 : 1/2 , 1 : 1/3 ) = 2
Вместо переменной x5 в план войдет переменная x1.
Выразим переменную x1 через x5
x1 = 2+1/2x2-2x5
и подставим во все выражения.
x0 = 0+2/3(2+1/2x2-2x5)-21/6x2
x3 = 1-1/6(2+1/2x2-2x5)-11/12x2
x4 = 1-1/3(2+1/2x2-2x5)-2/3x2
После приведения всех подобных, получаем новую систему, эквивалентную прежней:
x0 = 11/3-15/6x2-11/3x5
x3 = 2/3-11/6x2+1/3x5
x1 = 2+1/2x2-2x5
x4 = 1/3-5/6x2+2/3x5
Полагая небазисные переменные x = (3, 1, 4) равными нулю, получим новый допустимый вектор и значение целевой функции:
x = (0, 15/6, 0, 0, 11/3), x0 = 11/3
Выражение для x0 не содержит положительных элементов.
Найден оптимальный план.
Окончательный вариант системы уравнений:
x0 = 11/3-15/6x2-11/3x5
x3 = 2/3-11/6x2+1/3x5
x1 = 2+1/2x2-2x5
x4 = 1/3-5/6x2+2/3x5
Оптимальный план можно записать так:
x1 = 2
x3 = 2/3
x4 = 1/3
F(X) = 3•2/3 + 0•2 = 11/3
Примечание:
- Число операций в симплекс-методе не превосходит n!/((n-m)!*m!)
- Решение х системы уравнений, в котором все небазисные переменные равны 0, называется базисным решение.
- Если все компоненты базисного решения неотрицательны, то оно называется допустимым базисным решение или опорным планом.
M-задача
задачи линейного программирования решение онлайн
Вы искали задачи линейного программирования решение онлайн? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и калькулятор онлайн симплексный метод, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «задачи линейного программирования решение онлайн».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте.
Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как задачи линейного программирования решение онлайн,калькулятор онлайн симплексный метод,калькулятор симплекс,калькулятор симплекс метод,калькулятор симплекс метода онлайн,метод искусственного базиса калькулятор онлайн,метод искусственного базиса онлайн калькулятор,метод оптимальных решений онлайн калькулятор,методы оптимальных решений калькулятор онлайн,методы оптимальных решений онлайн калькулятор,онлайн калькулятор метод искусственного базиса,онлайн калькулятор методы оптимальных решений,онлайн калькулятор симплекс метод,онлайн калькулятор симплекс метод с подробным решением,онлайн калькулятор симплекс метода,онлайн калькулятор симплексный метод,онлайн решение задач линейного программирования,онлайн решение задачи линейного программирования,онлайн решение симплекс метод,онлайн решение симплекс методом,решение задач линейного программирования онлайн,решение задач линейного программирования симплекс методом онлайн,решение задач симплекс методом онлайн,решение задач симплекс методом онлайн с решением,решение задачи линейного программирования онлайн,решение задачи линейного программирования симплекс методом онлайн,решение задачи симплекс методом онлайн,решение злп симплекс методом онлайн,решение онлайн симплекс методом,решение симплекс метод онлайн,решение симплекс методом,решение симплекс методом онлайн,решения задачи табличным симплексным методом онлайн,решить задачу линейного программирования онлайн,решить задачу линейного программирования симплекс методом онлайн,решить задачу симплекс методом онлайн,решить онлайн задачу линейного программирования,решить онлайн симплекс методом,решить симплекс методом задачу,решить симплекс методом задачу линейного программирования онлайн,решить симплекс методом онлайн,симплекс калькулятор,симплекс калькулятор онлайн,симплекс метод калькулятор,симплекс метод калькулятор онлайн,симплекс метод онлайн,симплекс метод онлайн калькулятор,симплекс метод онлайн калькулятор с подробным решением,симплекс метод онлайн решение,симплекс метод онлайн с параметром,симплекс метод онлайн с подробным решением,симплекс метод онлайн с подробным решением онлайн,симплекс метод решение онлайн,симплекс метод с параметром онлайн,симплекс онлайн,симплекс онлайн калькулятор,симплекс таблица онлайн,симплексный метод калькулятор онлайн,симплексный метод онлайн,симплексный метод онлайн калькулятор.
На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и задачи линейного программирования решение онлайн. Просто введите задачу в окошко и нажмите
«решить» здесь (например, калькулятор симплекс).
Где можно решить любую задачу по математике, а так же задачи линейного программирования решение онлайн Онлайн?
Решить задачу задачи линейного программирования решение онлайн вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.
Калькулятор симплексного метода — eMathHelp
Калькулятор решит данную задачу оптимизации с использованием симплексного алгоритма.
При необходимости он добавит резервы, излишки и искусственные переменные. В случае искусственных переменных для определения исходного решения используется метод Big M или двухфазный метод. Шаги доступны.
Целевая функция:
Развернуть?
Ограничения:
x_1+2x_2<=8,x_1+x_2<=6,x_1>=0,x_2>=0
Через запятую.
Метод искусственного стартового раствора:
Метод Big M Двухфазный метод
Если калькулятор что-то не рассчитал, или вы обнаружили ошибку, или у вас есть предложение/отзыв, пожалуйста, напишите его в комментариях ниже.
Ваш ввод
Максимум $$$Z = 3 x_{1} + 4 x_{2}$$$, при условии $$$\begin{case} x_{1} + 2 x_{2} \ leq 8 \\ x_{1} + x_{2} \leq 6 \\ x_{1} \geq 0 \\ x_{2} \geq 0 \end{cases}$$$.
Решение
Задача в канонической форме может быть записана следующим образом:
$$Z = 3 x_{1} + 4 x_{2} \to max$$$$\begin{cases} x_ {1} + 2 x_{2} \leq 8 \\ x_{1} + x_{2} \leq 6 \\ x_{1}, x_{2} \geq 0 \end{cases}$$
Добавить переменные (остаток или излишек), чтобы превратить все неравенства в равенства:
$$Z = 3 x_{1} + 4 x_{2} \to max$$$$\begin{cases} x_{1} + 2 x_ {2} + S_{1} = 8 \\ x_{1} + x_{2} + S_{2} = 6 \\ x_{1}, x_{2}, S_{1}, S_{2} \ geq 0 \end{case}$$
Запишите симплексную таблицу:
| Basic | $$$x_{1}$$$ | $$$x_{2}$$$ | $$$S_{1}$$$ | $$$S_{2}$$$ | Решение |
| $$$Z$$$ | $$$-3$$$ | $$$-4$$$ | $$$0 $$$ | $$$0$$$ | $$$0$$$ |
| $$$S_{1}$$$ | $$$1$$$ | $$$2$$$ | $$$1$$$ | $$$0$$$ | $$$8$$$ |
| $$$S_{2}$$$ | $$$1$$$ | $$$1$$$ | $$$0$$$ | $$$1$$$ | $$$6$$ $ |
Входная переменная $$$x_{2}$$$, потому что она имеет самый отрицательный коэффициент $$$-4$$$ в Z-строке.
| Базовый | $$$x_{1}$$$ | $$$x_{2}$$$ | $$$S_{1}$$$ | $$$S_{2} $$$ | Решение | Отношение | |
| $$$Z$$$ | $$$-3$$$ | $$$-4$$$ | $$$0$$$ | $$$0$$$ | $$$0$$$ | ||
| $$$S_{1}$$$ | $$$1$$$ | $ | $$2$$$ | $$$1$$$ | $$$0$$$ | $$$8$$$ | $$$\frac{8}{2} = 4$$$ |
| $$$S_{2}$$$ | $$$1$$$ | $$$1$$$ | $$$0$$$ | $$$1$$$ | $$$6$$ $ | $$$\frac{6}{1} = 6$$$ |
Выходная переменная равна $$$S_{1}$$$, поскольку она имеет наименьшее отношение.
Разделить строку $$$1$$$ на $$$2$$$: $$$R_{1} = \frac{R_{1}}{2}$$$.
| Базовый | $$$x_{1}$$$ | $$$x_{2}$$$ | $$$S_{1}$$$ | $$$S_{2} $$$ | Решение |
| $$$Z$$$ | $$$-3$$$ | $$$-4$$$ | $$$0$$$ | $$$0 $$$ | $$$0$$$ |
| $$$x_{2}$$$ | $$$\frac{1}{2}$$$ | $$$1$$$ | $$$\frac{1}{2}$$$ | $$$0$$$ | $$$4$$$ |
| $$$S_{2}$$$ | $$$1$$$ | $$$1$$$ | $$$0 $$$ | $$$1$$$ | $$$6$$$ |
Добавить строку $$$2$$$, умноженную на $$$4$$$, в строку $$$1$$$: $$ $R_{1} = R_{1} + 4 R_{2}$$$.
| Базовый | $$$x_{1}$$$ | $$$x_{2}$$$ | $$$S_{1}$$$ | $$$S_{2} $$$ | Решение |
| $$$Z$$$ | $$$-1$$$ | $$$0$$$ | $$$2$$$ | $$$0$$$ | $$$16$$$ |
| $$$x_{2}$$$ | $$ $\frac{1}{2}$$$ | $$$1$$$ | $$$\frac{1}{2}$$$ | $$$0$$$ | $$$4$ $$ |
| $$$S_{2}$$$ | $$$1$$$ | $$$1$$$ | $$$0$$$ | $$$1$$$ | $$$6$$$ |
Вычесть строку $$$2$$$ из строки $$$3$$$: $$$R_{3} = R_{3} — R_{2}$$$.
| Базовый | $$$x_{1}$$$ | $$$x_{2}$$$ | $$$S_{1}$$$ | $$$S_{2}$$ $ | Решение | |
| $$$Z$$$ | $$$-1$$$ | $$$0$$$ | $$$2$$$ | $$$0$$$ | $$$16$$$ | |
| $$$x_{2}$$$ | $$$\frac{1}{2}$$$ | $$$1$$$ | $$$ \frac{1}{2}$$$ | $$$0$$$ | $$$4$$$ | |
| $$$S_{2}$$$ | $$$\frac{1 {2}$$$ | $$$0$$$ | $$$- \frac{1}{2}$$$ | $$$1$$$ | $$$2$$$ |
Вводимая переменная $ $$x_{1}$$$, потому что у него самый отрицательный коэффициент $$$-1$$$ в Z-строке.
| Базовый | $$$x_{1}$$$ | $$$x_{2}$$$ | $$$S_{1}$$$ | $$$S_{2} | 0045 | $$$0$$$ | $$$16$$$ | |
| $$$x_{2}$$$ | $$$\frac{1}{2}$$$ | $ $$1$$$ | $$$\frac{1}{2}$$$ | $$$0$$$ | $$$4$$$ | $$$\frac{4}{\frac {1}{2}} = 8$$$ | ||
| $$$S_{2}$$$ | $$$\frac{1}{2}$$$ | $$$0$$$ | $$$- \frac{1}{2}$$$ | $$$1$$$ | $$$2$$$ | $$$\frac{2}{\frac{1}{ 2}} = 4$$$ |
Выходная переменная равна $$$S_{2}$$$, поскольку она имеет наименьшее отношение.
Умножить строку $$$2$$$ на $$$2$$$: $$$R_{2} = 2 R_{2}$$$.
| Базовый | $$$x_{1}$$$ | $$$x_{2}$$$ | $$$S_{1}$$$ | $$$S_{2} $$$ | Решение |
| $$$Z$$$ | $$$-1$$$ | $$$0$$$ | $$$2$$$ | $$$0$$ $ | $$$16$$$ |
| $$$x_{2}$$$ | $$$\frac{1}{2}$$$ | $$$1$$$ | $ $$\frac{1}{2}$$$ | $$$0$$$ | $$$4$$$ |
| $$$x_{1}$$$ | $$$1$$$ | $$$0$$$ | $$$-1$$$ | $$$2$$$ | $$$4$$$ |
Добавить строку $$$3$$$ в строку $$$1$$$: $$$R_{1} = R_{1} + R_{ 3}$$$.
| Базовый | $$$x_{1}$$$ | $$$x_{2}$$$ | $$$S_{1}$$$ | $$$S_{2} $$$ | Решение |
| $$$Z$$$ | $$$0$$$ | $$$0$$$ | $$$1$$$ | $$$2$$$ | $$$20$$$ |
| $$$x_{2}$$$ | $$$\frac{1}{2}$$$ | $$ $1$$$ | $$$\frac{1}{2}$$$ | $$$0$$$ | $$$4$$$ |
| $$$x_{1}$$$ | $$$1$$$ | $$$0$$$ | $$$-1$$$ | $$$2$$$ | $$$4$$$ |
Вычесть строку $$ $3$$$, умноженное на $$$\frac{1}{2}$$$ из строки $$$2$$$: $$$R_{2} = R_{2} — \frac{R_{3}} {2}$$$.
| Базовый | $$$x_{1}$$$ | $$$x_{2}$$$ | $$$S_{1}$$$ | $$$S_{2}$$ $ | Решение |
| $$$Z$$$ | $$$0$$$ | $$$0$$$ | $$$1$$$ | $$$2$$$ | 5 $$20$$$ |
| $$$x_{2}$$$ | $$$0$$$ | $$$1$$$ | $$$1$$$ | $$$-1 $$$ | $$$2$$$ |
| $$$x_{1}$$$ | $$$1$$$ | $$$0$$$ | $$$-1$$$ | $$$2$$$ | $$$4$$$ |
Ни один из коэффициентов Z-ряда не является отрицательным.
Оптимум достигнут.
Получено следующее решение: $$$\left(x_{1}, x_{2}, S_{1}, S_{2}\right) = \left(4, 2, 0, 0\right) $$$.
Ответ
$$$Z = 20$$$A достигается при $$$\left(x_{1}, x_{2}\right) = \left(4, 2\right)$ $$А.
Калькулятор симплексного метода — двухфазный онлайн 🥇
Если вы добрались до этого поста, вы, вероятно, студент, пытающийся понять линейное программирование, и вы не знаете, как решить эти проблемы с помощью симплекс-метода. Вот почему в PM Calculators мы создали онлайн-калькулятор симплекс-метода , который позволит вам разрабатывать задачи максимизации и минимизации, применяя традиционный симплекс-метод и двухфазный метод, когда это применимо. Наш инструмент имеет дружественный и простой в использовании дизайн.
Калькулятор симплексного метода — Бесплатная версия 906:20
Количество переменных:
Количество ограничений:
У вас уже есть членство?
Получить членство
Бесплатная версия калькулятора показывает вам каждую из промежуточных таблиц, которые создаются на каждой итерации симплекс-метода, чтобы вы могли проверить результаты, полученные при решении задачи вручную.
Расширенные функции онлайн-калькулятора симплекс-метода – Two-Phase
Посмотрим правде в глаза, симплекс-метод характеризуется тем, что является дотошной и непрактичной процедурой, потому что, если вы ошибетесь в промежуточном расчете, вы можете поставить под угрозу окончательное решение проблемы. В этом смысле учащемуся важно знать пошаговую процедуру получения каждого из значений в итерациях. Таким образом, в PM Calculators мы улучшили наше приложение, включив в него полное пошаговое объяснение расчетов по методу. Вы можете получить доступ к этому инструменту и другим (таким как калькулятор больших m и калькулятор графического линейного программирования), став членом нашего членства.
В рамках функциональности, которую считает это приложение, мы имеем:
- Возможность решать упражнения с 20 переменными и 50 ограничениями.
- Объяснение того, как определить условие оптимальности.
- Объяснение критериев для установления условия осуществимости.
- Подробная информация о расчетах, выполненных для получения вектора приведенных затрат, сводной строки и других строк таблицы.
- Для упражнений с искусственными переменными становится Калькулятор двухфазного метода .
- Объяснение особых случаев, таких как неограниченные и недопустимые решения.
Полные примеры работы приложения можно найти по этой ссылке.
Как пользоваться онлайн-калькулятором симплекс-метода
Для использования нашего инструмента необходимо выполнить следующие шаги:
- Введите количество переменных и ограничений задачи.
- Выберите тип проблемы: развернуть или свернуть .
- Введите коэффициенты целевой функции и ограничения. Вы можете вводить отрицательные числа, дроби и десятичные дроби (с точкой).
- Нажмите «Решить».
- Онлайн-программа адаптирует введенные значения к стандартной форме симплексного алгоритма и создаст первую таблицу .
- В зависимости от знака ограничений нормальный симплексный алгоритм или двухфазный метод используется.
- Мы можем видеть шаг за шагом итераций и таблиц калькулятора симплекс-метода.
- В последней части покажу результаты решения задачи.
Мы решили, что наше приложение может решать задачи с максимум 20 переменными и 50 ограничениями; это связано с тем, что упражнения с большим количеством переменных затруднили бы выполнение шагов с использованием симплекс-метода. Для проблем с большим количеством переменных мы рекомендуем использовать другой метод.
Пример
Ниже мы показываем некоторые справочные изображения шаг за шагом и результат следующего примера:
Для максимизации следующей задачи требуется:
Целевая функция Z = 3X 1 + 2X 2
При условии следующих ограничений
2x 1 + x 2 ≤ 18
2x 1 + 3x 2 ≤ 42
x 1 , x 2 2 stry stress 2 ≤ 42
x 1 .