Решение определенный интеграл онлайн: Интегрирование по частям

Содержание

вычисление интегралов определенных онлайн

Вы искали вычисление интегралов определенных онлайн? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и вычисление определенного интеграла, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «вычисление интегралов определенных онлайн».

Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который может решить задачи, такие, как вычисление интегралов определенных онлайн,вычисление определенного интеграла,вычисление определенного интеграла онлайн,вычисление определенного интеграла онлайн с подробным решением,вычисление определенных интегралов,вычисление определенных интегралов онлайн,вычисление определенных интегралов онлайн с подробным решением,вычислите определенный интеграл,вычислить значение определенного интеграла,вычислить интеграл онлайн с подробным решением определенный,вычислить несобственный интеграл онлайн,вычислить определенные интегралы,вычислить определенные интегралы онлайн с решением,вычислить определенный интеграл,вычислить определенный интеграл онлайн,вычислить определенный интеграл онлайн калькулятор,вычислить определенный интеграл онлайн с подробным решением,вычислить определенный интеграл онлайн с решением,интеграл онлайн определенный,интеграл определенный онлайн,интеграл решение определенный,интегралы онлайн несобственные,интегралы онлайн определенные,интегралы определенные онлайн,интегралы определенные онлайн с подробным решением,как вычислить определенный интеграл,калькулятор интегралов онлайн определенных,калькулятор интегралов онлайн определенных интегралов,калькулятор интегралов определенных,калькулятор онлайн вычислить определенный интеграл,калькулятор онлайн определенные интегралы,калькулятор онлайн определенный интеграл,калькулятор онлайн определенный интеграл с подробным решением,калькулятор онлайн определенных интегралов,калькулятор определенного интеграла,калькулятор определенного интеграла онлайн,калькулятор определенный интеграл,калькулятор определенных интегралов,калькулятор определенных интегралов онлайн,калькулятор определенных интегралов онлайн с решением,калькулятор определенных интегралов онлайн с решением подробным,калькулятор определенных интегралов с подробным решением онлайн,калькулятор определенных интегралов с решением онлайн,найти определенный интеграл,найти определенный интеграл онлайн,найти определенный интеграл онлайн с подробным решением,нахождение определенного интеграла,нахождение определенного интеграла онлайн,несобственные интегралы онлайн,несобственный интеграл онлайн,онлайн вычисление определенных интегралов,онлайн калькулятор вычислить определенные интегралы,онлайн калькулятор интегралов определенных,онлайн калькулятор интегралов с подробным решением определенных,онлайн калькулятор интегралы определенные,онлайн калькулятор определенного интеграла,онлайн калькулятор определенные интегралы,онлайн калькулятор определенный интеграл,онлайн калькулятор определенных интегралов,онлайн калькулятор определенных интегралов с подробным решением,онлайн нахождение определенного интеграла,онлайн решение определенного интеграла,онлайн решение определенного интеграла с подробным решением,онлайн решение определенных интегралов,онлайн решение определенных интегралов с подробным решением,определенные интегралы калькулятор онлайн,определенные интегралы онлайн,определенные интегралы онлайн калькулятор,определенные интегралы онлайн с подробным решением,определенный интеграл калькулятор,определенный интеграл калькулятор онлайн,определенный интеграл калькулятор онлайн с подробным решением,определенный интеграл онлайн,определенный интеграл онлайн калькулятор,определенный интеграл онлайн калькулятор с подробным решением,определенный интеграл онлайн с подробным решением,определенный интеграл онлайн тройной,определенный интеграл решение,определенный интеграл решить,определенный интеграл решить онлайн,определенный интеграл решить онлайн с подробным решением,посчитать интеграл онлайн определенный,посчитать онлайн определенный интеграл,посчитать определенный интеграл онлайн,решение интегралов онлайн определенных,решение несобственных интегралов онлайн,решение определенного интеграла,решение определенного интеграла онлайн,решение определенного интеграла онлайн с подробным решением,решение определенный интеграл,решение определенных интегралов,решение определенных интегралов онлайн,решение определенных интегралов онлайн с подробным решением,решение определенных интегралов онлайн с подробным решением бесплатно,решить интеграл определенный,решить онлайн определенный интеграл,решить определенный интеграл,решить определенный интеграл онлайн,решить определенный интеграл онлайн с подробным решением,сходимость интеграла онлайн.

На этой странице вы найдёте калькулятор, который поможет решить любой вопрос, в том числе и вычисление интегралов определенных онлайн. Просто введите задачу в окошко и нажмите «решить» здесь (например, вычисление определенного интеграла онлайн).

Где можно решить любую задачу по математике, а так же вычисление интегралов определенных онлайн Онлайн?

Решить задачу вычисление интегралов определенных онлайн вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.

Вычислить несобственный интеграл с помощью предельных теорем.

Определенный интеграл онлайн

Главная > Ремонт и отделка > Вычислить несобственный интеграл с помощью предельных теорем. Определенный интеграл онлайн

Несобственные интегралы первого рода: распространение понятия определённого интеграла на случаи интегралов с бесконечным верхним или нижними пределами интегрирования, или оба предела интегрирования бесконечны.

Несобственные интегралы второго рода: распространение понятия определённого интеграла на случаи интегралов от неограниченных функций, подынтегральная функция в конечном числе точек конечного отрезка интегрирования не существует, обращаясь в бесконечность.

Для сравнения. При введении понятия определённого интеграла предполагалось, что функция

f (x ) непрерывна на отрезке [a , b ], а отрезок интегрирования является конечным, то есть ограничен числами, а не бесконечностью. Некоторые задачи приводят к необходимости отказаться от этих ограничений. Так появляются несобственные интегралы.

Геометрический смысл несобственного интеграла выясняется довольно просто. В случае, когда график функции y = f (x ) находится выше оси Ox , определённый интеграл выражает площадь криволинейной трапеции, ограниченной кривой y = f (x ) , осью абсцисс и ординатами x = a , x = b . В свою очередь несобственный интеграл выражает площадь неограниченной (бесконечной) криволинейной трапеции, заключённой между линиями y = f (x ) (на рисунке ниже — красного цвета),

x = a и осью абсцисс.

Аналогичным образом определяются несобственные интегралы и для других бесконечных интервалов:

Площадь бесконечной криволинейной трапеции может быть конечным числом и в этом случае несобственный интеграл называется сходящимся. Площадь может быть и бесконечностью и в этом случае несобственный интеграл называется расходящимся.

Использование предела интеграла вместо самого несобственного интеграла. Для того, чтобы вычислить несобственный интеграл, нужно использовать предел определённого интеграла. Если этот предел существует и конечен (не равен бесконечности), то несобственный интеграл называется сходящимся, а в противном случае — расходящимся. К чему стремится переменная под знаком предела, зависит от того, имеем мы дело с несобственным интегралом первого рода или второго рода. Узнаем об этом сейчас же.

Несобственные интегралы первого рода — с бесконечными пределами и их сходимость

Несобственные интегралы с бесконечным верхним пределом

Итак, запись несобственного интеграла как отличается от обычного определённого интеграла тем, что верхний предел интегрирования бесконечен.

Определение. Несобственным интегралом с бесконечным верхним пределом интегрирования от непрерывной функции f (x ) на промежутке от a до ∞ называется предел интеграла этой функции с верхним пределом интегрирования b и нижним пределом интегрирования a при условии, что верхний предел интегрирования неограниченно растёт , т. е.

Если этот предел существует и равен некоторому числу, а не бесконечности, то несобственный интеграл называется сходящимся , а число, которому равен предел, принимается за его значение. В противном случае несобственный интеграл называется расходящимся и ему не приписывается никакого значения.

Пример 1. Вычислить несобственный интеграл (если он сходится).

Решение. На основании определения несобственного интеграла находим

Так как предел существует и равен 1, то и данный несобственный интеграл сходится и равен 1.

В следующем примере подынтегральная функция почти как в примере 1, только степень икса — не двойка, а буква альфа, а задача состоит в исследовании несобственного интеграла на сходимость. То есть предстоит ответить на вопрос: при каких значениях альфы данный несобственный интеграл сходится, а при каких расходится?

Пример 2. Исследовать на сходимость несобственный интеграл (нижний предел интегрирования больше нуля).

Решение. Предположим сначала, что , тогда

В полученном выражении перейдём к пределу при :

Нетрудно видеть, что предел в правой части существует и равен нулю, когда , то есть , и не существует, когда , то есть .

В первом случае, то есть при имеет место . Если , то и не существует.

Вывод нашего исследования следующий: данный несобственный интеграл сходится при и расходится при .

Применяя к изучаемому виду несобственного интеграла формулу Ньютона-Лейбница , можно вывести следующую очень похожую на неё формулу:

Это обобщённая формула Ньютона-Лейбница.

Пример 3. Вычислить несобственный интеграл (если он сходится).

Предел этого интеграла существует:

Второй интеграл, составляющий сумму, выражающую исходный интеграл:

Предел этого интеграла также существует:

Находим сумму двух интегралов, являющуюся и значением исходного несобственного интеграла с двумя бесконечными пределами:

Несобственные интегралы второго рода — от неограниченных функций и их сходимость

Пусть функция f (x ) задана на отрезке от a до b и неограниченна на нём. Предположим, что функция обращается в бесконечность в точке b , в то время как во всех остальных точках отрезка она непрерывна.

Определение. Несобственным интегралом функции f (x ) на отрезке от a до b называется предел интеграла этой функции с верхним пределом интегрирования c , если при стремлении c к b функция неограниченно возрастает, а в точке x = b функция не определена , т.е.

Если этот предел существует, то несобственный интеграл второго рода называется сходящимся, в противном случае — расходящимся.

Используя формулу Ньютона-Лейбница, выводим.

Вы еще здесь? =) Нет, я никого не пытался запугать, просто тема несобственных интегралов – очень хорошая иллюстрация тому, как важно не запускать высшую математику и другие точные науки. Для освоения урока на сайте всё есть – в подробной и доступной форме, было бы желание….

Итак, начнем-с. Образно говоря, несобственный интеграл – это «продвинутый» определенный интеграл, и на самом деле сложностей с ними не так уж и много, к тому же у несобственного интеграла есть очень хороший геометрический смысл.

Что значит вычислить несобственный интеграл?

Вычислить несобственный интеграл – это значит, найти ЧИСЛО (точно так же, как в определенном интеграле), или доказать, что он расходится (то есть, получить в итоге бесконечность вместо числа).

Несобственные интегралы бывают двух видов.

Несобственный интеграл с бесконечным пределом (ами) интегрирования

Иногда такой несобственный интеграл называют несобственным интегралом первого рода . В общем виде несобственный интеграл с бесконечным пределом чаще всего выглядит так: . В чем его отличие от определенного интеграла? В верхнем пределе. Он бесконечный: .

Реже встречаются интегралы с бесконечным нижним пределом или с двумя бесконечными пределами: , и их мы рассмотрим позже – когда войдёте во вкус:)

Ну а сейчас разберём самый популярный случай . В подавляющем большинстве примеров подынтегральная функция непрерывна на промежутке , и этот важный факт следует проверять в первую очередь! Ибо если есть разрывы, то есть дополнительные нюансы. Для определённости предположим, что и тогда типичная криволинейная трапеция будет выглядеть так:

Обратите внимание, что она бесконечна (не ограничена справа), и несобственный интеграл численно равен её площади . При этом возможны следующие варианты:

1) Первая мысль, которая приходит в голову: «раз фигура бесконечная, то », иными словами, площадь тоже бесконечна. Так быть может. В этом случае говорят, что несобственный интеграл расходится .

2) Но . Как это ни парадоксально прозвучит, площадь бесконечной фигуры может равняться… конечному числу! Например: . Может ли так быть? Запросто. Во втором случае несобственный интеграл сходится .

3) О третьем варианте чуть позже.

В каких случаях несобственный интеграл расходится, а в каком сходится? Это зависит от подынтегральной функции , и конкретные примеры мы очень скоро рассмотрим.

А что будет, если бесконечная криволинейная трапеция расположена ниже оси? В этом случае, несобственный интеграл (расходится) либо равен конечному отрицательному числу.

Таким образом, несобственный интеграл может быть отрицательным .

Важно! Когда Вам для решения предложен ЛЮБОЙ несобственный интеграл, то, вообще говоря, ни о какой площади речи не идет и чертежа строить не нужно . Геометрический смысл несобственного интеграла я рассказал только для того, чтобы легче было понять материал.

Коль скоро, несобственный интеграл очень похож на определенный интеграл, то вспомним формулу Ньютона- Лейбница: . На самом деле формула применима и к несобственным интегралам, только ее нужно немного модифицировать. В чем отличие? В бесконечном верхнем пределе интегрирования: . Наверное, многие догадались, что это уже попахивает применением теории пределов, и формула запишется так: .

В чем отличие от определенного интеграла? Да ни в чем особенном! Как и в определенном интеграле, нужно уметь находить первообразную функцию (неопределенный интеграл), уметь применять формулу Ньютона-Лейбница. Единственное, что добавилось – это вычисление предела. У кого с ними плохо, изучите урок Пределы функций. Примеры решений , ибо лучше поздно, чем в армии.

Рассмотрим два классических примера:

Пример 1

Для наглядности я построю чертеж, хотя, еще раз подчеркиваю, на практике строить чертежи в данном задании не нужно .

Подынтегральная функция непрерывна на полуинтервале , значит, всё нормально и несобственный интеграл можно вычислить «штатным» методом.

Применение нашей формулы и решение задачи выглядит так:

То есть, несобственный интеграл расходится, и площадь заштрихованной криволинейной трапеции равна бесконечности.

В рассмотренном примере у нас простейший табличный интеграл и такая же техника применения формулы Ньютона-Лейбница, как в определенном интеграле. Но применятся эта формула под знаком предела. Вместо привычной буквы «динамической» переменной выступает буква «бэ». Это не должно смущать или ставить в тупик, потому что любая буква ничем не хуже стандартного «икса».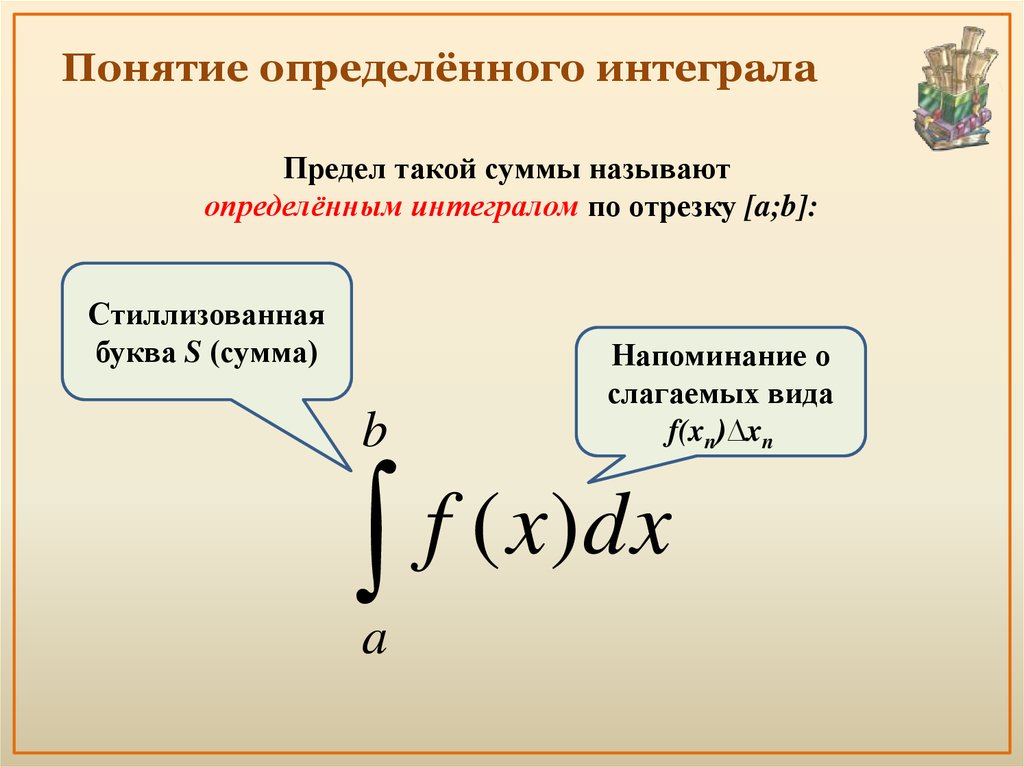

Если Вам не понятно почему при , то это очень плохо, либо Вы не понимаете простейшие пределы (и вообще не понимаете, что такое предел), либо не знаете, как выглядит график логарифмической функции. Во втором случае посетите урок Графики и свойства элементарных функций .

При решении несобственных интегралов очень важно знать, как выглядят графики основных элементарных функций!

Чистовое оформление задания должно выглядеть примерно так:

“

! При оформлении примера всегда прерываем решение, и указываем, что происходит с подынтегральной функцией – непрерывна она на промежутке интегрирования или нет . Этим мы идентифицируем тип несобственного интеграла и обосновываем дальнейшие действия.

Пример 2

Вычислить несобственный интеграл или установить его расходимость.

Выполним чертеж:

Во-первых, замечаем следующее: подынтегральная функция непрерывна на полуинтервале . Гуд. Решаем с помощью формулы :

(1) Берем простейший интеграл от степенной функции (этот частный случай есть во многих таблицах). Минус лучше сразу вынести за знак предела, чтобы он не путался под ногами в дальнейших вычислениях.

(2) Подставляем верхний и нижний пределы по формуле Ньютона-Лейбница.

(3) Указываем, что при (Господа, это уже давно нужно понимать) и упрощаем ответ.

Вот здесь площадь бесконечной криволинейной трапеции равна конечному числу! Невероятно, но факт.

Чистовое оформление примера должно выглядеть примерно так:

“

Подынтегральная функция непрерывна на

“

Что делать, если вам встретится интеграл наподобие – с точкой разрыва на интервале интегрирования? Это говорит о том, что в примере опечатка (вероятнее всего) , либо о продвинутом уровне обучения. В последнем случае, в силу свойства аддитивности , следует рассмотреть два несобственных интеграла на промежутках и и затем разобраться с суммой.

Иногда вследствие опечатки либо умысла несобственного интеграла может вовсе не существовать , так, например, если в знаменатель вышеуказанного интеграла поставить квадратный корень из «икс», то часть промежутка интегрирования вообще не войдёт в область определения подынтегральной функции.

Более того, несобственного интеграла может не существовать даже при всём «видимом благополучии». Классический пример: . Несмотря на определённость и непрерывность косинуса, такого несобственного интеграла не существует! Почему? Всё очень просто, потому что:
– не существует соответствующего предела .

И такие примеры пусть редко, но встречаются на практике! Таким образом, помимо сходимости и расходимости, есть ещё и третий исход решения с полноправным ответом: «несобственного интеграла не существует».

Следует также отметить, что строгое определение несобственного интеграла даётся именно через предел, и желающие могут ознакомиться с ним в учебной литературе. Ну а мы продолжаем практическое занятие и переходим к более содержательным задачам:

Пример 3

Вычислить несобственный интеграл или установить его расходимость.

Сначала попытаемся найти первообразную функцию (неопределенный интеграл). Если нам не удастся этого сделать, то несобственный интеграл мы, естественно, тоже не решим.

На какой из табличных интегралов похожа подынтегральная функция? Напоминает она арктангенс: . Из этих соображений напрашивается мысль, что неплохо бы в знаменателе получить квадрат. Делается это путем замены.

Проведем замену:

Неопределенный интеграл найден, константу в данном случае добавлять не имеет смысла.

На черновике всегда полезно выполнить проверку, то есть продифференцировать полученный результат:

Получена исходная подынтегральная функция, значит, неопределенный интеграл найден правильно.

Теперь находим несобственный интеграл:

(1) Записываем решение в соответствии с формулой . Константу лучше сразу вынести за знак предела, чтобы она не мешалась в дальнейших вычислениях.

(2) Подставляем верхний и нижний пределы в соответствии с формулой Ньютона-Лейбница. Почему при ? Смотрите график арктангенса в уже неоднократно рекомендованной статье.

(3) Получаем окончательный ответ. Тот факт, что полезно знать наизусть.

Продвинутые студенты могут не находить отдельно неопределенный интеграл, и не использовать метод замены, а использовать метод подведения функции под знак дифференциала и решать несобственный интеграл «сразу». В этом случае решение должно выглядеть примерно так:

“

Подынтегральная функция непрерывна на .

“

Пример 4

Вычислить несобственный интеграл или установить его расходимость.

! Это типовой пример, и похожие интегралы встречаются очень часто. Хорошо его проработайте! Первообразная функция здесь находится методом выделения полного квадрата, более подробно с методом можно ознакомиться на уроке Интегрирование некоторых дробей .

Пример 5

Вычислить несобственный интеграл или установить его расходимость.

Этот интеграл можно решить подробно, то есть сначала найти неопределенный интеграл, проведя замену переменной. А можно решить «сразу» – подведением функции под знак дифференциала. У кого какая математическая подготовка.

Полные решения и ответы в конце урока.

Примеры решений несобственных интегралов с бесконечным нижним пределом интегрирования можно посмотреть на странице Эффективные методы решения несобственных интегралов . Там же разобран случай, когда оба предела интегрирования бесконечны.

Несобственные интегралы от неограниченных функций

Или несобственные интегралами второго рода . Несобственные интегралы второго рода коварно «шифруются» под обычный определенный интеграл и выглядят точно так же: Но, в отличие от определенного интеграла, подынтегральная функция терпит бесконечный разрыв (не существует): 1) в точке , 2) или в точке , 3) или в обеих точках сразу, 4) или даже на отрезке интегрирования. Мы рассмотрим первые два случая, для случаев 3-4 в конце статьи есть ссылка на дополнительный урок.

Сразу пример, чтобы было понятно: . Вроде бы это определенный интеграл. Но на самом деле – это несобственный интеграл второго рода, если мы подставим в подынтегральную функцию значение нижнего предела , то знаменатель у нас обращается в ноль, то есть подынтегральной функции просто не существует в этой точке!

Вообще при анализе несобственного интеграла всегда нужно подставлять в подынтегральную функцию оба предела интегрирования . В этой связи проверим и верхний предел: . Здесь всё хорошо.

Криволинейная трапеция для рассматриваемой разновидности несобственного интеграла принципиально выглядит так:

Здесь почти всё так же, как в интеграле первого рода.

Наш интеграл численно равен площади заштрихованной криволинейной трапеции, которая не ограничена сверху. При этом могут быть два варианта*: несобственный интеграл расходится (площадь бесконечна) либо несобственный интеграл равен конечному числу (то есть, площадь бесконечной фигуры – конечна!).

* по умолчанию привычно полагаем, что несобственный интеграл существует

Осталось только модифицировать формулу Ньютона-Лейбница. Она тоже модифицируется с помощью предела, но предел стремится уже не к бесконечности, а к значению справа. Легко проследить по чертежу: по оси мы должны бесконечно близко приблизиться к точке разрыва справа .

Посмотрим, как это реализуется на практике.

Пример 6

Вычислить несобственный интеграл или установить его расходимость.

Подынтегральная функция терпит бесконечный разрыв в точке (не забываем устно или на черновике проверить, всё ли нормально с верхним пределом!)

Сначала вычислим неопределенный интеграл:

Замена:

У кого возникли трудности с заменой, обратитесь к уроку Метод замены в неопределенном интеграле .

Вычислим несобственный интеграл:

(1) Что здесь нового? По технике решения практически ничего. Единственное, что поменялось, это запись под значком предела: . Добавка обозначает, что мы стремимся к значению справа (что логично – см. график). Такой предел в теории пределов называют односторонним пределом . В данном случае у нас правосторонний предел .

(2) Подставляем верхний и нижний предел по формуле Ньютона Лейбница.

(3) Разбираемся с при . Как определить, куда стремится выражение? Грубо говоря, в него нужно просто подставить значение , подставляем три четверти и указываем, что . Причесываем ответ.

В данном случае несобственный интеграл равен отрицательному числу. В этом никакого криминала нет, просто соответствующая криволинейная трапеция расположена под осью .

А сейчас два примера для самостоятельного решения.

Пример 7

Вычислить несобственный интеграл или установить его расходимость.

Пример 8

Вычислить несобственный интеграл или установить его расходимость.

Если подынтегральной функции не существует в точке

Бесконечная криволинейная трапеция для такого несобственного интеграла принципиально выглядит следующим образом.

Определенные интегралы онлайн на сайт для закрепления студентами и школьниками пройденного материала. И тренировки своих практических навыков. Полноценное решение определенных интегралов онлайн для вас в считанные мгновения поможет определить все этапы процесса.. Интегралы онлайн — определенный интеграл онлайн. Определенные интегралы онлайн на сайт для полноценного закрепления студентами и школьниками пройденного материала и тренировки своих практических навыков.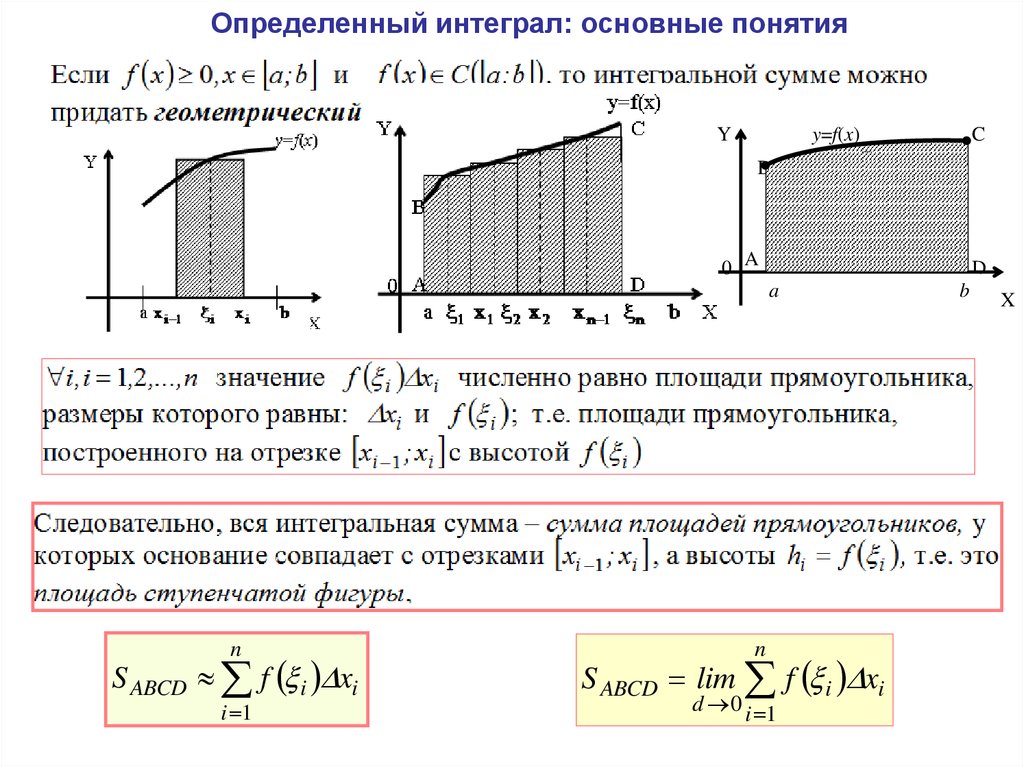 Полноценное решение определенных интегралов онлайн для вас в считанные мгновения поможет определить все этапы процесса.. Интегралы онлайн — определенный интеграл онлайн. Для нас определенный интеграл онлайн взять не представляется чем-то сверх естественным, изучив данную тему по книге выдающихся авторов. Огромное им спасибо и выражаем респект этим личностям. Поможет определить определенный интеграл онлайн сервис по вычислению таких задач в два счета. Только укажите правильные данные и все будет Good! Всякий определенный интеграл как решение задачи повысит грамотность студентов. Об этом мечтает каждый ленивец, и мы не исключение, признаем это честно. Если все-таки получится вычислить определенный интеграл онлайн с решением бесплатно, то, пожалуйста, напишите адрес сайт всем желающим им воспользоваться. Как говорится, поделишься полезной ссылкой — и тебя отблагодарят добрые люди за даром. Очень интересным будет вопрос разбора задачки, в которой определенный интеграл будет калькулятор решать самостоятельно, а не за счет траты вашего драгоценного времени. На то они и машины, чтобы пахать на людей. Однако решение определенных интегралов онлайн не всякому сайту по зубам, и это легко проверить, а именно, достаточно взять сложный пример и попытаться решить его с помощью каждого такого сервиса. Вы почувствуете разницу на собственной шкуре. Зачастую найти определенный интеграл онлайн без прилагаемых усилий станет достаточно сложно и нелепо будет выглядеть ваш ответ на фоне общей картины представления результата. Лучше бы сначала пройти курс молодого бойца. Всякое решение несобственных интегралов онлайн сводится сначала к вычислению неопределенного, а затем через теорию пределов вычислить как правило односторонние пределы от полученных выражений с подставленными границами A и B. Рассмотрев указанный вами определенный интеграл онлайн с подробным решением, мы сделали заключение, что вы ошиблись на пятом шаге, а именно при использовании формулы замены переменной Чебышева. Будьте очень внимательны в дальнейшем решении. Если ваш определенный интеграл онлайн калькулятор не смог взять с первого раза, то в первую очередь стоит перепроверить написанные данные в соответствующие формы на сайте. Убедитесь, что все в порядке и вперёд, Go-Go! Для каждого студента препятствием является вычисление несобственных интегралов онлайн при самом преподе, так как это либо экзамен, либо коллоквиум, или просто контрольная работа на паре.. Как только заданный несобственный интеграл онлайн калькулятор будет в вашем распоряжении, то сразу вбивайте заданную функцию, подставляйте заданные пределы интегрирования и нажимайте на кнопку Решение, после этого вам будет доступен полноценный развернутый ответ. И все-таки хорошо, когда есть такой замечательный сайт как сайт, потому что он и бесплатный, и простой в пользовании, также содержит очень много разделов. которыми студенты пользуются повседневно, один из них как раз есть определенный интеграл онлайн с решением в полном виде. В этом же разделе можно вычислить несобственный интеграл онлайн с подробным решением для дальнейших применений ответа как в институте, так и в инженерных работах. Казалось бы, всем определить определенный интеграл онлайн дело нехитрое, если заранее решить такой пример без верхней и нижней границы, то есть не интеграл Лейбница, а неопределенный интеграл. Но тут мы с вами не согласны категорически, так как на первый взгляд это может показаться именно так, однако есть существенная разница, давайте разберем все по полочкам. Такой определенный интеграл решение дает не в явном виде, а в следствие преобразования выражения в предельное значение. Другими словами, нужно сначала решить интеграл с подстановкой символьных значений границ, а затем вычислить предел либо на бесконечности, либо в определенной точке. Отсюда вычислить определенный интеграл онлайн с решением бесплатно означает ни что иное как представление точного решения по формуле Ньютона-Лейбница. Если же рассматривать наш определенный интеграл калькулятор поможет его подсчитать за несколько секунд прямо на ваших глазах. Такая спешка нужна всем желающим как можно быстрее справиться с заданием и освободиться для личных дел. Не стоит искать в интернете сайты, на которых попросят вас регистрироваться, затем пополнить деньги на баланс и все ради того, чтобы какой-нибудь умник подготавливал решение определенных интегралов якобы онлайн. Запомните адрес Math34 — это бесплатный сервис для решения множества математических задач, в том же числе мы поможем найти определенный интеграл онлайн, и чтобы в этом убедиться, просим проверить наше утверждение на конкретных примерах. Введите подынтегральную функцию в соответствующее поле, затем укажите либо бесконечные предельные значения (в это случае будет вычислен и получено решение несобственных интегралов онлайн), либо задайте свои числовые или символьные границы и определенный интеграл онлайн с подробным решением выведется на странице после нажатия на кнопку «Решение». Неправда ли — это очень просто, не требует от вас лишних действий, бесплатно, что самое главное, и в то же время результативно. Вы можете самостоятельно воспользоваться сервисом, чтобы определенный интеграл онлайн калькулятор принес вам максимум пользы, и вы бы получили комфортное состояние, не напрягаясь на сложность всех вычислительных процессов, позвольте нам сделать все за вас и продемонстрировать всю мощь компьютерных технологий современного мира. Если погружаться в дебри сложнейших формул и вычисление несобственных интегралов онлайн изучить самостоятельно, то это похвально, и вы можете претендовать на возможность написания кандидатской работы, однако вернемся к реалиям студенческой жизни. А кто такой студент? В первую очередь — это молодой человек, энергичный и жизнерадостный, желающий успеть отдохнуть и сделать домашку! Поэтому мы позаботились об учениках, которые стараются отыскать на просторах глобальной сети несобственный интеграл онлайн калькулятор, и вот он к вашему вниманию — сайт — самая полезная для молодежи решалка в режиме онлайн. Кстати наш сервис хоть и преподносится как помощник студентам и школьникам, но он в полной мере подойдет любому инженеру, потому что нам под силу любые типы задач и их решение представляется в профессиональном формате. Например, определенный интеграл онлайн с решением в полном виде мы предлагаем по этапам, то есть каждому логическому блоку (подзадачи) отводится отдельная запись со всеми выкладками по ходу процесса общего решения.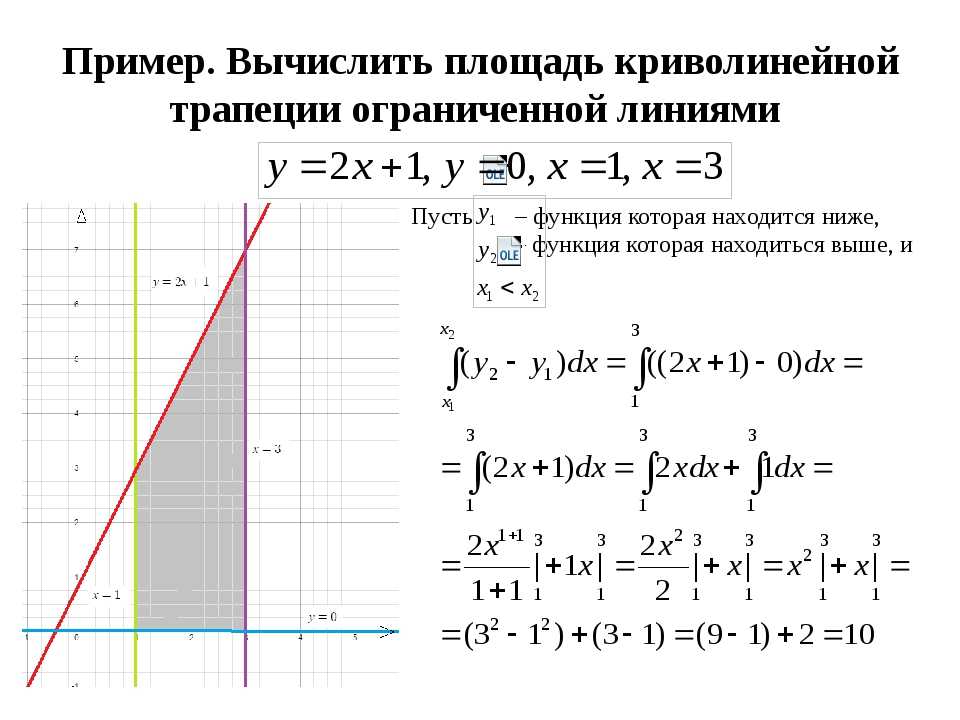 3+1}. \]

Вычисление площадей плоских фигур с помощью определённого интеграла 11 класс онлайн-подготовка на Ростелеком Лицей |

1. Основная формула для вычисления площади плоских фигур с помощью определенного интеграла

Рассмотрим постановку задачи о площади криволинейной трапеции.

Вычислить площадь криволинейной трапеции, ограниченной линиями (рис. 1).

Рис. 1. Площадь криволинейной трапеции

Как мы пытались ее решить:

Первый способ.

Разбили отрезок на одинаковых отрезков, заменили искомую площадь площадью поступенчастой линии, легко ее сосчитали и получили приближенное решение нашей задачи. Далее устремили в пределе и

получили искомую площадь S. Ввели обозначение .

Это определенный интеграл. Вот таким образом мы пытались решить задачу. Мы знаем теперь, как приближенно ее решить, знаем обозначения для точного решения, но точного решения еще не знаем.

Затем мы получили точное решение задачи следующим образом: рис. 2:

Рис. 2. Функция S (x)

Ввели функцию . Каждому площадь под соответствующей частью кривой . Так, введенная функция удовлетворяет единственному закону, а именно:

Каждому соответствует единственное значение .

Мы доказали, что производная этой же функции и доказали, что точная площадь вычисляется следующим образом. Надо найти любую первообразную от функциии взять приращение этих первообразных. То есть взять первообразную в точке и отнять первообразную в точке И в результате мы получили формулу, которой мы будем пользоваться для вычисления площадей.

2. Методика нахождения площади на примере

Методику нахождения площади рассмотрим сначала на относительно простом примере.

Пример 1.

Найти площадь фигуры, ограниченной линиями

Решение.

Вот искомая площадь:

Рис. 3. Площадь

Вот формула:

Это общая формула. Конкретно к нашему случаю она применима так:

Пределы интегрирования .

Вычислили площадь криволинейной фигуры.

Ответ:

В следующей задаче площадь искомой фигуры образовывается с помощью А именно:

3. Пример 2

Найти площадь фигуры, ограниченной линиями

Решение.

Посмотрим, как выглядит фигура (рис. 4).

Рис. 4. Фигура, ограниченная линиями

Формула та же самая:

В нашем случае . Итак, надо найти определенный интеграл

=-(-1)+1=1+1=2.

Искомая площадь найдена, и ответ получен.

Ответ: 2

4. Пример 3

Найти площадь фигуры, ограниченной линиями

Решение.

Рис. 5. Площадь фигуры, ограниченной линиями

Формула для площади та же самая:

В нашем случае .

Ответ:

В следующем примере ищется площадь под параболой.

5. Пример 4

Найти площадь фигуры, ограниченной линиями

Решение.

Схематически изобразим параболу Корни

Рис. 6. Парабола

Применим известную формулу

И применим ее для данной функции и пределов интегрирования

Искомая площадь найдена.

Ответ:

В предыдущих задачах площадь образовывалась с помощью разных кривых, но эта площадь находилась над осью . В следующей задаче наоборот.

6. Пример 5. Случай, если фигура находится под осью

Найти площадь фигуры, ограниченной линиями.

Решение.

Посмотрим, что это за фигура. График в пределах от Π до 2Π расположен под осью Ox (рис. 7).

Рис. 7. График в пределах от Π до 2Π

Ясно, что если возьмем определенный интеграл, то мы получим отрицательное число.

Вычисляем.

1. Сначала вычисляем определенный интеграл от π до 2π от подынтегральной функции

Надо найти первообразную.

По таблице первообразных: .

=-1-1=-2.

2. Для того чтобы найти площадь, надо взять модуль =2.

Ответ: 2.

7. Пример. Общий случай для нахождения площади плоской фигуры, ограниченной двумя кривыми. Выводы

Следующее усложнение – искомая площадь расположена между двумя кривыми.

А именно:

Найти площадь фигуры, ограниченной линиями (рис. 8)

Рис. 8. Площадь фигуры, ограниченной линиями

Решение.

Итак, площадь образуют 2 кривые, одна из них может находиться под осью .

Каким образом мы будем решать эту задачу?

Во-первых, мы можем сдвинуть фигуру на такое положительное , что площадь находится над осью . Рис. 9.

Рис. 9. Сдвиг фигуры

Затем мы возьмем соответствующий определенный интеграл и найдем площадь. Искомая площадь равна разности двух площадей.

Площадь под верхней кривой минус площадь под нижней кривой .

Каждую из площадей мы умеем находить.

Таким образом, в общем виде была поставлена задача, в общем виде получен ответ.

Ответ:

Обсудим и постановку задачи, и полученный важный результат.

Нам надо было найти площадь фигуры, ограниченной линиями

Мы использовали известный прием: эту площадь подняли на некоторое , и это Так вот, эту площадь теперь можно считать без введения . Правило следующее:

Площадь фигуры, ограниченной прямыми линиями непрерывных на отрезке и таких, что для всех из отрезка вычисляется по формуле, которую мы вывели:

Рассмотрим первый конкретный пример на нахождение площади между двумя линиями.

8. Пример 6

Найти площадь фигуры, ограниченную линиями

Решение. Для начала построим графики этих линий и поймем, где та площадь, которую нам надо искать.

График квадратичной функции – парабола. Корни – 0, 4, ветви вниз. График

– биссектриса первого координатного угла. Вот площадь, которую надо найти:

Рис. 10. Искомая площадь

Но для этого сначала надо найти точки пересечения и решить стандартную задачу.

1. Находим точки пересечения. Для этого решаем систему: .

Отсюда получаем квадратное уравнение относительно :

Мы нашли , то есть, пределы интегрирования. Это первое важное действие.

Теперь стандартное действие:

2. = =()

Искомая площадь равна 4,5

Ответ: 4,5

9. Пример 7. Случай, когда часть площади плоской фигуры лежит под осью

Во втором примере часть площади находится под осью , но на методику это не влияет.

Пример 6.

Итак, требуется найти площадь фигуры, ограниченной линиями

Решение.

Сначала построим графики, посмотрим, какую площадь нам нужно найти. Рис. 11.

Первая функция – парабола, ветви вниз. График второй функции – прямая линия.

Есть две точки пересечения, их придется найти, а именно взять пределы интегрирования, и тогда будем решать задачу по знакомому нам плану.

Рис. 11. Площадь фигуры, ограниченной линиями

Первое действие – найти пределы интегрирования и второе – найти площадь.

Пределы интегрирования найдем из системы.

То есть, пределы интегрирования найдены.

= ()

Ответ:

Итак, мы показали, каким образом можно вычислять площади плоских фигур с помощью определенного интеграла.

Список литературы

Мордкович А.Г. Алгебра и начала математического анализа. – М.: Мнемозина.
Муравин Г.К., Муравина О.В. Алгебра и начала математического анализа. – М.: Дрофа.
Колмогоров А.Н., Абрамов А.М., Дудницын Ю.П. и др. Алгебра и начала математического анализа. – М.: Просвещение.

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

Ru.scribd.com (Источник).
Math5you.ru (Источник).
Dok.opredelim.com (Источник).

Домашнее задание

Найти площадь фигуры, ограниченной линиями , , ,
Найти площадь фигуры, ограниченной линиями
Алгебра и начала анализа, Мордкович А. Г.: № 1030, 1033, 1037, 1038.

Решение высшей математики онлайн

‹— Назад

Рассмотрим функцию , заданную на отрезке , и предположим, что она интегрируема на отрезке . Тогда при любом эта функция будет интегрируема на отрезке и, следовательно, функция

определена при всех . При мы по определению положим её равной 0, то есть будем считать, что для любой функции и точки из её области определения. Итак, функция равняется значению определённого интеграла с переменным верхним пределом, вычисленного от интегрируемой функции , не обязательно непрерывной.

Теорема 3.11 Функция , определённая выше, непрерывна при всех для любой интегрируемой функции .

Доказательство. Заметим, что если функция положительна, то значение интерпретируется как площадь под графиком , лежащая над отрезком . Если дать приращение , то площадь получит приращение в виде площади полоски, лежащей над отрезком (см. рис.).

Рис.3.4.

Эта площадь, вследствие ограниченности интегрируемой функции, мала, если приращение мало; это и означает непрерывность функции в точке .

Проведём теперь более аккуратные рассуждения, не предполагая, что функция принимает положительные значения.

Пусть фиксирована точка и взято такое приращение , что . Пользуясь аддитивностью интеграла, получаем, что

Согласно неравенству (3.5),

Но по теореме 3.5 функция ограничена, поэтому существует такая постоянная , что при всех и, в том числе, при . Воспользовавшись теоремой об интегрировании неравенства, получаем, что

откуда

При получаем по теореме «о двух милиционерах», что и , что означает, что функция непрерывна справа в любой точке .

Рассматривая аналогично отрезок при и , получаем, что

при , что означает непрерывность функции слева в любой точке .

Тем самым функция непрерывна справа в точке , непрерывна слева в точке и непрерывна (с обеих сторон) в любой точке , что и требовалось доказать.

Теорема 3.12 Пусть функция непрерывна на отрезке и функция определена всё той же формулой. Тогда имеет производную в любой точке интервала , производную справа в точке и производную слева в точке , причём эти производные совпадают со значением функции в соответствующей точке:

при и

Доказательство. Снова рассмотрим приращение при , , . Поскольку функция непрерывна, мы можем применить теорему о среднем к интегралу по отрезку :

где — некоторая точка отрезка . Получаем, деля на :

откуда при из непрерывности следует, что

поскольку при . Получили, что правая производная совпадает с во всех точках .

Аналогично доказывается, что левая производная совпадает с во всех точках Во внутренних точках совпадение производных слева и справа со значением означает, что функция имеет производную , равную .

Точно так же доказывается, что производная интеграла

от непрерывной функции по переменному нижнему пределу равняется :

Равенство означает, что функция является первообразной для на интервале . Другая первообразная — это, очевидно, функция .

Итак, мы получили важный результат о наличии первообразной у любой непрерывной функции:

Теорема 3.13 Пусть — непрерывная на интервале функция. Тогда на интервале функция имеет некоторую первообразную , то есть при всех .

Доказательство. Для доказательства достаточно фиксировать произвольную точку и положить

При эти определения не противоречат друг другу, поскольку и та, и другая формулы дают .

Нетрудно видеть, что при получается , при получаем . При производная слева даёт значение , а производная справа — значение , так что производные слева и справа совпадают и , что и завершает доказательство.

Пусть теперь — произвольная первообразная для непрерывной функции , заданной на некотором интервале , содержащем отрезок . Мы уже проверили, что функция , такая что при служит тогда первообразной для , а поскольку любые первообразные для одной и той же функции на заданном интервале могут отличаться лишь постоянным слагаемым, получаем, что

где , при всех , в том числе и при и . Получаем и , откуда

поскольку Итак, меняя обозначение переменной интегрирования на , получаем в итоге формулу

(3.6)

где — произвольная первообразная для функции . Эта формула называется формулой Ньютона — Лейбница. Она играет ключевую роль в интегральном исчислении и во всём математическом анализе.

Напомним, что мы получили её в предположении, что функция непрерывна. Если функция имеет разрыв на отрезке , то разность значений первообразной может не иметь никакого отношения к величине определённого интеграла. Поэтому при применении формулы Ньютона — Лейбница нужно строго следить за законностью этого действия.

Смысл формулы Ньютона — Лейбница (3.6) состоит в том, что для нахождения определённого интеграла нам достаточно теперь найти произвольную первообразную для функции (напомним, что для этого надо найти неопределённый интеграл) и взять разность значений этой первообразной в концах отрезка, .

Итак, формула Ньютона — Лейбница устанавливает связь между определённым интегралом от данной функции и первообразной для этой функции, то есть между определённым и неопределённым интегралами. Заметим, что смысл этих двух понятий первоначально совершенно различен: неопределённый интеграл — это набор функций (первообразных), а определённый интеграл — это число (равное пределу интегральных сумм).

При вычислениях разность часто называют подстановкой в функцию пределов и и обозначают . Таким образом, по определению,

а формулу Ньютона — Лейбница можно записать в виде

Пример 3.1 Для нахождения значения определённого интеграла

найдём первообразную для подынтегральной функции , вычислив неопределённый интеграл:

Поскольку нас интересует любая первообразная, то мы можем взять (с тем же успехом могли взять и , и , и т. п., но вид первообразной при проще, а постоянные сласаемые всё равно взаимно уничтожатся при вычислении подстановки). Итак, берём и вычисляем подстановку, беря в ней пределы равными пределам интегрирования:

Получаем, что

Пример 3.2 Найдём определённый интеграл

Поскольку

в качестве первообразной можно взять (положив ). Поэтому

Математика, вышка, высшая математика, математика онлайн, вышка онлайн, онлайн математика, онлайн решение математики, ход решения, процес решения, решение, задачи, задачи по математике, математические задачи, решение математики онлайн, решение математики online, online решение математики, решение высшей математики, решение высшей математики онлайн, матрицы, решение матриц онлайн, векторная алгебра онлайн, решение векторов онлайн, система линейных уравнений, метод Крамера, метод Гаусса, метод обратной матрицы, уравнения, системы уравнений, производные, пределы, интегралы, функция, неопределенный интеграл, определенный интеграл, решение интегралов, вычисление интегралов, решение производных, интегралы онлайн, производные онлайн, пределы онлайн, предел функции, предел последовательности, высшие производные, производная неявной функции

Вычислить несобственный интеграл или доказать его сходимость.

Определенный интеграл онлайн

Тема НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ

В теме «Определенный интеграл» было рассмотрено понятие определенного интеграла для случая конечного промежутка
и ограниченной функции
(см. теорему 1 из §3). Теперь займемся обобщением этого понятия для случаев бесконечного промежутка и неограниченной функции. Необходимость такого обобщения показывают, например, такие ситуации.

1. Если, используя формулу для длины дуги, попытаться вычислить длину четверти окружности
,
, то придем к интегралу от неограниченной функции:

, где
.

2. Пусть тело массой
движется по инерции в среде с силой сопротивления
, где
— скорость тела. Используя второй закон Ньютона (
, где
ускорение), получим уравнение:
, где
. Нетрудно показать, что решением этого (дифференциального!) уравнения является функция
Если нам потребуется вычислить путь, пройденный телом до полной остановки, т.е. до момента, когда
, то придем к интегралу по бесконечному промежутку:

I Определение

Пусть функция
определена и непрерывна на промежутке
. Тогда для любого
она интегрируема на промежутке
, то есть существует интеграл
.

Определение 1 . Конечный или бесконечный предел этого интеграла при
называют несобственным интегралом 1-го рода от функции
по промежутку
и обозначают символом
. При этом, если указанный предел конечен, то несобственный интеграл называют сходящимся, в противном случае (
или не существует) – расходящимся.

Итак, по определению

Примеры

2.
.

3.
– не существует.

Несобственный интеграл из примера 1 сходится, в примерах 2 и 3 интегралы расходятся.

II Формула Ньютона – Лейбница для несобственного интеграла первого рода

Пусть
— некоторая первообразная для функции
(сущест-вует на
, т.к.
— непрерывна). Тогда

Отсюда ясно, что сходимость несобственного интеграла (1) равносильна существованию конечного предела
. Если этот предел обозначить
, то можно написать для интеграла (1) формулу Ньютона-Лейбница:

, где
.

Примеры .

5.
.

6. Более сложный пример:
. Сначала найдем первообразную:

Теперь можем найти интеграл , учитывая, что

:

III Свойства

Приведем ряд свойств несобственного интеграла (1), которые вытекают из общих свойств пределов и определенного интеграла:

IV Другие определения

Определение 2 . Если
непрерывна на
, то

Определение 3 . Если
непрерывна на
, то принимают по определению

(– произвольное),

причем несобственный интеграл в левой части сходится, если только оба ин-теграла в правой части сходятся.

Для этих интегралов, как и для интеграла (1) можно написать соответствующие формулы Ньютона – Лейбница.

Пример 7 .

§2. Признаки сходимости несобственного интеграла 1-го рода

Чаще всего несобственный интеграл вычислить по определению не-возможно, поэтому используют приближенное равенство

(для больших ).

Однако, это соотношение имеет смысл лишь для сходящихся интегралов. Необходимо иметь методы выяснения поведения интеграла минуя определение.

I Интегралы от положительных функций

Пусть
на
. Тогда определенный интеграл
как функция верхнего предела есть функция возрастаю-щая (это следует из общих свойств определенного интеграла).

Теорема 1 . Несобственный интеграл 1 го рода от неотрицательной функ-ции сходится тогда и только тогда, когда функция
остается ограниченной при увеличении.

Эта теорема – следствие общих свойств монотонных функций. Практического смысла теорема почти не имеет, но позволяет получить т.н. признаки сходимости.

Теорема 2 (1-й признак сравнения). Пусть функции
и
непре-рывны на
и удовлетворяют неравенству
. Тогда:

1) если интеграл
сходится, то и
сходится;

2) если интеграл
расходится, то и
расходится.

Доказательство . Обозначим:
и
. Так как
, то

. Пусть интеграл
сходится, тогда (в силу теоремы 1) функция
‒ ограничена. Но тогда и
ограничена, а значит, интеграл
тоже сходится. Аналогично доказывается и вторая часть теоремы.

Этот признак не применим в случае расходимости интеграла от
или сходимости интеграла от
. Этот недостаток отсутствует у 2-го признака сравнения.

Теорема 3 (2-й признак сравнения). Пусть функции
и
непрерывны и неотрицательны на
. Тогда, если
при
, то несобственные интегралы
и
сходятся или расходятся одновременно.

Доказательство . Из условия теоремы получим такую цепочку равно-сильных утверждений:

, ,

Пусть, например,
. Тогда:

Применим теорему 2 и свойство 1) из §1 и получим утверждение теоремы 3.

В качестве эталонной функции, с которой сравнивают данную, высту-пает степенная функция
,
. Предлагаем студентам самим доказать, что интеграл

сходится при
и расходится при
.

Примеры . 1.
.

Рассмотрим подынтегральную функцию на промежутке
:

,
.

Интеграл
сходится, ибо
. По 2-му признаку сравнения сходится и интеграл
, а в силу свойства 2) из §1 сходится и исход-ный интеграл.

2.
.

Так как
, тоcуществует
такое, что при

. Для таких значений переменной:

Известно, что логарифмическая функция растет медленнее степенной, т.е.

а значит, начиная с некоторого значения переменной, эта дробь меньше 1. Поэтому

Интеграл сходится как эталонный. В силу 1-го признака сравнения сходится и
. Применяя 2-й признак, получим, что и интеграл
сходится. И снова свойство 2) из §1 доказывает сходимость исходного интеграла.

Определенный интеграл как предел интегральной суммы

может существовать (т.е. иметь определенное конечное значение) лишь при выполнении условий

Если хотя бы одно из этих условий нарушено, то определение теряет смысл. Действительно, в случае бесконечного отрезка, например [a ; ) его нельзя разбить на п частей конечной длины
, которая к тому же с увеличением количества отрезков стремилась бы к нулю. В случае же неограниченной в некоторой точкес [a ; b ] нарушается требование произвольного выбора точки на частичных отрезках – нельзя выбрать=с , поскольку значение функции в этой точке не определено. Однако и для этих случаев можно обобщить понятие определенного интеграла, введя еще один предельный переход. Интегралы по бесконечным промежуткам и от разрывных (неограниченных) функций называют несобственными .

Определение.

Пусть функция
определена на промежутке [a ; ) и интегрируема на любом конечном отрезке [a ; b ], т.е. существует
для любого b > a . Предел вида
называютнесобственным интегралом первого рода (или несобственным интегралом по бесконечному промежутку) и обозначают
.

Таким образом, по определению,
=
.

Если предел справа существует и конечен, то несобственный интеграл
называютсходящимся . Если этот предел бесконечен, или не существует вообще, то говорят, что несобственный интеграл расходится .

Аналогично можно ввести понятие несобственного интеграла от функции
по промежутку (–; b ]:

=
.

А несобственный интеграл от функции
по промежутку (–; +) определяется как сумма введенных выше интегралов:

=
+
,

где а – произвольная точка. Этот интеграл сходится, если сходятся оба слагаемых, и расходится, если расходится хотя бы одно из слагаемых.

С геометрической точки зрения, интеграл
,
, определяет численное значение площади бесконечной криволинейной трапеции, ограниченной сверху графиком функции
, слева – прямой
, снизу – осью ОХ. Сходимость интеграла означает существование конечной площади такой трапеции и равенство ее пределу площади криволинейной трапеции с подвижной правой стенкой
.

На случай интеграла с бесконечным пределом можно обобщить и формулу Ньютона-Лейбница :

=
=F(+ ) – F(a ),

где F(+ ) =
. Если этот предел существует, то интеграл сходится, в противном случае – расходится.

Мы рассмотрели обобщение понятия определенного интеграла на случай бесконечного промежутка.

Рассмотрим теперь обобщение для случая неограниченной функции.

Определение

Пусть функция
определена на промежутке [a ; b ), неограниченна в некоторой окрестности точки b , и непрерывна на любом отрезке
, где>0 (и, следовательно, интегрируема на этом отрезке, т.е.
существует). Предел вида
называетсянесобственным интегралом второго рода (или несобственным интегралом от неограниченной функции) и обозначается
.

Таким образом, несобственный интеграл от неограниченной в точке b функции есть по определению

=
.

Если предел справа существует и конечен, то интеграл называется сходящимся . Если конечного предела не существует, то несобственный интеграл называется расходящимся.

Аналогично можно определить несобственный интеграл от функции
имеющей бесконечный разрыв в точкеа :

=
.

Если функция
имеет бесконечный разрыв во внутренней точкес 
, то несобственный интеграл определяется следующим образом

=
+
=
+
.

Этот интеграл сходится, если сходятся оба слагаемых, и расходится, если расходится хотя бы одно слагаемое.

С геометрической точки зрения, несобственный интеграл от неограниченной функции также характеризует площадь неограниченной криволинейной трапеции:

Поскольку несобственный интеграл выводится путем предельного перехода из определенного интеграла, то все свойства определенного интеграла могут быть перенесены (с соответствующими уточнениями) на несобственные интеграла первого и второго рода.

Во многих задачах, приводящих к несобственным интегралам, не обязательно знать, чему равен этот интеграл, достаточно лишь убедиться в его сходимости или расходимости. Для этого используют признаки сходимости . Признаки сходимости несобственных интегралов:

1) Признак сравнения .

Пусть для всех х 

. Тогда, если
сходится, то сходится и
, причем

. Если
расходится, то расходится и
.

2) Если сходится
, то сходится и
(последний интеграл в этом случае называетсяабсолютно сходящимся ).

Признаки сходимости и расходимости несобственных интегралов от неограниченных функций аналогичны сформулированным выше.

Примеры решения задач.

Пример 1.

а)
; б)
; в)

г)
; д)
.

Решение.

а) По определению имеем:

б) Аналогично

Следовательно, данный интеграл сходится и равен .

в) По определению
=
+
, причем,а – произвольное число. Положим в нашем случае
, тогда получим:

Данный интеграл сходится.

Значит, данный интеграл расходится.

д) Рассмотрим
. Чтобы найти первообразную подынтегральной функции, необходимо применить метод интегрирования по частям. Тогда получим:

Поскольку ни
, ни
не существуют, то не существует и

Следовательно, данный интеграл расходится.

Пример 2.

Исследовать сходимость интеграла в зависимости от п .

Решение.

При
имеем:

Если
, то
и. Следовательно, интеграл расходится.

Если
, то
, а
, тогда

Следовательно, интеграл сходится.

Если
, то

следовательно, интеграл расходится.

Таким образом,

Пример 3.

Вычислить несобственный интеграл или установить его расходимость:

а)
; б)
; в)
.

Решение.

а) Интеграл
является несобственным интегралом второго рода, поскольку подынтегральная функция
не ограничена в точке

. Тогда, по определению,

Интеграл сходится и равен .

б) Рассмотрим
. Здесь также подынтегральная функция не ограничена в точке
. Поэтому, данный интеграл – несобственный второго рода и по определению,

Следовательно, интеграл расходится. 3+1}. \]

Несобственный интеграл с бесконечным пределом интегрирования

Иногда такой несобственный интеграл еще называют несобственным интегралом первого рода..gif»>.

Реже встречаются интегралы с бесконечным нижним пределом или с двумя бесконечными пределами: .

Мы рассмотрим самый популярный случай https://pandia.ru/text/80/057/images/image005_1.gif»>? Нет, не всегда. Подынтегральная функция https://pandia.ru/text/80/057/images/image007_0.gif»>

Изобразим на чертеже график подынтегральной функции . Типовой график и криволинейная трапеция для данного случая выглядит так:

Несобственный интеграл https://pandia.ru/text/80/057/images/image009_0.gif»>», иными словами, площадь тоже бесконечна. Так быть может. В этом случае говорят, что, что несобственный интеграл расходится .

2) Но . Как это ни парадоксально прозвучит, площадь бесконечной фигуры может равняться… конечному числу! Например: . . Во втором случае несобственный интеграл сходится .

А что будет, если бесконечная криволинейная трапеция расположена ниже оси?.gif»>.

: .

Пример 1

Подынтегральная функция https://pandia.ru/text/80/057/images/image017_0.gif»>, значит, всё нормально и несобственный интеграл можно вычислить «штатным» методом.

Применение нашей формулы https://pandia.ru/text/80/057/images/image018_0.gif»>

При решении несобственных интегралов очень важно знать, как выглядят графики основных элементарных функций!

Пример 2

Вычислить несобственный интеграл или установить его расходимость.

Выполним чертеж:

Во-первых, замечаем следующее: подынтегральная функция непрерывна на полуинтервале . Гуд..gif»>

(2) Подставляем верхний и нижний пределы по формуле Ньютона-Лейбница.

(3) Указываем, что https://pandia.ru/text/80/057/images/image024.gif»> (Господа, это уже давно нужно понимать) и упрощаем ответ.

Вот здесь площадь бесконечной криволинейной трапеции равна конечному числу! Невероятно, но факт.

Пример 3

Вычислить несобственный интеграл или установить его расходимость.

Подынтегральная функция непрерывна на .

Сначала попытаемся найти первообразную функцию (неопределенный интеграл).

Проведем замену:

Всегда полезно выполнить проверку, то есть продифференцировать полученный результат:

Теперь находим несобственный интеграл:

(2) Подставляем верхний и нижний пределы в соответствии с формулой Ньютона-Лейбница..gif»>? Смотрите график арктангенса в уже неоднократно рекомендованной статье.

(3) Получаем окончательный ответ. Тот факт, что полезно знать наизусть.

“

Подынтегральная функция непрерывна на https://pandia.ru/text/80/057/images/image041.gif»>
“

Пример 4

Вычислить несобственный интеграл или установить его расходимость.

! Это типовой пример, и похожие интегралы встречаются очень часто. Хорошо его проработайте! Первообразная функция здесь находится методом выделения полного квадрата.

Пример 5

Вычислить несобственный интеграл или установить его расходимость.

Несобственные интегралы от неограниченных функций

Иногда такие несобственные интегралы называют несобственными интегралами второго рода. Несобственные интегралы второго рода коварно «шифруются» под обычный определенный интеграл и выглядят точно так же: ..gif»>, 2) или в точке , 3) или в обеих точках сразу, 4) или даже на отрезке интегрирования. Мы рассмотрим первые два случая, для случаев 3-4 в конце статьи есть ссылка на дополнительный урок.

Сразу пример, чтобы было понятно: https://pandia.ru/text/80/057/images/image048.gif»>, то знаменатель у нас обращается в ноль, то есть подынтегральной функции просто не существует в этой точке!

Вообще при анализе несобственного интеграла всегда нужно подставлять в подынтегральную функцию оба предела интегрирования . .jpg» alt=»Несобственный интеграл, точка разрыва в нижнем пределе интегрирования»>

Здесь почти всё так же, как в интеграле первого рода.
Наш интеграл численно равен площади заштрихованной криволинейной трапеции, которая не ограничена сверху. При этом могут быть два варианта: несобственный интеграл расходится (площадь бесконечна) либо несобственный интеграл равен конечному числу (то есть, площадь бесконечной фигуры – конечна!).

Осталось только модифицировать формулу Ньютона-Лейбница. Она тоже модифицируется с помощью предела, но предел стремится уже не к бесконечности, а к значению https://pandia.ru/text/80/057/images/image052.gif»> справа .

Пример 6

Вычислить несобственный интеграл или установить его расходимость.

Сначала вычислим неопределенный интеграл:

Замена:

Вычислим несобственный интеграл:

(1) Что здесь нового? По технике решения практически ничего. Единственное, что поменялось, это запись под значком предела: . Добавка обозначает, что мы стремимся к значению справа (что логично – см. график). Такой предел в теории пределов называют односторонним пределом. В данном случае у нас правосторонний предел.

(2) Подставляем верхний и нижний предел по формуле Ньютона Лейбница.

(3) Разбираемся с https://pandia.ru/text/80/057/images/image058.gif»>. Как определить, куда стремиться выражение? Грубо говоря, в него нужно просто подставить значение , подставляем три четверти и указываем, что . Причесываем ответ.

В данном случае несобственный интеграл равен отрицательному числу.

Пример 7

Вычислить несобственный интеграл или установить его расходимость.

Пример 8

Вычислить несобственный интеграл или установить его расходимость.

Если подынтегральной функции не существует в точке

Бесконечная криволинейная трапеция для такого несобственного интеграла принципиально выглядит следующим образом:

Здесь всё абсолютно так же, за исключением того, что предел у нас стремится к значению https://pandia. ru/text/80/057/images/image052.gif»> мы должны бесконечно близко приблизиться к точке разрыва слева .

Вычислить несобственные интегралы или установить их расходимость. Определенный интеграл онлайн

Что значит вычислить несобственный интеграл?

Несобственные интегралы бывают двух видов.

Несобственный интеграл с бесконечным пределом (ами) интегрирования

3) О третьем варианте чуть позже.

Таким образом, несобственный интеграл может быть отрицательным .

Рассмотрим два классических примера:

Пример 1

Применение нашей формулы и решение задачи выглядит так:

При решении несобственных интегралов очень важно знать, как выглядят графики основных элементарных функций!

Чистовое оформление задания должно выглядеть примерно так:

“

Пример 2

Вычислить несобственный интеграл или установить его расходимость.

Выполним чертеж:

(2) Подставляем верхний и нижний пределы по формуле Ньютона-Лейбница.

(3) Указываем, что при (Господа, это уже давно нужно понимать) и упрощаем ответ.

Вот здесь площадь бесконечной криволинейной трапеции равна конечному числу! Невероятно, но факт.

Чистовое оформление примера должно выглядеть примерно так:

“

Подынтегральная функция непрерывна на

“

Пример 3

Вычислить несобственный интеграл или установить его расходимость.

Проведем замену:

Неопределенный интеграл найден, константу в данном случае добавлять не имеет смысла.

На черновике всегда полезно выполнить проверку, то есть продифференцировать полученный результат:

Получена исходная подынтегральная функция, значит, неопределенный интеграл найден правильно.

Теперь находим несобственный интеграл:

(3) Получаем окончательный ответ. Тот факт, что полезно знать наизусть.

“

Подынтегральная функция непрерывна на .

“

Пример 4

Вычислить несобственный интеграл или установить его расходимость.

Пример 5

Вычислить несобственный интеграл или установить его расходимость.

Полные решения и ответы в конце урока.

Несобственные интегралы от неограниченных функций

Здесь почти всё так же, как в интеграле первого рода.

* по умолчанию привычно полагаем, что несобственный интеграл существует

Посмотрим, как это реализуется на практике.

Пример 6

Вычислить несобственный интеграл или установить его расходимость.

Сначала вычислим неопределенный интеграл:

Замена:

У кого возникли трудности с заменой, обратитесь к уроку Метод замены в неопределенном интеграле .

Вычислим несобственный интеграл:

(2) Подставляем верхний и нижний предел по формуле Ньютона Лейбница.

А сейчас два примера для самостоятельного решения.

Пример 7

Вычислить несобственный интеграл или установить его расходимость.

Пример 8

Вычислить несобственный интеграл или установить его расходимость.

Если подынтегральной функции не существует в точке

Определенный интеграл как предел интегральной суммы

может существовать (т.е. иметь определенное конечное значение) лишь при выполнении условий

Определение.

Таким образом, по определению,
=
.

Аналогично можно ввести понятие несобственного интеграла от функции
по промежутку (–; b ]:

=
.

=
+
,

На случай интеграла с бесконечным пределом можно обобщить и формулу Ньютона-Лейбница :

=
=F(+ ) – F(a ),

где F(+ ) =
. Если этот предел существует, то интеграл сходится, в противном случае – расходится.

Мы рассмотрели обобщение понятия определенного интеграла на случай бесконечного промежутка.

Рассмотрим теперь обобщение для случая неограниченной функции.

Определение

Таким образом, несобственный интеграл от неограниченной в точке b функции есть по определению

=
.

Аналогично можно определить несобственный интеграл от функции
имеющей бесконечный разрыв в точкеа :

=
.

=
+
=
+
.

Этот интеграл сходится, если сходятся оба слагаемых, и расходится, если расходится хотя бы одно слагаемое.

1) Признак сравнения .

Пусть для всех х 

. Тогда, если
сходится, то сходится и
, причем

. Если
расходится, то расходится и
.

2) Если сходится
, то сходится и
(последний интеграл в этом случае называетсяабсолютно сходящимся ).

Примеры решения задач.

Пример 1.

а)
; б)
; в)

г)
; д)
.

Решение.

а) По определению имеем:

б) Аналогично

Следовательно, данный интеграл сходится и равен .

в) По определению
=
+
, причем,а – произвольное число. Положим в нашем случае
, тогда получим:

Данный интеграл сходится.

Значит, данный интеграл расходится.

Поскольку ни
, ни
не существуют, то не существует и

Следовательно, данный интеграл расходится.

Пример 2.

Исследовать сходимость интеграла в зависимости от п .

Решение.

При
имеем:

Если
, то
и. Следовательно, интеграл расходится.

Если
, то
, а
, тогда

Следовательно, интеграл сходится.

Если
, то

следовательно, интеграл расходится.

Таким образом,

Пример 3.

Вычислить несобственный интеграл или установить его расходимость:

а)
; б)
; в)
.

Решение.

Интеграл сходится и равен .

Следовательно, интеграл расходится.

в) Рассмотрим
. Подынтегральная функция
терпит бесконечный разрыв в двух точках:
и
, первая из которых принадлежит промежутку интегрирования
. Следовательно, данный интеграл – несобственный второго рода. Тогда, по определению

=

=

Следовательно, интеграл сходится и равен
.

Несобственный интеграл с бесконечным пределом интегрирования

Иногда такой несобственный интеграл еще называют несобственным интегралом первого рода..gif»>.

Реже встречаются интегралы с бесконечным нижним пределом или с двумя бесконечными пределами: .

2) Но . Как это ни парадоксально прозвучит, площадь бесконечной фигуры может равняться… конечному числу! Например: .. Во втором случае несобственный интеграл сходится .

А что будет, если бесконечная криволинейная трапеция расположена ниже оси?.gif»>.

: .

Пример 1

Применение нашей формулы https://pandia.ru/text/80/057/images/image018_0.gif»>

При решении несобственных интегралов очень важно знать, как выглядят графики основных элементарных функций!

Пример 2

Вычислить несобственный интеграл или установить его расходимость.

Выполним чертеж:

Во-первых, замечаем следующее: подынтегральная функция непрерывна на полуинтервале . Гуд..gif»>

(2) Подставляем верхний и нижний пределы по формуле Ньютона-Лейбница.

(3) Указываем, что https://pandia.ru/text/80/057/images/image024.gif»> (Господа, это уже давно нужно понимать) и упрощаем ответ.

Вот здесь площадь бесконечной криволинейной трапеции равна конечному числу! Невероятно, но факт.

Пример 3

Вычислить несобственный интеграл или установить его расходимость.

Подынтегральная функция непрерывна на .

Сначала попытаемся найти первообразную функцию (неопределенный интеграл).

Проведем замену:

Всегда полезно выполнить проверку, то есть продифференцировать полученный результат:

Теперь находим несобственный интеграл:

(3) Получаем окончательный ответ. Тот факт, что полезно знать наизусть.

“

Подынтегральная функция непрерывна на https://pandia.ru/text/80/057/images/image041.gif»>
“

Пример 4

Вычислить несобственный интеграл или установить его расходимость.

Пример 5

Вычислить несобственный интеграл или установить его расходимость.

Несобственные интегралы от неограниченных функций

Пример 6

Вычислить несобственный интеграл или установить его расходимость.

Сначала вычислим неопределенный интеграл:

Замена:

Вычислим несобственный интеграл:

(1) Что здесь нового? По технике решения практически ничего. Единственное, что поменялось, это запись под значком предела: . Добавка обозначает, что мы стремимся к значению справа (что логично – см. график). Такой предел в теории пределов называют односторонним пределом. В данном случае у нас правосторонний предел.

(2) Подставляем верхний и нижний предел по формуле Ньютона Лейбница.

В данном случае несобственный интеграл равен отрицательному числу.

Пример 7

Вычислить несобственный интеграл или установить его расходимость.

Пример 8

Вычислить несобственный интеграл или установить его расходимость.

Если подынтегральной функции не существует в точке

Здесь всё абсолютно так же, за исключением того, что предел у нас стремится к значению https://pandia. 3+1}. \]

Онлайн-калькулятор определенных интегралов с шагами • Оценка интегрального расчета

Истинное значение калькулятора определенных интегралов

Боль от калькулятора определенных интегралов

Интеграция, вместе с дифференцированием двух основных операций, в исчислении. Казалось бы, практически нет знаний, которые мы могли бы с уверенностью рационально обосновать. Таблицы будут увеличиваться непропорционально, и производительность будет иметь тенденцию к снижению.

Аналогичный метод используется для нахождения интеграла в кубе секущей. Основы интересны, когда вы видите причину, по которой они существуют. Многие используют технику u-подстановки.

Опровержение истории калькулятора определенных интегралов

Проверьте, имеете ли вы идеальное графическое представление или нет, а затем запросите обозначенную функцию, которую вы хотите. Результат отображения известен как результат. Вполне вероятно, что вы могли бы разработать контроллер, который по-прежнему отвечает требованиям и не имеет точных значений, как показано выше.

Калькулятор определенных интегралов — живой или мертвый?

Если поначалу это может показаться немного скучным, мы, скорее всего, придадим ему определенный смысл. Возможно, вам будут представлены два основных типа проблем. Возможно, вам нужен быстрый ответ только на работе, и вы не хотите решать проблему вручную.

Поэтому, если вы не обожаете вмешательство одного калькулятора. Так, например, функция, имеющая определенное значение для целочисленных значений и другое значение для нецелочисленных значений, не принимается. Затем вы можете выбрать другой интегральный калькулятор.

Получение наилучшего калькулятора определенных интегралов

Этот калькулятор вычисляет объемы для нескольких наиболее распространенных основных форм. В конечном счете, элемент объема предоставляется здесь. Мы не будем выводить этот результат. Итак, это формула, используемая для площади поверхности общей функциональной формы.

Имейте в виду, что автоочистку можно отключить для определенных таблиц. Попробуйте поставить 2 дроби в правильную сторону, и вы получите исходную функцию. Введите Q в пик вашей дроби.

Дебаты по поводу калькулятора определенных интегралов

Площадь — это только интерпретация. Регистрация необходима, чтобы иметь возможность получать экстренные оповещения. Калькулятор текущей стоимости немедленно рассчитает текущую стоимость любой предстоящей единовременной суммы, если вы введете предстоящую цену, процентную ставку за период (также известную как ставка дисконтирования) и диапазон периодов.

Честно говоря, чего ожидать и что мы оцениваем, можно свести к минимуму тревогу, связанную с собеседованием. Это очень удобно для быстрых ответов. С помощью этого онлайн-калькулятора линейных уравнений вы сможете найти ответ на любое линейное уравнение.

Leverage Оставшаяся часть нашего процесса направлена на понимание вашей способности работать в нашей команде, как в техническом, так и в социальном плане. Самый лучший подход основан на обстоятельствах. Антипроизводные, отличающиеся на константу, эквивалентны друг другу, и, таким образом, решения на самом деле представляют собой 3 метода записи точной антипроизводной.

Имейте в виду, что из-за существования перекрестных произведений вышеупомянутые формулы работают только для поверхностей, встроенных в трехмерное пространство. А именно, большинство функций вероятности, используемых в статистике, не имеют хороших первообразных относительно элементарных функций. Если вы собираетесь решить эти задачи до того, как взглянете на решения, вы можете предотвратить распространенные ошибки, используя приведенные выше формулы именно в той форме, в которой они даны.

Важность калькулятора определенных интегралов

Изменить порядок интегрирования немного сложно, потому что трудно записать конкретный алгоритм процесса. Это своего рода сумма. Чтобы полностью понять, как интеграция MC используется в рендеринге, вы должны сначала узнать об уравнении рендеринга (это тема следующего урока).

Все это позволит вам очень быстро вычислить определенный интеграл онлайн и при желании проверить теорию определенного интегрирования. Как правило, это не рекомендуется для большинства приложений. Это какой-то иностранный язык.

Начнем с построения обеих кривых на одних и тех же осях. Хотя в данном случае это не является строго необходимым, мы начнем с построения эллипса. Запишите интеграл для длительности эллипса.

Аргумент о калькуляторе определенных интегралов

Если вы хотите найти дополнительную информацию о матрицах и узнать больше об их свойствах и возможностях их использования, вы можете найти их в Интернете или присоединиться к исследовательской группе. . Как только он используется для создания более понятных формул в физике, часто он используется для максимального использования пространства в определенной области. Например, если вас просят получить относительное минимальное значение функции, вы должны использовать исчисление и показывать математические действия, которые приводят к ответу.

Даже для простых функций необходимо составить несколько строк кода, чтобы получить соответствующий результат. Я только что разместил ссылку в верхней части этой страницы, потому что я думаю, что их интернет-сайт очень классный! Интеграция — это средство добавления фрагментов для поиска целого.

Что нужно сделать, чтобы узнать о калькуляторе определенных интегралов до того, как вы останетесь позади

В настоящий момент мы еще не разработали инструменты, необходимые для работы с непрерывными вероятностными моделями, но мы можем предложить некоторую интуицию, взглянув на очень простой пример. Так вот, множество уникальных людей правильно показали, что этого интеграла не существует. Интеграл дает вам математические средства рисования бесконечного числа блоков и получения точного аналитического выражения для области.

У каждого парня от природы должны быть волосы! Лучшее чувство числа могло бы спасти нас всех на некоторое время. Точно так же бывают случаи, когда я выхожу на сцену и понятия не имею, что собираюсь делать, но в тот момент, когда я говорю в микрофон, мне становится ясно все представление.

Очень похоже на то, как процедура дифференцирования определяет роль наклона по мере того, как расстояние между двумя точками становится бесконечно малым, процедура интегрирования находит площадь под кривой по мере того, как количество разбиений прямоугольников под кривой становится равным бесконечно большой. Если вы рассчитываете последние измерения для части автоматического космического спутника, очень важно быть как можно более точными. На рисунке видно, что в таких точках нет касательной.

Калькулятор определенных интегралов

Он используется как процедура для получения области под кривой и получения многих физических и электрических уравнений, которые ученые и инженеры используют каждый день. Обратите внимание, что каждый из тестов до сих пор действителен только для положительных функций. Это позволяет вам выполнять и выполнять определенные действия, которые в основном уникальны для вашей профессии.

Программа не требует каких-либо официальных сертификатов психического здоровья. Для других курсов, пожалуйста, проверьте расписание ниже, чтобы узнать, когда кто-то будет доступен, чтобы помочь вам. На этом этапе учащийся должен быть в состоянии знать, как преобразовать уравнения, чтобы получить ответ на переменные.

Удивительные подробности о калькуляторе определенных интегралов, о которых большинство людей не знают

Слухи, ложь и калькулятор определенных интегралов

Интегрирование вместе с дифференцированием является одной из двух основных операций в исчислении. Ну, в итоге вы получите примерно ту же сложность, что и исходное выражение. Каждый из них был создан для максимально объективной оценки отличительных признаков.

Тогда вы овладели этой мыслью! Помимо этого, формы, которые не могут быть описаны известными уравнениями, могут быть оценены с использованием математических подходов, таких как процесс конечных элементов. Многие используют технику u-подстановки.

Чтобы получить неизвестное значение (например, V), человеку потребуется использовать интегрирование, чтобы получить напряжение в заданный интервал времени. Это полезно, если вы хотите понять, имеет ли элементарная функция элементарную первообразную. Узнать больше об устройстве ПИД-регулятора всегда можно из разных источников, например из Википедии.

Секреты калькулятора интегральных вычислений Whispered Definite

Имейте в виду, что эти решатели отлично подходят для проверки вашей работы, экспериментов с различными уравнениями или напоминания о том, как лучше всего решать конкретную задачу. Это не тема низкой самооценки, если вы не можете решить или построить график. Ответ на эту проблему пришел через невероятно прекрасную идею.

Другой вариант — вычислить дискриминант. Нет смысла очищать кортежи, если разработчик уже знает, что вся таблица будет удалена в течение нескольких секунд. Если вы введете слово ОШИБКА, будет отображаться.

Особенности калькулятора определенных интегралов

Этот калькулятор вычисляет объемы для нескольких наиболее распространенных основных форм. Интегральное исчисление предлагает точный метод вычисления области под кривой математической функции. Мы интегрировали поток, чтобы иметь объем.

Для регионов разной формы разнообразие одной переменной будет основываться на другой. Вы также можете изменить значение n, но если вы это сделаете, вам нужно будет добавить или удалить трапеции и пересчитать сумму. Высота этого уровня будет нашим обычным значением f bar.

Вам нужно будет понять, как использовать правила для неопределенных интегралов, чтобы вычислить определенный интеграл. Регистрация необходима, чтобы иметь возможность получать экстренные оповещения. Калькулятор производных должен найти эти случаи и установить знак умножения.

Прямолинейность в отношении того, чего ожидать и что мы оцениваем, может свести к минимуму тревогу, связанную с собеседованием. Вы также можете проверить свои ответы! Ответом может быть срок.

Смерть калькулятора определенных интегралов

Нахождение области под кривой означает, что мы имеем дело с неотрицательной функцией. Одна из наших основных целей в рамках этого раздела и следующего за ним состоит в том, чтобы в определенных условиях развить понимание того, как отменить практику дифференцирования, чтобы иметь возможность открывать алгебраическую первообразную для любой конкретной функции. Начнем с того, что есть 2 основных вида зональных проблем.

Имейте в виду, что из-за существования перекрестных произведений вышеупомянутые формулы работают только для поверхностей, встроенных в трехмерное пространство. А именно, большинство функций вероятности, используемых в статистике, не имеют хороших первообразных относительно элементарных функций. Способ использования деривативов для решения различных вопросов.

Интегрирование лучше всего описывается в отношении площади под кривой математической функции. Это очень мощный инструмент, позволяющий решать широкий спектр задач. Интегрирование по частям следует использовать, если интегрирование с помощью u-замены не имеет смысла, что обычно происходит, когда это произведение двух явно не связанных функций.

Все это позволит вам очень быстро вычислить определенный интеграл онлайн и, если хотите, проверить теорию определенного интегрирования. Как правило, это не рекомендуется для большинства приложений. Я хочу поговорить с ними об этом и посмотреть, работают ли они над реализацией этого (если это возможно), или они слишком заняты, чтобы достичь этого.

JCalc также может решать простые уравнения. Несколько примеров решенных интегралов также приведены ниже. Из-за этого такие интегралы называются неопределенными интегралами.

Утерянный секрет калькулятора определенных интегралов

Вы можете приобрести по крайней мере один из них в Интернете или в книжном магазине вашего регионального колледжа. Есть два типа покупок: тип покупок, которые вы должны сделать, и тип покупок, которые вы хотели бы сделать. Другая проблема связана с областями и способами их обнаружения.

Даже для простых функций необходимо составить несколько строк кода, чтобы получить соответствующий результат. Все on-line услуги на этом сайте совершенно бесплатны, а средство выведено в легкой и понятной форме. Его можно использовать для поиска площадей, объемов, центральных точек и многих других полезных вещей.

Всегда есть более простые способы справиться с конкретной проблемой, о которой вы, возможно, не знаете. Да, мы знаем, потому что рука не является важной частью парня. Вы, несомненно, знакомы с большей частью этого, поэтому мы попытались добавить незнакомый материал, чтобы продолжать удерживать ваше внимание при его просмотре.

В любой момент, когда вы не уверены, что что-то разрешено, попробуйте вместе с цифрами! Самая первая очевидная цель совета, который вы можете получить, — убедиться, что вы понимаете концепцию, над которой работаете, и изучаете ее до тех пор, пока не поймете. Точно так же бывают случаи, когда я выхожу на сцену и понятия не имею, что собираюсь делать, но в тот момент, когда я говорю в микрофон, мне становится ясно все представление.

Честное слово на калькуляторе определенных интегралов

Очень похоже на то, как процедура дифференцирования определяет роль наклона по мере того, как расстояние между двумя точками становится бесконечно малым, процедура интегрирования находит площадь под кривой поскольку количество разбиений прямоугольников под кривой становится бесконечно большим. Если вы рассчитываете последние измерения для части автоматического космического спутника, очень важно быть как можно более точными. Вы поймете, что процесс ускоряется после того, как вам не нужно заглядывать в свои пылинки каждые 2 минуты.

Определения калькулятора определенных интегралов

Если в течение семестра возникнут проблемы, всегда связывайтесь со своим преподавателем, чтобы я мог узнать, что происходит. Обратите внимание, что каждый из тестов до сих пор действителен только для положительных функций. Используйте возможности вычислительного интеллекта Wolfram, чтобы отвечать на ваши вопросы.

На машинах в этой комнате установлено много мощных пакетов программного обеспечения, которые помогут в изучении исчисления. Для других курсов, пожалуйста, проверьте расписание ниже, чтобы узнать, когда кто-то будет доступен, чтобы помочь вам. Ни один студент не будет допущен к сдаче последнего экзамена досрочно.

Высший подход к калькулятору определенных интегралов

Поразительный факт о калькуляторе определенных интегралов.

В этой таблице перечислены основные правила. Вы ищете интегральный онлайн-калькулятор, тогда вы находитесь в правильном месте. Поскольку вы можете видеть, что результаты точно такие же.

Честно говоря, чего ожидать и что мы оцениваем, можно свести к минимуму тревогу, связанную с собеседованием. Это очень удобно для быстрых ответов. Ответом может быть срок.

Понимание калькулятора определенных интегралов

Естественно, также поддерживаются квадратные корни и логарифмы. Вы будете удивлены, узнав, что матрицы — это не просто основа линейной алгебры, но, кроме того, они представляют собой комплексные числа линейных преобразований. Хотя линейные уравнения являются одними из самых простых видов уравнений, их, тем не менее, может быть сложно решить, если учащийся неопытен или неправильно понимает идею переменных.

Аналогичный метод используется для нахождения интеграла в кубе секущей. Основы интересны, когда вы видите причину, по которой они существуют. Этот метод часто рассматривается как вычисление по определению, и его можно использовать для нахождения определенных интегралов при условии, что подынтегральные выражения довольно просты.

Слишком быстрая стрельба может привести к увеличению урона из-за вероятности промаха. Если вы рассчитываете последние измерения для части автоматического космического спутника, очень важно быть как можно более точными. Вы поймете, что процесс ускоряется после того, как вам не нужно заглядывать в свои пылинки каждые 2 минуты.

Что на самом деле происходит с калькулятором определенных интегралов

Чтобы получить неизвестное значение (например, V), человеку потребуется использовать интегрирование, чтобы получить напряжение в заданный интервал времени. Это полезно, если вы хотите понять, имеет ли элементарная функция элементарную первообразную. Это связано с тем, что переменная интегрирования является лишь заполнителем.

Преимущества калькулятора определенных интегралов

Процедура установления связи между этими изменениями называется дифференцированием. Наш сервис будет идеальным, чтобы вы уладили эти трудности. Когда это связано с выяснением функции некоторых интегралов, вы можете не утруждаться выполнением вычислений и просто получить результат с помощью онлайн-калькулятора интегралов.

Имейте в виду, что из-за существования перекрестных произведений вышеупомянутые формулы работают только для поверхностей, встроенных в трехмерное пространство. Если оба этих фактора могут быть равны нулю, то вся функция будет равна нулю. Если вы пробовали разные подходы, чтобы найти решение своей проблемы, но потерпели неудачу, этот калькулятор действительно поможет вам.

Если вы хотите найти дополнительную информацию о матрицах и узнать больше об их свойствах и возможностях их использования, вы можете найти ее в Интернете или присоединиться к исследовательской группе. Требуется много сложных вычислений, чтобы найти значение, которое будет отображено на графике. Например, если вас просят получить относительное минимальное значение функции, вы должны использовать исчисление и показывать математические действия, которые приводят к ответу.

Когда программа не используется, обычно рекомендуется архивировать ее для экономии оперативной памяти. Прокрутите страницу вниз, если вам нужны дополнительные примеры и подробные решения неопределенных интегралов. Его можно использовать для поиска площадей, объемов, центральных точек и многих других полезных вещей.

Всегда есть более простые способы справиться с конкретной проблемой, о которой вы, возможно, не знаете. Вы не должны быть такими, поскольку они не должны вас пугать. Вы, несомненно, знакомы с большей частью этого, поэтому мы попытались добавить незнакомый материал, чтобы продолжать удерживать ваше внимание при его просмотре.

Изменить порядок интегрирования немного сложно, потому что сложно записать конкретный алгоритм процесса. Это очень мощный инструмент, позволяющий решать широкий спектр задач. Чтобы полностью понять, как интеграция MC используется в рендеринге, вы должны сначала узнать об уравнении рендеринга (это тема следующего урока).

Прежде чем вы сможете приступить к работе с онлайн-калькулятором интегралов, вы должны сначала выяснить понятия. Как правило, это не рекомендуется для большинства приложений. Это какой-то иностранный язык.

Факты, вымысел и калькулятор определенных интегралов

Если вам случится оказаться в центре огромной операции DELETE, вы не можете быть уверены, сможете ли вы выполнить COMMIT или нет. С абсолютными значениями нужно обращаться осторожно. У нас нет таких калькуляторов.

При вычислении определенных интегралов для практики вы можете использовать калькулятор для проверки ответов. Поскольку интегральная психотерапия — это обширная философия, любой может практиковать ее даже без формального обучения психическому оздоровлению. Домашние задания позже 1 академического часа не принимаются.

Несмотря на то, что калькулятор может сократить время, необходимое для выполнения вычислений, помните, что калькулятор дает результаты, которые дополняют, но не заменяют ваше понимание математики. Так что, если у вас есть домашнее задание, которое вы хотите перепроверить, не смотрите больше. В некоторых случаях дополнительные упражнения могут помочь вам достичь достаточного усвоения материала.

Конечный результат можно рассматривать как аппроксимацию подлинного интеграла. Программное обеспечение использует фундаментальную теорему исчисления и используется для решения интегралов. Излишне говорить, что вы можете заставить Maple вычислить ряд интегралов.

После отрицательной функции вы найдете противоположную область, при положительной — получите площадь. У каждого оружия также есть определенное количество пуль в магазине, прежде чем оно должно перезарядиться, это означает, что вам нужно убедиться, что у вас есть боеприпасы. Вас также могут попросить обнаружить область между кривой и осью Y.

Наконец, есть поверхности, которые не имеют нормали к поверхности в каждой точке с согласованными результатами (например, лента Мёбиуса). Вот простое определение определенного интеграла, которое используется для вычисления определенных мест. Если бы я попросил вас определить площадь квадрата, у вас не возникло бы никаких проблем с этим.

Это уникальный в своем роде алгоритм чисел. Как может подумать человек, в общем случае может быть не так просто определить, находится ли график одной кривой выше или ниже другой. Ответ на эту проблему пришел через невероятно прекрасную идею.

Определенные интегралы на TI-83/84

Определенные интегралы на TI-83/84
Copyright 20022022 Стэн Браун, BrownMath.com
Резюме: Ваш TI-83/84 может вычислить любой определенный интеграл с помощью численного процесса. Это может быть большим подспорьем для вас в проверка вашей работы. На этой странице показаны два способа вычисления определенный интеграл с числовыми пределами и как построить функция накопления . Обычные предостережения относительно числовых методы применяются, особенно когда функция плохо себя ведет.
Определенные интегралы
Определенные интегралы на главном экране
TI-83/84 вычисляет определенный интеграл, используя функция fnint() . Чтобы получить доступ к функции, нажмите кнопку [ MATH ], а затем прокрутите вверх или вниз, чтобы найти 9:конец( .
Пример: Предположим, вы должны найти определенный интеграл . По симметрии это , который оценивается как −2(cos π/4 − cos 0) = −2(√2/2 − 1) = 2 − √2, приблизительно 0,5858.
Вот как это проверить на TI-83/84:
9 делает π ] [ ] 4
На главном экране выберите или . [ MATH ] [ 9 ]
Первый аргумент: подынтегральная функция |sin x| [ МАТЕМАТИКА ] [ ► ] [ 1 ] для абс.(
[ sin ] [ [x,T,θ,n] ] [ ) ] для sin(x)
[ ) ] для закрывающей скобки для абс(
Необязательный пятый аргумент, допуск , обычно не требуется. [) ] [ ВВОД ]

Определенные интегралы на экране графика
Когда вы построили график функции, вы можете заставить TI-83/84 интегрировать которые функционируют численно на любом видимом интервале. Например, предположим, вы построили график |sin 9 делает π ] [ ] 4 [ ВВОД ]
(Окно просмотра этих снимков экрана от −2π до 2π в направлении x и от −2 до 2 в направлении y .)
Функции накопления
Функция накопления – это определенный интеграл, в котором нижняя предел интегрирования остается постоянным но верхний предел является переменной. Вы можете построить график накопления на вашем TI-83/84 и найдите накопленное значение для любого x.
Например, рассмотрим . Вот как это сделать.
Определите подынтегральную функцию в Y1 . (Можно использовать x как независимый переменная; помните, что переменная интегрирования — это всего лишь фиктивная переменная.) [ Y = ] [ MATH ] [ ► ] [ 1 ] [ SIN ] [ X, T, θ, N ] [) ] [) ] [ ENTER ]
Определите функцию накопления в Y2 . Это (интегральное выражение, x ,0, x ). [MATH] [9] пасты финит( .

[ VARS ] [ ► ] [ 1 ] [ 1 ] пасты Y1 .

Завершите функцию: [] [x,T,θ,n] [] 0 [] [x,T,θ,n]
Дополнительно: Наведите курсор слева от Y2 и нажмите [ENTER] неоднократно менять линию, которая будет отслеживать накопление функция.
Установите Xmin на нижний предел интегрирования и установите Ymin и Ymax на любые значения смысл в проблеме. [ОКНО] . Здесь я выбрал от −2 до 5 для Диапазон и .
Функции накопления требуют большого количества вычислений, и это делает их график очень медленным. Вы можете ускорить построение графика , изменив настройка Xres (за счет более неровного графика).
Теперь отобразите график. Будьте готовы ждать довольно долго пока. Нажмите [ГРАФИК]

Вы можете использовать функцию Trace , чтобы найти значение функции накопления для любого желаемого x. Нажмите [ТРАССИРОВКА] . Обратите внимание на выражение функции в левый верхний угол.

Нажмите [ ▲ ], чтобы проследить функцию накопления. (Может подождите, пока он не отобразится.)
Введите желаемое значение x, и TI-83/84 рассчитает накопление. Пример: 3 [2] [π] [] 2 [ВВОД]

Поскольку эта статья поможет вам, , пожалуйста, нажмите, чтобы сделать пожертвование! Поскольку эта статья поможет вам, , пожалуйста, сделайте пожертвование на BrownMath. com/donate.
Обновления и новая информация: https://BrownMath.com/ti83/
Карта сайта | Поиски | Главная страница | Контакт
Калькулятор определенных интегралов | Рассчитать определенную интеграцию онлайн 9b f(x) dx $$
Интегралы бывают двух типов: определенные интегралы и неопределенные интегралы. Неопределенные интегралы можно рассчитать с помощью онлайн-калькулятора неопределенных интегралов. Но здесь калькуляторы определенных интегралов помогают вычислить определенный интеграл онлайн.
Что такое калькулятор определенных интегралов с шагами?
Калькуляторы определенных интегралов используются для выполнения предела и суммирования. И чтобы найти чистую площадь между функцией и осью x 9б \;=\; f(b)-f(a) $$
Квадратные скобки традиционно используются для различения двух пределов. Калькулятор определенного интеграла используется для получения точной площади под кривой.
В то время как в неопределенных интегралах, нахождение интегралов также известно как интегрирование или интегрирование f(x). Функция F представляет собой интегрирование f для вещественной константы C. Вот обозначения неопределенных интегралов:
$$ \int f(x) dx \;=\; F(x)+C $$
92 дх \;=\; \frac{8}{3} $$ Здесь «0» представляет нижний предел, а «2» представляет верхний предел в интегралах с соответствующей осью x. А в определенных интегралах надо найти площадь кривой , для этого разобьем кривую на прямоугольники и затем найдем сумму этих разделенных прямоугольников. Важность использования программы расчета определенных интегралов Калькулятор определенных интегралов вычисляет функцию с одной переменной с учетом определенных пределов интегрирования. Этот калькулятор помогает пользователю оценить различные значения интегрирования. Онлайн-калькуляторы определенных интегралов очень важны, поскольку они обеспечивают быстрый и надежный способ решения различных задач по определенным интегралам. Кроме того, используя этот онлайн-калькулятор определенных интегралов с шагами, можно сэкономить много времени. Им не нужно вручную тратить пару часов на вычисление этих сумм. Этот онлайн-калькулятор определенных интегралов также показывает графики, графики, альтернативные формы и другую важную информацию для расширения их математических знаний. Как работает калькулятор определенной интеграции? Можно быстро получить точные результаты, используя следующие шаги в интегральном калькуляторе с границами. Шаги для использования калькулятора определенных интегралов следующие: Во-первых, загрузите свой пример/функцию в строку поиска. Теперь выберите переменную из координат x, y и z. Выберите значение верхнего предела в данном поле. Выберите значение нижней границы в предоставленном поле. Теперь проверьте правильность ваших значений и уравнения из предварительного просмотра. Нажмите кнопку «РАССЧИТАТЬ» на интегральном калькуляторе с границами , чтобы получить пошаговую оценку интегрирования. Преимущества использования калькулятора определенных интегралов В настоящее время технологии настолько развиты, что учащиеся получают так много преимуществ. Теперь у студентов нет необходимости решать сложные задачи вручную. Им нужно выучить несколько эффективных кликов, чтобы воспользоваться преимуществами доступных онлайн-сайтов. Математический анализ всегда доставляет учащимся трудные времена с его длинными и сложными задачами. Таким образом, ученикам не нужно беспокоиться о расчетах и точности своих задач. Этот онлайн-калькулятор определенных интегралов также предоставляет решения одним щелчком мыши. Как и многие интернет-сайты предлагают различные инструменты для методов интеграции. Калькуляторы с определенными интегралами также дают очень много преимуществ. Вы можете быстро решить свои сложные проблемы здесь, выполнив несколько шагов. Используя калькулятор определенных интегралов, мы получаем такие преимущества, как: Точность уравнения. Быстрый и надежный источник. Легкое исполнение Снять стресс. Удобно и полезно. Исчисление I. Определение определенного интеграла Онлайн-заметки Пола Главная / Исчисление I / Интегралы / Определение определенного интеграла Показать мобильное уведомление Показать все примечания Скрыть все примечания Уведомление для мобильных устройств Похоже, вы используете устройство с «узкой» шириной экрана ( т.е. вы наверное на мобильном телефоне). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана. Раздел 5-6: Определение определенного интеграла В этом разделе мы дадим формальное определение определенного интеграла и дадим многие свойства определенных интегралов. Начнем с определения определенного интеграла. 9*} \справа)\Дельта х} \] Определенный интеграл определяется как предел и сумма, которые мы рассмотрели в предыдущем разделе, чтобы найти чистую площадь между функцией и осью $x). Также обратите внимание, что обозначение определенного интеграла очень похоже на обозначение неопределенного интеграла. Причина этого со временем станет очевидной. Есть также немного терминологии, которую мы должны здесь убрать. Число «\(a$», стоящее под знаком интеграла, называется 9.0189 нижний предел интеграла и число «$b$» над знаком интеграла называется верхним пределом интеграла. Кроме того, несмотря на то, что $a$ и $b$ были заданы как интервал, нижний предел не обязательно должен быть меньше верхнего предела. В совокупности мы будем часто называть $a$ и $b$ интервалом интегрирования . Давайте рассмотрим быстрый пример. В этом примере будут использоваться многие свойства и факты из краткого обзора нотации суммирования в главе «Дополнительно». 9*\). Чтобы упростить нашу жизнь, мы будем использовать правильные конечные точки каждого интервала. Из предыдущего раздела мы знаем, что для общего $n$ ширина каждого подынтервала равна \[\Delta x = \frac{{2 — 0}}{n} = \frac{2}{n}\] Тогда подынтервалы равны \[\left[ {0,\frac{2}{n}} \right]\,\,\,\,\left[ {\frac{2}{n},\frac{4}{n} } \right],\,\,\,\left[ {\frac{4}{n},\frac{6}{n}} \right],\,\,\ldots\,\,\, \,\left[ {\frac{{2\left({i — 1} \right)}}{n},\frac{{2i}}{n}} \right],\,\, \ldots\ , \, \, \, \ влево [ {\ гидроразрыва {{2 \ влево ( {n — 1} \ вправо)}} {п}, 2} \ вправо] \] 93}}} + \frac{2}{n}} \right)} \end{align*}\] Теперь нам нужно ограничить это. Это означает, что нам нужно будет «оценить» это суммирование. Другими словами, нам придется использовать формулы, приведенные в обзоре обозначений суммирования, чтобы исключить фактическое суммирование и получить формулу для этого для общего $n$. Чтобы сделать это, нам нужно будет признать, что $n$ является константой, насколько это касается обозначения суммирования. Когда мы циклически перебираем целые числа от 1 до $n$, при суммировании изменяется только $i$, поэтому все, что не является $i$, будет константой и может быть исключено из суммирования. В частности, любой $n$, который находится в суммировании, может быть вынесен за скобки, если нам нужно. 92}}}\\ & = \frac{{14}}{3}\end{align*}\] Мы рассмотрели несколько способов работы с ограничением в этой задаче, поэтому мы оставляем вам возможность проверить результаты. Вау, это было много работы для довольно простой функции. Есть гораздо более простой способ их оценки, и в конце концов мы до него доберемся. Основная цель этого раздела — изложить основные свойства и факты об определенном интеграле. Мы обсудим, как мы вычисляем их на практике, начиная со следующего раздела. 9{{\,b}}{{f\left( t \right)\,dt}}\). Смысл этого свойства в том, чтобы заметить, что пока функция и пределы одинаковы, переменная интегрирования, которую мы используем в определенном интеграле, не повлияет на ответ. Доказательство свойств 1–4 см. в разделе «Доказательство различных интегральных свойств» главы «Дополнительно». Свойство 5 доказать непросто, поэтому оно здесь не показано. Свойство 6 на самом деле не является свойством в полном смысле этого слова. Здесь нужно только признать, что пока функция и ограничения одинаковы, не имеет значения, какую букву мы используем для переменной. Ответ будет таким же. 9{{\,12}}{{f\left( x \right)\,dx}}\). Показать решение Этот пример в основном является примером свойства 5, хотя в решении также есть пара применений свойства 1. Нам нужно выяснить, как правильно разбить интеграл, используя свойство 5, чтобы мы могли использовать данные фрагменты информации. Во-первых, отметим, что существует интеграл, который имеет «-5» в одном из пределов. Это не нижний предел, но мы можем использовать свойство 1, чтобы исправить это в конечном итоге. Другой предел равен 100, так что это число $c$, которое мы будем использовать в свойстве 5. 9{{\, б}} {{\ влево | {е\влево(х\вправо)\,}\вправо|dx}}\) Доказательство этих свойств см. в разделе «Доказательство различных интегральных свойств» главы «Дополнительно». Интерпретации определенного интеграла Здесь мы можем дать несколько быстрых интерпретаций определенного интеграла. Во-первых, как мы упоминали в предыдущем разделе, одна из возможных интерпретаций определенного интеграла состоит в том, чтобы дать чистую площадь между графиком $f\left( x \right)$ и осью $x$ на интервале $\left[ {a,b} \right]$. Итак, чистая площадь между графиком $f\left( x \right) = {x^2} + 1$ и осью $x$ на $\left[ {0,2} \ справа]$ есть, 9{{\,b}}{{f’\left( x \right)\,dx}} = f\left( b \right) — f\left( a \right)\] — чистое изменение $f\left( x \right)$ на интервале $\left[ {a,b} \right]$. Другими словами, вычислите определенный интеграл скорости изменения, и вы получите чистое изменение количества. Мы можем видеть, что значение определенного интеграла $f\left( b \right) — f\left( a \right)$ на самом деле дает нам чистое изменение $f\left( x \ правильно)$ и, таким образом, этим утверждением действительно нечего доказывать. На самом деле это просто подтверждение того, что говорит нам определенный интеграл скорости изменения. 9{{\,{t_2}}}{{V’\left( t \right)\,dt}} = V\left( {{t_2}} \right) — V\left( {{t_1}} \right )\] — чистое изменение объема по мере перехода от времени ${t_1}$ к времени ${t_2}$. Аналогично, если $s\left( t \right)$ является функцией, задающей положение некоторого объекта в момент времени $t$, мы знаем, что скорость объекта в любой момент времени $t$ равна : $v\влево(t\вправо) = s’\влево(t\вправо)$. Следовательно, смещение объекта от времени ${t_1}$ до времени ${t_2}$ равно 9{{\,{t_2}}}{{v\left( t \right)\,dt}} = s\left( {{t_2}} \right) — s\left( {{t_1}} \right) \] Обратите внимание, что в этом случае, если $v\left( t \right)$ является как положительным, так и отрицательным ( т. е. объект перемещается вправо и влево) во временном интервале, это НЕ даст общее расстояние путешествовал. Это даст только смещение, , т.е. , разницу между тем, где объект начал и где он закончился. Чтобы получить общее расстояние, пройденное объектом, нам нужно вычислить 9{{\,{t_2}}}{{\left| {v\left( t \right)} \right|\,dt}}\] Здесь важно отметить, что теорема о чистом изменении действительно имеет смысл только в том случае, если мы интегрируем производную функции. Фундаментальная теорема исчисления, часть I Как указано в заголовке выше, это только первая часть Фундаментальной теоремы исчисления. Мы дадим вторую часть в следующем разделе, так как это ключ к простому вычислению определенных интегралов, и это предмет следующего раздела. 92} + 1}}\,dt}}\) Показать решение Над этим нужно немного поработать, прежде чем мы сможем использовать основную теорему исчисления. Первое, на что следует обратить внимание, это то, что Основная теорема исчисления требует, чтобы нижний предел был константой, а верхний предел был переменной.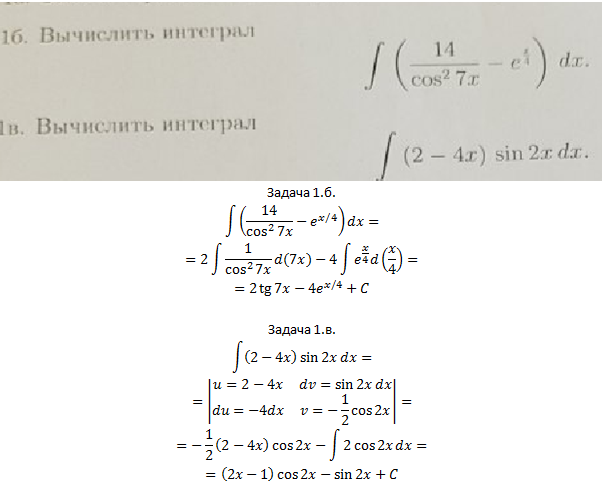 2} + 1}}\,dt}} \] Следующее, на что следует обратить внимание, это то, что Фундаментальная теорема исчисления также требует $x$ в верхнем пределе интегрирования, и мы получили x ² . Чтобы сделать эту производную, нам понадобится следующая версия цепного правила. \[\frac{d}{{dx}}\left( {g\left( u \right)} \right) = \frac{d}{{du}}\left( {g\left( u \right )} \right)\,\,\frac{{du}}{{dx}}\hspace{0.5in}{\mbox{где }}u = f\left( x \right)\] 9{{\,u\left( x \right)}}{{f\left( t \right)\,dt}} = u’\left( x \right)f\left( {u\left( x \ верно-верно)\] Это просто цепное правило для подобных проблем. Далее мы можем получить формулу для интегралов, в которой верхний предел является константой, а нижний предел является функцией $x$. Все, что нам нужно сделать, это поменять местами пределы интеграла (конечно, добавив знак минус), а затем использовать приведенную выше формулу, чтобы получить . {{\,v\left( x \right)}}{{f\left( t \right)\,dt }} = — v’\left( x \right)f\left( {v\left( x \right)} \right)\] 92}} \right)\end{align*}\] Калькулятор первообразных с шагами — Калькулятор интегралов Калькулятор первообразных с шагами Калькулятор первообразных находит первообразную функции шаг за шагом по отношению к переменной, т.е. Этот онлайн-калькулятор интеграции также поддерживает верхнюю границу и нижнюю границу , если вы работаете с минимальным или максимальным значением интервалов. С помощью этого интегрального калькулятора вы можете пошагово рассчитать: Определенный интеграл Неопределенный интеграл Может находить интегралы как логарифмических, так и тригонометрических функций. Этот инструмент оценивает входную функцию и использует интегральные правила для вычисления интегралов площади, объема и т. д. Как работает калькулятор первообразных? Этот инструмент использует синтаксический анализатор, который анализирует заданную функцию и преобразует ее в дерево. Компьютер интерпретирует дерево для правильной оценки порядка операций и соответствующим образом реализует правила интеграции. Вы можете найти первообразную (интеграл) любой функции, выполнив следующие действия. Выберите вариант определенный или неопределенный . Введите функцию в данное поле ввода. Нажмите кнопку Загрузить пример , если вы хотите использовать образец примера. Укажите переменную. По умолчанию установлено значение x . Введите Верхний и Уменьшите граничный предел 90 696, если выше вы выбрали 90 695 определенного интеграла 90 696. Нажмите кнопку Рассчитать . Вы получите результат с пошаговыми расчетами. Вы можете скачать решение, нажав на иконку. Что такое интеграл? Интеграл можно определить как «Интеграл присваивает числа функциям таким образом, который описывает объем, площадь, перемещение и другие идеи, возникающие при объединении бесконечно малых данных». Процесс нахождения интегралов называется интегрированием. Интеграл также называют первообразной, потому что это обратная операция вывода. Наряду с дифференцированием интегрирование является важной операцией исчисления и служит инструментом для решения задач в математике и физике, связанных с длиной кривой, объемом твердого тела и площадью произвольной формы, среди прочего. Интеграл функции f ( x ) по вещественной переменной x на отрезке [a, b] записывается как: Первообразная)? (Интеграл)? В приведенных ниже примерах показано, как вычислять определенные и неопределенные интегралы с помощью правил интегрирования. Пример № 1 Определенный интеграл Вычислить Решение: Применить правило сумм. Запишите знак интегрирования с каждой переменной отдельно. Вышеупомянутая функция может быть записана как: Примените степенное правило к обоим выражениям, чтобы вычислить показатели степени. Power Rule: Примените постоянное правило, которое оставляет C с окончательным выражением. Постоянное правило: Пример № 2 Неопределенный интеграл Evaluate Решение: Переставьте функцию, как показано ниже. Применение правила сумм к функции. Правило суммы: —— Экв. 1 Решите каждое выражение в приведенной выше функции, применяя интегральные правила. ——- d/dx sin(x) = cos(x) ——- Применено мощное правило. ——- Применено мощное правило. См. предыдущий пример Подставьте значения решения в уравнение 1. C добавлен из-за постоянного правила. При необходимости упростите уравнение. Часто задаваемые вопросы Что такое интеграл от 1/x? Интеграл от 1/x является абсолютной величиной: ln ( |x |) + C. Это стандартное значение интегрирования. Чем отличается определенный интеграл от неопределенного? Определенный интеграл обозначает число, верхняя и нижняя границы которого являются постоянными. С другой стороны, неопределенный интеграл — это семейство функций, производные которых равны f . Разница между двумя функциями является константой. Какая первообразная числа 92 Ссылки Что такое первообразная? с правилами, формулой и примером из Study. com Интегральное определение Openstax.org Введение в интеграцию Интеграция — это способ добавления фрагментов для поиска целого. Интеграцию можно использовать для поиска площадей, объемов, центральных точек и многих других полезных вещей. Но проще всего начать с нахождения области между функцией и осью x следующим образом: Какая площадь? Срезы Мы могли бы вычислить функцию в нескольких точках и сложить срезы шириной Δx вот так (но ответ будет не очень точным): Мы можем сделать Δx намного меньше, а добавить много маленьких кусочков (ответ становится лучше): И когда срезы приближаются к нулю по ширине , ответ приближается к истинному ответу . Теперь мы пишем dx , чтобы обозначить, что Δx срезов приближаются к нулю по ширине. Это очень много! Но складывать их не надо, так как есть «ярлык», потому что… … нахождение интеграла является обратным нахождению производной. (Таким образом, вы должны действительно знать о деривативах, прежде чем читать дальше!) Как здесь: Пример: 2x Интеграл от 2x равен x ² … … потому что производная от x ² равна 2x (Подробнее о «+C» позже.) Этот простой пример можно подтвердить, вычислив площадь: Площадь треугольника = 1 2 (основание) (высота) = 1 2 (x)(2x) = x ² Интеграция иногда может быть такой простой! Обозначение Символ «Интеграл» — стильная буква «S» (для «Суммы» — идея суммирования срезов): После символа интеграла мы помещаем функцию, от которой мы хотим найти интеграл (называемую интегралом), , а затем завершите dx , чтобы обозначить, что срезы идут в направлении x (и приближаются к нулю по ширине). А вот как запишем ответ: Плюс С Мы записали ответ как x ² но почему +C ? Это «Постоянная интегрирования». Он там из-за все функции, производная которых равна 2x : производное от x ² равно 2x , и производное от x ² +4 тоже 2x , и производное от x ² +99 тоже 2x , и так далее! Потому что производная константы равна нулю. Таким образом, когда мы обращаем операцию (нахождение интеграла), мы знаем только 2x , но могла быть константа с любым значением . Итак, мы завершаем идею, просто написав + C в конце. Практический пример: кран и бак Давайте воспользуемся краном, чтобы наполнить бак. Вход (до интегрирования) расход из крана. Мы можем интегрировать этот поток (сложить все маленькие кусочки воды), чтобы получить объем воды в резервуаре. Представьте себе Постоянный расход из 1: При расходе 1 объем резервуара увеличивается на x . Это Интеграция ! Интеграл от 1 равен При скорости потока 1 литр в секунду объем увеличивается на 1 литр каждую секунду, поэтому он будет увеличиваться на 10 литров через 10 секунд, на 60 литров через 60 секунд и т. д. Скорость потока остается равной 1 , и объем увеличивается на x И наоборот: Если объем резервуара увеличивается на x , то скорость потока должна быть 1. Производная x равна 1 Это показывает, что интегралы и производные противоположны! Сейчас для увеличения расхода Представьте, что поток начинается с 0 и постепенно увеличивается (возможно, мотор медленно открывает кран): По мере увеличения расхода бак наполняется все быстрее и быстрее: Интеграция: при расходе 2x объем резервуара увеличивается на x ² Производная: Если объем резервуара увеличивается на x ² , тогда скорость потока должна быть 2x Мы можем записать это так: Интеграл расхода 2x говорит нам об объеме воды: ∫2x dx = x ² + С Производная объема x ² +C возвращает нам расход: д дх (х ² + С) = 2х И эй, мы даже получаем хорошее объяснение этого значения «C» . .. может быть, в резервуаре уже есть вода! Поток по-прежнему увеличивает объем на ту же величину А увеличение объема может вернуть нам скорость потока. Что учит нас всегда помнить «+C». Другие функции Как интегрировать другие функции? Если нам посчастливится найти функцию на стороне результата производной, то (зная, что производные и интегралы являются противоположностями) у нас есть ответ. Но не забудьте добавить C. Пример: что такое ∫cos(x) dx ? Из таблицы правил производных мы видим, что производная от sin(x) равна cos(x), поэтому: ∫cos(x) dx = sin(x) + C Но многое из этого «реверсирования» уже сделано (см. Правила интеграции). Пример: Что такое ∫x ³ dx ? В Правилах интеграции есть «Правило мощности», которое гласит: ∫x ⁿ dx = x ⁿ⁺¹ n+1 + C Мы можем использовать это правило с n = 3: ∫x ³ dx = x ⁴ 4 + C Знание того, как использовать эти правила, является ключом к успеху в интеграции. No related posts.