Вычитание и сложение дробей
Предположим, вы выполнили часть домашнего задания вчера и еще часть сегодня. Должен же быть способ подсчитать, сколько домашней работы осталось и сколько всего вы сделали, верно? Вы можете выполнять операции сложения, вычитания, умножения и деления дробей точно так же, как и с целыми числами! В этой статье мы собираемся изучить, как именно выполнять вычитание и сложение дробей.
Правила и шаги: Сложение и вычитание дробей
Дробь — это число, выраженное в виде частного. Многие числа представлены таким образом, и это означает, что они не являются целыми числами. Частное состоит из старшего числа, числителя , и меньшего числа, знаменателя .
Как мы видим ниже, числитель расположен над горизонтальной линией, а знаменатель под ней. В математике эта горизонтальная линия эквивалентна символу деления. Таким образом, дробь представляет собой деление верхнего числа (числителя) на нижнее число (знаменатель).
Пример дроби с обозначением числителя и знаменателя — StudySmarter Originals
Дроби с одинаковым знаменателем
При сложении и вычитании дробей следует помнить одно важное правило: Если дроби нужно складывать или вычитать имеют одинаковые знаменатели, их числители можно складывать или вычитать, сохраняя знаменатель постоянным. Это правило является основой для всех операций сложения и вычитания дробей.
Проиллюстрируем этот процесс более подробно. Предположим, мы хотим вычислить . Поскольку знаменатели идентичны, мы можем просто выполнить вычитание числителей, сохраняя знаменатель постоянным (т. Е. Знаменатель = 9). Другими словами, мы выполняем 5 — 4 = 1 на числителях. Окончательный ответ: Шаги можно записать так:
Дроби с разными знаменателями
Прежде чем складывать или вычитать дроби с разными знаменателями, мы должны манипулировать дробями так, чтобы у них были одинаковые знаменатели. Для этого нам сначала нужно найти наименьший общий знаменатель (LCD).
Наименьший общий знаменатель (LCD) двух дробей — это наименьший возможный знаменатель, который может быть общим для каждой дроби, сохраняя при этом числовое значение каждой дроби одинаковым.
Чтобы найти наименьший общий знаменатель двух дробей, важно сначала убедиться, что каждая дробь представлена в самой упрощенной форме. Это означает, что все общие множители в числителе и знаменателе исключены. Следующим шагом является рассмотрение или перечисление всех множителей каждого знаменателя. Затем мы можем выбрать наименьшее кратное, общее для обоих списков. Это наименьший общий знаменатель! Рассмотрим подробнее этот процесс на следующем примере.
Найдите наименьший общий знаменатель дробей и
1. Убедитесь, что каждая дробь представлена в самой упрощенной форме.
Первая дробь, которую мы видим, не в самой упрощенной форме. Мы можем упростить эту дробь, убрав коэффициент 32 сверху и снизу.
Вторая дробь уже в самом упрощенном виде, так как нет множителей, которые можно вынести как из верха, так и из низа.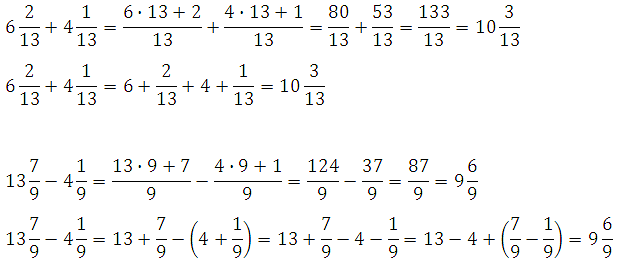
Это оставляет нас с дробями и
2. Перечислите кратные каждого знаменателя.
Кратные 2: 2, 4, 6, 8, 10, 12, 14…
Кратные 10: 10, 20, 30, 40, 50, 60, 70…
Из каждого из этих списков видно, что 10 — это наименьшее кратное, общее для обоих знаменателей. Следовательно, это наименьший общий знаменатель .
После нахождения ЖК-дисплея можно использовать следующую процедуру для сложения или вычитания дробей с разными знаменателями:
Шаг 1: Установите знаменатель каждого члена с наименьшим общим знаменателем (LCD).
Шаг 2: Установите числитель каждого члена равным.
Шаг 3: Теперь, когда все знаменатели одинаковы, вы можете складывать или вычитать члены в числителе, чтобы получить ответ.
Сложите дроби и
Из нашего предыдущего примера мы знаем, что наименьшее общее кратное и равно 10.
1.
Установите знаменатель каждого члена с наименьшим общим знаменателем (LCD).
и
2. Установить числитель каждого члена равным
Поскольку исходный знаменатель второй дроби уже равен 10, ее числитель не нужно преобразовывать.
У нас остались дроби и
3. Теперь, когда все знаменатели одинаковы, вы можете сложить члены в числителе, чтобы получить ответ.
В этом примере использовался более длинный способ вычисления; однако, как только вы поймете основы, вам будет намного проще выполнять следующие вычисления:
Примеры сложения и вычитания дробей
(1) Вычислить
Решение:
знаменатели одинаковы, мы можем напрямую вычесть числители.
(2) Оценка
Решение:
LCM знаменателей (18 и 12) составляет 36. С. (20, 12, 30 и 3) равно 60.
Чтобы сложить или вычесть смешанные дроби, сначала преобразуйте их в неправильные дроби, а затем продолжите стандартный процесс.
Сложение и вычитание смешанных дробей
Смешанная дробь — это число, представленное как целое число и частное, например
Сложение и вычитание смешанных дробей требует преобразования их в неправильные дроби. Затем мы можем выполнить стандартный процесс сложения и вычитания дробей, как мы это делали раньше. Неправильная дробь – это дробь, числитель которой больше или равен знаменателю.
Чтобы преобразовать смешанную дробь в неправильную дробь, мы должны преобразовать целую числовую часть смешанной дроби в дробь с тем же знаменателем, что и в частном. Затем мы просто добавляем их. Давайте посмотрим на пример.
Преобразуйте следующую смешанную дробь в неправильную дробь.
Решение:
1. Преобразовать целую числовую часть неправильной дроби в дробь с тем же знаменателем, что и у частного.
2. Добавьте эту новую дробь к частному исходной смешанной дроби, чтобы получить неправильную дробь.
И так получаем результат:
Оценка
Решение:
Преобразование смешанных фракций в ненадлежащие фракции, которые мы получаем:
положительных и отрицательных дробей
Как и любое другое число, которое вы встретите, дроби могут быть положительными или отрицательными. К счастью, правила сложения и вычитания положительных и отрицательных дробей такие же, как и для любого другого числа! Давайте посмотрим на несколько примеров, чтобы увидеть, как это работает.
(1) Вычислить
Решение:
Вычитание отрицательного числа аналогично сложению. Таким образом, наша сумма становится:
(2) Оценка
Решение:
Поскольку добавление отрицательного отрицательного, что и вычитание, наша сумма становится:
(3) Оценка
Решение:
При вычитании отрицательного числа из отрицательного мы складываем числа, но сохраняем знак минус.
Итак,
Сложение и вычитание десятичных дробей
Десятичные дроби – это дроби, знаменатель которых несколько кратен десяти, например .
Десятичные дроби складываются и вычитаются почти так же, как и любые другие дроби, рассмотренные ранее. Во-первых, они должны быть преобразованы в форму с наименьшим общим знаменателем, а затем числители могут быть добавлены или вычтены по мере необходимости. Удобная вещь в сложении и вычитании десятичных дробей заключается в том, что наименьший общий знаменатель всегда является наибольшим знаменателем в сумме! Давайте рассмотрим еще несколько примеров.
(1) Оценить
Решение:
Сначала мы приводим каждое к наименьшему общему знаменателю, который, как мы видим, равен 100.
И затем выполняем сложение.
(1) Оценка
Решение:
Сначала мы преобразуем каждый в самый низкий общий знаменатель, который мы видим, — 1000.
, а затем мы выпускаем субтракцию.
Вычитание и сложение дробей — основные выводы
- Если дроби, которые нужно складывать или вычитать, имеют одинаковые знаменатели, их числители можно просто складывать или вычитать, сохраняя знаменатель постоянным.
- Если нам нужно складывать или вычитать дроби с разными знаменателями, мы сначала манипулируем дробями так, чтобы они имели одинаковые знаменатели.
- Чтобы сложить или вычесть смешанные дроби, сначала преобразуйте их в неправильные дроби.
- Сложение и вычитание положительных и отрицательных дробей работает так же, как и любое другое число.
Упростить калькулятор алгебраических фракций — Google Suce
ALLBILDERVIDEOSBüchermApsNewshopping
Sucoptionen
Упрощение калькулятора — Algebraulator — Algebraulator. шаг за шагом. … Чтобы упростить выражение с дробями, найдите общий знаменатель, а затем .
.. 92
Simplify Calculator — MathPapa
www.mathpapa.com ›simplify-calculator
Упрощает выражения шаг за шагом и показывает работу! Этот калькулятор решит ваши проблемы.
Алгебраические дроби Калькулятор и решатель — SnapXam
www.snapxam.com › калькуляторы › алгебраическ…
Алгебраические дроби Калькулятор онлайн с решением и шагами. Подробные пошаговые решения ваших задач с алгебраическими дробями онлайн с помощью нашей математики …
Калькулятор упрощения — Mathway
www.mathway.com › Калькулятор › упрощение-калькулятор
Калькулятор упрощения позволяет взять простое или сложное выражение, упростить и привести его к простейшей форме.
Ähnliche Fragen
Как упростить алгебраические дроби с разными знаменателями?
Упрощение — Сокращение простых или сложных дробей с помощью … — QuickMath
quickmath.com › алгебра › отменить › базовый
Уменьшите или упростите дробь с помощью нашего бесплатного пошагового математического калькулятора.
… Когда дроби содержат алгебраические выражения, необходимо множить …
Калькулятор алгебраических дробей — Polymathlove.com
Добро пожаловать в наш пошаговый математический решатель! Решить · Упростить · Фактор · Расширить · График · GCF · LCM. калькулятор алгебраических дробей. Похожие темы: алгебра два …
Упрощение алгебраических дробей — калькулятор Casio fx-85GT fx-83GT
www.youtube.com ›Смотреть
05.05.2015 · dɪsᴄᴏᴠᴇʀ mᴏʀᴇ aᴛ tʜᴇ cᴀʟᴄᴜʟᴀᴛᴏʀ gᴜɪᴅᴇ wᴇʙsɪᴛᴇ ➜ http://snip.ly/uqds7n 💢gᴇᴛ a cʟᴀsɪᴢ nᴏᴏ …
Dauer: 7:59
767676767676767676: 6. 05.05.2015
калькулятор упрощения алгебраических дробей — Skilifting & Bike
skiliftingbike.it › упрощение расчета алгебраических дробей…
Онлайн-калькулятор упрощающих выражений от BYJU ускоряет вычисления и отображает упрощенную форму алгебраическое выражение в …
Упрощение калькулятора шаг за шагом — Igro.it
pdus.igro.